Unlike skeletal muscle, cardiac muscle is electrically coupled so that the wave of depolarization propagates from one cell to the next, independent of neuronal input. The heart is activated by capacitive currents generated when a wave of depolarization approaches a region of the heart that is at its resting potential. Unlike ionic currents, which are generated by the flux of charged ions across the cell membrane, capacitive currents are generated by the movement of electrons toward and away from the surfaces of the membrane.^2,³ The resulting decrease in positive charge at the outer side of the cell membrane reduces the negative charge on the intracellular surface of the membrane. These charge movements, which are carried by electrons, generate a capacitive current. When an excitatory stimulus causes the E_m to become less negative and beyond a threshold level (approximately −65 mV for working atrial and ventricular cardiomyocytes), Na⁺ channels activate (open) and permit an inward Na⁺ current (I_Na), resulting in a rapid shift of the E_m to a positive voltage range. This event triggers a series of successive opening and closure of selectively permeable ion channels. The direction and magnitude of passive ion movement (and the resulting current) at any given transmembrane voltage are determined by the ratio of the intracellular and extracellular concentrations and the reversal potential of that ion, with the net flux being larger when ions move from the more concentrated side.³

The threshold is the lowest E_m at which opening of enough Na⁺ channels (or Ca²⁺ channels in the setting of nodal cells) is able to initiate the sequence of channel openings needed to generate a propagated action potential. Small (subthreshold) depolarizing stimuli depolarize the membrane in proportion to the strength of the stimulus and cause only local responses because they do not open enough Na⁺ channels to generate depolarizing currents large enough to activate nearby resting cells (i.e., insufficient to initiate a regenerative action potential). On the other hand, when the stimulus is sufficiently intense to reduce the E_m to a threshold value, regenerative action potential results, whereby intracellular movement of Na⁺ depolarizes the membrane more, a process that increases conductance to Na⁺ more, which allows more Na⁺ to enter, and so on. In this fashion, the extent of subsequent depolarization becomes independent of the initial depolarizing stimulus, and more intense stimuli do not produce larger action potential responses; rather, an all-or-none response results.²

Electrical changes in the action potential follow a relatively fixed time and voltage relationship that differs according to specific cell types. Whereas the entire action potential takes several milliseconds in nerve cells, the cardiac action potential lasts several hundred milliseconds. The course of the action potential can be divided into five phases (numbered 0 to 4). Phase 4 is the resting E_m, and it describes the E_m when the cell is not being stimulated.

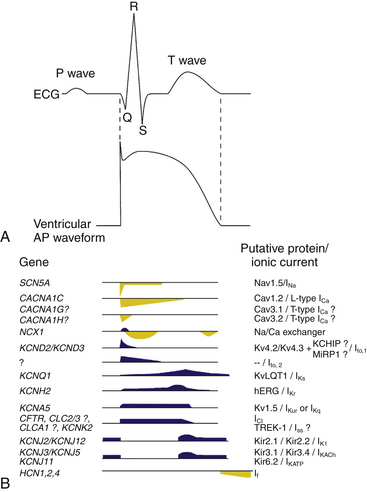
During the action potential, membrane voltages fluctuate in the range of −94 to +30 mV (Fig. 1-1). With physiological external K⁺, the reversal potential of K⁺ (E_K) is approximately −94 mV, and passive K⁺ movement during an action potential is out of the cell. On the other hand, because the calculated reversal potential of a cardiac Ca²⁺ channel (E_Ca) is +64 mV, passive Ca²⁺ flux is into the cell.⁵

FIGURE 1-1 A, Depiction of a standard ECG tracing with respect to its underlying ventricular action potential (AP). B, The different ionic currents (see text) that contribute to action potential generation and the putative encoding genes are shown. Depolarizing currents are shown in yellow, repolarizing currents in blue.

(Modified with permission from Saenena JB, Vrints CJ: Molecular aspects of the congenital and acquired long QT syndrome: clinical implications. J Mol Cell Cardiol 44:633-646, 2007.)

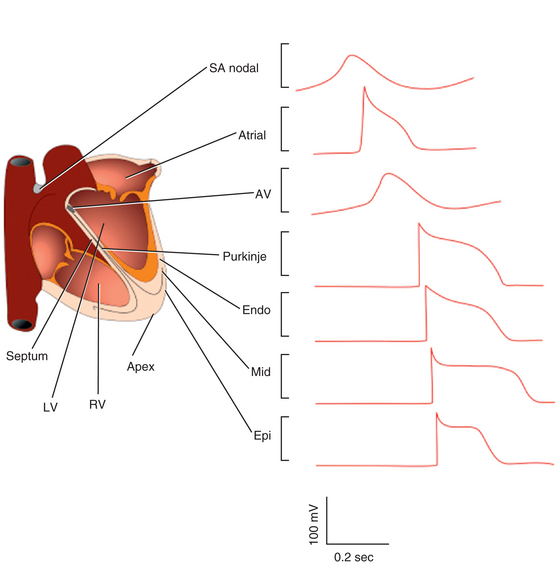
In normal atrial and ventricular myocytes and in His-Purkinje fibers, action potentials have very rapid upstrokes, mediated by the fast inward I_Na. These potentials are called fast response potentials. In contrast, action potentials in the normal sinus and atrioventricular (AV) nodal cells and many types of diseased tissues have very slow upstrokes, mediated by a slow inward, predominantly L-type voltage-gated Ca²⁺ current (I_CaL), rather than by the fast inward I_Na (Fig. 1-2). These potentials have been termed slow response potentials.^2,⁵

FIGURE 1-2 Action potential waveforms, displaced in time to reflect the temporal sequence of propagation, vary in different regions of the heart. AV = atrioventricular (node); endo = endocardial; epi = epicardial; mid = midmyocardial; LV = left ventricle; RV = right ventricle; SA = sinoatrial.

(Modified with permission from Nerbonne JM: Heterogeneous expression of repolarizing potassium currents in the mammalian myocardium. In Zipes DP, Jalife J, editors: Cardiac electrophysiology: from cell to bedside, ed 5, Philadelphia, 2009, Saunders, pp 293-305.)

The Fast Response Action Potential

Phase 4: The Resting Membrane Potential

The E_m of resting atrial and ventricular cardiomyocytes remains steady throughout diastole. The resting E_m is caused by the differences in ionic concentrations across the membrane and the selective membrane permeability (conductance) to various ions. Large concentration gradients of Na⁺, K⁺, Ca²⁺, and Cl⁻ across the cell membrane are maintained by the ion pumps and exchangers (Table 1-1).

TABLE 1-1 Intracellular and Extracellular Ion Concentrations and Equilibrium Potentials in Cardiomyocytes

Under normal conditions, the resting membrane is most permeable to K⁺ and relatively impermeable to other ions. K⁺ has the largest resting membrane conductance (g_K is 100 times greater than g_Na) because of the abundance of open K⁺ channels at rest, whereas Na⁺ and Ca²⁺ channels are generally closed. Thus, K⁺ exerts the largest influence on the resting E_m. As a consequence, the resulting E_m is almost always close to the K⁺ reversal potential (E_m approximates E_K). The actual resting E_m is slightly less negative than E_K because the cell membrane is slightly permeable to other ions.²

The inwardly rectifying K⁺ (Kir) channels underlie an outward K⁺ current (I_K1) responsible for maintaining the resting potential near the E_K in atrial, His-Purkinje, and ventricular cells, under normal conditions.^6,⁷ Kir channels preferentially allow currents of K⁺ ions to flow into the cell with a strongly voltage-dependent decline of K⁺ efflux (i.e., reduction of outward current) on membrane depolarization. As such, I_K1 is a strong rectifier that passes K⁺ currents over a limited range of E_m (see Chap. 2 for detailed discussion on the concept of rectification); at a negative E_m, I_K1 conductance is much larger than that of any other current, thus, it clamps the resting E_m close to the reversal potential for K⁺ (E_K). I_K1 density is much higher in ventricular than in atrial myocytes, a feature that protects the ventricular cell from pacemaker activity. By contrast, I_K1 is almost absent in sinus and AV nodal cells, thus allowing for relatively more depolarized resting diastolic potentials compared with atrial and ventricular myocytes (Table 1-2).²

TABLE 1-2 Regional Differences in Cardiac Action Potential

A unique property of Kir currents is the unusual dependence of rectification on extracellular K⁺ concentration. Specifically, on increase in extracellular K⁺, the I_K1 current-voltage relationship shifts nearly in parallel with the E_K and leads to a crossover phenomenon. One important consequence of such behavior is that at potentials positive to the crossover, K⁺ conductance increases rather than decreases, against an expectation based on a reduced driving force for K⁺ ions as a result of elevated extracellular K⁺ concentration.⁶^–⁸

The resting E_m also is powered by the Na⁺-K⁺ adenosine triphosphatase (ATPase) (the Na⁺-K⁺ pump), which helps establish concentration gradients of Na⁺ and K⁺ across the cell membrane. Under physiological conditions, the Na⁺-K⁺ pump transports two K⁺ ions into the cell against its chemical gradient and three Na⁺ ions outside against its electrochemical gradient at the cost of one adenosine triphosphate (ATP) molecule. Because the stoichiometry of ion movement is not 1:1, the Na⁺-K⁺ pump is electrogenic and generates a net outward movement of positive charges (i.e., an outward current). At faster heart rates, the rate of Na⁺-K⁺ pumping increases to maintain the same ionic gradients, thus counteracting the intracellular gain of Na⁺ and loss of K⁺ with each depolarization.

Although Ca²⁺ does not contribute directly to the resting E_m (since the voltage-activated Ca²⁺ channels are closed at the hyperpolarized resting E_m), changes in intracellular free Ca²⁺ concentration can affect other membrane conductance values. Increases in intracellular Ca²⁺ levels can stimulate the Na⁺-Ca²⁺ exchanger (I_Na-Ca), which exchanges three Na⁺ ions for one Ca²⁺ ion; the direction depends on the Na⁺ and Ca²⁺ concentrations on the two sides of the membrane and the E_m difference. At resting E_m and during a spontaneous sarcoplasmic reticulum Ca²⁺ release event, this exchanger would generate a net Na⁺ influx, possibly causing transient membrane depolarizations.³

Phase 0: The Upstroke—Rapid Depolarization

On excitation of the cardiomyocyte by electrical stimuli from adjacent cells, its resting E_m (approximately −85 mV) depolarizes, leading to opening (activation) of Na⁺ channels from its resting (closed) state and enabling a large and rapid influx of Na⁺ ions (inward I_Na) into the cell down their electrochemical gradient. As a consequence of increased Na⁺ conductance, the excited membrane no longer behaves like a K⁺ electrode (i.e., exclusively permeable to K⁺), but more closely approximates an Na⁺ electrode, and the membrane potential moves toward the Na⁺ E_ion (E_Na; see Table 1-1). Once an excitatory stimulus depolarizes the E_m beyond the threshold for activation of Na⁺ channels (approximately −65 mV), the activated I_Na is regenerative and no longer depends on the initial depolarizing stimulus; the influx of Na⁺ ions further depolarizes the membrane and thereby increases conductance to Na⁺ more, which allows more Na⁺ to enter.^2,⁹

Normally, activation of Na⁺ channels is transient; fast inactivation (closing of the pore) starts simultaneously with activation, but because inactivation is slightly delayed relative to activation, the channels remain transiently (less than 1 millisecond) open to conduct I_Na during phase 0 of the action potential before it closes. Additionally, the influx of Na⁺ into the cell increases the positive intracellular charges and reduces the driving force for Na⁺. When the E_Na is reached, no further Na⁺ ions enter the cell.⁹

The rate at which depolarization occurs during phase 0, that is, the maximum rate of change of voltage over time, is indicated by the expression dV/dt_max, which is a reasonable approximation of the rate and magnitude of Na⁺ entry into the cell and a determinant of conduction velocity for the propagated action potential.²

The threshold for activation of I_CaL is approximately −30 to −40 mV. Although I_CaL is normally activated during phase 0 by the regenerative depolarization caused by the fast I_Na, I_CaL is much smaller than the peak I_Na. The amplitude of I_CaL is not maximal near the action potential peak because of the time-dependent nature of I_CaL activation, as well as the low driving force (E_m − E_Ca) for I_CaL. Therefore, I_CaL contributes little to the action potential until the fast I_Na is inactivated, after completion of phase 0. As a result, I_CaL affects mainly the plateau of action potentials recorded in atrial and ventricular muscle and His-Purkinje fibers. On the other hand, I_CaL can play a prominent role in the upstroke of slow response action potentials in partially depolarized cells in which the fast Na⁺ channels have been inactivated.²

Phase 1: Early Repolarization

Phase 0 is followed by phase 1 (early repolarization) during which the membrane repolarizes rapidly and transiently to almost 0 mV (early notch), partly because of the inactivation of I_Na and concomitant activation of several outward currents. The transient outward K⁺ current (I_to) is mainly responsible for phase 1 of the action potential. I_to rapidly activates (with time constants less than 10 milliseconds) by depolarization and then rapidly inactivates (25 to 80 milliseconds for the fast component of I_to [I_to,f], and 80 to 200 milliseconds for the slow component of I_to [I_to,s]). The influx of K⁺ ions via I_to channels partially repolarizes the membrane, thus shaping the rapid (phase 1) repolarization of the action potential and setting the height of the initial plateau (phase 2; see Fig. 1-1). Additionally, an Na⁺ outward current through the Na⁺-Ca²⁺ exchanger operating in reverse mode likely contributes to early repolarization.^3,^6,¹⁰

Phase 2: The Plateau

Phase 2 (plateau) represents a delicate balance between the depolarizing inward currents (I_CaL and a small residual component of inward I_NaL) and the repolarizing outward currents (ultrarapidly [I_Kur], rapidly [I_Kr], and slowly [I_Ks] activating delayed outward rectifying currents; see Fig. 1-1). Phase 2 is the longest phase of the action potential, lasting tens (atrium) to hundreds of milliseconds (His-Purkinje system and ventricle). The plateau phase is unique among excitable cells and marks the phase of Ca²⁺ entry into the cell. It is the phase that most clearly distinguishes the cardiac action potential from the brief action potentials of skeletal muscle and nerve.²

I_CaL is activated by membrane depolarization, is largely responsible for the action potential plateau, and is a major determinant of the duration of the plateau phase. I_CaL also links membrane depolarization to myocardial contraction. L-type Ca²⁺ channels activate on membrane depolarization to potentials positive to –40 mV. I_CaL peaks at an E_m of 0 to +10 mV and tends to reverse at +60 to +70 mV, following a bell-shaped current-voltage relationship.³

Na⁺ channels also make a contribution, although minor, to the plateau phase. After phase 0 of the action potential, some Na⁺ channels occasionally fail to inactivate or exhibit prolonged opening or reopening repetitively for hundreds of milliseconds after variable and prolonged latencies, resulting in a small inward I_Na (less than 1% of the peak I_Na). This persistent or “late” I_Na (I_NaL), along with I_CaL, helps maintain the action potential plateau.^3,^11,¹²

I_Kr and I_Ks are activated at depolarized potentials. I_Kr activates relatively fast (in the order of tens of milliseconds) on membrane depolarization, thus allowing outward diffusion of K⁺ ions in accordance with its electrochemical gradient, but voltage-dependent inactivation thereafter is very fast. Hence, only limited numbers of channels remain in the open state, whereas a considerable fraction resides in the nonconducting inactivated state. The fast voltage-dependent inactivation limits outward current through the channel at positive voltages and thus helps maintain the action potential plateau phase that controls contraction and prevents premature excitation. However, as the voltage becomes less positive at the end of the plateau phase of repolarization, the channels recover rapidly from inactivation; this process leads to a progressive increase in I_Kr amplitudes during action potential phases 2 and 3, with maximal outward current occurring before the final rapid declining phase of the action potential.^6,^12,¹³

I_Ks, which is approximately 10 times larger than I_Kr, also contributes to the plateau phase. I_Ks activates in response to membrane depolarization to potentials greater than –30 mV and gradually increases during the plateau phase because its time course of activation is extremely slow, slower than any other known K⁺ current, and steady-state amplitude is achieved only with extremely long membrane depolarization. Hence, the contribution of I_Ks to the net repolarizing current is greatest late in the plateau phase, particularly during action potentials of long duration. Importantly, although I_Ks activates slowly compared with action potential duration, it is also slowly inactivated. As heart rate increases, I_Ks increases because channel deactivation is slow and incomplete during the shortened diastole. This allows I_Ks channels to accumulate in the open state during rapid successive depolarizations and mediate the faster rate of repolarization. Hence, I_Ks plays an important role in determining the rate-dependent shortening of the cardiac action potential.^6,¹²^–¹⁴

I_Kur is detected only in human atria but not in the ventricles, so that it is the predominant delayed rectifier current responsible for human atrial repolarization.^3,¹² The Na⁺-Ca²⁺ exchanger operating in forward mode and the Na⁺-K⁺ pump provide minor current components during phase 2.

Importantly, during the plateau phase, membrane conductance to all ions falls to rather low values. Thus, less change in current is required near plateau levels than near resting potential levels to produce the same changes in E_m. In particular, K⁺ conductance falls during the plateau phase as a result of inward rectification of I_Kr and I_K1 (that is, voltage-dependent decline of K⁺ efflux and hence reduction of outward current) on membrane depolarization, in spite of the large electrochemical driving force on K⁺ ions during the positive phase of the action potential (phases 0, 1, and 2). This property allows membrane depolarization following Na⁺ channel activation, slows membrane repolarization, and helps maintain a more prolonged cardiac action potential. This also confers energetic efficiency in the generation of the action potential.^6,^7,¹⁴

Experimental studies in wedge preparations strongly suggest the presence of a subpopulation of cells in the midmyocardium (referred to as the M cells) that exhibits distinct electrophysiological (EP) properties, although the presence of M cells has not been consistently confirmed by intact heart experiments.¹⁸^–²¹ The putative midmyocardial cells appear to have the longest action potential duration across the myocardial wall, largely attributed to their weaker I_Ks current but stronger late I_Na and Na⁺-Ca²⁺ exchanger currents. Hence, the M cells have been proposed to underlie the EP basis for transmural ventricular dispersion of repolarization and the T wave on the surface ECG, with the peak of the T wave (in wedge preparations) coinciding with the end of epicardial repolarization and the end of the T wave coinciding with the end of repolarization of the M cells. Although the role of M cells under physiological conditions remains controversial, these cells appear to have a significant role in arrhythmogenesis under a variety of pathological conditions, such as the long QT and Brugada syndromes, secondary to exaggeration of transmural repolarization gradients.^18,¹⁹

As noted, I_Kur is detected only in human atria and not in the ventricles, so that it is the predominant delayed rectifier current responsible for human atrial repolarization and is a basis for the much shorter duration of the action potential in the atrium (see Table 1-2).^3,¹²

I_K1 density is much higher in ventricular than in atrial myocytes, and this explains the steep repolarization phase in the ventricles (where the more abundant I_K1 plays a larger role in accelerating the terminal portion of repolarization) and the more shallow phase in the atria. The higher I_K1 channel expression in the ventricle protects the ventricular cell from pacemaker activity.^6,⁷

Changes in expression levels or gating properties of ion channels in pathological conditions can aggravate the regional heterogeneities in action potential duration and configuration that can be arrhythmogenic.^3,¹²

The Slow Response Action Potential

In normal atrial and ventricular myocytes and in the His-Purkinje fibers, action potentials have very rapid upstrokes mediated by the fast inward I_Na. These potentials are called fast response potentials. In contrast, action potentials in the normal sinus and AV nodal cells and many types of diseased tissue have very slow upstrokes, mediated predominantly by the slow inward I_CaL, rather than by the fast inward I_Na (see Fig. 1-2). These potentials have been termed slow response potentials.⁵

As noted, the action potentials of pacemaker cells in the sinus and AV nodes are significantly different from those in working atrial and ventricular myocardium. The slow response action potentials are characterized by a more depolarized E_m at the onset of phase 4 (−50 to −65 mV), slow diastolic depolarization during phase 4, reduced action potential amplitude, and a much slower rate of depolarization in phase 0 than that in the working myocardial cells, thus resulting in slow conduction velocity of the cardiac impulse in the nodal regions (see Table 1-2). Cells in the His-Purkinje system can also exhibit phase 4 depolarization under special circumstances.^6,⁷

Phase 4: Diastolic Depolarization

In contrast to working atrial and ventricular myocytes and fibers in the His-Purkinje system, which maintain a steady diastolic E_m level of approximately –85 mV, sinus and AV nodal excitable cells exhibit a spontaneous, slow, progressive decline in the E_m during diastole (spontaneous diastolic depolarization or phase 4 depolarization) that underlies normal automaticity and pacemaking function. Once this spontaneous depolarization reaches threshold (approximately −40 mV), a new action potential is generated.^2,^22,²³

The ionic mechanisms responsible for diastolic depolarization and normal pacemaker activity in the sinus node are still controversial. Originally, a major role was attributed to the decay of the delayed K⁺ conductance (an outward current) activated during the preceding action potential (the I_K-decay theory). This model of pacemaker depolarization lost favor on the discovery of the “funny” current (I_f), sometimes referred to as the pacemaker current. Other ionic currents gated by membrane depolarization (i.e., I_CaL and T-type Ca²⁺ currents), nongated and nonspecific background leak currents, and a current generated by the Na⁺-Ca²⁺ exchanger were also proposed to be involved in pacemaking.

Ic is a hyperpolarization-activated inward current (often referred to as the funny current because, unlike the majority of voltage-sensitive currents, it is activated by hyperpolarization rather than depolarization) that is carried largely by Na⁺ and, to a lesser extent, K⁺ ions. The I_f channels are deactivated during the action potential upstroke and the initial plateau phase of repolarization. However, they begin to activate at the end of the action potential as repolarization brings the E_m to levels more negative than approximately −40 to −50 mV, and they are fully activated at approximately −100 mV. Once activated, I_f depolarizes the membrane to a level where the Ca²⁺ current activates to initiate an action potential.³ At the end of the repolarization phase of the action potential, because I_f activation occurs in the background of a decaying outward time-dependent K⁺ current, the current flow quickly shifts from outward to inward, thus giving rise to a sudden reversal of voltage change (from repolarizing to depolarizing) at the maximum diastolic potential.²²^–²⁶

On the other hand, several studies have shown that I_f is not the only current that can initiate the diastolic depolarization process in the sinus node. In addition to voltage and time, the electrogenic and regulatory molecules on the surface membrane of sinus node cells are strongly modulated by Ca²⁺ and phosphorylation, a finding suggesting that intracellular Ca²⁺ is an important player in controlling pacemaker cell automaticity. Newer evidence suggests that the sarcoplasmic reticulum, a major Ca²⁺ store in sinus node cells, can function as a physiological clock within the cardiac pacemaker cells and have a substantial impact on late diastolic depolarization.

The sarcoplasmic reticulum generates spontaneous, rhythmic, local Ca²⁺ releases (via ryanodine receptors, RyR2) beneath the surface of the membrane, in the absence of Ca²⁺ overload. Activation of the local oscillatory Ca²⁺ releases is independent of membrane depolarization and is driven by a high level of basal state phosphorylation of Ca²⁺ cycling proteins. Critically timed Ca²⁺ releases occur during the later phase of diastolic depolarization in the form of multiple locally propagating wavelets beneath the cell membrane, and they activate the forward mode of the Na⁺-Ca²⁺ exchanger, thus resulting in an inward membrane current (I_Na-Ca). The I_Na-Ca causes the late diastolic depolarization to increase exponentially, driving the E_m to the threshold to activate a sufficient number of L-type Ca²⁺ channels and leading to generation of the upstroke of the next action potential. Although regulated by the E_m and submembrane Ca²⁺, the Na⁺-Ca²⁺ exchanger does not have time-dependent gating, as do ion channels, but generates an inward current almost instantaneously when submembrane Ca²⁺ concentration increases.^24,^25,^27,²⁸

Ca²⁺ influx via I_CaL during the action potential triggers Ca²⁺-induced Ca²⁺ release from the sarcoplasmic reticulum. The resulting global sarcoplasmic reticular Ca²⁺ depletion synchronizes the sarcoplasmic reticulum throughout the cell in a Ca²⁺-depleted state. Refilling of the sarcoplasmic reticulum ensures that the threshold of Ca²⁺ load required for spontaneous release is achieved at about the time when RyR2 inactivation is removed following prior activation; then the spontaneous local Ca²⁺ releases occur, thus activating I_Na-Ca to ignite the next action potential.^5,^24,²⁸

Such rhythmic, spontaneous intracellular Ca²⁺ cycling has been referred to as the intracellular Ca²⁺ clock. Phosphorylation-dependent gradation of speed at which Ca²⁺ clock cycles is the essential regulatory mechanism of normal pacemaker rate and rhythm. The robust regulation of pacemaker function is ensured by tight integration of the Ca²⁺ clock and the classic sarcolemmal ion channel clock (formed by voltage-dependent membrane ion channels) to form the overall pacemaker clock. The action potential shape and ion fluxes are tuned by membrane clocks to sustain operation of the Ca²⁺ clock, which produces timely and powerful ignition of the membrane clocks to effect action potentials.^24,^25,²⁸

There is some degree of uncertainty about the relative role of I_f versus that of intracellular Ca²⁺ cycling in controlling the normal pacemaker cell automaticity. Furthermore, the interactions between the membrane ion channel clock and the intracellular Ca²⁺ clock and cellular mechanisms underlying this internal Ca²⁺ clock are not completely elucidated. A further debate has arisen around their individual (or mutual) relevance in mediating the positive and negative chronotropic effects of neurotransmitters. Nevertheless, these interactions are of fundamental importance for understanding the integration of pacemaker mechanisms at the cellular level.^24,^25,²⁷

Phase 0: The Upstroke—Slow Depolarization

I_K1 is almost absent in sinus and AV nodal cells, thus allowing for relatively more depolarized resting diastolic potentials (−50 to −65 mV) compared with atrial and ventricular myocytes and facilitating diastolic depolarization mediated by the inward currents (e.g., I_f). At the depolarized level of the maximum diastolic potential of pacemaker cells, most Na⁺ channels are inactivated and unavailable for phase 0 depolarization. Consequently, action potential upstroke is mainly achieved by I_CaL.^6,⁷

L-type Ca²⁺ channels activate on depolarization to potentials positive to –40 mV, and I_CaL peaks at 0 to +10 mV. The peak amplitude I_CaL is less than 10% that of I_Na, and the time required for activation and inactivation of I_CaL is approximately an order of magnitude slower than that for I_Na. As a consequence, the rate of depolarization in phase 0 (dV/dt) is much slower and the peak amplitude of the action potential is less than that in the working myocardial cells.^5,^15,²⁹

Excitability

Excitability of a cardiac cell describes the ease with which the cell responds to a stimulus with a regenerative action potential. A certain minimum charge has to be applied to the cell membrane to elicit a regenerative action potential (i.e., the stimulus should be sufficiently intense to reduce the E_m to the threshold value); excitability is inversely related to the charge required for excitation.³

Excitability of a cardiac cell depends on the passive and active properties of the cell membrane. The passive properties include the membrane resistance and capacitance and the intercellular resistance. The more negative the E_m, the more Na⁺ channels are available for activation, the greater the influx of Na⁺ into the cell during phase 0, and the greater the conduction velocity. In contrast, membrane depolarization to approximately −60 to −70 mV can inactivate half the Na⁺ channels, and depolarization to −50 mV or less can inactivate all the Na⁺ channels, thereby rendering Na⁺ channels unavailable for mediating an action potential upstroke and reducing tissue excitability.⁵

On the other hand, supernormal excitability can be observed during a brief period at the end of phase 3 of the action potential. During the supernormal period, excitation is possible in response to an otherwise subthreshold stimulus; that same stimulus fails to elicit a response earlier or later than the supernormal period. Two factors are responsible for supernormality: the availability of fast Na⁺ channels and the proximity of the E_m to threshold potential. During the supernormal phase of excitability, the cell has recovered enough to respond to a stimulus (i.e., an adequate number of Na⁺ channels is available for activation). At the same time, because the E_m is still reduced, it requires only a little additional depolarization to bring the fiber to threshold; thus, a smaller stimulus than is normally required elicits an action potential.^30,³¹

Reduced membrane excitability occurs in certain physiological and pathophysiological conditions. Genetic mutations that result in loss of Na⁺ channel function, Na⁺ channel blockade with class I antiarrhythmic drugs, and acute myocardial ischemia can cause reduced membrane excitability.³²

Refractoriness

During a cardiac cycle, once an action potential is initiated, the cardiomyocyte becomes unexcitable to stimulation (i.e., unable to initiate another action potential in response to a stimulus of threshold intensity) for some duration of time (which is slightly shorter than the “true” action potential duration) until its membrane has repolarized to a certain level. This period of refractoriness to stimulation is physiologically necessary for the mechanical function of the heart; it allows only gradual recovery of excitability, thus permitting relaxation of cardiac muscle before subsequent activation. Additionally, the refractory period acts as a protective mechanism by preventing multiple, compounded action potentials from occurring (i.e., it limits the frequency of depolarization and heart rate). Therefore, this property is a determinant of susceptibility to arrhythmias.³³

There are different levels of refractoriness during the action potential. During the absolute refractory period (which extends over phases 0, 1, 2, and part of phase 3 of the action potential), no stimulus, regardless of its strength, can reexcite the cell. After the absolute refractory period, a stimulus may cause some cellular depolarization, but it does not lead to a propagated action potential. The sum of this period (which includes a short interval of phase 3 of the action potential) and the absolute refractory period is termed the effective refractory period (ERP). The ERP is followed by the relative refractory period, which extends over the middle and late parts of phase 3. During the relative refractory period, initiation of a second action potential is inhibited but not impossible; a larger-than-normal stimulus can result in activation of the cell and lead to a propagating action potential. However, the upstroke of the new action potential is less steep and of lower amplitude, and its conduction velocity is slower than normal. As noted, there is a brief period in phase 3, the supernormal period, during which excitation is possible in response to an otherwise subthreshold stimulus (supernormal excitability).

The refractory period is determined, in part, by the action potential duration and the E_m, and the degree of refractoriness primarily reflects the number of Na⁺ channels that have recovered from their inactive state. With repolarization, the Na⁺ channel normally recovers rapidly from inactivation (within 10 milliseconds) and is ready to open again. The ERP extends from phase 0 to approximately −60 mV during phase 3 of the action potential, a time during which it is impossible for the myocardium to respond with a propagated action potential, or even to a strong stimulus. The relative refractory period extends from approximately −60 mV during phase 3 to the end of phase 3 of the action potential. During this period, a depressed response is possible to a strong stimulus. Therefore, when premature stimulation occurs during the relative refractory period (i.e., before full recovery and at less negative potentials of the cell membrane), a portion of Na⁺ channels will still be refractory and unavailable for activation. Consequently, the I_Na and phase 0 of the next action potential will be reduced, and conduction of the premature stimulus will be slowed.^3,³²

In pacemaking tissues, I_Na is predominantly absent, and excitability is mediated by the activation of I_CaL. After inactivation, the transition of Ca²⁺ channels from the inactivated to the closed resting state (i.e., recovery from inactivation) is relatively slow. The time constant for recovery from inactivation depends on both the E_m and the intracellular Ca²⁺ concentration (typically 100 to 200 milliseconds at −80 mV and low intracellular Ca²⁺ concentration). This means that I_CaL must recover from inactivation between action potentials. As a result, excitability in pacemaking cells may not be recovered by the end of phase 3 of the action potential and full restoration of maximum diastolic potential, because L-type Ca²⁺ channels require longer time to recovery from inactivation to be able to mediate the upstroke of a new action potential. In other words, sinus and AV nodal cells remain refractory for a time interval that is longer than the time it takes for full voltage repolarization to occur, a phenomenon termed postrepolarization refractoriness.^5,²⁹ This can also occur during some disease states such as myocardial infarction.

Conduction

Cardiac excitation involves generation of the action potential by individual cells, followed by propagation of the electrical impulse along each cardiac cell and rapidly from cell to cell throughout the cardiac tissue. The propagating electrical wavefront interacts with structural boundaries that exist at the cellular level (cell membranes, intercellular gap junctions), as well as at the more macroscopic level (microvasculature, connective tissue barriers, trabeculation).

Conduction velocity refers to the speed of propagation of the action potential through cardiac tissue and is determined by source-sink relationships, which reflect the interplay between the active membrane properties of cardiac cells (i.e., electrical excitability or refractoriness of the source generating the action potential, or both) and the passive properties determined by cell-to-cell coupling and tissue geometry (sink).^3,³⁴

During action potential propagation, an excited cell serves as a source of electrical charge for depolarizing neighboring unexcited cells. The requirements of adjacent resting cells to reach the threshold E_m constitute an electrical sink (load) for the excited cell. For propagation to succeed, the excited cell must provide sufficient charge to bring the E_m at a site in the sink from its diastolic value to the threshold. Once threshold is reached and action potential is generated, the load on the excited cell is removed, and the newly excited cell switches from being a sink to being a source for the downstream tissue, thus perpetuating the process of action potential propagation. Action potentials are “regenerative” because they can be conducted over large distances without attenuation.

The current provided by the source must reach the sink. The pathway between the source and the sink includes intracellular resistance (provided by the cytoplasm) and intercellular resistance (provided by the gap junctions). Extracellular resistance plays a role, but it can often be neglected. The coupling resistance is mainly determined by resistance of the gap junctions. Therefore, the number and distribution of gap junctions, as well as the conductance of the gap junction proteins (connexins) and the geometry of the source-sink relationship, are important factors for conduction of the action potential.

The safety factor for conduction predicts the success of action potential propagation and is based on the source-sink relationship. The safety factor is defined as the ratio of the current generated by the depolarizing ion channels of a cell (source) to the current consumed during the excitation cycle of a single cell in the tissue (sink). Thus, the safety factor for propagation is proportional to the excess of source current over the sink needs. By this definition, conduction fails when the safety factor drops to less than 1 and becomes increasingly stable as it rises to more than 1. This concept of propagation safety provides information about the dependence of propagation velocity on the state of the ion channels, cell-to-cell coupling, and tissue geometry.

An action potential traveling down a cardiac muscle fiber is propagated by local circuit currents, much as it does in nerve and skeletal muscle. Conduction velocity along the cardiac fiber is directly related to the action potential amplitude (i.e., the voltage difference between the fully depolarized and the fully polarized regions) and the rate of change of potential (i.e., the rate of rise of phase 0 of the action potential [dV/dt]). These factors depend on the amplitude of I_Na, which, in turn, is directly related to the E_m at the time of stimulation, the availability of Na⁺ channels for stimulation, and the size of the Na⁺ electrochemical potential gradient across the cell membrane. A reduction in I_Na, leading to a reduction in the rate or amplitude of depolarization during phase 0 of the action potential, can decrease axial current flow (and therefore capacitive current) and slow conduction or produce conduction block. Tissues with high concentration of Na⁺ channels, such as Purkinje fibers, which contain up to 1 million Na⁺ channels per cell, have a large, fast inward current. The large I_Na spreads quickly within and between cells to support rapid conduction (approximately 4 m/sec). In contrast, at a less negative resting E_m, Na⁺ channel availability is limited because of the inactivation of a portion of the channels; hence, I_Na amplitude is attenuated, and the upstroke velocity is slowed. With progressive reduction of excitability, less Na⁺ source current is generated, and conduction velocity and the safety factor decrease monotonically. When the safety factor falls to less than 1, conduction can no longer be sustained, and failure (conduction block) occurs. Action potentials with reduced upstroke velocity resulting from partial inactivation of Na⁺ channels are called depressed fast responses.³⁵

In tissues with slow response action potentials (sinus and AV nodes), the upstroke of the action potential is formed by I_CaL rather than I_Na. Because I_CaL has lower amplitude and slower activation kinetics than I_Na, slow response action potentials exhibit lower amplitudes and upstroke velocities. Hence, slow conduction (approximately 0.1 to 0.2 m/sec) and prolonged refractoriness are characteristic features of nodal regions. These cells also have a reduced safety factor for conduction, which means that the stimulating efficacy of the propagating impulse is low, and conduction block occurs easily.

Excitation-Contraction Coupling

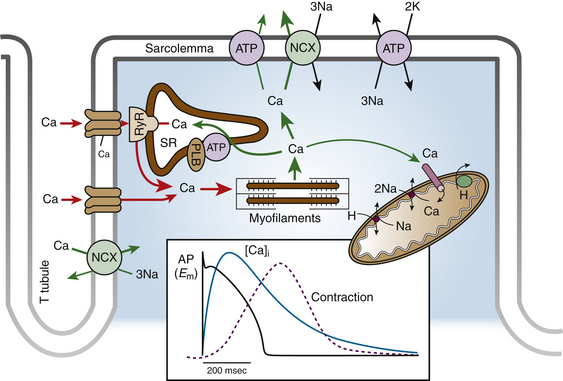
Excitation-contraction coupling describes the physiological process by which electrical stimulation of the cardiomyocytes (the action potential) results in a mechanical response (muscle contraction). The contraction of a cardiac myocyte is governed primarily by intracellular Ca²⁺ concentration (Fig. 1-3). Ca²⁺ enters the cell during the plateau phase of the action potential through the L-type Ca²⁺ channels that line areas of specialized invaginations known as transverse (T) tubules. Although the rise in intracellular Ca²⁺ is small and not sufficient to induce contraction, the small amount of Ca²⁺ entering the cell via I_CaL triggers a massive release of Ca²⁺ from the sarcoplasmic reticulum (the major store for Ca²⁺) into the cytosol by opening the RyR2 channels (present in the membrane of the sarcoplasmic reticulum) in a process known as Ca²⁺-induced Ca²⁺ release (CICR). Approximately 75% of Ca²⁺ present in the cytoplasm during contraction is released from the sarcoplasmic reticulum.