Suspensions
Susan A. Barker
Chapter contents
Solid particle–liquid vehicle interactions
The ‘electrical double layer’ theory
Factors affecting the electrical double layer
Particle movement in suspensions
Controlling particulate movement in suspensions
What is the desired sedimentation pattern?
Dispersibility issues – surface wetting
General suspension formulation considerations
Key points
Introduction
Suspensions are probably one of the most challenging pharmaceutical formulations that students and formulators are likely to encounter. Many of the issues relating to solution formulation development apply equally to suspension formulations, but there are several additional considerations relating to the solid component of the system and the interface between the solid and the liquid components. The intention of this chapter is to present these issues and discuss them in context, so that the reader will have a fundamental understanding of the science behind suspension formulation as well as the more patient-focused aspects.
The most important consideration in suspension formulation development is the interaction between the solid particles and the liquid vehicle, so this aspect will be considered in detail first in this chapter. Secondly, other considerations relating to the solid component will be discussed and finally aesthetic, patient-focused and practical matters will be reviewed.
Definition of a suspension
It is appropriate here to review the definition of a solution before going on to consider the definition of a suspension. Solutions are discussed in detail in Chapters 2 and 3. They can be formed from various combinations of phases. However, in pharmacy, the word ‘solution’, without further description, is generally understood to refer to a liquid system. A solution is a one-phase system where at equilibrium all the ingredients are dispersed evenly at a molecular level. Solutions are therefore optically clear as there are no solid particles remaining to disperse the light. In the context of a pharmaceutical formulation, the drug (solute) is added as a solid to the vehicle (solvent, most commonly water) and dissolves completely to give the formulation (a solution). Other formulation components, such as preservatives, buffers, flavours, etc., are added as required.
A pharmaceutical suspension is also a liquid system. However, in this case, the solid material (usually the drug) does not dissolve in the vehicle to any appreciable extent, but remains as solid particles which are distributed throughout the vehicle. Technically, the term suspension describes a dispersion of a solid material (the dispersed phase) in a liquid (the continuous phase) without reference to the particle size of the solid material. However, the particle size of the solid material can affect both its physical and chemical behaviour, so a distinction is usually made between a colloid or colloidal suspension with a particle size range of up to about 1 µm (see Chapter 5), and a ‘coarse dispersion’ with larger particles. Unfortunately, pharmaceutical suspensions fall across the borderline between colloidal and coarse dispersions, with solid particles generally in the range of 0.1 to 10 µm. Suspensions are not optically clear and will appear cloudy unless the size of the particles is within the colloidal range.
In the ideal suspension, the particles of the solid material are mono-dispersed spheres and are evenly suspended in three dimensions throughout the vehicle and remain so even after prolonged periods of time. Here, every dose from the suspension will contain the same amount of drug and will give the same clinical effect to the patient; such reproducibility is absolutely vital for all formulations, but is difficult to achieve with suspensions.
Solid particle–liquid vehicle interactions
Solid particle–liquid vehicle interactions determine the behaviour of suspensions and hence it is vital to have a working knowledge of them. Water is by far the most common vehicle used for pharmaceutical suspensions, due to its lack of toxicity, hence it is the interaction between water and the particles which is important. The behaviour of an individual particle will be discussed first, then the interactions between multiple particles. These issues are discussed in Chapter 5 in the context of dispersed systems in general and Chapter 4 discusses solid–liquid interfaces. The emphasis in this chapter is on pharmaceutical suspensions and the importance of particle charge and particle-particle interactions in successful suspension formulation.
The ‘electrical double layer’ theory
A solid material will not dissolve in a liquid vehicle unless it has some chemical similarity. Thus, drugs which are hydrophobic will not dissolve very well in water. Many modern drugs show very low aqueous solubility, because they are designed to fit into hydrophobic biological receptors, so although they may be very efficient once at their site(s) of action, they present a real challenge to the formulator, and many may be developed as suspension formulations.
An apparently odd characteristic of such hydrophobic drugs is that once dispersed as solid particles in an aqueous environment, they will acquire a charge. This is counter-intuitive, as hydrophobic materials will generally repel water; if they could ionize, they would be expected to show a reasonable degree of aqueous solubility and would not remain as solid particles within the aqueous dispersion. However, the charge produced is not as a result of ionization of the drug, rather it is due to the ionization of water:
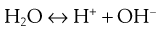(26.1)
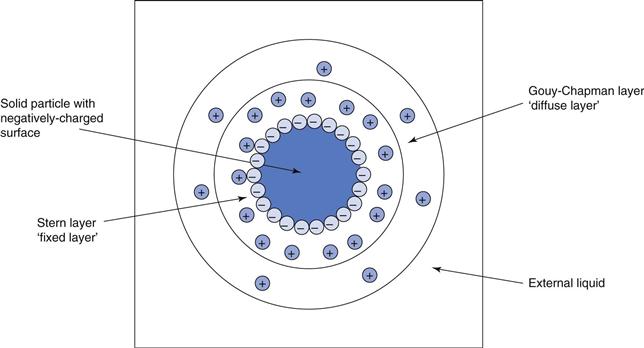
The liberated protons will then be solvated by intact water molecules to form hydronium ions (H3O+) and larger structures with more water molecules. One result of this is that they are generally less mobile than the hydroxide ions (OH−) produced from the initial ionization reaction shown in Equation 26.1. Some of the hydroxide ions will then collect on solid surfaces within the aqueous dispersion and give rise to an apparent negative charge on these surfaces. Overall, within the system, electrical neutrality must be maintained, so there will be a gradation of charge from a high negative charge on the surface of the particle down to no charge (overall neutrality) in the bulk vehicle. This gradation of charge occurs in two stages, giving rise to two ‘layers’ of charge surrounding the particle, hence the term electrical double layer.
Figure 26.1 illustrates a single solid particle in water, showing a negatively charged surface arising from the OH− ions. The innermost layer or ‘halo’ around the particle has a predominance of positively-charged ions. The outer layer or halo also has a predominance of positively-charged ions, but to a lesser extent than the inner layer. Finally the bulk vehicle has no overall net charge. Charges in the inner layer are held tightly to the particle and this is therefore known as the fixed layer, whereas charges within the outer layer are more mobile and can move away from the solid surface and hence this is denoted the ‘diffuse layer’. The two layers, fixed and diffuse, are also known as the Stern and Gouy-Chapman layers, respectively.
The rigidity with which the charges are held to the particle affects the intensity of charge at any point between the charged surface and the bulk external liquid. Throughout the fixed layer, there is a linear decrease of overall charge from the particle surface (high) to the edge of the fixed layer (lower). From this point until the edge of the diffuse layer, i.e. the beginning of the bulk liquid, there is an exponential decrease of charge. This phenomenon is discussed in Chapter 5.
Factors affecting the electrical double layer
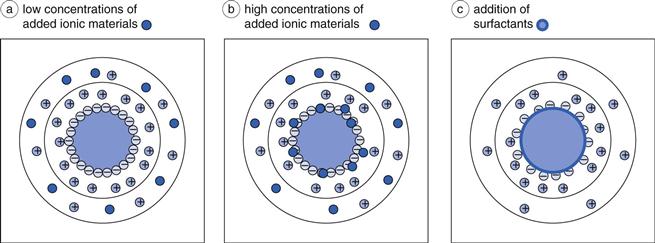
The addition of formulation excipients can change the behaviour of a solid particle in a suspension, by affecting either the fixed layer or the diffuse layer, or both. Materials which can ionize, for example sodium chloride, will increase the amount of mobile charges available in the system. At low to medium concentrations, for example 0.01 M, such charges are generally located only within the diffuse layer, as shown in Figure 26.2a, and therefore will not affect the surface potential ψ0 or the Stern potential ψδ (see Chapter 5 for explanations). The increase in the number of individual charges within the diffuse layer will result in easier neutralization of the remaining charge from the particle (ψδ) and hence will lead to a thinning of the diffuse layer. Mathematically, this is because the distance over which ψδ becomes ψδ/e, i.e. 1/κ (the ‘Debye-Hückel length’, Chapter 5), is smaller. It should be evident from the above discussion, that an increased concentration of the additional charges would be expected to lead to a greater reduction of 1/κ. In fact, the relationship is a square root one, in that 1/κ is inversely proportional to the square root of the ionic strength of the medium. This is the same as saying that κ (the ‘Debye-Hückel length parameter’, Chapter 5) is directly proportional to the square root of the ionic strength of the medium. Care must be taken, therefore, to consider the chemistry of dissolved ionic materials: the ionic strength of a calcium chloride (CaCl2) solution is higher than that of a sodium chloride (NaCl) solution of the same molar concentration. The effects of these two solutions on the electrical double layer will consequently be different.
Higher concentrations of ionic materials, for example 0.1 M, will not just result in a greater effect on the diffuse layer, but some of the charges will migrate through into the fixed layer and become adsorbed onto the surface of the particle itself, shown in Figure 26.2b. In this case, the charge on the particle surface will decrease, which will have the automatic effect of lowering the Stern potential and a secondary effect of reducing the zeta potential, as the charge reduction across the diffuse layer will begin at a different value.
Surfactants added into the system at concentrations below their critical micelle concentration (cmc) will localize on the surface of the particles, as shown in Figure 26.2c. At concentrations above the cmc, surfactant micelles will be formed, with a central hydrophobic core into which the hydrophobic drug may dissolve (Chapters 5 and 24). To avoid this, it is necessary to ensure that the surfactant concentration remains below the cmc. The addition of the surfactant to the surface of the particle will change the particulate charge, certainly in its magnitude but possibly also in its sign. The effects will be dependent on the chemistry of the surfactant itself, i.e. whether it is cationic, anionic or non-ionic. Such charge modification will affect the fixed layer directly, rather than the diffuse layer, and a variation in the surface charge will naturally lead to an alteration of the Stern potential. As described above, this will then have a secondary effect on the zeta potential, as the charge decay across the diffuse layer will start from a different value. Ionic surfactants can also release ionic components into the medium (e.g. Na+ ions from sodium lauryl sulphate), which will then have their own direct effects on the diffuse layer. The overall effect of addition of surfactants will need to be considered on a case-by-case basis, based on their chemistry.
The DLVO theory
Pharmaceutical suspensions are not composed of a single particle of drug suspended in a liquid medium, but rather of multiple particles; this leads to multiple particulate interactions. These interactions can, to some extent, be thought of as the interactions of the diffuse layers around individual particles and hence the electrical double layer provides the basis for understanding inter-particulate interactions. The DLVO theory describes these interactions.
The DLVO theory (Chapter 5 provides more detail) is concerned with predicting the stability of lyophobic (‘solvent-hating’) colloids and is relevant here because of the particle size of pharmaceutical suspensions. Essentially, it calculates the energies of attraction and repulsion between similar particles and predicts the overall energy of interaction. From this, deductions can be made as to the likely behaviour of the suspension, e.g. whether particles coalesce and settle, or remain evenly dispersed throughout the medium. This is arguably the most important question in pharmaceutical suspension formulation development, as a fundamental specification for such a formulation is dose reproducibility, which is most easily achieved from a system which remains well dispersed under all conditions.
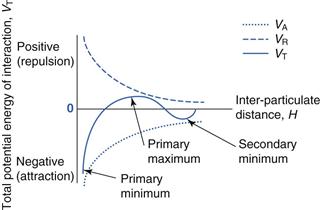
To calculate the total energy of interaction, VT, between two particles, the values of VA and VR are summed, as shown in Equation 26.2. VR is the energy of electrical repulsion and by convention this carries a positive sign. VA is the energy of Van der Waals attractions and by convention is given a negative sign.
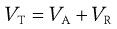(26.2)
Figure 26.3 shows the values of VA, VR and VT for two similar particles suspended in a medium and interacting. Further detailed relationships involving VA and VR can be found in Chapter 5. It is important to note that the VA and VR curves shown in Figure 26.3 are not mirror images of each other.
The easiest way to consider what happens when two particles interact is to remember that the VT line gives the overall energy of interaction and that this will change depending on the distance between the two particles. There are three important zones, or values of VT, in the DLVO diagram: the primary minimum, the secondary minimum and the primary maximum, and the behaviour of the suspension will be dependent on which zone the particles are in. It must also be remembered that all particles will have some thermal energy and will show some movement, whether caused by Brownian motion, the effects of gravity or by external agitation.
The primary minimum
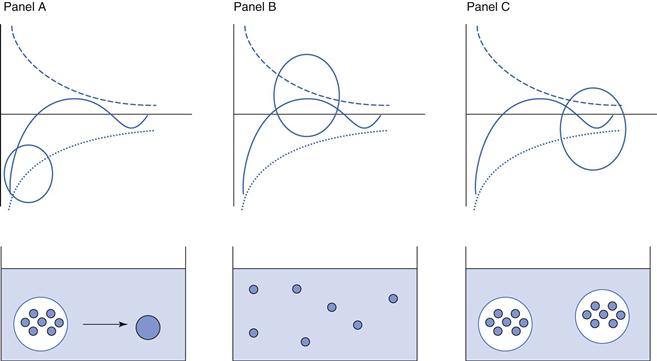
The ‘primary minimum’ zone is described as a ‘minimum’ because the total energy is calculated to be below zero (remember that repulsive energy is described as positive and attractive energy as negative). It is described as ‘primary’ because it is the largest negative deviation from zero. Particles in the primary minimum zone show a higher energy of attraction than repulsion and are therefore likely to move closer together. Imagine two particles are just far enough apart that the energy of attraction balances out the energy of repulsion, so that the overall energy of interaction is zero. Any movement of the particles which brings them closer together will result in an overall mathematical decrease in VT, i.e. VT is now attractive and the particles will continue to move closer together. As they do so, the strength of the overall attractive forces increases, moving the particles still closer together, resulting in a further increase in the attractive forces, and so on. The kinetic energy that the particles have (= kT, where k is the Boltzmann constant and T the temperature in Kelvin) is not high enough to overcome the attractive energy, VT and therefore the particles will eventually aggregate irreversibly. Particles will initially show ‘flocculation’, whereby the individual particles are loosely attracted to each other, but still act independently; subsequently they will demonstrate ‘coagulation’ where particles will collide and form larger particles. Such behaviour is undesirable for pharmaceutical suspensions as it will have serious negative effects on the reproducibility of dosing from the system. These changes are illustrated in panel A of Figure 26.4.
The primary maximum
The naming of the ‘primary maximum’ zone follows the same conventions as for the primary minimum. The primary maximum zone is described as a ‘maximum’ because the total energy is calculated to be above zero (using the convention of repulsive energy being positive and attractive energy being negative). It is described as ‘primary’ because it is the largest positive deviation from zero. Particles in the primary maximum zone show a higher energy of repulsion than attraction and are therefore likely to remain separate or ‘deflocculated’. This is illustrated in panel B of Figure 26.4. At first sight, this would appear to be a good formulation strategy for pharmaceutical suspensions, as if the particles can be forced into the primary maximum zone then they should remain independent and hence dosing would be expected to be reproducible. This is true when the kinetic energy of the particles is less than VT and they are, if anything, more likely to move away from each other, which will have the effect of decreasing the magnitude of VT but maintaining an overall repulsive effect. However, if the kinetic energy of the particles is high enough, for example if the temperature is increased, then this can overcome the energy barrier imposed by VT with the result that the particles can then move closer together. In this case, VT will initially decrease but remain repulsive, so the particles will still exist as independent entities. However, the magnitude of the difference between VT and the particles’ kinetic energy is now greater and therefore they are likely to move even closer together. At some point, the particles will be sufficiently close so that the overall energy of interaction becomes negative, i.e. it is now predominantly attractive, and the particles enter the primary minimum zone with the consequences described above. In summary, therefore, formulating pharmaceutical suspensions so that the particles are in the primary maximum zone can be considered to be risky.
The secondary minimum
Panel C of Figure 26.4, shows the behaviour within the secondary minimum zone. As its name suggests, the ‘secondary minimum’ gives rise to an overall attractive energy of interaction between particles, but of a lower magnitude than that seen in the primary minimum. The particles here show an overall limited attraction to each other and behave as ‘floccules’, loose aggregates of individual particles. Depending on the kinetic energy of the particles, their behaviour will vary slightly. If the kinetic energy is less than the VT, then the particles will move closer together under the influence of the VT, but will not collide and coalesce as the VT is still relatively weak. As the particles move further together, the attractive forces will reach their highest point (although not as strong as in the primary minimum zone) then decrease and overall VT becomes weakly repulsive, which will have the effect of forcing the particles apart. At this stage, VT once again dominates over the kinetic energy and the particles will be attracted weakly to each other. In essence, the particles are maintained in their flocculated state, that is they still exist as individual particles, but are loosely grouped together in floccules. If, however, the kinetic energy of the particles is greater than the VT, then the particles will be able to move further apart. As they do this, the overall VT will become less attractive and ultimately will become, to all practical purposes, zero. In this case, the particles will behave independently, will not flocculate and will not coalesce. In either case (kinetic energy greater to or less than VT), coalescence and coagulation of particles is minimal, and hence this is usually the desired strategy for developing pharmaceutical suspensions.
Controlling particulate behaviour in suspensions
From the discussion above, it can be seen that the behaviour of particles in suspension is complex, even when only two individual interacting particles are considered; the behaviour ultimately being dependent on the relative contribution of the repulsive and attractive energies at any separation distance. Examining the equations that govern these two aspects (Eqns 5.24 and 5.25, respectively, repeated here for convenience) can give some clues as to which factors can be manipulated during suspension formulation to alter the behaviour of the particles and which factors cannot be altered.
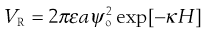(5.24)
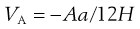(5.25)
A, the Hamaker constant (Eqn 5.25).
This factor is constant for each combination of particle and medium. As the particulate material within a pharmaceutical suspension is the drug, then the formulator has no opportunity to change the physicochemical nature of the particles. Although theoretically the medium may be altered, which will then change the Hamaker constant, most pharmaceutical suspensions, certainly those intended for oral drug delivery, are aqueous. Hence, the two components in the suspension which contribute to the Hamaker constant (the drug and water) are fixed, and this factor is, in effect, non-modifiable.
ε, the permittivity of the medium (Eqn 5.24).
The permittivity of the medium is related to its polarity, so therefore varying the medium will have a direct effect on the repulsive energy between particles in the system. Water is the most common medium for pharmaceutical suspensions and addition of dissolved solids, such as electrolytes, to water will have a relatively minor effect on its permittivity, compared to the effect of changing from water to, for example, oil. Overall, therefore, for the purposes of pharmaceutical suspensions, the permittivity can be considered to be that of water and will have limited variability.
H, distance between particles (Eqns 5.24 and 5.25).
The distance between particles can be considered to be both a cause and effect of the balance between the attractive and repulsive energies of the system, as discussed in the previous section: particles very far apart will have very limited interaction and particles located close to each other will be attracted or repelled depending on exactly how far apart they are, and may move in response to the dominant VT. Inter-particulate distance is difficult to control directly. It will be partly dependent on the mobility of the particles, i.e. their kinetic energy, which itself is dependent on the ambient temperature. The range of temperatures to which a pharmaceutical product is exposed is quite small, from fridge temperature (circa 5 °C) to 40 °C during product testing, so reducing the temperature to reduce mobility is not really a viable option. The inter-particulate distance is also dependent on the concentration of particles within the system, a higher concentration making it more likely that the particles will be physically located close to each other.
4 ψo, the surface potential (Eqn 5.24).
The physicochemical nature of the particles is fixed, as the formulator must work with the drug that is required, therefore the fundamental surface potential of the particles in an aqueous medium will also be fixed. However, it is easy to modify the surface potential of the particles by adsorbing materials at their surface; such materials most commonly being surfactants below their cmc.
5. κ, the Debye-Hückel reciprocal length parameter (Eqn 5.24).
The Debye-Hückel reciprocal length parameter is related to the distance over which the charge on the particle is reduced. It is dependent on the ionic strength of medium and can therefore be controlled easily by the addition of ionizable materials, such as sodium chloride.
6 a, the radius of particle (Eqns 5.24 and 5.25).
The radius of the particle (assuming sphericity) appears in both equations and so will affect both the attractive and repulsive energies. It can be relatively easily controlled by milling or micronization of larger particles to achieve a desired small particle size, or by crystal engineering techniques, intended to produce small particles directly from a solution. Assuming all other parameters in the two equations remain constant, variation in the particle size will have the same magnitude of effect on both VA and VR, and thereby VT. For example, doubling the particle size will double all three calculated values, and halving the particle size will halve them. In all cases, the sign of the VT, i.e. whether overall repulsive or attractive, will remain constant. Changing the particle size will have an effect, therefore, on the magnitudes of both the primary minimum and primary maximum and, depending on the relative extent of the kinetic energy compared to VT and the inter-particulate distance, may lead to increased or lowered stability, following the arguments presented above.
Effects of additives
As indicated in the above section, the addition of ionic or surfactant materials to a suspension formulation is likely to have an effect on the particulate behaviour, by changing the relative values of VA and VR. The effects can be rationalized by considering the electrical double layer on individual particles and how this affects the interaction between particles. Addition of low to medium concentrations of ionizable materials will result in higher concentrations of the positively charged ion in the diffuse layer surrounding a particle (remember that the particle will carry a negative charge in the absence of any absorbed material on its surface), which will allow charge neutralization to occur over a shorter range, i.e. the diffuse layer becomes thinner.
The practical significance of this is that the secondary minimum will be deeper, i.e. it will have a larger magnitude. This in turn means that the energy barrier to escaping the secondary minimum is now higher and the particles will require a larger value of kinetic energy to do so. Hence, more particles will be kept within this separation range. As described previously, the secondary minimum is generally considered to be desirable for pharmaceutical suspensions, as the particles will remain as loose floccules rather than becoming aggregated, and so it follows that addition of low to medium concentrations of ionic materials will be beneficial for pharmaceutical suspension formulations. However, the height of the energy barrier at the primary minimum will also be decreased, so if the particles have a high enough kinetic energy, for example from exposure to high temperatures or by vigorous shaking, then they could overcome this repulsive force and move closer together, finally entering the primary minimum and coalescing.
If the concentration of the ionic material is sufficiently high, then some of the counter-ion charges will penetrate to the particle surface and reduce the overall surface charge ψo and hence the Stern potential, ψδ, i.e. the charge at the edge of the fixed layer. Taken together with a high concentration of the added counter-ion charges in the diffuse layer, which will reduce the Debye-Hückel length, 1/κ, very quickly, this will have the effect of reducing VT to such an extent that the VA will dominate in the VT calculation at all separation distances. Hence, the particles remain attracted to each other at all length scales and are more likely to aggregate and coalesce.
Adding surfactants to the suspension formulation at a level below their cmc will result in their adsorption on the particle surface. This will alter the surface charge (ψo), thereby changing the value of VR with a consequent effect on VT. However, the size and magnitude of this effect will be dependent on the chemical characteristics of the surfactant and addition of surfactant may result in an increased or decreased chance of flocculation.
Particle movement in suspensions
There will always be some particle motion in a suspension formulation: very small particles will exhibit Brownian motion (Chapter 5), gravity will have the effect of causing the particles to sediment and the suspension may be shaken by the patient or during transportation. This motion can therefore affect the inter-particulate distance and by consequence the values of VA, VT and VR (above), potentially affecting the flocculation status of the suspension. When considering the effects of movement, it must be remembered that deflocculated systems behave as individual small particles, whilst flocculated systems behave as individual large particles with a porous structure. Flocculated and deflocculated systems will show different particulate behaviour as a result.
Diffusion
Brownian motion (Chapter 5) is the irregular movement of particles through the medium and is shown by particles up to approximately 1 to 2 µm radius. The result of Brownian motion is diffusion of the particles throughout the medium, from an area of high concentration to one of low concentration. Diffusion (Chapter 3) will therefore result in an improved, more homogeneous distribution of the particles throughout the system. It can be described by the Stokes-Einstein diffusion equation (Eqn 3.30). From Equation 3.30, it can be seen that reducing the particle size will increase the diffusion constant and, conversely, increasing the particle size will reduce it. There is an effective size range above which diffusion will be negligible, and for particles of radius greater than approximately 1 to 2 µm, diffusion can be ignored. As pharmaceutical suspensions may contain particles in the sub-micrometre range, diffusion may be an important contributor to particle movement. However, it is most likely to be observed with deflocculated systems, as these behave as independent particles, and less likely to be seen with flocculated systems. The latter behave as larger particles due to their agglomerated status, and they are therefore likely to be of a size above the effective cut-off for diffusional movement. Diffusion can be reduced by increasing the viscosity of the medium, with a value of 5 mPa s effectively reducing diffusion to zero. For comparison, water at 20 °C has a viscosity of 1 mPa s and a 2% w/v solution of low molecular weight hydroxypropyl methylcellulose (HPMC) has a viscosity of 5 mPa s at 20 °C.
Sedimentation
Sedimentation (also discussed in Chapters 5 and 6) is the downward movement of particles under gravity, and is observed for particles with radii of approximately 0.5 µm and greater. The vast majority of pharmaceutical suspensions will contain particles in this size range, so sedimentation is a significant cause of particle motion. Sedimentation is described by Stokes’ sedimentation equation (Eqn. 26.3), with the sedimentation velocity, v, predicting the speed of settling expected under particular conditions; higher values of v suggest greater likelihood of sedimentation. Here, the Stokes equation has been given in two equivalent forms, defined by the particle radius and diameter:
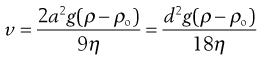(26.3)
where v is the sedimentation velocity, a and d are the particle radius and diameter respectively (the particle is assumed to be spherical), g is the acceleration due to gravity, ρ and ρ0 are the densities of the particles and the medium respectively, and η is the viscosity of the medium.
In the context of suspension formulation, Equation 26.3 shows that reducing the particle size will reduce the sedimentation rate, and conversely increasing the particle size will result in increased settling. Both flocculated and deflocculated systems will show sedimentation. Due to their relative sizes, flocculated systems will settle quickly whereas deflocculated systems will settle more slowly. Increasing the viscosity of the medium will reduce sedimentation, as will reducing the difference in density between the medium and the particle.
Controlling particulate movement in suspensions
Diffusion and sedimentation of particles within the suspension formulation will have opposite, but not equal, effects; sedimentation leading to increased proximity of particles and diffusion leading to greater dispersion of particles within the system. Particulate movement is almost inevitable in a liquid suspension system, with the overall result of a variation in the separation distance between particles, which has a direct consequence on the energies of interaction between particles and hence their flocculation behaviour. Increasing the separation distance will initially move particles away from the primary maximum zone into the secondary minimum zone, changing the nature of the system from a deflocculated to a flocculated one. Further outward movement will take the particles out of the secondary minimum zone and into an area of very little interaction, again changing the nature of the suspension, this time from a flocculated to an effectively deflocculated system. Decreasing the separation distance between particles will initially move them from the secondary minimum zone, showing flocculated behaviour, to the primary maximum zone, showing deflocculated behaviour. Further inward movement will result in the particles entering the primary minimum zone, leading to irreversible coagulation. It must be remembered that gravity works only in one direction (downwards) and that the base of the container is immobile, so ultimately the first settling particle or floccule will reach a point at which its travel stops and it rests on the inside bottom surface of the container. The second and subsequent sedimenting particles or floccules will then approach the first, fixed one, from above. The combination of gravitational force on the sedimenting particles or floccules and mechanical forces exerted by the mass of the sedimenting particles or floccules on those below will overcome VR, moving the particles into the primary minimum zone and irreversible coagulation.
Controlling the movement of particles within the suspension formulation is extremely important to maintain the desired flocculation status. Examination of Equations 3.30 and 26.3 that control diffusion and sedimentation respectively, will allow assessment of which factors can be manipulated and the likely results of such manipulation.
1 a, the radius of the particle.
Manipulation of particle size is relatively easily accomplished mechanically or via manipulation of crystallization techniques. Reducing particle size will increase diffusion and reduce sedimentation, with a larger effect on the sedimentation rate. Particle size reduction would generally be regarded as beneficial because of these effects. However, particle size is a key parameter governing particulate interactions as described by the DLVO theory and so manipulation of particle size will have a direct effect on VT and flocculation behaviour. Particle size will also have an effect on the dissolution behaviour of the drug, which is discussed below.
2 ρ, the density of the particle.
Particles are generally denser than the medium in which they are dispersed, and the greater the density difference, the faster the sedimentation rate. Reducing the particle density by changing crystallization methods is possible, but this will result in an increased particle size (if the total number of particles remains constant) or an increased number of particles (if the particle size remains constant); both of these leading to a change in the DLVO characteristics and flocculation behaviour of the system. So, although manipulation of the density of the particles seems an easy way of reducing the sedimentation rate, it has potential serious disadvantages. Diffusion is unaffected by particulate density.
3 ρo, the density of the medium.
Reducing the density difference between the particles and the medium will lead to a reduction in sedimentation rate, which is beneficial for pharmaceutical suspensions. This is most easily achieved by increasing the density of the medium. Although most pharmaceutical suspensions are based on water, addition of materials such as dextrose or some polymers will raise the density of the product sufficiently to reduce the observed sedimentation. It is best if these materials are non-ionic, as ionic materials will lead to a change in the flocculation behaviour of the particles, via movement of the counter-ion into the diffuse layers surrounding the particles.
4 η, the viscosity of the medium.
Raising the viscosity of the medium will reduce diffusion of the particles, with a value of 5 mPa s effectively decreasing the diffusion to zero. An increased viscosity will also reduce the particulate sedimentation rate. Overall, an increased viscosity is beneficial for pharmaceutical suspensions. The viscosity of water is very low (1 mPa s at 20 °C), but it can be easily modified via additives such as polymers, for example hydroxypropyl methylcellulose or sodium carboxymethylcellulose. In the latter case, however, effects on the electrical double layer around the particles and hence flocculation behaviour are likely to be seen due to the mobile Na+ ion.
5 T, temperature (in Kelvin).
Increasing the temperature will lead to an increase in the diffusion constant and hence greater particle mobility. Although not expressed explicitly in Equation 26.3, the viscosity of a given substance will change with temperature, affecting both diffusion and sedimentation. In reality, however, the range of temperatures to which a suspension is exposed (or should be exposed) is limited but uncontrolled outside the place of manufacture, and temperature should not be used as a tool with which to control particulate behaviour. Repeated cyclical variations in temperature will lead to Ostwald ripening, a deleterious effect, which will be discussed later.
Measuring particle movement
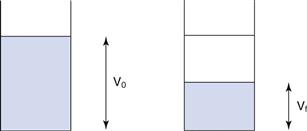
It is not straightforward to measure diffusion in a suspension formulation, but bulk sedimentation is very easy to observe. A known volume of the suspension with the solid particles dispersed as optimally as possible is placed in a graduated cylinder and left to stand, allowing sedimentation to occur. At certain time intervals, the volume of sediment is measured and the sedimentation volume ratio, F, calculated, as shown in Equation 26.4; the value of F is in the range of 0 to 1. Figure 26.5 illustrates this diagrammatically. The speed and extent of sedimentation can be observed visually and used to assess the behaviour of the formulation.
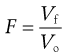(26.4)
where F is the sedimentation volume. Vo is the initial volume of suspension before settling and Vf is the final volume of sediment.
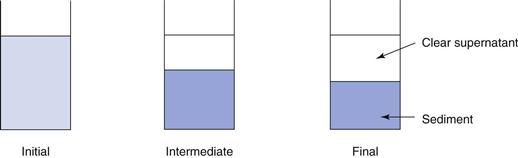
The sedimentation patterns of flocculated and deflocculated systems are different. In a flocculated system, the particles are arranged in loose aggregates or floccules, which behave as large, porous individual particles. These floccules will begin to sediment quickly, generally within a period of minutes, leaving a clear supernatant, and sedimentation will reach a maximum within a few hours or days. The sediment formed is loose and fluffy and can be easily redispersed by shaking, as both the individual floccule and the bulk sediment formed has the solvent medium incorporated into it. A high volume of sediment is observed, with calculated values of the sedimentation volume ratio, F, being up to 0.6. Figure 26.6 illustrates this, showing the initial condition, an ‘intermediate’ condition after a short period of time and the ‘final’ condition after a prolonged period.
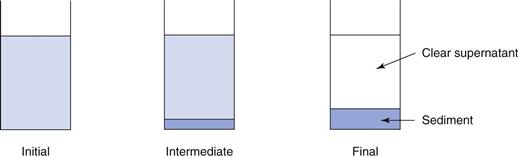
Deflocculated systems show a different pattern of sedimentation. As the particles behave independently, they will sediment slowly, reflecting their small size. Sedimentation takes some time, measured in days and weeks rather than minutes. In the initial stages of sedimentation, a small amount of compact sediment is observed at the base of the cylinder, with no, or limited clear supernatant being observed. Subsequently, the volume of sediment and the volume of clear supernatant both increase. The sediment formed is dense and compacted, described as being ‘caked’. Redispersion of the caked sediment is difficult, as little, if any, of the solvent medium can penetrate into it. A low final volume of sediment is observed, with calculated values of the sedimentation volume ratio, F, being as low as 0.1. Figure 26.7 illustrates this, showing the initial condition, an ‘intermediate’ condition after a short period of time (although longer than for flocculated systems) and the ‘final’ condition after a prolonged period.
What is the desired sedimentation pattern?
The question then arises as to which sedimentation pattern is best for a pharmaceutical suspension. Two factors need to be considered: speed of sedimentation and reversibility. A slow sedimentation rate would be optimal, suggesting that a deflocculated system is more desirable; however, reversibility is key to ensuring that dosing from the suspension is reproducible, and so a flocculated system would be better in this respect. Overall, as in many formulation challenges, a balance between opposing factors must be struck. Formulators may choose to develop a deflocculated system with no or minimal sedimentation, which will require greater viscosity and density adjustments to maintain the initial dispersion of particles. If the suspension is too viscous, then it may be difficult to pour from the container or to judge a dose accurately. A greater potential problem, though, is that, should changes to the particulate dispersion pattern occur, for example as a result of prolonged exposure to high temperatures, the particles may enter the primary minimum zone and irreversibly coagulate, resulting in catastrophic failure of the product. Alternatively, formulators may choose to develop a flocculated system with controlled slow sedimentation. This will require less viscosity and density adjustments than for a deflocculated system and will allow easy redispersion of particles upon shaking. However, patients and healthcare providers will need to be educated as to the vital importance of shaking the product before dispensing a dose and some people may find the separated product unexpected or unsightly.
Dispersibility issues – surface wetting
This chapter has focussed on the interactions of particles with the suspending medium, but with an implicit assumption that there is a suitable initial dispersion of the particles in the medium. It is vital that this initial dispersion is homogeneous at the single particle level to ensure that reproducible dosing is possible. However, pharmaceutical suspensions, by their very nature, involve the interaction of a non-dissolving hydrophobic solid with water and homogeneous individual particulate dispersion is not, in most cases, simple. A measurable surface tension will exist at the interface between the water and the solid, and the solid will not be easily wetted by the water; wettability being defined as the ability of a liquid to spread across a solid surface (discussed in Chapter 4). In order to reduce this surface tension and obtain a more energetically favourable situation, the solid particles are liable to clump together. In this way, the total particulate surface area in contact with the water is reduced; hence the total surface tension is reduced. The natural consequence is that the product is inhomogeneous, inelegant and reproducible dosing is not possible. A reduction in the surface tension between the particles and water is usually necessary to improve the wettability of the solvent over the solid, which will then promote even movement of the solvent across the particle surface and good dispersal of the particles throughout the medium. This is usually produced by the addition of a surfactant, below its cmc, to the medium.
Whether or not a given solid is likely to present dispersion problems can be assessed by examination of the contact angle made between the solid and a liquid when both are exposed to air. A compact of the solid is made and a drop of the liquid placed on its surface. The angle that the drop makes on the surface is then measured, as described in Chapter 4.
Generally, contact angle measurement should be used as a guide only, with values less than 90° indicating reasonable wetting would be expected and values greater than 90° suggesting that problems are likely to be observed during dispersion. Over-interpretation of very similar values of contact angle should be avoided. Wettability can be improved by the use of a surfactant below its cmc; comparison of the contact angles in the presence and absence of the surfactant aiding the assessment of its effectiveness.
Dissolution issues
Drugs are formulated as suspensions for oral delivery because they show limited aqueous solubility related to their target dose, and hence an aqueous solution formulation is not feasible. However, in order for the drug to be absorbed orally, it must be dissolved within the gastrointestinal tract and so dissolution behaviour must be considered. The Noyes-Whitney equation (Eqn 2.3) governs the rate of dissolution of solid materials into a liquid medium. The Noyes-Whitney equation, dissolution and solubility are discussed in greater detail in Chapter 2.
It is clear from the Noyes-Whitney equation that increasing the surface area, whilst keeping the total quantity of drug the same, will increase the dissolution rate of the drug. This in turn is likely to promote oral bioavailability, as typically poorly water-soluble drugs show dissolution rate-limited absorption. Surface area is related to particle size by:
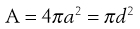(26.5)
where A is the surface area of the particles, and a and d are the particle radius and diameter, respectively.
Reducing the particle size of the drug will therefore result in increased dissolution once a pharmaceutical suspension is taken orally by the patient. However, there are a number of cautions to be borne in mind at this point. Changing the particle size will affect the inter-particulate interactions, as discussed above, and may alter the flocculation behaviour of suspensions. As the bioavailability is likely to be dependent on particle size, close control over the particle size and size distribution is required, in order to maintain batch-to-batch uniformity and promote a consistent therapeutic response after ingestion.
Ostwald ripening
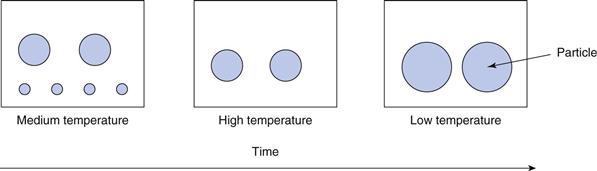
Even though the vast majority of the drug will be in the particulate state in a pharmaceutical suspension, there will always be a small amount in solution, dependent on its solubility. The equilibrium solubility of a solid in a liquid will change with temperature: raising the temperature will lead to an increase in the solubility, with a lowering of temperature resulting in a decrease in solubility. An unfortunate result of this temperature effect is Ostwald ripening, whereby small particles in suspension seem to disappear and large particles grow after repeated temperature changes in both directions. This can be explained as follows. There will always be a range of particle sizes in the suspension, although this range should be as narrow as possible to maintain consistency, and the product will ideally be formulated to be stored at room temperature (approximately 25 °C). If the suspension is exposed to a higher temperature, e.g. by placing in direct sunlight or during transportation, then the equilibrium solubility of the drug in the dispersing medium will increase. Dissolution proceeds from the surface of the particles, so even though the instantaneous removal of an individual drug molecule from a small particle into solution will be the same as that from a large particle, there are fewer molecules on the surface of a small particle and hence the particle surface of a smaller particle appears to recede more quickly than that of a larger particle. The net result is that all particles are slightly smaller and there is more drug in solution. If the suspension is then placed in lower temperature conditions, e.g. by storage in a refrigerator with a temperature circa 5 °C (usual range 2 to 8 °C), the equilibrium solubility of the drug will decrease to below the concentration now in solution (i.e. immediately after exposure to the higher temperatures) and the system is now super-saturated, which is energetically unfavoured. Some of the ‘excess’ drug will now precipitate out and will do so preferentially onto the larger particles, with their greater surface area, analogous to crystallization by seeding. At equilibrium of this stage, the smaller particles may have grown slightly, but the larger particles will have grown more. Overall, therefore, after one hot and cold cycle, the particle size distribution has changed in that the smaller particles are smaller and the larger particles are larger. Repeated temperature cycling aggravates this situation, with the result that the smaller particles dissolve completely and larger particles grow; the whole process being known as Ostwald ripening. This is summarized in Figure 26.8. A corresponding phenomenon occurs with droplets in emulsion (Chapter 27).
Ostwald ripening is a problem for pharmaceutical suspensions, as the particle size and size distribution will change as a result. Consequent effects on the DLVO behaviour of the particles will alter the flocculation profile of the suspension and hence the sedimentation behaviour. The dissolution profile following oral administration will also change, leading to potential bioavailability issues and variability in clinical effect. As the temperature cycling is likely to happen outside the manufacturer’s control, for example in the patient’s home, it is difficult to control, and variable effects between batches or between containers from the same batch are to be expected. The formulator needs to be aware of this and one relatively easy way of minimizing this is to ensure that the solubility profile of the drug in water is ‘flat’, i.e. over the temperature range that the product is likely to experience, the solubility changes only marginally.
General suspension formulation considerations
Pharmaceutically, suspensions are used in a wide range of applications, although oral dosing is the most common. The different routes of administration will present their own specific challenges. For example, a suspension prepared for nebulized inhalation therapy would need to be sterile, as would a suspension intended for ocular delivery. In both these cases, sterilization by terminal filtration would be unsuitable, as the suspended particles would generally be too large to pass through the 0.22 µm filters commonly used for microbial sterilization. Similarly, autoclaving is unlikely to be suitable as the high temperatures involved would affect the solubility of the drug and the physical structure of the suspension. Hence, aseptic preparation would have to be used to manufacture sterile suspensions. In oral dosing, organoleptic considerations apply, necessitating the use of colours and flavours, which are not relevant to the formulation of suspensions intended for topical application.
Solubility
The choice of developing a solution or a suspension formulation is ultimately made based on the aqueous solubility of the drug. The dose of the drug required will be decided by the clinical profile of the drug and therefore cannot be varied. Similarly, the dosing volume is largely fixed: an oral product would have a dosing volume of 5 mL and an eye-drop formulation a dosing volume of 10 µL. Once the equilibrium solubility of the drug in water is known, then simple calculation will establish whether a solution is likely to be possible or not. However, the situation is slightly more complex. A drug in a solution formulation must be mono-molecularly dispersed in the vehicle at manufacture, and remain so throughout the shelf-life of the product. A solution formulation, therefore, should not be produced near its solubility limit, as variations downwards in temperature, e.g. by refrigerated storage, will decrease the equilibrium solubility and potentially lead to precipitation. A general recommendation for solution formulations is to use the equilibrium solubility at 5 °C for solubility calculations and apply a safety factor, so that the maximum concentration of the formulation is significantly less than the equilibrium solubility and the chances of precipitation are minimized.
If the solubility calculations indicate that a suspension formulation is required, then the solubility profile of the drug as a function of temperature needs to be established. A fundamental requirement for suspension formulations is that the drug is suspended in the medium initially and remains so throughout its shelf-life. However, as discussed in previous sections, the drug needs to remain in the same dispersion state, i.e. degree of flocculation, throughout the shelf-life of the product, not merely remaining in suspension. Ostwald ripening must be avoided due to its potential deleterious consequences on product stability and clinical effect. An ideal solubility profile is flat, that is there is minimal change in the equilibrium solubility of the drug with temperature. Usually, the lower the aqueous solubility, the greater the chance of a flat profile being obtained. If the drug has some aqueous solubility, but not sufficient for a straight-forward solution to be developed, then the solubility of the drug may need to be suppressed, so as to maintain the suspended nature of the drug. Solubility suppression may be achieved by the addition of an anti-solvent. These materials act in the opposite manner to co-solvents, in that they reduce the aqueous solubility of the drug rather than enhance it, but they may be chemically the same as co-solvents, e.g. ethanol or polyethylene glycol. Variation of the pH of the medium may be appropriate if the drug is ionizable. Generally, pH manipulation is used to increase the solubility of drugs by forming the ionic species and allowing greater interaction with water, but the opposite intention can be used to find the pH of minimum solubility and use that for suspension formulation, assuming of course that the pH is acceptable for the intended route of administration. A weak acid will show low solubility in low pH conditions, whereas conversely a weak base will show low solubility in high pH conditions. A pro-drug such as an ester is also likely to show lower aqueous solubility than its counterpart ‘real’ drug, so is a potential formulation option. However, changes in the chemical structure of the drug will necessitate further expensive safety studies on the pro-drug as well as the actual drug.
Formulation excipients
A range of formulation excipients may need to be added to the suspension formulation. In each case, the potential effect of the excipient on the DLVO interaction of drug particles needs to be quantified and the formulation amended as necessary.
Flavours, sweeteners and colours
Products intended for oral dosing to children will generally require a colorant, sweetener and flavour to make them palatable (see Chapter 43). Although the intensity of taste of a drug molecule will be less in a suspension formulation than in a solution formulation, it still needs to be considered. The topic of taste masking is outside the scope of this chapter, but as a general rule, children prefer sweet and fruity tastes, although bitter tastes (most drugs are bitter) are best masked by another bitter taste such as grapefruit. The effects of flavours and colours on the physical behaviour of the suspension are likely to be limited, due to the low concentrations used, especially for colours. Traditionally, sugar (sucrose) has been used to sweeten oral formulations, but nowadays the use of sugar is severely restricted, due to concerns over dental caries and potential interference with diabetic glucose control. Several sweeteners are available, all of which are much sweeter than sugar, and hence are used in much lower concentrations. All of the common sweeteners are ionizable: saccharin is commonly used as the sodium salt and acesulfame is provided as the potassium salt, hence the effect of the mobile ions on the electrical double layer needs to be considered. Another consideration applies to aspartame: its degradation products include phenylalanine, so it should not be ingested by patients with the condition phenylketonuria, hence it may be reasonable to avoid its use, depending on the patient population to be treated.
Antimicrobial preservatives
Any time water is present in a multi-dose or non-sterile formulation, an antimicrobial preservative is required to prevent microbial contamination. A range of potential preservatives is available, including sorbic acid, benzoic acid, parabens, chloroform, sucrose and benzalkonium chloride (see Chapter 50). Sucrose has a preservative action at concentrations greater than or equal to 67% w/v. It is unlikely to be used in commercial products due to its cariogenic potential but may be encountered in extemporaneous products, albeit more likely in solution formulations. Sucrose will not interfere with the DLVO behaviour of the system as it does not ionize, so will not be localized in the diffuse layer, and will not adsorb onto the particle surface. It will, however, affect the density and viscosity of the system, and so will have an effect on the sedimentation profile of the suspension. Chloroform, likewise, is unlikely to be found in commercial products but is still included in several British Pharmacopoeial suspension and solution formulations. Benzalkonium chloride is typically used in aqueous eyedrop formulations at concentrations of about 0.01% w/w (approximately 0.3 mM). It is a cationic surfactant and will dissociate in aqueous solutions to produce Cl− ions and a long chain ionized surfactant moiety. Hence, it is likely to affect both the surface potential of the solid drug by deposition of the benzalkonium part of the molecule and the diffuse layer surrounding the solid particle by production of mobile Cl− anions. Benzalkonium chloride is not a ‘pure’ product, in that a range of molecules with varying hydrocarbon chain lengths will exist in each batch of ‘benzalkonium chloride’ (see Fig. 15.5), and thus inter-batch variation in its effect on the flocculation behaviour of the suspension may be expected. Sorbic acid and benzoic acid are both weak acids used in oral formulations at approximately 0.2% w/v (about 15 mM). They are most effective as preservatives in the unionized state, in which state they will not interfere with the flocculation behaviour of the drug. However, they both show mid-range pKa values of 4.8 (sorbic acid) and 4.2 (benzoic acid), so will be partially ionized in the pH conditions likely to be encountered in oral formulations. Some effect of charged moieties arising from this ionization is likely to be seen in the diffuse layer and hence this will directly affect the flocculation behaviour of the suspension. Sorbic acid is commonly used as the potassium salt and benzoic acid as the sodium salt. In this case, dissolution of the salt form into the aqueous vehicle will release the K+ or Na+ ions, which will directly affect the diffuse layer and hence flocculation. Parabens is a family of molecules based on para-hydroxybenzoic acid, with alkyl group esterification at the acid group. These are commonly used at a preservative concentration of approximately 0.2% w/v (about 10 mM). Parabens will not ionize at the pH conditions to be expected in a pharmaceutical product, so is unlikely to interfere with the flocculation behaviour of the particles.
Buffers
A buffer is defined as a mixture of a weak acid or base and one of its salts and is designed to maintain the pH of an aqueous system within very narrow limits. Buffers may be used in suspension formulations if a particular pH is required due to the route of administration, or if the solubility of the drug is suppressed by formulating at a particular pH, as discussed above. Due to its ionic nature, a buffer system will contribute charges to the formulation, which will affect the flocculation behaviour of the suspension by virtue of their being associated with the diffuse layer surrounding the particle. The use of a buffer may also affect the ionization state of other components, such as preservatives, with subsequent effects on their efficacy and the concentration required.
Chemical stabilizers
A range of chemical stabilizers may be used to improve the chemical stability of the drug. These include antioxidants, such as ascorbic acid, used at concentrations of approximately 0.2% w/v (about 10 mM), and sodium metabisulfite, used at levels of about 0.1% w/v (approximately 5 mM), and chelators such as ethylene diamine tetra-acetic acid (EDTA), commonly used as the disodium salt. As discussed above, if the additive ionizes to any appreciable extent, then it will potentially affect the stability of the product by interference with the diffuse layer.
Density and viscosity modifiers/suspending agents
Increasing the density of the suspension formulation may help to reduce the sedimentation rate of the dispersed particles. This may be achieved by the addition of a sugar such as dextrose or sucrose, which would not be expected to change the flocculation behaviour other than by retarding sedimentation. Sugars in low concentration provide an energy source for microbial contamination (at much higher concentrations, sugar solutions are hypertonic, leading to lysis of bacterial cells, and so are self-preserving), so adequate antimicrobial preservation would be required. Additionally, most medicines are formulated, if at all possible, as sugar-free products, so this would not necessarily be a recommended formulation strategy.
Viscosity modifiers are also known as suspending agents as they will reduce the sedimentation of the particles and keep them suspended for longer. The viscosity of the system can be easily adjusted by the additional of polymeric materials or inorganic materials such as clays. The target viscosity for each preparation needs to be defined so as to maintain the particles in their suspended state for as long as possible, i.e. to retard sedimentation. However, this must be balanced against the ease of use of the product; whilst a very viscous suspension will show little, if any, sedimentation, it is unlikely to be patient-friendly. The product must be pourable from a bottle onto a spoon for oral use or dispensable through a nozzle if it is intended for ocular or nasal use.
Cellulosic materials are commonly used as viscosity enhancers in suspension formulations. Cellulose itself is a linear polymer of D-glucose, with individual glucose units being linked via β(1→4) glycosidic bonds; the number of repeating units may run into the thousands. Cellulose ethers are more often used and these are obtained from native cellulose by chemical treatment with an appropriate reagent, replacing the hydrogen on the hydroxyl group of the glucose residue with an appropriate alkyl, hydroxyalkyl or carboxyalkyl group. There are three hydroxyl groups on each glucose residue in the cellulose chain, and the extent of conversion is measured by the degree of substitution. This can take values of anything up to 3, with non-integer numbers (e.g. 1.5) reflecting the fact that there will be an element of inhomogeneity along the cellulose backbone after reaction. Methyl (—CH3) group substitution gives methylcellulose (MC), which is water-soluble, but ethyl (—CH2CH3) group substitution produces ethylcellulose, which is water-insoluble. Substitution with a 2-hydroxypropyl (—CH2CH(OH)CH3) group produces hydroxypropylcellulose (HPC) and mixed substitution of methyl and 2-hydroxypropyl groups results in hydroxypropyl methylcellulose (HPMC). Carboxymethylcellulose (CMC) is prepared from cellulose by the addition of carboxymethyl groups (—CH2COOH) to the glucose residues. It is often used as its sodium salt, denoted sodium carboxymethylcellulose (NaCMC). All five cellulosic polymers mentioned (MC, HPC, HPMC, CMC and NaCMC) are water-soluble and are available in a range of molecular weights and degrees of substitution, which leads to a range of solution viscosities being easily obtainable by manipulation of the chemical properties and concentrations of the polymers used. Generally speaking, the polymers will not interfere with the flocculation behaviour of the particles. However, the ionic nature of NaCMC will directly lead to the production of Na+ ions in solution, which will migrate into the diffuse layer around the particles and affect their flocculation behaviour, so care should be taken with this excipient.
Alginic acid, a polymer derived from seaweed, can also be used to enhance the viscosity of the medium and reduce sedimentation. It consists of residues of β-D-mannuronic acid, and α-L-guluronic acid joined via a (1→4) link; macroscopically, the polymer consists of linear blocks of one or other of the two individual components, with a third type of block showing an alternating structure of the two residue types. This structural variety is a consequence of its natural origin, different sources producing alginic acid with different blocking arrangements, and gives rise to varying properties once in solution. Alginic acid is easily ionized and is commonly used as the sodium salt, so in this case, it will have a direct effect on flocculation behaviour. In the presence of divalent cations, such as calcium (Ca2+), alginic acid will behave as a chelator, with one Ca2+ ion being bound to two ionized acid residues (—COOH), giving rise to an ‘egg box’ structure for the polymer and an increase in viscosity in the solution. In terms of suspension formulation, therefore, addition of alginic acid, either as the intact acid or as the sodium salt, will extract Ca2+ ions from the surroundings if they are present in the formulation. The effects of this will be both to change the flocculation behaviour of the particles and to increase the viscosity of the system.
Traditionally, clays and gums were used to thicken suspensions and to retard sedimentation. Clays are water-insoluble inorganic materials that, when dispersed in water, will absorb water into their structure rather than dissolve. A clay suspension shows some rheological structuring and will retard the sedimentation of other materials suspended with it, such as the drug in pharmaceutical suspensions. Ultimately, the clay will itself sediment as it is in suspension rather than in solution, as are the polymers discussed above. An example of a clay is bentonite, used in the British Pharmacopoeia (BP) formula for Calamine Lotion BP. ‘Gum arabic’ is derived from the sap of Acacia trees and chemically is composed of a complex mixture of saccharides and glycoproteins. Once dissolved in water, gum arabic forms a reasonably viscous solution which can be used to retard sedimentation of suspended materials. Depending on the source, for example precisely which species of Acacia tree, the chemical composition will be different and hence the suspending capabilities will be variable. Tragacanth, sometimes known as gum tragacanth is another complex polysaccharide mixture, derived from the sap of plants of the Astragalus genus. As with gum arabic, it is used to increase the viscosity of the suspending medium and to retard sedimentation of the drug particles. Clays and gums are natural materials and are subject to much greater batch to batch variation than synthetic or semi-synthetic materials, and so have fallen out of favour as pharmaceutical excipients, where close control and predictability of physical and/or chemical behaviour is a pre-requisite.
Wetting agents
Wetting agents are used to improve the flow of the liquid vehicle across the particle surface, which in turn improves the homogeneity of distribution of the drug particles throughout the formulation. They do this by reducing the interfacial tension between the solid particle and liquid medium, as discussed earlier. Wetting agents are typically surfactants below their critical micelle concentration (cmc). Above the cmc, micelles are formed with a hydrophobic core and the hydrophobic drug will begin to dissolve into this region, thus affecting the structure of the system. Hence, the level of the surfactant is kept below the cmc. Surfactants will localize on the surface of the particle, affecting the surface charge, ψ0. The overall effect will be determined by the chemical nature of the surfactant and may be an increase or a decrease in the magnitude of the charge, but keeping the same sign (i.e. negative) or may even result in a change of sign (i.e. the particle effectively becomes positively charged). Each of these changes will have a direct effect on the Stern potential, ψδ and an indirect effect on the thickness of the diffuse layer, resulting in alteration of the flocculation behaviour of the system. Additionally, ionic surfactants such as sodium lauryl sulphate will release mobile ions when dissolved and will have a separate effect on the diffuse layer.
Flocculation modifiers
In previous sections, the necessity of understanding particulate behaviour in suspension was stressed. The electrical double layer surrounding individual particles will have a significant effect on the DLVO behaviour of interacting particles (Chapter 5), leading to flocculation or deflocculation depending on the relative extent of the attractive and repulsive energies at any separation distance. Materials which deposit onto the surface of the particle, such as surfactants, will affect the surface potential, ψ0, leading to a secondary effect on the thickness of the diffuse layer by changing the Stern potential, ψδ. Materials which ionize in solution, such as preservatives and buffers, will lead to mobile charges being taken into the diffuse layer, resulting in a thinning of the diffuse layer and, generally, increased flocculation behaviour.
Excipients are added to pharmaceutical suspension formulations for various good scientific reasons, such as buffering, antimicrobial preservation, viscosity modification, etc, as discussed above. However, their combined effects on the particulate behaviour must be understood and quantified. The last excipient to be added to the suspension formulation is the flocculation modifier, its function being to adjust the flocculation status of the particles to that which is intended. The quantity of flocculation modifier required must be determined last, once the levels and effects of all other functional excipients have been resolved. It is no good, for example, defining the level of the flocculation modifier to give perfect flocculation behaviour and then adding a buffer to the system, which will release mobile ions into the diffuse layer and change the flocculation status. Flocculation modifiers are ionic materials which ionize once in solution in the suspension medium. Typically, sodium chloride (NaCl) is used. The effect of the flocculation modifier on the flocculation behaviour of the particles is dependent on the ionic strength in solution and therefore a multivalent salt (e.g. calcium chloride, CaCl2) will have a greater effect than a monovalent salt (e.g. NaCl).
Colloid stabilizers
A colloid stabilizer is a material which will prevent or retard the coalescence of particles suspended in a medium and, as such, will encompass any material acting on the particle surface or in the diffuse layer. However, the term is usually understood to mean surfactants which are deposited on the particle surface, which are discussed above.
Stability considerations for suspensions
General chemical stability considerations apply to suspensions as much as to any other formulation. The drug must remain chemically stable over the intended shelf-life of the product (and allowing some time as a ‘margin of error’ afterwards) and specifications will be in place for the maximum permitted levels of specified degradation products (these will be determined for each drug independently, based on safety considerations). If the chemical degradation pathway of the drug is determined, then the appropriate chemical preservative(s) can be added to the suspension. Similarly, the effect of temperature on the chemical stability of the drug needs to be established, to assess whether any temperature restrictions are necessary during storage or transport.
However, physical stability is equally important for suspension formulations. Sedimentation should ideally be kept to a minimum as discussed previously, and where sedimentation is permitted or unavoidable, easy redispersion of the sediment is necessary. The patient or carer should be able to redisperse the sediment by inversion and gentle shaking of the bottle only; the bottle should carry an appropriate instruction. The redispersion pattern should be established, testing at suitable time intervals and under various storage conditions, and used as a measure during shelf-life determinations. Visual assessment of sediment redispersion on shaking is useful, but can only provide a general indication of whether there is a problem or not. A more quantitative approach is taken by assessing the particle size distribution and drug content of representative samples taken from the top, middle and bottom of the container. Ideally, these should be consistent across depth and over time, meeting the pre-set product specifications.
Manufacturing considerations
Suspensions are more challenging to prepare than solution formulations. On both a dispensary and factory scales, the most important part of the process is the initial dispersion stage, whereby the powdered drug is mixed with the carrier vehicle. If this is not performed adequately, then the particles are liable to cake. Poor initial dispersion will also lead to swift coagulation and sedimentation. Suspensions are bulky for manufacturers to produce. They require large quantities of pharmaceutical-grade water, necessitating in most cases a water processing plant to produce the water (on a dispensary scale, pre-packaged Purified Water BP would be used). Packaging of the suspension into containers will require a stirred hopper to minimize settling during the packaging process and the effect of shear at the dispensing nozzle on the suspension will need to be considered. A consideration with all products is cost. The drug is usually the most expensive item in the formulation, particularly for an investigative drug not yet licensed, and this will be no different for suspensions.
Summary
Suspensions are one of the most challenging pharmaceutical formulations that students and formulators are likely to meet. Successful suspension development is dependent on a basic understanding of the interactions between particles in the suspension and between particles and other formulation ingredients.
Bibliography
1. Kulshreshtha KA, Singh ON, Wall GM. Pharmaceutical Suspensions: From Formulation Development to Manufacturing. New York: Springer; 2009.
2. Nielloud F, Marti-Mestres G. Pharmaceutical Emulsions and Suspensions. New York: Marcel Dekker Inc.; 2000.
3. Rowe RC, Sheskey PJ, Cook WG, Fenton ME. Handbook of Pharmaceutical Excipients. 7th edn London: The Pharmaceutical Press; 2012.
4. Schramm LL. Emulsions, Foams and Suspensions: Fundamentals and Applications. Germany: Wiley-VCH; 2005.
