Sample Problems Using Respiratory Equations
The following measurements are made:
1. Calculate minute ventilation ( ), dead space–to–tidal volume ratio (VD/VT), alveolar volume (VA), and alveolar ventilation (
), dead space–to–tidal volume ratio (VD/VT), alveolar volume (VA), and alveolar ventilation (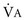 ).
).
2. If extra tubing with a volume of 250 mL were added to the system in a position such that it provided additional dead space, what would be the new VD/VT?
3. With the new system as described in Question 2, what would be the new PaCO2?
4. Going back to the original conditions (without added extra tubing), the ventilator settings are changed to new settings:
a. Calculate the new 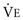 , VA,
, VA, 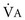 , and VD/VT.
, and VD/VT.
b. What would happen to PaCO2 on the new settings?
c. What would you expect PECO2 to be if you now measured it?
5. Using the original ventilator settings and arterial blood gases as given, calculate the alveolar-arterial difference in partial pressure of oxygen (AaDO2).
6. After the patient is improved, arterial blood gases measured with the patient breathing room air are as follows:
7. The next day, the patient’s arterial blood gas values on room air are as follows:
Answers
1. 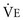 = 1000 mL/breath × 10 breaths/min = 10,000 mL/min = 10 L/min
= 1000 mL/breath × 10 breaths/min = 10,000 mL/min = 10 L/min
VD/VT = (40 mm Hg − 30 mm Hg)/40 mm Hg = 0.25
VA = VT − VD = 1000 mL − (0.25 × VT) = 1000 mL − 250 mL = 750 mL
2. New VD = 250 mL + 250 mL = 500 mL
3. Because PaCO2 is inversely proportional to 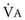 , the new PaCO2 can be calculated from the old and the new
, the new PaCO2 can be calculated from the old and the new 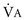 (assuming
(assuming 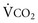 remains constant).
remains constant).
As per Problem 1, old 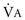 = 7.5 L/min
= 7.5 L/min
New VA = 1000 mL − new VD = 1000 mL − 500 mL = 500 mL
4. On the basis of the new settings:
a. 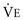 = 500 mL/breath × 20 breaths/min = 10 L/min
= 500 mL/breath × 20 breaths/min = 10 L/min
b. New PaCO2 is inversely proportional to the ratio of the new 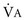 to the old
to the old 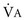 .
.
c. Because VD/VT = (PaCO2 − PECO2)/PaCO2, substitute the known values and solve the equation for PECO2.
5. PAO2 = (0.4 × 713 mm Hg) − (40 mm Hg/0.8) = 285 mm Hg − 50 mm Hg = 235 mm Hg

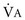 = V
= V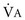 = 500 mL/breath × 10 breaths/min = 5 L/min
= 500 mL/breath × 10 breaths/min = 5 L/min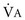 = 2/3 × old
= 2/3 × old 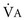
 = 250 mL/breath × 20 breaths/min =
= 250 mL/breath × 20 breaths/min =  /old
/old 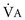 = (5 L/min)/(7.5 L/min) = 2/3
= (5 L/min)/(7.5 L/min) = 2/3