Reference ranges and normal values

Published on 04/03/2015 by admin

Filed under Hematology, Oncology and Palliative Medicine

Last modified 22/04/2025

Print this page

This article have been viewed 12165 times

Chapter 2 Reference ranges and normal values

A number of factors affect haematological values in apparently healthy individuals. As described in Chapter 1, these include the technique and timing of blood collection, transport and storage of specimens, differences in the subject’s posture when the sample is taken, prior physical activity and whether the subject is confined to bed. Variation in the analytic methods used may also affect the measurements. These can all be standardized.

More problematic are the inherent variables as a result of sex, age, occupation, body build, genetic background and adaptation to diet and to environment (especially altitude). These factors must be recognized when establishing physiologically normal values. Furthermore, it is difficult to be certain in any survey of a population for the purposes of obtaining data from which normal ranges may be constructed, that the ‘normal’ subjects are completely healthy and do not have nutritional deficiencies, mild chronic infections, parasitic infestations or the effects of smoking.

Haematological values for the normal and abnormal will overlap and a value within the recognized normal range may be definitely pathological in a particular subject. For these reasons the concept of ‘normal values’ and ‘normal ranges’ has been replaced by reference values and the reference range, which is defined by reference limits and obtained from measurements on the reference population for a particular test. The reference range is also termed the reference interval.^1,² Ideally, each laboratory should establish a databank of reference values that take account of the variables mentioned earlier and the test method, so that an individual’s result can be expressed and interpreted relative to a comparable apparently normal population, insofar as normal can be defined.

Recently new haematological parameters such as immature forms of cells, red cell fragments and detection of functional iron deficiency or malarial infection have become available. Currently these parameters are only used for research and, as internal quality control or external quality assessments are not yet available for some of these tests, their use in clinical decision making is not recommended.³

Reference ranges

A reference range for a specified population can be established from measurements on a relatively small number of subjects (discussed later) if they are assumed to be representative of the population as a whole.² The conditions for obtaining samples from the individuals and the analytic procedures must be standardized, whereas data should be analysed separately for different variables such as individuals who are in bed or ambulant, smokers or non-smokers and so on. One approach is that specimens are collected at about the same time of day, preferably in the morning before breakfast; the last meal should have been eaten not later than 9 p.m. on the previous evening and at that time alcohol should have been restricted to one bottle of beer or an equivalent amount of other alcoholic drink.⁴ An alternative approach is that, unless a test is usually done on a fasting patient, specimens are collected throughout the day on subjects who are not fasting or resting, as this will produce a reference range that is more relevant to results from patients. It is sometimes appropriate that the reference population is defined as having normal results for specific laboratory tests. For example, if determining a reference range for blood count components it may be necessary, in some populations, to exclude iron deficiency and β thalassaemia heterozygosity.

Statistical procedures

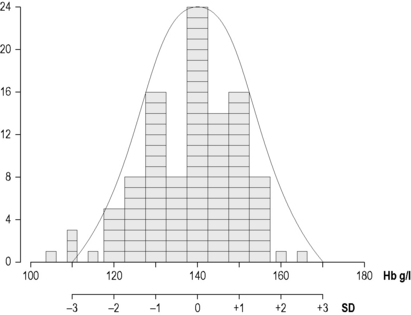
In biological measurements, it is usually assumed that the data will fit a specified type of pattern, either symmetric (Gaussian) or asymmetric with a skewed distribution (non-Gaussian). With a Gaussian distribution, the arithmetic mean (×) can be obtained by dividing the sum of all measurements by the number of observations. The mode is the value that occurs most frequently and the median (m) is the point at which there are an equal number of observations above and below it. In a true Gaussian distribution they should all be the same. The standard deviation (SD) can be calculated as described on p. 625.

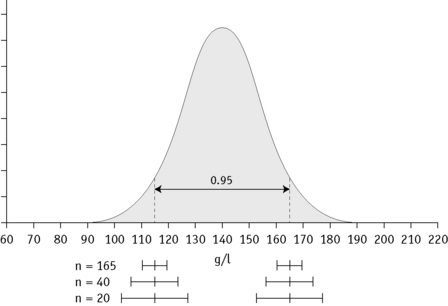
If the data fit a Gaussian distribution, when plotted as a frequency histogram the pattern shown in Figure 2.1z is obtained. Taking the mode and the calculated SD as reference points, a Gaussian curve is superimposed on the histogram. From this curve, practical reference limits can be determined even if the original histogram included outlying results from some subjects not belonging to the normal population. Limits representing the 95% reference range are calculated from arithmetic mean ± 2SD (or more accurately ± 1.96SD).

Figure 2.1 Example of establishing a reference range. Histogram of data of Hb measurements in a population, with Gaussian curve superimposed. The ordinate shows the number that occurred at each reference point. The mean was 140 g/l; the reference ranges at 1SD, 2SD and 3SD are indicated.

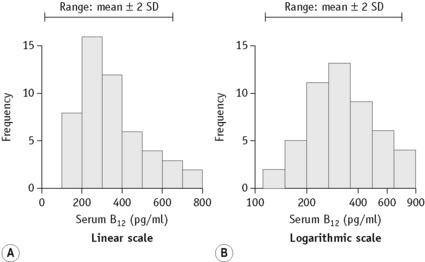
When there is a log normal (skew) distribution of measurements, the range to –2SD may even extend to zero (Fig. 2.2A). To avoid this anomaly, the data should be plotted on semilogarithmic graph paper to obtain a normal distribution histogram (Fig. 2.2B). To calculate the mean and SD the data should be converted to their logarithms. The log-mean value is obtained by adding the logs of all the measurements and dividing by the number of observations. The log SD is calculated by the formula on p. 625 and the results are then converted to their antilogs to express the data in the arithmetic scale. This process is now generally carried out using an appropriate statistical computer program.

Figure 2.2 Example of conversion to a log normal distribution. Data of serum vitamin B₁₂ measurements in a population. (A) Arithmetic scale: mean 340; 2SD range calculated as 10–665 pg/ml. (B) Geometric scale: mean 308; 2SD range calculated as 120–780 pg/ml.

When it is not possible to make an assumption about the type of distribution, a non-parametric procedure may be used instead to obtain the median and SD. To obtain an approximation of the SD, the range that comprises the middle 50% spread (i.e. between 25% and 75% of results) is read and divided by 1.35. This represents 1SD.

Confidence Limits

In any of the methods of analysis, a reasonably reliable estimate can be obtained with 40 values, although a larger number (≥120) is preferable (Fig. 2.3).⁵ When a large set of reference values is unattainable and precise estimation is impossible, a smaller number of values may still serve as a useful clinical guide. Confidence limits define the reliability (e.g. 95% or 99%) of the established reference values when assessing the significance of a test result, especially when it is on the borderline between normal and abnormal. Calculation of confidence limits is described on p. 625. Another important measurement is the coefficient of variation (CV) of the test because a wide CV is likely to influence its clinical utility (see p. 625).

Figure 2.3 Effect of sample size on reference values. A smoothed distribution graph was obtained for Hb measurement from a group of normal women; the ordinate shows the frequency distribution. The 95% reference interval is defined by the lower and higher reference limits, which are 115 and 165 g/l, respectively. The confidence levels for these values are shown for three sample sizes of 20, 40 and 165 values, respectively.

Normal reference values

The data given in Tables 2.1, 2.2 and 2.3 provide general guidance to normal reference values that are applicable to most healthy adults and children, respectively, in industrialized countries. The data have been derived from personal observations as well as various published reports.⁶^–¹¹ However, slightly different ranges may be found in individual laboratories where different analysers and methods are used. The reference interval, which comprises a range of ± 2SD from the mean, indicates the limits that should cover 95% of normal subjects; 99% of normal subjects will be included in a range of ± 3SD. Age and sex differences have been taken into account for some values. Even so, the wide ranges that are shown for some tests reflect the influence of various factors, as described below. Narrower ranges would be expected under standardized conditions. Because modern analysers provide a high level of technical precision, even small differences in successive measurements may be significant. It is thus important to establish and understand the limits of physiological variation for various tests. The blood count data and other test results can then provide sensitive indications of minor abnormalities that may be important in clinical interpretation and health screening.

Table 2.1 Haematological values for normal adults (predominantly from Europe and North America) expressed as a mean ± 2SD (95% range)

Red blood cell count
Men	5.0 ± 0.5 × 10¹²/l
Women	4.3 ± 0.5 × 10¹²/l
Haemoglobin concentration^a
Men	150 ± 20 g/l
Women	135 ± 15 g/l
Packed cell volume (PCV) or Haematocrit (Hct)
Men	0.45 ± 0.05 (l/l)
Women	0.41 ± 0.05 (l/l)
Mean cell volume (MCV)
Men and women	92 ± 9 fl
Mean cell haemoglobin (MCH)
Men and women	29.5 ± 2.5 pg
Mean cell haemoglobin concentration (MCHC)
Men and women	330 ± 15 g/l
Red cell distribution width (RDW)
As coefficient of variation (CV)	12.8 ± 1.2%
As standard deviation (SD)	42.5 ± 3.5 fl
Red cell diameter (mean values)
Dry films	6.7–7.7 μm
Red cell density	1092–1100 g/l
Reticulocyte count	50–100 × 10⁹/l (0.5–2.5%)
White blood cell count	4.0–10.0 × 10⁹/l
Differential white cell count
Neutrophils	2.0–7.0 × 10⁹/l (40–80%)
Lymphocytes	1.0–3.0 × 10⁹/l (20–40%)
Monocytes	0.2–1.0 × 10⁹/l (2–10%)
Eosinophils	0.02–0.5 × 10⁹/l (1–6%)
Basophils	0.02–0.1 × 10⁹/l (<1–2%)
Lymphocyte subsets (approximations from ranges in published data)
CD3	0.6–2.5 × 10⁹/l (60–85%)
CD4	0.4–1.5 × 10⁹/l (30–50%)
CD8	0.2–1.1 × 10⁹/l (10–35%)
CD4/CD8 ratio	0.7–3.5
Platelet count	280 ± 130 × 10⁹/l
Bleeding time^b
Ivy’s method	2–7 min
Template method	2.5–9.5 min
Thrombin time	15–19 s
Plasma fibrinogen concentration	1.8–3.6 g/l
Euglobulin clot lysis time	90–240 min
Plasminogen concentration^d	0.75–1.60 u/ml
Antithrombin concentration^d	0.75–1.25 u/ml
Protein C concentration^d
Functional	0.70–1.40 u/ml
Antigen	0.61–1.32 u/ml
Protein S concentration^d
Total antigen	0.78–1.37 u/ml
Free antigen	0.68–1.52 u/ml
Pre-menopausal women^c	0.55–1.55 u/ml
Function	0.60–1.35 u/ml
Pre-menopausal women	0.55–1.35 u/ml
Heparin cofactor II concentration^d	0.55–1.45 u/ml
Median red cell fragility (MCF) (g/l NaCl)
Fresh blood	4.0–4.45 g/l NaCl
After 24 h at 37°C	4.65–5.9 g/l NaCl
Cold agglutinin titre (4°C)	<64
Blood volume (normalized to ‘ideal weight’)
Red cell volume
Men	30 ± 5 ml/kg
Women	25 ± 5 ml/kg
Plasma volume	45 ± 5 ml/kg
Total blood volume	70 ± 10 ml/kg
Red cell lifespan	120 ± 30 days
Serum iron
Men and women	10–30 μmol/l (0.6–1.7 mg/l)
Total iron-binding capacity	47–70 μmol/l (2.5–4.0 mg/l)
Transferrin saturation	16–50%
Serum ferritin concentration
Men	15–300 μg/l (median 100 μg/l)
Women	15–200 μg/l (median 40 μg/l)
Serum vitamin B₁₂ concentration	180–640 ng/l
Serum folate concentration	3–20 μg/l (6.8–45 nmol/l)
Red cell folate concentration	160–640 μg/l (0.36–1.45 μmol/l)
Plasma haemoglobin concentration	10–40 mg/l
Serum haptoglobin concentration
Radial immunodiffusion	0.8–2.7 g/l
Haemoglobin binding capacity	0.3–2.0 g/l
HbA₂	2.2–3.5%
HbF	<1.0%
Methaemoglobin	<2.0%
Sedimentation rate (mm in 1 h at 20 ± 3°C)
Men
17–50 years	≤10
51–60 years	≤12
61–70 years	≤14
>70 years	≤30
Women
17–50 years	≤12
51–60 years	≤19
61–70 years	≤20
>70 years	≤35
Plasma viscosity
25°C	1.50–1.72 mPa/s
37°C	1.16–1.33 mPa/s

a Haemoglobin concentration may sometimes be reported as g/dl.

b Bleeding time is no longer recommended for routine assessment of haemostasis but may be useful in suspected collagen disorders.

c From Dykes AC, Walker ID, McMahon AD et al 2001 Protein S antigen levels in 3788 healthy volunteers. British Journal of Haematology 113:636–641.

d These ranges are for general guidance only as each laboratory should establish its own normal range.

Table 2.2 Haematological values for normal infants (amalgamation of data derived from various sources; expressed as mean ± 2SD or 95% range)^a

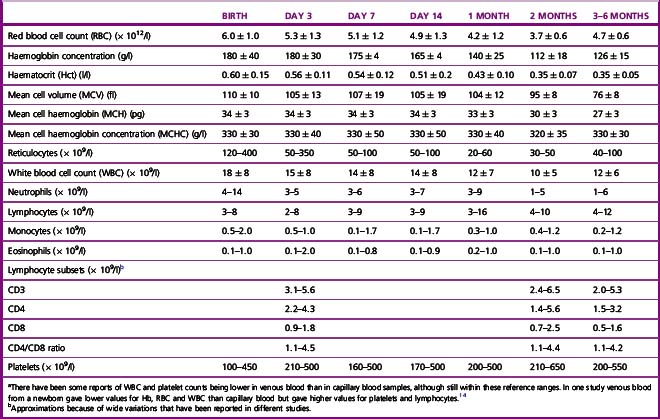
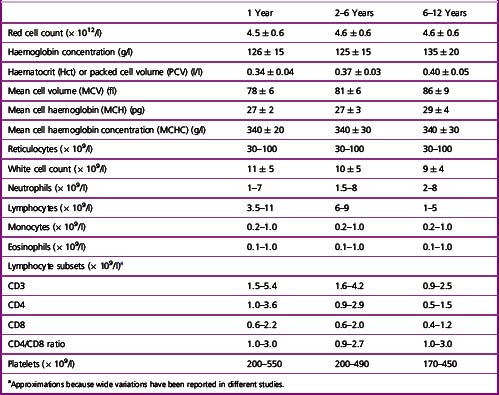
Table 2.3 Haematological values for normal children (amalgamation of data derived from various sources; expressed as mean ± 2SD or 95% range)

It should be noted that in Table 2.1 the differential white cell count is shown as percentages and in absolute numbers. Automated analysers provide absolute counts for each type of leucocyte and because proportional (percentage) counting is less likely to indicate correctly their absolute increase or decrease, the International Council for Standardization in Haematology has recommended that the differential leucocyte count should always be given as the absolute number of each cell type per unit volume of blood.¹² The neutrophil:lymphocyte ratio obtained from a differential leucocyte count should be regarded only as an approximation.

Reference ranges for pre-term infants vary with gestational age. In infants in the USA between 22 and 41 weeks’ gestation, the packed cell volume increased from 40 to 52 l/l, the haemoglobin from 140 to 170 g/l and the platelet count from 200 to 250 × 10⁹/l, whereas the MCV and MCH gradually decreased from 121 to 105 fl and 40.5 to 35.5 pg, respectively.¹³

Physiological variations in the blood count

Red Cell Components

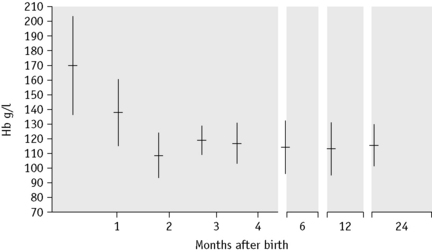
There is considerable variation in the red blood cell count (RBC) and haemoglobin concentration (Hb) at different periods of life and there are also transient fluctuations, the significance of which is often difficult to assess. At birth the Hb is higher than at any period subsequently (Table 2.2). The RBC is high immediately after birth,⁶ and values for Hb >200 g/l, RBC higher than 6.0 × 10¹²/l and a haematocrit (Hct) over 0.65 are encountered frequently when cord clamping is delayed and blood from the placenta and umbilical artery re-enter the infant’s circulation. After the immediate postnatal period, the Hb falls fairly steeply to a minimum by about the 2nd month (Fig. 2.4). The RBC and Hct also fall, although less steeply, and the cells may become microcytic with the development of iron deficiency. The changes in the mean cell haemoglobin (MCH), mean cell haemoglobin concentration and mean cell volume (MCV) from the neonate through infancy to early childhood are shown in Tables 2.2 and 2.3.

Figure 2.4 Changes in Hb values in the first 2 years after birth. The perpendicular lines show means and 2SD ranges.

The Hb and RBC increase gradually through childhood to reach almost adult levels by puberty.⁷ However, in a health survey of apparently normal men and women in Britain, mean Hb values of 145 g/l for men and 128 g/l for women have been reported;⁹ the lower normal limits for Hb (i.e. 2SD below the mean) are usually taken as 130 and 120 g/l, respectively, but in some apparently normal men and women lower limits of 120 and 110 g/l, respectively, have been noted. Statistically, at least 1% of a normal population have levels more than 3SD below the mean, but in some studies there have been considerably larger numbers.⁹ It is possible that some have nutritional deficiencies, especially iron deficiency, without clinical effects. The levels in women tend to be significantly lower than those of men.⁹ Apart from a hormonal influence on haemopoiesis, iron deficiency is likely to be a factor influencing the difference; the extent to which menstrual blood loss is a significant factor is not clear because a loss of up to 100 ml of blood with each period may lead to iron depletion without causing anaemia.¹⁵ There may be ethnic differences in Hb. A major 6-year survey in the USA has shown that in socially comparable populations the Hb in Black Americans is 5–10 g/l lower than their White counterparts at all ages and as much as 20 g/l lower in the first 2 years of life.¹⁶

Pregnancy

In normal pregnancy, there is an increase in erythropoietic activity.¹⁷ However, at the same time, an increase in plasma volume occurs,¹⁸ and this results in a progressive decrease in Hb, Hct and RBC (Table 2.4). The level returns to normal about a week after delivery. There is a slight increase in MCV during the 2nd trimester.¹⁹ Serum ferritin decreases in early pregnancy and usually remains low throughout pregnancy, even when supplementary iron is given.²⁰

Table 2.4 Haemoglobin concentration values in pregnancy

1st trimester	124–135 g/l
2nd trimester	110–117 g/l
3rd trimester	106–109 g/l^a
Mean values postpartum
Day 2	104 g/l
Week 1	107 g/l
Week 3	116 g/l
Month 2	119 g/l

a Higher values (120 g/l or higher) may be found when supplementary iron is being given.

The Elderly

In healthy men and women, Hb, RBC, Hct and other red cell indices remain remarkably constant until the 6th decade. Anaemia becomes more common in those older than 70–75 years ^21,²² and is associated with poor clinical outcomes due to poorer cognitive status, increased frailty and an elevated risk of hospitalization and of complications during hospitalization.²³ In the elderly, the difference in Hb between men and women is less than in younger subjects, so that a difference of 20 g/l in younger age groups is reduced to 10 g/l or less in the elderly. There is a concomitant increase in serum iron in women, although serum ferritin levels remain higher in men than in women. Factors which contribute to the lower Hb in the elderly include renal insufficiency, inflammation, testosterone deficiency, diminished erythropoiesis, stem cell proliferative decline and myelodysplasia.^24,²⁵ Moderate or severe anaemia should never be attributed to ageing per se until underlying disease has been excluded; however, a significant number of elderly subjects with anaemia have no identifiable clinical or nutritional causes.

Exercise

Optimal athletic performance depends on proper function of many organs, including the blood. Several haematological parameters can affect or be influenced by physical activity including blood cells and coagulation mechanisms.²⁶ For example endurance athletes may develop so-called ‘sports anaemia’, which is thought to be the result of increased plasma volume.^27,²⁸ Increasing oxygen delivery by raising the haematocrit is a simple acute method to improve athletic performance. Legal means of raising the haematocrit include altitude training and hypoxic tents. Illegal means include blood doping and the administration of erythropoietin (EPO) (see Chapter 6).²⁹ Endurance athletes may also have decreased levels of serum iron and ferritin, possibly associated with loss of iron in sweat. Conversely, in sprinters who require a short burst of very strenuous muscular activity, there is a transient increase in RBC by 0.5 × 10¹²/l and in Hb by 15 g/l, largely because of reduction in plasma volume and to a lesser extent the re-entry into the circulation of cells previously sequestered in the spleen.³⁰ The effects of exercise must be distinguished from a form of haemolysis known as ‘runner’s anaemia’ or ‘march haemoglobinuria’, which occurs as a result of pounding of the feet on the ground.³¹

Posture

There is a small but significant alteration in the plasma volume with an increase in haemoglobin and Hct as the posture changes from lying to sitting, especially in women ³²; conversely, changing from walking to lying down results in a 5–10% decrease in the Hb and Hct. Thus, subjects should rest for 5–10 min before their blood is collected. The difference in position of the arm during venous sampling, whether dependent or held at atrial level, can also affect the Hct.

These aspects highlight the relevance of using a standardized method for blood collection, although this is not necessarily practicable in routine practice. This is discussed in Chapter 1 and the differences between venous and capillary blood are described on p. 5.

Diurnal and Seasonal Variation

Changes in Hb and RBC during the course of the day are usually slight, about 3%, with negligible changes in the MCV and MCH. However, variation of 20% occurs with reticulocytes.⁸ Studies of diurnal variation of serum erythropoietin have shown conflicting results.³³ Pronounced, but variable, diurnal variations are seen in serum iron and ferritin and in patients taking iron-containing supplements.^34,³⁵ It has been suggested that minor seasonal variations also occur, but the evidence for this is conflicting.³⁶^–³⁸

Altitude

The effect of altitude is to reduce plasma volume, increase the Hb and Hct and raise the number of circulating red cells with a lower MCV.³⁹ The magnitude of the polycythaemia depends on the degree of hypoxaemia. At an altitude of 2000 m (c 6500 ft), Hb is c 8–10 g/l and Hct is 0.025 higher than at sea level; at 3000 m (c 10 000 ft), Hb is c 20 g/l and Hct is 0.060 higher and at 4000 m (c 13 000 ft) Hb is 35 g/l and Hct is 0.110 higher. Corresponding increases occur at intermediate and at higher altitudes.⁴⁰ These increases appear to be the result of both increased erythropoiesis which is secondary to the hypoxic stimulus and the decrease in plasma volume that occurs at high altitudes.

Smoking

Cigarette smoking affects Hb, RBC, Hct and MCV (see p. 20).

Leucocyte Count

The effect of age is indicated in Tables 2.1, 2.2 and 2.3; at birth, the total leucocyte count is high; neutrophils predominate, reaching a peak of c 13.0 × 10⁹/l within 6–8 h for neonates of >28 weeks’ gestation and 24 h for those delivered at <28 weeks.¹³ The count then falls to c 4.0 × 10⁹/l over the next few weeks and then to a level at which the count remains steady. The lymphocytes decrease during the first 3 days of life often to a low level of c 2.0–2.5 × 10⁹/l and then rise up to the 10th day; after this time, they are the predominant cell (up to about 60%) until the 5th to 7th year, when they give way to the neutrophils. From that age onwards, the levels are the same as for adults.⁷ There are also slight sex differences; the total leucocyte count and the neutrophil count may be slightly higher in girls than in boys,⁷ and in women than in men.⁴¹ After the menopause, the counts fall in women so that they tend to become lower than in men of similar age.⁴¹

People differ considerably in their leucocyte counts. Some tend to maintain a relatively constant level over long periods; others have counts that may vary by as much as 100% at different times. In some subjects, there appears to be a rhythm, occurring in cycles of 14–28 days and in women this may be related to the menstrual cycle or to oral contraception.⁴¹ There is no clearcut diurnal variation, but minimum counts are found in the morning with the subject at rest and during the course of a day there may be differences of 14% for the total leucocyte count, 10% for neutrophils, 14% for lymphocytes and 20% for eosinophils;⁸ in some cases this may result in a reversed neutrophil:lymphocyte ratio. Random activity may raise the count slightly; strenuous exercise causes increases of up to 30 × 10⁹/l, partly because of mobilization of marginated neutrophils and changes in cortisol levels.⁴² Large numbers of lymphocytes and monocytes also enter the bloodstream during strenuous exercise. However, there have also been reports of neutropenia and lymphopenia in athletes undergoing daily training sessions.^43,⁴⁴

Epinephrine (adrenaline) injection causes an increase in the numbers of all major types of leucocytes (and platelets), possibly reflecting the extent of the reservoir of mature blood cells present not only in the bone marrow and spleen but also in other tissues and organs of the body. Emotion may possibly cause an increase in the leucocyte count in a similar way. A transient lymphocytosis with a reversed neutrophil:lymphocyte ratio occurs in adults with physical stress or trauma.⁴⁵ The effect of ingestion of food is uncertain. Cigarette smoking has an effect on the leucocyte count (see p. 20).

A moderate leucocytosis of up to 15 × 10⁹/l is common during pregnancy, owing to a neutrophilia, with the peak in the 2nd trimester.¹⁹ The count returns to non-pregnancy levels a week or so after delivery.⁴⁶

In individuals of African ancestry there is a tendency for the neutrophil:lymphocyte ratio to be reversed primarily due to a reduction in neutrophil count. This is thought to be due to genetic rather than environmental factors because significantly lower leucocyte counts, especially neutrophil counts, have also been observed in Africans and Afro-Caribbeans living in Britain.⁴⁷ ‘Benign ethnic neutropenia’ occurs in up to 5% of African Americans and is defined as a neutrophil count <1.5 × 10⁹/l without overt cause or complications.⁴⁸ A region on chromosome 1, possibly the Duffy Null polymorphism, has recently been associated with the difference in WBC and neutrophil count between African Americans and European Americans.⁴⁹ Elderly people receiving influenza vaccination show a lower total leucocyte count owing to a decrease in lymphocytes.⁵⁰

Platelet Count

There is a slight diurnal variation in the platelet count of about 5%;⁸ this occurs during the course of a day as well as from day-to-day. Within the wide normal reference range, there are some ethnic differences and in healthy West Indians and Africans platelet counts may on average be 10–20% lower than those in Europeans living in the same environment.⁵¹ There may be a sex difference; thus, in women, the platelet count has been reported to be about 20% higher than in men.⁵² A decrease in the platelet count may occur in women at about the time of menstruation. There are no obvious age differences; however, in the 1st year after birth the platelet count tends to be at the higher level of the adult normal reference range. Strenuous exercise causes a 30–40% increase in platelet count;⁴² the mechanism is similar to that which occurs with leucocytes.

Other Blood Constituents

As with the blood count, variations from normal reference values occur in respect of sex, age, exercise, stress, diurnal fluctuation and so on. These are described in the relevant chapters.

Effects of Smoking

Both active and passive cigarette smoking have a significant effect on many haematological normal reference values.^53,⁵⁴ Some effects may be transient and their severity varies between individuals as well as by the number of cigarettes smoked. Smoking ≥10 cigarettes a day results in slightly higher Hb, Hct and MCV.^38,⁵⁵ This is probably at least in part a consequence of the accumulation of carboxyhaemoglobin in the blood together with a decrease in plasma volume. After a single cigarette, the carboxyhaemoglobin level increases by about 1%,⁵⁶ and in heavy smokers the carboxyhaemoglobin may constitute c4–5% of the total Hb. Smoking may be associated with polycythaemia.⁵⁷

The leucocyte count increases, largely as a result of an increase in the neutrophils and neutrophil function may be affected.^53,⁵⁸ Smoking may also cause an increase in CD4-positive lymphocytes and total lymphocyte count.^53,^58,⁵⁹

Smokers tend to have higher platelet counts than nonsmokers, but the counts decrease rapidly on cessation of smoking.⁵³ Studies of platelet aggregation and adhesiveness have given equivocal results, but there appears to be a consistent increase in platelet turnover with decreased platelet survival and increased plasma β-thromboglobulin. Elevated fibrinogen concentration (with increased plasma viscosity) and reduced protein S have been reported, but smoking does not seem to have any consistent effects on the fibrinolytic system.⁵³

The influence of smoking on the blood is summarized in Table 2.5.

Table 2.5 ^aEffects of cigarette smoking⁵³^–⁵⁹

Increased	Decreased
Haemoglobin concentration (Hb)	Plasma volume
Red cell count (RBC)	Protein S
Haematocrit (Hct)
Mean cell volume (MCV)
Mean cell haemoglobin (MCH)
White cell count (WBC)
Neutrophil count
Lymphocyte count
T cells (CD4-positive)
Monocyte count
Carboxyhaemoglobin (>2%)
Platelet count (transient)
Mean platelet volume
Fibrinogen concentration
β-thromboglobulin concentration
von Willebrand factor
Red cell mass
Haptoglobin concentration
Plasma viscosity
Whole blood viscosity
Erythrocyte sedimentation rate (ESR)