The second, more common error is a type II or β error.² This represents the probability of incorrectly concluding that a difference does not exist between therapies when in fact it does. This is analogous to missing the signal for the noise. Here, the key issue is the natural degree of variability among study subjects, independent of what might be due to treatment effects. When small but real differences exist between groups and there is enough variability among subjects, the study requires a large sample size to be able to show a difference. Missing the difference is a β error, and the power of a study is 1 − β. Study power is driven by sample size. The larger the sample, the greater the power to resolve small differences between groups.

Frequently, when a study fails to show a difference between groups, there is a tendency to assume that there is in fact no difference between them.³ What is needed is an assessment of the likelihood of a difference being detected, given the sample size and subject variability. Although the authors should provide this, they frequently do not, thereby leaving readers to perform their own calculations or refer to published nomograms.⁴^,⁵ Arbitrarily, we say that a power of 80%, or the chance of detecting a difference of a specified amount given a sample size of n, is acceptable. If the penalties for missing a difference are high, other values for power can be selected, but the larger the power desired, the larger the sample size required.

Multiple Tests

If the chance that a study or statistical test reports a false-positive result is 1 in 20 (assuming that the level of significance is set at P > .05), the chances of at least one of several tests being falsely positive is [1 − (0.95)ⁿ], where n is the number of studies performed. Thus, for six comparisons in which P < .05 determines rejection of the null hypothesis, there is a 25% chance that at least one false-positive conclusion has been accepted. Several strategies can be used to deal with this problem. Methodologically, protection is afforded by specifying comparisons beforehand, thus reducing the random nature of these comparisons. In other settings, such as secondary data analysis for developing new questions, it is not possible to do this. At a minimum, the bar for rejection of the null hypothesis should be raised. For example, the Bonferroni correction divides the nominal .05 level of significance by the number of tests performed such that for six tests, the value needed for acceptance of any hypothesis is P < .0083.

Confidence Intervals

The hypothesis-testing strategy just described is intended to yield an all-or-nothing answer. The null hypothesis is either accepted or rejected. It is often of more use, particularly when describing the relationships between risk factors and outcome, to note the intensity (risk or odds) and direction of the association, as well as the degree to which variability affects the precision of its estimate. This is accomplished in the form of a confidence interval (CI). A 95% CI describes the mean ± 2 standard deviations. Stated another way, given a sample with a mean and a 95% CI, one can be 95% certain that the true population mean falls within the limits given by the CI. In comparing two means, odds ratios, or risk rates, when the 95% CIs of the means do not overlap, there is a 95% chance that they were drawn from different populations, analogous to rejecting the null hypothesis for P < .05.The advantage of CIs is that by providing a range of reasonable possible rates, they are easier to incorporate into the clinical setting, where the precision of the research environment may be lacking.

Univariate versus Multivariate Techniques

A comparison between a single risk factor and an outcome is called univariate analysis and is often described by odds ratios. Multivariate analysis considers the impact of a variety of potential risk factors on an outcome. Logistic regression is one such technique and is useful when the outcome can be divided into membership in one of two groups, such as failure/success or alive/dead. The interpretation of such models is that a risk factor that is statistically part of the model has an association with the outcome that is independent of the other items in the equation. Multivariate analyses also allow investigation of the interplay between risk factors by demonstrating how the consideration of additional factors influences the associations already present in the model. Regression models can be prone to “overmodeling” the data, or describing patterns that are unique to the particular dataset used in their creation. Determining the validity of the model requires testing the degree to which the model predicts an outcome from risk factors when applied to other datasets not used in development of the model.

Events over Time/Survival Analysis

Frequently, an outcome measure is described as the time to a particular event, such as the time to tumor progression, stroke, or death. Data may best be described in these cases by using Kaplan-Meier or life-table techniques that incorporate both the group membership of the individuals under study and the length of time that they have been part of the group. The graphic reproduction of this analysis is the common survival curve. Survival curves of different cohorts can be compared by using a log-rank test or Breslow-Day statistic. The impact of different factors on a survival curve can be modeled in a multivariate fashion, logically similar to that described for binary outcomes in logistic regression. The Cox proportional hazards model is the most commonly used vehicle for this type of analysis.

Statistics and Probability in Diagnosis

The diagnosis of neurosurgical illness, as in other fields, requires the development of a list of possible explanations for the patient’s complaints to form a differential diagnosis. As an example, imagine the scenario of a hydrocephalic child with his first shunt placed 3 months earlier who now has a 2-day history of vomiting and irritability. An experienced clinician hearing this story would quickly formulate a list of possible diagnoses, including otitis media, gastroenteritis, constipation, upper respiratory infection, and of course, shunt malfunction. Through a series of additional questions about the medical history and a physical examination, the clinician would be able to narrow this list down considerably to one or two possibilities. Additional tests such as computed tomography (CT) or a shunt tap would then be used to either support or refute particular diagnoses.

Pretest and Posttest Probability—A Bayesian Approach

At the onset, certain quickly ascertainable features about a clinical encounter should lead to the formation of a baseline probability of the most likely diagnoses for the particular clinical findings. In the example just presented, among all children seen by a neurosurgeon within 3 months of initial shunt placement, about 30% will subsequently be found to have shunt malfunction.⁶ Before any tests are performed or even a physical examination completed, elements of the history provided allow the clinician to form this first estimate of the likelihood of shunt failure. The remainder of the history and physical findings allow revision of that probability, up or down. This bayesian approach to diagnosis requires some knowledge of how particular symptoms and signs affect the baseline, or the “pretest” probability of an event. The extent to which a particular clinical finding or diagnostic study influences the probability of a particular end diagnosis is a function of its sensitivity and specificity, which may be combined into the clinically more useful likelihood ratio.⁷ Estimates of the pretest probability of disease tend to be situation specific; for example, the risk of failure of a cerebrospinal fluid (CSF) shunt after placement is heavily dependent on the age of the patient and the time elapsed since the last shunt-related surgical procedure.⁸ Individual practitioners can best provide their own data for this by studying their own practice patterns.

Properties of Diagnostic Tests

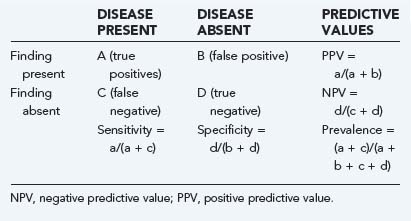
Elements of the history, physical examination, and subsequent diagnostic studies can all be assessed to describe their properties as predictors of an outcome of interest. These properties may be summarized as sensitivity, specificity, positive and negative predictive values, and likelihood ratios, as illustrated in Table 11-1.

TABLE 11-1 The Two-by-Two Table for Diagnosis

Sensitivity indicates the percentage of patients with a given illness who have a positive clinical finding or study. In other words, that a straight leg raise test has a sensitivity of 80% for lumbar disk herniation in the setting of sciatic pain means that 80 of 100 patients with sciatica and disk herniation do, in fact, have a positive straight leg raise test.⁹ In Table 11-1, sensitivity is equal to a/(a + c). Conversely, specificity, equal to d/(b + d) in Table 11-1, refers to the number of patients without a clinical diagnosis who also do not have a clinical finding. Again, using the example of the evaluation of low back pain in patients with sciatica, a positive straight leg raise test has about 40% specificity, which means that of 100 patients with sciatica but without disk herniation, 40 will have a negative straight leg raise test.

Sensitivity and specificity are difficult to use clinically because they describe clinical behavior in a group of patients known to carry the diagnosis of interest. These properties provide no information about performance of the clinical factor in patients who do not have the disease and who probably represent the majority of patients seen. Sensitivity ignores the important category of false-positive results (Table 11-1, B), whereas specificity ignores false-negative results (Table 11-1, C). If the sensitivity of a finding is very high (e.g., >95%) and the disease is not overly common, it is safe to assume that there will be few false-negative results (C in Table 11-1 will be small). Thus, the absence of a finding with high sensitivity for a given condition will tend to rule out the condition. When the specificity is high, the number of false-positive results is low (B in Table 11-1 will be small), and the absence of a symptom will tend to rule in the condition. Epidemiologic texts have suggested the mnemonics SnNout (when sensitivity is high, a negative or absent clinical finding rules out the target disorder) and SpPin (when specificity is very high, a positive study rules in the disorder), although some caution may be in order when applying these mnemonics strictly.¹⁰

However, when sensitivity or specificity is not as high or a disease process is common, the more relevant clinical quantities are the number of patients with the symptom or study result who end up having the disease of interest, otherwise known as the positive predictive value [PPV = a/(a + b)]. The probability of a patient not having the disease when the symptom or study result is absent or negative is referred to as the negative predictive value [NPV = d/(c + d)]. Subtracting NPV from 1 gives a useful “rule out” value that provides the probability of a diagnosis even when the symptom is absent or the study result negative.

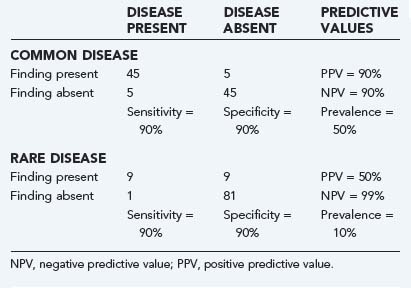
A key component of these latter two values is the underlying prevalence of the disease. Examine Table 11-2. In both the common disease and rare disease case, the sensitivity and specificity for the presence or absence of a particular sign are each 90%, but in the common disease case, the total number of patients with the diagnosis is much larger, thereby leading to much higher positive and lower negative predictive values. When the prevalence of the disease drops, the important change is the relative increase in the number of false versus true positives, with the reverse being true for false versus true negatives.

TABLE 11-2 The Impact of Prevalence on Positive Study Findings in Diagnosis

The impact of prevalence plays a particularly important role when one tries to assess the role of screening studies in which there is only limited clinical evidence that a disease process is present. Examples include the use of screening magnetic resonance imaging studies for cerebrovascular aneurysms in patients with polycystic kidney disease ¹¹ and routine use of CT for follow-up after shunt insertion¹² and for determining cervical spine instability in patients with Down syndrome,¹³ as well as to search for cervical spine injuries in polytrauma patients.¹⁴^,¹⁵ In these situations, the low prevalence of the disease makes false-positive results likely, particularly if the specificity of the test is not extremely high, and usually results in additional, potentially more hazardous and expensive testing.

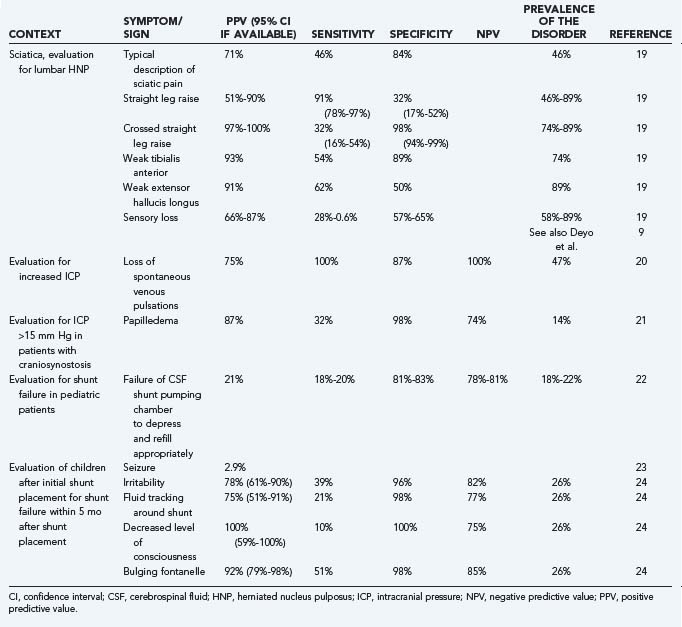
Likelihood ratios (LRs) are an extension of the previously noted properties of diagnostic information. LRs express the odds (rather than the percentage) of a patient with a target disorder having a particular finding present as compared with the odds of the finding in patients without the target disorder. An LR of 4 for a clinical finding indicates that it is four times as likely for a patient with the disease to have the finding as those without the disease. The advantage of this approach is that odds ratios, which are based on sensitivity and specificity, do not have to be recalculated for any given prevalence of a disease. In addition, if one starts with the pretest odds of a disease, this may be simply multiplied by the LR to generate the posttest odds of a disease. Nomograms exist to further simplify this process.¹⁶ A number of useful articles and texts are available to the reader for further explanation.¹⁷^,¹⁸ Table 11-3 gives examples of the predictive values of selected symptoms and signs encountered in clinical neurosurgical conditions.^9,¹⁹^–²⁴

TABLE 11-3 Symptoms, Signs, and Predictive Values

Clinical Decision Rules

The preceding examples demonstrate the mathematical consequences of the presence of a single symptom or sign on the diagnostic process. The usual diagnostic process involves the integration of different symptoms and signs, often simultaneous with the process of generating a differential diagnosis. Clinical decision rules or decision instruments allow integration of multiple symptoms or signs into a diagnostic algorithm. The desired properties of such algorithms depend on the disease process studied, the consequences of false-positive and false-negative results, and the risk and cost of evaluation maneuvers. For example, the National Emergency X-Radiography Utilization Study (NEXUS) sought to develop a clinical prediction rule to determine which patients require cervical spine x-ray assessment after blunt trauma.¹⁵

Measurement in Clinical Neurosurgery

Neurosurgeons have become increasingly aware of the need to offer concrete scientific support for their medical practices. Tradition and reasoning from pathophysiologic principles, although important in generating hypotheses, are not a substitute for scientific method. Coincident with this move toward empiricism has been the recognition that traditional measures of outcome, such as mortality and morbidity rates, are insufficient to capture important changes in functional status. Similarly, traditional outcomes as recorded in the medical record lack precision and reproducibility. Aware that better outcome assessments are required to better provide information on treatment choices, we must ask two important questions. What should we measure? How should we measure it?

Surrogate versus True End Points

In determining what should be measured, one starting point is the question, “What does the patient care about?” Even though this may seem obvious, in the settings of research, quality control, and economic analysis, outcomes that are not clearly of interest to the patient are regularly used. For example, fusion rates have commonly been used for assessing the outcomes of spinal surgery. Yet this is clearly a substitute or surrogate end point for what the patient cares about—that the pain be relieved or function improved. Improvement in one does not always equate with improvement in the other. Other neurosurgical examples of surrogate end points include shunt revision rates, extent of surgical resection (e.g., in an 80-year-old with an acoustic neuroma, the degree of resection may be only partially correlated with overall patient outcome), and CSF flow analysis after posterior fossa decompression. In many cases, an argument can be made that changes in the surrogate measure translate into tangible improvements for the patient. However, there remain numerous situations in which that relationship falters and misses important outcomes for the patient.

Surrogate or intermediate end points clearly have a role early in the investigation of a therapy. They are usually chosen because they are easily quantifiable and generally reproducible. However, the evidence used to justify the widespread application of a technology or procedure should include a broader assessment of the overall impact of the intervention on the target population.

Techniques of Measurement

Quantifying clinical findings and outcomes remains one of the largest stumbling blocks in performing and interpreting clinical research. Although outcomes such as mortality and some physical attributes such as height and weight are easily assessed, many of the clinical observations and judgments that we make are much more difficult to measure. All measurement scales should be valid, reliable, and responsive. A scale is valid if it truly measures what it purports to measure. It is reliable when it reports the same result for the same condition, regardless of who applies it or when they do so. It is responsive when meaningful changes in the item or event being measured are reflected as changes in the scale.²⁵ The complexity of neurologic assessment has led to a proliferation of such measurement scales.²⁶

Validity

The validity of a scale can be assessed along both logical and numerical lines. Face validity assesses whether a scale appears on the surface to measure its targeted outcome. For example, a scale to measure outcome with respect to activities of daily living that focused predominantly on physical pain measurement would have questionable face validity. Although a scale would not deliberately be designed to miss its target, this can happen when an established scale is used to assess a different disease process.

Content validity is a similar concept that arises out of scale development. In the course of developing scales, a series of domains are determined. For example, again referring to the activities of daily living, the functional independence measure has domains of self-care, sphincter control, mobility and transfer, location, communication, and social cognition.²⁷ The more completely that a scale addresses the perceived domains of interest, the better its content validity.

Construct validity refers to the degree to which the scale correlates with predictions based on the understanding of the disease process itself. A pathophysiologic understanding of a disease process should generate hypotheses about the performance of a scale in particular clinical settings. For example, if an instrument is developed to assess patients with tethered cord syndrome and then applied in a screening setting to a population of children with incontinence, the few patients found with tethering lesions should score significantly higher on the scale than children with other causes of incontinence.

Criterion validity refers to performance of the new scale in comparison to a previously established standard. Simplified shorter scales that are more readily usable in routine clinical practice should be expected to have criterion validity when compared with longer, more complex research-oriented scales.²⁸

Reliability

To be clinically useful, a scale should give a consistent report when applied repeatedly to a given patient. Reliability and discrimination are intimately linked in that the smaller the error attributable to measurement, the finer the resolving power of the measurement instrument. Measurement in part involves determining differences, so the discriminatory power of an instrument is of critical importance. Although often taught otherwise, reliability and agreement are not the same thing. An instrument that produces a high degree of agreement and no discrimination between subjects is, by definition, unreliable. This need for reproducibility and discrimination is dependent not only on the nature of the measurement instrument but also on the nature of the system being measured. An instrument found reliable in one setting may not be so in another if the system being measured has changed dramatically. Mathematically, reliability is equal to subject variability divided by the sum of subject and measurement variability.²⁵ Thus, the larger the variability (error) caused by measurement alone, the lower the reliability of a system. Similarly, for a given measurement error, the larger the degree of subject variability, the less the impact of measurement error on overall reliability. Reliability testing involves repeated assessments of subjects by the same observers, as well as by different observers.

Reliability is typically measured by correlation coefficients, with values ranging between 0 and 1. Although there are several different statistical methods of determining the value of the coefficient, a common strategy involves the use of analysis of variance (ANOVA) to produce an intraclass correlation coefficient (ICC).²⁹ The ICC may be interpreted as representing the percentage of total variability attributable to subject variability, with 1 being perfect reliability and 0 being no reliability. Reliability data reported as an ICC can be converted into a range of scores expected simply because of measurement error. The square root of (1 − ICC) gives the percentage of the standard deviation of a sample expected to be associated with measurement error. A quick calculation brings the ICC into perspective. For an ICC of 0.9, the error associated with measurement is (1 − 0.9)^0.5, or about 30% of the standard deviation.²⁵ Reliability measures can also be reported with the κ statistic, discussed more fully in the next section as a measure of clinical agreement.³⁰

Internal consistency is a related property of scales that are used for measurement. Because scales should measure related aspects of a single dimension or construct, responses on one question should have some correlation to responses on another question. Although a high degree of correlation renders a question redundant, very limited correlation raises the possibility that the question is measuring a different dimension or construct. This has the effect of adding additional random variability to the measure. There are a variety of statistics that calculate this parameter, the best known of which is Cronbach’s alpha coefficient.³¹ Values between 0.7 and 0.9 are considered acceptable.²⁵

Clinical Agreement

The success of measurement instruments and clinical decision rules such as those described earlier depends on the degree to which two or more clinicians can agree on the observed findings. Observations that are difficult to reproduce from examiner to examiner are of much less value in predicting the presence of significant injury, illness, or subsequent prognosis. Clinical agreement can be divided into intrarater and interrater reliability, depending on the likelihood of one individual identifying the same findings in a series of assessments done at different times or the probability of two independent evaluators arriving at the same conclusion given the same material to observe.

One of the common statistical ways to measure agreement is the κ statistic.³²^,³³ It attempts to compensate for the likelihood of chance agreement when only a few possible choices are available. If two observers identify the presence of a clinical finding 70% of the time in a particular patient population, by chance they will agree on the finding 58% of the time (Table 11-4). If they actually agree 80% of the time, the κ statistic for this clinical parameter is 80% to 58% actual agreement beyond chance and 100% to 58% potential agreement beyond chance. This is equal to 0.52. Interpretation of these κ values is somewhat arbitrary, but by convention, κ values of 0 to 0.2 indicate slight agreement; 0.2 to 0.4, fair agreement; 0.4 to 0.6, moderate agreement; and 0.8 to 1.0, high agreement.³⁴

TABLE 11-4 Clinical Agreement

The concept of clinical agreement can be broadened to apply not only to individual symptoms, signs, or tests but also to whole diagnoses; for example, Kestle and colleagues reported that a series of objective criteria for establishing the diagnosis of shunt malfunction have a high degree of clinical agreement (κ = 0.81) with the surgeon’s decision to revise the shunt.³⁵

The κ statistic is commonly used to report the agreement beyond that expected by chance alone and is easy to calculate. However, concern has been raised about its mathematical rigor and its usefulness for comparison across studies (for a detailed discussion see http://ourworld.compuserve.com/homepages/jsuebersax/kappa.htm#start).³⁶^,³⁷

Responsiveness

Measurement is largely a matter of discrimination among different states of being, but change needs to be both detected and meaningful. Between 1976 and 1996, Bracken and associates performed a series of randomized controlled trials (RCTs) to evaluate the role of corticosteroids in the management of acute spinal cord injury.³⁸^–⁴⁰ In the last two trials, the main outcome measure was performance on the American Spinal Cord Injury Association (ASIA) scale. Both studies demonstrated small positive benefits in preplanned subgroup analyses for patients receiving methylprednisolone. Subsequent to their publication, however, controversy arose regarding whether the degree of change demonstrated on the ASIA scale is clinically meaningful and justifies the perceived risk of increased infection rates with the therapy. The scale itself assesses motor function in 10 muscle groups on a 6-point scale from 0 (no function) to 5 (normal function and resistance). Sensory function is assessed in 28 dermatomes for both pinprick and light touch. In the first National Acute Spinal Cord Injury Study (NASCIS 1), the net benefit of methylprednisolone was a mean motor improvement of 6.7 versus 4.8 on a scale of 0 to 70. What is unclear from the scale is whether changes of this degree produce any significant functional improvement in a spinal cord injury patient.⁴¹^–⁴³ Presumably seeking to address this question, the last of these trials included a separate functional assessment, the functional independence measure. This multidimensional instrument assesses the need for assistance in a variety of activities of daily living. A change in this measure, at least on face, produces a more obvious change in functional state than does the ASIA scale. Indeed, a small improvement in the sphincter control subgroup of the scale was seen in the NASCIS 3 trial, although considering the scale as a whole, no improvement was seen.³⁸

Measurement Instruments

A large number of measurement instruments are now in regular use for the assessment of neurosurgical outcomes. Table 11-5 lists just a few of these,⁴⁴^–⁸⁴ as do other summaries.⁸⁵ Several types of instruments are noted. First, a number of measures focus on physical findings, such as the Glasgow Coma Scale (GCS), Mini-Mental Status Examination, and House-Brackmann score for facial nerve function. These measures are specific to a disease process or body system. A second group of instruments focus on the functional limitations produced by the particular system insult. A third group of instruments look at the role that functional limitations play in the general perception of health. Instruments that assess health status or health perceptions, such as the 36-item short-form health survey (SF-36) or Sickness Impact Profile, measure in multiple domains and are thought of as generic instruments applicable to a wide variety of illnesses. Others instruments include both general and disease-specific questions. The World Health Organization defines health as “a state of complete physical, mental, and social well-being and not merely the absence of disease or infirmity.”⁸⁶ In this context, it is easy to see the importance of broader measures of outcome that assess quality of life. Finally, economic measures such as health utilities indices are designed to translate health outcomes into monetary terms.⁸⁷

TABLE 11-5 Common Measurement Instruments in Neurosurgery

DISEASE PROCESS/SCALE	FEATURES	REFERENCE
Head Injury
Glasgow Coma Scale (GCS)	Examination scale: Based on eye (1-4 points), verbal (1-5 points), and motor assessment (1-6 points)	44
Glasgow Outcome Scale	1, Dead; 2, vegetative; 3, severely disabled; 4, moderately disabled; 5, good	45
DRS (disability rating scale)	Score of 0 (normal) to 30 (dead); incorporates elements of the GCS and functional outcome	46
Ranchos Los Amigos	I, No response; II, generalized response to pain; III, localizes; IV, confused/agitated; V, confused/nonagitated; VI, confused/appropriate; VII, automatic/appropriate; VII, purposeful/appropriate	47
Mental Status Testing
Folstein’s Mini-Mental State Examination	11 Questions: orientation, registration (repetition), attention (serial 7s), recall, language (naming, multistage commands, writing, copying design)	48, 49
Cognitive Testing
Wechsler Adult Intelligence Scale (WAIS)	The standard IQ test for adults with verbal (information, comprehension, arithmetic, similarities, digit span, vocabulary) and performance domains (digit symbols, picture completion, block designs, picture arrangement, object assembly)⁵⁰	51
Epilepsy
Engel class	I: Seizure free (with or without auras) II: Rare seizures (almost seizure free) III: Worthwhile improvement IV: No worthwhile improvement

52 Movement Disorders Unified Parkinson’s Disease Rating Scale Subscales for mentation/mood (0-16), activities of daily living (0-52), motor examination, including speech and tremor (0-108), and complications from therapy (0-23) 53 Ashworth scale (spasticity)

1: No increase in tone

2: Slight increase in tone, “catching” in flexion/extension

3: Passive movement difficult, moderate increase in tone

4: Passive movement difficult; substantial increase in tone

5: Rigid extremity

54 Vascular Hunt & Hess 0, Unruptured; 1, mild headache or nuchal rigidity; up to 5, deep coma 55, 56 WFNS grading scale 0, Unruptured; 1, GCS score of 15 without major focal deficit. Scale up to 5, GCS score of 3 with or without deficit 57 NIH stroke scale 15-Item scale: level of consciousness, visual symptoms, facial and limb weakness, ataxia, sensory loss, neglect, and language dysfunction 58 Ranklin Disability Scale, modified RDS (Modified version)

0: No symptoms

1: No significant disability, with symptoms

2: Slight disability, independent

3: Moderate disability—requires assistance, ambulatory

4: Moderately severe disability—requires assistance, not ambulatory

5: Severe disability—bedridden, incontinent, constant care

Original version had no grade 0 and grade 1 equivalent to grade 2 above

59, 60 Cranial Nerve House/Brackmann scale for facial nerve function 0, Normal function; to 6, complete paralysis, based on appearance during casual observation, appearance at rest, and appearance with motion. Cut point at 3 vs. 4 for complete eye closure 61 Spine Trauma ASIA classification Radicular motor function at 5 upper extremity and lower extremity levels (0-5 each), light touch (0-2), and pinprick (0-2) for each of 28 levels. Maximum (L + R) motor = 100, sensory = 112 per modality 62 Frankel/ASIA impairment

E: Normal motor/sensory function

D: Motor function below injury level generally ⩾3/5 strength

C: Motor function below injury level generally <3/5 strength

B: Limited motor function below injury, sensation preserved through sacral levels

A: No motor/sensory function below level of injury

63 Peripheral Nerve Trauma Medical Research Council grading system Scores strength 0-5. Similar to ASIA motor grading 64 Degenerative Spine North American Spine Society questionnaire Separate cervical and lumbar instruments. Combines both disease-specific questions and SF-36. Normative data published 65 Oswestry low back pain disability questionnaire 10 Domains, including pain intensity, personal care, lifting, walking, sitting, standing, sleeping, sex life, social life, and traveling; 6-item scale per domain 66 Japanese Orthopedic Association scale Reported for cervical myelopathy: Scores 0-2 to 0-4 for motor function in arm and leg; sensory function in arm, leg, and trunk; and sphincter dysfunction. Higher scores signify greater function 67 Hydrocephalus HOQ (Hydrocephalus Outcome Questionnaire) 51-Question disease-specific multidimensional outcome measure developed and validated for pediatric hydrocephalus. Responses scored to yield overall score from 0 to 1. Can be converted to health utility score 68, 69 Craniofacial Whitaker grade

I: No need for additional surgery

II: Minor surgery advisable for soft tissue revision or bone contouring

III: Major osteotomy or bone grafting required, although this would be less extensive than the original procedure

IV: Major surgery required that equals or exceeds the extent of the original procedure

70 Oncology Karnofsky performance scale 100-Point scale (scored by 10s) from 100 (normal) to 0 (dead) that measures degree of dependence; <70 is no longer independent 71 EORTC QLC 30- Multidimensional quality-of-life measures used for glioma outcomes 72, 73 University of Toronto 16 Items from Sickness Impact Profile, 13 items specific to brain tumor patients with an overall assessment question, question answered by visual analog–type scale between descriptive extremes 72 Functional Functional independence measure (FIM) 7-Point scale from independence to total assistance applied to 6 ADL areas: self-care (eating, grooming, bathing, dressing, and toilet), sphincter control, transfers, locomotion (walking and stairs), communication, and social cognition 74 WeeFIM Modification of FIM for pediatric patients 75, 76 Barthel index 10-Item (or 15 if the Granger modification version) score addressing ADLs (feeding, transfers, toiletry, etc). Each item scored for dependent vs. independent with several items at intermediate grade. Score of 0-100 (0-20 for modification) 77, 78 Pain McGill Pain Questionnaire Very common in use. Adjectival description of pain to assess three domains: sensory-discriminative, motivational-affective, and cognitive-evaluative. Adjective selected by patient carries intensity weighting. Several scoring systems exist 79 Visual analog scale Ruler scale of 0-10 for pain 80 General/Multidimensional SF-36 and shorter forms 36 Questions. Domains: physical activity, social activity, societal role, pain, mental health, emotions, vitality, and health perceptions. Can be self-administered; current testing involves Web-based applications. Scoring is out of 100 for each of the 8 domains, with higher scores indicating better health. Physical and mental summary scores also available 81 Sickness Impact Profile 136 Questions. Domains/categories: Physical—ambulation, mobility, body care, and movement; Psychosocial—social interaction, communication, alertness behavior, emotional behavior, sleep and rest, eating, home management, recreation and pastimes, employment 82 Nottingham Health Profile 38 Questions. Domains: physical mobility, energy level, pain, emotional reactions, sleep, and social isolation. Can be combined to summary measure 83, 84

ADLs, activities of daily living; ASIA, American Spinal Cord Injury Association; EORTC, European Organization for Research and Treatment of Cancer; NIH, National Institutes of Health; SF-36, short-form health survey (36 items); WFNS, World Federation of Neurological Surgeons.

Choosing a Specific Measure

From the standpoint of study design, the choice of measures is driven by the study question and context. When a study focuses on a narrow clinical question, focused measurement instruments are appropriate. However, the more varied the interventions considered and broader the generalizations the authors wish to draw, the more generic the outcome measure should be.

Functional outcome measures assess the impact of physiologic changes on more general function. Evidence from these sources may be more compelling than changes in physiologic parameters (see discussion on the NACSIS trials earlier). Even more broadly, health status measures place the loss of function in the context of the patient’s global health picture. These measures are particularly useful when comparing across disease processes or comparing healthy and diseased populations. A common strategy is to incorporate both system/disease-specific and generic outcome measures in the same study. Authors and readers must be clear which of these represents the primary outcome measure of the study. When the purpose of the study is to measure the economic impact of a therapy or its “utility” in an economic context, summary measures that report a single score rather than a series of scores for different domains are necessary. In many cases it is appropriate to have the quality-of-life measure as the principal outcome assessment tool. For example, in assessments of therapy for glioblastoma multiforme, efforts to extend survival have thus far been only minimally successful. Studies focusing on maximizing quality of life with the available modalities are often the best ones to provide information on therapeutic decision making.⁸⁸

Rating scales and quality-of-life assessment measures need not be limited to research studies. Familiarity with these measures can lead to their introduction into general clinic practice and thereby give the practitioner a more effective way to communicate with others and assess individual results. The “Guidelines for the Management of Acute Cervical Spine and Spinal Cord Injuries” offers as a guideline that the functional independence measure be used as a clinical assessment tool by practitioners when assessing patients with spinal cord injury.⁸⁹ Practical considerations dictate that instruments used in the conduct of routine care be short and feasible to perform. However, ad hoc modification or simplification of instruments to suit individual tastes or needs voids the instruments’ validation and reduces comparability with other applications. Access to many of the outcome measures listed in Table 11-5 is available through the Internet.

Specific Study Designs

Clinical researchers and clinicians using clinical research must be familiar with the various research designs available and commonly used in the medical literature. To better understand the features of study design, it is helpful to consider factors that limit the ability of a study to answer that question. In this context, it is easier to understand the various permutations of clinical research design. Elementary epidemiology textbooks broadly divide study designs into descriptive and analytic studies (Table 11-6).⁹⁰ The former seek to describe health or illness in populations or individuals but are not suited to describing causal links or establishing treatment efficacy. Comparisons can be made with these study modalities only on an implicit, or population, basis. Thus, a death rate may be compared with a population norm or with death rates in other countries. Analytic or explanatory studies have the specific purpose of direct comparison between assembled groups and are designed to yield answers concerning causation and treatment efficacy. Analytic studies may be observational, as in case-control and cohort studies, or interventional, as in controlled clinical trials. In addition to being directed at different questions, different study designs are more or less robust in managing the various study biases that must be considered as threats to their validity (Table 11-7).¹^,⁹¹

TABLE 11-6 Study Designs

	EXAMPLE	LIMITATIONS (TYPICAL)
Descriptive Studies
Population correlation studies	Rate of disease in population vs. incidence of exposure in population	No link at the individual level, cannot assess or control for other variables. Used for hypothesis generation only
	Changes in disease rates over time	No control for changes in detection techniques
Individuals
Case reports and case series	Identification of rare events, report of outcome of particular therapy	No specific control group or effort to control for selection biases
Cross-sectional surveys	Prevalence of disease in sample, assessment of coincidence of risk factor and disease at a single point in time at an individual level	“Snapshot” view does not allow assessment of causation, cannot assess incident vs. prevalent cases. Sample determines degree to which findings can be generalized
Descriptive cohort studies	Describes outcome over time for specific group of individuals, without comparison of treatments	Cannot determine causation, risk of sample-related biases
Analytic Studies
Observational
Case control	Disease state is determined first. Identified control group retrospectively compared with cases for presence of particular risk factor	Highly suspect for bias in selection of control group. Generally can study only one or two risk factors
Retrospective cohort studies	Population of interest determined first, outcome and exposure determined retrospectively	Uneven search for exposure and outcome between groups. Susceptible to missing data, results dependent on entry criteria for cohort
Prospective cohort studies	Exposure status determined in a population of interest, then monitored for outcome	Losses to follow-up over time, expensive, dependent on entry criteria for cohort
Interventional
Dose escalation studies (phase I)	Risk for injury from dose escalation	Comparison is between doses, not vs. placebo. Determines toxicity not efficacy
Controlled nonrandom studies	Allocation to different treatment groups by patient/clinician choice	Selection bias in allocation between treatment groups
Randomized controlled trials	Random allocation of eligible subjects to treatment groups	Expensive. Experimental design can limit generalizability of results
Meta-analysis	Groups randomized trials together to determine average response to treatment	Limited by quality of original studies, difficulty combining different outcome measures. Variability in base study protocols

After Hennekens C, Buring J. Epidemiology in Medicine. Boston: Little, Brown; 1987.

TABLE 11-7 Common Biases in Clinical Research

BIAS NAME	EXPLANATION
Sampling Biases
Prevalence-incidence	Drawing a sample of patients late in a disease process excludes those who have died of the disease early in its course. Prevalent (existing) cases may not reflect the natural history of incident (newly diagnosed) cases
Unmasking	In studies investigating causation, factors that cause symptoms, which in turn cause a more diligent search for the disease of interest. An example might be whether a particular medication caused headaches, which led to the performance of more magnetic resonance imaging studies and resulted in an increase in the diagnosis of arachnoid cysts in patients taking the medication. The conclusion that the medication caused arachnoid cysts would reflect unmasking bias
Diagnostic suspicion	A predisposition to consider an exposure as causative prompts a more thorough search for the presence of the outcome of interest
Referral filter	Patients referred to tertiary care centers are often not reflective of the population as a whole in terms of disease severity and comorbid conditions. Natural history studies are particularly prone to biases of this sort
Chronologic	Patients cared for in previous periods probably underwent different diagnostic studies and treatments. Studies with historical controls are at risk
Nonrespondent/volunteer	Patients who choose to respond or not respond to surveys or follow-up assessments differ in tangible ways. Studies with incomplete follow-up or poor response rates are prone to this bias
Membership bias	Cases or controls drawn from specific self-selected groups often differ from the general population. The result of this bias is the assumption that the group’s defining characteristic is the cause of their performance with respect to a risk factor
Intervention Biases
Co-intervention	Patients in an experimental or control group systematically undergo an additional treatment not intended by the study protocol. If a treatment were significantly more painful than a control procedure, a potential co-intervention would be increased analgesic use postoperatively. A difference in outcome could be due to either the treatment or the co-intervention
Contamination	When patients in the control group receive the experimental treatment, the potential differences between the groups are masked
Therapeutic personality	In unblinded studies, the belief in a particular therapy may influence the way in which the provider and patient interact and alter the outcome
Measurement
Expectation	Prior expectations about the results of an assessment can substitute for actual measurement. In assessments of either diagnosis or therapy, belief in the predictive ability or therapeutic efficacy increases the likelihood that a positive effect will be measured. Unblinded studies and those with a subjective outcome measure are prone to this bias
Recall	In cohort and case-control studies, different assessment techniques or frequencies applied to those with the outcome of interest may increase the likelihood of detection of a risk factor, in particular, asking cases multiple times vs. controls improves chances for recall. This bias applies especially to retrospective studies and is the inverse of the diagnostic-suspicion bias (see earlier)
Unacceptability	Measurements that are uncomfortable, either physically or mentally, may be avoided by study subjects
Unpublished scales	The use of unpublished outcome scales has been shown in certain settings to result in a greater probability of the study finding in favor of experimental treatment⁹¹
Analysis
Post hoc significance	When decisions regarding levels of significance or statistical measures to be used are determined after the results are analyzed, it is more likely that a significant result will be found. It is very unlikely that authors would state this in a manuscript, but protection is afforded by publication of the study methods in advance of the study itself
Data dredging	Asking multiple questions of a dataset until something with statistical significance is found. Subgroup analysis, depending on whether preplanned and coherent with the study aims and hypotheses, may also fall into this category

From Sackett DL. Bias in analytic research. J Chronic Dis. 32:51, 1979.

Descriptive Studies

Case Reports and Case Series

Currently, case reports and case series account for the bulk of the neurosurgical literature. These studies properly have their place in describing new or unusual medical events. In such studies there is an implicit comparison to what is usual or ordinary in clinical practice. They can suggest possible causes and treatments for events but can offer only limited support for clinical practice patterns and do not provide for hypothesis testing. The main advantage of these types of studies is that they are easy and inexpensive to complete. They can also provide data important in designing subsequent, more complex investigations, particularly if standard outcome measures are used in the analysis.

Cross-Sectional Surveys

These studies attempt to determine the presence of disease and potential exposure causing the disease in individuals at a single point in time. Usually based on interview or questionnaire, such studies can generally be accomplished relatively inexpensively and quickly in comparison to the cohort studies that they mimic. The principal limitation is that because the data are collected at a single point in time, they cannot be used to determine the causal relationship between an exposure and the disease of interest. In addition, the single time assessment does not allow understanding of the course of illness.

Descriptive Cohort Studies

Cohort studies as described more fully later can be primarily descriptive rather than analytic. That is, they can seek to describe events occurring in a defined population over time rather than drawing conclusions about causation, as is usually the case with the classically described cohort study. Simple natural history studies that do not attempt to analyze prognostic factors fit into this category.

Analytic Studies

Case-Control Studies

The aforementioned study methods lack control groups, thus making direct comparisons impossible. Almost always performed retrospectively, a case-control study seeks to make up for this deficiency by selecting a control group of patients who can then be compared with the cases of interest. Originally designed to assess causation in rare diseases in which a cohort would have to be prohibitively large to detect enough cases, the relative simplicity and easy retrospective application of this methodology have made for widespread use. Patients with the disease or outcome of interest are identified first. Then, a control population not showing the disease or outcome of interest is determined, and the two groups are assessed for the presence of particular risk factors. The result is typically an odds ratio, which is the odds of the risk factor in the cases versus the controls. Controls must be selected such that if the disease had developed in them, they would have been eligible to be cases. Controls may be selected at random from a sample, but because such studies are usually small in total number, it is generally important to balance or match the cases and controls for important prognostic factors so that these do not obscure associations between the outcome and the factor of interest. From the standpoint of bias, case-control studies are most susceptible in the choice and assignment of control patients and in the way in which the two groups are screened for the presence of risk factors. Controls are often “historical.” Such controls are open to a chronology bias based on changes in practice patterns and the influence of changing technology over time.

The reader will note that a case-control study provides an odds ratio rather than a relative risk. This is because by virtue of the control selection process, a case-control study does not provide information on the actual incidence of a risk factor in a group. A case-control study, because of the nonrandom selection of controls, cannot offer any protection against unknown confounding variables.

Cohort Studies

Cohort studies are primarily used to assess the role of common exposures with modest effects on disease incidence or progression. They can help establish an appropriate temporal relationship between exposure and outcome and can investigate a number of potential risk factors for a disease outcome simultaneously. An important subclass or variant of the cohort study, the natural history study, is discussed more fully later. In the traditional cohort study, investigators assemble a large group of individuals. This group is then assessed for a variety of exposures and monitored, usually by serial assessment over time, to determine the subsequent occurrence of outcome events. Drawing all the members of the cohort from the same setting is one of the ways in which studies of this type try to minimize selection bias. Keys to study design include a constant method of assessment for all members of the cohort regardless of potential exposure and complete follow-up. As opposed to the odds ratios reported in case-control studies, cohort studies report a relative risk because the structure of the study allows a comparative incidence of the outcome to be calculated.

In prospective cohort studies, the outcome events are unknown at the time that the study is started and patients are observed into the future. In retrospective cohort studies, the investigator is looking backward to determine the exposure history for the cohort after the outcome is already known. As always, a prospective study is more robust methodologically because it offers much better protection against assessment biases for the exposure. Retrospective studies are at risk for diagnostic-suspicion bias by investigating those with the outcome of interest more closely than those without, thereby biasing the reported relative risks. Prospective studies however, face a greater problem with losses to follow-up.

Diagnosis and Patient Assessment Studies

Studies looking at the discriminatory power of diagnostic tests or strategies ask the general question, “How well do the results of this diagnostic test predict the presence or absence of the sought-after disease?” Most often such studies take on the general form of a cohort study. The group of patients with the suspected disease is the cohort (e.g., all adult patients undergoing major surgery at a particular institution). The cohort is assessed for the presence of a risk factor (positive duplex scan of the lower extremity for clots) and then monitored for an outcome, which is usually the result of the “gold standard” diagnostic test (presence of deep venous thrombosis on venography).⁹² Like other cohort studies, studies looking at diagnostic accuracy are susceptible to bias when knowledge of the gold standard result can influence interpretation of the diagnostic study under question, or the reverse. This is similar to recall bias or diagnostic-suspicion bias for the more typical prospective and retrospective cohort studies.

Selection of the cohort under study is of particular importance in studies evaluating diagnosis in terms of the generalizability of the results. The cohort should consist of patients similar in all respects to those to whom the investigator wishes to apply the diagnostic test or algorithm at the conclusion of the study. Any referral filter biases and other typical sampling biases seen in cohort studies must be addressed.

The study methodology should allow assessment of observer agreement or variability, as well as the diagnostic properties of sensitivity, specificity, PPV, and NPV, as described in preceding sections.

Natural History Studies

Usually a variant of a cohort design, natural history studies observe a group of patients drawn from a defined population over time to determine the occurrence of particular outcome events such as mortality, rebleeding rates, stroke rates, and others. In essence, the study seeks to determine how accurately the future outcome can be predicted by a group of know predictors. Studies of this sort occupy a critical place in clinical reasoning because they can provide information about the consequences of a decision not to treat. Natural history studies do not replace a randomized comparison between placebo and treatment, but they are often the starting point for therapy decisions in the absence of such studies and frequently provide the framework for subsequent randomized comparisons. The line between a natural history study and a case series with long-term follow-up may seem a fine one, but the key is in determining the degree to which the study patients are representative of the population as a whole and the degree to which the follow-up investigations are evenly applied. The literature regarding the debate on the hemorrhage rate for unruptured aneurysms smaller than 1 cm provides numerous examples of this type of study and highlights the potential bias in studies of this type.⁹³^–⁹⁶ Critical in such studies is the development of an inception cohort. These individuals should have been identified at a clearly defined and similar point in their disease process. For example, if a study attempts to define the risk for hemorrhage after radiosurgery for an arteriovenous malformation and the study population consists of patients 4 or more years after the procedure, an important group, those who suffer hemorrhage before 4 years, will be missed. Because the hemorrhage rate appears different over time after radiosurgery, the study will report a rate that is biased in favor of a lower value. Thus, a set of inclusion and exclusion criteria must be specified for such studies, and it is to similar patients that the study results can be applied. To provide generalizable conclusions, the cohort being observed must be representative of the population of interest. As is true for all cohort studies, all members of the cohort must undergo the same degree of scrutiny for the outcome of interest, and assessors should be blinded to potential associated risk factors for the outcome of interest to prevent a more careful search for the outcome of interest in certain patients.

Large Database Studies: Case Registries and Administrative Databases

Although randomized clinical trials are generally acknowledged to be the strongest source of evidence for comparing treatment efficacy, randomization is sometimes too difficult, too costly, or impossible, and a nonrandomized study is the best option. Even though most such studies are conducted with single-center, retrospective methods, large multicenter patient databases often offer investigators an advantage in cost, convenience, or statistical power. These databases usually fall into one of two general types, case registries and administrative databases, although these types represent ends of a spectrum rather than mutually exclusive categories. The differences between databases constrain their value for different types of investigations, and most database studies are performed by investigators who did not design the data collection process.

Case registries contain data on patients with a specific diagnosis or procedure, often collected by a voluntary group of treating physicians who design and maintain the registry to facilitate observational research in a given clinical subject area. Neurosurgical examples include the Glioma Outcomes Project ⁹⁷ and the Ontario Carotid Endarterectomy Registry.⁹⁸ Some case registries are maintained by government agencies, such as the Veterans Administration National Surgical Quality Improvement Program (NSQIP) registry⁹⁹ or population-based cancer registries ranging from state registries to the nationally representative Surveillance, Epidemiology, and End Results (SEER) database.¹⁰⁰ Drug or device companies sometimes maintain case registries, particularly in the postmarketing phase of development when use is widespread and unregulated, and these registries can be valuable in studying rare instances of harm from therapies. Case registries may or may not achieve complete identification and enrollment of the target patient population and are usually rich in detailed demographic and clinical data. Some large clinical trials can also serve as detailed case registries for secondary research goals besides the primary trial question, especially if additional data can be acquired to address new hypotheses. For example, secondary analyses of chemotherapy trials have shown that extensive resection of pediatric malignant gliomas confers a survival benefit¹⁰¹ and that pediatric subspecialists are more likely to achieve gross total resection of pediatric brain tumors.¹⁰² Many trials intentionally lay the groundwork for subsequent correlative research by mandating tissue collection in tumor banks, imaging study archives, and long-term clinical follow-up.

Administrative databases typically include all patients treated at participating institutions or in geographic areas and contain relatively little clinical detail about individual patients. Data collection in administrative databases is typically mandated by state or federal government and is often closely tied to hospital billing for diagnoses and procedures, so patients’ primary diagnoses and procedures are coded more reliably than secondary procedures or comorbid conditions. An example of an administrative database is the Nationwide Inpatient Sample (NIS) maintained by the U.S. Agency for Healthcare Research and Quality.¹⁰³ This database contains information on about 20% of all inpatient admissions to U.S. nonfederal hospitals, thus providing a very large sample size, and was constructed by using sophisticated sampling methods to allow ready generalization to the U.S. population as a whole. The level of clinical detail is low, disease-specific measures are largely absent, and there is no way to track patient outcomes after hospital discharge. State administrative databases usually include all patient care within the boundaries of the state, and some allow tracking of a single patient across multiple sequential hospital admissions, but most do not. National or regional administrative databases exist for many countries outside the United States; Canada and the Scandinavian countries are frequent sites for research.

Depending on the characteristics of the individual databases, it is sometimes possible to link two disparate data sets—by using personal identifiers for patients who are contained in both—to gain additional depth of analysis. An example is the linked SEER-Medicare database,¹⁰⁴ which offers the ability to identify all incident cases of cancer in defined geographic areas (through SEER data) combined with detailed clinical information on the Medicare population that extends both before and after diagnosis (through billing data).

Using Large Databases

Given the extremely large size and low cost of using many available administrative and case registry databases, the possibility of economically studying treatment effects even for relatively rare procedures has obvious appeal. Unfortunately, there are significant barriers to using most large databases for this purpose, especially administrative databases. First, accurately identifying a defined incident patient cohort may be difficult because diagnoses and procedures are often coded with unfamiliar schemes. For example, the NIS identifies diagnoses and procedures with codes from the International Statistical Classification of Diseases, ninth revision (ICD-9), which do not always correspond to familiar clinical diagnostic categories or Current Procedural Terminology (CPT) codes. Codes are frequently applied ambiguously or incorrectly.¹⁰⁵ Accurate coding of novel treatments is particularly unlikely because there is a considerable lag before the ICD-9 scheme can be modified to reflect changing practice. Even the histologic diagnoses that sometimes underlie diagnostic coding can be unreliable because there is no central pathologic review.¹⁰⁶^,¹⁰⁷ Second, because such studies are nonrandomized, accurate risk adjustment for individuals is necessary to ensure a level playing field for assessing treatment efficacy. However, important risk factors may be undercoded or even absent (e.g., functional status, specific neurological symptoms, time since the onset of symptoms, subarachnoid hemorrhage severity, or tumor size). Case registries are much more likely than administrative databases to contain the data needed for accurate risk adjustment—indeed, case registries are often used to develop risk adjustment methods for clinical use. Third, many initial signs of neurological disease can also represent complications of neurosurgical treatment, and distinguishing between the two is not possible in many administrative databases.¹⁰⁸ Fourth, long-term follow-up of patient status and subsequent treatment is poor in most large databases, and detailed outcome information is not usually available. In contrast, because most clinical trials are powered to show the benefit of a treatment, their ability to identify rare but serious treatment morbidity is usually poor. Large databases offer higher sensitivity for detecting these rare treatment toxicities or patient safety events such as retained foreign bodies after surgery.

Although treatment efficacy is often better studied by using smaller databases specifically designed for that purpose, large multicenter databases are ideally suited for conducting many other specific types of outcome study. For example, studying the practical application of a treatment in real-life situations (as opposed to the highly controlled setting of most clinical trials) offers a chance to examine effectiveness in a more diverse patient population. In “pattern of care” studies, the aim is to measure the application of a treatment (often one already known to be effective, such as radiation therapy after tumor resection) to find evidence of underuse, overuse, or misuse.⁹⁷ In small-area studies, the number of procedures per capita is measured in small, defined geographic areas; a large variation in use of a procedure (as seen for carotid endarterectomy and back surgery) is interpreted as showing lack of consensus on the appropriate application of a treatment.¹⁰⁹ Volume-outcome studies test whether providers with larger annual volumes of care for a diagnosis or procedure provide better outcomes for their patients; accurate risk adjustment is important to remove bias caused by healthier patients obtaining care at specialized centers.¹¹⁰ Closely related studies compare outcomes for generalist providers versus specialists or older versus younger surgeons. When procedures are performed by surgeons from two or more different specialties, such as carotid endarterectomy, outcome differences and sometimes differences in processes of care can be measured.¹¹¹ Disparity studies examine equity of care; treatment outcomes may vary in relation to socially defined patient characteristics such as race, ethnicity, education, or socioeconomic status.¹¹² Differences in access to high-quality care, as reflected by large-volume or other more direct quality measures, are another focus of disparities research. In many of these types of studies, the health care system—rather than the patient—is the one whose “disease” is being diagnosed, and a comprehensive multicenter data source is the only possible starting point for the investigation.

Experimental Studies

Dose Escalation Studies

Phase I drug studies are intended to measure drug toxicity and determine pharmacokinetics, often for chemotherapeutic agents. They can suggest efficacy only in the most limited way. They lack a control group and numerically are usually too small to draw meaningful conclusions about the effects of therapy. Their main purpose is to provide planning information and lend support to the assessment of a particular protocol in a larger study. This study methodology has not typically been applied to surgical interventions (see later).

Randomized Clinical Trials

These studies are true clinical experiments and provide the best evidence for clinical practice. As noted previously, random allocation of study subjects offers the most reliable protection against the various sample biases discussed earlier. The precise design of trials of this kind is a science unto itself, but the basic features of a trial can be summarized as follows.

Hypothesis

All RCTs must begin with a hypothesis. For statistical reasons, this is usually stated as absence of the relationship that the experimenter hopes to show. This null hypothesis is then tested to determine whether the data are sufficiently outside the expectations of this null hypothesis to warrant rejection of it and acceptance of the counter position. Equivalence trials, in which the aim is to demonstrate that two therapies have the same efficacy (see later), adopt a different logic such that the null hypothesis is that the therapies are different. The experiment is then designed to show, given the difference predicted by the hypothesis, that the likelihood of failing to find this difference in the study sample is sufficiently outside expectation to warrant rejection of the hypothesis that a difference as large as proposed actually exists.

Determination of the Population To Be Studied

All studies must specify, by means of inclusion and exclusion criteria, on whom the experiment is to be performed. This defines the study population. The results of a study can safely be applied only to this group of patients. If the study population is defined too narrowly, the results will affect only a small number of patients, but too broad a study population will increase the variability of outcomes seen and make it more difficult to detect the signal amid the noise. In general, a trial should seek to include types of patients thought most likely to benefit from the planned intervention. Exclusion criteria are used to refine the entry criteria, eliminate otherwise eligible patients who cannot undergo any of the experimental therapies planned in the study, or remove individuals with other conditions that predispose them either toward or away from the outcome of interest (see discussion on managing confounding factors earlier).

Because all studies are conducted on a subset or sample of the study population defined by the inclusion and exclusion criteria, sample selection is a critical potential source of bias. Ideally, a random sample of the study population would be considered. However, rarely is it possible to study a random sample of persons with an illness in clinical medicine. Most often, patients in clinical trials will represent a convenience sample of the study population who in particular volunteer to be part of the trial. Because a patient’s participation in trials is not a random event, identifying and reporting the characteristics of patients who were eligible to participate in a trial but did not do so are considered an essential part of trial methodology.

Measurements of Baseline Factors

To demonstrate that the selected sample is indeed representative of the study population, detailed baseline characteristics of the patients in the trial must be provided. These data are also used to demonstrate that randomization has been successful in balancing the known potential confounding variables mentioned earlier.

Allocation

The process of assigning patients to either treatment or control groups is known as allocation. To be effective, allocation must be a truly random process. By this we mean that no other force besides chance can be operating in the assignment process. Pseudorandom processes, such as assignment by medical record number or day of the week, fail this test and introduce bias. To see this, imagine a patient who is otherwise eligible to participate in a study but possesses a risk factor that the study investigator thinks makes the patient an unacceptable candidate for one or other of the study arms. With randomization by day of the week or medical record number, the investigator can determine to which arm of a study a patient would be allocated before actually committing the patient to the study and then selectively exclude that patient.

Maneuver

The maneuvers to be performed in the experimental and control groups must be specified so that they can be repeated by others. The degree to which maneuvers are repeatable has a strong influence on whether and to whom the results of the study can be generalized. Compliance with the specified maneuver by intraoperative or postoperative imaging, an outside observer, or blood chemistry for drug studies is generally important to document. This guards against the bias of contamination, as mentioned previously.

Measuring Outcomes

The choice of outcome measures for studies has already been discussed. In designing the protocol for measurement, the main issue is to avoid or limit the impact of the potential observer biases of those doing the measuring. The two ways that this is generally accomplished are by the use of blinding techniques and by the use of outcome measures that leave as little room as possible for variation in interpretation. The ideal situation is to blind both the patient and the observer to the patient’s treatment allocation, the so-called double-blind study. Measurements made under these circumstances are unlikely to suffer from systematic error. In addition, the more objective or “hard” an outcome measure (such as mortality or stroke rates), the more robust its resistance to the same type of bias.

Analyzing Results

The methods and number of assessments to be used in determining the study results should be determined before data collection begins. This can be ensured by publication of the study methods as the study begins. Ideally, those analyzing the data, at least for the initial report of the study results, should be blinded to which group received experimental versus control treatment (triple blinding: subjects, observers, and analysts). In general, the more specific the questions and the better the overall study design, the simpler the statistical analysis required to assess the role of chance. Repeating the analysis on specific subgroups of patients is a common practice that can yield useful information but can also lead to false conclusions. Subgroup analyses should be planned and reported before the study begins and should make sense with the underlying hypothesis. This is not to say that unusual findings cannot be reported, but the weight or value of conclusion based on post hoc analytic approaches must be limited and the results regarded more as clues for future investigations.

Frequently, not all the study subjects will complete the study protocol in the desired fashion. Some may decide to withdraw from the study or be intolerant of the treatment to which they were allocated. How should a study assess subjects? In general, the principle of “once randomized, always analyzed” applies, and patients should be included in the group in which it was intended for them to be treated, regardless of the actual treatment that they received. This intention-to-treat principle is another safeguard against bias because patients often withdraw or change treatments for reasons specific to that treatment. Thus, eliminating them from analysis of the results reintroduces bias that randomization was supposed to control. This is not an absolute rule, however. Clinical trials can be regarded as studies of either efficacy or effectiveness. Efficacy trials are usually among the early studies of a clinical investigation and ask the question, “Can a therapy work under ideal circumstances?” If a study is assessing efficacy, it may be reasonable to consider only patients who successfully completed the maneuver when the reasons for noncompliance clearly do not relate to the therapy directly. Hypothetically, in an early trial of the efficacy of a drug therapy for subarachnoid hemorrhage, patients who received the wrong medication because of a pharmacy error may reasonably be excluded; however, those who are withdrawn from the study because of hypotension at the time of medication administration clearly should not be. Effectiveness studies ask the question, “Can a therapy work in general practice?” In such studies, all the variables are considered important, and a pure “intention-to-treat” analysis is the standard.

Reporting Results

Publication of results, especially negative results, is of paramount importance. Much has been written about publication biases wherein positive trials are more likely to be submitted and accepted for publication than those with negative results. Standardized reporting of clinical trials is encouraged. The CONSORT (Consolidated Standards in Reporting Trials) statement offers a step-by-step checklist of the necessary components of a clinical trial report.¹¹³

Special Issues in Surgical Randomized Controlled Trials

Randomized trials involving surgical maneuvers face particular methodologic challenges that differ from those in trials of medical therapy. Such challenges include the difficulty in standardizing an operative maneuver. In addition to the patient’s compliance with the prescribed allocation, the surgeon performing the procedure must be “compliant” with the technique being studied, both by desire and by ability. Therefore, surgeon eligibility must be specified in the study protocol. Controversy exists over the timing of a surgical trial relative to introduction of the procedure into clinical practice because of the potential “learning curve” for the procedure. Similarly, great controversy exists over the role of a placebo, or sham, control for surgical maneuvers.¹¹⁴^,¹¹⁵ In most settings it is not possible to blind the patient or the surgeon to the allocation group. To avoid bias in outcome assessment, strategies such as outcome assessment by members other than the surgical team and the inclusion of “hard” outcome measures are used. Further discussion on the evaluation of surgical techniques is included later and may be found in the text by Spilker.¹¹⁶

Meta-analysis

In some descriptions of the “hierarchy of evidence,” there is a level above the large, well-conducted RCT—a meta-analysis of RCTs without significant heterogeneity.¹¹⁷ This means, in essence, that when several well-designed trials are available with generally similar results, those results gain in credibility over a single trial. Although this makes intrinsic sense, there are special problems that arise in collecting and combining data from individual trials that deserve special attention.

A “meta-analysis” is usually understood to be a mathematical combination of collected effect sizes from more than one individual trial. Meta-analysis involves four steps: formulating an answerable question, collecting data, examining its quality, and finally combining it to give a single estimate of treatment effect.

A well-defined clinical question is required as a starting point for the study. Questions that are answerable through meta-analysis are typically those about the effect of a given treatment for which the researcher knows (or suspects) that more than one applicable trial already exists, especially when there is uncertainty about the treatment’s effect because of the existing trials being too small to produce a definitive answer individually or when there is apparent conflict between existing trials’ results. The unit under examination in meta-analysis is the individual research trial itself, so instead of specifying the study patient population and sampling methods, a protocol must describe a specific strategy for identifying all relevant studies in both the published and unpublished literature, as well as inclusion and exclusion criteria to determine which of the identified studies are appropriate to include. An element of subjective judgment enters here; for example, when trials differ in patient population (should pediatric studies be included?) or in treatment details (all calcium channel blockers or just nimodipine?), bias can be minimized by specifying these choices in a written protocol before the search is done.

Data for the meta-analysis are collected from a systematic review of published and unpublished evidence relevant to the chosen clinical question. When the review is complete, the meta-analyst next extracts the data from the primary trials that were located in the search, assesses the quality of the trials resulting from the search, and decides whether to proceed with combining their results. In extracting data from primary trials, a basic choice is whether to rely on published data only or to seek data on individual patients from the trialists who conducted the primary studies (an individual patient data meta-analysis). Individual patient data meta-analyses have much greater power for identifying the influence of patient characteristics (such as age or disease severity) on treatment effects, but they require the cooperation of the original trialists and are very resource intensive.¹¹⁸^,¹¹⁹

Trials differ in quality as well, and meta-analysts make choices here by necessity. The simplest and most common form of quality judgment is to limit the analysis to randomized trials. Incorporating nonrandomized studies into a meta-analysis, especially when there are no randomized studies to act as an internal gold standard, carries all the bias of the original studies into the analysis and can lead to seriously misleading conclusions. This is because the mathematical process of meta-analysis will isolate and magnify any consistent biases in the original studies just as efficiently as it can detect weak treatment effects that are common to the studies—the “garbage in, garbage out” problem. Many standardized instruments are available for assessing the “quality” of both randomized ¹²⁰^,¹²¹ and observational treatment trials¹²² based on various details of the trials’ methods and reporting, but none has been shown to correlate predictably with larger or smaller treatment effect estimates. Nonetheless, researchers often include a comparison between treatment effect estimates derived from high- and low-quality trials as a sensitivity analysis.

The final step in meta-analysis, the statistical process of combining the study results to yield a single unified conclusion, is based on the idea that studies addressing a similar question come from a population of such studies that should produce answers that vary in a predicable fashion around the “true” answer. Almost any measure of treatment effect, such as odds ratios or risk differences, can be combined in a meta-analysis.¹²³^,¹²⁴ Two basic methods used are the fixed-effects method, which assumes that all trials provide individual estimates of the same treatment effect, and random-effects methods, which assume that the true treatment effect might differ slightly between trials (usually a safer and more conservative assumption).¹²⁴ After a summary measure of treatment effect is constructed with appropriate confidence intervals, researchers next derive a measure of the heterogeneity present in the analysis.¹²⁵ This is a measure of the degree to which trials’ results differ from one another in excess of what would be expected from the play of chance. When a large degree of heterogeneity between trials is detected in a meta-analysis, the summary measure of treatment effect may not be applicable to all the patients or treatments, or both, included in the individual trials. However, advanced techniques sometimes demonstrate important differences between trial characteristics that predict the treatment effects seen in the original trials.¹²⁶^,¹²⁷ For example, a treatment’s efficacy might differ in specific patient populations defined by age or disease severity, or one drug or operative technique might work better than another.

Many meta-analyses on neurosurgical topics already exist and can often be found by searching PubMed and using the publication type “meta-analysis” in combination with appropriate subject descriptors. With few exceptions, as more evidence accumulates on a given clinical question, a meta-analysis will need to be revised and updated.

The Systematic Review

Combining evidence from multiple sources is frequently required to assess treatment effects. The traditional literature review, usually written by a recognized expert, is a common means of combining results from many studies to give a broader view of the field. Typical goals of an expert review can include describing recent progress or the present state of the art in a research or clinical area, calling attention to unsolved problems, or proposing new solutions to recognized problems; reviews are an efficient way for readers to gain currency in a broader subject area than single research papers typically address. However, the traditional expert review is a subjective and qualitative process that is subject to citation bias on the part of the individual review author or authors. Most such reviews contain no description of the methods used for identifying primary studies or for weighing their relative merits when conflict between studies is found.¹²⁸^–¹³¹

In contrast to the traditional expert review, a structured review contains a description of the protocol that the authors used for identifying primary studies in the field and attempts complete coverage of a given field or specific clinical question. Systematic reviews have increased in number very rapidly over the past 2 decades. About half of published systematic reviews combine the results of primary studies by using meta-analysis, a mathematical technique described earlier in this chapter.¹³²

Systematic reviews on treatment questions require an extensive literature search, beginning with the use of several medical literature databases (such as PubMed and EMBASE, in addition to specific databases of clinical trials), but also including citation-based searching to identify trials that are referenced in the identified literature or that include identified trials in their own reference lists, hand searching of appropriate journals and abstract sources, identification of relevant “gray literature” such as conference proceedings or abstracts, and consultation with experts in the field to identify additional published or unpublished data.¹³³ The goal is to identify all evidence, both published and unpublished, that has a bearing on the chosen question. The reason that unpublished data are important is because trials that are never published or are delayed in publication (whether as a result of the author’s actions or the peer review process) are especially likely to have negative results (the “file drawer” problem). Reviews limited to published results are thus skewed toward trials with positive results, an effect known as publication bias.¹³⁴^,¹³⁵ One way of avoiding publication bias is to require all clinical trials to be registered with a central authority (such as clinicaltrials.gov) before starting so that unpublished clinical trials can be readily located. Many medical journals require such registration before they will accept a clinical trial report for review. Some systematic reviews end with too little evidence or too poor-quality evidence to combine in a meta-analysis. This is, unfortunately, common in neurosurgery.¹³⁶^,¹³⁷ The Cochrane Collaboration offers online systematic reviews on a broad range of medical topics,¹³⁸^–¹⁴² which are updated regularly by the original analysis team or their successors, and also provides protocols and software to aid in performing new meta-analyses at www.cochrane.org.

Evaluating New Technologies

With multiple techniques of evaluation available and the many new techniques, drugs, devices, and variations being proposed every year, how does one rationally evaluate new therapies proposed for neurological practice?

The process of evaluation and introduction of new drugs into practice is well defined. A four-phase process closely monitored by the Food and Drug Administration (FDA) is followed. Because the FDA must approve the safety and effectiveness of specific indications for pharmaceuticals before they can be marketed for that indication, the pharmaceutical companies that develop these drugs have a strong economic incentive to support the evaluation process. The four phases are pharmacokinetic and pharmacologic evaluation, efficacy and short-term side effect estimation, clinical trials, and postmarketing surveillance.

• Phase I. The drug is first introduced into human use. Pharmacokinetics, dose levels, and short-term toxicity are studied.

• Phase II. The drug is administered to enough patients with a proposed indication to estimate both effectiveness and short-term safety. These estimates form the basis for design of a more definitive clinical trial in the next phase.

• Phase III. A clinical trial is conducted that attempts to provide clear evidence regarding the efficacy of the drug for the proposed indication.

• Phase IV. Once the drug is approved and released for sale, a less rigid system of postmarketing surveillance is in place. Physicians are requested to report any adverse events thought to be related to the medication to the FDA. Postmarketing surveillance has occasionally identified sufficient longer term safety and side-effect concerns to result in withdrawal of FDA approval for the medication.

Evaluation of new surgical procedures is not nearly so tightly regulated, although the intellectual and scientific principles are very similar. Governmental regulation of the process is limited because there is no commercial entity corresponding to the pharmaceutical industry that supports the development of new procedures and profits from their use. When new procedures involve new devices, the FDA has a limited authority to monitor the marketing of such devices. However, many devices are marketed through the 510 (k) exception, which allows the device to be marketed if it is substantially similar to a device in use for the proposed indication before 1976.

Governmental regulation aside, the scientific principles of developing and evaluating a new surgical intervention are very similar to those for drugs.

In phase I, presumably worked out in either animal or cadaver dissections, the procedure is first applied to patients to determine its feasibility and refine the techniques. One would ordinarily expect that a novel procedure would be applied in circumstances in which no standard procedure was available that was thought to have a reasonable chance of successfully treating the patient’s problem. One would expect the responsible surgical investigator to have had the procedure reviewed by peers with appropriate experience relevant to the problem at hand. At the end of this first phase of development and evaluation, one would expect that the procedure had become relatively standardized, that the major difficulties encountered had been solved, that the major risks associated with the procedure were identified, and that the investigator had a relatively clear idea of which patients might benefit from the operation. It would then be time to move into the second phase of evaluation, estimation of efficacy and risk. Perhaps the best rule of thumb that surgeons could apply to determine when the procedure should move from phase I to phase II evaluation is to recognize that when they are ready to begin to apply the new procedure to a specific category of patients on a regular basis, it is time to determine how safe and effective the procedure is.

Phase II evaluation requires application of the procedure to a larger number of patients with relatively uniform disease. Here the investigator should develop a protocol with inclusion and exclusion criteria, predefined measures of outcome and success, and monitoring for specific complications. It is possible to estimate statistically how many patients would need to be included to provide estimates of safety and effectiveness to specified levels of confidence. These results should be evaluated by disinterested parties (neither members of the surgical team nor the patient and family) to avoid the sometimes overwhelming bias introduced by the desire of the surgeon and patient to have a successful outcome in a desperate situation. The end result of such an evaluation may be that the procedure appears to be sufficiently safe and effective to be recommended for wider use or that the results are not as good as expected and further development to improve effectiveness or safety is required. Such further development should be done in a phase I–like setting and followed by another phase II evaluation. When the surgeon, based on phase II experience and confirmed by disinterested observers, is convinced that the procedure has sufficient value and safety that it should be taught to other surgeons so that they can apply it in their practice, it is time for evaluation in a clinical trial.

Phase III evaluation should generally occur within the context of a randomized clinical trial. For all the reasons discussed earlier in this chapter, randomization confers a degree of protection from erroneous conclusion caused by bias that can be achieved in no other way. There are a few unusual exceptions to the need for a randomized clinical trial to validate a new drug or procedure. In the relatively unusual circumstance in which the natural history of the disease is well defined and uniform and there is no existing treatment of substantial benefit, a new procedure shown in phase II evaluation to have a substantial positive impact on the disease unobtainable by other means probably does not require further evaluation. Such an example would be a procedure that cured 50% (or perhaps even 25%) of patients with glioblastoma. The monotonously fatal natural history of this disease is well documented, and current best treatments measure their success in weeks or months of lengthened survival. A procedure that demonstrated 5-year survival in 25% or 50% of patients would not require a randomized clinical evaluation. For most procedures, however, the effects are more modest, the natural history of the disease being treated less clear, and the outcomes often subjective. In these cases, the risks of biased outcome assessment are so high that randomization is a necessary evaluation tool.

When the phase III evaluation stage is reached, the procedures should be well standardized, able to be taught to a large number of investigators, and have clear inclusion and exclusion criteria and well-established objective outcome measures. Under these circumstances, the conduct of such a clinical trial is not difficult, although a good deal of work is required to obtain and analyze the data.

If the phase III evaluation establishes the efficacy and safety of the procedure, it should become part of standard clinical practice. However, evaluation of the procedure should not end at that point in time.

Phase IV evaluation should begin. The transition from a controlled clinical trial to standard clinical practice introduces much larger variation in surgical diagnostic and technical skill, disease severity, patient compliance, and follow-up. Unless great care is taken, surgeons may undertake the operation without sufficient training to carry it out successfully. They may apply it to patients for whom it has not been tested, and they may not evaluate critical outcome parameters to assess the effectiveness of the procedure in their own practice. Therefore, the main goal of the fourth phase of evaluation is to assess the effectiveness of an operation with proven efficacy once it is introduced into practice. This is primarily the realm of outcome science. The rigid controls of the phase III evaluation no longer apply, but the careful principles of scientific observation do. Such careful observations on a large scale could validate or invalidate additional indications for the procedure, assess the effectiveness of surgeon training, and monitor the effects of minor variations in the procedure on outcome. This type of evaluation has not been widely practiced. Because of the lack of strict governmental oversight and a significant funding source for such large-scale studies, they are relatively uncommonly done. There is therefore wide variation in the utilization and outcome of “standard” surgical procedures (Dartmouth Atlas of Health Care, http://www.dartmouthatlas.org/).

Evidence-Based Approach to Practice

“Evidence based” has become a fashionable phrase in modern medical practice. Many practicing neurosurgeons confronted with this term are perplexed. They believe that they have always practiced neurosurgery based on evidence and that existing methods of evaluating neurosurgical practice have led to substantial progress and do not understand what all the fuss is about. The “fuss” centers on emerging new understanding of evidence quality, more refined understanding of the pervasiveness of subtle forms of bias and distorting conclusions about therapeutic efficacy, and information from outcomes science indicating that efficacious procedures may not be effective in community practice.

The following definition of “evidence-based practice” answers many of the criticisms put forth: “a paradigm of neurosurgical practice in which best available evidence is consistently consulted first to establish principles of diagnosis and treatment that are artfully applied in light of the neurosurgeon’s training and experience informed by the patient’s individual circumstances and preferences to regularly produce the best possible health outcomes.”¹⁴³ A brief introduction for neurosurgeons is available.¹⁴⁴ For the practitioner of neurosurgery, there are several skills and understandings necessary to appropriately incorporate a growing body of sound scientific evidence into clinical practice, including critical analysis of single articles in the published literature, systematic review (summarization) of critically analyzed published literature, and practice outcome assessment. The first of these skills is the ability to critically evaluate a clinical article. There are several excellent resources available for self-education in this regard (Table 11-8).^17,^18,^143,¹⁴⁵^–¹⁷² The online version of this text offers a summary of the key questions to ask in reviewing clinical articles.

TABLE 11-8 Resources for Self-Education in Evidence-Based Practice

Haynes RB, Sackett DL, Guyatt GH. Clinical Epidemiology: How To Do Clinical Practice Research, 3rd ed. Philadelphia: Lippincott Williams & Wilkins; 2006

Sackett DL, Straus SE, Richardson WS, et al. Evidenced Based Medicine. How to Practice and Teach EBM. Edinburgh: Churchill Livingstone; 2000

“Users’ Guides to the Medical Literature” published in the Journal of the American Medical Association^17,^18,¹⁴⁵^–¹⁷⁰ and in book form: Rennie D, Guyatt GH, Meade M, et al. Users’ Guides to the Medical Literature: A Manual for Evidence-Based Clinical Practice, 2nd ed. New York: McGraw Hill; 2008¹⁷¹

Haines SJ, Walters BC. Evidence-Based Neurosurgery: An Introduction. New York: Thieme; 2006 ¹⁴³

Pollock BE. Guiding Neurosurgery by Evidence. Basel: Karger; 2006 ¹⁷²

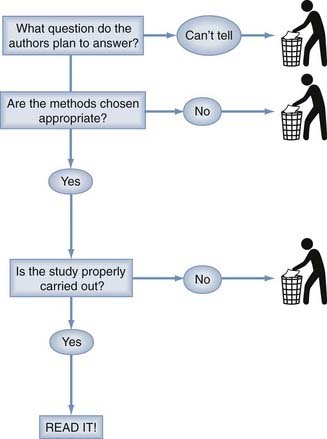
Because critical analysis of an article can be a time-consuming process, it is necessary to have a way of screening all the literature that appears in an ever-increasing volume these days. Our method for screening journal articles is diagrammed in Figure 11-1.The first step is to determine from the abstract or introductory paragraph what question the article proposes to answer. Is this an article on the prognosis of a disease, either untreated (i.e., natural history) or treated? Does it concern the usefulness of a diagnostic test or the value of a treatment modality? Does this article propose to review the existing literature on one of these topics or to assess the economic aspects of a health care intervention? If it is not clear from this preliminary information what questions the authors propose to answer, there is virtually no prospect of obtaining useful information from the article and time is better spent screening the next.