What Is Re-entry?

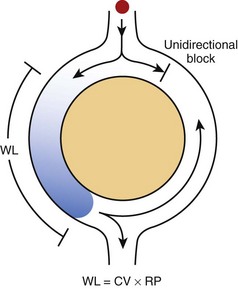
In its simplest form, re-entry is the circulation of the cardiac impulse around an obstacle; this leads to repetitive excitation of the heart at a frequency that depends on the conduction velocity of the circulating impulse and the perimeter of the obstacle (Figure 4-1).² According to the original description by George Mines, which was published in The Journal of Physiology in 1913, re-entry occurs around a fixed anatomic obstacle, and the physical disruption of the surrounding circuit will interrupt the activity. As illustrated in Figure 4-1, the initiation of the re-entrant activity depends on the occurrence of a unidirectional block in which activation takes place in only one direction within the circuit.

Figure 4-1 Circus movement re-entry around a ring of heterogeneous tissue surrounding an anatomic obstacle. re-entry is initiated by the application of a premature stimulus (red dot) to the upper branch. As the impulse enters the ring, it encounters tissue recovered on the left side. However, the tissue on the right has not yet recovered from previous excitation (not shown), and unidirectional block occurs. As a result, the wavefront begins to rotate around the obstacle. If the pathlength is long enough or the conduction velocity is slow enough, sufficient time is available for recovery on the upper right side of the ring, and sustained re-entry will be initiated. Note that in this hypothetical example, wavelength (WL), which is equal to the product of conduction velocity (CV) times refractory period (RP), is much shorter than the path length.

It is clear from Figure 4-1 that the rotation time around the circuit should be longer than the recovery period of all segments of the circuit. The extra time required for the impulse to successfully complete a rotation may result from a relatively large circuit, a relatively slow conduction velocity of the impulse, or the relatively short duration of the refractory period. Hence, the “wavelength,” which may be calculated roughly as the product of the refractory period and the conduction velocity, must be shorter than the perimeter of the circuit. An excitable region will separate the front of the impulse from its own refractory tail (i.e., excitable gap) and re-excitation will ensue.

Re-entry is responsible for various arrhythmias, including supraventricular and ventricular extrasystoles, atrial flutter, atrioventricular (AV) nodal reciprocating tachycardias, supraventricular tachycardias associated with accessory AV pathways, bundle branch ventricular tachycardias, and monomorphic ventricular tachycardias associated with myocardial infarction.

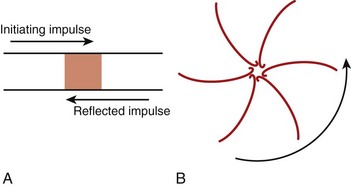
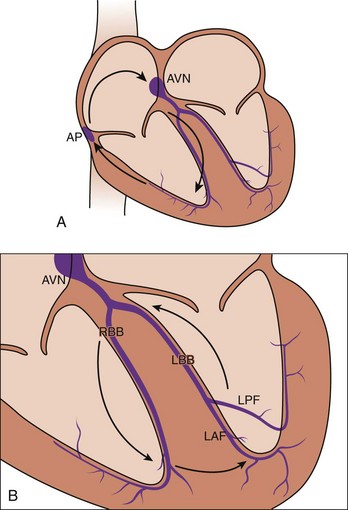
The classic model of anatomically determined re-entry depicted in Figure 4-1 is directly applicable to specific cases of tachyarrhythmias. These include supraventricular tachycardias occurring within the AV node or those using accessory pathways, as well as bundle branch re-entrant tachycardia. However, other types of re-entrant arrhythmias require somewhat different explanations for their mechanisms. For example, the cellular basis of closely coupled ventricular extrasystoles initiated somewhere in the Purkinje fiber network can be explained by the so-called reflection mechanism described by Antzelevitch et al in 1980 (Figure 4-2, A).³ Recently, reflection to and from an accessory pathway was shown to be a potential mechanism for the initiation of atrial fibrillation in patients with manifest (pre-excited) Wolff-Parkinson-White (WPW) syndrome.⁴

Figure 4-2 Two different forms of functional re-entry (i.e., in the absence of an anatomic obstacle). A, Reflection, where re-entry occurs over a single pathway in a linear bundle (e.g., a Purkinje fiber) across an area of depressed excitability (shaded). B, Functional re-entry in two-dimensional myocardium. Curved lines are isochrone lines showing consecutive positions of the wavefront. The curved arrow indicates the direction of rotation.

In the absence of a predetermined obstacle or circuit (Figure 4-2, B), however, many tachyarrhythmias that originate in the myocardium (atrial or ventricular) require mechanisms whereby re-entrant activation may occur as vortices of electrical excitation rotating around an area of myocardium. Accordingly, the impulse must circulate around a region of quiescence. In 1977, Allessie et al⁵ explained such functionally determined re-entry by proposing the so-called leading circle hypothesis, with its two variants of “anisotropic” re-entry described in 1988 by Dillon et al⁶ and “figure-of-8” re-entry proposed by El-Sherif⁷ in 1985. A somewhat different postulate for vortex-like re-entry, the “spiral wave re-entry” hypothesis, was put forth by Davidenko et al⁸ in 1992 and is derived from the theory of wave propagation in excitable media. Spiral wave re-entry attempts to provide a unifying explanation for the mechanisms of monomorphic and polymorphic ventricular tachycardias as well as the mechanism of fibrillation.

Circus Movement Re-entry

Undoubtedly, the concept of circus movement re-entry, in which a cardiac impulse travels around a predetermined circuit or around an anatomic obstacle, may be applied successfully to various clinical situations. Two clear examples of re-entrant arrhythmias based on the circus movement mechanisms are (1) supraventricular tachycardias observed in patients with WPW syndrome and (2) bundle branch re-entrant ventricular tachycardia, which is more commonly seen in patients with idiopathic dilated cardiomyopathy. All conditions required by the original idea of circus movement re-entry may be found in these two types arrhythmias, as follows:

Figure 4-3 A, Atrioventricular re-entry in the presence of an accessory pathway (AP). B, Bundle branch re-entry using the right bundle branch (RBB) and the left anterior fascicle (LAF) as the two major components of the circuit. AVN, Atrioventricular node; LBB, left bundle branch; LPF, left posterior fascicle.

Functionally Determined Re-entry

As Mines noted in 1913, circus movement re-entry results when an electrical impulse propagates around a one-dimensional circuit or ring-like structure. Although the model is entirely applicable to arrhythmias such as those observed in the presence of AV accessory pathways, it may not represent a realistic model for re-entrant arrhythmias occurring in the atria or ventricles. Re-entrant activity may, indeed, occur in the absence of a predetermined circuit—as shown later in 1973 and 1977 by Allessie, Bonke, and Schopman—where the electrical impulse may rotate around a region that is anatomically normal and uniform but functionally discontinuous.

In 1924, Garrey⁹ presented in an article in Physiological Reviews the first description of re-entrant excitation in the absence of anatomic obstacles in experimental studies on circus movement in the turtle heart. Garrey’s observations suggested that point stimulation of the atrium was sufficient to initiate a regular wave of rotation around the stimulus site. Subsequently, in 1946, Wiener and Rosenblueth¹⁰ developed the first mathematical model of circus movement re-entry, which supported waves of rotation around a sufficiently large barrier, but they could not demonstrate re-entry in the absence of an obstacle. This prompted Wiener and Rosenblueth to suggest that perhaps Garrey may have unwittingly produced a transient artificial obstacle near the stimulation site.

The “Leading Circle” Model

In 1973, Allessie, Bonke, and Schopman provided the first direct experimental demonstration that the presence of an anatomic obstacle is not essential for the initiation or maintenance of re-entry. These authors studied the mechanism of tachycardia in small pieces of isolated rabbit left atrium by applying single premature stimuli. Through multiple electrode mapping techniques, they demonstrated, in 1973 and 1977, that the tachycardias were based on rotating waves and suggested that such waves were initiated as a result of unidirectional block of the triggering premature input. Transmembrane potential recordings demonstrated that cells at the center of the vortex were not excited but developed local responses, which led to the development of the “leading-circle” concept of functional re-entry.

According to the leading-circle concept of Allessie and colleagues, in the absence of an anatomic obstacle, the dynamics of re-entry are determined by the smallest possible loop in which the impulse can continue to circulate. Under these conditions, the wavefront must propagate through relatively refractory tissue, in which case no “fully excitable gap” will be present and the wavelength will be very close to the length of the circuit. The leading circle idea paved the way for major advances in the understanding of functional re-entry. It served as a platform for developing a unifying hypothesis (spiral wave re-entry) that explains most of the major properties of functionally determined re-entry, which are commonly observed in normal cardiac muscle in experiments. This includes the phenomenon of re-entry “drift” described by Davidenko et al⁸ in 1992 and Pertsov et al¹¹ in 1993. Re-entry drift results in beat-to-beat changes in the location of the rotation center (see Drifting Vortices and Ventricular Fibrillation).

Anisotropic Re-entry

In 1986, Spach and Dolber¹² implicated microscopic structural complexities of the cardiac muscle in the mechanism of re-entrant activation in both atria and ventricles, particularly in relation to the orientation of myocardial fibers, the manner in which the fibers and fiber bundles are connected to each other, and the effective electrical resistivities that depend on fiber orientation. Because of these structural properties, propagation velocity in the cardiac muscle is three to five times faster in the longitudinal axis of the cells than along the transverse axis. Mapping studies performed by Peters and Wit¹³ in 1998, using multiple extracellular electrodes have shown that, in the setting of myocardial infarction, re-entry may occur in the survival epicardial rim of tissue. Under such conditions, the wave circulates around a functionally determined elongated region of block, the so-called line of conduction block (Figure 4-4, A). Based on the orientation of the line of block, it was thought that anisotropic propagation played a major role both in the initiation as well as in the maintenance of re-entry in ventricular tissue surviving a myocardial infarction (Figure 4-4, B). In addition, propagation velocity is exceedingly slow at the edges of the lines of block, which has also been attributed to anisotropic propagation.

Figure 4-4 Anisotropic re-entry around a line of block. Top panel, Curved lines are isochrones. The distance between lines denotes velocity of propagation. Velocity is faster in the horizontal direction than around the pivot points. Bottom panel, Example of re-entry around a line of block that was recorded in an isolated Langendorff-perfused murine heart with optical mapping. White lines are 1-ms isochrones. Time scale, 0 to 40 ms.

Figure-of-8 Re-entry

Figure-of-8 re-entry, described in 1987 by El-Sherif, Gough, and Restivo, has been recognized as an important pattern of re-entry in the late stages of myocardial infarction. In most cases, two counter-rotating waves coexist at a relatively short distance from each other (Figure 4-5). As described for the case of single re-entrant circuits, each wave of the figure-of-8 re-entry circulates around a thin line or arc of block. The region separating the lines of block is called the common pathway. A detailed description of the common pathway is of great practical importance, since there is evidence that it could be a strategic region for surgical or catheter ablation in this type of re-entry. In fact, unlike other forms of functionally determined re-entry, figure-of-8 re-entry may, indeed, be interrupted by physical disruption of the circuit. Several studies have attempted to describe the characteristics of propagation in the common pathway. However, the properties of the common pathway are still not clearly defined. It effectively behaves like an isthmus limited by two functionally determined barriers. In addition, there are two wavefronts that interact in the common pathway. As a result, propagation may be determined by a combination of factors other than those analyzed in most experimental studies such as anisotropy. The study of propagation across an isthmus and the influence of wavefront curvature may have significant implications in understanding the properties of the common pathway, as discussed in the next section.

Figure 4-5 Figure-of-8 re-entry. Left panel, Figure-of-8 re-entry consisting of two counter-rotating wavefronts, one in the clockwise direction and the other in the counterclockwise direction, around their respective lines of block. The wavefronts coalesce in the lower part of the circuits, and they move at varying velocities across the common pathway. Right panel, Activation map. Figure-of-8 re-entry recorded in optical mapping of an isolated Langendorff-perfused murine heart. White lines, 1-ms isochrones. Temporal scale, 0 to 17 ms.

Spiral Wave Re-entry

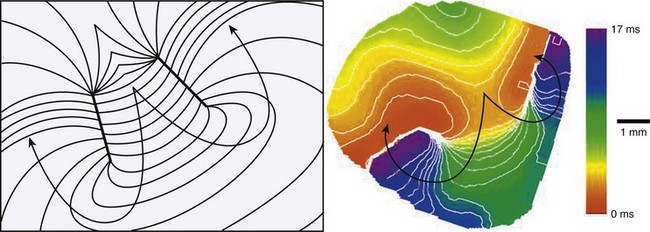
According to traditional concepts proposed by Allessie and colleagues, circus movement re-entry may be initiated in the heart because block is predetermined by the inhomogeneous functional characteristics of the tissue, whereas spiral waves could be formed in the heart even if cardiac muscle was completely homogeneous in its functional properties as shown by Davidenko et al⁸ in 1992, Pertsov et al¹¹ in 1993, and Winfree¹⁴ in 1998. This is because the initiation of rotating activity may depend solely on transient local conditions (e.g., the conditions created by cross-field stimulation).¹ Moreover, according to the traditional concept of re-entry, the circulation of the activity occurs around an anatomically or functionally predetermined circuit, and the rotating activity cannot drift. In other words, the circuit gives rise to and maintains the rotation. However, spiral waves occur due to initial curling of the wavefront; in fact, the curvature of the wavefront determines the size and shape of the region, called the core, around which activity rotates (Figure 4-6). Importantly, the core remains unexcited by the extremely curved activation front and it is readily excitable.¹ This explains the mechanism underlying the drift of spirals.

Figure 4-6 Spiral wave re-entry. Top panel, The activation front has increasing curvature from the periphery to the center. At the tip, the curvature is so extreme that the activation front cannot propagate into the core. Note that the activation front meets its tail of refractoriness (dotted line) at a specific point known as the phase singularity. Bottom panel, left, Phase map snapshot of a rotor recorded in an isolated Langendorff-perfused murine heart. The different colors denote the different phases of the action potential: green = upstroke; red, yellow, and purple = repolarization; and blue = resting (inset, colored action potential). The site where all the colors converge is the phase singularity. Bottom panel, right, Fluorescence amplitude map (blue = low, yellow = high) highlighting the core of the rotor of the left panel. The core is delineated in blue, inside which the signal amplitude is much smaller than that recorded away from the core (compare the two 100-ms single-pixel recordings from the core versus those far away).

Modes of Initiation of Spiral Wave Re-entry

In 1946, Weiner and Rosenblueth¹⁰ published a theoretical description of the mechanisms of initiation of flutter and fibrillation in cardiac muscle in the presence as well as in the absence of anatomic obstacles. They proposed that wave rotation around single or multiple obstacles was required for the initiation and maintenance of both types of arrhythmias, which they assumed to result from a single re-entrant mechanism.

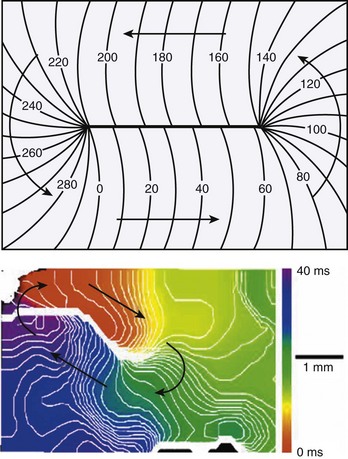
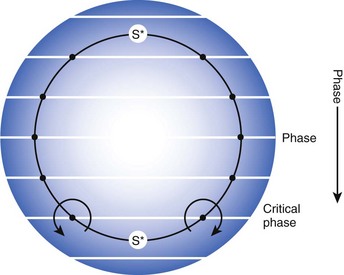
More than three decades later, another theory of initiation of vortices in two dimensions was suggested, and it has been supported by experiments in a number of different excitable media. It is based on Winfree’s “pinwheel experiment” protocol carried out in 1990.¹⁵ As shown in Figure 4-7, this protocol involves crossing a spatial gradient of momentary stimulus with a spatial gradient of phase (i.e., refractoriness, established by prior passage of an activation front through the medium). In accordance with this theory, when a stimulus of the right size (S*) is given at the proper time, mirror image vortices begin to rotate around crossings of critical contours of transverse gradients of phase and stimulus intensity. On the basis of this theory, a vulnerable domain was described. Its timing occurred just before complete recovery from previous excitation. Thus, with its limits of timing and stimulus intensity, the idea of vulnerable domain was similar to the empirical concept of the vulnerable period. In a 1988 study, Shibata et al¹⁶ demonstrated the application of Winfree’s theory to the induction of ventricular fibrillation (VF) in the heart. They concluded that the response to administered shocks during the vulnerable period is a complex one. However, in accordance with theory, during pacing of the ventricles, if a shock of the proper amplitude and delay is applied during the vulnerable period, two counter-rotating vortices can be formed. Thus, as predicted by theory, vortices can be formed even in the normal myocardium. Subsequently, in 1989, Frazier et al¹⁷ used an extracellular recording array with a modification of the pinwheel experiment, the so-called twin-pulse protocol, to demonstrate the mechanism of re-entry and fibrillation in the canine heart. They used the term critical point to refer to a phase singularity and provided strong support for what is referred to as the critical point hypothesis for the initiation of vortex-like re-entry and fibrillation. They also demonstrated that an upper limit of vulnerability for VF exists and that during the vulnerable period, if shock with a strength that is larger than a certain limit is applied, then VF will most likely not be induced.

Figure 4-7 Winfree’s pinwheel experiment. The circular surface represents a two-dimensional sheet of cardiac muscle. The horizontal white lines indicate different phases of the action potential. The white circles represent the critical magnitude (S*) of a stimulus applied at the center of the tissue. The black dots represent different stimuli occurring at the indicated phases. At the crossing of S* with the critical phase, two counter-rotating vortices emerge.

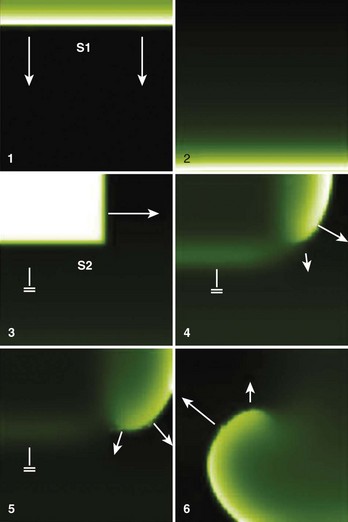
Another approach for initiating vortices is the cross-field stimulation protocol. This method is different from the pinwheel protocol in that it does not require a large stimulus. As shown in Figure 4-8, in cross-field stimulation, a conditioning stimulus (S1) is used to initiate a plane wave propagating in one direction. Subsequently, a second stimulus, S2, is applied perpendicular to S1 and timed in such a way as to allow interaction of the S2 wavefront with the recovering tail of the S1 wave. The S2 wavefront cannot invade the refractory tissue at the site of the interaction with the S1 wave tail; consequently, a wavebreak or phase singularity is formed at the end of the S2 wave, and rotation about this point occurs.

Figure 4-8 Cross-field stimulation protocol used to initiate spiral wave (vortex-like) activity in a square sheet of murine action potential model that was generated by the chapter authors. At time 1, an S1 stimulus is applied to the entire upper border of the sheet. At time 2, the wavefront in white reaches the bottom border followed by its tail of refractoriness (fading green). At time 3, an S2 stimulus is applied when the upper border has not yet fully recovered from previous excitation. Consequently, at time 4, the S2 wavefront cannot propagate downward and blocks (white broken lines) but propagates from left to right (white arrow), developing a pronounced curvature a the tip. At times 5 and 6, the wavefront has curled sufficiently to initiate sustained spiral wave activity.

(From Noujaim SF, Pandit SV, Berenfeld O, et al: Up-regulation of the inward rectifier K+ current (I_K1) in the mouse heart accelerates and stabilizes rotors, J Physiol 578[Pt 1]:315–326, 2007.)

Spontaneous Formation of Rotors

A major contribution of wave propagation theory in excitable media to the understanding of the mechanisms of initiation re-entrant arrhythmias is the concept of wavebreak, which explains how the interaction of a wavefront with an obstacle can lead to wavefront fragmentation and rotor formation.¹⁴ The re-entrant wave can begin as a single vortex, as a pair of counter-rotating vortices, or as two pairs of counter-rotating vortices.

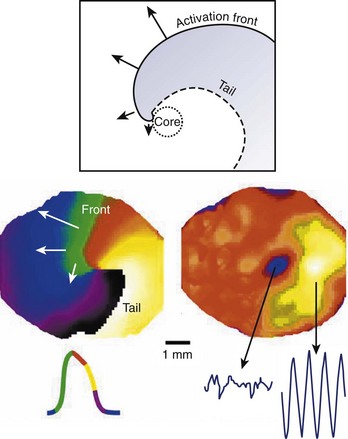
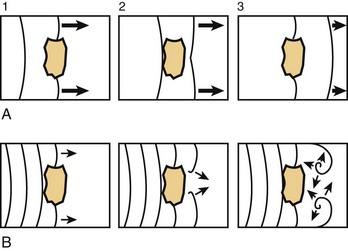
The concept of wavebreak is illustrated schematically in Figure 4-9, which shows the dynamics of the interaction of a wavefront with an anatomic obstacle in a two-dimensional sheet of cardiac tissue with two different excitability conditions. In A, when tissue excitability is normal, after circumnavigating the obstacle, the broken ends of the wave join together, the previous shape of the wavefront is regained, and the wave continues. However, in B, when excitability is low, the broken ends of the wave do not fuse. Instead, the broken ends rotate in the opposite direction. As illustrated by the diagrams in Figure 4-10, during “normal” propagation, which is initiated by a linear source (planar wave, A) or a point source (circular wave, B), the wavefront is always followed by a recovery band or wave tail. Under these conditions, the front and tail never meet, and the distance between them corresponds to the wavelength of the excitation. In contrast, as shown in C, the broken waves demonstrate a unique feature whereby the front and the tail meet at the wavebreak. In this situation, the wavefront curls, and its velocity decreases toward the wavebreak. In fact, at the wavebreak, the curvature is so pronounced that the wavefront fails to activate the tissue ahead. Consequently, the wavebreak effectively serves as a pivoting point, which forces the wavefront to acquire a spiral shape as it rotates around the core.¹

Figure 4-9 Initiation of functional re-entry by the interaction of a wavefront with an anatomic obstacle in a rectangular sheet of cardiac muscle. Two conditions of tissue excitability are represented. A, Under conditions of high excitability, quasi-planar wavefronts initiated at the left border move rapidly toward the obstacle, break, circumnavigate the obstacle, and then fuse again to continue propagating toward the right border. B, When excitability is lower, conduction velocity is slower. After reaching the obstacle, the wavefront breaks. However, in this case, the newly formed wavebreaks detach from the obstacle as they move toward the right border and begin to curl, giving rise to two counter-rotating spirals.

Figure 4-10 Expected conditions of propagation of different types of waves in a homogeneous and isotropic sheet of cardiac muscle (top panels) and in experiments the chapter authors performed in isolated Langendorff-perfused murine hearts (bottom panels, colored phase maps). A, Planar wave initiated by stimulation of the entire bottom border of the sheet or the top left corner of the field of view in the optical mapping experiment. B, Circular wave initiated by point stimulation in the center of the sheet or the center of the field of view in the optical mapping experiment. C, Spiral wave initiated by cross-field stimulation or burst pacing in the experiment. Note that for both planar and circular waves, the wavefront never meets the refractory tail. In contrast, during spiral wave activity, the wavefront and the wave tail meet at the wavebreak (WB), or where all the phases of the action potential converge in the experiment. In the phase maps, the wavefront is in green, and the wave tail is in red, yellow, and purple (inset at bottom, colored action potential).

Multitudes of obstacles, both anatomic and functional, are present in cardiac tissue. However, the excitation of the heart, which is triggered by signals that originate in the sinus node and subsequently propagate throughout the atria and the ventricles, occurs repeatedly in a rhythmic manner. This process occurs without the induction of arrhythmias because the normal sequence of activation through the His-Purkinje system prevents the formation of wavebreaks. Consequently, the presence of obstacles is not a sufficient condition for the establishment of re-entry. Using a voltage-sensitive dye in conjunction with a high-resolution video imaging system, Cabo et al demonstrated that certain critical conditions must be met in order for unexcitable obstacles to destabilize propagation and produce self-sustained vortices that result in uncontrolled high-frequency stimulation of the heart.¹⁸ They demonstrated that the critical condition is the excitability of the tissue such that when the tissue excitability is low, a broken wave will contract and vanish (i.e., conduction will be blocked). However, at an intermediate level of excitability, the broken wave detaches from the barrier and forms a vortex in a manner visually similar to the separation of the main stream from a body in a hydrodynamic system, where there is subsequent eddy formation during turbulence. Moreover, Cabo et al demonstrated that high-frequency stimulation, which decreases excitability, also resulted in the detachment of the broken wave and the generation of vortices in the presence of anatomic obstacles. This phenomenon has been termed vortex shedding. In summary, the dynamics of wavebreaks are determined by (1) the critical curvature of the wavefront (i.e., the curvature at which propagation fails), (2) the excitability of medium, and (3) the frequency of stimulation or wave succession.

Role of Wavebreaks in Ventricular Fibrillation

Under normal conditions of excitability and stimulation, the interaction of the wavefront with an obstacle does not produce a wavebreak. However, when the excitability is lowered, wavebreaks may be initiated and persist after the collision of the front with the appropriate anatomic or functional obstacles. As predicted by theory, the obstacle size must be equal to or greater than the width of the wavefront for perturbation of propagation to occur. At a propagation speed of 50 cm/s, the wavefront width (i.e., the spatial spread of the action potential upstroke) in normal cardiac muscle is approximately 1 mm.¹ Consequently, obstacles of 1 mm or larger have the potential to generate wavebreaks in the propagating waves and producing vortex-like re-entry.

Clearly, numerous conditions can lead to the formation of wavebreaks. However, what is the relationship between wavebreaks and ventricular fibrillation (VF)? The authors hypothesize that the numerous fragmented wavefronts observed during VF form as the result of the interaction of waves emanating from a high-frequency source with the obstacles present in cardiac tissue.¹ Because of their lateral instability, some waves may shrink and undergo decremental conduction, but other waves may continue unchanged until annihilated by other waves. Still others may undergo curling and form new rotors. The final result is the fragmentation of the mother waves away from the source into multiple short-lived daughter waves that produce a complex pattern of propagation during VF.

Mechanisms of Maintenance of Ventricular Fibrillation

Rotors and Ventricular Fibrillation

Rotors are thought to be the major organizing centers of re-entrant arrhythmias, so much investigation has focused on rotors as the underlying mechanism for VF in the heart. However, two schools of thought have emerged. On one hand, many recently proposed mechanisms for fibrillation have focused on the transience and instability of rotors. These mechanisms suggest that the breakup of rotors results in the “turbulent” nature of fibrillation. One such mechanism, the restitution hypothesis, suggests that fractionation of the rotor ensues when the oscillation of the action potential duration is of sufficiently large amplitude to block conduction along the wavefront.^22,25 Another mechanism for breakup focuses on the fact that propagation within the three-dimensional myocardium is highly anisotropic because of the intramural rotation of fibers; this produces the twisting and instability of the organizing center (filament), which results in multiplication following repeated collisions with boundaries in the heart.²⁶

Studies by the authors of this chapter have also focused on rotors as the primary engines of fibrillation. However, here the breakup of the rotor is not regarded as the underlying mechanism of VF. Rather, it is proposed that VF is a problem of self-organization of nonlinear electrical waves with both deterministic and stochastic components.^1,24 This has led to the hypothesis that there is spatial as well as temporal organization during VF in the structurally normal heart, although there is a wide spectrum of behavior during fibrillation. On one end, it has been demonstrated that a single drifting rotor can give rise to a complex pattern of excitation that is reminiscent of VF.²⁷ On the other end, it has been suggested that VF is the result of a high-frequency, stable source and that the complex patterns of activation are the result of the fragmentation of emanating electrical activity from that source (i.e., fibrillatory conduction).^28,29 In the following sections, these two extremes are examined.

Drifting Vortices and Ventricular Fibrillation

Using optical mapping in the structurally normal isolated Langendorff-perfused rabbit heart, Gray et al studied the applicability of spiral wave theory to VF.^24,27 In that study, they demonstrated the presence of a drifting rotor on the epicardial surface of the heart. Simultaneous recording of a volume-conducted ECG and fluorescence imaging showed that a single, rapidly moving rotor was associated with turbulent polymorphic electrical activity, which was indistinguishable from VF. It was assumed that rotors were the two-dimensional epicardial representation of a three-dimensional scroll wave. In addition, computer simulations incorporating a realistic three-dimensional heart geometry and appropriate model parameters demonstrated the ability to form a rapidly drifting rotor similar to that observed in the experiments.^24,27 Frequency analysis of the irregular ECGs for both experiments and simulations showed spectra that were consistent with previously published data. Furthermore, Gray et al confirmed, through the Doppler relationship, that the width of the frequency spectrum can be related to the frequency of the rotation of the rotor, the speed of its motion, and the wave speed.³⁰

Fibrillatory Conduction

Some forms of fibrillation depend on the uninterrupted periodic activity of discrete re-entrant circuits. The faster rotors act as dominant frequency sources that maintain the overall activity. The rapidly succeeding wavefronts emanating from these sources propagate throughout the ventricles and interact with tissue heterogeneities, both functional and anatomic, leading to fragmentation and wavelet formation.¹

Zaitsev et al,²⁸ using spectral analysis of optical epicardial and endocardial signals for sheep ventricular slabs, have provided additional evidence suggesting that fibrillatory conduction may be the underlying mechanism of VF. Zaitsev and colleagues presented data showing that the dominant frequencies of excitation do not change continuously on the ventricular surfaces of slabs. Rather, the frequencies are constant over regions termed domains; moreover, only a small number of discrete domains are found on ventricular surfaces. Zaitsev and colleagues²⁸ also demonstrated that the dominant frequency of excitation in the adjacent domains is often related to the fastest dominant frequency domain in 1 : 2, 3 : 4, or 4 : 5 ratios, and this was suggested to be the result of intermittent, Wenckebach-like conduction block at the boundaries between domains.²⁸ Thus, they concluded that in their model, VF could have resulted from a sustained high-frequency, three-dimensional intramural scroll wave, which created complex patterns of propagation as the result of fragmentation when waves emanating from a high-frequency scroll interacted with tissue heterogeneities.

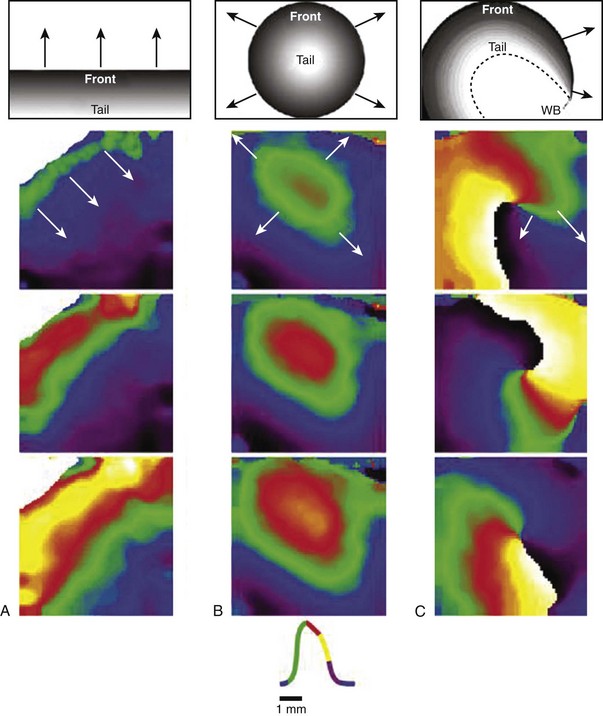
Samie et al²⁹ presented new evidence in the isolated Langendorff-perfused guinea pig heart that strongly supports the hypothesis that fibrillatory conduction from a stable high-frequency re-entrant source is the underlying mechanism of VF. Samie et al²⁹ obtained optical recordings of potentiometric dye fluorescence from the epicardial ventricular surface along with a volume-conducted “global” ECG. Spectral analysis of optical signals (pixel by pixel) was performed, and the dominant frequency (DF, peak with maximal power) from each pixel was used to generate a DF map. Pixel-by-pixel fast Fourier transformation (FFT) analysis revealed that DFs are distributed throughout the ventricles in clearly demarcated domains. The highest frequency domains are always found on the anterior wall of the left ventricle. Correlation of rotation frequency of rotors and the fastest DF domain strongly suggests that rotors are the underlying mechanism of the fastest frequencies. Further analysis of optical recordings has demonstrated that fragmentation of wavefronts emanating from high-frequency rotors occurs near the boundaries of the DF domains. The results demonstrate that in the isolated guinea pig heart, a high-frequency re-entrant source that remains stationary in the left ventricle is the mechanism that sustains VF.

Moreover, experiments and simulations have attributed the stabilization of the high-frequency rotors driving VF in the left ventricle of the guinea pig heart to the presence of a gradient in the inwardly rectifying potassium (K) current (I_K1) whereby I_K1 is larger in the left ventricle compared with that in the right ventricle.²⁹ I_K1 is a K current that (1) contributes to the resting membrane potential, (2) controls the approach of the membrane voltage to the range where sodium (Na) channels activate to give rise to the upstroke, and finally (3) modulates the final phase of repolarization. However, in the experiments of Samie et al, there no direct link was demonstrated at the molecular level between the stability of rotors in the left ventricle of the fibrillating guinea pig heart and I_K1.²⁹ As a result, Noujaim and colleagues³¹ used a murine model of cardiac-specific Kir2.1 upregulation, where I_K1 density was consequently increased by about 12-fold to investigate rotor behavior in such a substrate. It was found that the increased I_K1 serves to stabilize and accelerate rotors responsible for re-entrant VT and VF.³¹ The experiments and numerical simulations suggested that during re-entry, the larger I_K1 accelerates conduction velocity, decreases the core size, and hyperpolarizes the resting membrane potential.³¹ The combination of these factors leads to the generation of very fast and stable rotors. As discussed in earlier sections, wavebreaks and fibrillatory conduction can be characteristics of VF. The authors of this chapter recently examined the role of the slow component of the delayed rectifier K current (I_Ks) in wavebreak formation and fibrillatory conduction.³² In single cells, I_Ks has been shown to contribute to repolarization and postrepolarization refractoriness, where because of its slow kinetics of activation and deactivation, I_Ks accumulates in a deactivated state in response to fast, repetitive stimuli.³² As a result, the pool of deactivated channels will serve to oppose a carefully timed depolarization stimulus, even after the myocyte has fully repolarized and the Na channels have recovered from inactivation; this leads to the failure of action potential generation, hence the notion of postrepolarization refractoriness. Using numerical simulations and monolayers of neonatal rat ventricular myocytes expressing I_Ks via viral transfer of KvLQT1-minK fusion protein (the respective α- and β-subunits of the channel responsible for carrying I_Ks), Munoz et al showed that I_Ks is an important player in the formation of wavebreaks and fibrillatory conduction during excitation patterns that closely resemble those recorded during ventricular fibrillation.³²

Acknowledgment

This work is supported in part by National Heart and Blood Institute, National Institutes of Health, grants P01-HL039707 and P01-HL087226; R01-HL080159 and R01 HL60843; by a Leducq Foundation International Network grant (JJ); and by an AHA postdoctoral fellowship (SFN).