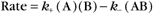CHAPTER 5 Macromolecular Assembly
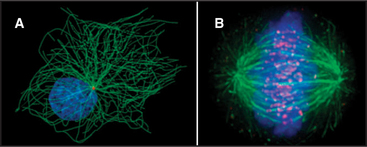
The discovery that dissociated parts of viruses can reassemble in a test tube led to the concept of self-assembly, one of the central principles in biology. In vitro analysis of true self-assembly from purified components of viruses, bacterial flagella, ribosomes, and cytoskeletal filaments has revealed the general properties of these processes. For example, large biological structures, such as the mitotic spindle (Fig. 5-1), are constructed from molecules that assemble by defined pathways without the aid of templates. Even large cellular components, such as chromosomes, nuclear pores, transcription initiation complexes, vesicle fusion machinery, and intercellular junctions, assemble by the same strategy. The properties of the constituents determine the assembly mechanism and architecture of the final structure. Weak but highly specific noncovalent interactions hold together the building blocks, which include proteins, nucleic acids, and lipids.
Assembly of macromolecular structures differs fundamentally from the template-specified, enzymatic mechanisms with which cells replicate genes (see Chapter 42) and translate genes into RNAs and proteins (see Chapters 15 and 17). Macromolecular assembly does not require templates and rarely involves enzymatic formation or dissolution of covalent bonds. When enzymatic processing occurs during the assembly of some viruses (see Example 7 later in the chapter, in the section titled “Regulation by Accessory Proteins”), collagen (see Fig. 29-6), and elastin (see Fig. 29-11), it usually precludes reassembly of the dissociated parts.
Assembly of Macromolecular Structures from Subunits
The use of subunits provides multiple advantages for assembly processes, as was originally pointed out by Crane (Box 5-1). These advantages include the following:
BOX 5-1 Crane’s Hypothesis
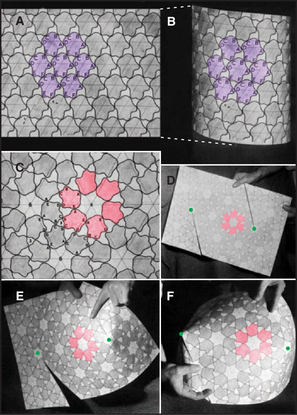
In 1950, the physicist H. R. Crane predicted in Scientific Monthly that all macromolecular structures in biology are assembled from multiple subunits and according to the laws of symmetry. A symmetric structure is composed of numerous identical subunits, all in equivalent environments (i.e., making identical contacts with their neighbors). For example, Figure 5-2A shows a plane hexagonal array, with each subunit making identical contacts with the six surrounding subunits. This is the most efficient way to fill a flat surface with globular subunits.
Crane also predicted that elongated tubular structures are assembled with symmetry. This type of symmetry is known as a helix. One way of constructing a helix is to take a plane hexagonal array, cut it along one of its lattice lines, and roll it up into a tube (Fig. 5-2B). The bonds between adjacent subunits are nearly identical in the plane array and the helical tube, except for the fact that each bond is distorted just enough to roll the sheet into a tube. Introduction of fivefold vertices into a hexagonal array allows it to fold up into a closed polygon (Fig. 5-2D–F).
Assembly of large structures from subunits conserves the genome. The assembly of macromolecular structures from identical subunits, like bricks in a wall, obviates the need to specify separate parts. For example, a plant virus, the tobacco mosaic virus (TMV; see Example 4 in this chapter), consists of 2130 protein subunits of 158 amino acids and a single-stranded RNA molecule of 6390 nucleotides. Having a separate gene for each viral coat protein would require 1,009,620 nucleotides of RNA, which would be about 160-fold longer than the entire viral RNA! The virus conserves its genome by using a single copy of the coat protein gene (474 nucleotides—7.4% of the genome) to make 2130 identical copies of protein that assemble into the virus coat.
Using small subunits improves the chance of synthesizing error-free building blocks. All biological processes are susceptible to error, and protein synthesis by ribosomes is no exception (see Chapter 17). The error rate of translation is about 1 in 3000 amino acid residues. Therefore, the odds that any given amino acid residue is correct are 0.99967. With these odds, the chance that a TMV subunit will be translated correctly is 0.99967158, or 0.949. Thus, about 95% of all TMV coat proteins in an infected cell are perfect, providing an ample supply of subunits with which to construct an infectious virus. Of the 5% of subunits with a mistake, some will be functional and others will not, depending on the nature and position of the amino acid substitution. Some amino acid substitutions pass unnoticed, whereas others result in loss of function. By contrast, the chance of correctly synthesizing the viral coat, if TMV coated its RNA with one huge polypeptide with 336,540 residues, would be only 0.99967336540, or 1.87 × 10−49.
Construction from subunits provides a mechanism for eliminating faulty components. Given that a significant fraction of all proteins have minor errors, good and bad subunits can be segregated on the basis of their ability to form correct bonds with their neighbors at the time of assembly. Many faulty subunits will not bond and thus are simply excluded from the final structure.
Subunits can be recycled. Many macromolecular structures assemble reversibly, and because they are built of subunits, the subunits can be reused later. For example, the subunits of the mitotic spindle microtubules reassemble into the interphase array of microtubules (Fig. 5-1; see also Chapter 44). Subunits in actin (see Example 1) and myosin (see Example 2) filaments are also recycled.
Assembly from subunits provides multiple opportunities for regulation. Simple modifications of subunits can regulate the state of assembly. For example, many intermediate filaments disassemble during mitosis when their subunits are phosphorylated by protein kinases (see Figs. 35-4 and 44-6).
Specificity by Multiple Weak Bonds on Complementary Surfaces
Stable macromolecular assemblies require intermolecular interactions stronger than the forces tending to dissociate the subunits. Subunits diffusing independently in an aqueous milieu have a kinetic energy of about 2.5 kJ mol−1 at 25°C. Interactions in macromolecular assemblies must be strong enough to overcome this thermal energy, which tends to pull them apart. Forces holding subunits together can be estimated from analysis of atomic structures (see Examples 1, 5, and 6) and the effects of solution conditions on the stability of assemblies (see Example 2).
Subunits of macromolecular assemblies are usually held together by the same four weak interactions (see Fig. 4-4) that stabilize folded proteins: the hydrophobic effect, hydrogen bonds, electrostatic interactions, and van der Waals interactions. Although none of these interactions is particularly strong on its own, stable association of macromolecular subunits is achieved by combining the effects of multiple weak interactions. This is possible because the free energy changes contributed by each weak interaction are added together. With a small correction for entropy changes, the overall binding constant for the association of subunits is the product of the equilibrium constants for each weak interaction [KA = (K1)(K2)(K3)(…)(Kn)].
Far from being a liability, multiple weak interactions provide assembly systems with the ability to achieve exquisite specificity that is derived from the “fit” between complementary surfaces of interacting molecules (see Examples 4 and 5). Complementary surfaces are important for three reasons. First, atoms that have the potential to form hydrogen bonds or electrostatic bonds must be placed in a complementary arrangement for the bonds to form. Second, complementary surfaces can exclude water between subunits, as required for the hydrophobic effect. Third and most important, repulsive forces arising from collisions between even a few atoms on imperfectly matching surfaces are strong enough to effectively cancel interactions between two potential bonding partners.
Many assembly reactions take advantage of flexibility in the protein subunits. In viral capsids (see Examples 5 and 6), hinges between the domains of the protein subunits provide the necessary flexibility to allow them to fit into more than one geometrical position. In some assemblies, flexible polypeptide strands knit subunits together (see Examples 1, 5, and 6). In other cases, assembly is coupled to the folding of the subunit proteins (see Examples 3, 4, and 6).
Symmetrical Structures Constructed from Identical Subunits with Equivalent (or Quasi-equivalent) Bonds
Studies of relatively simple systems composed of identical subunits, such as viruses and bacterial flagella, have provided most of what is known about assembly processes. The symmetry of these structures makes them ideal for analysis by X-ray crystallography and electron microscopy, and their biochemical simplicity facilitates analysis of assembly mechanisms. Subunits in asymmetric assemblies, such as transcription factor complexes (see Fig. 15-8), are likely to interact in the same way.
Subunits Arranged in Hexagonal Arrays in Plane Sheets
The simplest way to pack globular subunits in a plane is to form a hexagonal array with each subunit surrounded by six neighbors. This happens if one puts a layer of marbles in the bottom of a box and then tilts the box. A hexagonal array maximizes contacts between the surfaces of adjacent subunits. Membranes are the only flat surfaces in cells, and a number of membrane proteins crowd together in hexagonal arrays on or within the lipid bilayers. Connexons of gap junctions (Fig. 5-3), bacteriorhodopsin of purple membranes (see Fig. 7-7), and porin channels of bacterial membranes (see Fig. 7-7) all form regular hexagonal arrays in the plane of the lipid bilayer. Clathrin coats form hexagonal nets on the surface of membranes (Fig. 5-3).
Helical Filaments Produced by Polymerization of Identical Subunits with Like Bonds
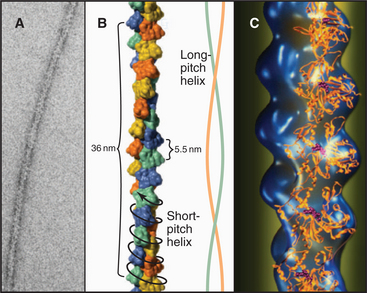
Helical arrays of identical subunits form cytoskeletal filaments (see Examples 1 and 2), bacterial flagella (see Example 3), and some viruses (see Example 4). In helice subunits are positioned like steps of a spiral staircase. Each subunit is located a fixed distance along the axis and rotated by a fixed angle relative to the previous subunit. Helices can have one or more strands. TMV has one strand of subunits (see Example 4), whereas bacterial flagella have 11 strands (see Example 3). Helices can be either solid, like actin filaments (see Example 1), or hollow, like bacterial flagella (see Example 3) and TMV (see Example 4).
The asymmetry of protein subunits gives most helical polymers in biology a polarity (see Examples 1, 3, and 4). Different bonding properties at the two ends of the polymer have important consequences for their assembly and functions. Myosin filaments (see Example 2) have a bipolar helix, a rare form of symmetry. (The DNA double helix [see Fig. 3-3] is geometrically symmetric, with one strand running in each direction, but the order of its nucleotide subunits gives each strand a polarity.)
Spherical Assemblies Formed by Regular Polygons of Subunits
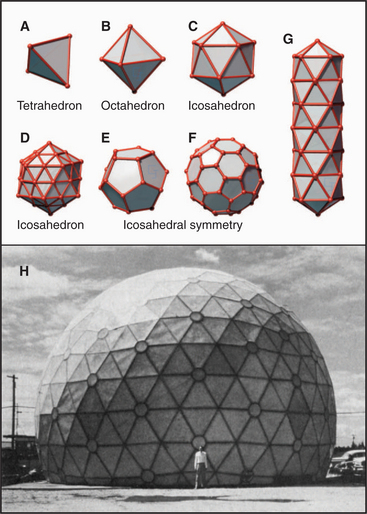
Geometric constraints limit the ways that identical subunits can be arranged on a closed spherical surface with equivalent or nearly equivalent contacts between the subunits. By far, the most favored arrangement is based on a net of equilateral triangles. On a plane surface, these triangles will pack hexagonally with sixfold vertices (Fig. 5-2). Since the time of Plato, it has been appreciated that introducing vertices surrounded by three, four, or five triangles will cause such a network of triangles to pucker and, given an appropriate number of puckers, to close up into a complete shell (Fig. 5-4). Four threefold vertices make a tetrahedron, six fourfold vertices make an octahedron, and 12 fivefold vertices make an icosahedron. Remarkably, no other ways of arranging triangles will complete a shell. In addition to threefold, fourfold, or fivefold vertices that introduce puckers, a closed polygon can contain additional triangular faces and sixfold vertices to expand the volume. The sixfold vertices can be placed symmetrically with respect to the fivefold vertices to produce a spherical shell or asymmetrically to form an elongated structure (Fig. 5-4G).
Most closed macromolecular assemblies in biology are polygons with fivefold vertices (see Examples 5 to 7). (The cubic iron-carrying protein ferritin is an exception.) An important reason for this is that most structures require some sixfold vertices to provide sufficient internal volume. This favors fivefold vertices for the puckers, as they require much less distortion of the subunits located on the triangular faces of the hexagonal plane sheet than do threefold or fourfold vertices. Further, the distortion in the contacts between the triangles is minimized if the fivefold vertices are in equivalent positions. Closed icosahedral shells can be assembled from any type of asymmetrical subunit given two provisions: (1) The subunit must be able to form bonds with like subunits in a triangular network; and (2) these subunits must be able to accommodate the distortion required to form both fivefold and sixfold vertices. Both fibrous (Fig. 5-5B) and globular subunits (see Examples 5 to 7) can fulfill these criteria.
These considerations indicate that subunits in a closed macromolecular assembly must be arranged in rings of five or six. A simple variation has three like protein subunits on each face, but three different protein subunits, or more than three like subunits, can be used on each face to construct icosahedrons. The closest packing is achieved if the protein subunits form pentamers and hexamers, but other arrangements on the 20 faces of an icosahedron are possible (see Example 6).
New Properties from Sequential Assembly Pathways
All self-assembly processes depend on diffusion-driven, random, reversible collisions between the subunits. As is described in Chapter 4, the rate equation for such a second-order bimolecular reaction is
where k+ is the association rate constant; k– is the dissociation rate constant; and (A), (B), and (AB) are the concentrations of the reactants and products. Elongation of actin filaments (see Example 1) illustrates this mechanism.
The rate of dissociation (k–) determines which complexes formed by random collisions are stable enough to participate in an assembly pathway. Specificity is achieved by rapid dissociation of nonspecific complexes. The sequence of random collisions, each followed by separation or bonding, can be viewed as a scanning process that allows each molecule to sample a variety of interactions. At cellular concentrations (see Fig. 3-3), intermolecular collisions between macromolecules are extremely frequent but usually involve irrelevant molecules or molecules that could assemble but that collide in the wrong orientation. Given these frequent random collisions, it is extremely important that proteins not be intrinsically “sticky.” Dissociation of unrelated molecules that have collided by chance is just as important as is the formation of specific associations. Because interactions of individual atoms on the surfaces of proteins are relatively weak, random collisions are very brief unless two complementary surfaces collide in an orientation that is close enough to allow a large number of simultaneous weak interactions or to allow flexible strands to intertwine two subunits. Molecules with poorly aligned or uncomplementary surfaces rapidly dissociate by diffusing away from each other. This is how specific associations are achieved by random collisions.
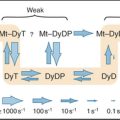
The stability of macromolecular complexes varies considerably owing to two factors. First, collision complexes have a wide spectrum of dissociation rate constants ranging from greater than 1000 s−1 for very unstable complexes to less than 0.00001 s−1 for very stable complexes. (The former complexes have a half-life of 0.7ms, whereas the half-life of the latter is 16h. See Box 4-2 for an explanation of half-times.) Second, conformational changes often follow formation of a collision complex between subunits. These reactions are difficult to observe, but assembly of bacterial flagella provides one clear example (see Example 3). Because the equilibrium constants for all of the coupled reactions are multiplied, such conformational changes can provide the major change in free energy holding a structure together (see Fig. 4-4). The weakly associated conformation characteristic of a free subunit can be thought of as an unsociable state, whereas the strongly associated conformation found in a completed structure is considered an associable state.
Although all assembly reactions occur by chance encounters, large structures usually assemble by specific pathways in which new properties emerge at most steps. A new binding site for the next subunit may emerge from a conformational change in a newly incorporated subunit or by juxtaposition of two parts of a binding site on adjacent subunits. Such emergent properties favor addition of subunits in an orderly fashion until the process is completed. The assembly of myosin (see Example 2), tomato bushy stunt virus (see Example 5), and bacteriophage T4 (see Example 7) illustrates control of assembly by emergent properties.
Initiation of assembly is frequently much less favorable than its propagation. Free subunits associating randomly cannot participate in all the stabilizing interactions enjoyed by a subunit joining a preexisting structure. Consequently, assembly of the first few subunits to form a “nucleus” for further growth may be thousands of times less favorable than the steps that follow during the growth of the assembly (see Example 1). The chance of dissociation from the assembly is reduced once subunits can engage in the full complement of bonds made possible by conformational changes that stabilize the structure. Cells often solve the nucleation problem by constructing specialized structures to nucleate the formation of macromolecular assemblies (see Examples 3 and 6; also see Figs. 33-12, 33-13, and 34-16). Nucleation is not always the slowest step; in the case of myosin minifilaments, the initial step is the fastest (see Example 2).
Regulation at Multiple Steps on Sequential Assembly Pathways
Many assembly reactions proceed spontaneously in vitro, but all seem to be tightly regulated in vivo. For example, at the time of mitosis, cells disassemble their entire microtubule network and reassemble the mitotic spindle with the same subunits (Fig. 5-1). The following are some examples of the mechanisms that cells use to control assembly processes.
Regulation by Subunit Biosynthesis and Degradation
Cells regulate the supply of building blocks for assembly reactions. For example, a feedback mechanism controls the concentration of tubulin subunits available to form microtubules. The concentration of unpolymerized tubulin regulates the stability of tubulin mRNA. Experimental release of tubulin subunits in the cytoplasm results in degradation of tubulin mRNA and a decline in the rate of tubulin synthesis. On the other hand, red blood cells regulate the assembly of their membrane skeleton (see Fig. 7-7) by synthesizing a limiting amount of one subunit of the spectrin heterodimer. Following assembly of the membrane skeleton, proteolysis destroys the excess of the other subunit.
Regulation of Nucleation
Regulation of a rate-limiting nucleation step is particularly striking in the case of microtubules. Microtubule nucleation from subunits is so unfavorable that it rarely, if ever, occurs in a cell. Instead, all the microtubules grow from a discrete microtubule organizing center (Fig. 5-1). In animal cells, the principal microtubule organizing center is the centrosome, a cloud of amorphous material surrounding the centrioles (see Fig. 34-16). Varying the number, position, and activity of microtubule organizing centers helps cells to produce completely different microtubule arrays during interphase and mitosis.
Regulation by Changes in Environmental Conditions
Weak bonds between subunits allow cells to regulate assembly processes with relatively mild changes in conditions, such as in pH or ion concentrations. For example, when TMV infects a plant cell, the low concentration of Ca2+ in cytoplasm promotes disassembly of the virus because Ca2+ links the protein subunits together (see Example 4). Uncoating the RNA genome begins a new cycle of replication.
Regulation by Covalent Modification of Subunits
Phosphorylation of specific serine, threonine, or tyrosine residues (see Fig. 25-1) can regulate interactions of protein subunits in macromolecular assemblies. This is an excellent strategy because cell cycle and extracellular signals can control the activities of the kinases that add phosphate and the enzymes, called protein phosphatases, that reverse the modification. Given the uniform bonding between subunits of symmetrical macromolecular structures, phosphorylation of the same amino acid residue on each subunit can cause the whole structure to disassemble.
Reversible phosphorylation regulates the assembly of the nuclear lamina, the filamentous network that supports the nuclear envelope (see Fig. 14-8). At the onset of mitosis, a protein kinase adds several phosphate groups to the lamina subunits (see Fig. 44-6). The network of filaments falls apart when negatively charged phosphate groups overcome the weak interactions between the protein subunits. Removing these phosphates at the end of mitosis is one step in the reassembly of the nucleus. Similarly, phosphorylation of centrosomal proteins may be responsible for changes in their microtubule nucleation properties during mitosis (Fig. 5-1).
Several other chemical modifications regulate assembly reactions. Proteolysis is a drastic and irreversible modification used in the assembly of the bacteriophage T4 head (see Example 7) and collagen (see Fig. 29-4). Collagen is an extreme example, since its assembly also requires hydroxylation of prolines and lysines, glycosylation, disulfide bond formation, oxidation of lysines, and chemical cross-linking. Subunits in other assemblies are modified by methylation, acetylation, glycosylation, fatty acylation, tyrosination, polyglutamylation, or link-age to ubiquitin (or related proteins).
Regulation by Accessory Proteins
Self-assembly processes were originally thought to require only the components found in the final structure, but many assembly reactions either require or are facilitated by auxiliary factors. The molecular chaperones that promote protein folding (see Fig. 17-13) also promote assembly reactions. In fact, bacterial mutations that compromised assembly of bacteriophages led to the discovery of the original chaperonin-60, GroEL (see Fig. 17-16). This class of chaperones also facilitates assembly of oligomeric proteins, such as the chloroplast enzyme RUBISCO. These effects of chaperones may simply be due to their role in preventing aggregation during the folding of subunit proteins prior to their assembly. They may also participate directly in macromolecular assembly reactions, but this has not been proven.
Bacteriophage assembly also requires accessory proteins coded by the virus. T4 uses accessory proteins to assemble its head. Often, proteolysis destroys these accessory proteins prior to insertion of the viral DNA (see Example 7). Bacteriophage P22 uses an accessory “scaffolding protein” to guide assembly of its icosahedral capsid protein. The building blocks are apparently heterodimers or small oligomers of the two proteins. Scaffolding protein forms an internal shell inside the capsid. Before the DNA is inserted, the scaffolding proteins exit intact from the head (by an unknown mechanism) and recycle to promote the assembly of another virus.
Accessory molecules can specify the size of assemblies. The length of the RNA genome precisely regulates the size of TMV (see Example 4). A giant a-helical polypeptide called nebulin runs from end to end of skeletal muscle actin filaments, determining their length (see Chapter 39). By contrast, a kinetic mechanism determines the length of skeletal muscle myosin filaments (see Example 2).
Numerous proteins regulate assembly of the cytoskeleton, and some are incorporated into the polymer network. Taking actin as an example, different classes of proteins regulate nucleotide exchange, determine the concentration of monomers available for assembly, nucleate and cap the ends of filaments, sever filaments, and cross-link filaments into bundles or random networks (see Fig. 33-10). Similar regulatory proteins likely are involved in other macromolecular assemblies, such as microtubules, intermediate filaments, myosin filaments, and coated vesicles.
EXAMPLE 1 Actin Filaments: Rate-Limiting Nucleation and the Concept of Critical Concentration
Actin filaments consist of two strands of subunits wound helically around one another (Fig. 5-5). (The structure can also be described as a single short-pitch helix with all of the subunits repeating every 5.5nm.) Each subunit contacts two subunits laterally and two other subunits longitudinally. Hydrogen bonds, electrostatic bonds, and hydrophobic interactions stabilize contacts between subunits. Subunits all point in the same direction, so the polymer is polar. The appearance of actin filaments with bound myosin (see Fig. 33-8) originally revealed the polarity now seen directly at atomic resolution. The decorated filament looks like a line of arrowheads with a point at one end and a barb at the other.
Actin binds adenosine diphosphate (ADP) or adenosine triphosphate (ATP) in a deep cleft. Irreversible hydrolysis of bound ATP during polymerization complicates the assembly process in a number of important ways (see Fig. 33-8). Here, assembly of ADP-actin, a relatively simple, reversible reaction, illustrates the concepts of nucleation and critical concentration.
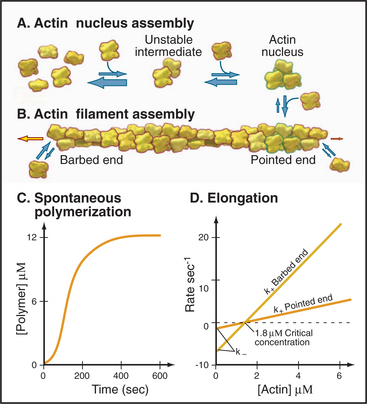
Initiation of polymerization by pure actin monomers, also called nucleation, is so unfavorable that polymer accumulates only after a lag (Fig. 5-6C). This time is required to nucleate enough filaments to yield a detectable rate of polymerization. Initiation of each new filament is slow because small actin oligomers are exceedingly unstable. Actin dimers dissociate on a microsecond time scale, so their concentration is low, making addition of a third subunit rare. Actin trimers are the nucleus for filament growth (Fig. 5-6A) because they are more stable than dimers and can add further monomers rapidly. A trimer is a reasonable nucleus, since it is the smallest oligomer with a complete set of intermolecular bonds. Unfavorable nucleation reduces the chance that new filaments form spontaneously. This enables the cell to control this reaction with specific nucleating proteins (see Figs. 33-12 and 33-13).
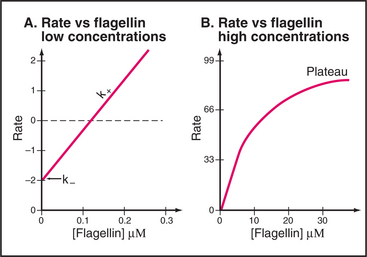
Elongation of actin filaments is a bimolecular reaction between monomers and a single site on each end of the filament (Fig. 5-6B–D). The growth rate of each filament is directly proportional to the concentration of subunits. (In a bulk sample, the rate of change in polymer concentration by elongation is proportional to both the concentrations of filament ends and subunits.) If the rate of assembly is graphed as a function of the concentration of actin monomer, the slope is the association rate constant, k+. The y-intercept is the dissociation rate constant, k–. The elongation rate is zero where the plot crosses the x-axis. This monomer concentration is called the critical concentration. Above this concentration, polymers grow longer. Below this concentration, polymers shrink. Polymers grow until the monomer concentration falls to the critical concentration. At the critical concentration, subunits bind and dissociate at the same rate. The rates of association and dissociation are somewhat different at the two ends of the polar filament. The rapidly growing end is called the barbed end, and the slowly growing end is called the point-ed end.
EXAMPLE 2 Myosin Filaments: New Properties Emerge as the Filaments Grow
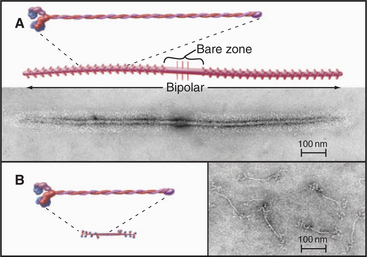
Myosin-II forms bipolar filaments held together by interactions of the a-helical, coiled-coil tails of the molecules (Fig. 5-7). Antiparallel overlap of tails forms a central bare zone flanked by filaments with protruding heads. On either side of the bare zone, parallel interactions extend the filament. The simplest myosin-II minifilaments from nonmuscle cells consist of just eight molecules (Fig. 5-7B). Muscle myosin filaments are much larger but are built on the same plan (Fig. 5-7A). Molecules are staggered at 14.3-nm intervals in these filaments. This arrangement maximizes the ionic bonds between zones of positive and negative charge that alternate along the tail. Hydrophobic interactions are also important; 170 water molecules dissociate from every molecule incorporated into a muscle myosin filament.
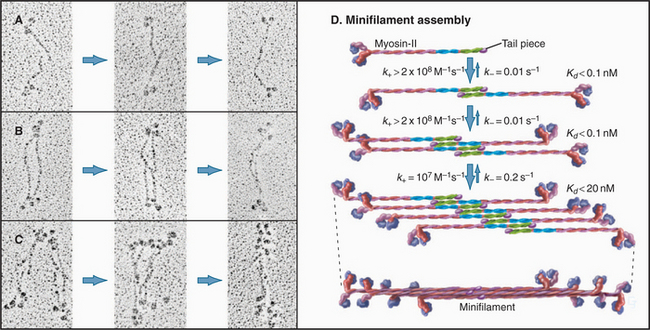
Myosin-II minifilaments form in milliseconds by three successive dimerization reactions (Fig. 5-8). Under experimental conditions in which filaments are partially assembled, antiparallel dimer and antiparallel tetramer intermediates can be detected. Computer modeling of the time course of assembly provides limits on the rate constants for each transition. The association rate constants for formation of dimers and tetramers are larger than those predicted by diffusional collisions. Perhaps the long tails of the subunits form a variety of weakly bound complexes that rearrange rapidly to form stable intermediates without dissociating.
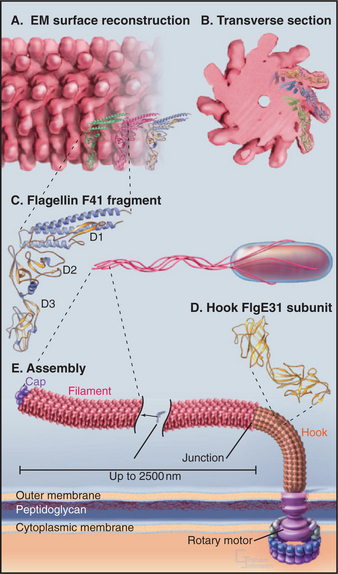
EXAMPLE 3 Bacterial Flagella: Assembly with a Rate-Limiting Folding Reaction
Bacterial flagella are helical polymers of a protein called flagellin (Fig. 5-9). Eleven strands of subunits surround a narrow central channel.
Nucleation of a flagellar filament is even less favorable than for an actin filament, so assembly from purified flagellin depends absolutely on the presence of preexisting flagellar ends. Bacteria use structures called the base plate and hook assembly to initiate flagellar growth and to anchor the flagellum to the rotary motor that turns it (see Fig. 38-24).
Amazingly, flagella grow only at the end located farthest from the cell. Flagellin subunits synthesized in the cytoplasm diffuse through the narrow central channel of the flagellum (Fig. 5-9) out to the distal tip, where a cap consisting of an accessory protein prevents their escape before assembly.
Elongation of a filament by addition of purified flagellin is expected to be a bimolecular reaction dependent on the concentrations of flagellin monomers and polymer ends. This behavior is observed at low concentrations of flagellin, where the rate of elongation is proportional to the concentrations of flagellin and nuclei (Fig. 5-10A). Unexpectedly, the rate of elongation plateaus at a maximum of about three monomers per second at high subunit concentrations (Fig. 5-10B). This rate-limiting step is thought to be a relatively slow conformational change that is required before the next subunit can bind. The parts of the flagellin monomer that form the core of the polymer are disordered in solution, so the slow step may involve folding of these disordered peptides into a-helices that interact to form the two concentric cylinders inside the flagellum. Slow folding converts an unsociable monomer into an associable subunit of the flagella and allows further growth.
EXAMPLE 4 Tobacco Mosaic Virus: A Helical Polymer Assembled with a Molecular Ruler of RNA
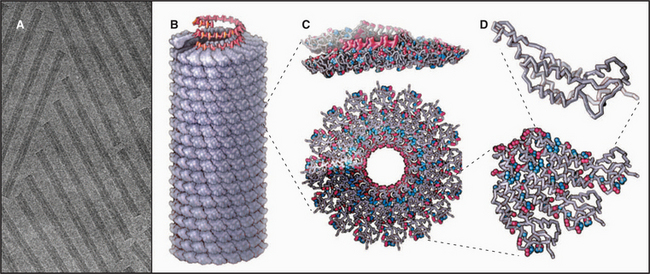
Tobacco mosaic virus (TMV) was the first biological structure recognized to be a helical array of identical subunits, and it was the first helical protein structure to be determined at atomic resolution (Fig. 5-11). The virus is a cylindrical copolymer of one RNA molecule (the viral genome) and 2130 protein subunits. The protein subunits are constructed from a bundle of four a-helices, shaped somewhat like a bowling pin. These subunits pack tightly in the virus and are held together by hydrophobic interactions, hydrogen bonds, and salt bridges. The RNA follows the protein helix in a spiral from one end of the virus to the other, nestling in a groove in the protein subunits. This groove is lined with arginine residues to neutralize the negative charges along the RNA backbone (Fig. 5-11C-D). Each protein subunit also makes hydrophobic and electrostatic interactions with three of the RNA bases.
Production of infectious TMV from RNA and protein subunits was the first self-assembly reaction reproduced from purified components. At the time, during the 1950s, newspapers proclaimed, “Scientists create life in a test tube!”
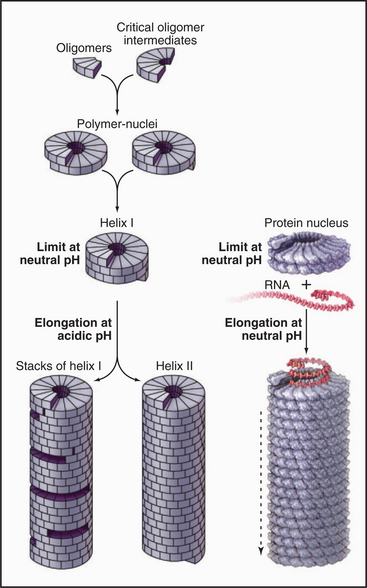
RNA regulates assembly of the protein subunits in two ways. First, RNA allows the protein to polymerize at a physiological pH. Protein alone forms helical polymers of varying lengths at nonphysiological acidic pH; but at neutral pH, it forms only unstable oligomers of 30 to 40 protein subunits, slightly more than two turns of the helix (Fig. 5-12). Monomers and small oligomers of coat protein exchange rapidly with these oligomers, but disorder in the polypeptide loops lining the central channel limits growth beyond 40 subunits. RNA promotes folding of these disordered loops, acting as a switch to drive propagation of the helix by the incorporation of additional protein subunits. Second, RNA is the molecular ruler that determines the precise length of the assembled virus. Only after interacting with RNA at the growing end of the polymer can subunits fold into a structure compatible with a stable virus.
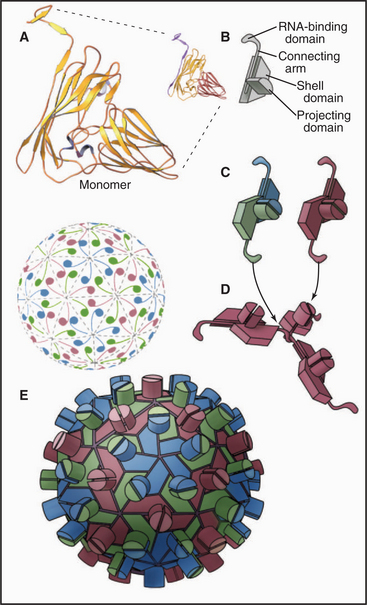
EXAMPLE 5 Tomato Bushy Stunt Virus: Flexibility within Protein Subunits Accommodates Quasi-equivalent Bonding
The first atomic structure of a virus (tomato bushy stunt virus, TBSV) revealed that the flexibility required to form both fivefold and sixfold icosahedral vertices lies within the protein subunit rather than in the bonds between subunits. The 180 identical subunits associate in pairs in two different ways, distinguished in Figure 5-13 by the green-blue and red colors. The blue subunit of the green-blue pairs is used exclusively for fivefold vertices. Three red subunits and three green subunits form six-fold vertices. External contacts of both green-blue and red pairs with their neighbors are similar, but the contacts between pairs of red subunits differ from pairs of green-blue subunits. The difference is achieved by changing the position of the amino-terminal portion of the coat protein polypeptide chain. Two subunits in green-blue pairs pack tightly against each other, providing the sharp curvature required at fivefold vertices. In red dimers, the amino-terminal peptide acts as a wedge to pry the inner domains of the subunits apart and flatten the surface, as is appropriate for sixfold vertices. Thus, the flexible arm acts like a switch to determine the local curvature. This subunit flexibility accommodates the 12-degree difference in packing at fivefold and sixfold vertices. Other spherical viruses use a similar strategy to achieve quasi-equivalent packing of identical subunits.
Icosahedral plant viruses like TBSV assemble from pure protein and RNA. An attractive hypothesis is that local information built into the growing shell specifies the pathway, as follows. Building blocks are dimers of coat protein. To initiate assembly, three dimers in the red conformation bind a specific viral RNA sequence, forming a structure similar to a sixfold vertex. Folding of the arms in this nucleus forces the next three dimers to take the green-blue conformation, since no intermolecular binding sites are available for their arms. The greater curvature of the green-blue dimers dictates that fivefold vertices form at regular positions around the nucleating sixfold vertex. Additional fivefold vertices form appropriately as positions for this more favored association become available around the growing shell. The beauty of this idea is that local information (the availability of intermolecular binding sites for strands) automatically favors the insertion of green-blue or red dimers, as appropriate, to complete the icosahedral shell.
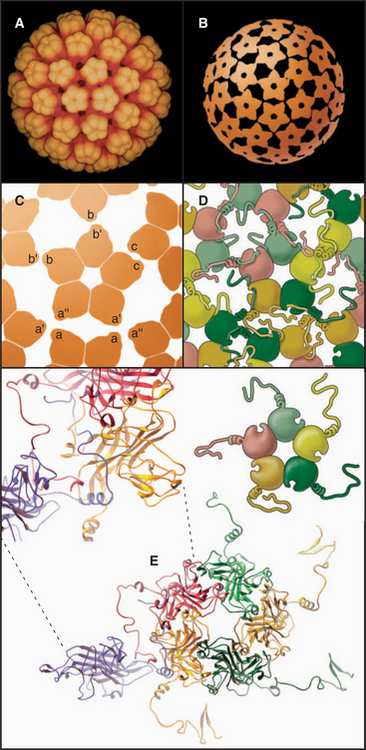
EXAMPLE 6 Simian Virus 40: Quasi-equivalent Bonding of Protein Subunits with a Flexible Adapter
Flexible polypeptide strands, even more extensive than those of plant viruses, lace together the icosahedral capsid of DNA tumor viruses of animal cells, such as polyomavirus (Fig. 5-14A) and simian virus 40 (SV40) (Fig. 5-14B-E). The geometry is more complicated than that of TBSV, since all 360 subunits are clustered in groups of five, called pentamers. Bonds between subunits within these pentamers are all identical. Icosahedral geometry is achieved by surrounding 12 pentamers with 5 other pentamers, and surrounding the remaining 60 pentamers with 6 pentamers.
EXAMPLE 7 Bacteriophage T4: Three Irreversible Assembly Pathways Form a Metastable Structure
Bacteriophage T4 is a virus of the bacterium Escherichia coli (Fig. 5-15). Genetic analysis established that more than 49 distinct gene products contri-bute to assembly of this virus. Three separate, multicomponent substructures—heads, tails, and tail fibers—assemble along independent pathways and combine to form the virus (Fig. 5-16). Emergence of new properties automatically orders the steps along each pathway, so assembly occurs sequentially even in the presence of reactive pools of all of the subunits. A good product is ensured because defective subassemblies fail to attach and are rejected.
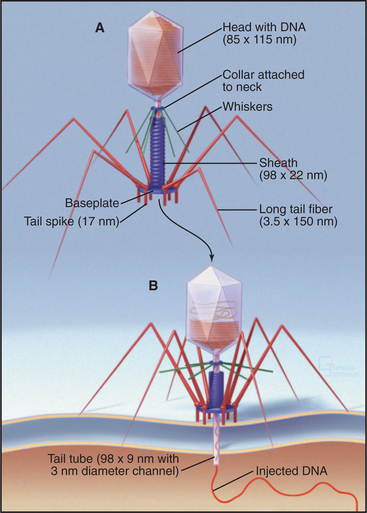
(Reference: Leiman PG, Chipman PR, Kostyuchenko VA, et al: Three-dimensional rearrangement of proteins in the tail of bacteriophage T4 on infection of its host. Cell 118:419–429, 2004. Also see the movie on the journal web site: http://download.cell.com/supplementarydata/cell/118/4/419/DC1/leiman-et-al.movie-2.)
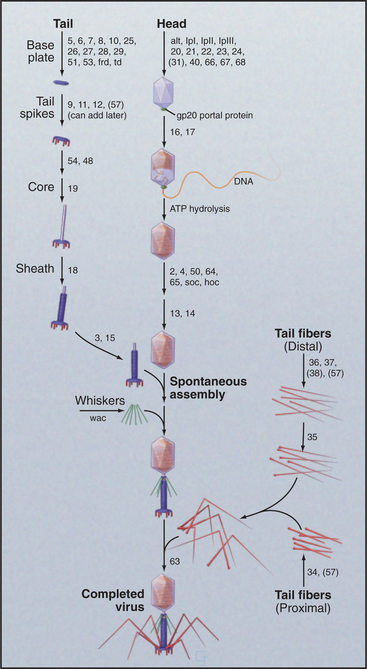
Figure 5-16 assembly pathway of bacteriophage t4. The numbers refer to genes required at each step.
(Redrawn from Wood WB, Edgar RS, King J, et al: Bacteriophage assembly. Fed Proc 27:1160–1166, 1968.)
A protein complex nucleates the growth of a preliminary version of the icosahedral head and later attaches one vertex of the head to the tail. A complex of the major head protein with several accessory proteins adds to the growing head. The accessory proteins end up inside the precursor head. After proteolysis cleaves 20% of the peptide from the N-terminus of the major head protein and degrades the accessory proteins, a major conformational change shifts part of the head protein from inside to outside and expands the volume of the head by 16%. Then, an ATP-driven rotary motor inserts the 166,000-base-pair DNA molecule into the head through a hole in a vertex. This motor, one of the strongest in nature, can produce a force of 70pN, enough to compress the DNA inside the head to a pressure of 60 atmospheres. Within the head, the pressurized DNA is restrained in a near-crystalline, metastable state until it is released during infection of the E. coli host.
When tail fibers contact a susceptible bacterium, dramatic structural changes in the sheath force the tail core through both bacterial membranes in a syringe-like fashion (Fig. 5-15B). The base plate changes from a hexagon into a six-pointed star that cuts loose the central plug with its attached tail core. The weakness of the contacts between sheath and core allows the sheath to “recrystallize” into its preferred short, fat, helical form. Because the sheath is firmly attached at both the base plate and the top of the tail core, this spring-like contraction drives the core through the base plate into the bacterium. This action also unplugs the head, allowing the pressurized DNA to extrude through the channel in the core into the bacterium. Thus, the linear assembly reactions and an ATPase motor produce a machine that can, when triggered, do physical work.
Caspar DLD. Virus structure puzzle solved. Curr Biol. 1992;2:169-171.
Caspar DLD, Klug A. Physical principles in the construction of regular viruses. Cold Spring Harbor Symp Quant Biol. 1962;27:1-24.
Harrison SC. What do viruses look like? Harvey Lect. 1991;85:127-152.
Leiman PG, Chipman PR, Kostyuchenko VA, et al. Three-dimensional rearrangement of proteins in the tail of bacterio-phage T4 on infection of its host. Cell. 2004;118:419-429. [Also see movie on the journal web site: http://download.cell.com/supplementarydata/cell/118/4/419/DC1/leiman-et-al.movie-2.].
Liddington RC, Yan Y, Moulai J, et al. Structure of simian virus 40 at 3.8 A resolution. Nature. 1991;354:278-284.
Namba K, Stubbs G. Structure of tobacco mosaic virus at 3.6 A resolution: Implications for assembly. Science. 1986;231:1401-1406.
Oosawa F, Asakura S. Thermodynamics of the Polymerization of Protein. New York: Academic Press, 1975.
Pollard TD, Blanchoin L, Mullins RD. Biophysics of actin filament dynamics in nonmuscle cells. Ann Rev Biophys Biomolec Struct. 2000;29:545-576.
Rossmann MG, Mesyanzhinov VV, Fumio Arisaka F, Leiman PG. The bacteriophage T4 DNA injection machine. Curr Opin Struct Biol. 2004;14:171-180.
Simpson AA, Tao Y, Leiman PG, et al. Structure of the bacteriophage phi29 DNA packaging motor. Nature. 2000;408:745-750.
Sinard JH, Pollard TD. Acanthamoeba myosin-II minifilaments assemble on a millisecond time scale with rate constants greater than those expected for a diffusion limited reaction. J Biol Chem. 1990;265:3654-3660.
Smith DE, Tans SJ, Smith SB, et al. The bacteriophage straight phi29 portal motor can package DNA against a large internal force. Nature. 2001;413:748-752.
Wood WB. Genetic control of bacteriophage T4 morphogenesis. Symp Soc Dev Biol. 1973;31:29-46.