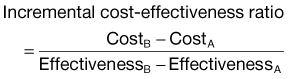Introduction to Cost-Effectiveness Analysis

Published on 10/02/2015 by admin

Filed under Emergency Medicine

Last modified 22/04/2025

Print this page

rate 1 star rate 2 star rate 3 star rate 4 star rate 5 star
Your rating: none, Average: 0 (0 votes)

This article have been viewed 1084 times

218 Introduction to Cost-Effectiveness Analysis

Emilie S. Powell, Brian W. Patterson

image      Key Points

• Cost-effectiveness analysis (CEA) is a method for evaluating and comparing the outcomes and costs of interventions designed to improve health.

• CEA is an increasingly important component of the medical literature because it drives both clinical and policy decisions that affect the practice of emergency medicine.

• The output of any CEA model is contingent on appropriate and accurate input data.

• The primary outcome of importance in a CEA is the incremental cost-effectiveness ratio, or ICER, which represents the incremental change in cost and effectiveness when choosing one strategy over another.

• CEA model outcomes incorporate a degree of uncertainty based on input data, which is quantified in the process of sensitivity analysis.

What Is Cost-Effectiveness Analysis?

A key skill for emergency physicians is effective integration of new interventions into existing clinical practice. Physicians have classically been trained and have become comfortable with more traditional methodologies of evaluating new interventions and treatment modalities, such as randomized controlled trials, but are often less comfortable in applying techniques such as cost-effectiveness analysis (CEA). As health care resources become more limited, costs rise, and treatment options expand, interventions and treatments are increasingly being compared and evaluated on the basis of cost.1

CEA falls under the broad umbrella of comparative effectiveness research, which refers to any study that compares the effectiveness of two or more strategies with or without regard to cost. CEA is a method for evaluating and comparing the outcomes and costs of interventions designed to improve health.2 Although many methodologies fall under the umbrella of CEA, they all share the common goal of reporting outcomes as a cost per achieving a unit of health effect (i.e., lives saved, year of life gained, quality-adjusted year of life gained). CEA tracks costs and effectiveness for a number of strategies by using both real and modeled data, compares the cost-effectiveness of the strategies, and then accounts for uncertainty in the data through sensitivity analyses.3

How Does Cost-Effectiveness Analysis Affect the Emergency Physician?

CEA is becoming an increasingly important input into health policy decisions; however, the methodology does have limitations. CEA cannot incorporate all aspects of a decision, and the results are only as good as the data available to input into the analyses. Economic analyses such as CEA cannot capture every input necessary to make health care decisions and should not be reported as scientific fact, but models and their results may be reported as aids in decision making.4 An additional criticism of CEA is that although the economic models have become increasingly complex to better represent reality, they have also become increasingly opaque to the lay reader, thus making it difficult for those without a background in economics to personally interpret the results.1 Despite these limitations, CEA offers the benefit of adding perspective to difficult questions regarding treatment choices in the setting of limited resources.2,5,6 If emergency physicians are to act as decision makers in our changing practice environment, it is essential to have an understanding of the basic principles of CEA.

Methodology in Cost-Effectiveness Analysis

Components of A Cost-Effectiveness Analysis

CEA has four main components: inputs (costs and effectiveness and the perspective from which these variables are determined), the model, primary outcomes, and sensitivity analyses. Inputs are known values gathered from primary research, previously published literature, or estimation and are incorporated into a model. The model is the computational framework created to combine these known values along with clinical probabilities to output the overall cost-effectiveness of an intervention or set of interventions. Uncertainty in the model is evaluated and reported through sensitivity analyses.

All CEAs starts with a focused clinical question that drives collection of data for analysis and allows appropriate interpretation of results. As an example for the proceeding sections, we will consider a hypothetic CEA created to answer a clinical question. Suppose an emergency department (ED) is attempting to create a cost-effective strategy for stratification of cardiac risk in low-risk patients with chest pain. After a normal electrocardiogram and two negative cardiac enzyme tests, these low-risk patients could either be sent home or be admitted to the hospital for an exercise stress test. A CEA could be created to answer the following question: “Among low-risk patients seen in the ED with chest pain, is adding admission for an exercise stress test more cost-effective than discharging the patient directly home?”

Inputs

Perspective

An important characteristic of any CEA is the perspective from which the analysis is conducted. The cost and effectiveness of an intervention may vary depending on the perspective. Common perspectives include those of the patient, the insurer, the employer, the hospital, or society, to name a few. For instance, from the perspective of an insurer, the cost of an intervention for a patient whom it insures is simply the amount of money paid to physicians and hospitals. However, from the perspective of an employer who provides health care insurance, the cost of an intervention additionally includes loss of productivity while the employee is ill and undergoing the intervention. The choice of perspective is of critical importance in performing and interpreting a CEA because it determines the relevance of the study for decision making.

Although one can perform a CEA from a vast number of perspectives, the most common is the societal perspective, which will be used for our example. In a CEA conducted from the societal perspective, the analyst considers all parties affected by the intervention and all costs related to the intervention, regardless of who experiences these costs and effects. Because the societal perspective includes all costs and health effects, it does not necessarily give an individual group the information necessary to make decisions on which interventions to implement. However, the societal perspective is used most commonly because it has several benefits.3 It is standardized and therefore allows comparison of various interventions across a broad spectrum of disciplines in medicine and society when making policy decisions. It is fair: if all decisions in health care were made from a societal standpoint, resources would be allocated to provide the most benefit to the most people. Moreover, although other perspectives may be more useful for individual groups, these perspectives do not necessarily take into account the cost or harm seen by those outside the sphere of the analyst’s perspective that the societal perspective takes into account.

Costs

Costs may be gathered from several different sources: institutional data, Medicare or other payment records, or elsewhere in the published literature. In our example study, the costs associated with the hospital stay, such as the cost of an exercise stress test and hospital admission, could be taken from institutional data. Because the study is conducted from a societal perspective, the true cost of these interventions to the hospital (as opposed to hospital charges) would need to be calculated. Other costs included in the study, such as the cost of a day of missed work and the cost of outpatient medical treatment of coronary artery disease (CAD), could be taken from the economic or medical literature. When evaluating a CEA, it is important to verify that the authors included all relevant costs for the stated perspective of the study and that these costs are plausible.

Effectiveness

In CEA, each strategy has an associated effectiveness. The effectiveness (sometimes referred to in the economic literature as utility) can be expressed with a number of different metrics. The most common measure is “life-years gained” or “lives saved.” Traditionally, most medical and public health studies use “life-years,” whereas CEAs in transportation and environmental policy use “lives saved.”7

Even though life-years may be used alone as an effectiveness measure, they are generally adjusted to account for quality of life or disability. Without adjustment, two interventions would have the same effectiveness based on life-years even if one substantially increased quality of life without any extension in life expectancy. The most common adjustment unit is the quality-adjusted life-year (QALY), although other units such as disability-adjusted life-year are sometimes used.8

Several methods can be used for quality-adjusting life-years to arrive at QALYs. All methods seek to find the value placed on various disease states among a group representing the interests of either a patient population or society. One commonly used method is known as the time trade-off. In a time trade-off, subjects are asked to choose between remaining in a particular health state for a fixed length of time or “trading off” that time for some shorter amount of time in perfect health. The ratio of time traded gives the QALY equivalent for the health state. For instance, if respondents would choose to equate 6 months of perfect health with 1 year in a health state, each year in that state would be worth 0.5 QALYs. Another commonly used method for quality adjustment is the standard gamble. Respondents choose between remaining in a health state or taking a gamble on a treatment that will either kill them or restore them to perfect health. If a patient in a particular health state is willing to take a 50-50 chance of dying or being restored to perfect health, that state is valued at 0.5 QALYs.

These methodologies for quality adjustment have limitations. Not all patients will value quality of life and disease states the same. The life-year–to-QALY conversion is not standard or universal, and when evaluating a CEA, one should verify that the adjustments seem appropriate. Controversy exists regarding the most appropriate derivation method, and the different approaches to derive QALYs may deliver different results even with the same respondent.

In our example model we could track the effectiveness of several outcomes. Our first outcome could be a disease-free outcome; this would represent the average quality-adjusted life span of CAD-free patients following discharge from the ED after a negative work-up. Another outcome would be a true diagnosis of CAD. Patients found to have CAD in the hospital would probably have a lower quality-adjusted life expectancy than those without CAD but would benefit from treatment of the disease. A third outcome would be patients discharged from the ED after a false-negative work-up; that is, those who have CAD but are sent home thinking that they are well. These patients would probably have the shortest life expectancy.

Clinical Probabilities

To build a model, in addition to the cost and effectiveness of the strategies, a set of clinical probabilities must be created to govern how patients flow through the model. Similar to cost and effectiveness measures, these probabilities can be derived from a number of sources, from primary institutional data to educated estimation. Our model would include population characteristics such as the prevalence of CAD, as well as test characteristics such as the sensitivity and specificity of an exercise stress test in detecting clinically relevant CAD. Anywhere a chance node lies on a decision tree, a model must contain a corresponding set of probabilities that dictate the outcomes from that node.

Discounting

An important aspect of economic analyses is the practice of discounting. Many CEAs take into account costs and health states that occur years in the future from the time of an intervention. To compare future costs and utilities with those occurring in the present, future costs and utilities are devalued at a constant yearly rate to reflect their lower opportunity cost. For example, if one needs to pay for a health intervention, clearly it is preferable to pay the same sum of money 10 years from now rather than paying today because the sum of money used for payment in the future could be invested in the meantime to generate further revenue. Therefore, a discount rate is applied to compare present and future events. The discount rate for all costs and utilities is generally approximately 3% to 5% per year in health economic analyses. Even though this value is commonly used, there is little agreement among economists regarding what represents an appropriate discount rate and exactly how this rate should be calculated.9,10

The Model

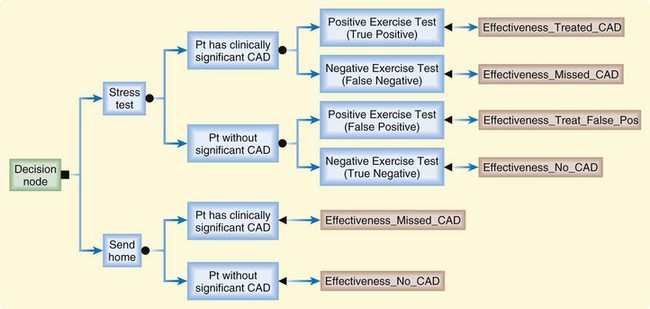
Mathematic models are used in CEA to simulate the chain of events surrounding alternative interventions so that the costs and outcomes related to the choice of one medical intervention over another can be tracked. Although it is theoretically possible to complete a CEA by measuring every variable prospectively, the broad scope of most CEAs necessitates at least some component of mathematic modeling.11,12 A successful model is transparent, internally consistent, reproducible, and interpretable.13 Multiple modeling methodologies are used in modern CEAs; here we will cover the two most common: decision tress and Markov models. Decision trees depict decisions and chance events as branches of a tree. Computerized decision trees can track the costs and outcomes associated with various health interventions. Graphic branches in the tree represent a chain of related events, and nodes in the branches represent decisions, such as a choice between competing strategies, or chances, such as the chance of a complication developing after an intervention. Figure 218.1 depicts a simple decision tree.

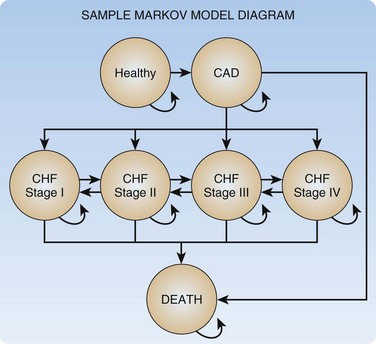
image

Fig. 218.1 Sample decision tree.

The square represents a decision node, circles represent chance nodes, and triangles represent terminal nodes. Costs are tracked at each branch along the chain, and each terminal node is associated with an effectiveness. Clinical probabilities are documented below the nodes. CAD, Coronary artery disease; Pt, patient.

Certain situations are difficult to model with decision trees alone; especially problematic are episodic or recursive disease states (i.e., a chronic disease with frequent exacerbations). For these situations more complex models, such as Markov models, are used. A Markov model consists of a set of health states, as well as allowable transitions between these states. The model moves forward with discrete steps in time; at each time step the model allows patients to transition between states along allowable transitions according to predefined transition probabilities. Markov models can be constructed independently or be inserted into decision trees. If in our example CEA we wish to model CAD in more detail and specifically include ischemic congestive heart failure states, we could use a Markov model as depicted in Figure 218.2.

image

Fig. 218.2 Sample Markov model.

Circles represent health states, and arrows represent allowable transitions between states. Each arrow is associated with a transition probability that governs the percentage of patients who make that transition at each time step. Arrows that point back at the same circle indicate the associated chance of remaining in the same state. The model can track cost and effectiveness associated with staying in a particular health state, as well as with making the transition between states. CAD, Coronary artery disease; CHF, congestive heart failure.

Primary Outcomes

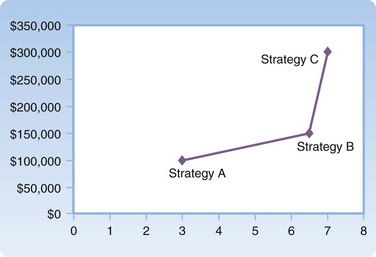
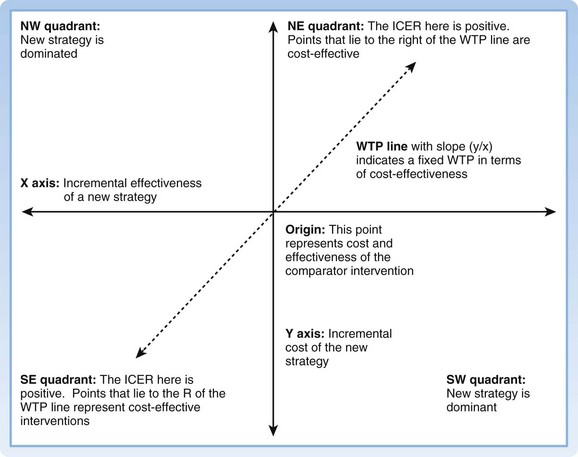
The most basic outcome from any CEA is a cost-effectiveness ratio (CE ratio), in which the cost of an intervention is placed in the numerator and the measure of effectiveness in the denominator; for instance, “dollars per QALY.” The CE ratio can then be compared with a predetermined “willingness to pay” to determine whether the intervention is cost-effective. Frequently, from a societal perspective a CE ratio is not particularly useful by itself because it involves a large number of societal costs and outcomes. It is often more useful to view the cost-effectiveness of one intervention versus another. The cost-effectiveness frontier graphically shows this difference, with cost on the y-axis and effectiveness on the x-axis (Fig. 218.3). To numerically compare two strategies, we use the incremental cost-effectiveness ratio (ICER). The ICER represents the incremental change in cost and effectiveness when choosing one strategy over another. For example, if the ICER for strategy A versus strategy B is $10 per QALY, by choosing to implement strategy A over strategy B, an additional $10 is spent for one additional QALY. A strategy is said to be dominant if it is both less costly and more effective than the comparator strategy. When interpreting ICERs it is important to remember two key points. First, the ICER is only as good as the value of the comparators. One can always make a strategy look good by comparing it with something bad. Second, ICERs should be reported only when positive. A negative ICER can mean one of two opposite scenarios: the new strategy is dominant, or the new strategy is dominated (more costly and less effective). The cost-effectiveness plane may be used as an intuitive way to understand and report ICERs between two strategies14 (Fig. 218.4).

image

Fig. 218.3 Cost-effectiveness frontier.

The total cost of a strategy is plotted against each strategy’s effectiveness. This graph gives a representation of the additional life years gained for the additional cost of a strategy. The slope of the line connecting two points is mathematically equivalent to the incremental cost-effectiveness ratio.

image

Fig. 218.4 Incremental cost-effectiveness plane.

ICER, Incremental cost-effectiveness ratio; WTP, willingness to pay.

Sensitivity Analyses

The point estimate of cost-effectiveness provided from a model is known as the “base case.”15 There is likely to be some uncertainty associated with the inputs of any model, and expressing this uncertainty in the outcome is a critical component of any CEA.9,12 The degree to which a model’s outcome changes with changes in particular inputs is referred to as its sensitivity. Examination of uncertainty in a CEA consists of varying input parameters and measuring the effects on results through sensitivity analyses. Sensitivity can be calculated on a number of levels.

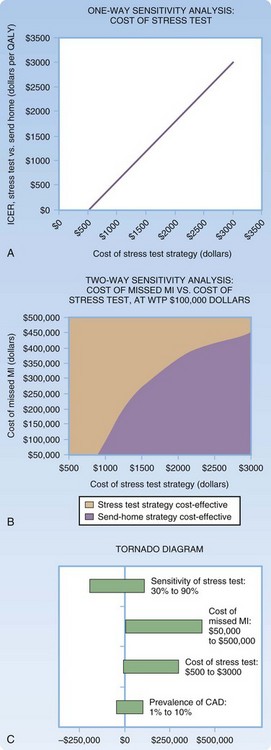
image Facts and Formulas

image

image

Sensitivity analyses may be reported as a threshold value (i.e., a threshold value on an input beyond which the intervention is cost-effective) or continuously, in which the resultant cost-effectiveness is considered across a range of input values.16 A one-way sensitivity analysis is the most basic form of sensitivity analysis. It demonstrates the variability in cost-effectiveness of an intervention or group of interventions based on variation of a single input. A two-way sensitivity analysis varies two variables simultaneously to capture their interaction. Any number of parameters can be varied simultaneously, although it is challenging to graphically depict sensitivity analyses beyond two way. Figure 218.5 depicts examples of one- and two-way sensitivity analyses for our example model, as well as an example of a tornado diagram, another commonly used methodology for reporting sensitivity. Tornado diagrams give a graphic representation of the magnitude of a number of one-way sensitivity analyses simultaneously but do not incorporate interaction between these variables.

image

Fig. 218.5 A-C, Sensitivity analyses. CAD, Coronary artery disease; ICER, incremental cost-effectiveness ratio; MI, myocardial infarction; QALY, quality-adjusted life year; WTP, willingness to pay.

The goal of multivariate sensitivity analysis is to gain a sense of model uncertainty by varying all variables simultaneously. It allows the generation of true confidence intervals of the inputs. The confidence interval for an ICER is dependent on the confidence intervals of all model inputs, as well as the structure of the model. Several methods have been described for empiric calculation of confidence intervals, but there is no consensus method. Most commonly, “bootstrap methods” are used, in which iterative methods are used to create confidence intervals from the data after the model has been run.17

The most common bootstrap method for calculating multivariate sensitivity is the Monte Carlo method. In a Monte Carlo analysis, each input in a model is replaced by a distribution representing the uncertainty surrounding the input variable. For instance, in our sample decision tree we may know that the incidence of CAD in the patient population in question is 0.1, with a 95% confidence interval of 0.05 to 0.15, normally distributed. To perform a Monte Carlo sensitivity analysis, we would replace our incidence point probability with a normal distribution of probabilities with a mean of 0.1 and standard deviation of 0.025. We would perform a similar replacement for all model inputs with uncertainty. The model would then be run many times (generally at least 1000).17 For each iteration of the model, the computer picks a value for each input based on the probability distribution. In the case of our CAD incidence distribution, most iterations would have values near the mean of 0.1, but some iterations would pick outlier values such that over the course of 1000 runs, the values picked would form the distribution specified. Each model run creates an individual ICER. These ICERs then form a distribution, the characteristics of which (standard deviation and confidence intervals) reflect the uncertainty of the model as whole.

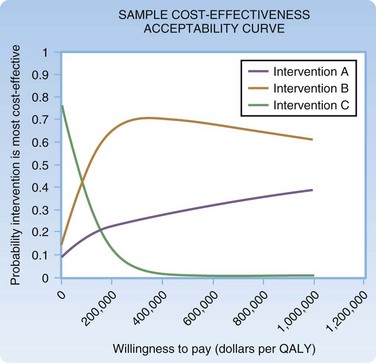
Several methods can be used for reporting confidence intervals generated from multivariate sensitivity analyses. In an ICE scatterplot (Fig. 218.6), individual runs of a multivariate Monte Carlo analysis are plotted as individual points on a cost-effectiveness plane.18 Figure 218.7 shows a sample cost-effectiveness acceptability curve in which individual model runs are compiled to form a probability distribution that reflects the likelihood that a given intervention is cost-effective at a given willingness to pay.17

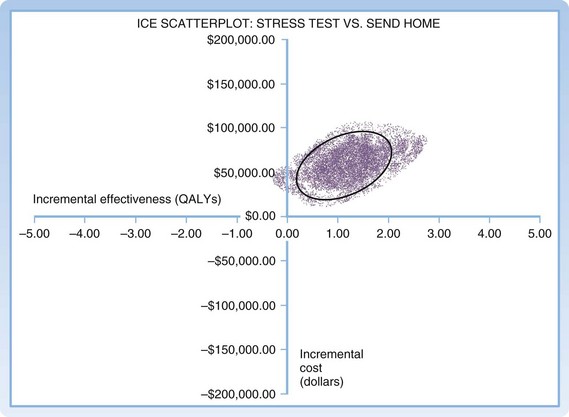
image

Fig. 218.6 Monte-Carlo sensitivity analysis: ICE scatterplot.

ICE, Incremental cost-effectiveness; QALYs, quality-adjusted life years.

image

Fig. 218.7 Cost-effectiveness acceptability curve.

This curve displays the output of a multivariate sensitivity analysis as a function of willingness to pay. At each dollar value, the y-value of the line corresponds with the probability that the intervention is the most effective without exceeding that dollar value per effectiveness unit. QALY, Quality-adjusted life year.

Evaluating a Cost-Effectiveness Analysis

See Box 218.1 for a sample approach to critically evaluating a CEA. Though not the only approach or an all-inclusive list, it provides a framework for assessing the impact of a particular study on a clinical question. See “Suggested Readings” for more in-depth analysis.12,19–22

Box 218.1 Template for Critiquing a Cost-Effectiveness Analysis

1. What is the research question being asked?

a. From what perspective is the analysis conducted, and is this appropriate?
b. What population is specifically modeled or studied?
c. Are all appropriate interventions or strategies included in the comparison?
d. Was the choice of units describing the costs and effectiveness of the evaluated strategies appropriate?

2. What is the quality of the evidence?

a. Are the sources of model parameter values stated clearly?
b. Is uncertainty of the source data described (ranges given for all parameters)?
c. Is the search strategy used to identify model data described and adequate?
d. Were future costs and consequences discounted appropriately?

3. Is the model’s design valid?

a. Is the structure of the model consistent with the stated research question?
b. Are the disease states in the model driven by a sound biologic model of the underlying disease (as opposed to data available during construction of the model)?
c. Were all important and relevant costs and consequences for each alternative identified and valued credibly?
d. Are model assumptions clearly stated and reasonable?
e. Is the model as transparent and reproducible as possible while adequately representing the disease and interventions studied?

4. Are the base case results presented?

a. Are all strategies present in the base case results?
b. Are appropriate incremental cost-effectiveness ratios calculated for all relevant comparisons?

5. Was an appropriate sensitivity analysis performed?

a. Do the ranges of possible variable values accurately reflect the uncertainty of the data?
b. Was a multivariate sensitivity analysis performed?
c. Are outputs of the sensitivity analysis reported appropriately?

6. Is the model externally consistent?

a. Are any relevant studies or models identified for comparison?
b. Does the discussion include and address all points of concern?

Suggested Readings

Black WC. The CE plane: a graphic representation of cost-effectiveness. Med Decis Making. 1990;10:212–214.

. Cost-effectiveness analysis. Jamison DT, Breman JG, Measham AR, et al. Priorities in health. Washington, DC: International Bank for Reconstruction and Development/The World Bank Group; 2006:39–57. http://files.dcp2.org/pdf/PIH/PIH.pdf. Full text available online at

O’Brien BJ, Briggs AH. Analysis of uncertainty in health care cost-effectiveness studies: an introduction to statistical issues and methods. Stat Methods Med Res. 2002;11:455–468.

Russell LB, Gold MR, Siegel JE, et al. The role of cost-effectiveness analysis in health and medicine. Panel on Cost-Effectiveness in Health and Medicine. JAMA. 1996;276:1172–1177.

Sox HC, Blatt MA, Higgins MC, et al. Medical decision making. Woburn, Mass: Butterworth-Heinemann; 1988.

References

1 Congressional Budget Office. Research on the comparative effectiveness of medical treatments: issues and options for an expanded federal role. 2007. http://www.cbo.gov/sites/default/files/cbofiles/ftpdocs/88xx/doc8891/12-18-comparativeeffectiveness.pdf.

2 Cost-effectiveness analysis. In: Jamison DT, Breman JG, Measham AR, et al. Priorities in health. Washington, DC: International Bank for Reconstruction and Development/The World Bank Group; 2006:39–57.

3 Russell LB, Gold MR, Siegel JE, et al. The role of cost-effectiveness analysis in health and medicine. Panel on Cost-Effectiveness in Health and Medicine. JAMA. 1996;276:1172–1177. http://files.dcp2.org/pdf/PIH/PIH.pdf. Full text available online at

4 Weinstein MC, O’Brien B, Hornberger J, et al. Principles of good practice for decision analytic modeling in health-care evaluation: report of the ISPOR Task Force on Good Research Practices—modeling studies. Value Health. 2003;6:9–17.

5 Neumann PJ, Greenberg D. Is the United States ready for QALYs? Health Aff (Millwood). 2009;28:1366–1371.

6 Neumann PJ, Weinstein MC. Legislating against use of cost-effectiveness information. N Engl J Med. 2010;363:1495–1497.

7 Hammitt JK. Valuing “lives saved” vs. “life-years saved.”. Risk Perspect. 2008;16:5.

8 Sox HC, Blatt MA, Higgins MC, et al. Decision making when the outcomes have several dimensions. In: Sox HC, Blatt MA, Higgins MC, et al. Medical decision making. Woburn, Mass: Butterworth-Heinemann; 1988:201–236.

9 Weinstein MC, Siegel JE, Gold MR, et al. Recommendations of the Panel on Cost-effectiveness in Health and Medicine. JAMA. 1996;276:1253–1258.

10 Krahn M, Gafni A. Discounting in the economic evaluation of health care interventions. Med Care. 1993;31:403–418.

11 Brennan A, Akehurst R. Modelling in health economic evaluation. What is its place? What is its value? Pharmacoeconomics. 2000;17:445–459.

12 Sculpher M, Fenwick E, Claxton K. Assessing quality in decision analytic cost-effectiveness models. A suggested framework and example of application. Pharmacoeconomics. 2000;17:461–477.

13 Decision analytic modelling in the economic evaluation of health technologies. A consensus statement. Consensus Conference on Guidelines on Economic Modelling in Health Technology Assessment. Pharmacoeconomics. 2000;17:443–444.

14 Black WC. The CE plane: a graphic representation of cost-effectiveness. Med Decis Making. 1990;10:212–214.

15 Siegel JE, Weinstein MC, Russell LB, et al. Recommendations for reporting cost-effectiveness analyses. Panel on Cost-Effectiveness in Health and Medicine. JAMA. 1996;276:1339–1341.

16 Sox HC, Blatt MA, Higgins MC, et al. Cost-effectiveness analysis and cost-benefit analysis. In: Sox HC, Blatt MA, Higgins MC, et al. Medical decision making. Woburn, Mass: Butterworth-Heinemann; 1988:317–335.

17 O’Brien BJ, Briggs AH. Analysis of uncertainty in health care cost-effectiveness studies: an introduction to statistical issues and methods. Stat Methods Med Res. 2002;11:455–468.

18 Briggs AH. Handling uncertainty in cost-effectiveness models. Pharmacoeconomics. 2000;17:479–500.

19 Drummond MF, Richardson WS, O’Brien BJ, et al. Users’ guides to the medical literature. XIII. How to use an article on economic analysis of clinical practice. A. Are the results of the study valid? Evidence-Based Medicine Working Group. JAMA. 1997;277:1552–1557.

20 McCabe C, Dixon S. Testing the validity of cost-effectiveness models. Pharmacoeconomics. 2000;17:501–513.

21 Department of Clinical Epidemiology and Biostatistics MUHSC. How to read clinical journals: VII. To understand an economic evaluation (part A). Can Med Assoc J. 1984;130:1428–1434.

22 Department of Clinical Epidemiology and Biostatistics MUHSC. How to read clinical journals: VII. To understand an economic evaluation (part B). Can Med Assoc J. 1984;130:1542–1549.

Related posts:

Pediatric Abdominal Disorders Pancreatic Disorders Altered Mental Status and Coma Esophageal Disorders Vasculitis Syndromes Pericarditis, Pericardial Tamponade, and Myocarditis