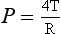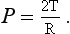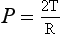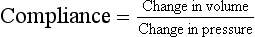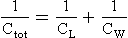ELASTIC PROPERTIES OF THE RESPIRATORY SYSTEM
Introduction
The most commonly used model of lung inflation is a toy balloon. Many of the principles that follow can be demonstrated by this model. For example, if you inflate a balloon and prevent the air escaping by blocking the neck with your finger (Fig. 3.1A), the elastic recoil of the balloon will be proportional to its elastance (1/compliance, see below) and will produce a recoil pressure. The pressure inside the balloon will be the same throughout if no flow is taking place into or out of the balloon. These observations demonstrate important principles of lung function.

Fig. 3.1 (A) Balloon demonstrating elastic recoil. (B) Physiological model of the respiratory system.
An even more physiological model of the respiratory system can be made by suspending a balloon in a jar with a piston at its base, like a large syringe (Fig. 3.1B). In this case the balloon represents the lungs, the jar represents the chest wall and the piston represents the diaphragm. Lowering the piston reduces the pressure round the balloon (intrapleural pressure) and causes it to inhale.
Intrapleural pressure (Ppl)
For an object to be stretched or in some other way distorted it must be subjected to a force. In the case of a three-dimensional object this force may be pressure. In our simple model of breathing (Fig. 3.1A), inspiration would be inflation of the balloon and expiration deflation. The pressure that brings about inflation in Figure 3.1A would be applied to the inside. There is a pressure gradient from inside the balloon to outside. The other, more complicated, way for us to inflate the balloon would be to reduce the pressure outside it using the jar and plunger (Fig. 3.1B): again there is a pressure gradient from inside to outside the balloon, and this is the way we inflate our lungs.
Another way of visualizing what is happening in the space between the lungs and chest wall is to imagine a syringe with two plungers being pulled in opposite directions (Fig. 3.2).
You can see from such a model that intrapleural pressure is negative with respect to atmospheric pressure. What is not immediately obvious is that intrapleural pressure is also negative with respect to air pressure within the alveoli, because the alveoli are connected to the atmosphere by a system of open tubes, the bronchial tree (Fig. 3.3).
This means a hole made between either the atmosphere or the alveoli and the intrapleural space will allow the pressure surrounding the lung to rise and the lung to collapse: this dangerous condition is called a pneumothorax.
Because the lungs are to some extent suspended from the trachea and rest on the diaphragm, they behave like a child’s ‘slinky’ (a very soft spring), held at one end and supported from underneath. Gravity causes the spring or lungs to slump under their own weight (Fig. 3.4).
The physical basis of lung compliance
The elasticity of lung tissue
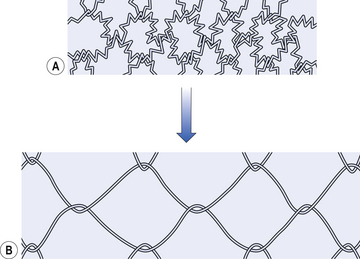
It might be reasonably assumed that the elastic properties of the lungs are due to the yellow elastin fibres of the lung parenchyma, the fibre type that gives most other organs their elasticity. In fact, only about half the elastic recoil of the lungs comes from the elastin fibres in the alveolar walls, bronchioles and capillaries. Also present in the lungs are collagen fibres, which are less easily stretched and limit overexpansion of the lung. The elastin fibres act in a rather complicated way to provide elasticity. The fibres are kinked and bent round each other, and during inspiration unfold and rearrange in a manner that has been likened to the straightening of the fibres of a nylon stocking when it is put on (Fig. 3.6).
The liquid lining of the lungs
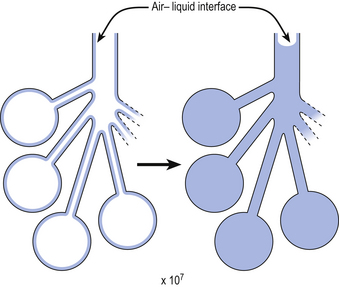
So, about half the elastic recoil of the lungs comes from the elastic properties of their tissues, just as there is recoil in an inflated rubber balloon. The remaining half of the elastic recoil of the lungs comes from their unique structure of millions of tiny bubble-like alveoli, lined with liquid and connected to the atmosphere by a series of tubes (the bronchial tree). The importance of this structure was demonstrated by von Neergaard, in 1929, when he showed that an isolated lung completely filled with water is about twice as easy to inflate as one filled with air. The cause of this change in ease of inflation lies in the removal of the air–liquid surface that lines the millions of spherical bubbles surrounded by lung tissue by filling the air space with water to form one single small air–liquid interface somewhere in the trachea (Fig. 3.7).
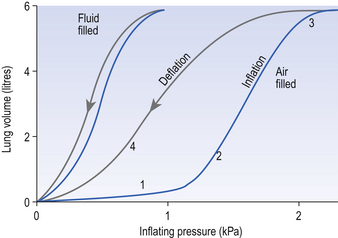
Not only does filling a lung with fluid make it easier to inflate, it also abolishes the hysteresis seen in the normal lung. Hysteresis (Greek, hysterion, to lag behind) means that inflation of the lung follows a different pressure/volume relationship from deflation (Fig. 3.8). It requires a greater pressure to reach a particular lung volume when you are inflating it than to hold it at that volume when you are deflating it. Something is ‘propping the lung alveoli open’. These peculiar changes are due to the nature of bubbles and the properties of the liquid that makes up the liquid lining of the lung. We need to consider the nature of the surface of liquids, the nature of bubbles and the very special properties of the liquid lining of the alveoli to understand static and dynamic compliance of the lungs.
The surface of liquids
That liquids form a clear boundary between themselves and the air above them could almost be a definition of a liquid. That this boundary is under tension or stress is clearly seen in the liquids we come across in everyday life: the surface of a cup of coffee, if touched lightly with a spoon, seems to leap up to the spoon. This is the effect of surface tension (Fig. 3.9).
The ‘skin’ or surface of a liquid exists because at the surface there is an imbalance of the forces acting on the molecules at the surface, as explained in the Appendix (p. 153).
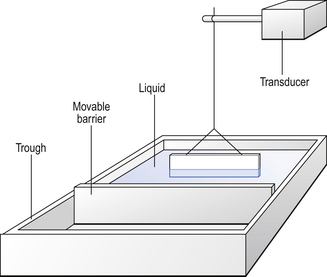
Just as mechanical and chemical systems move to a state of minimal energy (maximum entropy), so surfaces seek minimal energy and hence minimal area (this is why water droplets are spheres, the shape that has minimal surface for a given mass). The tendency to reduce in surface area produces tension in a liquid surface which can be measured by a surface balance (Fig. 3.10). In this, a bar of metal dips into the liquid and is exposed to the same forces as act on molecules at the surface of liquids, or the coffee spoon. These forces can be measured by a sensitive transducer. The total force will depend on the surface tension and the length of the bar, and the units of surface tension are therefore N m−1. The surface balance was modified to produce the Wilhelmi Balance by the ingenious addition of a movable barrier that can compress the surface of the liquid in the balance trough. Under these circumstances the depth of the liquid alters as the barrier is moved, but this doesn’t matter as it is the air–liquid interface that is important. If pure water is placed in a Wilhelmi Balance, moving the barrier to and fro, expanding and contracting the surface, has no effect on the measured surface tension. If, however, a phospholipid of the type found lining the alveoli of the lungs is placed on the surface of the liquid it spreads out to form a layer between water and air, and the surface tension changes as the barrier advances, forcing the phospholipid molecules closer together, or retreats allowing them to separate. The tension reaches a minimum when all the phospholipid molecules are neatly packed as a single layer on the surface. When the surface area is reduced further the molecules pile up on each other and the tension begins to rise again. It is possible to measure the size of the molecules of the phospholipid from the area of the surface at which the surface tension is minimal.
The nature of bubbles
They will have noticed that once a complete sphere has formed the bubble is stable. While there is a hole in the bubble, however, through the pipe or wire loop, if you stop blowing the bubble immediately collapses, returning to a flat layer of soap stretched across the pipe or loop. The molecular basis of this effect is explained in the Appendix (p. 156).
where P is the excess pressure (Pa), T is the surface tension (N m−1) of the liquid making up the bubble, and R is the radius (m) of the bubble. The constant 4 appears in this equation because a bubble has two surfaces exposed to the air. For alveoli whose outer surface is in contact with the lung tissue it becomes:
The nature of the liquid lining of alveoli
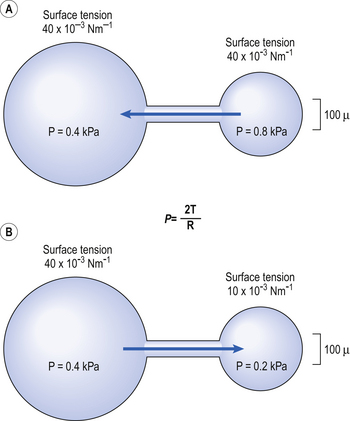
From the Laplace Relationship we can see, somewhat surprisingly, that the pressure in a small bubble can be expected to be greater than the pressure in a large one. This might lead us to anticipate problems in the lungs, as there exists a whole variety of sizes of alveoli, those at the top being larger than those at the bottom (see Chapter 5). Under these circumstances an unstable situation might be expected to arise, with small alveoli (containing higher pressure) emptying into large ones (containing lower pressure) (Fig. 3.11A). The nature of the liquid lining of the lungs provides an ingenious solution to this problem.
The liquid lining of the lungs can be extracted by washing them out with saline (bronchial lavage). The washed-out liquid can then be investigated in a Wilhelmi Balance, where it shows some interesting and useful properties. Adding the extract to water in the balance reduces the surface tension from 70 to 40 × 10−3 N m−1. Surface tension falls even further when the surface is compressed, reaching a minimum below 10 × 10−2 N m−1 This effect is due to surfactant secreted by type II cells of the alveolar epithelium (Fig. 3.12).
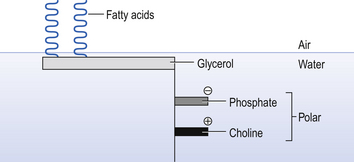
The surfactant spreads over the inner surface of the alveoli and into the bronchioles. It is made up of dipalmitoyl phosphatidylcholine: the structure of this and the way it arranges itself at an air–liquid interface is shown in Figure 3.13.
The straight structure of these molecules enables them to pack more closely during expiration than would other shapes. This packing and unpacking during inspiration and expiration causes surface tension to decrease and increase in a manner that produces the characteristic hysteresis of the lungs. The change in surface tension also provides the solution to the problem posed earlier of the alveoli of different sizes containing different pressures, and the tendency for the small to empty into the large (Fig. 3.11A). If the surface tension in the large alveolus is sufficiently greater than the tension in the small the effect of the larger radius (R) in the Laplace Relationship
will be matched or even overpowered by changes in tension (T).
And this is what happens in the lung. The surface tension changes to match the radius, so that all alveoli contain about the same air pressure and the small do not tend to empty into the large (Fig. 3.11B).
The air pressure inside an alveolus not only resists the effects of surface tension causing the alveolus to collapse, but also resists exudation of fluid from pulmonary capillaries into the alveolar space. If surface tension is reduced at any particular air pressure within an alveolus more of that air pressure will be available to resist exudation and prevent pulmonary oedema.
The presence of surfactant is clearly important to normal lung function. It:
The opening and closing of alveoli
Range 1 of Figure 3.8 is the result of alveoli staying shut despite increased inflation pressure.
Range 2 begins at about 1 kPa, when alveoli begin to pop open and the lung inflates with very little increase in pressure.
Range 3 is where tissue elasticity, particularly from collagen fibres, stiffens the lung.
Range 4 is deflation, where hysteresis of surfactant ‘props open’ the alveoli.
Static compliance
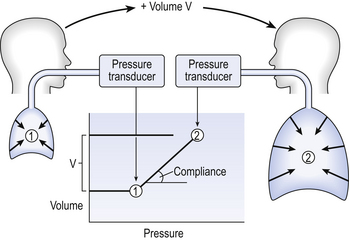
Neither pressure nor volume has the dimensions of time, and therefore these measurements can be made under static conditions where the subject breathes in slightly, relaxes his respiratory muscles while measuring mouth pressure with a transducer; he then breathes in a known volume and again relaxes against the transducer. The slope of the pressure–volume graph so formed is his total static compliance (Fig. 3.14).
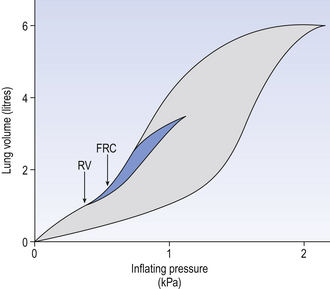
The slope of the line that makes up the loop in Figure 3.15 is the compliance of the lungs, which in this case have been taken out of the body. This loop describes the condition of the lungs from total collapse to maximum volume.
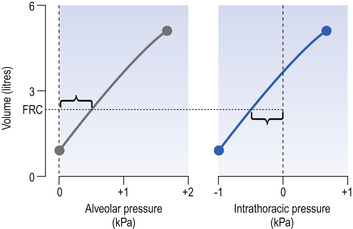
In normal breathing there are about 3.0 L of air left in the lungs at the end of expiration (FRC), and we seldom inhale to total lung capacity (TLC). Most quiet breathing takes place within the shaded area of Figure 3.15, which shows less hysteresis than the total collapse to total volume manoeuvre, but still shows that compliance reduces due to airway collapse when residual volume (RV) is approached.
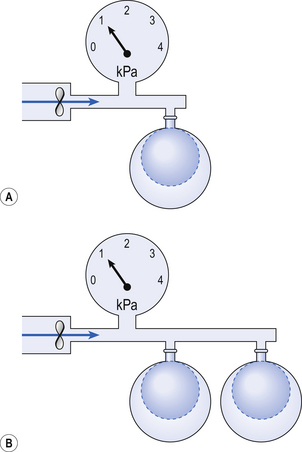
If you connect a single balloon to the pump and it inflates 2 L the balloon has a compliance (volume increase/pressure) of 2 L kPa−1 (Fig. 3.16A).
If two balloons are connected to the pump they will both be subjected to a pressure of 1 kPa and increase in volume by 2 L each (4 litres in all), which gives the sys-tem a compliance (volume increase/pressure) of 4 L kPa−1 (Fig. 3.16B).
Dynamic compliance
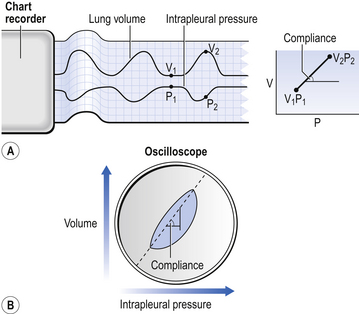
The ‘static conditions’ referred to above and in Figure 3.14 consist of the lung neither inhaling nor exhaling while pressure is being measured. These no-flow conditions only occur at two points during normal breathing: at the peak of inspiration and at the trough of expiration (Fig. 3.17).
This fact can be used to measure compliance while the subject is breathing – dynamic compliance – by measuring intrapleural pressure and lung volume at the same time (Fig. 3.17A). Alternatively, these two variables can be displayed as a loop (Fig. 3.17B), and in this case the angle of the long axis of the loop (volume/pressure) represents dynamic compliance. In this case the area of the loop represents the work of breathing.
The thoracic cage
At the end of expiration the lungs do not collapse totally because the thoracic cage is holding them out in a slightly expanded condition. This means that the thorax is slightly pulled in. Because of this the elasticity of the thorax initially helps inspiration. The thorax reaches its neutral position at about two-thirds vital capacity, and after that the direction of its elastic forces is in favour of expiration (Fig. 3.18).
Total compliance (Ctot)
Because the lungs fit inside the thorax, rather like the innertube inside a tyre, they must be treated as elements in parallel rather than in series when their properties are added together (Fig. 3.19).
Because the compliance of the lungs and that of the chest wall are about the same (2 L kPa−1), an artificial ventilator needs to apply twice the normal change in intrapleural pressure to the air in the lungs of a paralysed patient to produce the normal volume change.
Factors affecting lung compliance
• Lung size. The principles of calculating specific compliance (see above) tell us that although a man has a greater compliance than a mouse, this is due to the difference in the amount of lung being inflated. The lung volume at which compliance is measured is a different effect from that of the amount of lung present, and also exerts an effect.
• Recent pattern of breathing. Compliance is affected by breath-holding and recent pattern of breathing, probably owing to redistribution of air in the lungs, closing and opening of alveoli, stress relaxation and changes in circulation.
• Age. Because a large part of lung compliance is due to a surface tension effect that does not age, there is little effect of healthy ageing on compliance.
• Posture. The changes in lung compliance seen with posture are probably due to the effect of posture on lung volume.
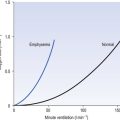
• Disease. Most diseases of the lung – congestion, fibrosis, consolidation, respiratory distress syndrome – decrease its compliance. Emphysema is unique in that static compliance is increased owing to the loss of lung tissue. Even in emphysema, however, dynamic compliance is decreased because of the disordered distribution of ventilation.