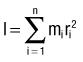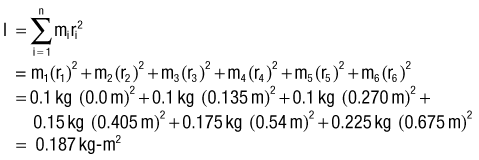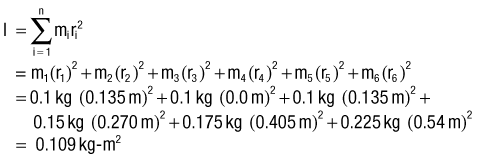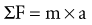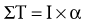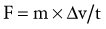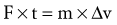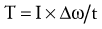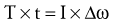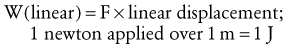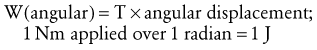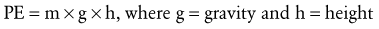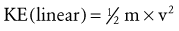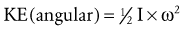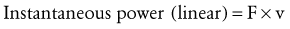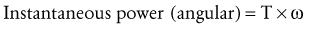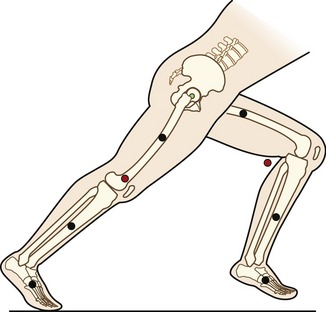
In addition to the human body as a whole, each segment, such as the arm or trunk, also has a defined center of mass. In the lower extremity, for example, the major segments include the thigh, shank (lower leg), and foot. Figure 4-1 shows the center of mass of these segments for the lower extremities of a sprinter, indicated by black circles. The location of the center of mass within each segment remains fixed, approximately at its midpoint. In contrast, however, the location of the center of mass of the entire lower extremity changes with a change in spatial configuration of the segments (compare red circles in Figure 4-1). As shown for the left (flexed) lower extremity, the specific configuration of the segments can displace the center of mass of the lower limb outside the body. Additional information regarding the center of mass of body segments is discussed later in this chapter under the topic of anthropometry.

FIGURE 4-1. Lower extremities of a sprinter are illustrated, showing the centers of mass for the thigh, shank (lower leg), and foot segments as black circles. The center of mass for each lower extremity is shown as a red circle. The center of mass of the sprinter’s left lower extremity exists outside of the body. The axis of rotation of the right hip is indicated by the smaller green circle.

The mass moment of inertia of a body is a quantity that indicates its resistance to a change in angular velocity. Unlike inertia, its linear counterpart, the mass moment of inertia depends not only on the mass of the body, but, perhaps more important, on the distribution of its mass with respect to an axis of rotation.⁷ (Mass moment of inertia is often indicated by I and is expressed in units of kilograms-meters squared [kg-m²]). Because most human motion is angular rather than linear, the concept of mass moment of inertia is very relevant and important. Consider again the two positions of the lower extremities of the sprinter in Figure 4-1. Within each segment, the individual centers of mass of the thigh, shank, and foot are in the same location in both lower extremities; however, because of the different degrees of knee flexion, the distances of the centers of mass of the shank and foot segments have changed relative to the hip joint. As a consequence the mass moment of inertia of each entire limb changes; the right extended (and “longer”) lower extremity has a greater mass moment of inertia than the left. (Another way of conceptualizing the increase is to note that as the knee extends, the center of mass of the entire right lower extremity, depicted by the red circle, moves farther from the hip, thereby increasing its mass moment of inertia.) The ability to actively change an entire limb’s mass moment of inertia can profoundly affect the muscle forces and joint torques necessary for movement. For example, during the swing phase of running, the entire lower limb functionally shortens by the combined movements of knee flexion and ankle dorsiflexion (as in the left lower extremity in Figure 4-1). The lower limb’s reduced mass moment of inertia reduces the torque required by the hip muscles to accelerate and decelerate the limb during swing phase. This concept can be readily appreciated during the swing phase while running with the knees held nearly extended (increased I), or almost fully flexed (decreased I).

The concept of mass moment of inertia applies to both rehabilitation and recreational settings. Consider, for example, the design of a prosthesis for the person with a lower limb amputation. The use of lighter components in the foot prosthesis, for example, not only reduces the overall mass (and weight) of the prosthesis, but also results in a change in the distribution of the mass to a more proximal location in the leg. As a result, less resistance is imposed on the remaining limb during the swing phase of gait. The benefit of these lighter components is realized in terms of lessened energy requirements for the person with an amputation. Changing footwear can also make a difference. Consider changes in the mass moment of inertia and resultant required torques for gait when the person changes from wearing a lightweight tennis shoe to a wearing a heavy winter boot.

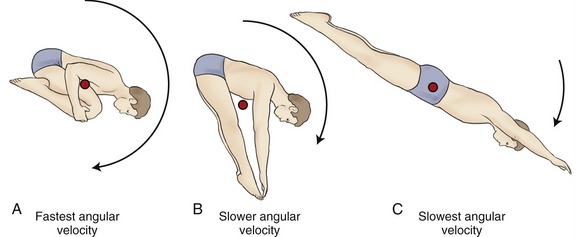
Athletes often attempt to control the mass moment of inertia of their entire body by altering the position of their individual body segments relative to the axis of rotation. This concept is well illustrated by divers who reduce their moment of inertia in order to successfully complete multiple somersaults while in the air (Figure 4-2, A). The athlete can assume an extreme “tuck” position by placing the head near the knees, holding the arms and legs tightly together, thereby bringing their segments’ centers of gravity closer to the axis of rotation. Based on the principle of “conservation of angular momentum,” reducing the body’s mass moment of inertia results in an increased angular velocity. Conversely, the athlete could slow the rotation by assuming a “pike” (see Figure 4-2, B) position and increasing the body’s moment of inertia, or assuming a “layout” position (see Figure 4-2, C), which maximizes the body’s mass moment of inertia and greatly slows the body’s angular velocity.

FIGURE 4-2. A diver illustrates an example of how the mass moment of inertia around a medial-lateral axis (red circle) can be altered through changes in position of the extremities. In position A, the diver decreases the mass moment of inertia, which increases the angular velocity of the spin. In positions B and C, the extremities are positioned progressively farther from the axis, and the angular velocity is progressively slower.

SPECIAL FOCUS 4-1 A Closer Mathematic Look at the Concept of Mass Moment of Inertia

Thus far in this chapter, the concept of mass moment of inertia (I) has been described primarily from a functional standpoint. It may be instructive, however, to consider this physical property from a more mathematic perspective. I is formally defined in the following equation, in which n indicates the number of particles in a body, m_i is the mass of each particle in the body, and r_i is the distance of each particle to the axis of rotation.

Mass Moment of Inertia

(Equation 4.2)

As a way to further explore Equation 4.2, it will be used to determine how the grip applied to a baseball bat dramatically affects its mass moment of inertia and therefore the difficulty in swinging the bat. The bat illustrated in Figure 4-3 is considered to consist of six point masses (m₁ to m₆), ranging from 0.1 to 0.225 kg, each located 0.135 m from another. During the swing the batter rotates the bat; for illustration purposes the axis of this rotation is positioned as Y₁ (red line). If the bat is not sized correctly for the batter, the batter will often “choke up” by shifting his or her grip farther down the bat; again, for illustration purposes, the axis is now positioned as Y₂ (blue line). The calculations shown in the box demonstrate how the distribution of the mass particles, relative to a given axis of rotation, dramatically affects the mass moment of inertia of the rotating bat. First consider Y₁ as the axis of rotation. The mass moment of inertia of the bat is determined using Equation 4.2 and substituting known values. Next, consider Y₂ as the axis of rotation. The important point here is that the mass particles are distributed differently when each axis is considered separately. As seen in the calculations, the mass moment of inertia when considering Y₂ as the axis is 58% of that if Y₁ is the considered axis. This means that the batter could achieve the same angular acceleration with 58% less torque. Or, for the same torque, the bat would accelerate 1.72 times as fast. This is a significant functional advantage gained by choking up on the bat; the bat is easier to swing, although its mass and weight have not changed. The reason for the reduced moment of inertia is that mass points m₂ through m₆ are closer to the Y₂ axis. This is very significant mathematically when one considers that the mass moment of inertia of each point is related to the square of the distance to the axis.

FIGURE 4-3. A baseball bat is shown with a potential to rotate around two separate axes of rotation (Y₁, Y₂). The set of calculations associated with each axis of rotation shows how the distribution of mass relative to the axis of rotation affects the mass moment of inertia. The bat is assumed to consist of six mass points (m₁ to m₆), ranging from 0.1 to 0.225 kg, located at equal distances from one another.

Y₁ Axis of Rotation

Y₂ Axis of Rotation

The mass moment of inertia of human body segments is more difficult to determine than for the baseball bat, although they are based on the same mathematic principle. Much of the difficulty stems from the fact that segments in the human body are made up of different tissues, such as bone, muscle, fat, and skin and are not of uniform density. Values for the mass moment of inertia for each body segment have been generated from cadaver studies, mathematic modeling, and various imaging techniques.3,8

NEWTON’S SECOND LAW: LAW OF ACCELERATION

Force (Torque)-Acceleration Relationship: Newton’s second law states that the linear acceleration of a body is directly proportional to the force causing it, takes place in the same direction in which the force acts, and is inversely proportional to the mass of the body. Newton’s second law generates an equation that relates force (F), mass (m), and acceleration (a) (Equation 4.1). Conceptually, Equation 4.1 defines a force-acceleration relationship. Considered a cause-and-effect relationship, the left side of the equation, force (F), can be regarded as a cause because it represents a pull or push exerted on a body; the right side, m × a, represents the effect of the pull or push. In this equation, ΣF designates the sum of, or net, forces acting on a body. If the sum of the forces acting on a body is zero, acceleration is also zero and the body is in linear equilibrium. As previously discussed, this case is described by Newton’s first law. If, however, the net force produces acceleration, the body will accelerate in the direction of the resultant force. In this case, the body is no longer in equilibrium.

Newton’s Second Law of Linear Motion Quantifying a Force

(Equation 4.1)

Force is measured in newtons, where 1 newton (N) = 1 kg-m/sec².

The rotary or angular counterpart to Newton’s second law states that a torque will cause an angular acceleration of a body around an axis of rotation. Furthermore, the angular acceleration of a body is directly proportional to the torque causing it, takes place in the same rotary direction in which the torque acts, and is inversely proportional to the mass moment of inertia of the body. (The italicized words denote the essential differences between the linear and angular counterparts of this law.) For the rotary condition, Newton’s second law generates an equation that relates the torque (T), mass moment of inertia (I), and angular acceleration (α) (Equation 4.3). (This chapter uses the term torque. The reader should be aware that this term is interchangeable with terms moment and moment of force.) In this equation, ΣT designates the sum of, or net, torques acting to rotate a body. Conceptually, Equation 4.3 defines a torque–angular acceleration relationship. Within the musculoskeletal system, the primary torque producers are muscles. A contracting biceps muscle, for example, produces a net internal flexion torque at the elbow. Neglecting external influences such as gravity, the angular acceleration of the rotating forearm is proportional to the internal torque (i.e., the product of the muscle force and its internal moment arm) but is inversely proportional to the mass moment of inertia of the forearm-and-hand segment. Given a constant internal torque, the forearm-and-hand segment with the smaller mass moment of inertia will achieve a greater angular acceleration than one with a larger mass moment of inertia. (A smaller mass moment of inertia can be achieved by moving a cuff weight from the wrist to the mid-forearm, for example.) Understand that this inertial resistance to the angular acceleration of the limb applies even in the absence of gravity. For example, consider the positions of the lower limb in Figure 4-1 but with the person on his or her side in a “gravity eliminated” position. Because of changes in the mass moment of inertia, less muscular effort will be required to flex the hip with the knee also flexed than with the knee extended.

Newton’s Second Law of Rotary Motion Quantifying a Torque

(Equation 4.3)

Torque is expressed in newton-meters, where 1 Nm = 1 kg-m² × radians/sec².

Impulse-Momentum Relationship: Additional relationships can be derived from Newton’s second law through the broadening and rearranging of Equations 4.1 and 4.3. One such relationship is the impulse-momentum relationship.

Acceleration is the rate of change of velocity (Δv/t). Substituting this expression for linear acceleration in Equation 4.1 results in Equation 4.4. Equation 4.4 can be further rearranged to Equation 4.5.

(Equation 4.4)

(Equation 4.5)

Application of a linear impulse (force multiplied by time) leads to a change in linear momentum (mass multiplied by a change in linear velocity).

The product of mass and velocity on the right side of Equation 4.5 defines the momentum of a moving body. Momentum describes the quantity of motion possessed by a body. Momentum is generally represented by the letter p and has units of kilogram-meters per second (kg-m/sec). An impulse is a force applied over a period of time (the product of force and time on the left side of Equation 4.5). The linear momentum of an object such as a moving car is changed by the application of a force over a given time. When a quick change in momentum is required (during an emergency stop, for instance), a very large brake force is applied for a short time. Less brake force for the same time, or the same brake force for even less time, results in a smaller change in momentum. Impulse and momentum are vector quantities. Equation 4.5 defines the linear impulse-momentum relationship.

The impulse-momentum relationship provides another perspective from which to study human performance, as well as to gain insight into injury mechanisms. At certain locations the body develops mechanisms and structures to lessen peak external load forces. For example, when landing from a jump, peak forces can be reduced throughout the joints of the lower extremities if the impact of the landing is prolonged by more “give” in the muscles—through a lower level and prolonged eccentric activation. As another example, as the foot contacts the ground during normal gait, the fat pad over the plantar surface of the calcaneus cushions the interaction between the foot and the ground and works to decrease peak reaction forces. Running footwear often augments this function with shock-absorbing outsoles to further cushion the impact of the foot on the ground. Bicycle helmets, rubber or springed flooring, and protective padding are additional examples of equipment designs intended to reduce injuries by increasing the duration of impact in order to minimize the peak force of the impact.

Newton’s second law involving torque can also apply to the rotary case of the impulse-momentum relationship. Similar to the substitutions and rearrangements for the linear relationship, the angular relationship can be expressed by substitution and rearrangement of Equation 4.3. Substituting Δω/t (rate of change in angular velocity) for α (angular acceleration) results in Equation 4.6. Equation 4.6 can be rearranged to Equation 4.7—the angular equivalent of the impulse-momentum relationship. Torque and angular momentum are also vector quantities.

(Equation 4.6)

(Equation 4.7)

Application of an angular impulse (torque multiplied by time) leads to a change in angular momentum (mass moment of inertia times a change in angular velocity).

SPECIAL FOCUS 4-2 A Closer Look at the Impulse-Momentum Relationship

Numerically, an impulse can be calculated as the product of the average force (N) and its time of application. Impulse can also be represented graphically as the area under a force-time curve. Figure 4-4 displays a force-time curve of the horizontal component of the anterior-posterior shear force applied by the ground against the foot (ground reaction force) as an individual runs across a force plate embedded in the floor. The curve is biphasic: the posterior-directed impulse during initial floor contact is negative, and the anterior-directed impulse during propulsion is positive. If the two impulses (i.e., areas under the curves) are equal, the net impulse is zero, and there is no change in the momentum of the system. In this example, however, the posterior-directed impulse is greater than the anterior, indicating that the runner’s forward momentum is decreased.

FIGURE 4-4. Graphic representation of the areas under a force-time curve showing the (A) posterior-directed and (B) anterior-directed impulses of the horizontal component of the ground reaction force while running.

Work-Energy Relationship: To this point, Newton’s second law has been described using (1) the force (torque)-acceleration relationship (Equations 4.1 and 4.3) and (2) the impulse-momentum relationship (Equations 4.4 through 4.7). Newton’s second law can also be restated to provide a work-energy relationship. This third approach can be used to study human movement by analyzing the extent to which work causes a change in an object’s energy. Work occurs when a force or torque operates over some linear or angular displacement. Work (W) in a linear sense is equal to the product of the magnitude of the force (F) applied against an object and the linear displacement of the object in the direction of the applied force (Equation 4.8). If no movement occurs in the direction of the applied force, no mechanical work is done. Similar to the linear case, angular work can be defined as the product of the magnitude of the torque (T) applied against the object, and the angular displacement of the object in the direction of the applied torque (Equation 4.9). Work is expressed in joules (J).

SPECIAL FOCUS 4-3 Positive Work, Negative Work, and “Isometric Work”

As described, linear work is found by multiplying an applied force by the object’s displacement in the direction of the applied force. Consider, for example, the linear force applied by the contracting elbow flexor muscles to flex the elbow and bring the hand to the mouth. In a linear sense, the work is the product of the muscles’ contractile force and the distance the muscles shortened. In an angular sense, the rotary work is computed by the torque applied by the elbow flexors and the amount of flexion (in radians) occurring at the elbow. In this case the work is positive because the rotation of the forearm is in the same direction as the applied torque. In addition, the elbow flexors are shortening through concentric activation, and the work is being performed by the muscles. In contrast, when the elbow flexors are active, but the elbow is extending (e.g., when slowly lowering a weight), the elbow flexors are lengthening through an eccentric activation, and the work is being performed on the muscles. In this case, because the rotation is in a direction opposite to the applied torque, the work is negative. The final scenario is when the elbow flexors are active but no movement is taking place, as when a muscle is active isometrically. In this case, even though considerable metabolic energy may be expended, no mechanical work is being performed.

Relationships between Work (W), Potential Energy (PE), and Kinetic Energy (KE)

(Equation 4.8)

(Equation 4.9)

Just as the impulse-momentum relationship describes the change in momentum caused by a force applied over a given time, the work-energy relationship describes the change in kinetic energy caused by a force applied over a given displacement. Using the example described earlier can illustrate the similarity in these concepts. The kinetic energy of an object such as a moving car is changed by the application of a force over a displacement. When a quick change in kinetic energy is required (e.g., for an emergency stop), a very large brake force is applied over a short displacement. Less brake force for the same displacement or the same brake force applied for even less displacement results in a smaller change in kinetic energy. Work and displacement are vector quantities.

The work-energy relationship does not take into account the time over which the forces or torques are applied. Yet in most daily activities it is often the rate of performing work that is important. The rate of performing work is defined as power. The ability for muscles to generate adequate power may be critical to the success of movement or to the understanding of the impact of a treatment intervention. On the basketball court, for example, it is often the player’s vertical speed at takeoff that determines success in achieving a rebound. Another example of the importance of the rate of work can be appreciated in an elderly person with Parkinson’s disease who must cross a busy street in the time determined by a pedestrian traffic signal.

Average power (P) is work (W) divided by time (Equation 4.10). Because work is the product of force (F) and displacement (d), the rate of work at any instant can be restated in Equation 4.11 as the product of force and velocity. Angular power may also be defined as in the linear case, using the angular analogs of force and linear velocity: torque (T) and angular velocity (ω), respectively (Equation 4.12). Angular power is often used as a clinical measure of muscle performance. The mechanical power produced by the quadriceps, for example, is equal to the net internal torque produced by the muscle times the average angular velocity of knee extension. Power is often used to designate the net transfer of energy between active muscles and external loads. Positive power reflects the rate of work done by concentrically active muscles against an external load. Negative power, in contrast, reflects the rate of work done by the external load against eccentrically active muscles.

Power (P)

(Equation 4.10)

(Equation 4.11)

(Equation 4.12)

Table 4-2 summarizes the definitions and units needed to describe many of the physical measurements related to Newton’s second law.

TABLE 4-2.

Physical Measurements Associated with Newton’s Second Law

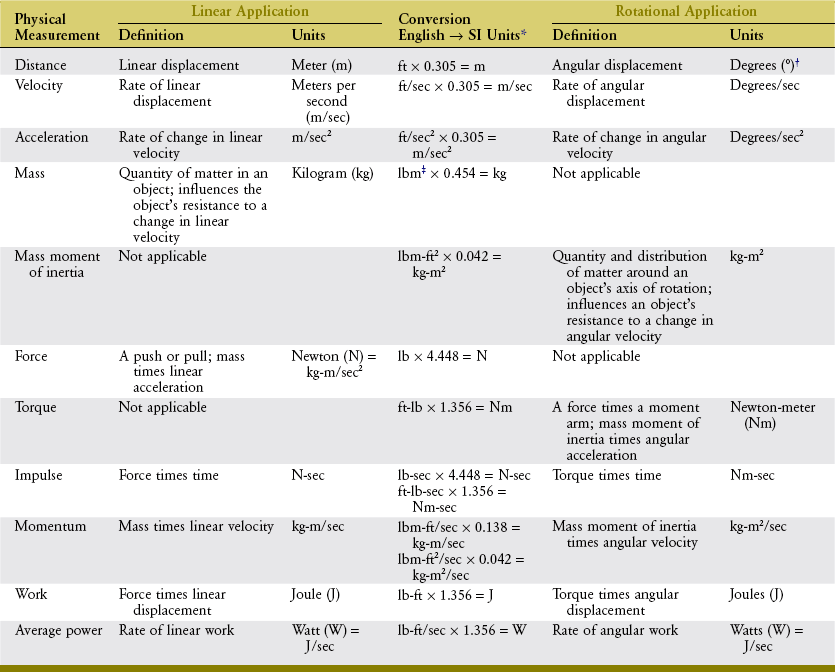
^*To convert from English units to SI units, multiply the English value by the number in the table cell. To convert from SI units to English, divide by that number. If two equations are in the cell, the upper equation is used to convert the linear measure, and the lower equation is used to convert the angular measure.

^†Radians, which are unitless, may be used instead of degrees (1 radian = about 57.3 degrees).

^‡The English unit of a mass is a pound-mass (lbm) or slug.

NEWTON’S THIRD LAW: LAW OF ACTION-REACTION

Newton’s third law of motion states that for every action there is an equal and opposite reaction. This law implies that every effect one body exerts on another is counteracted by an effect that the second body exerts on the first. The two bodies interact simultaneously, and the consequence is specified by Newton’s law of acceleration (ΣF = m × a); that is, each body experiences a different effect, and that effect depends on its mass. For example, a person who falls off the roof of a second-story building exerts a force on the ground, and the ground exerts an equal and opposite force on the person. Because of the huge discrepancies in mass between the earth and the person, the effect, or acceleration experienced by the person, is much greater than the effect “experienced” by the ground. As a result, the person may sustain significant injury.

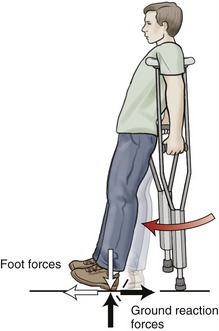
Another example of Newton’s law of action-reaction is the reaction force provided by the surface on which one is walking or standing. The foot produces a force against the ground, and in accordance with Newton’s third law, the ground generates a ground reaction force in the opposite direction but of equal magnitude (Figure 4-5). The ground reaction force changes in magnitude, direction, and point of application on the foot throughout the stance period of gait. Newton’s third law also has an angular equivalent. For example, during an isometric exercise, the internal and external torques are equal and in opposite rotary directions.

FIGURE 4-5. The action of the forces produced between the ground and foot are illustrated during the contact phase of the “swing-through” method of crutch-assisted walking. The action of the foot forces (white arrows) is counteracted by the ground reaction forces (black arrows). If the horizontal component of the ground reaction force (caused by friction) is less than the horizontal component of the foot force, the foot will slide forward on the floor according to Newton’s second law: F = m × a.

INTRODUCTION TO MOVEMENT ANALYSIS: SETTING THE STAGE FOR ANALYSIS

The previous section describes the nature of the cause-and-effect relationships between force and motion as outlined by Newton’s laws. Now that this foundation has been established, this section introduces the steps and conventions used to formally analyze movement. Special attention is paid to the analysis of internal and external forces and torques and how these variables affect the body and its joints. This section should fully prepare the reader to follow the mathematic solutions to three sample problems constructed in the next section.

Anthropometry

Anthropometry is derived from the Greek root anthropos, man, + metron, measure. In the context of human movement analysis, anthropometry may be broadly defined as the measurement of certain physical design features of the human body, such as length, mass, weight, volume, density, center of gravity, and mass moment of inertia. Knowledge of these parameters is often essential to conducting kinematic and kinetic analyses for both normal and pathologic motion. Variables such as mass and mass moment of inertia of individual limb segments, for example, are needed to determine the inertial properties that muscles must overcome to generate movement. Anthropometric information is also valuable in the design of the work environment, furniture, tools, and sports equipment.

Much of the information pertaining to the body segments’ center of gravity and mass moment of inertia has been derived from cadaver studies.3,4 Other methods for deriving anthropometric data include mathematic modeling and imaging techniques, such as computed tomography and magnetic resonance imaging. Table 4-3 lists data on the weights of body segments and the location of the center of gravity. (The specific details contained in this table will be needed to solve selected parts of the biomechanical problems posed in Appendix I, Part B).

TABLE 4-3.

Anthropometric Data on Body Segments’ Weight and Center of Gravity Location in the Anatomic Position (Extremity Data Are Unilateral Only)

Compiled results in Winter DA: Biomechanics and motor control of human movement, ed 3, New York, 2005, John Wiley & Sons. Mass moments of inertia are not included in this table because the focus of this chapter is limited to static analysis.

^*Even though some definitions listed in this table do not represent the endpoints of the segment, they are easily identified locations on the human. The values for segment weight and center of gravity location in this table take into consideration the discrepancy between the definition of the segment and the true endpoints. For example, the segment definition for the forearm is the same for the forearm-and-hand, but the percentages listed for the segment weight and center of gravity location of the forearm-and-hand are higher, taking into consideration the mass of the hand.

Free Body Diagram

The analysis of movement requires that all forces that act on the body be taken into account. Before any analysis, a free body diagram is constructed to facilitate the process of solving biomechanical problems. The free body diagram is a “snapshot” or simplified sketch that represents the interaction between a body and its environment. The body under consideration may be a single rigid segment, such as the foot, or it may be several segments, such as the head, arms, and trunk. When the body consists of several segments, these are assumed to be rigidly connected together into a single rigid system.

A free body diagram requires that all relevant forces acting on the system are carefully drawn. These forces may be produced by muscle, gravity (as reflected in the weight of the segment), fluid, air resistance, friction, and ground reaction forces. Arrows are used to indicate force vectors.

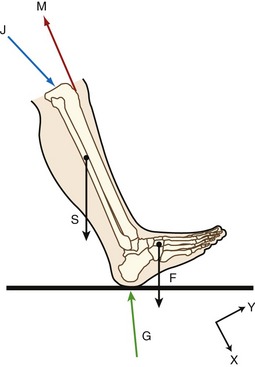
How a free body diagram is configured depends on the intended purpose of the analysis. Consider the example presented in Figure 4-6. In this example, the free body diagram represents the shank-and-foot at the instant of initial heel contact during walking. The free body diagram involves figuratively “cutting through” the desired joint(s) to isolate or “free” the body of interest. In the example presented in Figure 4-6, the knee joint was cut through to isolate the shank-and-foot segment. The effects of active muscle force are usually distinguished from the effects of other soft tissues, such as passive tension created in stretched joint capsule and ligaments. Although the contribution of individual muscles acting across a joint may be determined, a single resultant muscle force (M) vector is often used to represent the sum total of all individual muscle forces. Other forces external to the system are added to the diagram, which may include the ground reaction force (G) and weight of the shank-and-foot segments (S and F). As specified by Newton’s third law, the ground reaction force is the force developed in response to the foot striking the earth.

FIGURE 4-6. Free body diagram of the shank-and-foot at the instant of heel contact during walking. The segment is isolated by figuratively “cutting through” the knee joint. Relevant forces are drawn in as shown. The X-Y coordinate reference frame is placed so the X axis is parallel with the shank.

An additional force is identified in Figure 4-6: the joint reaction force (J). This force includes joint contact forces as well as the net or cumulative effect of all other forces transmitted from one segment to another. Joint reaction forces are caused “in reaction” to other forces, such as those produced by activation of muscle, by passive tension in stretched periarticular connective tissues, and by gravity (body weight). As will be discussed, the free body diagram is completed by defining an X-Y coordinate reference frame and writing the governing equations of motion.

Clinically, reducing joint reaction force is often a major focus in treatment programs designed to lessen pain and prevent further joint degeneration in persons with arthritis. Frequently, treatments are directed toward reducing joint forces through changes in the magnitude of muscle activity and their activation patterns or through a reduction in the weight transmitted through a joint. Consider the patient with osteoarthritis of the hip joint as an example. The magnitude of the hip joint’s reaction force may be decreased by having the person reduce walking velocity, thereby lessening the magnitude of muscle activation. Highly cushioned shoes may be recommended to reduce impact forces. In addition, a cane may be used to reduce forces through the hip joint.1,10,13 If obesity is a factor, a weight-reduction program may be recommended.

STEPS FOR CONSTRUCTING THE FREE BODY DIAGRAM

The key elements needed to begin solving problems related to human movement are to determine the purpose of the analysis, identify the free body of interest, and indicate all the forces that act on that body. The following example presents steps to assist with construction of a free body diagram.

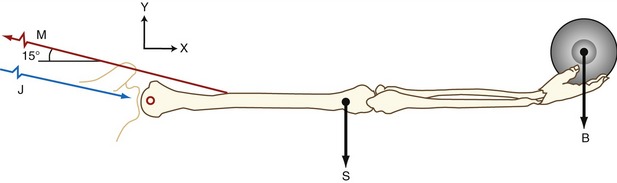
Consider the situation in which an individual is holding a weight out to the side, as shown in Figure 4-7. This free body is assumed to be in static equilibrium, and the sum of all forces and the sum of all torques acting on the body are equal to zero. One purpose of the analysis might be to determine how much muscle force is required by the glenohumeral joint abductor muscles (M) to keep the arm abducted to 90 degrees; another purpose might be to determine the magnitude of the glenohumeral joint reaction force (J) during this same activity.

FIGURE 4-7. A frontal plane depiction of a free body diagram isolating the system as a right arm and ball combination: resultant shoulder abductor muscle force (M); glenohumeral joint reaction force (J); segment weight (S); and ball weight (B). The axis of rotation is shown as an open red circle at the glenohumeral joint. The X-Y coordinate reference frame is placed so the X axis is parallel with the upper extremity. (Modified from LeVeau BF: Williams & Lissner’s biomechanics of human motion, ed 3, Philadelphia, 1992, Saunders.)

Step I of constructing the free body diagram is to identify and isolate the free body under consideration. In this example, the glenohumeral joint was “cut through,” and the free body is the combination of the entire arm and the resistance (exercise ball weight).

Step II involves defining a coordinate reference frame that allows the position and movement of a body to be defined with respect to a known point, location, or axis (see Figure 4-7, X-Y coordinate reference frame). More detail on establishing a reference frame is discussed ahead.

Step III involves identification and inclusion of all forces that act on the free body. Internal forces are those produced by muscle (M). External forces include the force of gravity on the mass of the exercise ball (B), as well as the force of gravity on the arm segment (S). Although not relevant to Figure 4-7, other examples of external forces could include forces applied by therapists, cables, resistance bands, the ground or other surface, air resistance, and orthotics. The forces are drawn on the figure while specifying their approximate point of application and spatial orientation. For example, vector S acts at the center of gravity of the upper extremity, a location determined by using anthropometric data, such as those presented in Table 4-3.

The direction of the muscle force (M) is drawn to correspond to the line of muscle pull and in a direction to generate torque that opposes the net torque produced by the external forces. In this example the torque produced by the external forces, S and B, tends to rotate the arm in a clockwise, adduction, or −Z direction. The line of force of M, therefore, in combination with its moment arm, creates a torque in a counterclockwise, abduction direction, or +Z direction. (The convention of using + or −Z to designate rotation direction is described ahead.)

Step IV of the procedure is to show the joint reaction force (J), in this case created across the glenohumeral articulation. Initially the direction of the joint reaction force may not be known, but, as explained later, it is typically drawn in a direction opposite to the pull of the dominant muscle force. The precise direction of J can be determined after static analysis is carried out and unknown variables are calculated.

Step V involves writing the three governing equations required to solve two-dimensional (2D) static equilibrium problems encountered in this chapter. The equations are: ΣTorque_Z = 0; ΣForce_X = 0; ΣForce_Y = 0. These equations are explained later in the chapter.

Steps in Constructing the Free Body Diagram

Step I: Identify and isolate the free body under consideration.

Step II: Establish a coordinate reference frame.

Step III: Draw the internal (muscular) and external forces that act on the system.

Step IV: Draw the joint reaction force.

Step V: Write the governing equations of motion.

SPATIAL REFERENCE FRAMES

In order to accurately describe motion or solve for unknown forces, a spatial reference frame needs to be established. This information allows the position and direction of movement of a body, a segment, or an object to be defined with respect to some known point, location, or segment’s axis of rotation. If a reference frame is not identified, it becomes very difficult to interpret and compare measurements in clinical and research settings.

A spatial reference frame is arbitrarily established and may be placed inside or outside the body. Reference frames used to describe position or motion may be considered either relative or global. A relative reference frame describes the position of one limb segment with respect to an adjacent segment, such as the foot relative to the leg, the forearm relative to the upper arm, or the trunk relative to the thigh. A measurement is made by comparing motion of an anatomic landmark or coordinates between segments of interest. Goniometry provides one example of a relative reference frame used in clinical practice. Elbow joint range of motion, for example, describes a measurement using a relative reference frame defined by the long axes of the upper arm and forearm segments, with an axis of rotation through the elbow.

Relative reference frames, however, lack the information needed to define motion with respect to a fixed point or location in space. To analyze motion with respect to the ground, direction of gravity, or another type of externally defined reference frame in space, a global (laboratory) reference frame must be defined. Excessive anterior or lateral deviations of the trunk during gait are examples of a measurement made with respect to a global reference frame. In these examples, the position of the trunk is measured with respect to an external vertical reference.

Whether motion is measured via a relative or global reference frame, the location of a point or segment in space can be specified using a coordinate reference frame. In laboratory-based human movement analysis, the Cartesian coordinate system is most frequently employed. The Cartesian system uses coordinates for locating a point on a plane in 2D space by identifying the distance of the point from each of two intersecting lines, or in three-dimensional (3D) space by the distance from each of three planes intersecting at a point. A 2D coordinate reference frame is defined by two imaginary axes arranged perpendicular to each other with the arrowheads pointed in positive directions. The two axes (labeled, for example, X and Y) may be oriented in any manner that facilitates quantitative solutions (compare Figures 4-6 and 4-7, for example). A 2D reference frame is frequently used when the motion being described is predominantly planar (i.e., in one plane), such as knee flexion and extension during gait.

In most cases, human motion occurs in more than one plane. In order to fully describe this type of motion, a 3D coordinate reference frame is necessary. A 3D reference frame typically has three axes (X, Y, and Z), each perpendicular (or orthogonal) to another. As with the 2D system, the arrowheads point in positive directions. A universal convention for orienting this triplanar coordinate system in space is based on the right-hand rule. This rule is used throughout most quantitative biomechanical studies (see Special Focus 4-4).

Throughout most of this textbook, the terminology used to describe linear direction within planes (such as the direction of a muscle force or an axis of rotation around a joint) is less formal than that dictated by the right-hand rule. As described in Chapter 1, linear direction in space is loosely described relative to the human body standing in the anatomic position, using terms such as anterior-posterior, medial-lateral, and vertical. Although useful for most qualitative or anatomic-based descriptions, this convention is not well suited for quantitative analyses, such as those introduced later in this chapter. In these cases, the Cartesian coordinate system is used, and the orientation of its 3D axes is designated by the right-hand rule.

SPECIAL FOCUS 4-4 The “Right-Hand Rule”: a Convention for Completely Describing the Spatial Orientation of a Three-Dimensional Coordinate Reference Frame

When a Cartesian coordinate system is set up, the direction or orientation of the orthogonal axes is not arbitrary. A convention must be used to facilitate the sharing of research from different laboratories throughout the worldwide scientific community. Using Figure 4-7 as an example, the X and Y axes are in the plane of the page or, relative to the subject, parallel with the frontal plane. (It is often most convenient, although not mandatory, to orient the X-Y axes so that the X axis is parallel with the body segment of interest.) A third axis, the Z axis, must be defined. Although not drawn in the figure, the Z axis is oriented perpendicular to the X-Y plane. By convention, the direction of the arrowheads shown on the X-Y coordinate reference frame indicates positive directions. As shown in Figure 4-7, positive X direction is to the right and positive Y direction is upward. The right-hand rule can be used to define the direction (+ or −) of the Z axis. Applying the right-hand rule is performed by laying the ulnar border of your right hand along the X axis, with the straight fingers pointing in a positive X direction (toward the ball on the model). Your hand should be positioned along the X axis so that when your fingers flex, they curl from the positive X direction toward the positive Y direction. Your extended thumb is pointing out of the page, thereby defining the direction of the positive Z axis. By necessity, the −Z axis is oriented perpendicularly into the page. Using the right-hand rule means that only two axes ever need to be defined and shown; use of the right-hand rule allows the third axis to be completely described.

SPECIAL FOCUS 4-5 Another Use of the “Right-Hand Rule”: a Guide for Describing the Direction of Angular Motion and Torque

Another use of the right-hand rule is to define the rotation direction of angular motion and torque. Consider once again, the coordinate reference frame depicted in Figure 4-7. This reference frame indicates that the path of humeral motion (abduction) is in the X-Y (frontal) plane, around a perpendicular anterior-posterior axis (or, as described in Special Focus 4-4, the Z axis). The right-hand rule is again applied to Figure 4-7 as follows. Begin by aligning the ulnar side of your right hand parallel with the arm segment of the model, so that flexing your fingers curls them in the rotation path of shoulder abduction. The direction of your extended thumb points in the +Z direction, indicating abduction is a positive Z rotation. Shoulder adduction is in a negative Z direction.

This right-hand rule is also used to describe the rotary direction of torque. Again the right hand is used, curling your fingers in the path of motion produced by the torque. Returning to Figure 4-7, force M, produced by the shoulder abductor muscles, generates a +Z torque, whereas the shoulder adductor muscles (not shown) generate a −Z torque. With the coordinate reference frame oriented as shown, the shoulder abductors will always generate a +Z torque, regardless of concentric action (associated with a +Z motion), or eccentric action (associated with a −Z motion).

Rotary or angular movements or torques are often described as occurring in a plane, around a perpendicular axis of rotation. In most kinesiologic literature, a segment’s rotation direction is typically described by terms such as flexion and extension and, to a lesser extent, clockwise or counterclockwise rotation.

Buy Membership for Rheumatology Category to continue reading. Learn more here