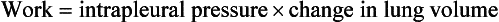AIRFLOW IN THE RESPIRATORY SYSTEM
Introduction
• blocking of the airway by secretions, e.g. in bronchitis
• reduction in airways diameter due to contraction of smooth muscle in its walls or swelling due to inflammation, e.g. in asthma and bronchitis
• collapse of the airways due to disruption of the supporting parenchyma, e.g. in emphysema, or changes in intrapleural pressure, as in cough.
How airflow is brought about
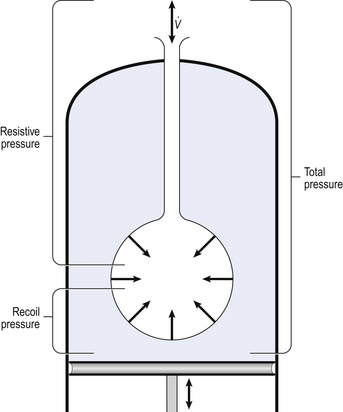
Our model from the previous chapter, which represents the respiratory system as a balloon inside a container like a syringe, is often used to illustrate the two components of intrapleural pressure mentioned above and illustrated in Figure 4.1. The plunger of the syringe represents the diaphragm, the walls of the syringe represent the chest wall, the balloon represents the alveoli, and the narrow tube represents the airways of the lung.
1. The changes in intrapleural pressure that bring about breathing can be superimposed on a small lung volume (the balloon being only slightly inflated) or on a large lung volume (the balloon very inflated). Understandably, to hold the balloon at a large volume requires greater effort, and this is what happens, for example, in asthma, where the patient breathes at an increased lung volume to keep his airways open.
2. Airflow only takes place from a region of high pressure to a region of low pressure along the airway. Therefore, at two times in each respiratory cycle (when inspiration has just ceased and is about to become expiration, or when expiration has just ceased and is about to become inspiration) there is no flow, and pressure is the same all the way from the lips to the alveoli. This fact can be used to measure dynamic lung compliance (see Fig. 3.17). It should also be noted that under conditions of normal breathing the pressure in the airways is much closer to atmospheric pressure than the pressure in the intrapleural space.
3. Recoil of the lungs produces a pressure which resists inspiration but assists expiration. This is analogous to pushing a car up a hill: the weight of the car represents recoil pressure and resists going up (inspiration). The weight of the car would, however, assist going down (expiration). This effect of helping expiration and hindering inspiration is seen in flow/volume loops used to test lung function.
The nature of airflow
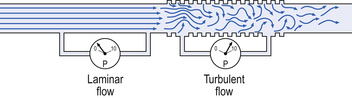
Flow in a long straight smooth tube becomes turbulent when Reynolds’ Number, which is calculated as 2rvd/η (r = radius of tube, v = velocity of flow, d = gas density, η = gas viscosity) exceeds 2000. Under turbulent conditions flow varies with the square root of the driving pressure, i.e. it is very much more difficult to produce the same flow when flow is turbulent (Fig. 4.2).
The major determinant of flow – radius
where r is the radius of the tube, η is the viscosity of the gas, and l is the length of the tube. This relationship applies to gas flow in the long straight smooth tubes under stable conditions – hardly conditions that apply to the lungs. However, it can be roughly applied to breathing, and you may notice that the most important factor affecting airflow in this equation is the radius of the tube, which is raised to the fourth power (r4). This means that if you reduce the radius by half and keep everything else constant, the flow will be reduced to 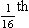 .
.
Laminar flow in a tube can be represented as a series of cylinders moving down the tube, with the central cylinder moving fastest. The outermost cylinder is stationary and is in fact a layer of the original gas in the tube left behind as the new gas moves forward, as shown in Figure 4.4.
These apparently esoteric considerations have important consequences in respiratory medicine. For example, adequate ventilation of the alveoli of the lungs can be achieved with a surprisingly small tidal volume, provided a high enough frequency of ‘breathing’ is used. This phenomenon is seen in clinical conditions when high-frequency artificial ventilation of the lungs is used where we want to avoid movements of the chest wall – in trauma victims with a crushed chest, for example. The patient is successfully artificially ventilated with a tidal volume less than his or her anatomical dead space (see p. 64) and frequencies up to 50 Hz. A ‘spear’ of fresh air in the centre of the airways penetrates deeper into the lungs than might be expected and provides adequate ventilation.
Airways resistance and obstructive pulmonary disease
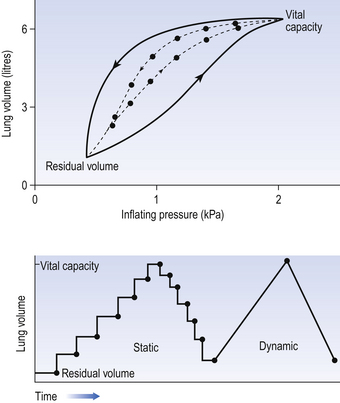
We have established that it takes a greater pressure to inflate the lungs than simply to hold them in a steady inflated state. This extra pressure is required to produce flow in the airways. We have also seen that the relationship between pressure and volume on slowly inflating and deflating the lungs is not a straight line, as you would get with a rubber balloon, but rather a loop, with a greater pressure needed to inflate the lungs to a given volume than that which exists at the same volume when they are being allowed to deflate (Fig. 4.3).
The small dotted loop in Figure 4.3 was produced by inflating and deflating the lungs extremely slowly, a situation that is called pseudostatic. If we were to carry out this inflation and deflation at a normal breathing rate (12 times per minute, say) the loop would be wider (the solid line), with inflation pressures required for a given volume being greater than under the static conditions and deflation pressures being less.
This situation arises because energy is used up to propel the air along the airways; the airways can be said to resist flow in a phenomenon known as airways resistance. This resistance during laminar flow can be thought of as the friction between the layers of air as they are pushed down the airway. Pushing a pile of typing paper or a pack of cards across a table gives a good idea of what is happening (Fig. 4.4).
As its name implies, airways resistance is analogous to electrical resistance. To measure the electrical resistance of a length of wire you need to know two things, the potential difference (voltage) between the two ends of the wire, and the current flowing in the wire. Using reasonable currents (that do not overheat the wire) we find that the relationship between voltage (V) and current (I) is a straight line (Fig. 4.5).
This is Ohm’s Law, and the slope of the line (V/I) is the resistance of the wire in ohms.
The slope of the line is the airway resistance of the tube in kPa 1−1 s.
Two important points arise from this apparently innocuous statement:
1. Airways resistance is a dynamic property and can only be measured when flow is taking place.
2. The figures used above to arrive at the figure of 0.2 kPa 1−1 apply equally well if flow is in an inspiratory or an expiratory direction: they are a property of the tube, not the direction of the flow.
The clinical situation
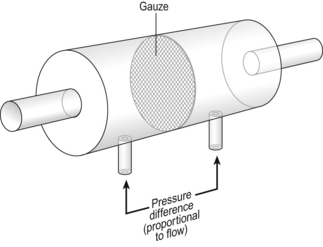
Airways resistance changes in disease and its measurement has been the focus of interest of doctors for many years. Measurement of airflow is not difficult and is usually accomplished using an instrument known as a pneumotachograph, which itself illustrates the principle of airways resistance. The pneumotachograph consists of a tube through which the subject breathes (Fig. 4.6).
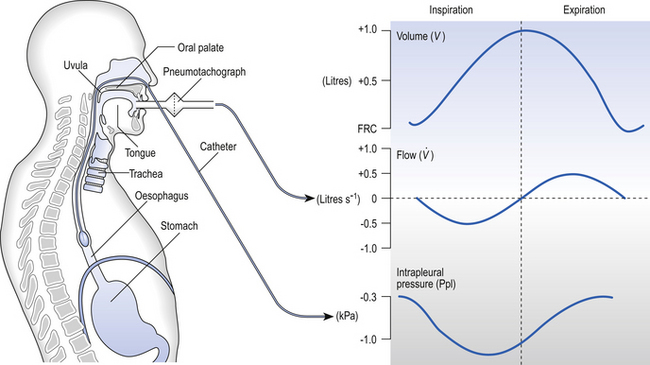
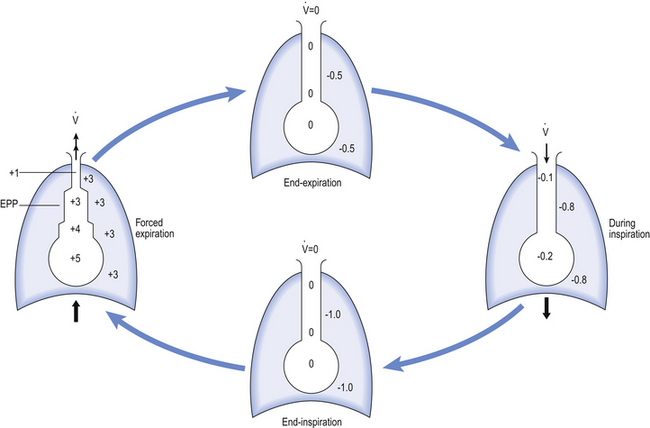
One way of getting round the problem of measuring the driving pressure is to use the fact that it is the change in alveolar pressure that brings about flow and stretches the lungs against recoil pressure. Consider the changes in intrapleural pressure and recoil pressure due to the elasticity of the lungs in a single respiratory cycle (Fig. 4.7).
Subtract changes in recoil pressure from changes in intrapleural pressure and you are left with the changes in alveolar pressure that produce changes in airflow – the two variables we are interested in to measure resistance. This subtraction process can be done instantaneously electronically, and so we need to know the changes in recoil pressure, which can be worked out from lung compliance, and the changes in intrapleural pressure, which we obtain by measuring changes in the pressure inside the oesophagus passing through the intrapleural space.
The whole-body plethysmograph
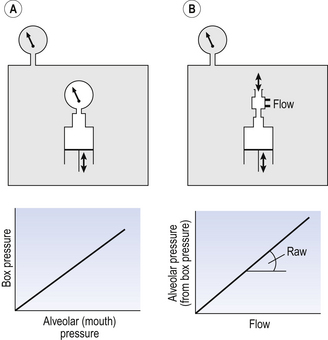
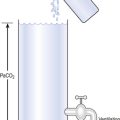
This consists of an airtight box in which the subject sits. It depends on the principle that the total quantity of air in the box (inside the patient’s lungs and around him in the box) is the same throughout the measurement – the box is airtight. The patient first pants against a closed shutter while the pressure changes in his mouth and the pressure changes in the box are measured simultaneously. The pressure changes at his mouth are assumed to be the same as those in the alveoli (by the same arguments as in the interrupter technique above). Pressure changes in the box while the patient is panting because he is compressing and decompressing the air in his lungs and therefore changing the volume of his chest in the closed box. (Consider him like the syringe in Figure 4.8: when he compresses the air in his chest he decompresses the air in the box, and when he decompresses the air in his chest he compresses the air in the box.)
The pressure changes in the box are therefore related to pressure changes in the alveoli, and so by measuring box pressure change and flow while the patient breathes through a pneumotachograph, we can measure his airways resistance. Other uses of the whole-body plethysmograph are described in Chapter 11.
Sites of airways resistance
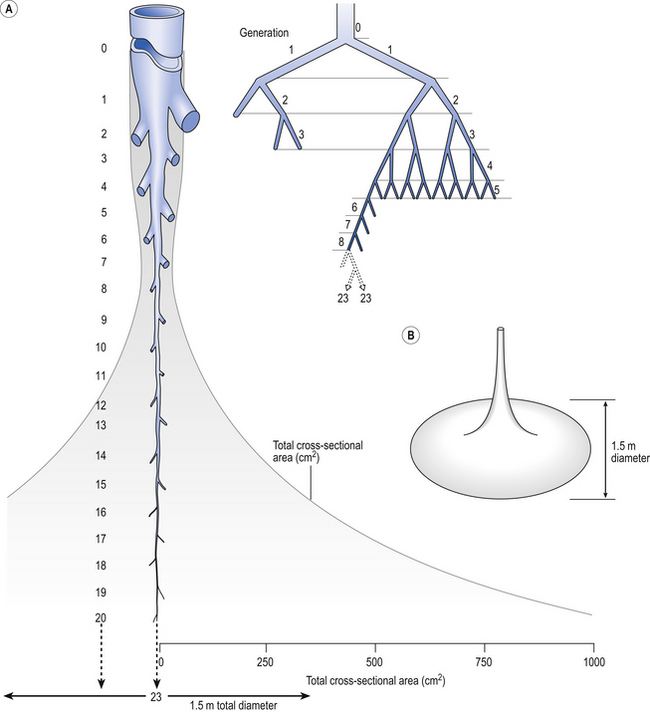
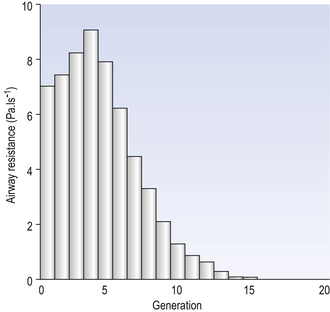
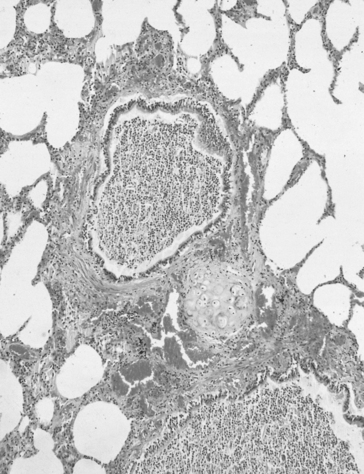
Of the approximately half total airway resistance existing below the larynx 80% resides in the trachea and bronchi. This is difficult to reconcile with Poiseuilles’s law (p. 46, 156) that the airway resistance of a tube is proportional to the fourth power of its radius, as the trachea and main bronchi are the largest tubes in the bronchial tree. The explanation for this is that the number of airways doubles at each airway branching (each airway normally splits into two daughters), therefore the number (n) at each generation (g) (see p. 15) is n = g2, starting with the two main bronchi as generation 1 (Fig. 4.9). This rapid increase in numbers more than offsets the decrease in diameter of the individual members of each generation, and the total cross-sectional area increases dramatically. The bronchi extend from generation 1 to 16, with the small bronchi (generations 5–11; 3.5–1 mm diameter) not being directly attached to the lung parenchyma. They are supported against collapse by cartilage and the transmural pressure gradient, which it is now believed rarely reverses sufficiently to cause complete collapse of these airways.
At the other extreme of the size range are the large airways, the trachea and main bronchi. Because these are few in number they form the narrowest part of the bronchial tree, but are well armoured against collapse by incomplete rings of cartilage in their walls. Even they can, however, be profoundly influenced by physiological conditions, such as cough, where positive pressure surrounding them squeezes them shut.
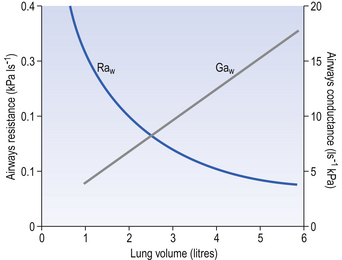
The most important parts of the bronchial tree in terms of physiological control of airways resistance are the smaller bronchi and bronchioles. Not only do they contain virtually no supporting cartilage, but innervated smooth muscle, which can contract to reduce their diameter, makes up a large part of their walls. In addition, they are found at a level in the bronchial tree where the increase in number of airways has not yet exerted its effect (generations 7–14; Fig. 4.9), and therefore cross-sectional area is relatively small. If the airways resistance of each generation is compared the small bronchi are seen to have less resistance than the larger generations (Fig. 4.10). However, the important point is that the resistance of these smaller airways is variable (particularly in disease) and is under the influence of bronchomotor tone. Their content of smooth muscle and lack of support by cartilage makes these airways prone to influence by neural and hormonal factors that affect their muscle tone, and physical factors such as the pull of surrounding tissue (radial traction, see p. 53). Their position at a relatively narrow part of the bronchial tree makes them particularly important in terms of obstruction by inflammatory swelling or mucus.
Asthma and airways smooth muscle
Bronchomotor tone
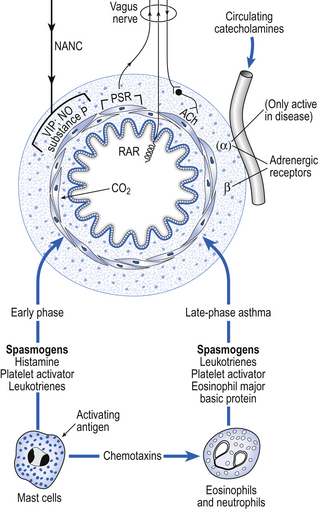
Physiological control of airways smooth muscle involves several mechanisms (Fig. 4.11).
• Parasympathic nerves. Efferent preganglionic fibres of this most important system run in the vagus nerve to ganglia located in the wall of the small bronchi. Postganglionic fibres release acetylcholine, which stimulates muscarinic receptors on the smooth muscle fibres, causing them to contract. Atropine blocks these receptors, and injections of atropine in a normal individual can reduce airways resistance by about 30%. This limited response demonstrates that parasympathetic nerves, though important, are not the only method of bronchomotor control.
• Sympathetic nerves. Most organs with a parasympathetic nerve supply also have a sympathetic input. In the case of the lungs this nerve supply does not extend as far as the bronchial smooth muscle. Any sympathetic effects seen in the lung are due to circulating catacholamines. The general lack of importance of nerves to lung function is demonstrated by the success of lung transplants, in which the donated lungs are completely denervated.
• Circulating catecholamines. The membrane of airways smooth muscle carries β2 receptors which, when stimulated by the naturally occurring catecholamine adrenaline (epinephrine), or drugs such as salbutamol, relax smooth muscle, inhibit the action of mast cells and improve mucociliary activity. They therefore form an important treatment for asthma. α-Adrenergic agents only cause contraction of bronchial smooth muscle in diseased states.
• Non-adrenergic non-cholinergic systems (NANC). The airways are also provided with an autonomic nerve supply which is neither adrenergic nor cholinergic. The efferent fibres run in the vagus nerves and mainly release an inhibitory neurotransmitter which relaxes the airways. The identity of the transmitter is still open to question, although vasoactive intestinal peptide (VIP) and nitric oxide are strong candidates. This NANC inhibitory system is the main neurotransmitter-mediated relaxant system of the airways. However, bronchoconstrictor NANC mediators can also be released by this system. They included substance P and neurokinin A, which may have a role in the delayed phase of asthma.
• Mast cell degranulation. Mast cells are plentiful in the walls of the airways. Allergens interact with IgE antibodies on their surface, causing them to undergo the process of degranulation, which is the rapid release (within 30 s) of preformed mediators, including histamine, heparin, serotonin, lysosomal enzymes and chemotactic factors. Prostaglandins and slow-reacting substances are synthesized and released some time later. It is now accepted that mast cell degranulation is responsible for less than 30% of the bronchoconstriction of asthma, let alone the physiological control of bronchiolar smooth muscle.
• Neutrophils and eosinophils. Although degranulation of mast cells is of limited importance in the physiological control of airway resistance, and its role restricted to the immediate phase of asthma, neutrophil and eosinophil chemotactic factors are of such importance in the late (inflammatory) phase that is has been suggested that asthma should be called ‘chronic desquamating eosinophilic bronchiolitis’, because of the degree of involvement of these cell types.
• Rapidly adapting pulmonary receptors (irritant and cough receptors). Stimulation of these receptors in the airways by inhalation of particles, chemicals, or by disease provokes contraction of airways smooth muscle by a reflex with both its arms in the vagus nerves. This contraction of the airways may improve the efficiency of coughing, but is not helpful in conditions of asthma.
• Slowly adapting pulmonary receptors. These receptors also have their afferent nerves in the vagus. Their activity reduces bronchomotor tone. They are stimulated by stretching the lungs, so a large breath – a sigh, for example – dilates the airways both by passive stretch and by this reflex effect.
• Carbon dioxide. This gas causes bronchodilation by direct relaxing action on the bronchial smooth muscle. In those parts of the lung that are underventilated carbon dioxide will build up, dilate the airways and improve ventilation locally.
The factors involved in the immediate and late phases of asthma which influence bronchomotor tone are illustrated in Figure 4.11.
Pharmacological treatment of asthma
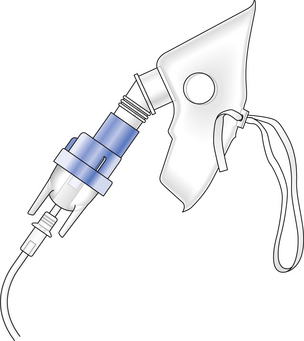
The treatment of asthma may address the early (bronchoconstrictor) or late (inflammatory) phases of the disease frequently with drugs delivered directly to the airway, as droplets produced by a nebulizer. One of the many types used in hospitals in shown in Figure 4.12.
Bronchodilators – early phase treatment
• β2 Adrenoreceptor agonists – These include salbutamol and terbutaline, which are usually given as an aerosol. These drugs act directly to relax bronchial smooth muscle, and also inhibit degranulation of mast cells.
• Xanthines – Of these, aminophylline is often the first choice of treatment for an acute attack. The mode of action of theophylline is still unclear, but may involve enzyme inhibition in bronchial smooth muscle.
• Muscarinic receptor antagonists – By blocking the activity of parasympathetic (vagal) nerves on the bronchial smooth muscle, drugs such as ipratropium bromide reduce any reflex component of an asthmatic attack.
Anti-inflammatories – late-phase treatment
• Glucocorticoids – given prophylactically as an aerosol, beclometasone, betamethasone or budesonide inhibit the late-phase response by inhibiting the generation of PAF (platelet-activating factor) and eicosanoids from mast cells, platelets, macrophages and eosinophils.
• Sodium cromoglicate – used prophylactically, cromoglicate appears to reduce hyperreactivity by depressing axon reflexes triggered by stimulation of rapidly adapting (irritant) receptors in the airways.
• Histamine receptor antagonists – H1 antagonists such as azelastine and ketotifen are being used in mild asthma as a supplement for other drugs used in the early phase.
Clinical definitions
In the spectrum of obstructive pulmonary disease, between the ‘reversible airway obstruction’ of asthma and irreversible diseases such as emphysema, which are permanent – in the case of emphysema, as a result of loss of lung tissue – comes chronic bronchitis, which is almost inevitably associated with a greater or lesser degree of emphysema. The bronchitic element of this combination of diseases is fairly easily diagnosed by the chronic production of mucus. The emphysematous component is much more difficult to quantify during life and so, if for no other reason, the term chronic obstructive pulmonary disease (COPD) is useful to describe this combination, if only to cover our uncertainty.
Bronchitis and mucus
The airways are lined from nose to alveoli by a watery layer containing mucus. The normal mucus film within the lungs is approximately 5–10 μm thick and consists of two layers, the layer next to the airway wall is more watery to allow the cilia of the ciliary escalator to work, brushing the overlying more viscous layer, together with any foreign particles it contains, towards the mouth. Mucus is produced by ducted seromucous glands deep in the bronchial walls and goblet cells in the bronchial epithelium. The accumulation of mucus results from excess production, drying of the surface, failure of the ciliary escalator to clear it, or infection making it too viscous to be moved. This results effectively in a narrowing or total blockage of the airways (Fig. 4.14). The secretion of mucus is normally controlled by vagal reflexes and local chemical stimulation. Curry and other spicy foods provoke the vagal reflex, and tobacco smoke stimulates both mechanisms. In extreme cases of bronchitis mucus can solidify into tiny solid casts of the small airways, and chronic bronchitic patients cough up these casts.
Emphysema and radial traction
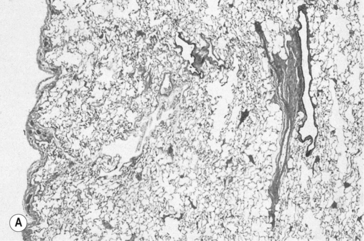
The effect of radial traction is less profound than this at the lung volumes involved in normal breathing, with changes in resistance due to this effect being proportional to lung volume. The effect is, however, of great importance at low lung volumes, with the airways collapsing when radial support disappears. At this point airways resistance begins to increase dramatically (Fig. 4.15).
Because of the weight of overlying tissue this closure begins first in the lower lobes of the lungs at a volume known as closing capacity (CC). In young people closing capacity is less than FRC and so closing does not occur during normal breathing. At about 65 years it becomes equal to FRC in the upright position, and greater than FRC when supine. Under these conditions blood is shunted (see p. 97) through the lungs without coming into contact with air, and this is an important aspect of desaturation of arterial blood with increasing age. Closure of the airways can be prevented by increasing the pressure within them, and many patients whose airways are closing in this way intuitively exhale through pursed lips, the positive pressure within the airway produced by this ‘pursed lip breathing’ helping keep their airways open.
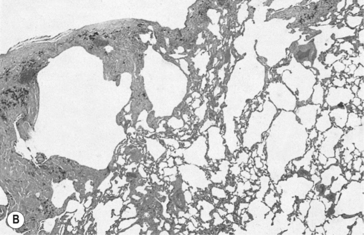
Emphysema is defined anatomically as an irreversible increase in the size of air spaces distal to the terminal bronchioles. The destruction of lung parenchyma that brings about this increase in size is now generally agreed to be due to uncontrolled action of proteolytic enzymes from leukocytes associated with pulmonary inflammation (Fig. 4.16). Cigarette smoke is again a major villain in the piece, stimulating elastase release from neutrophils. Lung elastase is normally inhibited by antiprotease enzymes, the most important of which is a1-antitrypsin. About 1 in 4000 people has a genetic deficiency of α1-antitrypsin, and therefore have a predisposition towards emphysema.
Airway collapse, owing to loss of radial traction, is exacerbated by changes in transmural pressure which brings about flow-related airway collapse, which we will consider next.
Intrapleural pressure and cough
When breathing becomes vigorous and expiration becomes active, conditions change. Passive expiration comes about because the elastic recoil of the lungs draws in the chest wall, which tends to spring out during normal tidal breathing. This action maintains a negative intrapleural pressure (see Fig. 3.2). When expiration is active, however, the internal intercostals and the abdominal muscles ‘squash’ the air out of the lungs by making intrapleural pressure positive with respect to the air in the airways. This can lead to dynamic airway collapse, with its associated expiratory flow limitation.
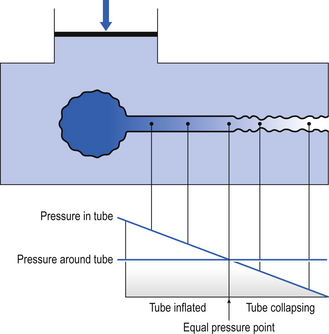
Under conditions of dynamic collapse the airways behave like a Starling Resistor (named after the physiologist who first described it). The Starling Resistor arises when air is being driven through a flexible tube by a pressure which is applied to the outside of the tube as well as the inside (Fig. 4.17). Inside the tube the pressure is being used up to drive the air along, and therefore pressure inside the tube falls from left to right. Outside the tube the pressure stays the same along the whole length of the tube. At a point somewhere along the tube the outside pressure exceeds the inside pressure and the tube collapses.
The concept of equal pressure point, where the pressures inside and outside the airway are equal, is frequently used to describe the state of the lungs in obstructive disease. At the equal pressure point the rigidity of the wall and surrounding parenchyma is the only factor holding the airway open. As lung volume decreases during expiration the equal pressure point moves progressively toward the smaller airways as the contribution to the pressure within the airways from elastic recoil is reduced (Fig. 4.18).
Collapsed areas trap air behind them, within the lung. Extra expiratory effort does not relieve this trapping, as it simply presses the collapsed area more firmly shut. In healthy lungs these conditions do not occur above functional residual capacity. In lungs affected by damage to the airway wall, or when the supporting parenchyma has been destroyed, collapse takes place at higher volumes. During expiration the collapsing segment vibrates and is a major source of the wheeze heard in many lung diseases. In emphysema the destruction of the supporting parenchyma is clearly the cause of loss of support of the airways; in asthma it is the high bronchomotor tone and oedema of the airways that augments collapse and increases the rate of pressure drop along the airway.
Clinical tests for changes in resistance
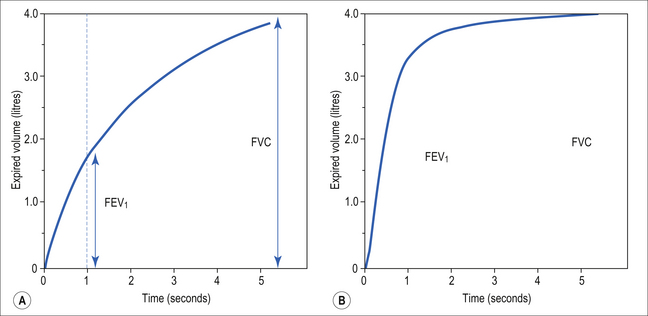
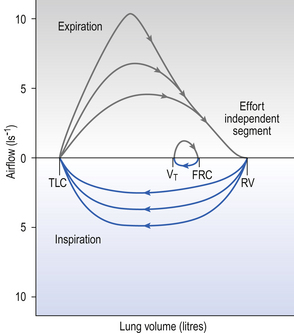
A most useful test for obstructive diseases is the flow/volume curve, or loop, which is obtained by a method described in Chapter 11. The peak flow obtained at large lung volumes depends largely on effort (Fig. 4.19), but to-ward the end of expiration there is an effort-independent segment of the loop where expiratory flow is determined by airway collapse below the equal pressure point. The alteration in this loop by disease is also dealt with in Chapter 11.
Work of breathing
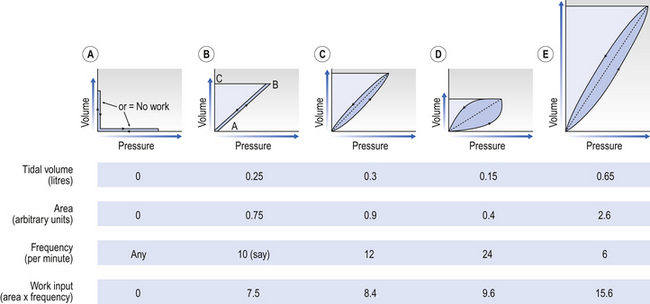
This is illustrated in Figure 4.20, where work in a lung is the product of the volume change and the pressure change producing it.
Deep slow breathing (panel (e) in Fig. 4.20) requires the most work to be done against elastic resistance, whereas rapid shallow breathing (panel (d)) works largely against airways resistance.
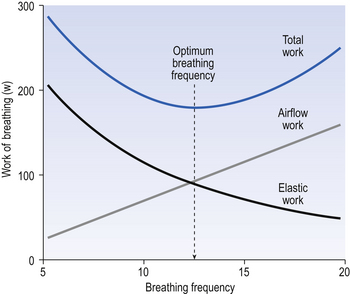
So, if you begin breathing slowly and deeply and increase the frequency while reducing the volume, work against elastic resistance decreases and work to produce airflow increases (Fig. 4.21). We automatically choose the best pattern of breathing in terms of work, probably as a result of subliminal information received from mechanoreceptors in the lungs (see Chapter 11).
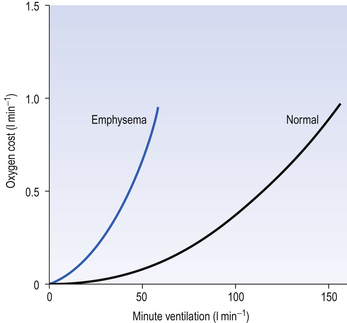
This system is quite efficient at minimizing the expenditure of energy by the respiratory muscles (as a fraction of our total energy use), and in healthy subjects the work done in breathing provides ‘good value’ in providing extra oxygen. For example, exercise is rarely limited by the respiratory system using too much energy. In diseased lungs, however, the airway resistance, elastic properties or the control system may be compromised, and the extra work done by the respiratory muscles to provide extra oxygen to the rest of the body during exercise demands more oxygen than it provides (Fig. 4.22), which of course is an untenable situation that limits the exercise.

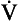 ) as:
) as: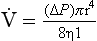
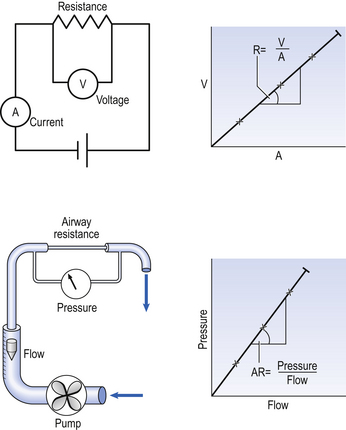
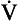 ) is also a straight line, like electrical resistance.
) is also a straight line, like electrical resistance.