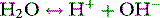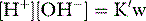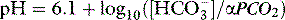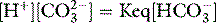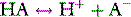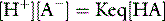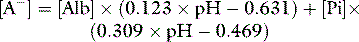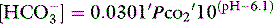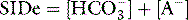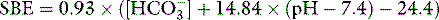Acid–base balance and disorders

Published on 27/02/2015 by admin

Filed under Anesthesiology

Last modified 22/04/2025

Print this page

This article have been viewed 1574 times

Chapter 84 Acid–base balance and disorders

Thomas J. Morgan

THEORETICAL CONSIDERATIONS

The structural integrity of intracellular enzymes is essential for survival. Proton activity at enzymatic sites of action in cytosol and organelles must be tightly controlled. In critical illness, with survival under threat, direct monitoring of any intracellular site remains an impractical ideal. Clinicians are obliged to track extracellular data, usually from tests on arterial blood, knowing that plasma pH exceeds intracellular pH by 0.6 pH units on average.

WATER DISSOCIATION AND ACID–BASE

Stewart reminded us of the central role of water in aqueous acid–base equilibria.¹ Mammals are approximately 60% water. It follows that the behaviour of water is fundamental to our understanding of acid–base physiology. Water (simplistically) dissociates as follows:

By the Law of Mass Action, at any equilibrium [H⁺] [OH⁻] = Kw [H₂O], where Kw is the temperature-dependent dissociation constant. Water is a vast proton reservoir, its concentration several orders of magnitude greater than that of its two dissociation products (55.5 M vs. 160 nM at 37 °C). When conditions favour proton release, for example with increased temperature, water dissociates and pH falls. With conditions less favourable, protons return to their source, and pH rises.

An advantage of its numeric predominance is that [H₂O] can be combined with Kw to form a new constant, K’w. The equilibrium equation then simplifies to:

Equation 84.1

pH AND ACID–BASE NEUTRALITY

The negative logarithm of the proton concentration, or more exactly proton ‘activity’, is termed pH. In aqueous solutions, neutrality occurs when [H⁺] = [OH⁻], so that ([H⁺])² = K’w. Thus neutral pH = 0.5 pK’w. At 37 °C, neutral pH is 6.8, which is the normal mean intracellular pH in health. The pH of the surrounding extracellular fluid, usually > 7.3, is relatively alkaline.

THE PaCO₂/PH RELATIONSHIP – THE ACID–BASE ‘WINDOW’ FOR CLINICIANS

About 15 moles of CO₂ are generated daily by aerobic metabolism. CO₂ travels along a partial pressure gradient from its intracellular source (PCO₂ > 50 mmHg) to the atmosphere (PCO₂ = 0.3 mmHg). The primary exit point is the lungs, with transit facilitated by a large, perpetually refreshed blood–air interface. En route, CO₂ equilibrates with all aqueous environments. The PCO₂ in any body fluid is thus an equilibrium value, determined by the interplay between regional CO₂ production, regional blood flow, alveolar perfusion and alveolar ventilation.

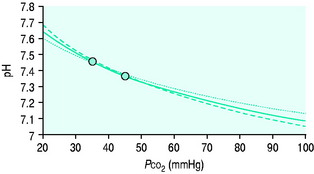
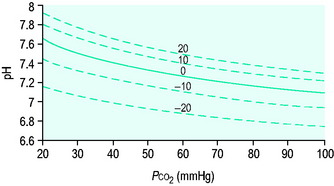
Clinicians use the relationship between arterial PCO₂ (PaCO₂) and arterial pH as the acid–base assessment platform. This is appropriate, because the PaCO₂/pH curve is a fundamental physiological property (Figure 84.1). Several factors determine the shape and position of this curve.

Figure 84.1 PCo₂/pH relationships. The solid line shows the normal in vivo PaCO₂/pH relationship. The normal PaCO₂ range is between the filled circles. To the left of the circles there is an increasing acute respiratory alkalosis, and to the right an increasing acute respiratory acidosis. The interrupted curve represents the normal in vitro whole blood relationship, and the dotted curve is the same relationship for separated plasma. A point of commonality exists at PCO₂ = 40 mmHg.

THE PaCO₂/pH RELATIONSHIP IS DEFINED BY SEVERAL SIMULTANEOUS EQUATIONS

In body fluids, pH is a function of water dissociation modified by CO₂, other weak acids and certain electrolytes. All equilibria obey the Laws of Mass Action and Mass Conservation, and must achieve overall electrical neutrality. Non-diffusible ions exert electrochemical forces across membranes, known as Gibbs Donnan effects, which influence the final acid–base result.

Therefore apart from Equation 1, several other equations must be satisfied simultaneously at any equilibrium. They relate to:

1 The interaction of carbon dioxide with water:

By applying the Law of Mass Action and substituting [dissolved CO₂] for [H₂CO₃], the following expression can be derived:

Equation 84.2

This is the Henderson–Hasselbalch equation, where α is the plasma CO₂ solubility coefficient (0.03), and 6.1 is the pKa, the negative logarithm of the dissociation constant. The Henderson–Hasselbalch equation generates the plasma [HCO₃⁻] in blood gas readouts.

2 Bicarbonate dissociation to carbonate. At equilibration:

Equation 84.3

3 Non-volatile weak acid dissociation. Fluid compartments have varying concentrations of non-CO₂ generating (non-volatile) molecules with weak acid properties. In other words, their overall negative charge alters in parallel with pH. In plasma, they consist mainly of albumin and to a lesser extent inorganic phosphate. In red cells haemoglobin predominates. Much smaller concentrations of non-volatile weak acid also appear in interstitial fluid, primarily as phosphate. For convenience, Stewart modelled all non-volatile weak acids in each compartment as having a single anionic form (A⁻) and a single conjugate base form (HA).

By applying the Law of Mass Action:

Equation 84.4

4 Conservation of mass. Stewart termed the total concentration of non-volatile weak acids in any compartment ‘A_TOT’, where A_TOT = [HA] + [A⁻]. A_TOT is an imposed mass constant. It does not vary with pH. A change in pH merely signals a shift in the balance between HA and A⁻.

5 Electrical neutrality, linked to Stewart’s concepts of strong ions and strong ion difference. Certain elements such as Na⁺, K⁺, Ca⁺⁺, Mg⁺⁺ and Cl⁻ exist as completely ionised entities in body fluids. At physiological pH this includes anions with pKa values of 4 or less, for example sulphate, lactate, and β-hydroxybutyrate. Stewart described compounds exhibiting this property as ‘strong ions’. In body fluids there is a surfeit of strong cations, referred to by Stewart as the strong ion difference (SID). In other words, SID = [strong cations] – [strong anions]. Being a ‘charge’ space, SID is expressed in mEq/l. SID calculated from measured strong ions in normal plasma is 42 mEq/l.

Hence, by the Law of Electrical Neutrality:

Equation 84.5

6 Gibbs Donnan forces. These alter equilibria across semipermeable membranes, with electrical gradients balanced against concentration gradients. The plasma compartment (volume 3 l), the erythrocyte compartment (volume 2 l) and the interstitial space (volume 13.5 l) each contains different concentrations of non-diffusible anions, mainly albumin or haemoglobin. Erythrocytes, which harbour most of these trapped negative charges, attract diffusible cations (such as Na⁺, K⁺) from adjacent compartments while repelling diffusible anions (primarily Cl⁻). However, several cations are continually redistributed against the Donnan forces by energy-dependent transmembrane pumps, to prevent cell swelling and haemolysis. Importantly, chloride, the major anion, remains fully susceptible to the Donnan effects.

The trapped anions have weak acid properties. Any pH shift alters their negative charge, driving further ionic redistributions, particularly chloride, between compartments. The net effect is that plasma SID goes up and down with PaCO₂ (Figure 84.2), the origin of the so-called Hamburger effect. Importantly, ionic shifts are confined within the total extracellular space, so that extracellular SID does not alter with PCO₂. This is fortuitous for clinicians, forming the basis of the CO₂ invariance of standard base excess (see below).

Figure 84.2 Gamblegrams of plasma strong and weak ions (in vitro data from CO₂ equilibrated normal blood). On the left, PCO₂ < 20 mmHg; on the right, the same blood with PCO₂ > 200 mmHg. The transition from hypocapnia to hypercapnia increases SIDa, with ionic redistribution between red cells and plasma due to altered Gibbs Donnan forces. There are almost identical increases in SIDe ([A⁻] + [HCO₃⁻]), also known as ‘buffer base’, although [A⁻] actually falls. Note that the SIG, which is SIDa minus SIDe, remains close to zero.

At any equilibrium, Equations 1–5 plus the Donnan equilibria must be satisfied simultaneously. In such a system, pH and HCO₃⁻, as well as CO₃²⁻, A⁻ and OH⁻, cannot be altered directly, only via any of three independent variables imposed on the system but not altered directly by the system. These are SID (total extracellular SID, immune to Gibbs Donnan forces), extracellular A_TOT, and PaCO₂, which is externally regulated by alveolar ventilation. Hence, in arterial blood, pH is defined by PaCO₂, extracellular SID and extracellular A_TOT.

Thus it can be seen that for any individual the PaCO₂/pH relationship is a unique acid–base ‘signature’ (Figure 84.1) and ultimately a complex function of extracellular SID and A_TOT.

WEAK IONS AND BUFFER BASE

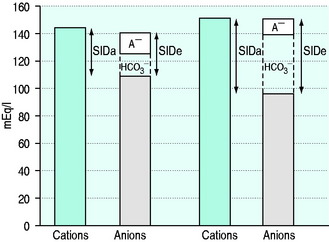
SID is a charge space. Weak ions, which arise from variably dissociating conjugate bases, occupy this space. These include H⁺, OH⁻, HCO₃⁻, CO₃²⁻ and A⁻. Their total net charge must always equal SID. However, HCO₃⁻ and A⁻, together known as the ‘buffer base’ anions, take up virtually the entire space on their own (Figure 84.2) since the other ions are measured in either micromoles/l or, in the case of protons, nanomoles/l. SID therefore not only dictates the buffer base concentration but is also numerically identical to it. In other words, SID = [HCO₃⁻] + [A⁻]. This fact, plus Figge’s linear approximations² for calculating A⁻, allows us to simplify Stewart’s equations in plasma, reducing them to three without sacrificing accuracy.³

[Alb] is albumin concentration expressed in g/l. [Pi] is phosphate concentration in mmol/l. PCO₂ is in mmHg. SIDe is effective SID, also known as ‘buffer base’ (Figure 84.2).

SID calculated from measured plasma concentrations of strong ions is termed the ‘apparent’ SID, or SIDa (Figure 84.2). Discrepancies between SIDe and SIDa imply the presence of unmeasured ions in plasma (see below).

ISOLATED CHANGES IN SID AND A_TOT

At any given PaCO₂, a falling SID or a rising A_TOT reduce pH, moving the equilibrium towards a metabolic acidosis. Conversely, a rising SID or a falling A_TOT create a metabolic alkalosis. Many argue that SID and A_TOT act individually and should therefore be regarded as independent metabolic acid–base variables. By this argument we could have a strong ion acidosis or alkalosis combined with either a hyperalbuminaemic (high A_TOT) acidosis or a hypoalbuminaemic (low A_TOT) alkalosis.⁴ However, SID and A_TOT do appear to be linked, with the SID set-point adjusting to A_TOT. In particular, SID seems to fall in hypoalbuminaemia, presumably by renal chloride adjustment.^5,⁶

HOW ACID–BASE DISTURBANCES AFFECT THE PACO₂/PH RELATIONSHIP

Acute respiratory disturbances move data points along the prevailing PaCO₂/pH curve, to the left in respiratory alkalosis, and to the right in respiratory acidosis (Figure 84.1). In contrast, metabolic disturbances (altered extracellular SID and/or A_TOT) shift the entire curve up or down (Figure 84.3). A down-shifted curve means that the pH at any given PaCO₂ is lower than normal, which – depending on the PaCO₂ – represents either a primary metabolic acidosis or else metabolic compensation for a respiratory alkalosis. With an up-shifted curve, the pH at any given PaCO₂ is higher than normal, signifying either a primary metabolic alkalosis or else compensation for a respiratory acidosis.

Figure 84.3 PaCO₂/pH curve shifts and associated SBE values (mEq/l). Alterations in metabolic acid–base status shift the curve down (SBE increasingly negative) or up (SBE increasingly positive).

TEMPERATURE CORRECTION OF BLOOD GAS DATA – ‘ALPHA-STAT’ VERSUS ‘PH-STAT’ APPROACHES

Blood gas analysers operate at 37 °C. Their software can convert pH and gas tensions to values corresponding to the patient core temperature for interpretation and action. This is the ‘pH-stat’ approach. The alternative is to act on values as measured at 37 °C – the ‘alpha-stat’ approach.

‘Alpha’ is the ratio of protonated imidazole to total imidazole on the histidine moieties in protein molecules. At 37 °C, under normal acid–base conditions, the mean intracellular pH is 6.8 (the neutral pH at 37 °C). Alpha is then approximately 0.55. Maintaining alpha close to 0.55 preserves enzyme structure and function, and is thus a fundamental goal.

‘Alpha-stat’ logic is best illustrated by considering blood in a blood gas syringe. When placed on ice, the PCO₂ falls as its solubility coefficient increases. Water dissociation is reduced, due to the hypocapnia and to the temperature-induced decrease in K’w. Consequently, there is a progressive alkalaemia, which on rewarming in the blood gas analyser reverts immediately. Throughout these phenomena, alpha stays constant. The reason is that the fall of the imidazole pKa with temperature is about half the fall in pK’w.

Hence, a simple way to keep alpha at 0.55 in hypothermia is to maintain uncorrected PaCO₂ and pH measurements in their 37 °C reference ranges.^7,⁸ This mimics the hypothermic physiology of ectothermic (cold-blooded) animals. Similar arguments apply in fever, the more common intensive care unit (ICU) scenario. Many intensivists follow the alpha-stat approach, whatever the core temperature.

Those who favour the pH-stat approach argue that it is more consistent with the physiology of hibernating endothermic mammals, and that it allows better maintenance of cerebral perfusion in hypothermia.⁹ This approach was used during an influential trial of mild hypothermia following out-of-hospital cardiac arrest.¹⁰

RENAL PARTICIPATION IN ACID–BASE

In the absence of renal function, there is a progressive metabolic acidosis. About 60 mEq of strong anions, particularly sulphate, but also hippurate and others, are produced daily as metabolic end-products. These accumulate in renal failure, reducing extracellular SID. So does free water, which brings sodium concentrations closer to chloride, again reducing SID. Hyperphosphataemia contributes by increasing A_TOT, although in acute renal failure this is commonly offset by coexistent hypoalbuminaemia.¹¹

Traditionally, renal acid–base homeostasis is described in terms of resorption of filtered bicarbonate primarily in the proximal tubule, and excretion of fixed acids through titration of urinary buffers, particularly phosphate, and through excretion of ammonium, primarily in the distal tubule.¹²

From the physical chemical perspective, the traditional analysis of renal acid–base homeostasis is misleading, since it is based on H⁺ or HCO₃⁻ ‘balances’. H⁺ and HCO₃⁻ are dependent variables, responsive exclusively to PCO₂, SID and A_TOT, and not subject to ‘in versus out’ balance sheets. The physical chemical explanation is simple. The kidneys regulate extracellular SID via urinary SID, the principal tool being tubular NH₄⁺ acting as an adjustable cationic partner for tubular Cl⁻ and other urinary strong anions.¹³ The kidneys also modify A_TOT via phosphate excretion, which is a totally different concept from that of ‘titratable acidity’.

ACID–BASE ASSESSMENT – THE TWO ‘SCHOOLS’

By convention, acid–base disorders are divided into respiratory (PaCO₂) and metabolic (non-PaCO₂). PaCO₂ is the undisputed index of respiratory acid–base status. Two ‘schools’, Boston and Copenhagen, separated by a large ocean,¹⁴ have formed around the identification and quantification of metabolic acid–base disturbances. Both succeed as navigation systems, if used correctly.

Stewart’s concepts neither invalidate nor supplant the traditional approaches,¹⁵^–¹⁷ but rather help us to understand their physiological basis, evaluate their relative merits, and extend their utility.¹⁸ SID by itself is not a reliable measure of metabolic acid–base status, for three reasons:

• Plasma SID, the only SID measurable by clinicians, is subject to Donnan effects, which means it varies with PaCO₂ (the only SID that does not is total extracellular SID).

• In any compartment, SIDa and at times SIDe can be quite inaccurate reflections of the true SID. For example, unmeasured strong anions give SIDa positive bias, and unmeasured weak anions such as infused gelatin give SIDe negative bias.

• SID on its own is only half the story, since metabolic acid–base status is a function of the interplay between SID and A_TOT. In a healthy individual a plasma SID of 42 mEq/l may be normal, but in the presence of hypoalbuminemia (reduced A_TOT) it represents a metabolic alkalosis. Hence there is little point in attempting to track SID clinically.

For a pure metabolic index to succeed, it must integrate the effects of extracellular SID and A_TOT, irrespective of the PaCO₂. The best of these (in the author’s opinion) is standard base excess, the flagship of the Copenhagen school. However, Boston school devotees can navigate quite successfully using empiric plasma bicarbonate-based ‘rules of thumb’.

BASE EXCESS AND STANDARD BASE EXCESS

In 1960, Siggaard-Andersen introduced ‘base excess’ (BE).¹⁹ BE was defined as zero when pH = 7.4, PCO₂ = 40 mmHg (both at 37 °C). If pH ≠ 7.4 or PCO₂ ≠ 40 mmHg, BE was defined as the concentration of titratable hydrogen ion required to return the pH to 7.4 while maintaining PCO₂ at 40 mmHg.

In the lead-up, Astrup, Siggaard-Andersen, Engel and others had equilibrated the blood of Danish volunteers with known CO₂ tensions at varying haemoglobin concentrations, after first adding known amounts of acid or base. The data were then used to create an ‘alignment nomogram’ which allowed the determination of BE from simultaneous measurements of pH, PCO₂ and haemoglobin concentration.

Seventeen years later, Siggaard-Andersen published the Van Slyke equation for calculating BE.²⁰ It was derived from known physical chemical relationships, and was claimed to match the empiric nomogram. The Van Slyke equation computes (Δ[HCO₃⁻] + Δ[A⁻]) – in other words, the deviation from normal of the buffer base concentration in whole blood. From the Stewart perspective, buffer base and SID are interchangeable terms. Hence Stewart would describe BE as the abnormality in whole blood SID at the prevailing A_TOT.

It became clear that BE loses its CO₂ invariance in vivo, where Gibbs Donnan forces drive ions between intravascular and interstitial compartments. As a result, a primary change in PaCO₂ shifts BE in the opposite direction. The solution was to calculate BE at a haemoglobin concentration of approximately 50 g/l, replicating the mean extracellular haemoglobin concentration and thus more closely modelling the extracellular environment.²¹ This is standard base excess (SBE).

As a metabolic acid–base index, SBE is close to ideal, being both quantitative and demonstrably independent of PacO₂.²² A useful formula is:

with SBE and [HCO₃⁻] values in mEq/l. This formula can be further refined to allow for changes in plasma A_TOT due to variations in albumin and phosphate.²³ However, because haemoglobin is the predominant weak acid, the end result is very similar.

A typical SBE reference range (in mEq/l) is −3.0 to +3.0. If SBE < −3.0 mEq/l, there is a down-shifted PaCO₂/pH curve. This could represent either a primary metabolic acidosis or else compensation for a primary respiratory alkalosis, depending on the PaCO₂ and the pH (see below). SBE quantifies the increase in extracellular SID (in mEq/l) needed to shift the curve back to the normal position without changing A_TOT (Figure 84.3). In terms of the original BE definition, this is roughly the required dose of sodium bicarbonate in mmol per litre of extracellular fluid. Similarly, if SBE is > 3.0 mEq/l, there is an up-shifted curve, either a metabolic alkalosis or compensation for a respiratory acidosis. The SBE is the decrease in extracellular SID needed to shift the curve back to the normal position at the prevailing A_TOT. Conceptually, it approximates the dose of HCl required per litre of extracellular fluid. SBE is thus ‘extracellular SID excess’ or ‘SIDex’.²⁴

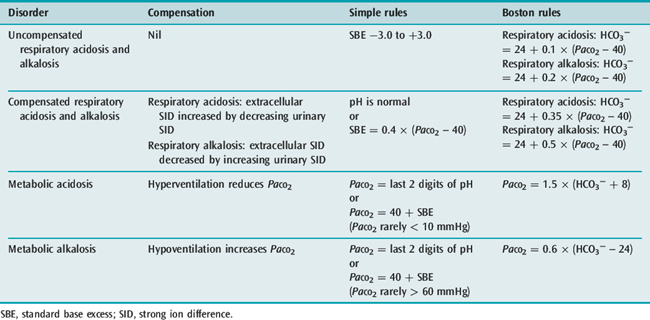
THE BICARBONATE-BASED APPROACH TO METABOLIC ACID–BASE – THE BOSTON ‘Rules Of Thumb’

Boston ‘school’ devotees calculate the plasma [HCO₃⁻] from the measured pH and PaCO₂, and match this value with the [HCO₃⁻] deemed appropriate for the measured PaCO₂, using empiric ‘rules of thumb’ derived from clinical and experimental data (Table 84.1).²⁵ An offset denotes a metabolic acid–base disturbance.

Table 84.1 Compensation – mechanisms and rules

The Boston method is largely qualitative, since by focusing on plasma bicarbonate alone it ignores the A⁻ component of the buffer base (SIDe) concentration (Figure 84.2). The Boston rules of thumb can only tell us whether the PaCO₂/pH curve is shifted up or down. Unlike SBE, they cannot tell us how much.

ACID–BASE DISORDERS – CLASSIFICATION

ACID–BASE ‘SCANNING TOOLS’

ELECTRICAL GAPS (Table 84.2)²⁸

Accumulating strong anions reduce SID, causing metabolic acidosis. Other than chloride and now increasingly L-lactate, strong anions are not routinely measured. However, they can be especially injurious, creating a need for rapid detection and early intervention. Critical care practitioners use electrical ‘gaps’ as early warning systems.

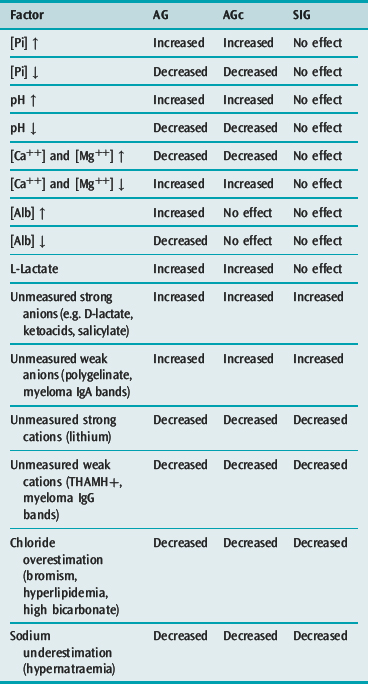
Table 84.2 Factors affecting the anion gap (AG), the albumin-corrected anion gap (AGc) and the strong ion gap (SIG)

Anion gap (AG)

The plasma AG is calculated (in mEq/l) as [Na⁺] + [K⁺] – [Cl⁻] – [HCO₃⁻], although [K⁺] is omitted in many laboratories. A typical reference range is 7–17 mEq/l. The AG quantifies [unmeasured anions] – [unmeasured cations], both strong and weak. The AG is increased by unmeasured anions, and reduced by unmeasured cations. In health, most of the AG consists of A⁻, the negative charge on albumin and phosphate. The AG is altered by A_TOT fluctuations, which affect A⁻ directly, and by severe pH disturbances, which act via the A⁻ component (Table 84.2). When used for its primary purpose, which is scanning for unmeasured strong anions, AG sensitivity and specificity are low.

Albumin-corrected anion gap (AGc)⁴

The AGc was devised to correct for variations in plasma [albumin]. It is calculated as AG + 0.25 × (40 – [albumin]), assuming a normal plasma [albumin] of 40 g/l. By attributing a fixed negative charge to albumin, and making no adjustment for pH, error remains. This is minor, except in severe alkalaemia.

Strong ion gap (SIG)

The SIG concept was proposed by Jones in 1990,²⁹ and progressed by others.^2,³⁰ It is calculated as SIDa – SIDe, where SIDa = [Na⁺] + [K⁺] + [Ca⁺⁺] + [Mg⁺⁺] – [Cl⁻] – [L-lactate], and SIDe = [A⁻] + [HCO₃⁻]. The unmeasured ions creating the ‘gap’ can be either strong or weak, but the term ‘strong ion gap’ has persisted.

In the absence of measurement error, the SIG should be zero unless there are unmeasured ions, the list of which is smaller than with AG and AGc (Table 84.2).²⁸ SIG is under evaluation as a scanning tool. Its signal is subject to the summated variability of multiple analytes. In many centres, the normal SIG is 4 mEq/l or more, the positive bias presumably due to locally adopted measurement technologies and variations in analytic reference standards. A refinement, ‘net unmeasured ions’ (NUI), has been successfully incorporated into an acid–base diagnostic module and linked to a laboratory information system.³¹

THE OSMOLAL GAP

The osmolal gap scans for unmeasured osmotically active molecules. It is calculated as measured osmolality − (1.86 × ([Na⁺] + [K⁺]) + [urea] + [glucose]). The normal osmolal gap is < 10 mosm/kg. If there is an unexplained high AGc, a simultaneously raised osmolal gap suggests poisoning by methanol or ethylene glycol. However, a number of other molecules elevate the osmolal gap. These include other alcohols, mannitol and glycine, acetone and glycerol in ketoacidosis, and unknown solutes in lactic acidosis and renal failure.

PRACTICAL CONSIDERATIONS

THE DIAGNOSTIC SEQUENCE

At the outset, the clinician examining a set of blood gases should ignore derived variables such as bicarbonate or standard base excess. Most (frequently all) of the important information can be gleaned from the measured variables, PaCO₂ and pH.

PRIMARY SURVEY

1 Take a history and perform a clinical examination.

2 Scan for primary disorders by matching the PaCO₂ and pH combination with one of nine possible scenarios (Table 84.3).

Table 84.3 Acid–base status – primary survey

pH	Paco₂ (mmHg)	Primary process(es)
7.35–7.45	35–45	None
7.35–7.45	> 45	1 Chronic respiratory acidosis or 2 Respiratory acidosis, metabolic alkalosis

7.35–7.45 < 35

1 Chronic respiratory alkalosis

2 Respiratory alkalosis, metabolic acidosis

< 7.35 < 35 Metabolic acidosis < 7.35 > 45 Respiratory acidosis < 7.35 35–45 Respiratory acidosis, metabolic acidosis > 7.45 > 45 Metabolic alkalosis > 7.45 < 35 Respiratory alkalosis > 7.45 35–45 Respiratory alkalosis, metabolic alkalosis

SECONDARY SURVEY

1 Apply ‘rules of thumb’ (Table 84.1) where applicable. This step assesses compensation for any primary acid–base disturbances.

2 Note absent or inappropriate respiratory compensation in primary metabolic acid–base disorders, and identify this as a separate acid–base disturbance. For example, in diabetic ketoacidosis, if the arterial pH = 7.20 and the PaCO₂ = 20 mmHg, the patient has a metabolic acidosis with normal respiratory compensation (Table 84.1). If, however, the pH = 7.20 with a PaCO₂ = 32 mmHg, the metabolic acidosis has an accompanying respiratory acidosis (despite the hypocapnia). This is a greater cause for concern, signalling imminent respiratory decompensation. Conversely, if at this pH, PaCO₂ = 12 mmHg, there is an accompanying respiratory alkalosis.

3 Calculate the AG or preferably the AGc. If either is elevated, unmeasured anions are likely. If low or negative, suspect laboratory error, but consider lithium intoxication, IgG myeloma and others (Table 84.2).

4 Compare any AGc elevation with the SBE or [HCO₃⁻]. An elevated AGc should be accompanied by a similar reduction in SBE or [HCO₃⁻]. If not, there are dual disorders. For example, if AGc = 20 mEq/l and SBE = −15 mEq/l, the metabolic acidosis is due to a combination of an unmeasured anion and a narrowed difference between chloride and sodium (a combined normal and raised anion gap metabolic acidosis). If AGc = 20 mEq/l and the SBE = 0 mEq/l, there is a combined metabolic alkalosis and anion gap metabolic acidosis.

5 If there is no obvious cause for an elevated AGc, perform specific assays (e.g. L-lactate, β-hydroxybutyrate, D-lactate, salicylate). A concurrently raised osmolal gap suggests methanol or ethylene glycol toxicity. Urinary organic anions may reveal pyroglutamate.³²

CLINICAL ACID–BASE DISORDERS

METABOLIC ACIDOSIS

In metabolic acidosis, the extracellular SID is low relative to A_TOT. This can represent a narrowing of the difference between [Na⁺] and [Cl⁻] (normal AGc, Table 84.4), or an accumulation of other anions (elevated AGc, Table 84.4). Although a normal AGc acidosis is often hyperchloraemic, the absolute [Cl⁻] is not important, just its value relative to [Na⁺].

Table 84.4 Causes of metabolic acidosis

Normal AGc	Raised AGc
Saline infusions	L-Lactate acidosis
Organic anion excretion	Ketoacidosis
Ketoacidosis	β-Hydroxybutyrate, acetoacetate
Glue sniffing (hippurate, benzoate)	Renal failure
Loss high SID enteric fluid	Sulphate, hippurate, urate, other organic anions
Small intestinal, pancreatic, biliary	Phosphate accumulation increases A_TOT
Urinary/enteric diversions	Ethylene glycol poisoning
High urinary SID	Glycolate, oxalate
Renal tubular acidosis	Methanol poisoning
High urinary SID	Formate
Post hypocapnia	Pyroglutamic acidosis
High urinary SID	Pyroglutamate
TPN and NH₄Cl administration	Toluene (glue sniffing)
	Hippurate, benzoate
	Short bowel syndrome
	D-lactate

AGc, albumin-corrected anion gap; SID, strong ion difference; TPN, total parenteral nutrition.

Clinical features

Clinical features are those of acidaemia itself (Table 84.5), combined with specific toxicities of individual anions. These include blindness and cerebral oedema (formate),³³ crystalluria, renal failure and hypocalcaemia (oxalate),³⁴ and tinnitus, hyperventilation and fever due to uncoupling of oxidative phosphorylation (salicylate).³⁵

Table 84.5 Adverse effects of metabolic acidosis

Reduced myocardial contractility, tachy- and bradydysrhythmias, systemic arteriolar dilatation, venoconstriction, centralization of blood volume

Pulmonary vasoconstriction, hyperventilation, respiratory muscle failure

Reduced splanchnic and renal blood flow

Increased metabolic rate, catabolism, reduced ATP synthesis, reduced 2,3-DPG synthesis

Confusion, drowsiness

Increased inducible nitric oxide synthase (iNOS) expression, proinflammatory cytokine release

Hyperglycaemia, hyperkalaemia

Cell membrane pump dysfunction

Bone loss, muscle wasting

The adverse effects of acidaemia (Table 84.5) are more prominent at pH < 7.2. Acidaemia also has potential benefits. For example, the Bohr effect increases tissue oxygen availability, although this is rapidly counteracted by reduced 2,3-diphosphoglycerate concentrations. Lowering pH is protective in a number of experimental hypoxic stress models.^36,³⁷ During mild acidaemia therefore, the net result of harm versus benefit can be debated.

Infusion-related acidosis ^38,³⁹

Large volumes of intravenous saline cause a normal AGc metabolic acidosis. The SBE rarely falls below −10 mEq/l. With appropriate respiratory compensation, the pH will frequently remain above 7.3. An unresolved question is whether this is severe enough to cause harm.

To balance saline, some Cl⁻ must be replaced with HCO₃⁻, or else with strong anions which undergo metabolic ‘disappearance’, such as lactate, gluconate or acetate. Enough chloride must be replaced to balance the fall in extracellular SID against the A_TOT dilution effect. Experimentally this value is 24 mEq/l.³⁸

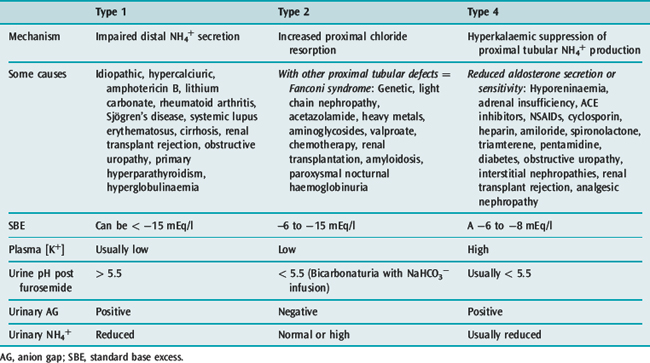
Renal tubular acidosis (RTA)

In RTA, urinary SID is inappropriately high in the setting of a low extracellular SID. The disturbance is in renal tubular Cl⁻ handling, either from reduced ammonium production proximally (Type 4) or distally (Type 1), or increased proximal tubular chloride resorption (Type 2). Causes are legion (Table 84.6).

Table 84.6 Types of renal tubular acidosis

Apart from treating underlying causes and preventing hypercalciuria, management in Types 1 and 2 RTA is based on administering sodium bicarbonate or citrate to correct extracellular SID, and preventing and treating hypokalaemia using potassium citrate (not chloride). In Type 4 RTA, inciting agents are ceased where relevant, and adrenal insufficiency treated with mineralocorticoid replacement. Alkali supplements and furosemide are occasionally necessary.¹²

Lactic acidosis

This is discussed in Chapter 15.

Management of metabolic acidosis

Management is directed at the underlying cause. When instituting mechanical ventilation, a sudden reduction in minute volume can be lethal. For example, a patient with an arterial pH of 6.9 and PaCO₂ of 10 mmHg is hyperventilating maximally. If the PaCO₂ is allowed to return to ‘normal’ (40 mmHg) on instituting mechanical ventilation, the arterial pH will immediately fall to 6.7. If the PaCO₂ is inadvertently allowed to rise to 60 mmHg, the pH will be 6.6.

Administration of buffers – sodium bicarbonate, ‘carbicarb’ and sodium lactate

In lactic acidosis and organic acidoses in general, it is difficult to justify the administration of buffers (see Chapter 15).⁴⁰ However, infusing NaHCO₃ to correct a severe normal AGc acidosis may be appropriate. Other conditions where NaHCO₃ administration is often indicated include severe hyperkalaemia, methanol and ethylene glycol poisoning, and tricyclic and salicylate overdose. A NaHCO₃ dose of 1 mmol/kg increases SBE approximately 3 mEq/l.

When administering NaHCO₃, the aim is to increase SID. The active agent is therefore sodium, not bicarbonate. The only reason NaOH is not used is its alkalinity (pH 14). However, two problems arise from the high CO₂ content (CO_2TOT) of NaHCO₃ (approximately 1028 mmol/l in a 1 M solution): one is the need for CO₂ impermeable storage; the other is the potential to create paradoxical intracellular respiratory acidosis, which can be demonstrated in vitro by adding NaHCO₃ to cultured cells.⁴¹

One approach is to reduce CO_2TOT, the trade-off being a rise in pH. In carbicarb (CO_2TOT = 750 mmol/l, PCO₂ = 2 mmHg, pH = 9.8), half the monovalent bicarbonate becomes divalent carbonate. Its use is still under evaluation. In Europe, sodium lactate (0.167 M, pH 6.9) is an alternative. The role of lactate is not to generate bicarbonate, but to undergo metabolic ‘disappearance’, leaving sodium to increase the SID.

Adding a weak base (B_TOT) will also shift the PaCO₂/pH curve upward. THAM (tris-hydroxymethyl aminomethane, or tris buffer) is a weak base with a pKa of 7.7 at 37 °C. THAM-H⁺ allows buffer base and thus SBE to increase without changing extracellular SID or A_TOT. THAM is CO₂ consuming, with good cell penetration, and causes an immediate intracellular metabolic and respiratory alkalosis. Presumably in CSF this phenomenon is behind its propensity to cause sudden apnoea. THAM accumulates in renal failure. Other problems include hyperosmolality, coagulation and potassium disturbances, and hypoglycaemia. The use of THAM requires further evaluation.

Finally, it should be recognised that to cause an appreciable increase in PaCO₂, NaHCO₃ has to be administered very rapidly (e.g. over 5 minutes).⁴² Even then the rise is transient, and usually less than 10 mmHg. With slow administration, over 30–60 minutes, NaHCO₃ should have minimal effects on CO₂ production and intravascular PCO₂. The exception is when pulmonary perfusion is massively reduced, such as in cardiac arrest.

Other potential adverse effects of buffer administration include a sudden increase in haemoglobin–oxygen affinity, the production of a hyperosmolar state, reduced [Ca⁺⁺] and [Mg⁺⁺], and rebound alkalosis on resolution of an organic acidosis.

METABOLIC ALKALOSIS

In metabolic alkalosis, extracellular SID is high relative to A_TOT. Metabolic alkalosis has been described as the most common acid–base disturbance. With modern definitions it is more often seen as part of a ‘mixed’ disorder.

Causes (Table 84.7)

Metabolic alkalosis can be precipitated by:

• low urinary SID

• loss of low SID enteric fluid

• gain of high SID fluid

Table 84.7 Metabolic alkalosis – causes

Low urinary SID	Enteric losses of low SID fluid	Gain of high SID fluid
Loop or thiazide diuretics	Pyloric stenosis, vomiting, nasogastric suction	NaHCO₃ administration
Post hypercapnia	Villous adenoma	Sodium citrate (plasma exchange, > 8 units stored blood)
Corticosteroids	Laxative abuse	Renal replacement fluids with high SID (> 35 mEq/l)
Cushing’s syndrome Primary mineralocorticoid excess Carbenoxolone Glycyrrhetinic acid (liquorice)		Milk-alkali syndrome
Hypercalcaemia
Milk-alkali syndrome
Magnesium deficiency
Bartter’s and Gitelman’s syndromes

SID, strong ion difference.

Clinical features

A high plasma pH (> 7.55) has a number of adverse effects (Table 84.8). Mortality in critical illness escalates as the pH rises above 7.55, although how much is causation versus association is unclear.

Table 84.8 Severe metabolic alkalosis – multisystem effects

Central nervous system

Vasospasm

Seizures

Confusion, drowsiness

Neuromuscular

Weakness, tetany, muscle cramps

Cardiovascular

Arrhythmias – supraventricular and ventricular

Decreased contractility

Respiratory

Decreased alveolar ventilation

Atelectasis, hypoxaemia

Metabolic

Hyperlactaemia

Low [Pi], [Ca⁺⁺], [Mg⁺⁺] and [K⁺]

Haemoglobin–oxygen affinity

Initially increased (until counteracted by increased 2,3-DPG)

Treatment

The first step is to remove the cause. Measures can then be instituted to accelerate the reduction in extracellular SID. They include:

• Correcting effective volume depletion (reduced skin turgor, postural hypotension, high urea:creatinine ratio, urinary [Cl⁻] < 20 mmol/l). Albumin preparations simultaneously increase A_TOT and reduce SID, and are thus likely to be more effective than saline.⁴³

• Administering KCl to correct potassium depletion. The vital component here is the chloride. Simplistically, potassium (strong cation) enters the depleted intracellular compartment in excess of chloride (strong anion), increasing extracellular SID. This explanation ignores associated Gibbs Donnan phenomena.

• Acetazolamide therapy to increase urinary SID (requires adequate renal function).

• Administration of HCl, which has a negative SID.^44,⁴⁵ Minute ventilation, hypercapnia and oxygenation generally (but not invariably) improve. For full correction the calculated HCl requirement (in mmol) is 0.3 × SBE × Wt (kg). HCl can be infused over 24 hours as a 0.2 M solution in dextrose through a central venous catheter. Regular checks of SBE (every 4 hours) are advisable. HCl can also be given indirectly, as NH₄Cl, or arginine or lysine hydrochloride. All require hepatic deamination.

• Renal replacement therapy.

Metabolic alkalosis in the setting of effective volume depletion has been termed ‘saline responsive’, in the sense that saline overcomes the alkalinising renal hypovolaemic response (low urinary SID). In fact, all metabolic alkaloses will respond if sufficient saline can be administered safely (see Infusion-related acidosis).

As with metabolic acidosis, care is required when instituting mechanical ventilation. Unless minute volume settings are reduced, it is possible to precipitate extreme alkalaemia.

RESPIRATORY ACIDOSIS

Causes (Table 84.9)

The risk is increased when CO₂ production is high and when ventilation is inefficient (large alveolar or apparatus dead space, respiratory muscle disadvantage due to hyperinflation).

Table 84.9 Some causes of respiratory acidosis

Mechanism/affected site	Acute	Chronic
Respiratory centre suppression	Sedative and narcotic drugs, CNS injury, CNS infection, brainstem vasculitis or infarction	Obesity hypoventilation syndrome
Airway obstruction	Inhalational injury, Ludwig’s angina, laryngeal trauma	Obstructive sleep apnoea, vocal cord paresis, subglottic and tracheal stenosis
Mechanical ventilation	Permissive hypercapnia
Neural/neuromuscular	Spinal cord injury, Guillain–Barré syndrome, myasthenia gravis, muscle relaxants, envenomation, acute poliomyelitis, critical illness weakness syndromes	Phrenic nerve damage, paraneoplastic syndromes, post-polio syndrome
Muscle	Myopathy, low [K⁺], high [Mg⁺], low [Pi], diaphragmatic injury, shock	Muscular dystrophies, motor neurone disease
Decreased chest wall compliance	Abdominal distension, burns, pneumothorax, large pleural effusions	Obesity, kyphoscoliosis, ankylosing spondylitis
Loss of chest wall integrity/geometry	Flail segment	Thoracoplasty
Increased small airways resistance	Asthma, bronchiolitis	Chronic obstructive pulmonary disease
Deceased lung compliance	Acute lung injury, pneumonia, pulmonary oedema, vasculitis, haemorrhage	Pulmonary fibrosis

Clinical features

These include the effects of acidaemia (Table 84.5). However, acute hypercapnia has important central nervous effects, including confusion, drowsiness, asterixis, fitting and raised intracranial pressure. Hypercapnia also activates the sympathetic–adrenal and renin–angiotensin systems, reducing renal blood flow, glomerular filtration rate and urine output.

Acute	Chronic
Hypoxaemia	Pregnancy
Hepatic failure	High altitude
Sepsis	Chronic lung disease
Asthma	Neurotrauma
Pulmonary embolism	Chronic liver dysfunction
Pneumonia, acute lung injury
CNS disorders – stroke, infection, trauma
Drugs – salicylates, selective serotonin reuptake inhibitors
Opiate and benzodiazepine withdrawal
Mechanical hyperventilation – intentional or inadvertent
Pain, anxiety, psychosis