Review of Basic Mathematical Skills
• Add, subtract, multiply, and divide whole numbers
• Add, subtract, multiply, and divide fractions and reduce fractions to the lowest terms
• Add, subtract, multiply, and divide mixed numbers and reduce to the lowest terms
• Add, subtract, multiply, and divide decimals and round them to a specific number place value
• Convert fractions to decimal fractions
• Convert among fractions, decimals, and percentages
• Express numbers in ratio and proportion and solve for unknowns
Fractions
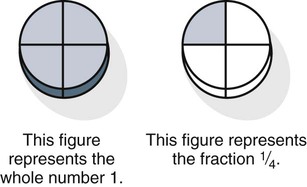
What Is a Fraction?
If you said the numerator is 5 and the denominator is 6, you are correct.
If a patient has 25 tablets in a prescription and takes 13 tablets, what is the fractional use?
Answer: 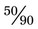 or
or 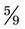 . (When
. (When 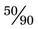 is divided by 10 in both the numerator and the denominator, the result is
is divided by 10 in both the numerator and the denominator, the result is 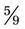 .)
.)
Decimals
What Is a Decimal?

| Three | the number to the left of the decimal point |
| and | the decimal point |
| Forty-seven | the number to the right of the decimal point |
| Hundredths | the place value of the decimal |
| One | the number to the left of the decimal point |
| and | the decimal point |
| Two hundred fifty | the number to the right of the decimal point |
| Thousandths | the place value of the decimal |
Ratios
Expressing Numbers as Ratios
When numbers are expressed in ratios, numbers that designate a quantity must be expressed in the same units of measure. For example, if the numerator of the ratio is expressed in inches, the denominator must also be expressed in inches. So to establish a ratio of 3 inches : 1 foot, the 1 foot must be changed to 12 inches (12″ = 1 foot). Now the ratio has the same unit of measure in inches and the ratio is 3″ : 12″, or the ratio is reduced to 1 : 4. Thus 3 qts : 1 gal (1 gal = 4 qt) becomes 3 qt : 4 qt, or the ratio 3 : 4. Conversions within and among units of measure will be presented in Chapters 3 and 4.
Quantities
Determining the Percentage of a Quantity
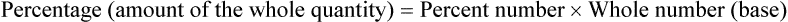
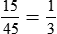
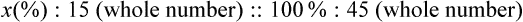
The fraction may be found in three ways:
1. Finding the percentage, as in “What is 50% of 15?”
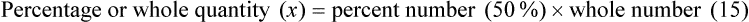
2. Find the whole quantity, as in “15 is 60% of what number?”
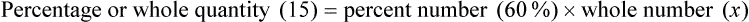
3. Finding the percent number, as in “5 is what percent of 15?”
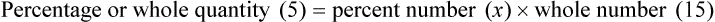
Review of Rules
Fractions
• To change an improper fraction to a mixed number, divide the numerator by the denominator.
• To change a mixed number to an improper fraction, multiply the denominator by the whole number and then add the numerator to the product obtained. This number then becomes the numerator for the fraction, and the denominator of the fraction retained is the original denominator.
• To reduce a fraction to the lowest term, divide both the numerator and denominator by the greatest common factor.
• To add or subtract fractions with a common denominator, add or subtract the numerators as indicated. Then write the sum or difference as the numerator for the fraction, and the common denominator becomes the denominator for the fraction. Reduce this fraction to the lowest term or change to a mixed number as indicated.
• For fractions with an uncommon denominator, the least common denominator must be found. The number that will divide exactly into the denominators must be found, and then the numerators of each fraction must be multiplied by the common number. After finding the common denominator, the mathematical calculation of adding or subtracting may be performed. When adding or subtracting fractions with uncommon denominators, add or subtract the numerators as indicated and then reduce to lowest terms or to the mixed number.
• To multiply fractions, multiply the numerators and multiply the denominators, with the product of the numerators being the new numerator and the product of the denominators being the new denominator. Reduce the fraction or change to a mixed number as indicated.
• To multiply mixed numbers, change the mixed number to an improper fraction and then multiply, as mentioned earlier with fractions.
• To divide fractions, invert the fraction that is the divisor and multiply the dividend by the inverted fraction—the remainder of the problem is actually like multiplying fractions. Reduce to the lowest term.
• To divide mixed numbers, change the mixed number to a fraction and then proceed as if the problem were a fractional unit. Reduce the fraction as needed or change to a mixed number as indicated.
Decimals
• To read a decimal, the number to the left of the decimal is a whole number, “and” is used to represent the decimal point, and the number to the right of the decimal point is read as a whole number value of the number farthest to the right including the decimal point as a number space, with “th” added to the number space. For example, 2.34 would be 2 and 34 hundredths.
• To round a decimal place to a certain place or determined number, begin at the farthermost right digit. If that number is 5 to 9, the second digit to the right will be increased by one (i.e., 1.567 would become 1.57). If the farthermost number is 0 to 4, the second number will remain the same. After determining the number of digits to remain, delete the excess numbers using the previous rule to the correct place (e.g., if 8.78934 is to be rounded to hundredths, the answer would be 8.79).
• To add or subtract decimal numbers, align the numbers, being sure that the decimal points are aligned. Add zeros at the end of the decimal fraction until all decimal numbers are the same length. Then add or subtract as for whole numbers, being sure the decimal point is correctly aligned in the answer. Whole numbers are understood to have a decimal point to the right of the number.
• To multiply decimal numbers, multiply the numbers as if the numbers are whole numbers, then count the numbers to the right of the decimal points and finally add a decimal point in the product so that there are as many decimal points in the product as in the numbers being multiplied.
• To divide a decimal number by a whole number, place the decimal point in the quotient directly above the decimal point in the dividend.
• To divide a decimal number by a decimal number, count the number of digits to the right of the decimal in the divisor; place a decimal point at the end of the same number of places in the dividend, moving the decimal point in place and adding zeros as needed; and then place the decimal point at that place in the quotient directly above the decimal point in the dividend. Divide the numbers as if the divisor is a whole number.
• To change a fraction to a decimal, divide the numerator by the denominator.
• To change a decimal to a fraction, place the decimal number as the numerator with the denominator being 1 plus the number of zeros as found in the decimal number and the decimal point (i.e., 0.01 would be 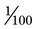 ). Reduce the fraction as appropriate.
). Reduce the fraction as appropriate.
Ratio, Proportion, and Percentages
• If two fractions are equivalent, the cross-products will be equal. If the cross-products in a proportional equation are equal, the fractions are equivalent or the proportion is true.
• If each member of an equality is multiplied by the same number, the products will be equal.
• If each member of an equality is divided by the same number, the quotients will be equal.
• To multiply or divide in %, first change the percentage to a decimal and then do the calculation.
• To change a percentage to a decimal form, multiply by 0.01 or move the decimal point two places to the left. To change decimal to percent, move the decimal point two places to the right. Think of the alphabet placement of “D” and “P.”
• To solve an unknown proportion, multiply the means or “insies” and the extremes or “outsies,” setting the equation with the unknown on the left being equal to the quotient numbers on the right. Then solve for the unknown.
• To solve a percent proportion, the “what” translates to the unknown or a letter, “of” translates to times or “×,” “is” translates to equal or “=,” and “%” may be either 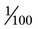 or 0.01 for multiplication of the percentage. Read the problem and insert the translation, then solve the unknown.
or 0.01 for multiplication of the percentage. Read the problem and insert the translation, then solve the unknown.
Estimating of Answers
• Estimation is the best check of a reasonable mathematical calculation. To estimate a number, mentally round of to a slightly larger or smaller number containing fewer significant figures (Example: 59 would be estimated to 60). Then do the calculation mentally knowing that the mental answer will be slightly higher or lower than the actual calculation but will be close to the desired answer.
• After estimating the answer, calculate the answer and then check against the estimated answer.

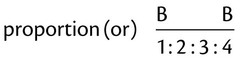
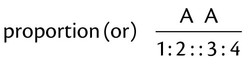
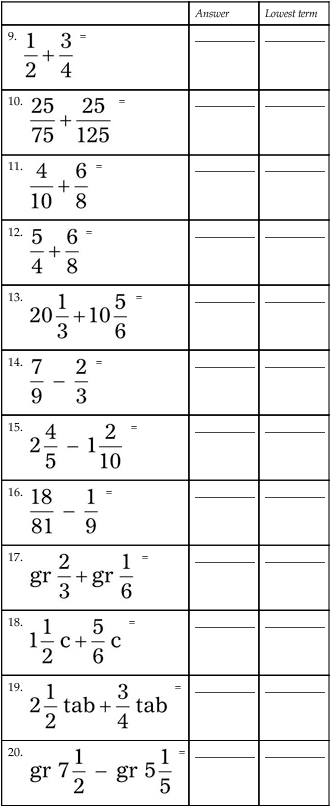
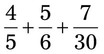 = __________
= __________ = __________
= __________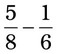 = __________
= __________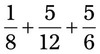 = __________
= __________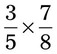 = __________
= __________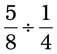 = __________
= __________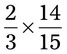 = __________
= __________ = __________
= __________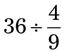 = __________
= __________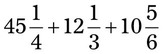 = __________
= __________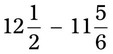 = __________
= __________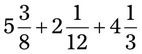 = __________
= __________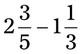 = __________
= __________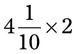 = __________
= __________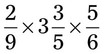 = __________
= __________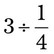 = __________
= __________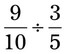 = __________
= __________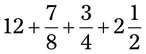 = __________
= __________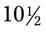 inches long. The physician asks you to be sure the person has sufficient amount to apply bandages daily for 2 weeks using approximately
inches long. The physician asks you to be sure the person has sufficient amount to apply bandages daily for 2 weeks using approximately 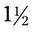 yards per bandage. How many rolls of adhesive should you be sure the patient buys?
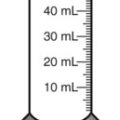
yards per bandage. How many rolls of adhesive should you be sure the patient buys?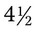 cups of water. How many milliliters would be in
cups of water. How many milliliters would be in 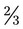 of the solution?
of the solution?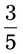 __________
__________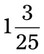 __________
__________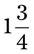 __________
__________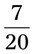 __________
__________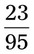 __________
__________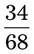 __________
__________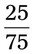 __________
__________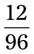 __________
__________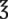 __________
__________ __________
__________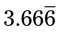 ; all the numbers in this example contain whole numbers, but they are not evenly divisible and may have decimal remainders.
; all the numbers in this example contain whole numbers, but they are not evenly divisible and may have decimal remainders.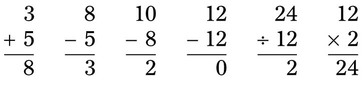
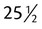 .
.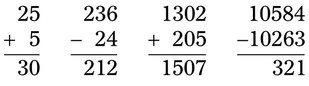
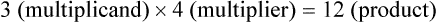


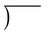 .” The number being divided is called the dividend, and the number used to divide is the divisor. The result of the division is the quotient.
.” The number being divided is called the dividend, and the number used to divide is the divisor. The result of the division is the quotient.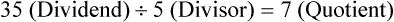
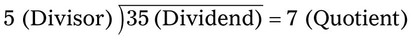
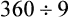
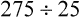
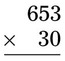 = __________
= __________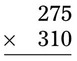 = __________
= __________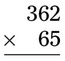 =
= =
=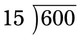 = __________
= __________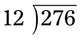 = __________
= __________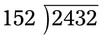 = __________
= __________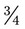 .
.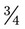 you are correct.
you are correct.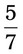

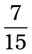
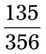
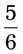

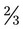 is written, the fraction actually means 2 ÷ 3. The following illustrates this in pharmaceutical terms:
is written, the fraction actually means 2 ÷ 3. The following illustrates this in pharmaceutical terms:
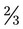 and
and 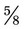 . An improper fraction is one in which the numerator is equal to or greater than the denominator, making the fraction a number of one or more such as
. An improper fraction is one in which the numerator is equal to or greater than the denominator, making the fraction a number of one or more such as 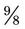 or
or 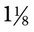 and
and  or 2. If the numerator and denominator are the same, the number becomes 1, such as
or 2. If the numerator and denominator are the same, the number becomes 1, such as 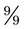 or
or 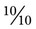 . An improper fraction may be written as a mixed number (a whole number and a fraction) or as an improper fraction (a fraction that has a numerator equal to or greater than the denominator). To change an improper fraction to a mixed number, the numerator is divided by the denominator and any remainder is written over the denominator, such as
. An improper fraction may be written as a mixed number (a whole number and a fraction) or as an improper fraction (a fraction that has a numerator equal to or greater than the denominator). To change an improper fraction to a mixed number, the numerator is divided by the denominator and any remainder is written over the denominator, such as 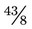 (an improper fraction) =
(an improper fraction) = 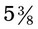 (a mixed number). (When 43 is divided by 8, the answer is 5 with a remainder of 3, so
(a mixed number). (When 43 is divided by 8, the answer is 5 with a remainder of 3, so 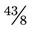 as a mixed number is
as a mixed number is 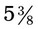 .) The remainder is the amount that is left over after the whole number has been divided into the numerator the maximum number of times (in this problem, 3 is the remainder that now is seen as
.) The remainder is the amount that is left over after the whole number has been divided into the numerator the maximum number of times (in this problem, 3 is the remainder that now is seen as 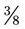 ). An improper fraction should always be reduced to a mixed number after calculations have been completed.
). An improper fraction should always be reduced to a mixed number after calculations have been completed.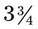 and
and 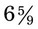 . To change a mixed number to an improper fraction, multiply the whole number by the denominator and add the amount found in the numerator (e.g.,
. To change a mixed number to an improper fraction, multiply the whole number by the denominator and add the amount found in the numerator (e.g., 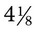 actually means that 4 is multiplied by 8 to provide the whole number of 32 and the 1 found in the numerator of the fraction is added to the total, or 32 + 1 = 33). The denominator remains the number found as the denominator of the mixed number, or
actually means that 4 is multiplied by 8 to provide the whole number of 32 and the 1 found in the numerator of the fraction is added to the total, or 32 + 1 = 33). The denominator remains the number found as the denominator of the mixed number, or 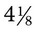 =
= 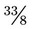 . Another example of changing a mixed number to an improper fraction is
. Another example of changing a mixed number to an improper fraction is 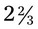 : 2 × 3 + 2 with the same denominator of 3 or
: 2 × 3 + 2 with the same denominator of 3 or 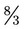 .
.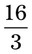 = __________
= __________ = __________
= __________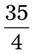 = __________
= __________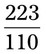 = __________
= __________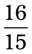 = __________
= __________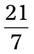 = __________
= __________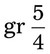 = __________
= __________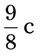 = __________
= __________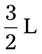 = __________
= __________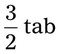 = __________
= __________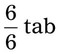 = __________
= __________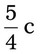 = __________
= __________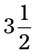 = __________
= __________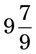 = __________
= __________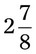 = __________
= __________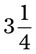 = __________
= __________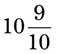 = __________
= __________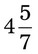 = __________
= __________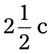 = __________
= __________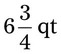 = __________
= __________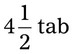 = __________
= __________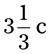 = __________
= __________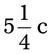 = __________
= __________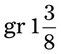 = __________
= __________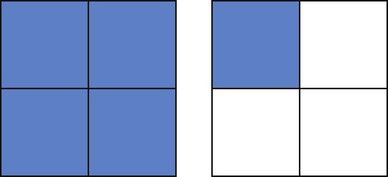

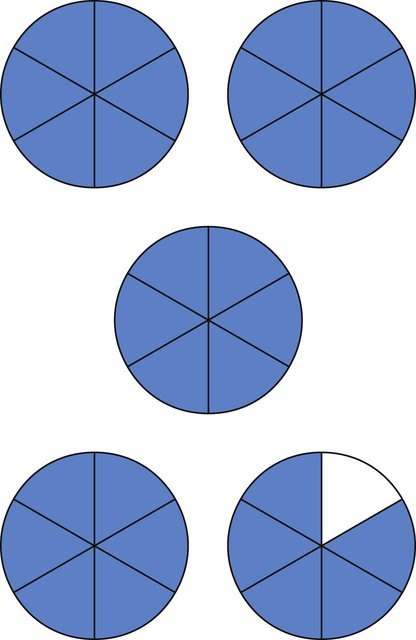

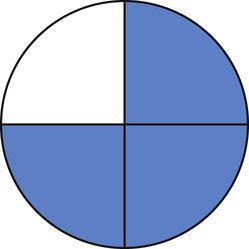
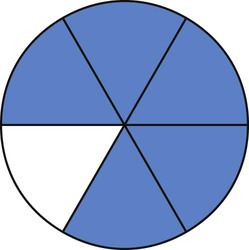
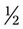 of a tablet. Fill in the following tablet to show this fraction.
of a tablet. Fill in the following tablet to show this fraction.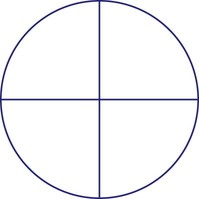
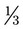 of a glass of water. On the glass, show
of a glass of water. On the glass, show 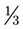 of the glass of water.
of the glass of water.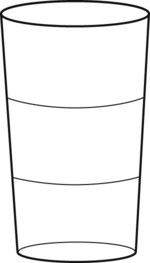
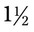 tablets four times a day. The prescription drug is in whole tablets. Show what the customer should do.
tablets four times a day. The prescription drug is in whole tablets. Show what the customer should do.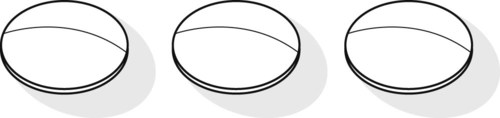
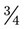 of a medicine dropper of medication. Indicate on the medicine dropper what you would show the customer as a dose.
of a medicine dropper of medication. Indicate on the medicine dropper what you would show the customer as a dose.
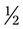 could be
could be 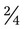 ,
, 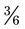 , or even
, or even 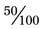 . For example, with
. For example, with 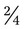 , the numerator and denominator can both be divided by 2 to give
, the numerator and denominator can both be divided by 2 to give 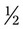 ; or with
; or with 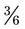 , both parts of the fraction can be divided by 3 for
, both parts of the fraction can be divided by 3 for 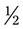 ; finally, with
; finally, with 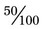 , both components of the fraction can be divided by 50 for
, both components of the fraction can be divided by 50 for 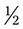 . Each of these fractions is actually one half of the total number of equivalent parts of a whole.
. Each of these fractions is actually one half of the total number of equivalent parts of a whole.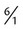 = 6.
= 6.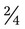 can be reduced by dividing by 2 [2 ÷ 2 = 1 and 4 ÷ 2 = 2] =
can be reduced by dividing by 2 [2 ÷ 2 = 1 and 4 ÷ 2 = 2] = 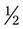 , or
, or 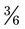 can be reduced by 3 [3 ÷ 3 = 1 and 6 ÷ 3 = 2] to =
can be reduced by 3 [3 ÷ 3 = 1 and 6 ÷ 3 = 2] to = 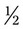 ). In each case the reduced fraction contains the same amount of space in each whole. The difference is that the number of divided pieces of the whole has changed. The fractions are comparable, although the actual numerators and denominators have been altered by division with a number that is common to both parts of the fraction. This is dividing by a common factor of the numerator and denominator (e.g., with the fraction
). In each case the reduced fraction contains the same amount of space in each whole. The difference is that the number of divided pieces of the whole has changed. The fractions are comparable, although the actual numerators and denominators have been altered by division with a number that is common to both parts of the fraction. This is dividing by a common factor of the numerator and denominator (e.g., with the fraction 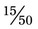 , both the numerator and denominator can be divided by 5, so the fraction can be reduced to
, both the numerator and denominator can be divided by 5, so the fraction can be reduced to 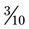 ).
).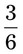 = __________
= __________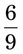 = __________
= __________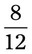 = __________
= __________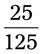 = __________
= __________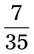 = __________
= __________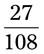 = __________
= __________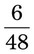 = __________
= __________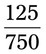 = __________
= __________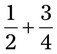 =
=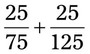 =
=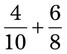 =
=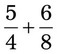 =
=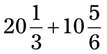 =
=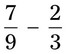 =
=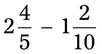 =
=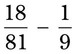 =
=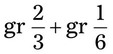 =
=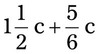 =
=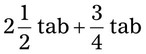 =
=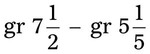 =
=
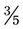 +
+ 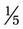 can be added by adding the numerators, or 3 and 1 [3 + 1] and placing the answer over the denominator of 5. This provides an answer of
can be added by adding the numerators, or 3 and 1 [3 + 1] and placing the answer over the denominator of 5. This provides an answer of 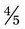 . To subtract
. To subtract 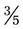 −
− 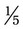 , subtract 1 from 3 [3 – 1]/5 for an answer of
, subtract 1 from 3 [3 – 1]/5 for an answer of 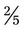 ).
).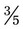 +
+ 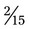 could easily be found because 15 is divisible by 5. To change
could easily be found because 15 is divisible by 5. To change 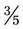 to the common denominator, divide the denominator 5 into the denominator 15 (3); then multiply the 3 (numerator) times 3 to calculate
to the common denominator, divide the denominator 5 into the denominator 15 (3); then multiply the 3 (numerator) times 3 to calculate 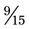 . Therefore
. Therefore 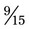 +
+ 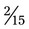 would provide an answer of
would provide an answer of 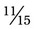 .
.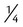 ,
,  ,
, 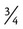 , 1, and so on to estimate the answer with any calculations with fractions. Estimate either slightly larger or slightly smaller numbers. Remember that this is an estimate not a specific answer. It is for comparison for your exact answer.
, 1, and so on to estimate the answer with any calculations with fractions. Estimate either slightly larger or slightly smaller numbers. Remember that this is an estimate not a specific answer. It is for comparison for your exact answer.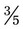 +
+ 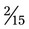 , the lowest common denominator is 15. The problem with the common denominator is
, the lowest common denominator is 15. The problem with the common denominator is 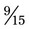 (15 ÷ 5 = 3; 3 × 3 = 9; so
(15 ÷ 5 = 3; 3 × 3 = 9; so 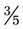 =
= 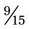 ) +
) + 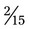 =
= 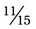 .
.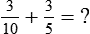
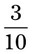 is okay. The common denominator for both fractions will be 10.
is okay. The common denominator for both fractions will be 10.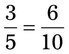
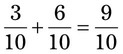
 , so now the problem is simply
, so now the problem is simply 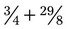 . The next step is to find the lowest common denominator; in this problem it is 8; 8 ÷ 4 = 2; 2 × 3 = 6; leading to the fraction
. The next step is to find the lowest common denominator; in this problem it is 8; 8 ÷ 4 = 2; 2 × 3 = 6; leading to the fraction 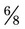 . The problem is now
. The problem is now 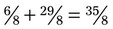 . This improper fraction can then be converted back to the mixed number of
. This improper fraction can then be converted back to the mixed number of 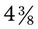 (35 ÷ 8 = 4 with a remainder of 3 or
(35 ÷ 8 = 4 with a remainder of 3 or 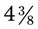 ). Here is one more example:
). Here is one more example: 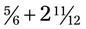 . First, change the mixed number to an improper fraction (12 × 2 +11 =
. First, change the mixed number to an improper fraction (12 × 2 +11 = 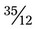 ). The problem now becomes
). The problem now becomes 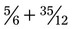 . The lowest common denominator is 12. To convert
. The lowest common denominator is 12. To convert 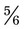 using the lowest common denominator would be
using the lowest common denominator would be 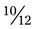 (12 ÷ 6 = 2; 2 × 5 = 10; so
(12 ÷ 6 = 2; 2 × 5 = 10; so 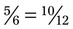 ). Next,
). Next, 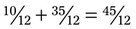 , or
, or 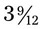 (45 ÷ 12 = 3 with a remainder of 9, or
(45 ÷ 12 = 3 with a remainder of 9, or 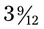 or
or 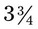 ). In this problem the fraction may be reduced.
). In this problem the fraction may be reduced.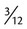 can be reduced to
can be reduced to 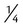 by dividing the numerator and denominator by 3.
by dividing the numerator and denominator by 3.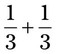 = __________
= __________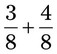 = __________
= __________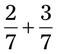 = __________
= __________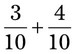 = __________
= __________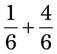 = __________
= __________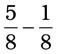 = __________
= __________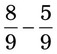 = __________
= __________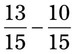 = __________
= __________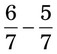 = __________
= __________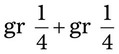 = __________
= __________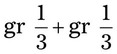 = __________
= __________ = __________
= __________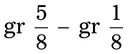 = __________
= __________ = __________
= __________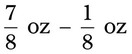 = __________
= __________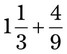 = __________
= __________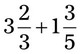 = __________
= __________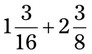 = __________
= __________ = __________
= __________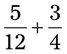 = __________
= __________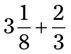 = __________
= __________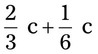 = __________
= __________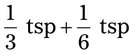 = __________
= __________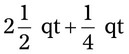 = __________
= __________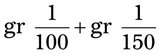 = __________
= __________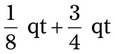 = __________
= __________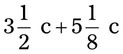 = __________
= __________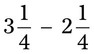 = __________
= __________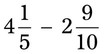 = __________
= __________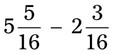 = __________
= __________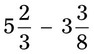 = __________
= __________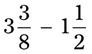 = __________
= __________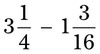 = __________
= __________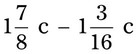 = __________
= __________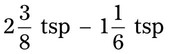 = __________
= __________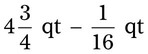 = __________
= __________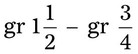 = __________
= __________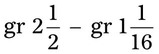 = __________
= __________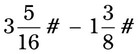 = __________
= __________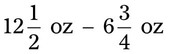 = __________
= __________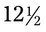 oz of the desired medication. A newer medication container holds
oz of the desired medication. A newer medication container holds 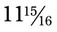 oz of the medication. A customer asks you to calculate the difference in the amount of medication in the two bottles. What is your answer? __________
oz of the medication. A customer asks you to calculate the difference in the amount of medication in the two bottles. What is your answer? __________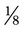 gallon. The second medication uses
gallon. The second medication uses 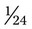 gallon. The third medication needs
gallon. The third medication needs 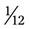 of a gallon. What is the total amount of distilled water used? __________
of a gallon. What is the total amount of distilled water used? __________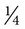 , gr
, gr 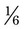 , and gr
, and gr 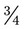 . Express the medication doses in a common denominator. __________ What is the total amount that has been used? __________ If the total medication is gr v, how many grains are left following the completion of the prescription preparations? __________
. Express the medication doses in a common denominator. __________ What is the total amount that has been used? __________ If the total medication is gr v, how many grains are left following the completion of the prescription preparations? __________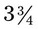 oz of a specific medication. In a day, you have used
oz of a specific medication. In a day, you have used 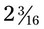 oz of that medication. How much medication will you have left for use to fill prescriptions the next day? __________
oz of that medication. How much medication will you have left for use to fill prescriptions the next day? __________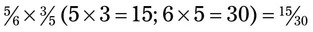 . In this example, 15 is a number that can be used to reduce to lowest terms (15 ÷ 15 = 1; 30 ÷ 15 = 2), giving the final answer of
. In this example, 15 is a number that can be used to reduce to lowest terms (15 ÷ 15 = 1; 30 ÷ 15 = 2), giving the final answer of 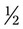 .
.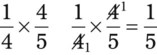
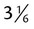 would be changed to
would be changed to 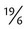 by multiplying 3 × 6 and adding the 1 in the numerator of the fraction, with the denominator remaining the same).
by multiplying 3 × 6 and adding the 1 in the numerator of the fraction, with the denominator remaining the same).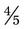 is inverted, the fraction would become
is inverted, the fraction would become 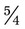 . In the problem
. In the problem 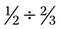 (
(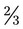 is the number to be inverted), the problem becomes
is the number to be inverted), the problem becomes 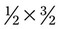 after the inversion of the numbers. After the inversion is complete, the remainder of the problem is actually multiplication of fractions. Remember to cancel any numbers that can be simplified to make the problem easier to solve. (Canceling numbers was shown earlier with the multiplication example.) To cancel a number, divide both the numerator and the denominator by a common number that will divide into both numbers evenly, or without a remainder. This is a shortcut used to reduce the value of the numerals in the fractions for ease of calculation. (Cancellation is used when fractions are being multiplied. Canceling cannot be accomplished if sums or differences are in numerators or denominators. If you question whether you can cancel, do not do it.) Then reduce the fraction further if this is possible. In the previous example, solving the problem gives an answer of
after the inversion of the numbers. After the inversion is complete, the remainder of the problem is actually multiplication of fractions. Remember to cancel any numbers that can be simplified to make the problem easier to solve. (Canceling numbers was shown earlier with the multiplication example.) To cancel a number, divide both the numerator and the denominator by a common number that will divide into both numbers evenly, or without a remainder. This is a shortcut used to reduce the value of the numerals in the fractions for ease of calculation. (Cancellation is used when fractions are being multiplied. Canceling cannot be accomplished if sums or differences are in numerators or denominators. If you question whether you can cancel, do not do it.) Then reduce the fraction further if this is possible. In the previous example, solving the problem gives an answer of 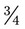 . Another example is
. Another example is 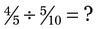 In this example, the problem is now
In this example, the problem is now 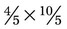 or simplified to 4 × 2 (10 ÷ 5) = 8, and 1 (5 ÷ 5) × 5 = 5, so the fraction is
or simplified to 4 × 2 (10 ÷ 5) = 8, and 1 (5 ÷ 5) × 5 = 5, so the fraction is 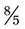 . This can be changed to a mixed number of
. This can be changed to a mixed number of 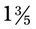 .
.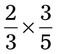 = __________
= __________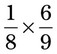 = __________
= __________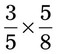 = __________
= __________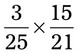 = __________
= __________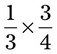 = __________
= __________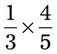 = __________
= __________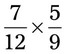 = __________
= __________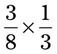 = __________
= __________ = __________
= __________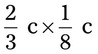 = __________
= __________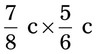 = __________
= __________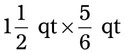 = __________
= __________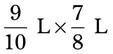 = __________
= __________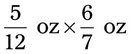 = __________
= __________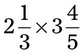 = __________
= __________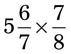 = __________
= __________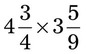 = __________
= __________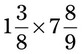 = __________
= __________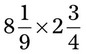 = __________
= __________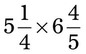 = __________
= __________ = __________
= __________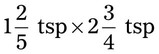 = __________
= __________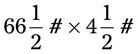 = __________
= __________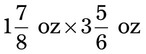 = __________
= __________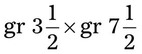 = __________
= __________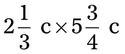 = __________
= __________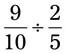 = __________
= __________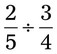 = __________
= __________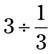 = __________
= __________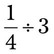 = __________
= __________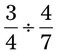 = __________
= __________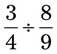 = __________
= __________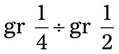 = __________
= __________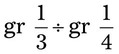 = __________
= __________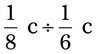 = __________
= __________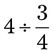 = __________
= __________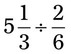 = __________
= __________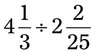 = __________
= __________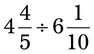 = __________
= __________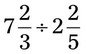 = __________
= __________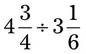 = __________
= __________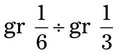 = __________
= __________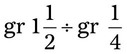 = __________
= __________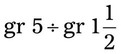 = __________
= __________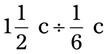 = __________
= __________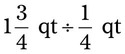 = __________
= __________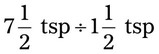 = __________
= __________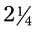 of a drug to be given tid. You have gr
of a drug to be given tid. You have gr 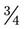 tabs in stock. How many tablets would you give with each dose? __________ How many tablets would you give in a day? __________ How many tablets would you need to fill this prescription for a 30-day supply? __________
tabs in stock. How many tablets would you give with each dose? __________ How many tablets would you give in a day? __________ How many tablets would you need to fill this prescription for a 30-day supply? __________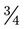 of the bottle. How many tablets do you have left in stock for filling future prescriptions? __________
of the bottle. How many tablets do you have left in stock for filling future prescriptions? __________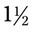 tsp, how many doses are in the bottle? __________. If the medication is given four times a day, how many days will this medication last? __________
tsp, how many doses are in the bottle? __________. If the medication is given four times a day, how many days will this medication last? __________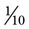 , 0.01 =
, 0.01 = 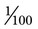 , or 0.001 =
, or 0.001 = 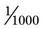 .
.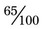 . (The decimal number is made into a fractional mixed number of 25 65/100.) With decimals, the numerator is the number following the decimal point. This number is placed over a number consisting of 1 followed by the number of zeros found in the number of the numerator. Thus 3.7 is
. (The decimal number is made into a fractional mixed number of 25 65/100.) With decimals, the numerator is the number following the decimal point. This number is placed over a number consisting of 1 followed by the number of zeros found in the number of the numerator. Thus 3.7 is 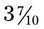 . With decimals, zeros may be added to or deleted from the end of the decimal without changing the actual value of the number. Thus 3.7 is the same value as 3.70 or 3.700. Likewise 5.050 is the same value as 5.05.
. With decimals, zeros may be added to or deleted from the end of the decimal without changing the actual value of the number. Thus 3.7 is the same value as 3.70 or 3.700. Likewise 5.050 is the same value as 5.05.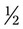 is 1 ÷ 2, or 1.0 ÷ 2, because 2 will not divide into 1. Thus 1.0 ÷ 2 = 0.5. Likewise,
is 1 ÷ 2, or 1.0 ÷ 2, because 2 will not divide into 1. Thus 1.0 ÷ 2 = 0.5. Likewise,  is 3 ÷ 4, or 3.0 ÷ 4. Thus 3 ÷ 4 = 0.75 is a decimal answer.
is 3 ÷ 4, or 3.0 ÷ 4. Thus 3 ÷ 4 = 0.75 is a decimal answer.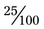 .
.

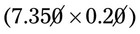 so that the problem now looks like 7.35 × 0.2 or an answer of 1.470. The zero in the answer should then be canceled (
so that the problem now looks like 7.35 × 0.2 or an answer of 1.470. The zero in the answer should then be canceled (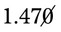 ) to give the final answer of 1.47.
) to give the final answer of 1.47.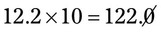 , or just move the decimal point one space to the right in the 12.2. or 122. If the multiplier is 100, then the decimal would be moved 2 places; with 1000, 3 places, etc.
, or just move the decimal point one space to the right in the 12.2. or 122. If the multiplier is 100, then the decimal would be moved 2 places; with 1000, 3 places, etc.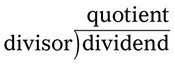
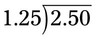 . If a decimal appears in the divisor, move the decimal to the right until the divisor is a whole number. Then move the decimal point in the dividend the same number of places to the right. For example, in the previous example, the problem would appear as
. If a decimal appears in the divisor, move the decimal to the right until the divisor is a whole number. Then move the decimal point in the dividend the same number of places to the right. For example, in the previous example, the problem would appear as 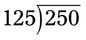 when the decimals in the divisor and dividend are both moved (
when the decimals in the divisor and dividend are both moved (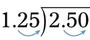 ). Place a decimal point on the quotient (answer) line directly above the decimal point in the dividend and add zeros behind the decimal point in the dividend if more places are necessary for dividing. The answer is then 2. For example, 1 ÷ 5 would be
). Place a decimal point on the quotient (answer) line directly above the decimal point in the dividend and add zeros behind the decimal point in the dividend if more places are necessary for dividing. The answer is then 2. For example, 1 ÷ 5 would be 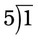 . In this problem, 5 cannot be divided into 1, so the problem must become
. In this problem, 5 cannot be divided into 1, so the problem must become 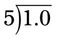 or 0.2 by placing the decimal point directly over the decimal point in the dividend and then dividing. Remember that if a whole number is not in front of the decimal point, a zero must be added to prevent medication errors. Another example would be 40.44 ÷ 0.4, which, when placed in the long division format, would be
or 0.2 by placing the decimal point directly over the decimal point in the dividend and then dividing. Remember that if a whole number is not in front of the decimal point, a zero must be added to prevent medication errors. Another example would be 40.44 ÷ 0.4, which, when placed in the long division format, would be 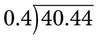 . Next, move the decimal in the divisor to the whole number 4 and move the decimal in the dividend to 404.4. For
. Next, move the decimal in the divisor to the whole number 4 and move the decimal in the dividend to 404.4. For 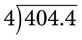 , the answer is 101.1. Be sure to fill in the 0 in the quotient when the number cannot be divided by the divisor, as in the “0” in 101.1.
, the answer is 101.1. Be sure to fill in the 0 in the quotient when the number cannot be divided by the divisor, as in the “0” in 101.1.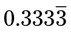 to the number of places that zeros are added to the dividend. In these cases, the number may be shown with a 3 with a line over the 3, meaning
to the number of places that zeros are added to the dividend. In these cases, the number may be shown with a 3 with a line over the 3, meaning 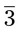 is a repeating number. In this case in the medical field, the 3 should be rounded to the hundredth place or 0.33. Again, remember to place the 0 in front of the decimal point.
is a repeating number. In this case in the medical field, the 3 should be rounded to the hundredth place or 0.33. Again, remember to place the 0 in front of the decimal point.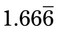 would be 1.67).
would be 1.67).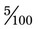 or 5 parts of 100.
or 5 parts of 100.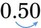 ) by multiplying by 100 and add the % sign. So 0.50 is equal to 50%. If the decimal does not have two places to the right of the decimal point, you must add a zero so that the decimal point can be moved two places because two decimal places are needed to multiply by 100; 0.5 would need a zero added (0.50) and then the decimal point should be moved two places (
) by multiplying by 100 and add the % sign. So 0.50 is equal to 50%. If the decimal does not have two places to the right of the decimal point, you must add a zero so that the decimal point can be moved two places because two decimal places are needed to multiply by 100; 0.5 would need a zero added (0.50) and then the decimal point should be moved two places (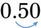 ) so that 0.5 becomes 50%. Finally, if the number is a whole number such as 5, two zeros must be added to the number to find the percentage. Thus 5, when multiplying by 100, two zeros would be added (
) so that 0.5 becomes 50%. Finally, if the number is a whole number such as 5, two zeros must be added to the number to find the percentage. Thus 5, when multiplying by 100, two zeros would be added (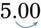 ), and 5 would become 500%.
), and 5 would become 500%.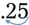 ). An example is 25% =
). An example is 25% = 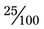 (or 25 ÷ 100) = 0.25. Remember, to prevent errors, always place a zero in front of the decimal place if no whole number is present. As with changing a decimal to a percentage, zeros may be added in front of the number as needed so that the two decimal places may be moved (e.g., 8% would become 0.08 [
(or 25 ÷ 100) = 0.25. Remember, to prevent errors, always place a zero in front of the decimal place if no whole number is present. As with changing a decimal to a percentage, zeros may be added in front of the number as needed so that the two decimal places may be moved (e.g., 8% would become 0.08 [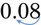 ] in decimals or 8/100).
] in decimals or 8/100).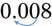 or 0.8 divided by 100).
or 0.8 divided by 100). ).
).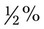 would first need to be converted to 0.5% (1 ÷ 2 = 0.5). Then convert the 0.5% to a decimal by moving the decimal two places to the left while adding the necessary zeros, or
would first need to be converted to 0.5% (1 ÷ 2 = 0.5). Then convert the 0.5% to a decimal by moving the decimal two places to the left while adding the necessary zeros, or 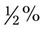 = 0.005 (
= 0.005 (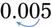 ). Remember that the calculation is actually dividing by 100.
). Remember that the calculation is actually dividing by 100.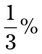 = __________
= __________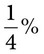 = __________
= __________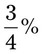 = __________
= __________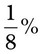 = __________
= __________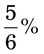 = __________
= __________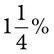 = __________
= __________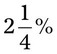 = __________
= __________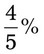 = __________
= __________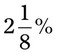 = __________
= __________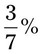 = __________
= __________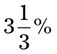 = __________
= __________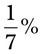 = __________
= __________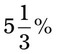 = __________
= __________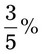 = __________
= __________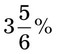 = __________
= __________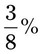 = __________
= __________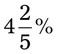 = __________
= __________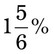 = __________
= __________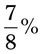 = __________
= __________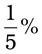 = __________
= __________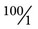 (the fraction for 100) and add the percent sign (%). This is the same step that was used to convert a fraction to a decimal. If the division is not even, round to ten-thousandths before converting the decimal to a percentage.
(the fraction for 100) and add the percent sign (%). This is the same step that was used to convert a fraction to a decimal. If the division is not even, round to ten-thousandths before converting the decimal to a percentage.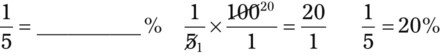
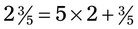 or
or 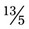 . Then multiply by 100:
. Then multiply by 100: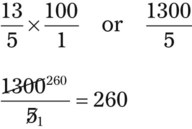
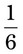 = __________%
= __________%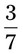 = __________%
= __________%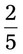 = __________%
= __________%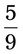 = __________%
= __________%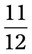 = __________%
= __________%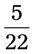 = __________%
= __________%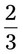 = __________%
= __________% = __________%
= __________%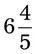 = __________%
= __________%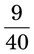 = __________%
= __________%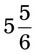 = __________%
= __________% = __________%
= __________%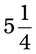 = __________%
= __________%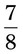 = __________%
= __________%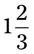 = __________%
= __________%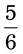 = __________%
= __________%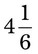 = __________%
= __________%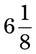 = __________%
= __________%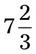 = __________%
= __________%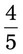 = __________%
= __________%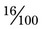 when changed to a fraction. This will reduce to
when changed to a fraction. This will reduce to 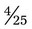 . Remember if the fraction is not reduced to the lowest term, it may be considered incorrect.
. Remember if the fraction is not reduced to the lowest term, it may be considered incorrect.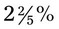 to a fraction, first change the mixed number to the improper fraction
to a fraction, first change the mixed number to the improper fraction 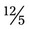 . Remember that when dividing in percentage, you are actually dividing by 100. The fraction is now
. Remember that when dividing in percentage, you are actually dividing by 100. The fraction is now 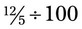 . To divide fractions, the fraction must be inverted so that the divisor becomes the dividend and the dividend becomes the divisor; thus the equation now is as follows:
. To divide fractions, the fraction must be inverted so that the divisor becomes the dividend and the dividend becomes the divisor; thus the equation now is as follows:
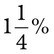 = __________
= __________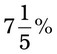 = __________
= __________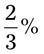 = __________
= __________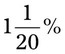 = __________
= __________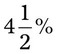 = __________
= __________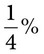 = __________
= __________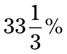 = __________
= __________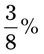 = __________
= __________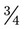 as a fractional expression would be 3 : 4 when written in ratio. Like a fraction, a ratio is the relative size of two quantities and should be reduced to lowest terms. Because of the relationship of the numbers in a ratio, the value of the ratio will not be changed if both the numerator and denominator are multiplied or divided by the same number. Multiplication and division are the only numeric operations that can be performed on a ratio without changing its value.
as a fractional expression would be 3 : 4 when written in ratio. Like a fraction, a ratio is the relative size of two quantities and should be reduced to lowest terms. Because of the relationship of the numbers in a ratio, the value of the ratio will not be changed if both the numerator and denominator are multiplied or divided by the same number. Multiplication and division are the only numeric operations that can be performed on a ratio without changing its value.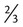 ).
).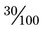 = 30 : 100.
= 30 : 100.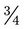 or 20 : 100 would be
or 20 : 100 would be 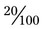 , which will reduce to
, which will reduce to 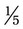 by dividing both the numerator and the denominator by 20.
by dividing both the numerator and the denominator by 20.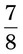 = __________
= __________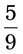 = __________
= __________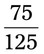 = __________
= __________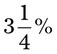 = __________
= __________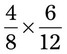 . When the fractions are cross-multiplied
. When the fractions are cross-multiplied 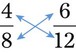 both answers will be 48, or the products will be equal.
both answers will be 48, or the products will be equal.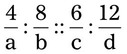 , we will multiply the two outside numbers (numbers a and d) or the extremes, and the two inside numbers (numbers b and c), or the means, so 4 × 12 and 6 × 8, with both answers being 48. The product of the means will always equal the product of the extremes in a true proportion. The computation of the problem can be checked by placing the answer into the unknown (x) and multiplying the means and extremes, checking that the answers are the same.
, we will multiply the two outside numbers (numbers a and d) or the extremes, and the two inside numbers (numbers b and c), or the means, so 4 × 12 and 6 × 8, with both answers being 48. The product of the means will always equal the product of the extremes in a true proportion. The computation of the problem can be checked by placing the answer into the unknown (x) and multiplying the means and extremes, checking that the answers are the same.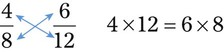
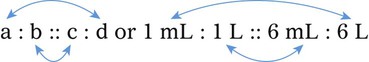
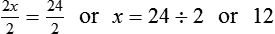
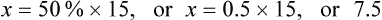
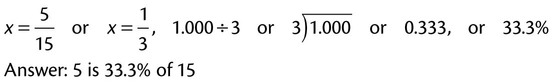

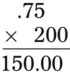
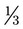 ? (Round to a whole number.) __________
? (Round to a whole number.) __________ of 48 mg? __________
of 48 mg? __________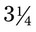 teaspoons are 20% of what total number of teaspoons? __________
teaspoons are 20% of what total number of teaspoons? __________
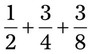 = __________ __________
= __________ __________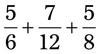 = __________ __________
= __________ __________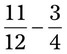 = __________ __________
= __________ __________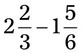 = __________ __________
= __________ __________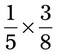 = __________ __________
= __________ __________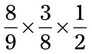 = __________ __________
= __________ __________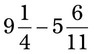 = __________ __________
= __________ __________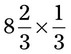 = __________ __________
= __________ __________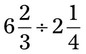 = __________ __________
= __________ __________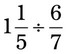 = __________ __________
= __________ __________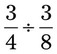 = __________ __________
= __________ __________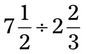 = __________ __________
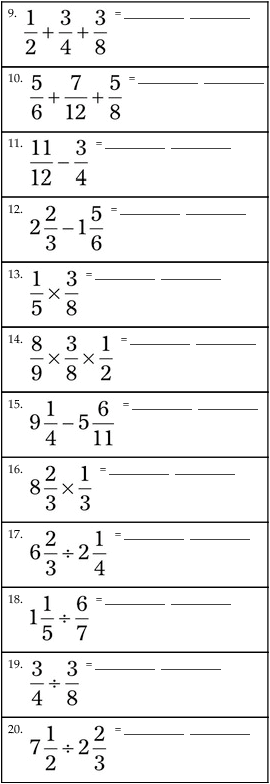
= __________ __________
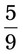 = __________
= __________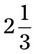 = __________
= __________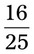 = __________
= __________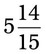 = __________
= __________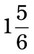 = __________
= __________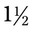 oz cough syrup. __________
oz cough syrup. __________