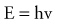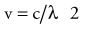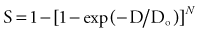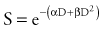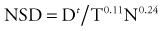Toward the closing years of the nineteenth century, many investigations into electricity characteristics were conducted, one of them demonstrating that electric potential placed across two separated platinum electrodes produces a spark.¹ British physicist William Crookes demonstrated that if the two electrodes were placed within an evacuated glass tube, the vacuum would eventually cause the walls of the vessel to fluoresce.² On November 8, 1895, Wilhelm Roentgen, while performing an experiment with the Crookes tube, accidentally left a piece of paper painted with barium platinocyanide nearby; he noted that the paper fluoresced and realized that this fluorescence of the paper could have been caused by a new, invisible type of ray that the tube was now emitting. Thus, the x-ray was discovered.

Radioactivity was discovered shortly after by Henri Becquerel, who investigated the capability of different substances to produce x-rays. He observed the darkening of photographic plates by uranium salts and concluded that the same x-rays were emitted spontaneously and continuously from the uranium.³ Pierre and Marie Curie, who read his results, coined the term radioactivity to describe this phenomenon. In 1898 they isolated a material with radioactivity 60 times higher than uranium and called it radium.⁴

These discoveries led to radiation biology experiments. The first documented experiment was performed unintentionally at about the same time, when Antoine Becquerel developed a “burn” on his chest from carrying a vial of radium salt in his vest pocket. It soon became apparent that radiation had the ability to produce profound biologic changes. In the beginning it was believed to be a magical cure for almost every known illness. The first documented success was reported in 1899 in Stockholm ⁵ by Thor Stenbeck, who treated a 49-year-old woman’s nasal basal-cell carcinoma. He delivered 100 treatments in the course of 9 months, and the patient was alive and well 30 years after the treatment. In 1901, Dr. Frand Williams in Boston reported on the successful treatment of a lip cancer.⁵ The early treatments often involved very large single exposures that resulted in extensive skin toxicities and other complications. Therefore, only superficial sites were originally treated by the direct application of radium.⁶ Eventually, physicians started to insert radium directly into deep-seated tumors, effectively beginning the field of brachytherapy.⁷

The use of external beam treatments made its leap in 1922 when Coutard and Hautant reported a new concept of fractionated treatments: advanced laryngeal cancer could be cured without severe toxicities using fractionated treatments.⁸ Advances in measurements were also achieved when the skin erythema dose (the dose of x-rays required to give a light skin reaction) was replaced by the roentgen in 1928,⁹ which was later replaced by the rad. The rad is the unit of absorbed dose and is a measure of the energy deposition per unit mass by all types of ionizing radiation. The next step was achieved with the development of higher-energy machines capable of depositing dose at depth.

As technology has progressed, radiation therapy (RT) has become increasingly sophisticated, with computer controls to deliver exact and modulated doses to depths and specific areas within the treatment field. The advances in energy technologies led to the routine use of high-energy and accurate deep-penetrating radiation produced by linear accelerators. Nuclear physics innovations produced many artificial radioisotopes, enabling the use of high-dose brachytherapy, which shortens treatment time and simplifies the radioprotection procedures.

Aside from the technology advances, radiation treatment has a special role in head and neck cancer (HNC), in which it has in many cases a major advantage over traditional surgery in its ability to preserve organs, improving quality of life without compromising the survival rate.

Basic Physics

Characteristics of Radiation

Radiation refers to the propagation of energy through space or a medium (Fig. 77-1). Radiation can be broadly classified as either particulate or electromagnetic. If the radiant energy is carried off by a particle that has rest mass, the radiation is called “corpuscular” or “particulate” radiation. Examples of particulate radiations are electrons, beta particles, protons, neutrons, and heavy charged particles.

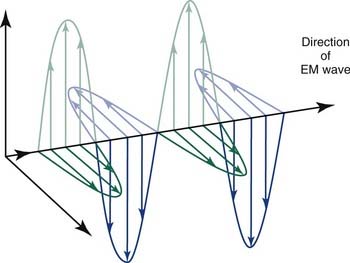
Figure 77-1. Propagation of electromagnetic (EM) radiation with oscillating electric and magnetic fields.

(From Saw CB. Foundation of Radiological Physics. Omaha, NE: C. B. Saw Publishing; 2004:10, with permission.)

Electron beams, which are produced in a linear accelerator, are widely available for the treatment of superficial lesions in clinical radiation oncology practice. In addition, mixed beams consisting of electron beams and photon beams are used to treat lesions that require higher surface doses. Negatrons from strontium Sr-90 are used in the treatment of restenosis in intravascular coronary brachytherapy. Although other forms of particulate radiation have been used experimentally in the past, their use has been limited to a few centers. The use of protons is gaining popularity in many centers specifically for pediatric tumors.

Electromagnetic radiation is a packet of energy (a photon) that propagates through space. It has no rest mass and propagates at the speed of light. This discrete energy (E) is related to its associated frequency (ν) as follows:

(Eq. 77-1)

where h is Planck’s constant, having a value of 6.626 × 10⁻³⁴ joule-second (J.s). The energy of a photon is often expressed in electron volts (eV). One eV represents the amount of energy required to accelerate an electron through a potential of one volt. The frequency (ν) of a photon is related to its wavelength (λ) as follows:

(Eq. 77-2)

where c = 3.0 × 108 m/sec, the speed of light in a vacuum. The waves of electromagnetic radiation are composed of oscillating electric and magnetic fields that are orthogonal to each other and to the direction of propagation, as shown in Figure 77-1. The electromagnetic spectrum spans a broad and continuous range from radiowaves to x-rays with wavelengths from 106 to 10⁻¹³ m. Radiation with wavelengths shorter than visible light is classified as ultraviolet rays, x-rays, and gamma rays. The boundaries between these regions are not sharply defined. For example, x-rays and gamma rays are indistinguishable except for their origins, one from the orbital electrons and the other from the nucleus, respectively. Different types of electromagnetic radiation interact differently with the same material (see Fig. 77-1).

Radiation Production by Radioactive Decay

As previously discussed, radioactivity is the phenomenon in which radioactive materials disintegrate by emitting radiation to achieve nuclear stability. The amount of radioactivity is measured in units of curie (ci), named after the Polish-born French scientist, Madame Curie. A curie is equal to 3.7 × 10¹⁰ disintegrations per second. A smaller unit, the millicurie (mci), is routinely used in the field of radiologic physics. The SI unit of radioactivity is the becquerel. It is equal to 1 disintegration/sec, typically denoted as the reciprocal of 1 second (s-1).Unstable nuclei decay by emitting alpha particles, beta particles, or gamma rays. An alpha particle (denoted by the symbol α) is actually stripped helium consisting of two protons and two neutrons. A negative beta particle (β⁻) carrying a unit negative charge (−1e) is called a negatron; a positive beta particle (β⁺) carrying a unit positive charge (+1e) is called a positron.

Unstable atoms de-excite by emitting x-rays. An atom is said to be in an excited state if any orbital electron is not in its lowest energy state. When an atom is in an excited state, an electron from the higher energy shell jumps into the vacant position. As a consequence of this transition, an x-ray is emitted. A cascade of x-rays can be emitted after a tightly bound electron is ejected. The process of ejecting an orbital electron is called ionization radiation.

Radiation Production from Linear Accelerators

Another type of radiation is termed bremsstrahlung ¹¹ (German for “braking radiation”), electromagnetic radiation produced by a sudden slowing down or deflection of charged particles (especially electrons) passing through matter near the strong electric fields of atomic nuclei.

Internal bremsstrahlung arises in the radioactive process of beta decay, which consists of the production and emission of electrons by unstable atomic nuclei or the capture by nuclei of one of their own orbiting electrons. These electrons, deflected from their own associated nuclei, emit internal bremsstrahlung. During the deceleration process, the electrons interact with the atomic nuclei, resulting in the emission of bremsstrahlung radiation. Before 1950, external beam RT was accomplished in this way, with a maximum energy of about 300 keV. As just stated, these x-rays are low in energy compared to what is used today, with the disadvantages of poor penetration and maximal deposition of dose at the skin.

Today, other types of radiation are produced in nuclear reactors, cyclotrons, and linear accelerators.

Interaction of X-Rays with Matter

After these high-energy x-rays are produced successfully, they can interact with matter via several different processes. Each interaction type has a probability, based on the composition of the matter and the energy of the x-rays. These interactions cause some photons (x-rays) to be removed from the forward-moving x-ray beam, an effect called attenuation, which is basically the loss of intensity and subsequent decrease in the deposition of dose as the beam reaches greater depths. The five possible interactions of x-rays with matter are as follows:

• Coherent scattering

• The photoelectric effect

• The Compton effect

• Pair production

• Photodisintegration

The most important of these interactions in RT are represented in Figure 77-2.

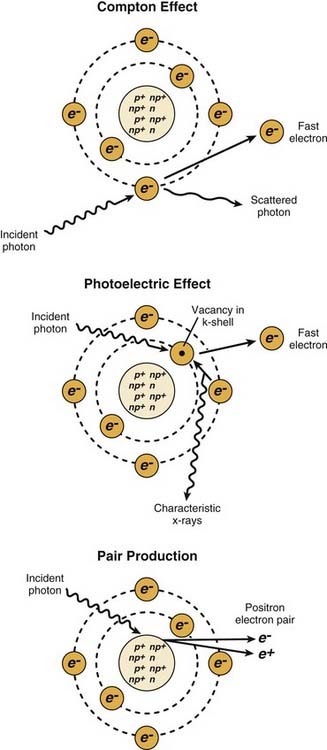
Figure 77-2. The major radiation interactions. e, electron; n, neutron; p, proton.

(Redrawn from Cox JD, Ang KK, eds. Radiation Oncology: Rationale, Technique, Results. 8th ed. St. Louis: Mosby; 2003:5.)

Deposition of Dose

The absorbed dose from an x-ray beam is the measure of the energy deposited by the beam and absorbed by the target. Radiation doses were historically measured by roentgen, which was a unit of exposure but did not quantify the dose the patient absorbs. In the late 1950s the rad, an abbreviation for “radiation-absorbed dose,” was introduced. The rad is equivalent to the deposition of 100 ergs (10⁻⁷ joules) per gram of material.

More recently, an international commission has agreed that radiation doses should be specified in terms of gray (Gy), which corresponds to the deposition of 1 joule per kilogram of material. Numerically, doses in rad can be converted to equivalent doses in Gy by dividing by 100 (i.e., 100 rad = 1 Gy). This is closely related to the observed biologic effects, how and where the dose is deposited is obviously very important. Because the amount of radiation absorbed by the target is assumed to be as stated previously, x-rays in the megavoltage energy range, such as those used in RT, exhibit the phenomenon of skin sparing, whereby the dose deposited in tissue is relatively low at the surface but increases rapidly over the first few millimeters. The region of rapidly increasing dose is known as the buildup region. This rapid increase occurs because of the forward-moving photons interacting with electrons of the target tissue via the interactions described previously. Because these electrons are also propelled forward but have a shorter course than the photons, there becomes an area at depth at which the number of electrons entering the plane of interaction from superficial interactions is exactly equal to the amount leaving the plane from interactions in that plane. This plane is termed the D_max, as it represents the maximum number of ionization events past this point; as more interactions between the photon beam and tissue occur, fewer photons are available to travel forward and deposit dose at greater depths. This process, as previously described, is called attenuation. How quickly a photon beam is attenuated (i.e., how much dose it deposits at depth) depends on qualities both within the beam and within the target tissue. The most substantial effect on depth dose from the photon beam itself is the beam’s energy.

Deposition of Energy

As a high-energy photon beam traverses through a medium, the atoms are excited and ionized. Of the two interacting processes, ionization is disruptive to atoms, changing the molecular integrity and leading to cell death in tissue. The ejected electrons undergo further interactions and deposit their energies to the medium through excitation and ionization. The amount of energy transferred to the electrons at the initial point of interaction is called kerma. The second stage of the energy-transfer process is called the absorbed dose. Not all the energy transferred to the medium at the initial point of interaction is absorbed. Some of the energy is radiated away as bremsstrahlung, and the remaining is called collision kerma. The absorbed dose is the energy retained in the medium along the path of the electrons. If the electron track has an appreciable length, the transfer of energy (kerma) and the absorption of energy (absorbed dose) take place at separate locations.

When a photon beam enters a medium, the initial ionization of atoms takes place at the surface. The energy is directly transferred to the ejected electrons, and therefore kerma has a maximum value at the surface. As the beam proceeds farther, the photon intensity decreases as a result of absorption and scatter. Hence kerma decreases as a function of depth into the medium. On the other hand, absorbed dose is initially low at the medium surface, increases to a maximum, and thereafter decreases as a function of depth. The region from the surface to depth of maximum dose is called the buildup region. The position of maximum absorbed dose is called the point of equilibrium, and the region beyond the maximum dose is the region of transient electronic equilibrium.

Radiation in Conventional Medicine

External beam radiotherapy is the most frequently used form of radiotherapy. With this technique, the patient lies on a bed and an external source of radiation is pointed at a particular part of the body. Kilovoltage (which may be either superficial or deep) x-rays are used for treating skin cancer and superficial structures. Megavoltage x-rays are used to treat deep-seated tumors (e.g., bladder, bowel, prostate, lung, brain). Megavoltage electrons are used mainly for treating superficial tumors.

The energy of diagnostic and therapeutic gamma rays and x-rays is expressed in kilovolts (kV)or megavolts (MV), whereas the energy of therapeutic electrons is expressed in terms of megaelectron volts (MeV). In diagnostic and therapeutic situations, this voltage is the maximum electric potential used by a linear accelerator to produce the photon beam. The beam is made up of a spectrum of energies: the maximum energy is approximately equal to the beam’s maximum electric potential times the electron charge. Thus, a 1-MV beam will produce photons of no more than about 1 MeV. The mean x-ray energy is only about a third of the maximum energy. Beam quality and hardness may be improved by special filters, which improve the homogeneity of the x-ray spectrum.

In the medical field, useful x-rays are produced when electrons are accelerated to a high energy. Some examples of x-ray energies used in medicine are as follows:

Diagnostic x-rays: 20 to 50 kV

Superficial x-rays: 50 to 200 kV

Orthovoltage x-rays: 200 to 500 kV

Supervoltage x-rays: 500 to 1000 kV

Megavoltage x-rays: 1 to 25 MV

Of these energy ranges, megavoltage x-rays are by far the most common in radiotherapy. Orthovoltage x-rays do have limited applications, and the other energy ranges are not typically used clinically.

Medically useful photon beams can also be derived from a radioactive source such as cobalt Co-60, iridium Ir-192, cesium Cs-137 and radium Ra-226 (which is no longer used clinically). Such photon beams, derived from radioactive decay, are more or less monochromatic and are properly termed gamma rays.

Orthovoltage x-rays are produced by linear accelerators operating at 200 to 500 kV. These are also known as “deep” or “superficial” machines, depending on their energy range. Orthovoltage units have essentially the same design as diagnostic x-ray machines. These machines are generally limited to less than 600 kV.

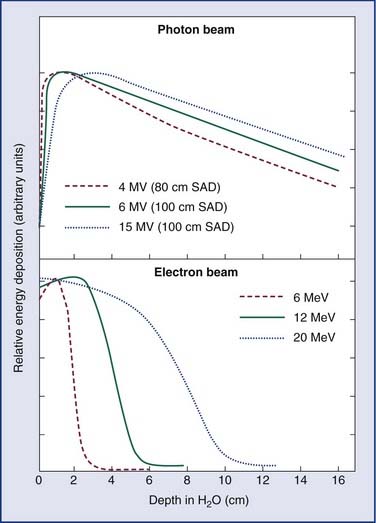
Linear accelerators (linacs) produce megavoltage x-rays. Commercially available medical linear accelerators produce x-rays and electrons with an energy range from 4 MeV up to around 25 MeV.¹¹ The x-rays themselves are produced by the rapid deceleration of electrons in a target material, typically a tungsten alloy, which produces an x-ray spectrum via bremsstrahlung radiation. The shape and intensity of the beam produced by a linear accelerator may be modified or collimated by a variety of means. Thus, conventional, conformal, intensity-modulated, tomographic, and stereotactic radiotherapy are all produced by specially modified linear accelerators (Fig. 77-3).

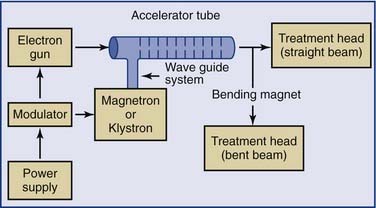
Figure 77-3. Block diagram of a typical medical linear accelerator.

(From Leibel SA, Phillips TL, eds. Textbook of Radiation Oncology. Philadelphia: WB Saunders; 1998:110.)

As the particle bundle passes through the tube it is unaffected, and the frequency of the driving signal and the spacing of the gaps between electrodes is designed so that the maximum voltage differential appears as the particle crosses the gap. This accelerates the particle, imparting energy to it in the form of increased velocity. At speeds near the speed of light the incremental velocity increase will be small, with the energy appearing as an increase in the mass of the particles

Additional magnetic or electrostatic lens elements may be included to ensure that the beam remains in the center of the tube and its electrodes (see Fig. 77-3).

Linear Accelerators

Linear accelerators typically produce beam energies ranging from 6 to 18 MeV, and the dose at depth increases with beam energy. Therefore, an 18-MeV photon beam would deliver more dose to a given depth in a patient than would a 6-MeV photon beam. An 18-MeV beam would also have more skin sparing (i.e., it would have a greater D_max). Another aspect that affects the depth dose is the size of the field of radiation used to treat the patient. With a larger field size, there is greater scattering of photons within the field during the interactions with electrons. This scatter effect leads to more interactions, which translate into a higher deposition of dose at depth. In other words, the dose at 10-cm depth within a patient from a photon beam that has a field size of 20 cm × 20 cm would be higher than the same photon beam with a field size of 5 cm × 5 cm. Many other factors go into the calculation of dose delivered at varying depths in a patient, including scatter from the collimators in the machine, blocks to shield normal tissue, and wedges and compensators (which are used to shape the photon beam). Another main modifier in the target tissue that affects dose at depth is the density of the tissue being treated. Lung, for example, being less dense than soft tissue, allows more photon transmission. Additionally, the inverse square effect, first noted by Roentgen, must be taken into account. All of these factors must be taken into consideration in the determination of the dose being delivered to structures within the patient. Calculation of the dose given to a tumor or other volumes within a patient is thus complex, requiring much more knowledge than simply how much x-ray dose the machine is putting out.

As an energy source, electrons differ from photons in that electrons travel only a certain (short) distance within tissue. They are very light particles compared with the nuclei of the target tissue with which they interact. Hence, the electrons lose a large fraction of their energy in a single process. This leads to much less skin sparing and the deposition of the majority of the dose in superficial tissues. Consequently, however, they are very useful for treatments in which the target of the radiation lies close to the surface of the patient, such as skin tumors (Fig. 77-4).

Figure 77-4. Typical depth-dose curves for megavoltage photon and electron beams commonly used in the therapy of head and neck cancers. The upper panel shows curves for 10 cm × 10 cm fields for a 4-megavolt (MV) (80-cm source axis distance [SAD]) linear accelerator (dashed line), a 6-MV (100-cm SAD) linear accelerator (solid line), and a 15-MV (100-cm SAD) linear accelerator (dotted line). The lower panel shows depth-dose curves for 10 cm × 10 cm fields for 6–megaelectron volt (MeV) (dashed line), 12-MeV (solid line), and 20-MeV (dotted line) electron energies.

Particle Beams

High-energy charged particle beams interact with tissues in a unique way. At first, the charged particles lose energy gradually, but there is an intense release of energy at the end of the range. This intense energy deposition is called the Bragg peak. This feature provides a means of delivering the maximum dose to a target at a specified depth. Often in clinical practice, the particle beams are modulated to change the energy, and hence the depth, to widen the dose deposition to cover the target, and this change is in addition to allowing optimized dose delivery.

In the strictest sense, the electron beams used in conventional radiotherapy facilities are a type of particle radiation, but this section is devoted to the heavier charged particles (e.g., protons, α-particles, heavy ions, π-mesons, and fast neutrons) used experimentally at a small number of radiotherapy centers throughout the world. These particles are of special interest because of their different radiobiologic properties or their better depth-dose characteristics, which allow for higher tumor doses without causing a commensurate increase in the dose to the surrounding healthy tissues.

One particle for which there has been a great amount of clinical work is the fast neutron.^12,¹³ Fast neutrons are of clinical interest because of their radiobiologic properties, which occur because of the much greater amount of energy they deposit when they go through tissue. Neutrons are neutral particles and interact with the atomic nuclei, producing “heavy” charged particles such as protons, α-particles, or nuclear fragments that in turn create a dense chain of ionization events as they go through tissue. The distribution of these secondary particles depends on the energy spectrum of the neutron beam, so the biologic properties of the beam depend strongly on its energy spectrum. Neutrons used in therapy generally are produced by accelerating charged particles, such as protons or deuterons, and impacting them on a beryllium target.

There is considerable interest in using charged particle beams directly for therapeutic purposes, which generally requires beams of much higher energy than those used to produce neutrons. The lighter particles, such as protons ¹⁴ and α-particles, are of interest because of their extremely favorable depth-dose characteristics. The radiobiologic properties of these beams are similar to those of conventional photon or electron beams. Heavy charged particles combine the favorable depth-dose properties of the proton and α-particle beams with the favorable biologic properties of the neutron beams. Energies are on the order of several hundred MeV per nucleon, rather than the few MeV per nucleon for the recoil fragments produced by neutrons. These highly energetic particles do not deposit much energy in tissue until they reach the end of their path, where they are moving slowly. Hence, they do not produce much radiation damage in the intervening tissues. Because of their extremely high cost and general unavailability, however, these beams are not widely in use. Interest in proton beams has grown, and the number of radiotherapy facilities using protons in the United States is expected to rise.

Treatment Aspects of External Beam Radiation

A series of technical tasks must be performed to prepare a patient to undergo external beam RT. The purpose of these tasks—simulation, treatment planning, verification, dose delivery, and quality assurance—is to ensure that high radiation doses are delivered to the patient in an accurate and controlled manner. Usually the processes of simulation, treatment planning, and verification take 1 to 3 days. The setup and treatment planning must be individualized to maximize the dose delivered to the target while minimizing the irradiation of surrounding normal tissue. Any inaccuracy in this process could cause further delay in the initiation of the radiation treatment.

During simulation, the patient setup is assessed for ease of positioning and daily reproducibility. This process involves the use of immobilization devices (anything that can hold a patient in position during treatment) and treatment aids (any kind of support to make patient comfortable). In most HNC cases, a mask that immobilizes the head and neck is used.

After the patient is immobilized, at least two reference points are marked on the patient with x-ray markers to define a reference plane close to the internal tumor target. The marking of the reference points is aided by the use of lasers. Next, the region of interest on the patient is scanned using computed tomography (CT), often using a dedicated CT-simulator scanner to obtain CT images for image-based treatment planning. The images are scanned to a treatment planning station. The radiation oncologist then outlines the tumor target region and critical surrounding normal structures on the axial images on the basis of the CT scan, and a prescribed dose with appropriate normal tissue margin is provided. On the basis of this information, a medical physicist or a medical dosimetrist designs an individualized treatment plan. The challenge in the plan is to deliver the prescribed dose uniformly to the tumor or tumor bed target while maintaining a very low dose to the critical normal structures. Although these goals are achievable, it takes time to arrive at an optimized individualized plan.

Aside from delivering the prescribed dose to the target and minimal dose to the surrounding critical structures, the individualized plan must be evaluated for deliverability—that is, the selected beam orientation must be such that the linear accelerator does not collide with the patient or the table, and the technical parameters of the patient’s plan must comply with the technical requirements of the delivery machine. Next, the individualized machine-delivery parameters are downloaded into a record verification system database. Patient verification is the process of ascertaining that the individualized plan is correct and deliverable. Correct here means that the patient is easily placed into treatment position, relatively comfortable, and immobile, the setup is reproducible, and the target is at the appropriate position relative to the isocenter according to the plan. Finally, there is clearance to avoid patient-equipment collision. During verification, orthogonal radiographs or individualized field radiographs are taken, with films or a portal imager, for assessment and for documentation of the setup. In addition, machine parameters are captured into the database. These images can be used to assist in repositioning the patient as necessary.

Typically, the radiation dose is delivered to the patient using a linear accelerator (Fig. 77-5). The radiation beam as produced is a forward peak; that is, it has extremely high intensity along the beam axis. It must pass through a conical metallic flattening filter to create a uniform field beam for clinical use. As the clinical beam exits the linear accelerator, it is collimated by a pair of jaws or a multileaf collimation (MLC) system (see Fig. 77-5). The multileaf collimation system is used to shield and protect normal structures (replacing the antiquated and cumbersome lead blocks). In addition, the system is used to modulate beam intensity in intensity-modulated RT. The linear accelerator has a gantry that allows the rotation of the treatment head around the patient. Hence, the radiation beam can be directed at the target from multiple positions to reduce dose to the normal tissues. Because of the high voltage, moving parts, and high dose, the linear accelerator must be properly calibrated and properly maintained for its safe use (see Fig. 77-5).

Figure 77-5. Photograph of a linear accelerator.

In addition to external beam therapy, radiation oncology departments offer brachytherapy services. In brachytherapy (brachy is derived from the Greek word for “short”), sealed radioactive sources are implanted near or directly into tumors. The principal advantage of brachytherapy has been its rapid dose fall-off away from the source. Brachytherapy is generally invasive. When the implant requires short-lived radioactive sources, preimplant dosimetry is performed to determine the number of sources required. After the number of sources has been determined, they are ordered from the vendors. When the sources arrive, they must be assayed and prepared for implantation. On the day of implantation, a final dosimetry plan is created and the sources (often in the form of seeds, as used in prostate brachytherapy) are implanted according to the new treatment plan. For cases involving sources with long half-lives, catheters are provided to the radiation oncologist for implantation. After the implantation, the patient must undergo simulation, and a final treatment plan is generated, similar to the process already described for external beam RT. With advances in computer technology, remote afterloading brachytherapy is now being practiced, in which radioactive sources are remotely loaded into a patient and can be retracted at any time if necessary.

Treatment Planning

Successful treatment planning is imperative to the success of a radiation treatment course. The goal is to identify the full extent of the tumor and areas of possible spread. Several considerations must be taken into account. They include the tumor histology, the extent of the gross disease, regions of microscopic spread but no gross disease, whether the treatment is being given postoperatively or in an undisturbed tumor bed, and the tolerances of adjacent structures. A plan must then be devised to treat this entire region to the dose desired for each region while keeping the volume of each normal tissue below its tolerance. After the image data sets are obtained in any type of simulation, careful review of the clinical data must be made to delineate the tissue in need of treatment. This volume to be treated is defined as the target volume and is created by adding three components together. First, the gross tumor volume (GTV) is noted. This volume is expanded to create the clinical target volume (CTV) by accounting for the areas at risk for spread, such as adjacent tissues or draining lymphatic regions. The planning target volume (PTV) is calculated by adding margin to correct for possible variability in daily positioning and patient motion during treatment.

The remainder of the planning process involves choosing the number of radiation beams required, the energy of these beams, and the angles and weighting of the beams needed to deliver the required radiation dose to the tumor with optimal sparing of normal tissues. After these beams are designed, digitally reconstructed radiographs are produced to reflect the designed treatment fields. The availability of three-dimensional treatment planning has allowed for greater complexity of plans in the attempt to increase the therapeutic ratio via the designing of radiation fields, because the doses to the tumor and normal organs can be evaluated accurately and three dimensionally. This evaluation process allows assessment of the possible toxicity that could result from the radiation treatment via the evaluation of a dose volume histogram, which shows the dose delivered throughout the volume of the organ.

Once treatment planning is completed, the patient begins the course of RT. The first step is to set up the patient to verify the simulation fields on the actual treatment machine. Each day, the patient is repositioned into the exact position in which the simulation and subsequent treatment planning were done. To aid in the repositioning, immobilization devices are often used, consisting of foam body casts or plastic head masks, as previously described. These are made prior to simulation and are kept for use throughout the entire radiation course. Laser lights that converge on the exact isocenter (the point around which the treatment machine rotates) of the treatment machine are available within the treatment room and are used to assist in this repositioning. As three-dimensional techniques allow for greater refinement of treatment volumes and of the increasing complexity of plans, exact daily repositioning is absolutely imperative.

When planning radiation treatment, one must keep in mind the dosages needed to control gross tumor-positive margins and microscopic disease. The probability of tumor control correlates with both the dose of radiation and the volume of the cancer. Radiation cell kill is basically an exponential function of dosage. As a result, the necessary dosage of radiation is roughly proportional to the number of cells in the tumor (tumor volume). Control of microscopic disease in HNC usually requires a dosage of approximately 50 Gy, whereas positive margins require 60 Gy, and adequate control of large (stages T3 and T4) tumors requires dosages in the range of 70 Gy.

Radiobiology

Radiation biology is the study of the effect of radiation on biologic systems. It includes everything from DNA strand breaks to genetic mutations to cellular nongenetic events such as apoptosis.

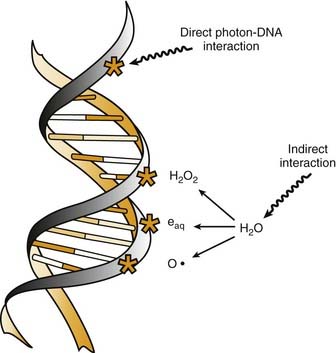
Radiation cell killing occurs when critical targets within the cell are damaged by radiation.¹⁵ A number of biologic molecules or structures are potential targets for radiation damage. According to most studies DNA is the most critical target for the biologic effects of radiation. On a molecular level, this effect requires the production of ionizations, which is why we refer to the process as ionizing radiation. The damage can occur directly when the radiation is absorbed by the DNA itself, because the atoms of the DNA become ionized and damaged. More commonly, however, it occurs indirectly through the following three modes of action^15,¹⁶:

• The effect of x-rays or gamma rays requires the generation of an intermediate ion. (By contrast, particulate types of ionizing radiation, such as α-particles, are directly ionizing and do not require an intermediate ion for effect.)

• The intermediate ion in most cases produces intermediate free radicals, which affect the DNA by breaking chemical bonds (the intermediate ion can also generate DNA damage directly: a less common event for photon ionizing radiation).

• Water molecules surrounding the DNA are ionized by the radiation, creating hydroxyl radicals, peroxide, hydrated electrons, and oxygen radicals.¹⁷

All of these species are highly reactive free radicals that, in turn, interact with the DNA and cause damage. Both ways eventually cause broken bonds in the DNA backbone, which can cause double-strand breaks, ultimately resulting in mitotic death (Fig. 77-6).

Figure 77-6. Two types of interactions are possible between x-rays and DNA: Direct interaction, in which x-ray interacts with the DNA molecule itself (this interaction is relatively rare); and indirect interaction, in which x-rays ionize water and the reactive species that are created interact secondarily with DNA, causing damage and DNA strand breakage.

(Redrawn from Lichter AS. Radiation therapy. In: Abeloff M, ed. Clinical Oncology. 2nd ed. London: Churchill Livingstone; 2000:423-470.)

These broken bonds can result in the loss of a base or of the entire nucleotide, or in complete breaking of one or both of the strands of DNA. Single-strand breaks are easily repaired with use of the opposite strand as a template. Therefore, single-strand breaks show little relation to cell killing, although they might result in mutation if the repair is incorrect. Double-strand breaks, on the other hand, are thought to be the most important lesion in DNA produced by radiation.¹⁸ Double-strand breaks, as the name implies, results in snapping of the chromatin into two pieces. These double-strand breaks can result in mutations or, most important, in cell killing.

A growing body of experimental data suggests that radiation damage to DNA is not the only mechanism by which ionizing radiation damages cells. Other mechanisms are apoptosis, cell cycle arrest, and mitotic death. One study has suggested that apoptosis can be triggered by radiation energy deposition in cell membranes.¹⁹ It has also been reported that direct radiation damage to mitochondria can trigger apoptosis.²⁰

Cell Cycle Arrest

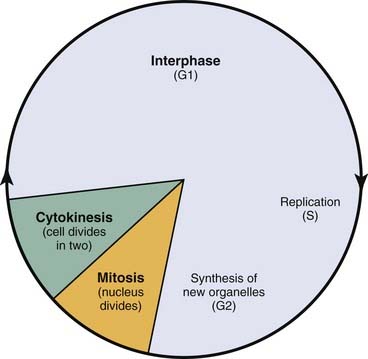
Radiation triggers signaling cascades leading to arrest, usually at the G1 and G2 checkpoints in the cell cycle.²¹ Cell cycle perturbations (Fig. 77-7) are seen characteristically after radiation exposure and were among the earliest observed biologic effects of radiation. Cells can show checkpoints or arrest in any phase of the cell cycle, although the best-described checkpoints with respect to radiation damage are the G1 and G2 checkpoints. Normal cells and those cancer cells that retain p53 function are blocked in the G1 phase of the cell cycle. This is a p53-mediated event.

Figure 77-7. Cell cycle.

Mitotic Death

Many cancer cells (typically those with loss or mutation in the p53 protein pathway) have lost the ability to stop in G1. These cells retain the ability to arrest in the G2 phase of the cell cycle. Even in cells that re-enter the cycle after the G2 checkpoint, however, cell death can still be seen and can take several forms. Some cells fail in cytokinesis and form multinucleated giant cells. Some undergo mitotic catastrophe as they attempt to undergo mitosis.

Radiosensitivity

Our main interest in radiobiology is in figuring out ways to improve the treatment toxicity ratio. One of the main concepts is radiation sensitivity, which refers to the relative susceptibility of cells, tissues, tumors, or organisms to radiation. However, tumor regression is not solely a function of tumor cell death, but is influenced by many factors, including the amount of extracellular stroma, the propensity of the tumor cells to undergo rapid rather than delayed death, and the resorption of radiation-inactivated cells (depopulation). A frequent misconception is that tumors should be more radiosensitive than normal tissues because they proliferate more rapidly. This misconception may go back 100 years. In 1906, only 11 years after the discovery of x-rays, Bergonie and Tribondeau formulated a “law” for the relationship between cellular radiosensitivity and reproductive capacity.²² They postulated that cells that have a higher proliferation rate are more radiosensitive than slowly proliferating cells. On a purely cellular basis, it is correct that cells in mitosis at the time of irradiation are more radiosensitive than cells in other phases of the cell cycle. However, many other factors, such as tissue- and host-specific factors, have important influence. In 1906, there was no appreciation of late-occurring normal tissue complications. Nowadays, we know that many slowly proliferating or nonproliferating normal tissues, such as the kidney, are highly radiosensitive; they just express radiation injury much later than rapidly proliferating tissues. Similarly, the proliferation rate of tumors does not predict their radio-curability. For example, rapidly proliferating tumors such as glioblastoma multiforme can be highly radioresistant.

Cell Survival

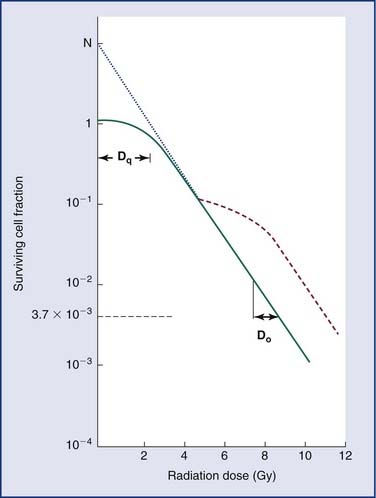
Loss of reproductive integrity in long-term survival assays is important to our understanding of the response of either a tumor or a normal tissue to radiation. When cells are exposed to lethal doses of radiation, they may not die immediately or within a few hours of treatment, or even sometimes within a single division of radiation. When cells have been observed by time-lapse cinematography after irradiation, some cells survive and go on to form colonies, and some die quickly. Others go through up to several rounds of abortive cell division before finally ceasing to divide. Radiation biologists have demonstrated that it is the proportion of cells capable of forming a colony by sustained cell division that most fully predicts the effects of a dose of radiation.²³ In order to eradicate or control a tumor; one must inactivate all clonogenic tumor cells. In other words, the treatment may fail if only one clonogen survives, because that cell can give rise to a regrowing tumor. In order to understand tumor control better, plots of the surviving fraction of cells as a function of the radiation dose have been performed. An example is shown in Figure 77-8.

Figure 77-8. A representative cell survival curve (solid line) for mammalian cells exposed to single doses of radiation. The surviving cell fraction is plotted on a logarithmic scale, and the radiation dose is plotted on a linear scale. D_q characterizes the width of the shoulder region, which in target theory also may be characterized by the extrapolation number, N. D_o characterizes the slope of the “straight line” portion of the curve. The dotted line shows the extrapolation of the linear portion of the curve back to the abscissa. The dashed line shows the regeneration of the cell survival curve if, after a certain amount of radiation is given, 6 to 8 hours are allowed to pass before additional radiation is given.

(Redrawn from Hall EJ. Radiobiology for the Radiologist. Philadelphia: JB Lippincott; 1994.)

By convention, the surviving cell fraction is plotted on a logarithmic scale, and the radiation dose is plotted on a linear scale. This curve is representative of most mammalian cells. Consider the solid curve in Figure 77-8, which represents the survival data. Note that there are two distinct regions to the curve. There is an initial region for low radiation doses, where the slope of the curve is shallow. In this region, small incremental changes in the amount of radiation are not very effective at increasing the number of cells killed. This is called the shoulder region, and its width is characterized by the parameter D_q. It is the distance along the dose axis at a surviving fraction of unity between the abscissa and the point where the extrapolated linear portion of the curve is intersected. It is a measure of the ability of the cells to repair small amounts of radiation damage. At higher doses of radiation, the curve becomes a straight line on a semilog plot. Its slope is characterized by D_o, which is the incremental dose change required to reduce the surviving cell fraction to 1/e of its value. The steeper the slope in this region, the smaller is the value of D_o and the more radiosensitive is the cell line. When extrapolated back to a zero radiation dose, it intersects the abscissa at a value N. A curve of this type can be modeled using the following equation:

(Eq. 77-3)

where S is the surviving fraction, D is the radiation dose, and N and D_o are as indicated in Figure 77-8. In target theory, N can be thought of as the number of distinct targets in the cell that should receive one radiation “hit” before the cell is inactivated.

A number of mathematical models have been devised to attempt to describe the shape of the cell survival curves that are observed experimentally, with an initial shallower slope, an eventual bending (the “shoulder”), and a final, steeper slope. These include target models, lethal and potentially lethal damage models, and repair saturation models. Some of these have been based on simple mathematical modeling without any real attempt to model known molecular events involved in cell killing, whereas others have been based on attempts to model some of the known molecular events (e.g., chromosome breaks or DNA repair) that are involved in cell killing. All of the models can describe the shape of the survival curve to a first approximation. None does so perfectly, and none takes into account all the events and all of the possible mechanisms involved in cell death. A model that has been most influential on clinical practice is the linear quadratic model,²⁴ because it is one of the models that best fits the behavior of cells after exposure to radiation doses within the range used in the clinic. The linear-quadratic model was devised by Keller and Rossi,²⁵ who proposed that radiation-induced cell killing resulted from two potential events, one with a linear relation to dose (exp[−αD]), the other having a quadratic relation to dose (exp[−βD²]). This was expressed mathematically by the “alpha-beta” equation, as follows:

(Eq. 77-4)

where S represents survival of a cell population after a dose, D (Fig. 77-9). It has been hypothesized that this equation actually represents a molecular reality.²⁶ Double-strand breaks in the DNA are lethal lesions that are produced by either one energy deposition, an event termed (αD), or by two separate events, each involving a single strand of DNA (βD²), which then interact. This hypothesis is now thought to be unlikely because of the low probability of two tracks interacting within a single double helix.

Figure 77-9. Dose-response curves for mammalian cells are adequately fitted by the linear-quadratic relationship, at least over the range of doses of concern in radiation therapy. The form of the equation is where S is the fraction of cells surviving a dose (D), and α and β are constants. Cell killing by the linear and quadratic term are equal when D = α/β.

(From Cox JD, Ang KK, eds. Radiation Oncology: Rationale, Technique, Results. 8th ed. St. Louis: Mosby; 2003:14.)

The α/β ratio, which is derived from Equation 77-4, represents a point on the survival curve at which the components of cell killing are equal to each other—that is, αD = βD², or D = α/β. In other words, for each cell population there is a dose of radiation in which the linear (α) and quadratic (β) contributions to cell killing are equal. The α/β ratio is specific to each cellular population and reflects the sensitivity of the cell to the two types of damage. Tissues that have an early response to radiation (skin, mucosa, and tumor cells) have a high α/β ratio. In other words, their survival curves stay straight for a longer period before the bend occurs, in which there is a higher contribution of single-event or α killing. Late-responding tissues, such as spinal cord, kidney, and muscle, have survival curves that bend earlier, with resultant lower α/β ratios. These late-responding tissues have shoulders on their survival curves within the range of doses commonly used in RT. This understanding led to the concept that altered fractionation schedules could be used to treat tumor populations more effectively with respect to damage to late-responding tissues.

Tissue-Radiation Characterizations

The main intent in clinical radiotherapy is to irradiate tumoral tissues while minimizing the damage to the surrounding healthy tissues. The four main concepts of clinical radiotherapy are known as “the four Rs of radiotherapy”: repair (of sublethal damage), redistribution (across the cell cycle), repopulation, and reoxygenation. Radiotherapy basically works not because tumors are more radiosensitive than normal tissue but because normal tissues are better at repair and repopulation. These four Rs also account for different response rates of tumors.²⁷^–²⁹

Dividing the total dose into a number of smaller fractions allows for normal tissue sparing because of the repair of sublethal damage between fractions; however, doing so may also influence tumor cells. Cells show increased survival with split-dose radiation because the shoulder of the survival curve must be repeated with every fraction. In other words, the shoulder of the survival curve represents the accumulation and repair of sublethal damage.

Fractionating the therapy also allows for reassortment or redistribution of tumor cells into radiosensitive phases of the cell cycle, according to several studies. The cells are radiosensitive early in the M phase but become more resistant toward the end of this phase. They are resistant in the early G₁ phase but then become more sensitive in the late G₁ and early S phases. They then become more resistant again in the late S and early G₂ phases. The exact mechanisms underlying this change in radiosensitivity are not clear, but it is interesting to note that at the beginning of mitosis, the DNA in the chromosomes aggregates into a discrete state; in the late S phase, the DNA content of the cell has doubled. These points in the cycle correspond, respectively, to the points of maximum and minimum radiosensitivity.

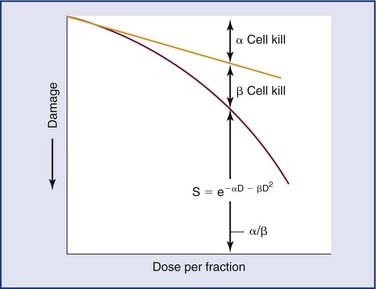
Reoxygenation of the tumor cells causes the cells to be more radiosensitive. The response of cells to ionizing radiation is strongly oxygen dependent, with well-oxygenated cells showing up to threefold greater sensitivity to the killing effects of ionizing radiation than the same cells under hypoxic conditions (Fig. 77-10).³⁰ Tumors tend to have a much higher proportion of hypoxic cells than normal tissues do. Therefore it is important to allow tumor cells to reoxygenate. However, if too much time occurs between fractions, repopulation or proliferation of the tumor cells could occur. Therefore the main issue is creating a balance between reoxygenation of the tumor and its repopulation and repair, and at the same time minimizing the damage to the surrounding tissue.

Figure 77-10. Illustration of the effects of fractionated radiotherapy on a heterogeneous cell population. Surviving cell fraction is plotted along the abscissa as a function of the radiation dose. The dose is given in increments, D, with the time interval between successive doses being long enough to allow for sublethal damage repair. The initial dose increment kills a greater fraction of well-oxygenated cells than it does their hypoxic counterparts. It also preferentially kills those cells in the radiosensitive phases of the cell cycle. The solid curve indicates when the remaining cells reoxygenate and redistribute along the cell cycle before the next radiation dose is given. The dashed curve indicates when there is no reoxygenation or redistribution, and successive radiation doses are delivered to a more radioresistant cell population. The figure is schematic and is not meant to represent any particular cell line.

Rapidly dividing tissues, including tissues such as the skin, mucous membranes, bone marrow, and tumor cells, are responsible for the acute toxicity following RT. The severity of acute toxicity correlates with the relationship between the rates of cell killing of early-responding tissues counteracted by regeneration by those tissues’ surviving stem cells. This balance is based mainly on total treatment time. Prolonging overall treatment time spares the patient from the severe acute toxicity caused by shorter, intense treatment courses. If the therapy is so intense and does not allow a sufficient number of stem cells to survive, the acute toxicity can progress to consequential late effects. Late-responding tissues are responsible for the late toxicity from RT. These tissues, such as the spinal cord, brain cells and connective tissue, are composed mostly of terminally differentiated cells with no reproducible cell population. Thus, there is usually no turnover of such cells within a radiation treatment course, and no opportunity or need for regeneration to occur during treatment. Therefore, unlike in early-responding tissues, the overall treatment time has little importance in determining toxicity in late-responding tissues. Instead, late toxicity depends mainly on total dose and dose per fraction.

Provided that full recovery occurs after each fraction, most late radiation effects show no dependence on the duration of treatment. In contrast, overall treatment time has a large effect on both acute toxicity in early-responding tissues and the cure of tumors. This implies that the tumors that show a decrease in curability with longer treatment times have a rapid regeneration in response to the cell killing that occurs with radiation.

In order to evaluate the impact of a radiation treatment, time-dose considerations are important in estimating the effect of a given total radiation dose.³¹ If the dose were given in a single fraction, then the healthy tissues would experience more cell killing than if it were given in a fractionated manner. This difference occurs because single fractions allow no opportunity for repair of sublethal damage. In general, smaller total radiation doses given over shorter total treatment times can produce the same normal tissue effects as larger total radiation doses given over longer intervals.

The classic measurements that illustrate this point are the isoeffect measurements on skin that were made by Strandquist.³² He showed that the isoeffect lines for various degrees of skin damage and for curing skin cancer were straight when plotted on a log-log scale of total dose versus time. Moreover, the lines appeared to have the same slope (i.e., were parallel). The required dose to produce a given effect was proportional to time to the 0.33 power. Ellis³³ extended this concept to clinical radiotherapy by allocating a portion of the exponent 0.33 to the overall treatment time, T, and a portion to the number of fractions, N. He defined the nominal standard dose (NSD) with the following equation:

(Eq. 77-5)

where D^t is the total radiation dose. The exponents in this expression are for skin and no doubt vary for other tissues.

Clinical Applications

Radiation Fractionation

Altered Fractionation Schedules

The highly fractionated radiotherapy protocols used today are based on the notions just discussed. They are a result of many years of clinical experience, and are extremely crucial for patients with HNC, in whom the radiation in most cases is a curative treatment. Side effects of treatment may have an impact on treatment and therefore may influence survival. In order to further improve the outcome, many studies have suggested different types of dosage prescriptions. The two main treatment methods that have been explored are hyperfractionation and accelerated fractionation treatment.

Several trials suggested the use of hyperfractionation, which involves the administration of multiple daily doses of radiation of such a size that the overall treatment time is about the same as for a conventionally fractionated course of once-a-day radiotherapy. The decreased size of each radiation fraction should permit utilization of a higher total dose without increasing late morbidity. Because normal tissues that show delayed toxicity (and hence long-term morbidity) are more dependent on the size of the individual dose than are tumors, decreasing the size of each radiation fraction should permit utilization of a higher total dose without increasing late morbidity. In practice, multiple daily treatments with smaller than conventional fraction sizes are given over approximately the same treatment duration. Typically, 1.1 to 1.2 Gy/fraction, two fractions per day, to total doses of 74 to 80 Gy have been employed.

Four prospective randomized trials comparing hyperfractionation with standard irradiation alone (without chemotherapy) have been performed.³⁴^–³⁷ In all studies locoregional control was significantly better for those patients treated with hyperfractionation and accelerated fractionation with a concomitant boost than for those treated with standard fractionation. The advantage ranged from an 8% to a 20% 2-year locoregional control rate. There was also a trend toward better disease-free survival with hyperfractionation. In one of the studies, which dealt specifically with oropharynx tumors, there was an improvement in overall survival: Overall survival rate at 42 months was 27% for the hyperfractionation arm and 8% for the conventional treatment arm (P = .03).³⁶ Survival rates were 40% for the hyperfractionated arm and 18% for the conventional RT arm (P = .06). All groups treated with altered fractionation RT had significantly greater late side effects than those undergoing conventional fractionation. The acute side effects of hyperfractionation were slightly more intense and common than with standard fractionation, but the long-term effects appear to be very similar.

Accelerated fractionation is the administration of multiple daily radiation doses of larger size to reduce the overall treatment time. The goal of accelerated fractionation is to prevent tumor repopulation during a course of radiation therapy. Clinical support for tumor cell proliferation during therapy is found in numerous studies that have shown a loss in tumor control with prolongation of overall treatment time in HNC. In general, accelerated treatments that employ continuous (rather than split-course) RT schedules without compromise in the total dose result in better local control. However, whether the added mucosal toxicity from this approach is justified by meaningful gains in survival remains an open question. The studies present a trend toward better primary tumor control in the hyperfractionation arm but no significant difference in overall survival. Comparison of accelerated RT with conventional RT for locoregionally advanced HNC has been tested in a considerable number of randomized trials.³⁴^–⁴¹ All of these trials used somewhat different dose fractionation schedules, and the results (in terms of both locoregional control and survival) are inconsistent. The only trial suggesting a survival benefit for this approach was the smallest.³⁹

The reasons for these inconsistent findings may be the differences in treatment regimens used. In some studies overall treatment time was decreased by more than 50%, necessitating a decrease in total dose by approximately 10% to 20%.^38,^40,⁴¹ This approach resulted in significantly better locoregional control in only one trial,³⁸ and none showed gains in overall survival. Another approach involved moderate reduction in the overall treatment time without a relevant compromise in total dose, with the use of split-course RT regimens.^34,^35,³⁸ With this strategy, no benefit in local control or survival has been observed, except for a significant improvement in local control in one of the trials.³⁵ This improvement did not translate into an improvement in overall survival, however. This lack of survival benefit has been attributed, at least in part, to the significantly higher rate of severe late toxicities in the accelerated treatment arm, which resulted in an increase in the non–cancer-related death rate.

Moderate reduction of the overall treatment time without a relevant compromise in total dose has also been achieved in two studies, with the use of six or seven fractions per week (compared with the usual five fractions weekly) without a split course.^39,⁴² Both of these studies showed a significantly improved local control rate in the accelerated treatment arm, and one demonstrated a trend for an improvement in overall survival.³⁹ Both studies demonstrated a significant increase in acute side effects. Whether late toxicity is also worse with the accelerated treatment approach is unclear. The available data are conflicting, with some trials suggesting no increase in late toxicity,³⁸ and others suggesting the opposite.³⁵

The benefit of altered fractionation RT for squamous cell HNC was addressed in a meta-analysis of 6515 patients enrolled in 15 selected trials comparing hyperfractionated or accelerated fractionation RT with conventional fractionation RT.⁴³ The majority were treated for stage III or IV disease. Compared with conventional fractionation RT, altered fractionation RT resulted in a statistically significant 18% reduction in rate of local failure at the primary site, corresponding to a 6.4% absolute reduction in rate of locoregional failure at 5 years. The improvement in locoregional control was more pronounced in patients undergoing hyperfractionated RT and in those treated with accelerated RT without dose reduction. A significant benefit in overall survival was also found; altered fractionation regimens reduced the risk of dying by 8%, which translated into an absolute survival benefit of 3.3% and 3.4% at 2 and 5 years, respectively. The magnitude of benefit was statistically significant in patients treated with hyperfractionated RT, but not for those undergoing accelerated fractionation RT, with or without a dose reduction. Although this meta-analysis demonstrates the advantage of hyperfractionation versus conventionally fractionated radiation, the standard of care today is chemoradiation, and these studies do not demonstrate superiority of any RT regimens over chemoradiation.

The benefit of combining radiosensitizing chemotherapy with hyperfractionated RT (CRT) schedules was shown in one study in which 116 patients with HNCs (approximately 53% of which were unresectable) were randomly allocated to undergo hyperfractionated RT either alone or with 5-fluorouracil (5-FU) and cisplatin.⁴⁴ At 3 years, CRT was associated with significantly higher rates of locoregional control (70% vs. 44%), a trend toward better relapse-free survival (61% vs. 41%, P = .08), and better overall survival (55% vs. 34%, P = .07). Toxicity, although high, was equivalent in the two groups. However, no trial has compared a regimen using hyperfractionated RT with or without chemotherapy directly with a regimen using concomitant CRT and conventional fractionation RT, the widely accepted standard of care, at least in the United States, for locoregionally advanced laryngeal and oropharyngeal cancers. These twice-daily treatments place greater time demands on the patient as well as on the treatment facility and may create problems with compliance. As a result, hyperfractionated regimens have not been widely adopted, at least in the United States.

Radiosensitizers

The two main options for improving radiation treatment outcome are modulation of the radiation itself, as already discussed, and helping the radiation to become more effective, known as radiosensitizing. A number of mechanisms have been proposed to explain radiation resistance or failure. These can be divided into mechanisms based on radiation dose and schedule, and genetic and epigenetic factors that affect the tumor and its response to radiation therapy. In this section the following existing strategies are discussed: (1) reducing hypoxia, (2) concomitant chemotherapy, and (3) targeted therapy.

Reducing Hypoxia

Within the tumor cell microenvironment, radiation therapy effectiveness is closely dependent on oxygen availability at the time of treatment. Hypoxic cells are 2.5 to 3 times less radiosensitive than well-oxygenated cells.^45,⁴⁶ The hypoxic cell fraction in solid tumors ranges from less than 1% to more than 50%.⁴⁷ Hypoxia in the tumor microenvironment may be a result of increased interstitial pressure, which leads to vascular collapse with resulting areas of transient or persistent hypoperfusion, local hypoxia, and acidosis.⁴⁸ Many patients with cancer are anemic, a factor that may also contribute to localized hypoxia and that has an adverse effect on curability of a tumor by radiation therapy.⁴⁹ In order to overcome the hypoxia, specific trials addressing this issue were performed. These explored the concept of increasing the delivery of oxygen, also known as hyperbaric oxygen therapy (HBO), which increases the amount of oxygen in the blood. The use of carbogen, also raises the local oxygen level. Although the use of HBO was associated with significant increases in response rate (clinical complete response rate 84% with HBO vs. 52% without it),⁵⁰ there were no significant differences in 5-year rates of local control or survival. Inhalation of carbogen (95% oxygen–5% carbon dioxide) during radiation therapy, often combined with accelerated radiation and oral nicotinamide (ARCON treatment)^6,⁷ has been suggested in several trials, and its benefit has not been confirmed.

A second approach to decreasing the impact of hypoxia is the use of hypoxic cell sensitizers, some of which have been used in concomitant chemotherapy regimens, including nimorazole and tirapazamine. Although results of initial clinical trials have been promising, so far there is no proven evidence for survival benefit.⁵¹^–⁵³

Several trials have evaluated the hypothesis that outcomes might be improved through correction of preexisting anemia using recombinant human erythropoietin (epoetin or darbepoetin); this hypothesis was supported by the results of uncontrolled studies.⁵² However, subsequent randomized trials directly testing this hypothesis did not confirm benefit and, in fact, suggested significantly worse locoregional control and overall survival outcomes, or both, in patients who received epoetin during therapy for HNC.^54,⁵⁵

Concomitant Chemotherapy

In general, there may be a synergistic effect between radiotherapy and chemotherapy that alters the radiobiologic parameters (α and β) or there may be an additive effect.

The additive effect may occur in two different ways, as follows:

1. The chemotherapy may be effective at eradicating micrometastases, thus reducing the incidence of distant metastases.

2. Spatial cooperation, meaning independent activity of each treatment modality (i.e., radiation within the treatment field and chemotherapy inside and outside the field) may occur. Toxicity independence (i.e., non-overlapping toxicity) allows for administration of each treatment modality at near full dose without a significant increase in normal tissue damage, although almost all chemoradiotherapy regimens are associated with higher rates of mucositis and other regional toxicities than radiation alone.

Alternatively, a synergistic effect may occur, through increased cytotoxic activity within the radiation field as a direct result of the interaction of chemotherapy with radiation. In this case, the drug is acting as a sensitizer, enhancer, or potentiator of radiation. A number of chemotherapy drugs act as direct cellular radiosensitizers in vitro. They include cisplatin, mitomycin C, 5-FU, hydroxyurea, bleomycin, paclitaxel, docetaxel, and cetuximab, a monoclonal antibody that is directed against the epidermal growth factor receptor, which is over-expressed in the majority of HNCs.

Synergistic or additive effects are thought to be due to the following mechanisms ⁵⁶^–⁵⁸:

• The drug may interfere with cellular DNA repair after sublethal or potentially lethal damage. This may be part of the mechanism of action of cisplatin.⁵⁶

• The drug may reduce tumor cell repopulation by enhancing the cytotoxic effect, particularly following fractionated RT.⁵⁷

• The drug may reduce the population of hypoxic tumor cells. Tumor cell oxygenation can be improved by reduction of interstitial pressure that follows successful cytoreduction.⁵⁶^–⁵⁸ Alternatively, hypoxic cells can be sensitized to radiation (or chemotherapy). Hypoxic cells can be killed with a hypoxic cell toxin; for example, mitomycin is preferentially activated in hypoxic cells,⁵⁸ and tirapazamine is another hypoxic cell toxin.

• The drug may kill radioresistant cells in the S phase of the cell cycle and increase cell cycle synchronization.⁵⁹ Hydroxyurea is an S phase–specific agent that inhibits ribonucleotide reductase. Therefore, it may have additive effects with radiation because it is toxic to S-phase cells that are considered radioresistant. It has also been shown to synchronize cells by inhibiting the entry of cells from the radiosensitive S phase. Paclitaxel works similarly as a cell cycle modifier: It causes accumulation of cells at the G2/mitosis phase of the cell cycle, at which both it and radiation are most effective.⁶⁰

Concomitant chemoradiation has been tested in several settings, for example as up-front curative treatment in resectable and unresectable tumors, postoperatively.

UNRESECTABLE TUMORS

Several meta-analyses have been performed to analyze the use of chemoradiotherapy in unresectable tumors. One meta-analysis of trials evaluating locoregional treatment with or without chemotherapy suggested that the magnitude of the absolute survival benefit with chemotherapy (given in any fashion with RT) was 4% at five years.⁶¹ The hazard ratio (HR) for death was 0.81 (95% confidence interval [CI] 0.76 to 0.88) with concomitant chemoradiotherapy compared with locoregional therapy alone, and the benefit was more pronounced with multiple-agent chemotherapy regimens (hazard ratio 0.69).

A second meta-analysis of randomized trials testing curative intent RT alone or with concurrent or alternating chemotherapy concluded that the addition of concurrent (but not induction) chemotherapy to conventional or altered fractionation RT prolonged survival by an average of 12 months.⁶² Benefit was most pronounced in those trials that used 5-FU or cisplatin-based chemotherapy (average survival prolongation 24 months and 16 months, respectively).

INDUCTION CHEMOTHERAPY

Some writers have suggested that the optimal regimen should include induction chemotherapy prior to chemoradiation. The rationale for using induction chemotherapy is that a reduction in the overall tumor burden will permit more effective local therapy: Radiotherapy can be directed against a smaller number of tumor cells, and early treatment of micrometastases may diminish the chance of developing gross metastatic disease. The reduction in tumor size and healing prior to definitive RT may improve functional outcomes. The response to chemotherapy may be an important predictor of survival, because various studies have shown that patients with a good response to induction chemotherapy have a better overall survival.

The majority of studies suggest that there is no obvious role for induction chemotherapy. Tumor cells that remain after chemotherapy are likely to be chemoresistant and to show cross-resistance to radiation therapy as well.⁶³ Delaying radiation treatment can lead to accelerated repopulation of surviving tumor clonogens, which occurs during an extended total treatment time. There are also practical issues. Induction chemotherapy is associated with increases in toxicity (compared with local therapy without chemotherapy), cost, and overall duration of treatment. Some patients receiving induction chemotherapy do not go on to receive definitive therapy because of the toxicities.

Several trials have compared different regimens of induction chemotherapy.^64,⁶⁵ The triple regimen of docetaxel or paclitaxel plus cisplatin and 5-FU has been compared with a regimen using cisplatin plus 5-FU in the setting of induction chemotherapy. The studies demonstrated that the taxane-containing regimen (with docetaxel or paclitaxel) provided superior outcomes, reporting a 14% improvement of overall survival at 3 years and improvement in median survival from 30 to 71 months.⁶⁵ However, neither of these studies compared induction chemotherapy with direct chemoradiation. In the study by Hitt and associates,⁶⁴ 13% of the patients assigned for the better-tolerated PCF induction regimen dropped out and did not receive the definitive treatment, a situation that might lead to worse survival than that with standard treatment. In order to answer this question, three large randomized trials have been initiated to test the benefit of adding induction chemotherapy to chemoradiotherapy. Until these trials are completed, this approach should be considered investigational.

ORGAN PRESERVATION

One of the main goals in chemoradiation treatment in HNC is the ability to preserve organs that would have been destroyed by surgery. Many studies have dealt with producing the optimal combination in order to preserve function.

The U.S. Department of Veterans Affairs (VA) Laryngeal Cancer Study was the first published randomized trial using neoadjuvant chemotherapy with the major endpoint of organ preservation.⁶⁶ In this study, 332 patients with advanced laryngeal cancer, either stage III (53%) or stage IV (47%), were randomly assigned in equal numbers to one of the following two regimens:

Arm 1—Induction chemotherapy followed by RT, with surgery reserved for salvage. Chemotherapy was given on a 21-day cycle. Clinical tumor responses were reassessed by physical examination and indirect laryngoscopy 18 to 21 days after the start of the second cycle of chemotherapy. The patients undergoing definitive RT received 66 to 76 Gy to the primary tumor site. The doses to the nodes varied according to initial nodal size, ranging from 50 Gy to 75 Gy. Patients with persistent disease in the larynx after RT underwent salvage laryngectomy, and patients with persistent disease in the neck underwent neck dissection alone. In addition, patients with late relapses underwent salvage laryngectomy.

Arm 2—Standard surgery and RT. These patients underwent total laryngectomy and most also underwent neck dissection. This surgery was followed by postoperative RT (PORT) (50 to 74 Gy). The results were as follows: 15% of patients had less than a PR and received standard laryngectomy, 31% had a clinical CR at the primary site, and 85% had a complete response (CR) or partial response (PR) of the primary and involved regional lymph nodes.

Outcome was reported at 33 months’ follow-up, and outcome measures of both survival and organ preservation were clearly delineated. Two-year survival was equivalent at 68% in the two treatment arms.

A second publication from the same study reported long-term survival in the chemoradiation group only.⁶⁷ At the time of that report, 53% survival was noted at 3 years. Patients who had a histologic CR had better survival than patients with persistence of tumor after chemotherapy.

The most significant findings in the VA studies were those related to organ preservation. In the patients randomly assigned to neoadjuvant chemotherapy followed by definitive radiotherapy, 66% of the survivors had a preserved larynx at 2-year follow-up, and 39% of the overall group were alive at 2 years with a functional larynx. A major conclusion of this study was that a significant number of patients could remain alive with a functional larynx after neoadjuvant chemotherapy with definitive RT. However, no survival advantage was seen.

Subsequently, Forastiere and colleagues ⁶⁸ compared RT alone with either induction chemotherapy followed by RT or concomitant CRT, with larynx preservation as the primary end point. In their initial report, 2-year laryngectomy-free survival rates significantly favored the concomitant chemoradiotherapy group (88% vs. 75% for neoadjuvant chemotherapy and 70% for RT alone), and the rates of local control were also significantly better (80%, 64%, and 58%, respectively).⁶⁸ There were no significant differences when induction chemotherapy followed by RT was compared with RT alone, and overall survival was nearly identical in all three groups (2-year and 5-year survival rates 74% to 76%, and 54% to 56%, respectively).

In a later report that this group presented at the 2006 meeting of the American Society of Clinical Oncology, there were no longer any differences in laryngectomy-free survival between the groups receiving concomitant chemoradiotherapy and induction chemotherapy followed by RT (47% versus 45% at 5 years, respectively, compared with 35% for RT alone).⁶⁹ However, the overall laryngeal preservation rate still favored concomitant therapy (84% versus 71% respectively, compared with 66% with RT alone), as did locoregional control rates. This study has established concomitant CRT as a standard of therapy in this setting.

POSTOPERATIVE TREATMENT

The treatment goals for patients with resectable locally advanced HNC are to maximize cure and to maintain functional status through organ preservation. Historically, surgery with postoperative radiotherapy (PORT) has been used for most patients with potentially resectable stage III or IV HNC. Indications for PORT include involved surgical margins, perineural involvement, bone or cartilage invasion, and advanced primary (T3 or T4) or nodal (N2 or N3) disease.

Two large trials have reported a survival benefit for combined chemotherapy and conventional fractionation over radiation alone after surgical resection among patients with locally advanced but resectable disease.^70,⁷¹ These benefits came at the cost of enhanced acute mucosal toxicity, although late toxicities were not more common.

In a multi-institutional trial sponsored by the European Organization Research and Treatment of Cancer (EORTC), 334 patients with high-risk resected squamous cell cancer (SCC) of the oral cavity, oropharynx, larynx, or hypopharynx were randomly assigned to RT alone or the same dose of RT with concomitant cisplatin.⁶² High-risk disease was defined as a T3 or T4 primary with any nodal stage (excepting T3N0 laryngeal cancer), involved surgical margins, extracapsular extension, perineural invasion, vascular invasion, or oral cavity/oropharyngeal primary sites with involvement of level IV or V lymph nodes.

At a median follow-up of 60 months, concomitant chemoradiotherapy was associated with significantly better 5-year rates of progression-free survival (47% vs. 36%) and overall survival (53% vs. 40%), fewer locoregional relapses (18% vs. 31%), and a significantly longer time to progression (55 versus 23 months) than those for PORT alone. In a similarly designed Radiation Therapy Oncology Group (RTOG) trial, 459 patients with resectable high-risk SCC of the oral cavity, oropharynx, larynx, or hypopharynx were randomly assigned to RT alone or the same doses of RT with concomitant cisplatin on days 1, 22, and 43.⁷⁰ The definition of “high-risk” differed somewhat from that used in the EORTC trial, consisting of positive resection margins, involvement of two or more lymph nodes, or extracapsular nodal extension. At a median follow-up of 46 months, chemoradiotherapy was associated with a significantly better 4-year disease-free survival (40% vs. 30%) and fewer locoregional relapses (19% vs. 30%) than those for PORT alone. The difference in overall survival was not statistically significant (hazard ratio 0.84, P =.19). As in the EORTC trial, the incidence of acute severe mucosal toxicity was significantly greater in the chemoradiotherapy group (77% vs. 34%). Long-term toxicity rates were comparable in the two groups, although data derived from larger numbers of patients undergoing definitive treatment suggest that the rate of long-term toxicity is higher in patients receiving chemoradiotherapy than in those undergoing RT alone.

In order to suggest treatment guidelines, risk stratification was addressed in a pooled analysis comparing the selection criteria, clinical and pathologic risk factors, and treatment outcomes of the EORTC and RTOG studies.⁷¹ The findings can be summarized as follows: Extracapsular extension and/or microscopically involved surgical margins were the only risk factors for which the effect on survival of adding chemotherapy to RT was statistically significant in both trials. There was a trend toward better survival in favor of chemoradiotherapy in the group of patients who had stage III or IV disease, perineural infiltration, vascular embolisms, and/or clinically enlarged level IV or V lymph nodes secondary to tumors arising in the oral cavity or oropharynx, but the differences were not statistically significant. Patients in whom two or more histopathologically involved lymph nodes without extracapsular extension was the only risk factor that did not seem to benefit from the addition of chemotherapy.

Targeted Therapy

In order to reduce side effects and optimize treatment, several studies have substituted chemotherapy with molecular targeting antibodies. The most prominent molecule thus far investigated has been cetuximab (Erbitux, IMC225), which is a monoclonal antibody that is directed against the epidermal growth factor receptor and often over-expressed in the majority of HNCs. Cetuximab inhibits receptor activity by blocking the ligand binding site. The benefit of cetuximab as a radiation sensitizer was tested in a multicenter trial ⁷² in which 424 patients with locoregionally advanced SCC of the oropharynx, hypopharynx, or larynx were randomly assigned to RT (once daily, twice daily, or with a concomitant boost, with the specific approach selected by each participating institution) with or without weekly concurrent cetuximab. The majority of patients underwent concomitant boost RT (56%), whereas once daily and twice daily fractionation schedules were used in 26% and 18% of patients, respectively. Cetuximab was administered at a dose of 400 mg/m² over 2 hours 1 week prior to RT, then at 250 mg/m² over 1 hour for subsequent weekly doses during the RT weeks. At a median follow-up of 54 months, the cetuximab-treated group had significantly better median (49 vs. 29 months) and 3-year survival rates (55% vs. 45%) than the group receiving RT alone. Locoregional control rates were also significantly better (50% vs. 41%, respectively), and there was also a suggestion of a higher laryngeal preservation rate in the cetuximab group (88% versus 80% at 3 years, respectively).⁷² The cumulative rates of distant metastases at 2 years were similar (16% versus 17%, respectively).⁷² Although cetuximab did not appear to exacerbate the toxic effects commonly associated with RT (i.e., mucositis, xerostomia, dysphagia, and weight loss), patients receiving combined therapy had a greater incidence of grade 3 or 4 skin toxicity (17% vs. 1% rate of acneiform rash, respectively).

These results are encouraging; however, cetuximab has not been directly compared with other agents as a radiosensitizer. Thus, its role, particularly in comparison with the current standard cisplatin-based chemoradiotherapy, remains uncertain. Nevertheless, it is approved in the United States in combination with RT for the treatment of locally or regionally advanced head and neck SCC. It could be considered in older patients with a borderline performance status (PS2) whose ability to tolerate cisplatin-based chemoradiotherapy is questionable.

The next generation of clinical trials is focusing on combinations of RT, cetuximab, and conventional cytotoxic chemotherapy agents. Although early reports using this approach are promising, it may result in greater toxicity, and incorporation of this strategy into clinical practice would be premature.⁷³

Advanced Radiation Technologies

In traditional irradiation of HNC, the placement of the radiation fields and their shapes were based on the bony anatomy acquired by the simulator diagnostic-quality films. During the late 1980s, advancements in computer technology and imaging introduced methods to identify the targets on CT scans and display the radiation beams in three dimensions relative to the anatomy. In addition, calculation and display of the radiation dose distributions and methods to evaluate and compare rival plans with dose-volume histograms (DVHs) became available. The introduction of multileaf collimators facilitated an increase in the number of beams that could be delivered without a large extension of treatment time. The result was the emergence of three-dimensional conformal radiotherapy (3DCRT), which allowed better precision of irradiation delivery to image-based targets and some improvements in the sparing of noninvolved critical tissue. Early studies of the utility of 3DCRT in HNC examined larynx,⁷³ nasopharynx,⁷⁴ hypopharynx,⁷⁵ and paranasal sinuses cancers.⁷⁶ These studies demonstrated a significant benefit for 3DCRT—better coverage of the tumors and reduced doses to critical tissue—over standard techniques.

Another step forward in the mid-1990s was the development of intensity-modulated radiotherapy (IMRT), which facilitated a higher degree of dose conformality and offered opportunities for additional clinical gains. More recently, imaging-guided radiotherapy (IGRT) has emerged, providing opportunities for better precision of patient setup and for tracking of tumor regression and anatomical changes in the noninvolved tissue during the course of radiation therapy. Other emerging technologies are new imaging modalities that enable study of the customization of the radiation dose according to the expected tumor biology, and the use of heavy particles like protons and carbon ions, which offer additional advantages in dose conformality.

Intensity-Modulated Radiotherapy

IMRT implies the use of radiation fields whose intensity varies across the field, depending on the thickness of the target and the existence of critical organs or critical noninvolved tissue in their path. Treating the targets with multiple beams of varying intensity allows a relatively uniform dose in an irregularly shaped target while avoiding a high dose to the surrounding structures. Two technologic developments made IMRT possible: the introduction of computer-controlled multileaf collimators, and the development of computerized optimization, or “inverse planning,” which determines the intensity of the beams required to satisfy a specified set of dose distributions. Inverse planning demands the planner to state the treatment goals, usually in terms of the dose and/or dose/volume goals for the targets, and the constraints for the critical normal tissue (the objective, or cost function). The computer attempts to achieve the desired outcome by iteration through numerous possible beam intensities. The desired solution is the dose distribution that minimizes the variance of the delivered dose relative to the objective function. For each target and noninvolved organ or tissue, an importance factor or weight is assigned, and the objective function is the sum of the variance terms representing each structure of interest, multiplied by the importance factor.

Intensity-Modulated Radiotherapy in Head and Neck Cancer

The anatomy of the neck is complex, with many critical and radiation-sensitive organs in close proximity to the targets. Tight dose gradients around the targets that limit the doses to the noninvolved tissue, features characteristic of IMRT, are desirable and offer the potential for therapeutic gains (Fig. 77-11). Noninvolved tissues, the sparing of which may offer tangible gains, include the major salivary glands, minor salivary glands dispersed within the oral cavity, the mandible, and the pharyngeal musculature. In the cases of nasopharyngeal and paranasal sinus cancers, critical normal tissues that may be partly spared using IMRT are the inner and middle ears, the temporomandibular joints, temporal brain lobes, and the optic pathways.

Figure 77-11. Intensity-modulated radiation therapy of head and neck cancer. Each green field represents a radiation field. The red field is the target, and the eyes are avoided.

In addition to sparing of noninvolved tissues, IMRT offers a potential for improved tumor control by reducing the constraints on the tumor dose due to critical organs. Examples include the spinal cord, brainstem, and optic pathways that occasionally limit the tumor boost doses in conventional RT. This goal is achieved by specifying a maximal dose to the critical organs and a high penalty in the optimization process if that dose is exceeded. In addition, IMRT eliminates the need for posterior neck electron fields, commonly used in conventional RT, and their associated dose deficiencies. Although IMRT in the head and neck is more feasible than in other sites because breathing-related organ motion is practically absent, other factors must to be taken into account, such as patient setup uncertainties, swallowing-related organ movements, and changes in target and organ positions related to tumor shrinkage and patient weight loss during therapy; these are discussed later.

Not every patient is expected to benefit from IMRT. Those who would benefit most are patients with paranasal sinus cancer in whom the targets are near the optic pathways, patients with oropharyngeal or nasopharyngeal cancer in whom standard RT fields would encompass most of the salivary glands, and patients in whom standard techniques would require a compromise in the tumor dose because of proximity of the tumor to the spinal cord or brainstem. For patients with laryngeal cancer and clinically noninvolved neck, who are receiving treatment to the larynx alone or who require irradiation of the neck encompassing the jugulodigastric nodes but not extending to the base of skull, IMRT may not be better than simpler techniques. The same applies to patients requiring irradiation to the ipsilateral neck alone.

Defining the Target: Imaging

The simulation contrast-enhanced CT is in most cases the only imaging modality required for the delineation of the targets. Magnetic resonance imaging (MRI) is a necessary adjunct to CT for tumors close to the base of skull, such as nasopharyngeal and paranasal sinus cancer, where it provides better details of tumor extension and of the parapharyngeal and retropharyngeal spaces than CT.^77,⁷⁸ Another potential imaging modality for this purpose is fluorodeoxyglucose-positron emission tomography (FDG-PET). However, in a series of HNCs in which CT, MRI, and FDG-PET were obtained, and surgery was then performed to validate the primary tumor extent and lymph node involvement, a rather limited benefit of FDG-PET over CT and MRI was found.⁷⁹ PET-derived gross tumor volumes were smaller than those derived from CT and MRI, and surgical specimens were even smaller. However, when examined in detail, despite overestimation in most dimensions, all three imaging modalities actually underestimated the mucosal extent of disease.⁷⁹ Therefore, physical examination and laryngoscopy findings should be part of the definition in addition to image modalities such as CT and PET.

Selection and Outlining of the Targets

Target Definitions in the Head and Neck

As described previously, the gross tumor volume (GTV) consists of the primary tumor and of lymph nodes with apparent or suspected metastasis. The clinical target volume (CTV) surrounding the primary tumor consists of tissue perceived to contain microscopic, subclinical tumor extension. In addition to the primary tumor CTV, the lymphatic CTVs consist of nodal areas that are at risk for metastatic disease but that do not match the radiologic criteria for involved nodes.

Selection and Delineation of the Lymphatic Clinical Target Volumes

Our knowledge of the pattern and risk of lymphatic drainage from different head and neck sites is based on the classic anatomical work of Rouviere,⁸⁰ which has been reviewed,⁸¹ the assessment of the location and prevalence of clinical neck metastasis by Lindberg⁸²; and the large experience with elective neck dissections providing information about microscopic metastases, which was reported by Byers and colleagues⁸³ and Shah.⁸⁴ A division of the neck into six levels has been developed by surgeons from Memorial Hospital and revised by Robbins and associates.^85,⁸⁶ The retropharyngeal nodes, which are not routinely dissected surgically, are not considered in the surgical neck levels classification but are important targets in the irradiation of nasopharyngeal and other advanced HNCs.⁸⁷

The Planning Target Volumes

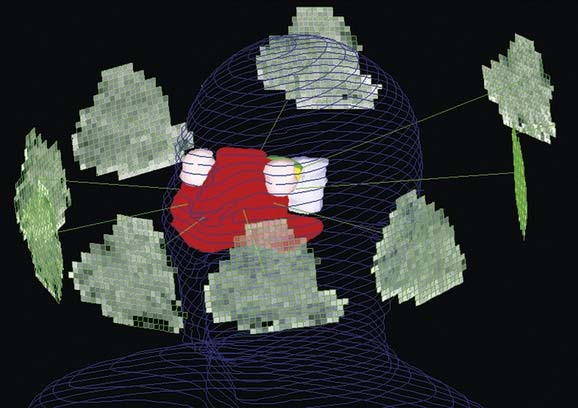
Once the GTVs and CTVs are outlined on the axial CT scans, a uniform expansion of these targets is performed to obtain the PTVs that accommodate setup uncertainties. Typically the magnitude of the margin is 3 to 5 mm, which means that an extra 5-mm ring of normal tissue around the target receives full dose. In a region with targets and organs at risk in close proximity, reducing this margin can potentially reduce treatment-related toxicity. Indeed, it has been estimated that each 1 mm of margin adds 1.3 Gy of dose to the parotid gland, which is particularly sensitive to low doses of radiation.⁸⁸ In order to reduce setup uncertainty, many groups have advocated daily imaging, with a position correction if the displacement from the original plan exceeds a threshold value. An example of the delineation of the targets and noninvolved structures in a case of oropharyngeal cancer is provided in Figure 77-12. The delivery of a single IMRT plan throughout the course of treatment provides better dose conformality than the use of several consecutive plans common in conventional radiotherapy, which consist of initial fields encompassing all targets followed with a boost to the gross tumor.⁸⁹ When a single plan is prescribed, the gross tumor PTV receives both a higher total dose and a higher dose per fraction than the PTVs of the subclinical disease. Owing to the differences in the daily fraction doses, a correction of the total dose to yield the normalized total dose for a 2-Gy fraction regimen is required. Therefore a standard IMRT plan would include 70 Gy over 35 fractions to the GTV, and lower fraction doses to the subclinical disease PTVs: 63 Gy to the high-risk and 56 to 59 Gy to lesser-risk elective targets, over 35 fractions (1.8 Gy and 1.6-1.7 Gy).

Figure 77-12. Dose prescription and specification and normal tissue dose constraints. Green represents the parotid gland; red represents CTV; yellow represents the constrictor muscle; and blue represents the 50 Gy line.

Dose and dose/volume specifications are made to impose constraints on the dose-volume histograms of the targets, noninvolved tissue of interest, and nonspecified tissue outside the targets. Radiation Therapy Oncology Group protocol H-0022 specified the prescription dose as the dose that encompasses at least 95% of the PTV. No more than 20% of the PTV can receive more than 110%, and no more than 1% of the PTV can receive less than 93%, of the prescribed dose.

Dose constraints regarding critical organs are usually stated in terms of the maximal dose. Commonly applied constraints in the head and neck are maximal doses of 45 Gy to the spinal cord, 54 Gy to the brainstem, 70 Gy to the mandible, and 50 to 55 Gy to the optic pathway.

The Optimization Process: The Number and Directions of the Beams

Although tomotherapy uses arcs around the patient, IMRT using multileaf collimators requires decisions regarding the number and orientation of the beams. It was suggested early on that if the number of segments (or beamlets) is large enough, the direction of the beams is not important, and coplanar beams arranged at equal distances around the patient’s head and neck would achieve satisfactory results. Most investigations of IMRT of the head and neck with multileaf collimators use this approach. The beam number should be odd, to prevent opposed beams, which would increase hot spots near their entrances to the neck. Nine beams arranged equidistantly (40 degrees apart) were found to be optimal: They provided better dose distributions than five or seven beams, whereas fifteen beams did not seem to improve the plans.⁹⁰

Clinical Results

Most studies comparing IMRT with conventional treatments are retrospective and therefore have a potential selection bias. IMRT is far more complex and time consuming than conventional radiotherapy. It is likely that different selection factors play a role in each institution: In patients who cannot tolerate lengthy treatment, those judged to be too sick to benefit from complex therapy, those requiring urgent start of therapy, more simple, conventional treatment may be selected. Therefore the comparison of IMRT with conventional RT in such situations would be futile. With this in mind, we would like to briefly summarize the existing results for specific sites.

Nasopharynx

The use of IMRT for the nasopharynx represents opportunities to spare many critical noninvolved structures and to improve tumor coverage, as detailed previously. These improvements have been demonstrated in several treatment planning exercises in nasopharyngeal and oropharyngeal tumors, in which IMRT plans were compared with “standard 3D” plans in the same patients.^91,⁹²

Two randomized prospective studies compared IMRT treatment with conventional treatment in early stage nasopharyngeal cancer.^93,⁹⁴ Both showed similar high rates of tumor control and a benefit for IMRT for sparing of salivary flow. One of these studies demonstrated a benefit for IMRT in patient-related xerostomia.⁹³

A large clinical series of IMRT of nasopharyngeal cancer has been reported by investigators at the University of California in San Francisco.⁹⁵ They studied 67 patients treated in the years 1995 to 2000. The GTV dose was 1.12 to 2.25 Gy/fraction to a total of 65 to 70 Gy, and the CTV dose was 1.8 to 2.0 Gy/fraction to a total of 50 to 60 Gy. In order to prevent under-dosing of the targets, the prescribed doses were typically the minimal doses encompassing the targets. The resulting delivered mean GTV dose was 74.5 Gy, at mean GTV fraction doses of 2.24 to 2.4 Gy. The resulting normalized total dose (calculated for late-responding tissue) was 80 Gy. This regimen yielded excellent locoregional tumor control: The rate was 97% at median follow-up of 31 months, with reasonable rates of acute toxicity. For re-irradiation of nasopharyngeal cancer, IMRT offers dose distribution advantages because it significantly reduces the extent of irradiation of the previously irradiated tissue volume. Lu and coworkers⁹⁶ described their experience with re-irradiation using IMRT for recurrent nasopharyngeal cancer. The rate of acute toxicity was acceptable, and at a median follow-up of 9 months, the locoregional control rate was 100%. Although longer follow-up is necessary, the preliminary toxicity and local control data for these recurrent cases are promising.⁹⁶

Paranasal Sinuses

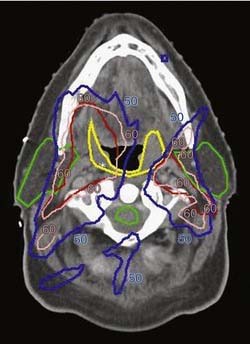
The main obstacle to adequate irradiation of tumors of the paranasal sinuses is the proximity of the optic pathways to the target in advanced cases. In these cases, IMRT can provide adequate target coverage while sparing the optic pathways (Fig. 77-13).

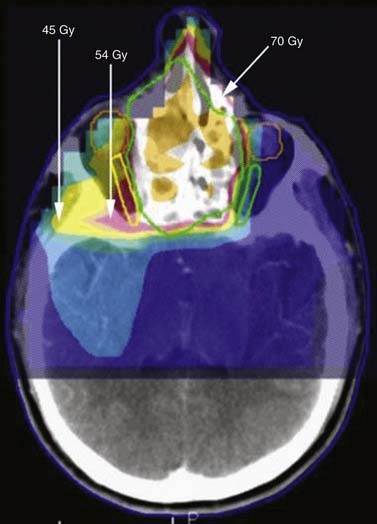
Figure 77-13. Radiation of sinuses with sparing of the optic nerves. Green represents GTV, to Gy dose; yellow is US Gy; and pink is SU Gy.

The group from the Royal Marsden Hospital found that compared with 3DCRT using the same beam arrangement, IMRT significantly reduced the dose to the optic nerves and improved PTV coverage.⁹⁷ Tsien and colleagues⁹⁸ at the University of Michigan found that IMRT planning in patients with nonresectable maxillary sinus cancer revealed no substantial difference between plans using an anterior field and two lateral fields and plans using nine equidistant beams arranged around the patient. Optimization using normal tissue complication probability (NTCP) of the optic nerves as an objective function was found to facilitate planning and to provide a basis for the assessment of the clinical trade-off between PTV coverage and ipsilateral optic nerve sparing.⁹⁸

A large clinical series of IMRT for paranasal sinuses was reported from Ghent University in Belgium.⁹⁹ 39 patients were treated postoperatively, and the 4-year actuarial local control after surgery and IMRT was more than 80% for patients with T1-4aN0M0 disease. In the group undergoing IMRT, there was significantly lower incidence of severe dry-eye syndrome than in the historical cohort.

Oropharynx

In general, all series investigating IMRT for oropharyngeal cancer have reported outstanding locoregional control rates.^92,¹⁰⁰ These series reported 2-year locoregional tumor control rates of 90% to 98% for patient populations who mainly had stage III or IV tumors. However, these results should be evaluated in the context of a likely selection bias and, importantly, with consideration of the emergence of human papillomavirus–related oropharyngeal cancer, which is associated with better prognosis.¹⁰¹

Some of the most reliable information gained from clinical series of IMRT for HNC in general, and oropharyngeal cancer in particular, relates to the pattern of tumor recurrences relative to the targets and the locally delivered doses. These data allow an assessment of the adequacy of target selection and delineation. In all reported cases, it seems that careful selection and delineation of the targets resulted in very few or no marginal or out-of-field recurrences. De Arruda and colleagues ¹⁰⁰ reported that all recurrences in their series were in-field. In the series by Chao and coworkers,¹⁰² most marginal recurrences were in the lower neck, which was treated with an anterior field that was matched to the IMRT-treated upper neck. In the series reported by Eisbruch and associates,⁸⁷ in which the majority of patients had oropharyngeal cancer, almost all recurrences were in-field, in high-risk volumes that had received the full prescribed doses.

Larynx and Hypopharynx

IMRT can improve target dose homogeneity for laryngeal and hypopharyngeal SCC while reducing the dose to the normal tissues at risk.¹⁰³^–¹⁰⁵ Clinical data on IMRT for laryngeal and hypopharyngeal SCC are scarce, however, and include limited numbers of patients within large heterogeneous series of multiple HN tumor sites.^87,^95,¹⁰⁵ In general, these series showed lower tumor control rates than those reported for oropharyngeal sites. Potential reasons could be patient selection factors. For example, at the University of Michigan, only patients with laryngeal cancer and advanced nodal disease receive IMRT. The reason is that for patients with nodal stage 0 to 1, the uppermost nodes at level II are the subdigastric nodes, which can be treated with conventional techniques while sparing the majority of the parotid glands and avoiding the oral cavity; the retropharyngeal nodes or level II near the base of skull are not at risk in these patients. Another small study has suggested a benefit in xerostomia without a compromise in local control (94% at 2 years) in advanced node-negative laryngeal cancer.¹⁰⁶

In general the main intent in IMRT planning is preservation of function. One of the main issues is reducing xerostomia via the sparing of the parotid salivary glands and submandibular glands. According to one study, the mean dose of 26 Gy is the threshold for parotid gland sparing (see Fig. 77-12),¹⁰⁷ and patients in whom at least one functioning parotid gland was spared enjoyed significant preservation of salivary flow and reduced xerostomia.

Other potential functional gains from IMRT compared with conventional RT include reduced long-term dysphagia. Sparing of pharyngeal constrictors and the glottic and supraglottic larynx may be beneficial in this regard.¹⁰⁸

Proton Therapy

Currently, all centers utilize photons, or high-energy x-rays, for their IMRT treatments. However, because of their inherent physical characteristics, protons are better able to concentrate dose inside targets and minimize dose to surrounding normal tissues. Most of the energy of a proton beam is deposited near the end of the beam path (Bragg peak), the location of which is determined by the energy of the beam. Thus, the target can be included in the tissue volume receiving the high dose while little is delivered before or after the beam passes through the target, and the integral dose delivered outside the targets is lower than the dose delivered using IMRT. Use of proton beams would be expected to reduce the risk of secondary malignancies, which is especially important in pediatric cancer patients.¹⁰⁹ With the use of inverse planning, intensity-modulated proton therapy (IMPT) can further improve the therapeutic index of radiotherapy. Several groups have published treatment planning comparisons of (photon) IMRT with IMPT.¹¹⁰^–¹¹² Using IMPT, mean doses to the organs at risk—the parotid glands, in particular—have been reduced by as much as 50%. However, because IMPT has been used for only a few years, long-term clinical treatment results are not yet available. The areas in the head and neck that could benefit from the added conformality achievable with protons are the paranasal sinuses and nasopharynx, which are often in close proximity to the optic nerves and chiasm, as well as the brain. Retrospective reviews of 3D conformal proton therapy suggest high local control rates with minimal toxicity, including preservation of vision in patients with advanced sphenoid sinus cancers.¹¹³

Neutron and Carbon Ion Therapy

In addition to protons, other particles have been used to treat HNCs. Neutrons have found a niche in treatment of salivary gland tumors, after a small trial randomly assigning patients to photon or neutron radiotherapy demonstrated a survival benefit for neutron therapy.¹¹⁴ Other ions, including helium, neon, and carbon, have been investigated over the past 50 years. Currently, carbon ion therapy shows the most promise. Compared with photons, carbon ions have the conformality advantage of protons, with the additional advantage of a greater relative biologic efficacy (RBE): A smaller dose of carbon ions is required to achieve the same biologic effect as a reference dose of photons. This difference is due to a higher linear energy transfer with carbon ions, which theoretically causes more irreparable DNA damage, is more effective in hypoxic cells, and is less subject to variation in radiosensitivity with cell cycle. Currently, few centers worldwide are able to treat with this modality. Initial results in adenoid cystic carcinoma and locally advanced SCC of the head and neck, which demonstrate excellent local control rates with low toxicities, are promising.¹¹⁵ However, long-term results are not yet available.

Imaging-Guided Radiotherapy

The term imaging-guided radiotherapy relates to the performance of patient and tumor imaging with electronic portal imaging devices (EPIDs) or CT before each fraction or every few fractions of therapy in order to ensure tracking of the tumor by the treatment beams. In cancer of the head and neck, where breathing-related motion is inconsequential, imaging-guided radiotherapy has two main goals, minimizing setup uncertainties, thereby enabling reduction of the PTV margins, and assessing anatomic changes in tumor and critical tissue during the course of therapy.

Tracking Anatomic Changes during Therapy

During the 6- to 7-week course of radiotherapy, many anatomic changes can occur. Because dose distributions achieved using IMRT have steep gradients, and PTV “safety” margins are becoming smaller, it is especially important to understand the consequences of anatomic changes during therapy for the dose to both targets and normal tissues. In definitive cases, the primary tumor, nodes, or both can shrink, whereas in postoperative cases, inflammation and edema can resolve. Additionally, weight loss, a common consequence of acute treatment toxicity, can lead to muscle wasting and shifting of both normal tissue and tumor positions. Barker and associates ¹¹⁶ conducted a detailed study of such anatomic changes during radiotherapy for HNC.¹¹⁶ The primary tumors and nodes were noted to shrink at a median rate of 1.8% of the initial volume per treatment day, so that on the last day of treatment, the median overall volume loss was close to 70%. The parotid glands moved medially during treatment, the median displacement at the end of therapy being 3.1 mm. These changes were highly correlated with patient weight loss. After publication of these findings, several investigators suggested replanning during treatment to minimize parotid gland dosage while maximizing tumor dosage. This issue is subject to ongoing studies.

Brachytherapy

As described previously, brachytherapy is localized radiotherapy that uses many radioactive isotopes, such as radium Ra-226 and cesium Cs-137 needles for implants in certain cases or afterloading techniques using iridium Ir-192 sources.¹¹⁷ These sources produce a lower-energy gamma ray, thus simplifying the radiation protection requirements associated with routine patient care. The sources are left in place for a specified time and then are removed. Alternatively, permanent implants using gold Au-198 and iodine I-125 can be used. These implants deliver their total radiation dose over the effective lifetime of the radioactive material. The obvious advantages of implants are better dose localization, which results in less radiation damage to the healthy tissue surrounding the tumor, and the relatively prolonged time over which the radiation is delivered. The disadvantages include lack of addressing subclinical disease and the requirement for general anesthesia in many cases.

External-beam radiation is given at the rate of 1.5 to 2.0 Gy per minute.¹¹⁸ A typical Ir-192 implant delivers its dose at the rate of 0.4 to 0.8 Gy per hour. High-dose-rate (HDR) remote afterloading devices have also been developed. These devices push a single, high-activity Ir-192 source through a set of interstitial catheters, and a computer program controls the source dwell time at various points throughout the implant. Typically, about 3.0 to 3.5 Gy is given to a distance of about 1 cm from the periphery of the catheters each treatment, and up to two daily treatments are given about 6 hours apart. Each treatment takes about 15 to 30 minutes, depending on the strength of the radioactive source and the complexity of the implant.

Radiation Side Effects

Acute Side Effects

Acute reactions that can occur during irradiation with or without chemotherapy are predictable toxicities, and depend on the dose and schedule of radiation therapy used and the accompanying chemotherapy. Such effects include mucositis, odynophagia, dysphagia, hoarseness, xerostomia, dermatitis, and weight loss. These effects occur to some degree in the majority of patients, but they are self-limited in duration.

Acute complications can interfere with and delay treatment. Even short delays can be deleterious, interfering with local tumor control.^119,¹²⁰ In one study, for example, a 5-day delay in completing RT was associated with a 3.5% to 8% reduction in local control for laryngeal cancers.¹²⁰ The effect was greater in tumors with a higher probability of local failure. In addition to treatment-related factors, the nature, frequency, and severity of complications are heavily influenced by tumor-related factors (e.g., location, invasion of vital structures) and patient-related factors (e.g., oral hygiene, nutritional status, continued tobacco use, and history of diabetes, collagen vascular disease or human immunodeficiency virus).

The following sections discuss the most common acute side effects:

Dermatitis

Radiation damage to stem cells in basal layers of the skin can give rise to a sunburn-like desquamation. This can be aggravated by chemotherapeutic agents such as 5-FU. These effects can occur as early as 2 weeks after the start of radiotherapy.

This side effect can be minimized through appropriate skin care, avoidance of exposure to potential chemical irritants, limitation of direct sun exposure, and avoiding application of lotions, ointments, or fragrances to the head and neck region to minimize the bolus effect that might alter the depth at which the maximum RT dose is delivered. IMRT typically worsens skin reaction because of the multiple target beams, but this effect can be reduced by specifying the skin as an avoidance structure and by treating the lower neck with an anterior beam rather than including it in the IMRT plan.

Xerostomia—

The severity of xerostomia resulting from RT for HNC depends on the volume of salivary tissue irradiated. Temporary loss of saliva is significant after about 10 Gy is delivered to the salivary glands, whereas administration of doses significantly higher than 26 Gy can cause permanent loss of function. Alteration in taste can also occur, and decreased oral intake may contribute to reduced saliva production.

Prevention of this side effect can be performed by reducing salivary gland dosage in formal planning. Some suggested that the use of amifostine may reduce xerostomia. The benefit of amifostine was shown in a landmark trial of 315 patients receiving RT alone (60 to 70 Gy in 1.8- to 2.0-Gy daily fractions), who were randomly assigned to receive either amifostine or no amifostine.¹²¹ Amifostine reduced the incidence of significant acute xerostomia from 78% to 51% and the incidence of significant chronic xerostomia at 12 months from 57% to 34%. This agent had no impact on rates of mucositis or on tumor control at 2 years.¹²¹ However, data on the effect of amifostine in the chemoradiation setup are conflicting,^122,¹²³ other than that it has severe side effects and is expensive and therefore has not been widely used.

Mucositis

Radiation-induced loss of stem cells in the basal layer interferes with the replacement of cells in the superficial mucosal layers when they are lost through normal physiologic sloughing. The subsequent denuding of the epithelium results in mucositis, which can be painful and can interfere with food intake and nutrition. Mucositis usually develops 2 to 3 weeks after the start of RT. The incidence of mucositis is variable, depending on the field, the total dose and duration of RT, and the concomitant administration of chemotherapy.¹²⁴ In one series, clinically significant mucositis occurred in 64% of patients receiving RT to the head or neck for any malignancy.¹²⁵ Both incidence and severity are higher in patients receiving chemoradiotherapy than in those undergoing RT alone. Chemotherapy can have a similar effect on the mucosa, and the combination of chemotherapy with RT increases the rate of mucositis especially when the modalities are delivered concurrently. Mucositis is managed symptomatically with scrupulous oral hygiene, dietary modification, and topical anesthetics. A variety of agents have been evaluated for use either prophylactically or after the onset of symptoms; their role in the treatment of radiation-induced mucositis is uncertain (Fig. 77-14).

Figure 77-14. Acute mucositis.

Late Toxicities

Xerostomia

Xerostomia is a frustrating side effect that may lead to many other effects. It often improves with time,¹²⁶ but it can be long-lasting or even permanent. Regarding treatment, several strategies may minimize the incidence of xerostomia. When possible, sparing one parotid gland and, if possible, the submandibular glands can greatly diminish the incidence of xerostomia.¹²⁷ Commercially available salivary substitutes or artificial saliva (oral rinses containing hyetellose, hyprolose, or carmellose) relieve the discomfort of xerostomia by temporarily wetting the oral mucosa. Although they can provide temporary relief, especially prior to eating, many patients must take frequent sips of water to remain comfortable. In addition to being inconvenient, this can lead to secondary problems such as nocturia from late night fluid intake in men with prostatic hypertrophy and in men and in women with small bladder capacity. In patients in whom untreated or unaffected residual salivary tissues are intact, sialagogues that stimulate salivary production may be used. Sialagogues can be characterized as gustatory, tactile, or pharmacologic. Gustatory stimuli such as acidic or bitter substances are most effective at stimulating salivary flow.¹²⁸ Sweet substances such as sugar-free hard candy also stimulate the flow of saliva, but to a lesser extent. Pharmacologic sialagogues, which are typically agonists of the muscarinic (M3) receptor, include pilocarpine and cevimeline. Of these, pilocarpine has been the most extensively investigated. Pilocarpine may improve or prevent xerostomia when given after completing radiotherapy. Improvement in symptoms may occur only after many weeks of treatment, and cholinergic side effects, in particular sweating, may stop a significant number of patients from continuing to use the drug.¹²⁸

Osteoradionecrosis

Osteoradionecrosis (ORN) of the jaw is a severe complication of RT for HNC. The presentation of post-RT ORN ranges from small asymptomatic bone exposures that remain stable for months to years and heal with conservative management, to severe necrosis necessitating surgical intervention and reconstruction. Depending on the location and extent of the lesion, symptoms can include pain, bad breath, dysgeusia, dysesthesia or anesthesia, trismus, difficulty with mastication, deglutition, and/or speech, fistula formation, pathologic fracture, and local, spreading, or systemic infection. The mandible is the most commonly affected bone, because in the majority of patients undergoing treatment for HNC, a large part of it is inevitably exposed to high RT doses. Another reason is the blood supply of the mandible, which is unilateral; the maxilla has bilateral blood supply. Maxillary ORN is reported infrequently, usually in the setting of irradiation for nasopharyngeal cancer (in which both jaws are at risk).

Mandibular ORN occurs in 5% to 10% of patients treated with conventional RT or high-dose-rate brachytherapy, and is severe in about 2%.^129,¹³⁰ The incidence of this complication appears to be higher with hyperfractionated regimens, especially with a short inter-fraction interval. In one study of 168 patients with oral cancer treated with hyperfractionated or conventional RT, the incidence of ORN was higher with hyperfractionated therapy (23% vs. 9%, respectively).¹³⁰ Tooth extraction and dental disease in irradiated regions are major factors in the development of both mandibular and maxillary ORN.^129,¹³⁰ Although opinion differs as to whether extraction of diseased and nonrestorable teeth should be performed before or after irradiation, many writers report that postirradiation extraction of such teeth produces a higher rate of mandibular ORN.¹³¹ Furthermore, at least some data suggest that mandibular ORN associated with postirradiation tooth extraction more often requires radical resection than does ORN that develops after pre-irradiation extraction (45% vs. 12%, respectively).¹³² Repair of nonrestorable and diseased teeth prior to RT may reduce the risk of this complication. However, most authorities do not recommend the pre-irradiation extraction of healthy or restorable teeth.

Ben-David and colleagues ¹³³ demonstrated that rates of ORN could be significantly lower if the following rules were observed: reducing the mandibular volumes receiving high doses, improved salivary flow rates and associated improved oral health, and uniform prophylactic dental care. For mild ORN, treatment with conservative débridement, antibiotics, and occasionally ultrasound is usually successful.¹³⁴ However, when bone and soft tissue necrosis are extensive, radical resection of the mandible with immediate microvascular reconstruction may provide better results.¹³⁵ Persistence of ORN despite aggressive treatment should raise the suspicion of recurrent cancer.¹³⁵

Hyperbaric oxygen therapy (HBO) has been suggested as a beneficial therapeutic maneuver in patients in whom ORN of the jaw develops after RT. ORN may be triggered by a predominantly fibro-atrophic mechanism.¹³⁶ At least in theory; HBO simulates the function of monocytes and fibroblasts, increasing collagen synthesis and vascular density. Despite this theoretical rationale, the available data are conflicting, as to clinical benefit, of HBO for both prevention and therapy of ORN. The benefit from HBO was called into question by results of a randomized multicenter trial in which 68 patients with overt mandibular ORN were randomly assigned to receive either 30 to 40 exposures to HBO or a placebo at 2.4 absolute atmospheres for 90 minutes.¹³⁷ Healing rates were equivalent in the two groups and in fact trended toward worse in the HBO group (19%, compared with 32% for placebo; P = .23). Although this was only a single study and did not include patients receiving HBO prior to dental extraction, its results raise doubt about the efficacy of HBO for ORN.

Fibrosis

A serious complication of RT in the treatment of cancer patients is the late-onset of fibrosis in normal tissues, including the neck, pharynx, esophagus, and temporomandibular joint. Radiation-induced fibrosis (RIF) is similar to inflammation, wound healing, and fibrosis of any origin. Typical histologic features include the presence of inflammatory infiltrates (particularly macrophages in the earlier stages of fibrosis), differentiation of fibroblasts into postmitotic fibrocytes, and changes in the vascular connective tissue with excessive production and deposition of extracellular matrix proteins and collagen. RIF can cause a wide range of clinical manifestations, including cutaneous induration, lymphedema, restrictions in joint motion, strictures and stenoses in hollow organs, and ulcerations. Specifically in the head and neck region it may cause trismus, which can progress over time. RIF in the esophagus and hypopharynx may lead to strictures, ulcerations, and fistula formation. Radiation fibrosis to the constrictor muscles may lead to chronic dysphagia. The best way to prevent this side effect is conformal planning to spare unnecessary radiation.

Thyroid Dysfunction

Irradiation of the low neck is associated with hypothyroidism. The incidence varies widely and is dose-dependent as well as time dependent, increasing with time elapsed since treatment. RT-induced hypothyroidism develops at a median of 1.4 to 1.8 years (range 0.3 to 7.2 years) after RT.¹³⁸ It is more common in patients undergoing both neck surgery and RT but is not higher in patients who undergo chemotherapy in addition to RT than in those who have RT alone.

Vascular Complications

Carotid artery rupture (also called carotid blowout syndrome) and oropharyngocutaneous fistula are major complications associated with RT to the neck. These sequelae occur almost exclusively in patients who have received combined surgery and RT. As an example, in one series of 46 patients with carotid artery rupture, 43 had undergone extensive primary and salvage radical surgery with intraoperative brachytherapy, external beam irradiation, or both.¹¹⁹ Both retrospective and prospective studies show that both carotid artery rupture and oropharyngocutaneous fistula occur more often with preoperative than postoperative irradiation.

Carotid rupture and fistula are rarely observed after definitive RT with or without concomitant chemotherapy but may be more common when tumor is invading the carotid sheath or extending into and occupying a large volume of the soft tissue of the neck.¹³⁹ Patients with ORN of the temporal bone after definitive treatment for nasopharyngeal cancer are also at risk for carotid artery rupture.

The most common angiographic abnormality seen in one study was one or more pseudoaneurysms.¹⁴⁰ Although this devastating complication can sometimes be managed with endovascular therapy, it recurs in up to 25% of patients, often as a manifestation of recurrent tumor or of multifocal iatrogenic arteriopathy and occasionally wound complications.

Neurologic Complications

Radiation therapy can cause toxicity to either the central or peripheral nervous system when these structures are included in the treatment field. Nervous system toxicity is usually subdivided into acute (during the course of radiation), early delayed (weeks to three months after radiation), and delayed reaction (after more than 3 months). Late toxicity is the most common.

A transient myelopathy may develop 2 to 6 months following spinal irradiation. This condition is widely believed to be due to temporary demyelination of the posterior columns of the spinal cord. Self limiting, it is generally not a precursor of chronic progressive myelitis. The characteristic manifestation is the development of Lhermitte’s sign, a nonpainful but unpleasant electric shock–like sensation that shoots down the spine during neck flexion. Increased spinal cord metabolic activity and PET imaging have been described in association with Lhermitte’s sign.

Radiation myelopathy may begin acutely, but more often the onset is insidious. Paresis, numbness, and sphincter dysfunction developing 6 to 12 months after irradiation are the typical manifestations of progressive radiation-induced myelitis. However, the initial signs can be subtle, such as decreased temperature sensation and decreased proprioception. These signs may stabilize or slowly progress inexorably to lower extremity weakness, footdrop, the Brown-Séquard syndrome, incontinence, hyperreflexia, loss of bowel and bladder function, and complete paresis below the irradiated section of the spinal cord. The risk of chronic radiation myelopathy rises progressively with the dose of radiation.¹⁴¹ Evidence derived from several large series suggests that the incidence of myelopathy is less than 0.5% after 50 Gy with conventional fractionation.¹⁴¹ The best estimate of the dose expected to cause a 5% risk of myelopathy within 5 years (sometimes called the TD 5/5) is approximately 60 Gy if the radiation is given in 1.8- to 2.0-Gy daily fractions. This dose value appears to be independent of the region or length of spinal cord treated. The risk of myelopathy increases rapidly with doses above 60 Gy, with one series reporting an incidence of 50% in patients receiving between 68 and 73 Gy to the spinal cord.¹⁴¹

Recent Posts

Meta

Categories

Search Engine

Radiotherapy for Head and Neck Cancer: Radiation Physics, Radiobiology, and Clinical Principles

Share this:

Related

Related posts: