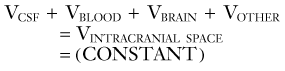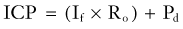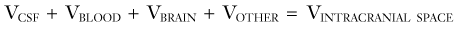Physiology of the Cerebrospinal Fluid and Intracranial Pressure

Published on 13/03/2015 by admin

Last modified 22/04/2025

Print this page

This article have been viewed 4822 times

CHAPTER 10 Physiology of the Cerebrospinal Fluid and Intracranial Pressure

The exquisite sensitivity of the central nervous system to physical and chemical injury has led to an ingenious series of protective and homeostatic systems that shroud, nurture, nourish, and maintain maximal function. These systems include rigid physical protection in the form of skull bones, hydraulic shock absorption in the form of cerebrospinal fluid (CSF), substrate supply and cellular homeostasis in the form of a rich vascular supply with continuous turnover of extracellular fluid, and protection from external noxious substances by the blood-brain barrier.

These highly developed protective systems can become detrimental, however, under certain pathologic conditions. In particular, encasement of brain tissue in a rigid structure (the skull) places an important constraint on the refined interplay between cerebral homeostatic processes, namely, volume regulation. Noncompressible matter such as fluid, when added to a rigid container, will generate pressure; in the case of the central nervous system, this results in the intracranial pressure (ICP). Under pathologic conditions, the intracranial volume and therefore ICP can rise, which presents a serious threat to the central nervous system. Furthermore, the effects of raised ICP can further contribute to the primary pathologic process.

A wide range of neurosurgical problems—including congenital lesions, neoplasms, metabolic and infectious syndromes, infarction, hemorrhage, and trauma—requires evaluation and treatment for elevated ICP. Effective clinical treatment of problems relating to raised ICP demands a detailed understanding of the physiologic mechanisms that generate and maintain normal ICP, the perturbations that lead to an elevated ICP, and the means by which elevated pressures can be reduced.

Historical Considerations

Although problems with brain swelling and the effects of removing pieces of skull were understood even in the times of Galen, Hippocrates, and the early Egyptian physicians, modern thinking about volume regulation inside the skull began with the writings of George Kellie and his mentor, Alexander Monro, who worked in Edinburgh at the turn of the 19th century. Monro,¹ in his seminal work on the brain and nervous system, wrote:

For, as the substance of the brain, like that of other solids of our body, is nearly incompressible, the quantity of blood within the head must be the same, or very nearly the same at all times, whether in health or disease, in life or after death, those cases only excepted in which water or other matter is effused, or secreted from the blood vessels; for in these a quantity of blood, equal in bulk to the effused matter, will be pressed out of the cranium.

Some years later, at a meeting of the Medico-Chirurgical Society of Edinburgh, George Kellie ² presented a report in which he advanced this idea and stated:

If these premises be true, it does not then appear very conceivable how any portion of the circulating fluid can ever be withdrawn from within the cranium, without its place being simultaneously occupied by some equivalent; or how anything new or exuberant can be intruded without an equivalent displacement.

These ideas later became recognized as the Monro-Kellie doctrine, which is formalized physiologically later. Subsequent advances in understanding ICP came with the ability to effectively monitor ICP under different circumstances. Quincke ³ first described lumbar puncture for the relief of “brain pressure” in 1911. However, it was not until the work of Guillaume and Janny⁴ in 1951 that ICP was continuously monitored. Lundberg⁵ later published results from a large series of patients in which he described several of the fundamental concepts used today in clinical ICP monitoring, including the Lundberg A, B, and C waves.

ICP monitoring today is considered commonplace in neurosurgical practice. ICP values are used as a measure of disease, as an indication of treatment response, and to monitor cerebral perfusion.

Normal Intracranial Pressure

The upper limit of normal ICP in adults and older children is usually given as 15 mm Hg, although the usual range is 5 to 10 mm Hg. Transient physiologic changes resulting from coughing or sneezing often produce pressures exceeding 30 to 50 mm Hg, but ICP returns rapidly to baseline levels.

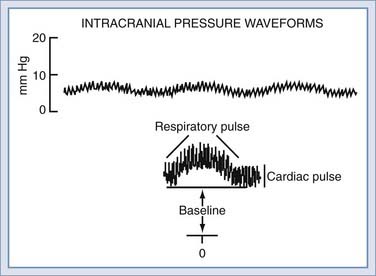
ICP can be measured by low-volume displacement transducers to interface with CSF pathways in the intraventricular, intraparenchymal, subdural, or epidural spaces. The ICP waveform is normally pulsatile and can be divided into three major components (Fig. 10-1). The baseline or average level is commonly referred to as the ICP; rhythmic components superimposed on this level are associated with cardiac and respiratory activity. To completely describe ICP, one should specify the magnitude of the baseline or “steady-state” level and the amplitude and periodicity of the pulsatile components. Changes in these pulsatile components can be one of the earliest signs that the ICP is beginning to rise, as a reflection of the increased conductance of pressure waves through a “tightening” brain.

FIGURE 10-1 Normal intracranial pressure (ICP) waveform. The baseline pressure level is affected by rhythmic components caused by cardiorespiratory activity. Mean arterial blood pressure fluctuation with heart rate causes small-amplitude rapid pulsation, and respiration causes larger amplitude fluctuations of lower frequency. ICP is completely described only by information about both the baseline level and the pulsatile components.

Cardiac and respiratory activity creates pulsatile components by cyclic changes in cerebral blood volume. Left ventricular contraction contributes the cardiac component, which has a frequency similar to the peripheral arterial pulse. The exact vessels that transmit the peripheral pulse remain to be established. Early studies suggested that the choroid plexus and pial arteries were responsible,⁶ although more recent analysis has implicated the high-compliance venous blood vessels.⁷

The respiratory contribution to the ICP waveform arises as a result of fluctuations in arterial blood pressure and cerebral venous outflow during the respiratory cycle, generated by pressure changes in the thoracic and abdominal cavities. During inspiration, there is a fall in arterial blood pressure and an increase in pressure gradient from cerebral veins to central venous capacitance vessels. This gradient drives cerebral venous return, which is therefore increased on inspiration, with a concomitant drop in cerebral blood volume. Mechanical ventilation and intrathoracic disease may considerably alter the respiratory contribution to the ICP waveform.

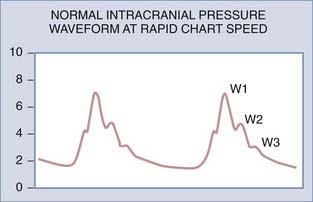
If the ICP waveform is examined in more detail and at a higher chart speed, the waveform of highest frequency can be seen to consist of as many as five smaller peaks. Three of these are relatively constant (Fig. 10-2): the percussion wave (W1), the tidal wave (W2), and the dicrotic wave (W3).⁷^,⁸ The percussion wave is the most constant in amplitude and derives from pulsations in large intracranial arteries.⁹ The tidal wave has a more variable shape and is thought to arise from brain elastance. The tidal wave and the dicrotic wave are separated by the dicrotic notch, which corresponds to the dicrotic notch in the arterial pulse waveform.

FIGURE 10-2 Normal ICP waveform at rapid chart speed. Several small components can be seen, the most constant of which are the percussion wave (W1), the tidal wave (W2), and the dicrotic wave (W3).

Physical Principles

ICP is synonymous with CSF pressure and is defined as the pressure that must be exerted against a needle introduced into the CSF space to just prevent escape of fluid. ICP depends on several parameters that are features common to any hydrodynamic system: the internal (intracranial) fluid volume, the elastance of the system, the contribution from the atmosphere, and the orientation of the craniospinal axis relative to the gravitational vector.

Pressure (P) is defined as force (F) per unit area (A). Pressures are usually reported in units of either millimeters of water (mm H₂O) or millimeters of mercury (mm Hg). This convention arose because a fluid column will exert a pressure at its base proportional to the height of the column (h), the density of the fluid (ρ), and the gravitational constant (g). Because, for a given fluid, g and ρ are constant, pressures can be compared by relation to the height of a given fluid. ICP is variably expressed in either millimeters of mercury or millimeters of water. Dividing the pressure in millimeters of water by 13.6 yields the equivalent pressure in millimeters of mercury; this constant is based on the ratio of the density of water to mercury. The SI unit for pressure is the pascal (Pa), which is defined as 1 newton (N)/square meter; 1 kilopascal (kPa) is 7.5 mm Hg or 102 mm H₂O.

In actual fact, three different pressures contribute to ICP: atmospheric pressure, hydrostatic pressure, and filling pressure. Atmospheric pressure is the component resulting from transmitted atmospheric pressure to the brain, and therefore absolute ICP varies with altitude. This pressure is principally transmitted through the vasculature ¹⁰; however, ICP is typically reported relative to atmospheric pressure, and this component is ignored.

As with any column of fluid, the skull and spinal canal experience hydrostatic pressure caused by the weight of their contents. The contribution of hydrostatic pressure depends on the weight of fluid and tissue above the point of measurement, divided by the cross-sectional area at that level. For example, lumbar CSF pressure is greater in the sitting position compared with the lateral decubitus position ¹¹^,¹² as a result of the hydrostatic difference; increasing degrees of head-down tilting further increase the contribution of hydrostatic pressure.

The filling pressure of the system is determined by the volume of the intracranial contents and the elastance of the enclosing structures. The intracranial contents consist of blood, brain, CSF, and any pathologic masses. Elastance is a system parameter that is defined by the pressure change per unit of volume change,¹³ namely, the corresponding pressure change for any given volume increase in craniospinal contents (Fig. 10-3A). The relationship is not necessarily linear across all volumes and not necessarily constant under all physiologic conditions. Compliance is the inverse of elastance, and both measures are useful for understanding the physiology of ICP. Elastance arises as a combined result of both distention and displacement. In other words, as volume is added to the system, there are two principal routes for compensation, either expansion or loss of volume. In a physiologic sense, this can occur either by distention of the spinal dura mater or by displacement of CSF and blood. These concepts are expounded on subsequently in the discussion of non–steady-state dynamics. Atmospheric pressure, hydrostatic pressure, and filling pressure all contribute to the concept of steady-state dynamics.

FIGURE 10-3 The pressure-volume curve and the pressure-volume index describe the response of ICP to the addition of volume. A, The normal curve shows how compliance changes as greater volumes are added. The CSF system is in the phase of spatial compensation at point a compared with spatial decompensation at point b. B, Graphing log ICP against volume change allows calculation of the pressure-volume index, which is widely used as a description of intracranial compliance.

Steady-State Dynamics

In the absence of disease, baseline ICP and the amplitude of the pulsatile components of ICP remain constant despite a variety of transient perturbations. As alluded to previously, the skull should be considered a rigid container of noncompressible elements. ICP therefore depends on the relative constancy of total volume inside the skull, contributed to by CSF, blood, and brain tissue. The ability of the dural coverings to distend is very limited; therefore, any change in volume of one of the three intracranial components must occur at the expense of the other two if ICP is to be maintained. The following equation describes this relationship:

This relationship encapsulates the concept of the Monro-Kellie doctrine. The presence of an abnormal component, such as a tumor or hematoma (represented by V_OTHER in the equation), demands reciprocal changes in the volumes of brain, blood, or CSF to maintain ICP at physiologic levels. Even the physiologic state is far from static; it is rather a dynamic equilibrium. Constant changes induced by the heartbeat, systemic blood pressure, fluid status, and intrathoracic pressure invoke transient changes within the intracranial compartment that are considered part of the steady state.

General Physiology of the Cerebrospinal Fluid

In the adult, approximately 87% of the typically 1500-mL intracranial space is occupied by the brain, 9% by compartmental CSF (ventricles, cisterns, and subarachnoid space), and 4% by blood.¹⁴ The extracellular space is in direct contact with CSF and forms approximately 15% of the total brain volume.¹⁵ Total CSF is considered to include compartmental CSF and the extracellular space.

Cranial CSF volume as assessed in humans by Tanna and colleagues ¹⁶ was found to have a mean of 164.5 mL, with a range of 62.2 to 267 mL. Ventricular volume also varies considerably, as assessed with magnetic resonance imaging, from 7.49 mL to 70.5 mL, with a mean of 31.9 mL. Reasons for such variation are not clear; however, the amount of CSF in any organism reflects a dynamic balance between production and clearance.

CSF is principally produced by the choroid plexuses, which are invaginations of the pia mater into the ventricular cavities, specifically in the roofs of the third and fourth ventricles and the walls of the lateral ventricles. At these points, fronds of densely branching blood vessels are invested by pia mater and covered by specialized ependymal cells, the choroidal epithelium. The surfaces of cells in this structure are densely covered with villous processes to increase the surface area. A second site of CSF production is the ventricular ependyma, the proportional contribution of which arguably ranges from 50% to 100%.¹⁷^,¹⁸

For a considerable time, CSF was described as an ultrafiltrate of plasma, implying that hydrostatic pressure within blood vessels forced protein-free fluid through interendothelial spaces.¹⁹ However, close analysis of the composition of CSF (Table 10-1) shows multiple differences in composition at the ionic level, which is strongly against the idea of a simple filtration or dialysis process. CSF, in general, has a higher sodium, chloride, and magnesium concentration than one would expect in a plasma filtrate. The concentrations of potassium, calcium, urea, and glucose are lower. The overall osmolality is, however, similar. Current thinking therefore holds that a simple filtration process is modified by energy-dependent secretion and reabsorption processes.

TABLE 10-1 Concentrations of Solutes (mEq/kg H₂O) in Plasma and Lumbar Cerebrospinal Fluid in Humans

SUBSTANCE	PLASMA	CSF
Sodium (Na⁺)	150	147
Potassium (K⁺)	4.63	2.86
Magnesium (Mg²⁺)	1.61	2.23
Calcium (Ca²⁺)	4.7	2.28
Chloride (Cl⁻)	99	113
Bicarbonate (HCO₃⁻)	26.8	23.3
Amino acids	2.62	0.72
Osmolality	289.0	289.0
pH	7.397	7.30

Cl⁻, Na⁺, and K⁺ from Fremont-Smith F, Dailey ME, Merritt HH, et al. The equilibrium between cerebrospinal fluid and blood plasma: I. The composition of the human cerebrospinal fluid and blood plasma. Arch Neurol Psychiatry. 1931;25(6):1271-1289; Mg²⁺ and Ca²⁺ from Hunter G, Smith HV. Calcium and magnesium in human cerebrospinal fluid. Nature. 1960;186:161-162; HCO₃⁻ and pH from Bradley RD, Semple SJ. A comparison of certain acid-base characteristics of arterial blood, jugular venous blood and cerebrospinal fluid in man, and the effect on them of some acute and chronic acid-base disturbances. J Physiol. 1962;160:381-391; osmolality from Hendry EB. The osmotic pressure and chemical composition of human body fluids. Clin Chem. 1962;8:246-265.

Estimates of the rates of CSF production can be made experimentally by examining the clearance or turnover of injected substances,²⁰ by marker dilution techniques,²¹ or by ventriculocisternal perfusion.²² Estimates with these techniques have yielded values in the range of 0.35 to 0.37 mL/min for humans.²³^,²⁴ More recently, flow voids in magnetic resonance signal within the CSF system have been used to estimate CSF production rates. Feinberg and Mark²⁵ estimated the flow of CSF through the aqueduct in humans, which should in principle equate to the flow of CSF secretion in the lateral and third ventricles, as 0.48 mL/min. There are variations in absolute rates of CSF production, however, that clearly relate to the absolute weight of choroid plexus tissue in each subject. Furthermore, rates of CSF production follow a diurnal variation, with peak production rates in the late evening and early morning.²⁶

Because there is a constant production of CSF, there must be removal of CSF at the same rate. CSF circulates from choroid plexus, through the ventricles, to the cisterna magna, basal cisterns, and subarachnoid space. The principal site of physiologic CSF drainage is into the dural venous system, through the dural venous sinuses. Evaginations of the arachnoid membrane protrude into the lumen of the dural veins and form the arachnoid granulations or villi. This forms a valvular connection between the subarachnoid space and the dural sinus so that blood cannot reflux into CSF. A higher hydrostatic pressure in the subarachnoid space drives the bulk flow of fluid in the forward direction, therefore draining CSF volume. Studies of these structures have revealed that they can allow molecules up to several microns to pass, but only unidirectionally.²⁷ CSF reabsorption has been shown to cease at CSF pressures of less than 5 mm Hg.²³

Cerebrospinal Fluid Dynamics

The nonpulsatile volume of CSF at any point in time is dependent on a balance between the rate of formation, the rate of absorption, and the volume sink in the skull. The interactions between these parameters can be addressed by a mathematical model that analyzes the physiologic mechanisms of (1) CSF formation, (2) volume storage or compliance, and (3) fluid absorption (Fig. 10-4).²⁸^,²⁹

FIGURE 10-4 Equivalent electrical circuit showing the principal factors that govern ICP. CSF formation is represented as a current source (I formation), CSF storage is represented by a capacitative element (C). Resistance to CSF outflow is represented by a resistive element (R), and dural sinus pressure is P_d. This framework has allowed accurate description of CSF dynamics.

(From Marmarou A, Shulman K, Rosende RM. A nonlinear analysis of the cerebrospinal fluid system and intracranial pressure dynamics. J Neurosurg. 1978;48:332-344.)

The formation of CSF can be depicted as a pump that continuously introduces fluid into the CSF spaces of the neural axis. The rate of formation of fluid (I_f) is considered constant and independent of the pressure that has to be pumped against, in accordance with observations that the rate of CSF formation is affected minimally, if at all, by changes in the ICP. The fluid enters a compliant storage space, which can expand to accommodate the added volume, and proceeds through outflow pathways to be absorbed across the arachnoid villi into the dural venous sinuses. The compliance mechanism is represented by an element (C) that decreases its compressibility with increasing volume, much like the resistance offered by a rubber balloon at maximal inflation. Both the resistance of the CSF channels leading to the arachnoid villi and the resistance of the villi to fluid flow are combined into a single resistance element (R_o). This component represents the total resistance to the outflow of the CSF, which under normal conditions remains fixed and independent of ICP. The final element of this model is the dural sinus pressure (P_d). Fluid crossing the arachnoid villi must overcome this exit pressure.

From this conceptual framework, a theory has been developed to describe the interaction of the formation, storage, and absorptive elements in the steady state. First, both pressure and volume are in equilibrium, and there can be no net increase or decrease in the total volume of the CSF. The CSF formed must pass through the absorptive elements so that no net fluid is stored.

Because all fluid formed passes through the resistive element (R_o), a pressure gradient will be developed across the absorptive element that is equal to the product of fluid formation (I_f) and the fluid resistance (R_o). The greater the magnitude of flow or resistance, the greater the pressure gradient (I_f × R_o). As long as the system is in equilibrium, the pressure of the CSF spaces must be of sufficient magnitude to drive fluid through the arachnoid villi at the same rate it is being formed. This requires that the CSF pressure (ICP) be equal to the sum of the pressure gradient across the absorptive element (I_f × R_o) and the exit pressure. The equation

shows that the steady-state ICP is proportional to three parameters: (1) the rate of CSF formation, (2) the resistance to CSF absorption, and (3) the dural sinus pressure. When these parameters remain constant, ICP is unchanged, and the compliance element does not actively participate in ICP regulation.

An increase in CSF formation, outflow resistance, or venous pressure at the site of fluid absorption can alter this dynamic equilibrium and result in elevated ICP. Mathematical modeling has shown that the contribution of the product of CSF formation rate and outflow resistance (I_f × R_o) is approximately 10% of the total ICP.²⁹ The remainder is attributed to the magnitude of the dural sinus pressure (P_d). With this distribution, the outflow resistance would have to increase markedly to cause a significant rise in the ICP. However, much smaller elevations of sagittal sinus pressure (P_d) caused by venous sinus obstruction would be transmitted directly to the CSF system, thus raising resting ICP. From the equation, it is clear that changes in these elements can occur independently of each other.

If P_d rises, CSF absorption can remain constant, and a shift to a new ICP equilibrium can occur. This concept is supported by the work of Johnston,³⁰ who demonstrated normal CSF resistance in the presence of raised ICP induced by venous obstruction.⁴^,³⁰ In this case, there is no net change in the CSF volume and presumably no change in the compliance element.

Pulsation Models of Communicating Hydrocephalus: A New Concept

The pulsation of ICP has been the subject of study for many years. More recently, it has been considered to be an integral part of a new concept of hydrocephalus whereby the ICP pulse is more than a CSF reflection of the cardiac and respiratory pulsation. In the new concept, the flow of the arterial pulsations into the cranium is considered to be sequential, beginning from the large subarachnoid arteries at the skull base to the small arterioles in the parenchyma. Pulsations are dissipated into the subarachnoid CSF and into the choroidal arteries and ventricular CSF. These pathways are arranged in a series-parallel array of arteries and CSF spaces. The bulk flow of blood that remains after the pulsations have been filtered out continues through the capillary pathways and represents a windkessel mechanism.³¹ Most important, this model provides an alternative view to the “bulk flow theory” causing ventricular enlargement. Increased impedance to pulsations in the subarachnoid space increases pulsations in the blood flow to the choroidal arteries and the choroid plexus, thereby increasing the pulsations in the ventricular CSF. The ventricular pulsations exceed those in the subarachnoid space, and it is theorized that a transmantle pulse pressure gradient and subsequent ventricular expansion result. This theory is now being explored by mathematical models and experimental studies in the laboratory and in the clinical setting.³²^,³³ Future work will focus on demonstrating that this model accounts for the pathologic changes seen in communicating hydrocephalus.

Cerebral Blood Volume and Flow

The other dynamic component of the equation representing the Monro-Kellie doctrine is cerebral blood volume (CBV). CBV and cerebral blood flow (CBF) are essentially functions of the cerebral arteriovenous pressure difference and cerebrovascular resistance, which is largely determined by vessel caliber. Although, as described previously, there are rhythmic changes in blood volume as a result of the cardiorespiratory cycles, both CBV and CBF are maintained within narrow limits by the process of autoregulation. Vascular tone is influenced by both physical (force) and chemical (pH, PCO₂) signals, with the aim of maintaining CBF across a wide range of both arterial blood pressures (50 to 160 mm Hg) and levels of tissue metabolism (PaCO₂, 20 to 70). The mean normal adult CBF is 53 mL/100 g per minute.

Non–Steady-State Dynamics

The preceding processes maintain a constant ICP while there is no CSF accumulation or other change in intracranial volume. Unfortunately, many pathologic states, such as hematoma, tumor, hydrocephalus, and cerebral edema, are associated with changes in intracranial volume, which can, in turn, cause elevated ICP.

The most common clinical cause of raised ICP is traumatic brain injury, the pathology of which encompasses several possible V_OTHERS. Brain edema contributes extra volume to the intracranial contents in the form of water. Trauma may induce intracerebral collections of blood in extradural, subdural, subarachnoid, or intraparenchymal locations, which each contribute extra volume. Furthermore, trauma may induce changes in V_BLOOD as a result of disrupted autoregulation and hyperemia. The extent to which elevated CBV contributes to ICP after traumatic brain injury seems small, however, compared with edema.³⁴

Subarachnoid hemorrhage after rupture of an intracranial aneurysm differs from other intracranial hemorrhage. Bleeding with arterial pressure can potentially cause ICP to rise instantaneously, and as ICP approaches the mean arterial blood pressure, bleeding slows, but cerebral perfusion pressure is critically low.³⁵ The cause of this rise in ICP is a combination of intraparenchymal blood collection, increased CBV, and a strong vasomotor reaction to the ensuing injury.³⁶

Brain tumors provide a slowly increasing V_OTHER, which provides time for the organism to make compensatory changes. Therefore, ICP problems with tumors occur less commonly; however, a sudden change in intracranial volume (such as a hemorrhage into the body of a tumor) in a system that is already compensated and therefore dynamically stressed can have disastrous results. Also, prolonged periods of increased hydrostatic pressure (such as lying down) can create substantial increases in ICP in such patients. This phenomenon, coupled with the diurnal variation in CSF secretion, may underlie the early morning headaches and nausea experienced by these patients.

Other clinical conditions can result in an elevated ICP, including hydrocephalus, idiopathic intracranial hypertension, meningitis, and arteriovenous malformations. In several of these conditions, a direct addition of intracranial volume is not the primary cause. For example, in hydrocephalus, an impaired CSF drainage system causes CSF accumulation. The cause of elevated ICP in idiopathic intracranial hypertension is not known, although again, CSF production and drainage have been implicated as has elevated venous pressure.³⁷ Meningitis can influence ICP in several patterns, either by blocking CSF drainage pathways or by stimulating marked cerebral edema. Arteriovenous malformation, in contrast, represents a significant increase in V_BLOOD that can secondarily create V_OTHER if it is involved in a hemorrhagic event.

Brain edema is a specific pathologic process arising in response to a wide range of cerebral pathologic changes. It is defined as an increase in the brain tissue water content and therefore can be thought of as contributing to V_OTHER or V_BRAIN. At the turn of the 20th century, Reichardt ³⁸ reported differences between a dry swollen brain and a wet edematous brain. Klatzo³⁹ subsequently paved the way for all future discussions of edema by introducing the terms cytotoxic and vasogenic to indicate intracellular and extracellular water accumulation, respectively. The latter of these is traditionally associated with an open blood-brain barrier and fluid leakage. However, this division is a simplification for two reasons. First, for brain tissue water to rise, even under cytotoxic conditions, water has to enter the tissue from an external source, the most likely of which is blood vessels. Therefore, even cytotoxic edema has a “vasogenic” origin. It is the pathologic cause and the final site of edema accumulation that must distinguish these phenomena. Furthermore, studies in traumatic brain injury have suggested that the vasogenic component of injury may have been overemphasized⁴⁰^,⁴¹ and that the importance of a disrupted blood-brain barrier lies in the provision of a low-resistance pathway for movement of water to cells that are swelling cytotoxically.⁴² The predominance of traumatic cellular edema has been supported by studies in head-injured patients.⁴³ Cytotoxic and vasogenic edema may not, therefore, be separable entities, and a recently proposed classification of edema based on the terms intact barrier and open barrier may have merit.⁴⁴

Several possible alterations in intracranial volume are discussed in the preceding paragraphs. When such changes occur rapidly or exceed the ability for compensation by reciprocal volume reductions, ICP may begin to rise. Under these conditions, more descriptors of ICP are required than in the steady state.

Intracranial Pressure in Idiopathic “Normal-Pressure” Hydrocephalus

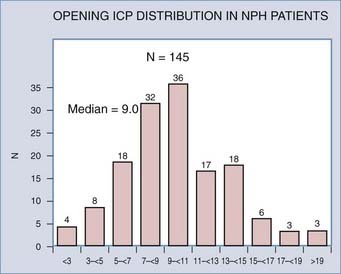
The term normal-pressure hydrocephalus was introduced in the thesis of Solomon Hakim in 1964 and the description later published in the landmark article by Adams and coworkers.⁴⁵ Together, they are credited with describing a specific syndrome associated with patients in whom ventricular enlargement occurred in the absence of elevated ICP and who presented with gait disturbance, dementia, and incontinence. Current guidelines for diagnosis and management of idiopathic normal-pressure hydrocephalus are now available.⁴⁶ According to these guidelines, the lumbar pressures for idiopathic normal-pressure hydrocephalus range from 60 to 240 mm H₂O. This range was arrived by consensus in a meeting of experts on the basis of their experience and what was reported in the available literature. Later, in a study of 151 patients diagnosed with idiopathic normal-pressure hydrocephalus, it was confirmed that the lumbar pressure measured in these patients varied over a wide range⁴⁷ (Fig. 10-5). Thus, the term normal-pressure hydrocephalus has been questioned as pressures varied considerably from the so-called normal pressure defined by Ekstedt.⁴⁸ Interestingly, the median pressure found by Marmarou⁴⁷ in patients with idiopathic normal-pressure hydrocephalus correlates well (9.0 mm Hg) with the value of the normal resting pressure by Ekstedt (10.0 mm Hg).

FIGURE 10-5 Distribution of lumbar pressure in patients with idiopathic “normal”-pressure hydrocephalus (NPH). Pressure varied over a wide range, calling normal-pressure hydrocephalus into question. The median pressure of 9.0 mm Hg was slightly lower than the average 10.0-mm Hg lumbar pressure found in patients without normal-pressure hydrocephalus.

Pressure-Volume Relationships

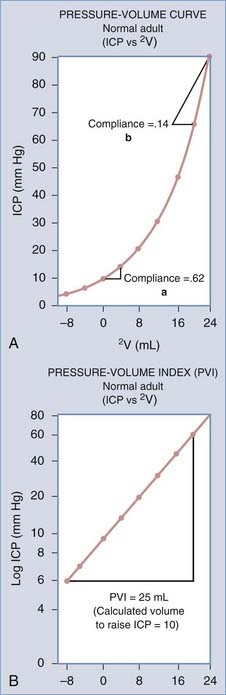
The relationship between intracranial volume and ICP is not linear. Volume-pressure relationships can be depicted by graphing the response of ICP to volume added into the neural axis (see Fig. 10-3). In the normal adult, Ryder and coworkers⁴⁹ showed that this relationship describes a hyperbolic curve. Along the flat portion of the curve, increases in volume affect ICP minimally because compensatory mechanisms can effectively maintain ICP in a normal range. This part of the curve is called the period of spatial compensation. As volume is added, the pressure changes per unit volume become increasingly large, and compliance lessens; this portion is called the period of spatial decompensation. Above 50 mm Hg, and as ICP approaches mean arterial pressure, the curve tends to flatten again; thus, the complete curve is not hyperbolic but rather sigmoid.

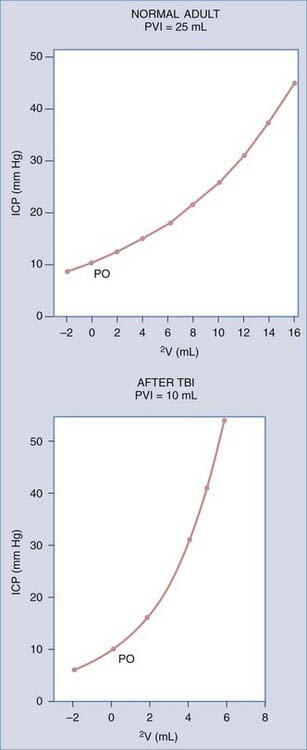
The reciprocal of the slope of this curve (ΔV/ΔP) represents the compliance of the system, which is maximal in the period of spatial compensation. The slope of the pressure-volume curve rises rapidly during spatial decompensation, and therefore compliance falls. Another method of expressing information about compliance is to plot ICP logarithmically against volume, which gives a straight line.⁵⁰ Its slope is the pressure-volume index (PVI), or the calculated volume in milliliters needed to raise ICP by a factor of 10 (Fig. 10-6A). In normal adults, PVI is 25 to 30 mL.⁵¹ When compliance is reduced by a pathologic process, PVI diminishes, and therefore small volume changes result in much greater pressure changes. Values less than 13 mL are considered clearly abnormal.⁵² PVI is age dependent, although normal infants have PVIs below 10 mL, and the adult PVI of 25 mL is reached at around 14 years of age.

FIGURE 10-6 Pressure-volume curves from a normal adult (A) and an adult with cerebral edema (B). In the pathologic state, the curve is steeper and the pressure-volume index (PVI) is greatly reduced as a result of V_OTHER. TBI, traumatic brain injury.

PVI can be measured clinically by infusion or withdrawal of small boluses of fluid in the CSF space, with concomitant measures of the pressure response. CSF outflow resistance can also be calculated from the rate decay of the pressure peak after a bolus infusion. A complete description of resistance measurement techniques is found in the report of Eklund and colleagues.⁵³ Methods of continuous PVI measurement have been devised with use of multiple time-averaged small-volume pulses.⁵⁴ Although these methods generate less pressure perturbation, they tend to underestimate compliance as measured with the conventional technique.

The compensatory abilities of brain, blood, and CSF at any given point on the pressure-volume curve are dependent on their respective volumes, their ease of egress from the skull, and the level of ICP at which the interactions are occurring, coupled with the rigidity of the skull. Although the brain occupies 80% of the intracranial space, this volume is effectively available for compensation only when increases in V_OTHER occur slowly. With more rapid changes, brain shifts and herniations are more likely to occur. Although blood and CSF occupy less of the intracranial space, their total volume can be reduced more rapidly.

These concepts become more complex, as do most models, when they are applied to clinical practice. Although short-term changes cause movement along a single pressure-volume curve, changing intracranial dynamics can create a new pressure-volume curve with time (Fig. 10-6B). Increases in CBV and cerebral edema are also likely to play a role in producing these dynamic pressure-volume interactions.⁵⁵ Thus, knowledge of the absolute pressure coupled with some expression of the slope of the ICP volume curve at any given time point provides a more complete description of the stability or instability of ICP.

Effects of Elevated Intracranial Pressure

Under non–steady-state conditions, failure of compensation mechanisms ultimately results in an elevated ICP, the pathologic consequences of which can be severe. First, continued perfusion of the brain relies on a cerebral arteriovenous pressure gradient. ICP is transmitted to the compliant cerebral veins, and therefore the cerebral perfusion pressure (CPP) is defined as the arterial inflow pressure minus ICP. If ICP increases, CPP falls; and if the lower limit of autoregulation is exhausted, CBF will begin to fall.

The autoregulatory reserve may be defined as the difference between the CPP at a given moment and the lower limit of autoregulation. Considering that the lower limit of autoregulation is within the range of 50 to 70 mm Hg, the autoregulatory reserve for a CPP of 90 would be 20 to 40 mm Hg. Thus, a CPP below the autoregulatory threshold exhausts the autoregulatory reserve.⁵⁶^–⁶⁰ When CPP decreases, the wall tension of reactive brain vessels decreases, thereby increasing the transmission of the arterial pulse wave to the intracranial contents.⁶¹ Similarly, when a reduction of CPP is caused by increased ICP, brain compliance decreases,²⁹^,⁶² which also serves to increase pulsatile transmission. Taken in concert, a decrease in CPP results in an increase of both blood pressure and ICP pulsatility. This relationship is highly predictive for fatal outcome⁶³ because as the ICP pulse amplitude levels off or starts to decrease, it implies that the cerebral vessels are no longer pressure reactive.

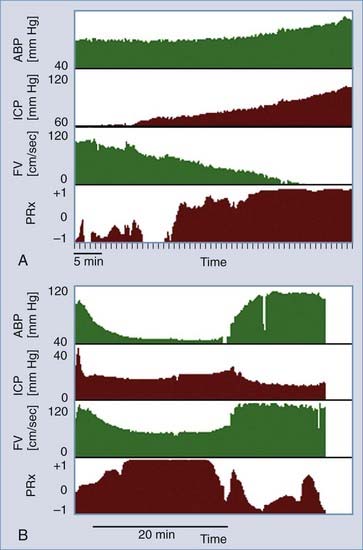
By use of these principles, it is clear that the correlation between spontaneous waves of blood pressure and ICP is dependent on the autoregulatory reserve. The correlation coefficient between changes in blood pressure and ICP is defined by Czosnyka ⁶¹ as the pressure reactivity index. An example of the use of the pressure reactivity index is illustrated in Figure 10-7. Examples of time-related changes of the pressure reactivity index are shown, in which the index increases from relatively low values (no association) to values approaching 1.0 (strong positive association). These values were calculated from a period of 1-hour terminal increase in ICP from 60 to 90 mm Hg in a head-injured patient who died (Fig. 10-7A). Figure 10-7B illustrates a transient change in pressure reactivity index during the period of an ICP plateau wave with rapid recovery when ICP returned to baseline. In summary, the pressure reactivity index provides a practical means of assessing the degree of autoregulation and is useful in elucidating the contribution of the cerebrovasculature to mechanisms causing ICP rise.

FIGURE 10-7 Examples of the use of the pressure reactivity index to assess autoregulatory reserve and to predict patient outcome. A, Mean arterial blood pressure (ABP), ICP, middle cerebral artery flow velocity (FV), and pressure reactivity index (PRx) in a patient with a fatal increase in ICP. The pressure reactivity index rises with ICP increase and remains high. B, Comparable data from a patient experiencing a plateau wave in ICP with subsequent recovery. It is notable how the pressure reactivity index falls with recovery and reduction in ICP.

(Courtesy of M. Czosnyka.)

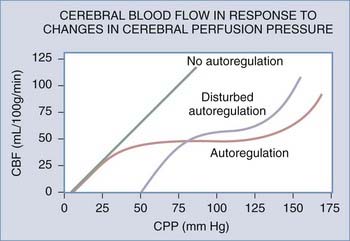
Furthermore, in many pathologic cases, autoregulation is disturbed so that the response curve is shifted to the right and is more linear (Fig. 10-8). This reduces the autoregulatory reserve for any given CPP. If the autoregulatory reserve is exhausted, CBF begins to fall, which ultimately causes tissue ischemia. Ischemia creates cytotoxic edema, which, in turn, contributes to the ICP elevation and low CPP. Clearly, a vicious circle of edema and ICP elevation can ensue if treatment attempts do not prevent this. A marked rise in ICP that will not respond to available treatments is called refractory ICP.

FIGURE 10-8 Cerebral autoregulatory curves. Normal autoregulation maintains cerebral blood flow across a range of mean arterial blood pressure. Disturbed autoregulation causes a shift of the curve to the right and introduces a more linear component (i.e., cerebral blood flow is less stable with rising mean arterial blood pressure). If autoregulation is completely abolished, cerebral blood flow rises linearly with mean arterial blood pressure.

A second problem with increased ICP arises from the generation of pressure gradients.⁶⁴^,⁶⁵ CSF will conduct the pressure generated by an increased volume in one region of the brain to others. There are specific anatomic sites where such pressure gradients may cause movement of brain tissue into an abnormal anatomic location—so-called herniation. Several types of herniation have been described, including downward transtentorial (central and uncal), subfalcine, upward transtentorial, and transforaminal.⁶⁶ Each syndrome has a characteristic clinical correlate.

Anatomically, in central transtentorial herniation, downward shift of the hemisphere and basal ganglia compresses and displaces the diencephalon through the tentorial incisura. Subsequent displacement of the brainstem will stretch the paramedian branches of the basilar artery, which, in turn, will contribute to the marked diencephalon and brainstem dysfunction. In uncal herniation, the uncus and hippocampal gyrus shift medially into the tentorial notch, which distorts the brainstem and creates significant dysfunction. Subfalcine herniation of the cingulate gyrus is caused by expansion of one hemisphere causing a movement of the cingulate gyrus under the falx cerebri. Cingulate herniation may compress the internal cerebral veins or the ipsilateral anterior cerebral artery. Lesions in the posterior fossa differ slightly in that they may cause upward transtentorial herniation as well as downward transforaminal herniation.

Symptoms and Signs of Elevated Intracranial Pressure

The degree of effect of a given ICP depends greatly on the nature and anatomic location of the underlying pathologic condition. The cardinal symptoms and signs of raised ICP include headache, vomiting, and papilledema. Vomiting without any associated nausea is especially suggestive of intracranial disease. Varying degrees of cranial nerve palsies may arise as a result of pressure on brainstem nuclei (particularly abducens palsies). Papilledema is a reliable and objective measure of raised ICP, with good specificity. However, its sensitivity is observer dependent, and symptoms suggestive of intracranial disease in the absence of papilledema should not be ignored.

Vital signs may also change under conditions of elevated ICP. The Cushing response, defined as arterial hypertension and bradycardia, arises as a result of either generalized central nervous system ischemia or local ischemia due to pressure on the brainstem.⁶⁷ Bradycardia is possibly mediated by the vagus nerve and can occur independently of hypertension. Abnormal respiration may also arise,⁶⁸ depending in part on the anatomic location of any lesion. Cheyne-Stokes respiration arises from damage to the diencephalic region, and sustained hyperventilation occurs in patients with dysfunction of the midbrain and upper pons.⁶⁹ Midpontine lesions cause slow respiration; pontomedullary lesions result in ataxic respirations; upper medullary lesions cause rapid, shallow breathing; and with greater medullary involvement, ataxic breathing predominates.

Herniation Syndromes

Tissue herniation is the most serious complication of raised ICP. Central herniation and uncal herniation cause the central syndrome and the uncal syndrome, respectively.⁷⁰ The central syndrome displays progressive dysfunction of structures in a rostral to caudal direction. Diencephalic structures are involved early, which may cause a change in behavior or even loss of consciousness. Diencephalic involvement also alters respiration, causing interruptions of sighing, yawning, or pausing; Cheyne-Stokes respiration may appear. Pupils become small, with a poor reactivity to light. A unilateral lesion can cause contralateral hemiparesis, with ipsilateral paratonia and decorticate responses. With progressive midbrain involvement, respiration becomes tachypneic, and the pupils fall into a midline fixed position. Internuclear ophthalmoplegia may arise, and motor examination will show bilateral decerebrate posturing. As the pons becomes involved, respiration remains rapid and shallow. Motor examination reveals flaccid extremities with bilateral extensor plantar responses. With progressive medullary involvement, respiration slows and becomes irregular with prolonged sighs or gasps. As hypoxia ensues, the pupils dilate, and brain death follows shortly thereafter.

In sharp contrast, the uncal syndrome often begins with a unilaterally dilated and poorly reactive pupil, which can arise even in the presence of a normal conscious level. The pupil will then fully dilate with external oculomotor ophthalmoplegia. If midbrain compression ensues, consciousness may be impaired, followed by contralateral decerebrate posturing. On occasion, posturing or hemiparesis may occur ipsilateral to the lesion as a result of pressure on the contralateral cerebral peduncle on the edge of the tentorium cerebelli.⁷¹ If the uncal syndrome is allowed to progress, extensor plantar response appears bilaterally, along with dilation of the contralateral pupil. Finally, patients will develop hyperpnea, midposition pupils, impaired oculovestibular response, and bilateral decerebrate rigidity. From this point, progression is as for the central syndrome.

Other compression and herniation syndromes may arise, including unilateral hemiparesis and hemianesthesia with compression of cortical structures or compression of the anterior cerebral artery with subfalcine herniation of the cingulate gyrus causing contralateral leg weakness. Although no less distressing for the patient, these symptoms represent a much lesser emergency than either the central or uncal syndrome does.

Intracranial Pressure Monitoring

Several published clinical trials show that monitoring of ICP, under situations in which ICP may be high, either facilitates outcome or promotes aggressive management.⁷²^–⁷⁴ There is strong clinical evidence that careful control of ICP is important,⁷⁵ and maintaining CPP under many different pathologic circumstances is of benefit for outcome.⁶⁰ An understanding of the indications for initiation of monitoring and the methods by which this can be done is important.

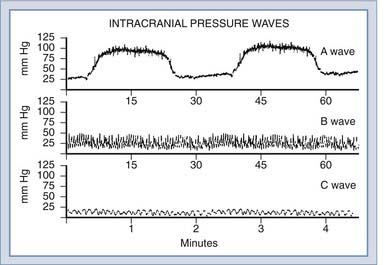
Initial work on direct monitoring of ICP by ventricular puncture was performed by Guillaume and Janny ⁴ and by Lundberg.⁵ In Lundberg’s classic report, he described three basic patterns of ICP waveform: A waves (plateau waves), B waves, and C waves (Fig. 10-9).

FIGURE 10-9 Lundberg’s classification of ICP waves. A waves or plateau waves are prolonged stable increases in ICP that spontaneously recover to a new higher baseline. B waves are short, modest elevations in ICP, and C waves are rapid sinusoidal fluctuations. These waves do not represent part of steady-state ICP dynamics. Their pathologic significance remains to be defined.

A waves, or plateau waves, are characterized by increases of ICP that are sustained for several minutes and then return spontaneously to a new baseline, which is usually slightly higher than the preceding one. Lundberg postulated that A waves are a result of an increase in cerebrovascular blood volume due to vasodilation. Rosner ⁷⁶^,⁷⁷ has postulated that these plateau waves are a normal compensatory response to decreases in CPP, and therefore effective management involves the use of vasopressors. Other more recent studies have suggested that vasopressors may enhance lesion size and edema formation.⁷⁸^,⁷⁹ The plateau wave itself is proposed to consist of four phases, called the drift phase, the plateau phase, the ischemic response phase, and the resolution phase.⁷⁶ The drift phase is characterized by a decline in CPP, which triggers vasodilation. This vasodilation increases ICP to the plateau level, for the plateau phase. This sudden reduction in CPP causes a degree of cerebral ischemia that triggers brainstem vasomotor centers to mount a Cushing response (ischemic response phase), which, in turn, restores CPP in the resolution phase.

Lundberg B waves are short elevations of a modest nature (10 to 20 mm Hg) that occur at a frequency of 0.5 to 2 Hz and are thought to relate to vasodilation secondary to respiratory fluctuations in PaCO₂. However, they are seen in ventilated patients, who in theory should have a constant PaCO₂; therefore, they are of only questionable clinical significance. Transcranial Doppler studies in humans have shown that B waves occur secondary to intracranial vasomotor waves, causing variations in CBF.⁸⁰ The physiologic basis for this cyclic change in vasomotor tone is not clear. B waves are believed to reflect increased ICP in a qualitative manner, as is the case with C waves, which are more rapid sinusoidal fluctuations occurring approximately every 10 seconds, corresponding to Traube-Hering-Mayer fluctuations in arterial pressure.

The decision to monitor a patient’s ICP is based on the premise that intracranial hypertension reduces CPP both focally and globally and can cause ischemia. The final result of elevated ICP is brain herniation and death, the imminent onset of which can be detected clinically. By monitoring ICP, such problems can be detected and treated much earlier. Furthermore, indiscriminate application of therapy for ICP reduction can be avoided, and if a ventriculostomy is used, there is the added advantage of being able to treat with CSF drainage. These advantages must be weighed against the possible complications of invasive monitoring.

Intracranial hypertension is found in 40% to 60% of severe head injuries and is a major factor in the deaths of 50% of all fatalities.⁸¹ Data from the Traumatic Coma Data Bank have shown that the proportion of hourly ICP recordings above 20 mm Hg is highly significant in predicting outcome.⁸² The role of ICP monitoring in adult brain trauma is clear; however, the role in nontraumatic settings depends on the nature and severity of the disease process. Management of intracranial hypertension may be beneficial in Reye’s syndrome⁸³ and other causes of fulminant hepatic failure,⁸⁴ although the complication rate is higher in these conditions.⁸⁵ In the case of intracranial tumors, ventricular catheters can provide temporary therapeutic ventricular decompression before and after resection of the tumor along with a rational means of testing the reestablishment of normal CSF pathways in the early postoperative period. The role of monitoring in metabolic encephalopathies, cerebral infarction, or diffuse cerebritis is less clear.

After trauma in adults, guidelines for ICP monitoring include a Glasgow Coma Scale score of 3 to 8 and an abnormal computed tomographic scan. In the presence of a normal computed tomographic scan, two or more of the following should prompt monitoring anyway: age older than 40 years, unilateral or bilateral motor posturing, or systolic blood pressure below 90 mm Hg.⁸⁶ Patients with a Glasgow Coma Scale score greater than 8 may benefit from ICP monitoring if computed tomographic scans demonstrate significant mass lesions or treatment is required for associated injuries.

Methods of Intracranial Pressure Measurement

Ventriculostomy coupled with a pressure transducer remains the “gold standard” for monitoring of ICP because of accuracy and ease of calibration. Access to CSF for dynamic testing and drainage to control ICP are additional benefits. Disadvantages are that catheter placement can be difficult when the ventricles are small or shifted from the midline, and the risk of infection rises in ventriculostomies after 5 days, although this risk can be lessened by tunneling the catheter under the skin. Current estimates have associated intraventricular monitoring with less than 2% hemorrhagic complications ⁸⁷ and less than 10% infective complications.⁸⁸^–⁹¹ Changing the catheter at regular intervals does not appear to reduce the infection rate.⁸⁹ Parenchymal monitors, in contrast, have less than 1% infective complications.⁷³

Alternative methods of monitoring ICP include the subarachnoid bolt,⁹² subdural catheter, epidural transducer,⁹³ and fiberoptic microtransducer.⁹⁴ The bolt and epidural transducer, although less invasive, are prone to inaccuracy because of their physical characteristics.⁹⁵^–⁹⁷ Fiberoptic catheter-transducers cannot be recalibrated externally; however, their accuracy in practice has proved excellent,⁹⁸ they are easy to place, and the complication rate is low because of their small size and lack of fluid coupling. All intraparenchymal monitors may be prone to regional inaccuracy, depending on their placement in relation to the site of any lesion,⁹⁹ given that elevated ICP may be regional. The choice of which measurement method to use should be based on the presentation of the patient and the planned treatment. There is no defined reference level for the use of transducers in the intensive care unit; however, the device is typically zeroed at the level of the foramen of Monro, using the external acoustic meatus as an anatomic landmark.

There is no uniform agreement about the critical level of ICP beyond which treatment is mandatory. Saul and Ducker ⁷⁴ demonstrated benefits by treating ICP above 15 mm Hg compared with a group of patients treated for ICP above 25 mm Hg. Marmarou and colleagues⁸² examined data from 428 patients and calculated the ICP threshold most predictive of 6-month outcome by logistic regression. The threshold that correlated best was 20 mm Hg, and this is the current level at which most centers begin treatment. Current opinion now regards CPP as the critical parameter that should be monitored in concert with ICP.

Management of Intracranial Pressure

Logically, the best therapy for intracranial hypertension is resolution of the cause of the increased pressure. However, when this is not possible, manipulation of the system by other means can lower ICP. No one therapy or series of therapies is appropriate for all cases of elevated ICP, and treatment strategy should be constantly reevaluated in the face of a dynamically changing pathologic condition.

The equation

provides a conceptual framework by which to consider the components of intracranial volume responsible for non–steady-state ICP situations and allows treatment to be directed in a focused manner (Table 10-2).

TABLE 10-2 Therapeutic Modalities for the Reduction of Raised Intracranial Pressure by the Intracranial Compartment of Action*

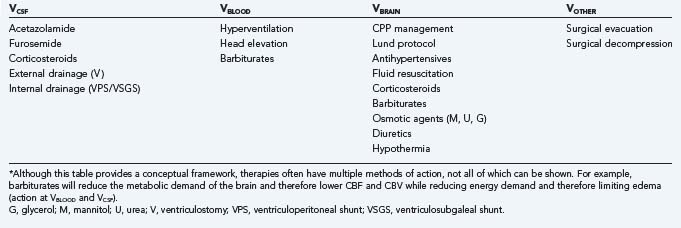
V_CSF

When hydrocephalus causes intracranial hypertension and its cause cannot be eradicated, temporary or permanent CSF diversion may be necessary. When obstruction of the CSF pathways by a tumor or other mass causes the hydrocephalus, it is usually possible, and indeed preferable, to treat the obstruction in an effort to open the CSF pathways.

If CSF diversion is required, options exist that permit temporary external drainage (ventriculostomy), temporary internal drainage (ventriculosubgaleal shunt), or permanent internal drainage (ventriculoperitoneal shunt, ventriculoatrial shunt, or third ventriculostomy). External ventriculostomy has value as a method for both measuring and controlling ICP, and the technique can be especially helpful in deciding whether a permanent internal drainage procedure will be of benefit. One approach to this includes CSF drainage against minimal resistance early on with eventual elevation of the drip chamber to a level commensurate with physiologic ICP. Pressure is monitored continuously, and CSF is allowed to escape when threshold ICP levels are exceeded. Maintenance of normal ICP and minimal volumes of CSF drainage usually indicate that a permanent shunt will not be needed.

A ventriculosubgaleal shunt provides a closed, temporary method for continuous CSF diversion. It involves placement of a ventricular catheter attached to a reservoir (with or without a valve mechanism) with a short side arm opening into the subgaleal space, which is dissected at the time of surgery. The ventriculosubgaleal shunt provides continuous ventricular decompression for several weeks to months without the need for percutaneous aspiration of the reservoir.

Permanent internal CSF diversion by ventriculoperitoneal shunt is attended by a full array of indications, technical considerations, and risks. Third ventriculostomy by both stereotactic and endoscopic techniques has been repopularized recently.¹⁰⁰ This technique offers an alternative in certain situations without the potential risks inherent in standard ventriculoperitoneal shunting.

When mechanical methods of CSF diversion are not possible or desirable, adjunctive therapy with medications such as acetazolamide, furosemide, and corticosteroids can transiently decrease CSF production. Acetazolamide, which inhibits carbonic anhydrase–mediated CSF production, is used most frequently. Reductions of CSF production by 16% to 66% have been achieved.²⁴ Synergy has been reported when acetazolamide is combined with furosemide.¹⁰¹ Acetazolamide also has a cerebral vasodilator effect, which may transiently worsen intracranial hypertension, and so its use is contraindicated in patients with closed head injury.¹⁰²

V_BLOOD

The role of V_BLOOD in the pathologic process of ICP is complicated. Excess amounts of intracranial blood (hyperemia) can clearly contribute to reduced compliance and elevations in ICP. Other causes of intracranial hypertension, however, can occur at the expense of V_BLOOD, which can, in turn, cause ischemia and brain edema. There is no absolute blood volume or CBF that is normal; these parameters are rather defined by the metabolic activity of the brain itself. For example, the mean absolute CBF of 53 mL/100 g per minute in normal subjects may be considered hyperemic in the anesthetized brain or ischemic in a portion of epileptic cortex.

In general terms, most of the CBV resides within the pial vessels and veins; however, the precapillary arterioles control CBF. Relationships among the various factors that reflect the status of CBF are complex and vary according to the timing of measurements, underlying pathologic process, presence or absence of hypoxia or ischemia, systemic blood pressure, ICP, cerebral metabolic rate, and arterial blood gases.

Extremes of CBF, both low and high, have been seen in patients with poor outcome after head injury.¹⁰³^–¹⁰⁶ Bouma and coworkers¹⁰⁷ showed that measurements of CBF performed within 6 hours of severe head trauma (Glasgow Coma Scale score ≤ 8) are reduced (22.5 ± 5.2 mL/l00 g per minute) and correlate well with Glasgow Coma Scale score and eventual outcome. These findings are more common in patients with bilateral diffuse injuries than in patients with mass lesions, who tend to have higher global CBF in the hemisphere of the mass lesion. Between 45% and 65% of head injury victims will exhibit hyperemia in the 12 to 24 hours after injury.¹⁰⁸^–¹¹⁰ The increase in CBF is presumably accompanied by increased CBV, which may contribute to intracranial hypertension. Increased CBF and CBV are seen in the acute encephalopathy of Reye’s syndrome as well. Clearly, ischemia and hyperemia are not constant phenomena but rather dynamically changing under the influence of several factors. In general, CBF tends to stabilize by 36 to 48 hours after injury.¹⁰³^,¹⁰⁵^,¹⁰⁸^,¹¹¹

This complex interplay of factors affecting V_BLOOD makes rational treatment difficult. The association among CBF, cerebral metabolic rate of oxygen, arteriovenous oxygen difference, and clinical parameters (ICP, Glasgow Coma Scale score, and outcome) is more easily documented by multivariate analysis than it is explained in terms of physiologic cause and effect. In general terms, as ICP increases, arteriovenous oxygen difference usually rises because of reductions in venous PO₂ caused by greater oxygen extraction. CBV increases with vasodilation in response to lowered CPP or a rise in PaCO₂. Hyperventilation therefore decreases total intracranial blood volume as hypocapnic vasoconstriction moves blood from the pial circulation to the veins and sinuses. Reductions of the cerebral metabolic rate of oxygen are seen after trauma, but these reductions may not reflect the energy demands of the injured brain. Some have attributed these reductions to mitochondrial incapacities or enzymatic deficits that render the neuron incapable of using oxygen.¹⁰⁷^,¹¹²

Understanding the role of CBF and CBV in situations of elevated ICP is hindered by difficulties in measuring CBF. Global CBF obtained by the Kety-Schmidt method includes the white matter but lacks anatomic information. Regional CBF determined by the xenon Xe 133 inhalation method largely ignores the contribution of the white matter, and focal areas of ischemia can be missed if they are surrounded by zones of relatively high flow.¹¹³ Magnetic resonance imaging–based measures of cerebral perfusion may yield accurate anatomic information but suffer from a degree of time averaging and lack of widespread availability. A further problem relates to differential sensitivities of structures to reduced flow. For example, the hippocampus may be acutely sensitive to even mild ischemia, whereas diminished CBF in the brainstem does not correlate with clinical estimates of brainstem function.⁵⁸

Although every effort should be made to prevent cerebral ischemia in the face of intracranial hypertension, treatment of hyperemia or increased CBV may be dangerous until more is understood about these pathophysiologic processes. However, some success has been reported with therapy that reduces CBV.¹¹⁴^,¹¹⁵ The most efficacious methods are hyperventilation and elevation of the head. Hyperventilation causes constriction of pial vessels when blood vessels retain CO₂ responsivity. Pressure autoregulation is frequently lost after head injury; however, CO₂ responsivity can be preserved in the absence of pressure autoregulation, and its prolonged loss is considered a grave sign.¹¹⁶ In adults, a 1-torr change in PaCO₂ is associated with a 3% change in CBF. Thus, vasoconstriction reduces CBV and therefore lowers ICP.

In addition to its effects on cerebrovascular tone, hyperventilation induces tissue alkalosis, which can buffer the intracellular and CSF acidosis seen after severe head injury.¹¹⁷ However, the benefits of hyperventilation may be short-lived, and higher levels can cause vasoconstriction sufficient to produce cerebral ischemia mediated through a mechanism that involves the loss of the CSF bicarbonate buffer.¹¹⁸^,¹¹⁹ In a randomized, prospective trial of head-injured patients, Muizelaar¹¹⁵ showed that hyperventilation to a PaCO₂ of 25 ± 2 in patients with a Glasgow motor scale of 4 or 5 resulted in Glasgow outcome scores at 6 months that were significantly worse than those in controls. Consequently, only moderate hyperventilation is necessary (32 to 35 torr), which is thought to be sufficient to avoid ischemic effects.

Some have advanced the concept of “inverse steal” to explain the risk of hyperventilation-induced ischemia. In patients with intact or supersensitive CO₂ responsivity, hypocapnia can lead to shunting of blood from high-resistance, maximally constricted vessels to low-resistance, dilated vessels that lack CO₂ responsivity.¹²⁰ These areas may be so severely damaged as to have low oxygen demand; thus, hyperventilation may tend to redistribute blood from viable tissue into nonviable tissue. When possible, these investigators recommend that arteriovenous oxygen difference and CBF be monitored along with ICP¹²¹ and that hyperventilation be performed cautiously in patients with evidence of cerebral ischemia. When hyperventilation is discontinued, it should be tapered during 24 to 48 hours. Abrupt discontinuation can cause vasodilation as the extracellular pH falls, resulting in ICP elevations.¹²²^,¹²³

Elevation of the head to 30 degrees decreases ICP by facilitating adequate venous drainage and possibly CSF drainage also. This degree of elevation does not alter CPP.¹²⁴ Feldman and associates¹²⁵ demonstrated the beneficial effects of head elevation on ICP clinically. In this study, CPP and CBF seemed unaffected by head position until the head was elevated to 60 degrees. Rotation of the head or flexion of the neck can also impair jugular venous flow and raise ICP.¹²⁶ Therefore, an effort should be made to maintain the head in a neutral position.

An intuitive mechanism by which CBV should be lowered is to lower mean arterial blood pressure and therefore CPP. This principle, coupled with a reduction of hydrostatic forces in damaged capillary beds, underlies the Lund protocol for raised ICP, which advocates reduced CPP, precapillary vasoconstriction with dihydroergotamine, and maintenance of plasma osmolarity with albumin infusion.¹²⁷ Initial clinical trials of this approach yielded outcomes no worse than those of more conventional techniques.¹²⁸

This protocol, however, is in stark contrast to the principles of CPP management, which promulgate that low CPP stimulates arteriolar vasodilation, causing increases in both CBV and ICP. By elevation of CPP with vasopressors, the blood vessel will be stimulated by the mechanisms of pressure autoregulation to vasoconstrict, consequently reducing the CBV and ICP.⁶⁰ This argument appears to hold only when pressure autoregulation is intact. Rosner also proposes that in many cases in which loss of pressure autoregulation is seen, the mechanism is not lost; rather, the curve is shifted to the right (see Fig. 10-8). By giving pressors, the vessel is manipulated back into a state in which it can autoregulate. If this is true, the real challenge is presented in distinguishing those brains that will benefit from CPP management. The possible risks of pressor therapy in areas in which the blood-brain barrier may be incompetent are unresolved. Several studies have questioned the safety of their use¹²⁹ and demonstrated ways in which pathologic changes can be worsened.⁷⁸^,⁷⁹

V_BRAIN

The third component contributing to ICP is the volume occupied by brain tissue. Increases in V_BRAIN occur most frequently as a result of cerebral edema, which is a nonspecific reaction to a variety of processes. Conceptually, treatment of increased ICP due to brain edema is directed toward removal of the cause of edema, control of its propagation, and enhancement of its clearance. Efforts to decrease the formation of vasogenic edema include prevention of cerebrovascular hypertension and appropriate choice of fluid resuscitation.

Control of systemic and cerebrovascular hypertension is especially important when intracranial hypertension exists or when cerebral autoregulation is impaired. The choice of antihypertensive drugs in patients with increased ICP is important. Hirose and coworkers and others showed that nifedipine, chlorpromazine, and reserpine decreased mean arterial pressure and increased ICP, thereby reducing CPP.¹³⁰^–¹³² These findings were more pronounced when ICP exceeded 40 mm Hg. In the same studies, thiopental decreased mean arterial pressure and ICP, leaving CPP unchanged, but caused respiratory depression, necessitating intubation and mechanical ventilation. Sodium nitroprusside is commonly used now for rapid control of blood pressure in adult critical care; however, despite its highly efficacious action, prolonged use is not considered safe because of a risk of cyanide ion toxicity.

In a laboratory study using inflated balloons to produce intracranial hypertension, sodium nitroprusside, nitroglycerin, and trimetaphan were used to reduce mean arterial pressure by 20%. All three drugs reduced regional CBF and CO₂ responsivity, leading the authors to recommend caution in their use for blood pressure control in patients with increased ICP. Propranolol has been shown to be superior to hydralazine for control of hypertension in head-injured patients because propranolol decreases both cardiac demands and serum levels of epinephrine and norepinephrine.¹³³

The choice of fluid resuscitation in the head-injured patient is critical. Approximately 10% to 15% of head-injured patients are hypotensive because of either the injury itself or associated injuries.¹³⁴ Aggressive correction of shock improves survival and clinical outcome; however, the osmolality of the blood has important implications for ICP. Isotonic fluids (e.g., 5% dextrose, 0.45% normal saline, 0.9% normal saline, and lactated Ringer’s solution) are in regular use, but hypotonic solutions have the potential to worsen cerebral edema. Hypertonic solutions have been advocated as a possible therapy for elevated ICP. Certainly, bolus doses of hypertonic saline appear to be beneficial¹³⁵; however, fluid replacement therapy with hypertonic saline has been shown to be both beneficial and detrimental for ICP in different studies.¹³⁶^,¹³⁷

Controversy exists as to whether colloids (molecular weight >8000 D) are more beneficial than crystalloids for fluid resuscitation. Some authors have found no difference, whereas Tranmer ¹³⁸ showed a definite advantage with use of the colloid hetastarch. In a laboratory model of vasogenic edema, treatment with colloid for 2 hours after injury produced no change in ICP, whereas infusions of normal saline and 5% dextrose in water led to elevations in ICP of 91% and 141%, respectively.

In the case of cytotoxic injury, efforts to decrease formation of edema center around correction of the cause of disordered cell function. With toxins, this involves treatment directed toward the causative agent. When anoxia or ischemia is the cause, their reversal may bring improvement if the duration of anoxia and ischemia has not been prolonged.

A second goal of treating ICP is to improve neuronal and axonal function and survival. A variety of agents have been tried,¹³⁹^–¹⁴⁸ some of which were able to influence cerebral edema formation (for review, see Smith and colleagues¹⁴⁹). Despite reasonable experimental success, no compound has yet been found to be of clinical benefit in limiting edema formation.

Steroids and barbiturates have been widely used for treatment of both vasogenic and cytotoxic edema; however, neither is wholly effective, and both have attendant problems. Steroids are of unquestionable value in the treatment of edema with brain tumors, but no definite benefits have been shown when they are used in patients with head injury.¹⁵⁰^–¹⁵⁵ A study has also indicated that the newer configurations of steroids, the 21-amino steroids or lazaroids, are also without beneficial effect in traumatic brain injury.¹⁵⁶ The mode of action of steroids in cerebral tumors is not clear, but dramatic effects on both edema¹⁵⁷ and function¹⁵⁸^,¹⁵⁹ can be seen. Corticosteroids have been shown to have widespread effects on membrane lipid hydrolysis and peroxidation, processes that are thought to be important for development of injury.¹⁶⁰^–¹⁶³

Use of steroids in subarachnoid hemorrhage has no proven benefit, but angiographically demonstrable vasospasm can be decreased by their use.¹⁶⁴ In cases of cerebral ischemia, steroids worsen outcome either by means of a direct glucocorticoid toxicity or as a consequence of elevated serum glucose levels, which exacerbate ischemic lactic acidosis.¹⁶⁵^,¹⁶⁶

Barbiturates are useful in a wide range of situations by decreasing the cerebral metabolic rate of oxygen, thus permitting tolerance of a degree of ischemia or anoxia not otherwise acceptable on the cellular level. This, in turn, lowers demand for CBF, which therefore tends to lower CBV and consequently ICP. Barbiturates seem to have maximal effect in situations in which CBF is greater than metabolism. In addition, Messeter and associates ¹⁶⁷ have shown that preservation of cerebral CO₂ responsivity can predict the response of ICP to iatrogenic barbiturate coma. When CO₂ responsivity was normal, barbiturates reduced CBF and normalized ICP in 75% of patients. When this response was reduced or absent, CBF was unchanged or increased, and ICP was reduced in only 20% of patients. Pentobarbital has proved more effective at control of ICP than phenobarbital or thiopental sodium.

Barbiturates are effective at reducing ICP, but in many studies they have not been shown to improve outcome.¹⁶⁸ Even prophylactic use of barbiturates has not improved outcome or led to easier control of ICP.¹⁶⁹ Considering the risks of high-dose barbiturates, their application is most appropriate for patients in whom conventional measures to control ICP have failed. Usually, a bolus of pentobarbital (5 to 10 mg/kg) is administered during 30 minutes, followed by a continuous hourly maintenance infusion of 1 to 5 mg/kg to achieve a serum concentration of 3.5 to 4.5 mg/100 mL¹⁷⁰ or 10 to 20 seconds of burst suppression monitored by bedside electroencephalography. Despite maintenance of normal blood volume and cardiac output, hypotension occurs in 50% of cases and is probably due to decreased peripheral vascular resistance. Volume expansion in addition to dopamine may be necessary to restore systemic blood pressure while maintaining the desired level of suppression. Other potential complications related to high-dose barbiturates include hyponatremia, pneumonia, and cardiac depression.

Barbiturates are anticonvulsant; however, as mentioned before, they should not be used unless all other options have been exhausted. Other prophylactic anticonvulsants, however, should be given. The incidence of seizures is 4% to 25% after injury and 50% after penetrating injuries.¹⁷¹ Seizures may increase ICP by several factors, including an increased metabolic demand, Valsalva maneuver, and release of excitotoxins.

Finally, V_BRAIN can be reduced by increasing the clearance of edema. Both osmotic and loop diuretics are widely used and can treat both vasogenic and cytotoxic edema.¹⁷²^–¹⁷⁴ Osmotic agents increase serum osmolality and create an osmotic gradient between the serum and brain. This effect draws free water from the brain into the intravascular compartment along the osmotic gradient. This is thought both to prevent edema formation and to speed clearance. However, osmotic agents transiently increase CBF independent of their effect on ICP, so their use in the presence of hyperemia and increased CBV may be contraindicated.

The drugs used most commonly for increasing intravascular osmolality are mannitol, urea, and glycerol. Mannitol (20% solution) is usually the agent of choice. Mannitol has a rapid effect on ICP, and it is therefore thought that a second mechanism of action may involve the rheologic characteristics of blood. Mannitol increases plasma volume, decreases hematocrit, and decreases blood viscosity, which can cause a vasoconstriction and a drop in ICP.¹⁷⁵^–¹⁷⁷

The dose of mannitol is 0.25 to 1 g/kg, and this can be given as a repeated bolus or, in smaller doses, as a continuous infusion. Complications with osmotic therapy are dehydration, electrolyte imbalance, and, with extreme hyperosmolarity, renal failure. Fluid replacement is aimed at preserving isovolemia while increasing serum osmolality. Osmolality should not exceed 320 mOsm/kg because the renal tubule can be easily injured, especially if other nephrotoxic drugs are used concomitantly. Maintenance of high serum mannitol levels can lead to penetration of mannitol into injured brain,¹⁷⁸ especially in areas of blood-brain barrier deficiency. In this case, the osmolality of brain tissue will tend to draw water into the tissue and worsen edema.¹⁷⁹

Mannitol is used more commonly than urea (30% solution) and glycerol (10% solution) because plasma and brain concentrations tend to equilibrate more rapidly with urea and glycerol than with mannitol. Glycerol can also cause hemolysis and renal failure when it is administered parenterally.¹⁸⁰ Because glycerol is metabolized, hyperosmolality lasts for less time than with mannitol. In one study comparing mannitol and glycerol, glycerol was less effective in reducing ICP.¹⁸¹

Loop diuretics such as furosemide and ethacrynic acid can be used in conjunction with mannitol to control ICP associated with edema.¹⁸²^,¹⁸³ Furosemide works synergistically with mannitol to remove free water and is most appropriate in patients with fluid overload. The addition of furosemide increases the likelihood of dehydration and loss of potassium.¹⁰² Although furosemide decreases CSF production, this effect probably does not contribute greatly to lowering of ICP in the acute setting.

Hypothermia was first reported for treatment of brain injury in the mid-20th century.¹⁸⁴^–¹⁸⁷ Recent reports have suggested a beneficial effect on ICP. Shiozaki and coworkers¹⁸⁷ found a statistically significant reduction in ICP in a group of severely injured patients with intracranial hypertension refractory to other treatment, including barbiturates. Marion and colleagues¹⁸⁸ also demonstrated that hypothermia could lower ICP and improve patient outcome at 3 and 6 months after injury. The ability of hypothermia to lower ICP probably relates to a depression of cerebral metabolic requirements as with barbiturates, coupled with a slowing of injurious cellular events (e.g., lipid peroxidation).