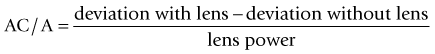1 Optics
Properties of Light
Light behaves both as waves and as particles (photons)
Its speed (velocity) (v) is directly proportional to wavelength (λ) and frequency (ν): v = λν
Index of refraction (n)
ratio of speed of light in a vacuum to speed of light in specific material (n = c/v)
Coherence
ability of 2 light beams to cause interference (large white source has a coherence close to zero)
Scattering
disruption of light by irregularities in light path; shorter wavelengths scatter to a greater extent
Refraction
Snell’s law
n sin (i) = n′ sin (r); n = refractive index of material; i = angle of incidence (measured from the normal); r = angle of refraction (measured from the normal) (Figure 1-2)
Critical angle
Example: Glass / air interface has a critical angle of 41°; critical angle of cornea = 46.5°
Prisms
Prisms displace and deviate light (because their surfaces are nonparallel); light rays are deviated toward the base; image is displaced toward the apex (Figure 1-3)
Prism diopter (PD, Δ)
displacement (in cm) of light ray passing through a prism, measured 100 cm (1 m) from prism
Angle of minimum deviation
total angle of deviation is least when there is equal bending at both surfaces of prism
Plastic prisms are calibrated by angle of minimum deviation: back surface parallel to frontal plane
Glass prisms are calibrated in Prentice position: back surface perpendicular to visual axis
Prism placed in front of the eye creates a phoria in the direction of the base
Stacking prisms is not additive; 1 prism in front of each eye is additive
Prismatic effect of lenses (Figure 1-4)
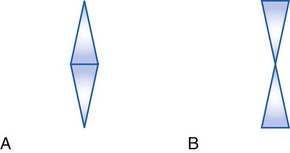
Figure 1-4 A, Plus lenses act like 2 prisms base to base. B, Minus lenses act like 2 prisms apex to apex.
Perceived movement of fixation target when lens moves in front of the eye:
Prentice’s rule
Example: Reading 1 cm below optical center: OD − 3.00; OS + 1.00 + 3.00 × 90
OD (Oculus Dexter – right eye): prism power = 1 cm × 3 D = 3 Δ BD
Net prismatic effect = 4 Δ (either BD over OD, or BU over OS)
Prismatic effect of bifocal glasses
Vergence
The amount of spreading of a bundle of light rays (wavefront) emerging from a point source
Direction of light travel must be specified (by convention, left to right)
Basic lens formula
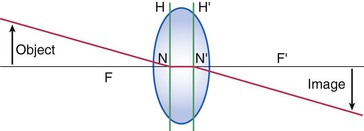
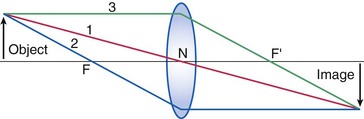
Objects and images
Lenses
Vertex distance conversion
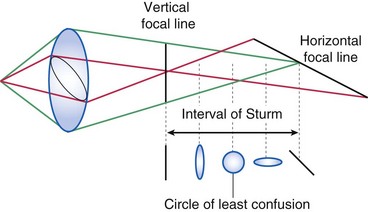
Pure cylindrical lens
power only in 1 meridian (perpendicular to axis of lens); produces focal line parallel to axis
Spherocylindrical lens
power in 1 meridian greater than other
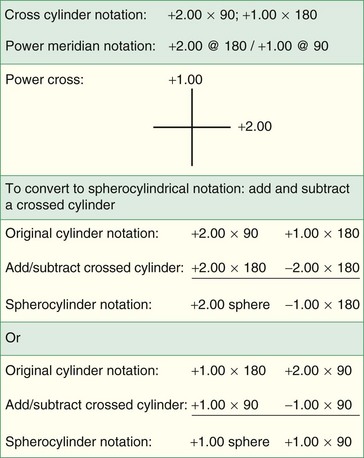
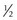 the cylinder; places circle of least confusion on retina
the cylinder; places circle of least confusion on retinaPower cross diagram
depicts 2 principal meridians of lens with the power acting in each meridian (90° from axis), rather than according to axis (Figure 1-9)
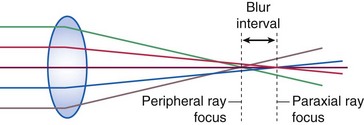
Aberrations
Lenses behave ideally only near optical axis; peripheral to this paraxial region, aberrations occur
Spherical
shape-dependent aberration; periphery of lens has increasing prismatic effect; thus, peripheral rays refracted farther than paraxial ones, producing a blur interval along the optical axis (Figure 1-10)
Magnification
Angular
Example: moon gazing with telescope
MA = xD = D/4 (standardized to 25 cm [ m], the near point of the average eye)
m], the near point of the average eye)
Size of image seen through glasses
Anisometropia
difference in power between the 2 eyes; every 1 D produces approximately 2% of aniseikonia
Aniseikonia
difference in image size between eyes from unequal magnification of correcting lenses
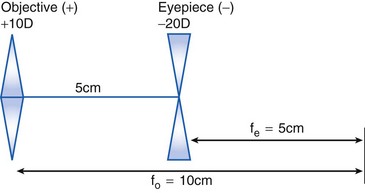
Telescopes
magnify objects by increasing angle that object subtends on retina
Mirrors
Objects and images
real if located on left side of mirror, virtual if on right side (inside) of mirror
Central ray
passes through center of curvature of mirror, not center of mirror
Eye as Optical System
Model Eye
Gullstrand studied the eye’s optical system and, based on average measurements (power = +58.64 D; F = 17.05 mm), he created a simplified model: the ‘reduced’ or ‘schematic’ eye (Figure 1-13): power = +60 D; F = 17 mm; F′ = 22.6 mm
Vision Measurements
Minimum discriminable
resolving power of eye; depends on ability to detect differences in light intensity
Minimum separable
smallest angle at which 2 separate objects can be discriminated; detection of a break in a line
Snellen acuity
based on angle that smallest letter subtends on retina; each letter subtends 5 minutes of arc at a specific distance (represented by the denominator [i.e. 20/40 letter subtends 5 minutes at 40 feet, 20/20 letter subtends 5 minutes at 20 feet]; the numerator is the testing distance); each stroke width and space subtends 1 minute (Figure 1-14)
Factors other than disease that reduce measured visual acuity
uncorrected refractive error, eccentric viewing, decreased contrast, smaller pupil size, older age
Legal blindness (in US)
visual acuity (VA) = 20/200 or worse or visual field (VF) < 20° in better-seeing eye
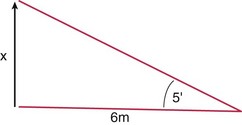
Refractive Error
Secondary focal point (F′) of eye is not located on retina (accommodation must be completely relaxed) (Figure 1-15):
Astigmatism
produces 2 focal lines rather than a single focal point (Table 1-1)
Acquired hyperopia
Acquired myopia
Accommodation
Eye gains plus power when crystalline lens becomes more convex
Accommodation response can be described as:
Amplitude of accommodation
total dioptric amount eye can accommodate
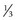 mm (33 cm); then, measure how near patient can read and convert into diopters; subtract far point from near point to determine amplitude
mm (33 cm); then, measure how near patient can read and convert into diopters; subtract far point from near point to determine amplitudeRange of accommodation
distance between far point and near point; measured with tape measure or accommodative rule
Theories of accommodation
Color Vision
Bezold-Brucke phenomenon
Luminosity curve
illustrates sensitivity to different wavelengths
Prescribing Glasses
Use cycloplegia in children and hyperopes to uncover full refractive error
Infants average 2 D of hyperopia; myopic shift between ages 8 and 13; most adults are emmetropic
Children (Table 1-3)
| Hyperopia: | ≥+5 D |
| Anisometropia | ≥1.5 D |
| Myopia: | |
| Up to age 1 | ≥−5 D |
| Ages 1–6 | ≥−3 D |
| Age >6 | ≥−1 D |
| Anisometropia | ≥3 D |
| Astigmatism: | |
| Up to age 1 | ≥3 D |
| Ages 1–6 | ≥2 D |
| Age >6 | ≥1 D |
| Anisometropia | ≥1.5 D |
Minus cylinder grinding
placing astigmatic correction on rear surface (closer to eye) is optically preferable
Bifocal add
place segments as high as practical in relation to optical centers of the distance lenses
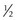 of measured accommodative amplitude in reserve to prevent asthenopic symptoms
of measured accommodative amplitude in reserve to prevent asthenopic symptoms
Example: Prince rule measures 2.0 D of amplitude; thus 1.0 D is available to patient
Contact Lenses (Cl)
Toric lens
Overall diameter
for a given base curve, increasing diameter increases the apical vault
Example: to tighten a lens, reduce radius of curvature or increase diameter
Accommodative demand
depends on magnification, which varies with different lens powers and vertex distances
Fitting rigid CL
SAM-FAP rule (’steeper add minus, flatter add plus’)
Power calculation
if trial lens not available for overrefraction
Evaluating fit
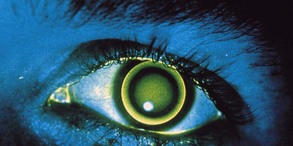
Figure 1-16 Fluorescein pattern of corneal contact lens fitted 1 D steeper than ‘flat K.’ Note the central clearance.
(From White P, Scott C: Contact lenses. In: Yanoff M, Duker JS (eds) Ophthalmology. London, Mosby, 1999.)
Low-Vision Aids
Intraocular Lenses (IOL)
Formulas for IOL calculation (see Ch. 10)
Lens position is important: 1 mm error = 1.0 D change in power
IOL power for a different lens = original IOL power ± difference in A constants
Ophthalmic Instruments
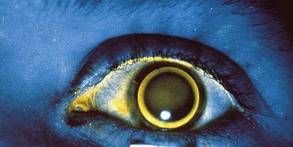
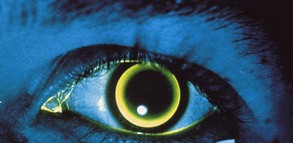
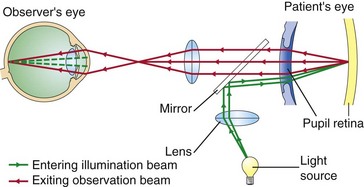
Direct ophthalmoscope (Figure 1-19)
Indirect ophthalmoscope (Figure 1-20)
Retinoscope
instrument to objectively measure refractive state of eye
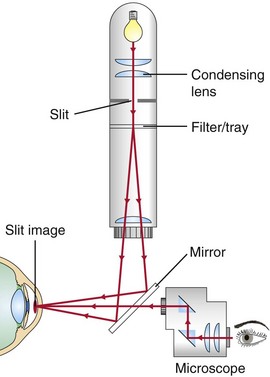
Slit-lamp biomicroscope (Figure 1-21)
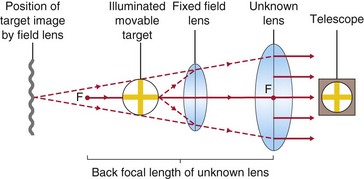
Lensometer
measures power of spectacle or CL using telescope to detect neutralization point; distance measurement is determined from back vertex power; add measurement is taken from front vertex power; prism measurement is derived from displacement of target pattern (Figures 1-22 and 1-23)
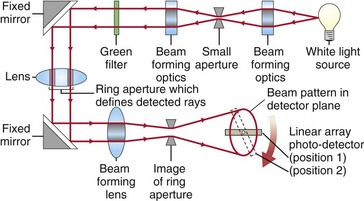
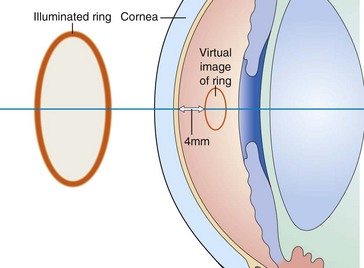
Keratometer
measures curvature of anterior corneal surface based on power of reflecting surface; measures only 2 paracentral points 3 mm apart; doubling of image prevents interference from eye movements (Figure 1-24)
Equations
Reduced schematic eye (calculations of retinal image size)
I = retinal image size, O = object size, X = distance to object
Reflecting power of a spherical mirror
f = focal length of mirror, r = radius of curvature of mirror, (− = convex; + = concave)
Power of lens at new vertex distance
D1 = original dioptric power of lens, D2 = new dioptric power, S = difference in location (m)
Total accommodation through telescope
AN = normal accommodation required, MA = telescope magnification
AC/A ratio (accommodative converge/accommodation):
(expressed as PD of deviation per D of accommodation)
Review Questions (Answers start on page 355)
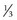 of a meter to the left of a +7 D lens. Where will its image come to focus?
of a meter to the left of a +7 D lens. Where will its image come to focus?
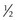 mm on a patient’s retina?
mm on a patient’s retina?
American Academy of Ophthalmology. Optics, Refraction, and Contact Lenses. vol 3. 2012. AAO. San Francisco.
Benjamin WJ. Borish’s Clinical Refraction, 2nd edn. Philadelphia: Elsevier; 2006.
MacInnes BJ. Ophthalmology Board Review: Optics and Refraction. St Louis: Mosby; 1994.
Milder B, Rubin ML, Weinstein GW. The Fine Art of Prescribing Glasses Without Making a Spectacle of Yourself. Gainesville: Triad Scientific Publications; 1991.
Rubin ML. Optics for Clinicians. Gainesville: Triad Scientific Publications; 1993.

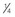 wavelength apart); interference filters (allow only green light out of the eye during fluorescein angiography); laser interferometry (retinal function test; optical coherence tomography [OCT])
wavelength apart); interference filters (allow only green light out of the eye during fluorescein angiography); laser interferometry (retinal function test; optical coherence tomography [OCT])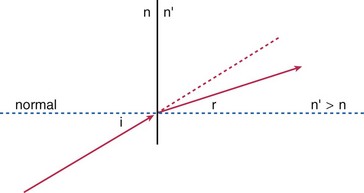

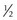 % (magnification decreases as plus power decreases)
% (magnification decreases as plus power decreases)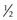 % (magnification decreases as lens thickness decreases)
% (magnification decreases as lens thickness decreases)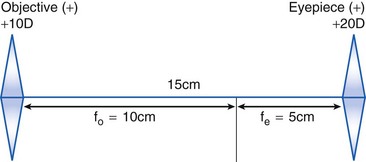
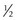 the radius of curvature (f = r/2)
the radius of curvature (f = r/2)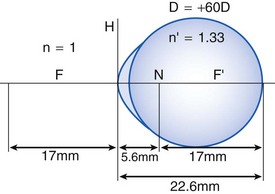
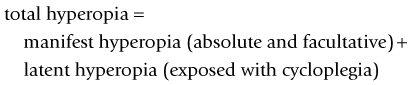


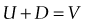
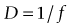
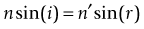

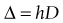
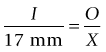
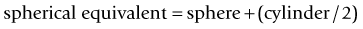
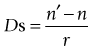
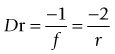
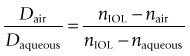
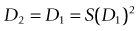
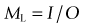
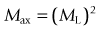
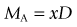
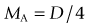
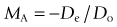
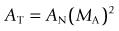
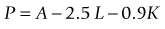
 m
m
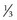 m, then remeasuring with +3 D sphere in front of both eyes
m, then remeasuring with +3 D sphere in front of both eyes