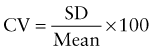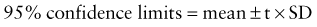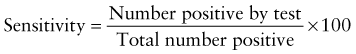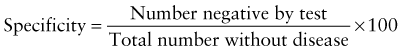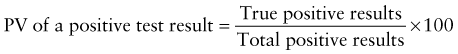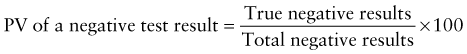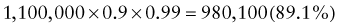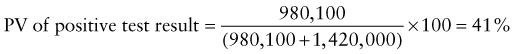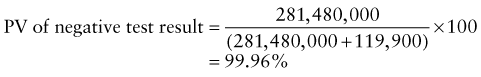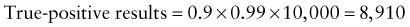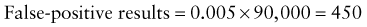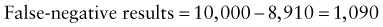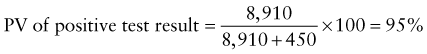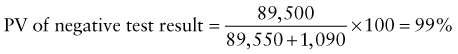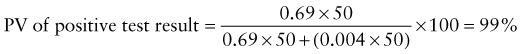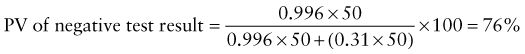Chapter 707 Laboratory Testing in Infants and Children
Reference intervals, more commonly known as normal values, are difficult to establish within the pediatric population. Differences in genetic composition, physiologic development, environmental influences, and subclinical disease are variables that need to be considered when developing reference intervals. Other considerations for further defining reference intervals include partitioning based on sex and age. The most commonly used reference range is generally given as the mean of the reference population ±2 standard deviations (SD). This is acceptable when the distribution of results for the tested population is essentially gaussian. The serum sodium concentration in children, which is tightly controlled physiologically, has a distribution that is essentially gaussian; the mean value ±2 SD gives a range very close to that actually observed in 95% of children (see Table 707-1 on the Nelson Textbook of Pediatrics website at www.expertconsult.com ![]() ). However, not all analytes have a gaussian distribution. The serum creatine kinase level, which is subject to diverse influences and is not actively controlled, does not show a gaussian distribution, as evidenced by the lack of agreement between the range actually observed and that predicted by the mean value ±2 SD. In these cases, a reference interval defining the 2.5-97.5th percentiles are typically used.
). However, not all analytes have a gaussian distribution. The serum creatine kinase level, which is subject to diverse influences and is not actively controlled, does not show a gaussian distribution, as evidenced by the lack of agreement between the range actually observed and that predicted by the mean value ±2 SD. In these cases, a reference interval defining the 2.5-97.5th percentiles are typically used.
Table 707-1 GAUSSIAN AND NONGAUSSIAN LABORATORY VALUES IN 458 NORMAL SCHOOL CHILDREN 7-14 YR OF AGE
| SERUM SODIUM (mmol/L) | SERUM CREATINE KINASE (U/L) | |
|---|---|---|
| Mean | 141 | 68 |
| SD | 1.7 | 34 |
| Mean ± 2 SD | 138-144 | 0-136 |
| Actual 95% range | 137-144 | 24-162 |
SD, standard deviation.
Accuracy and Precision of Laboratory Tests
where t is a constant derived from the number of replications. In most cases, t = 2.
Predictive Value of Laboratory Tests
In addition, there will be 281,480,000 true-negative results.
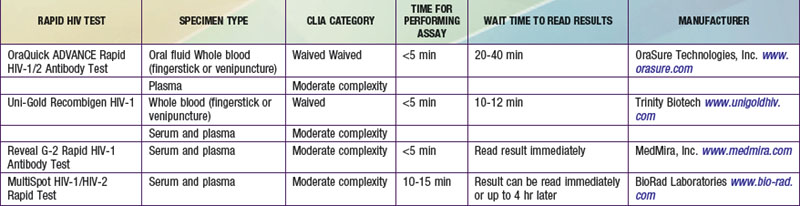
However, because of the long time needed to test for HIV antibodies, it was difficult to screen women during labor and provide the necessary therapy. Recently, rapid HIV antibody testing procedures using a fingerstick or venipuncture to obtain whole blood, plasma, or serum, and tests using oral fluid were approved (Table 707-2). The HIV test results are usually obtained in <20 min. The collection of oral fluid samples provides an alternative for individuals who avoid HIV testing because of their dislike of needlesticks. HIV testing using whole blood or oral fluid is classified as a waived test under the Clinical Laboratory Improvement Amendments of 1988 (CLIA), and these tests are allowed in a point-of-care setting. Waived tests are simple laboratory procedures that use methodologies that are so simple and accurate as to render the likelihood of an erroneous result by the user negligible. A positive rapid HIV test result is then confirmed by Western blot analysis or immunofluorescence assay.
Neonatal Screening Tests
In an attempt to standardize newborn screening programs, the American College of Medical Genetics recommends that every baby born in the USA be screened for a core panel of 29 disorders (Table 707-3). An additional 25 conditions were recommended as secondary targets because they may be identified while screening for the core panel disorders. The March of Dimes and the American Academy of Pediatrics also endorse the recommendation by the American College of Medical Genetics. However, expansion of the screening test menu raises several issues. For example, the cost of implementation can be significant because many states will need multiple MS/MS systems. In addition, staffing the laboratory with qualified technical personnel to run the MS/MS system and qualified clinical scientists to interpret the profiles can be a challenge. A number of false-positive results will also be obtained with these newborn screening programs. Many of these findings are due to parenteral nutrition, biologic variation, or treatment, and are not the result of an inborn error of metabolism. Therefore, qualified staff will be needed to ensure that patients with abnormal results are contacted and receive follow-up testing and counseling, if needed. Even with these concerns, the American College of Medical Genetics report is a step in the right direction toward standardizing guidelines for state newborn screening programs.
Testing in Refining a Differential Diagnosis
Serologic Testing
Using laboratory testing to refine a differential diagnosis poses problems, as exemplified by serologic testing for Lyme disease, which is a tick-borne infection by Borrelia burgdorferi that has various manifestations in both early and late stages of infection (Chapter 214). Direct demonstration of the organism is difficult, and serologic test results for Lyme disease are not reliably positive in young patients presenting early with erythema chronicum migrans. These results become positive after a few weeks of infection and remain positive for a number of years. In an older population being evaluated for late-stage Lyme disease, some individuals will have recovered from either clinical or subclinical Lyme disease and some will have active Lyme disease, with both groups having true-positive serologic test results. Of individuals without Lyme disease, some will have true-negative serologic test results, but a significant percentage will have antibodies to other organisms that cross react with B. burgdorferi antigens.
Laboratory Screening
Screening profiles (Table 707-4) are used as part of a complete review of systems, to establish a baseline value, or to facilitate patient care in specific circumstances, such as: (1) when a patient clearly has an illness, but a specific diagnosis remains elusive; (2) when a patient requires intensive care; (3) for postmarketing surveillance and evaluation of a new drug; and (4) when a drug is used that is known to have systemic adverse effects. Laboratory screening tests should be used in a targeted manner to supplement, not supplant, a complete history and physical examination.
| LABORATORY TEST | ASSESSMENT FACILITATED BY TESTS |
|---|---|
| Complete blood cell count and platelets | Nutrition, status of formed elements |
| Complete urinalysis | Renal function/genitourinary tract inflammation |
| Albumin and cholesterol | Nutrition |
| ALT, bilirubin, GGT | Liver function |
| BUN, creatinine | Renal function, nutrition |
| Sodium, potassium, chloride, bicarbonate | Electrolyte homeostasis |
| Calcium and phosphorus | Calcium homeostasis |
ALT, alanine aminotransferase; BUN, blood urea nitrogen; GGT, γ-glutamyltransferase.
American Academy of Pediatrics, American Thyroid Association. Newborn screening for congenital hypothyroidism. Pediatrics. 1987;80:745-749.
Bulterys M, Jamieson DJ, O’Sullivan MJ, et al. Rapid HIV-1 testing during labor: a multicenter study. JAMA. 2004;292:219-223.
Clayton EW. Issues in state newborn screening programs. Pediatrics. 1992;90:641-646.
Farrell PM, Kosrok MR, Rock MJ, et al. Early diagnosis of cystic fibrosis through neonatal screening prevents severe malnutrition and improves long-term growth. Pediatrics. 2001;107:1-13.
Galen RS, Gambino SR. Beyond normality. New York: Academic Press; 1975.
Hu LT, Klempner MS. Update on the prevention, diagnosis, and treatment of Lyme disease. Adv Intern Med. 2001;46:247-275.
National Newborn Screening and Genetics Resource Center (website) http://genes-r-us.uthscsa.edu. Accessed December 3, 2010
Rinaldo P, Tortorelli S, Matern D. Recent developments and new applications of tandem mass spectrometry in newborn screening. Curr Opin Pediatr. 2004;16:427-433.
Steere AC, Taylor E, McHugh GL, et al. The overdiagnosis of Lyme disease. JAMA. 1993;269:1812-1826.
Watson MS, Mann MJ, Lloyd-Puryear MA, et al. Newborn screening: towards a uniform screening panel and system. Genet Med. 2006;8(Suppl):S12-S252.
Wilcken B, Wiley V, Hammond J, et al. Screening newborns for inborn errors of metabolism by tandem mass spectrometry. N Engl J Med. 2003;348:2304-2312.
Zytkovicz TH, Fitzgerald EF, Marsden D, et al. Tandem mass spectrometric analysis for amino, organic, and fatty acid disorders in newborn dried blood spots: a two-year summary from the New England Newborn Screening Program. Clin Chem. 2001;47:1945-1955.