Health technology assessment

Published on 02/03/2015 by admin

Filed under Basic Science

Last modified 22/04/2025

Print this page

rate 1 star rate 2 star rate 3 star rate 4 star rate 5 star
Your rating: none, Average: 0 (0 votes)

This article have been viewed 1220 times

Chapter 5 Health technology assessment

Michael Rawlins

Synopsis

Health technology assessments bridge the gap between licensing and everyday clinical practice.

They involve:

• Defining the scope of the assessment.

• Assessing the overall clinical effectiveness.

• Assessing the cost-effectiveness.

The critical steps involve:

• A systematic review of the evidence.

• Estimating cost-effectiveness.

• Drawing appropriate conclusions on which decision-makers can act.

A cost–effectiveness analysis attempts to provide a rational basis for decision-making in the face of resource constraints.

Pharmacoeconomics involves trying to estimate the extra cost to the health-care system of adopting a product, in relation to the additional benefit the product might bring.

Health technology assessment, in its broadest application, involves a systematic assessment of the clinical and cost-effectiveness of either a single, or several similar, health technologies.

The term health technology encompasses all approaches to the prevention, screening, diagnosis and treatment of disease. Treatments, in health technology assessments, not only encompass pharmaceuticals (including vaccines) but can include devices and interventional (surgical) procedures as well as techniques such as physiotherapy, speech therapy or cognitive behavioural therapy. Although this chapter is concerned with health technology assessment as it relates to pharmaceuticals, the same approach is adopted in these other therapeutic areas.

For pharmaceuticals, health technology assessment of single products, or of a group of similar products, bridges the gap between licensing and use in everyday clinical practice. The process involves the close scrutiny of a product’s clinical effectiveness in comparison with other forms of treatment (including best supportive care), together with its cost-effectiveness in comparison with these same alternatives. It therefore goes further than the criteria for licensing (quality, safety and efficacy), and health technology assessment has sometimes been called ‘the fourth hurdle’.

A health technology assessment may be used by a variety of agencies. It may inform the decisions of individual practitioners in the treatment of their own patients or it may be used by a hospital to develop their treatment policies. Health technology assessments are critical for those developing clinical guidelines for the management of specific conditions; and they may be used by policy makers for an entire health-care system.

There are three stages in the health technology assessment of a product:

• Definition of the scope of the assessment.

• Assessment of its clinical effectiveness.

• Assessment of its cost-effectiveness.

The scope

Before embarking on the health technology assessment of a product the scope of the enquiry needs to be carefully defined:

1. Obviously the product, or group of products, under investigation needs to be characterised.

2. The nature of the comparator health technology (or technologies) also requires definition. Depending on the circumstances, the comparator might be another pharmaceutical product indicated for the same condition; it might be a device or procedure used for the same or similar purposes; or it might be ‘best supportive care’. In any event, the comparator should reflect current clinical practice.

Difficulties arise when a potential comparator is not licensed for a particular indication but is, nevertheless, used in clinical practice. This is a particular problem in the heath technology assessment of products for use in children and for whom potential comparators reflect ‘custom and practice’ even though unlicensed. The wise course of action, in such circumstances, is to include comparators that reflect current clinical practice.

3. At the start of any health technology assessment, the clinical outcome(s) of interest should be decided. The most desirable, of course, is the ‘ultimate outcome’, such as dead versus alive or recovered versus not recovered. There are circumstances, however, when an assessment is focused on an ‘intermediate’ (or surrogate) outcome where there is confidence that this reflects the ultimate outcome. For example, in the assessment of statins for the treatment of hypercholesterolaemia, a decision would need to be taken as to whether the long-term ‘ultimate’ outcome (i.e. reduction in coronary artery disease) should be used; or whether the assessment should be concerned with an ‘intermediate’ outcome (i.e. a reduction in LDL cholesterol).

4. The type of evidence required to demonstrate the effectiveness of a product must also be determined. In many instances this may be restricted to the results of randomised controlled trials. There may be circumstances where other study designs are more appropriate. In the assessment of a vaccine, for example, evidence from randomised controlled trials may usefully be supplemented by the results of observational studies that have examined its efficacy under circumstances that more closely reflect its performance in the ‘real world’.

5. Decisions must also be made about the form any economic evaluation should take. These include the economic perspective and the type of analysis that is most appropriate. These issues are discussed later.

Clinical effectiveness

An assessment of the clinical effectiveness of a product requires a full ‘systematic review’ of the available evidence. A systematic review involves four steps:

1 Developing the protocol

The development of a protocol for a systematic review is just as important in secondary research as it is for primary research. The objectives of the review will usually have been defined by the scope (as above). The protocol will, in addition, include the relevant:

• pharmacological product or therapeutic class

• comparator(s) which may include a non-pharmacological procedure

• study designs for assessing the effectiveness of the product

• clinical endpoints used in the studies that are to be included in the review.

2 Defining the methods

The literature search will, at a minimum, involve a comprehensive search of the three major electronic databases (MEDLINE, EMBASE and CENTRAL). Although there is some overlap between each database, one alone is inadequate. The usual approach is to start the search in a broad manner by looking at the abstracts of all the studies that appear to be relevant and then only include those that match the criteria that have been established for the review. In a review of the clinical effectiveness of statins, for example, the review criteria may have required the assessment to be restricted to randomised controlled trials where the outcome is the secondary prevention of vascular death or disability. All other study designs, involving different patient populations or surrogate outcomes, would be excluded. The search will also include any relevant references gleaned from scrutiny of the list of publications in the included studies.

One of the major problems in identifying appropriate studies in any systematic review is so-called ‘publication bias’. There is a tendency for negative studies, or those demonstrating only very modest benefits, to either remain unpublished or to be published in a non-English language journal. The inclusion of such studies is extremely important if a reliable indication of the product’s ‘effect size’ is to be made. Common techniques to avoid publication bias include enquiry of both the particular manufacturer as well as of known experts in the particular field. The assessment team must also decide whether to attempt to identify articles in non-English language journals and get them translated. This step substantially increases the cost of the review and is not invariably undertaken.

3 Analysing the data

After extracting the relevant data from each of the studies that meet the review inclusion criteria an ‘evidence table’ is constructed. In such a table the relevant data for each study are summarised and usually include:

• The study’s bibliographic reference.

• The type of study (e.g. randomised controlled trial, case–control study).

• Number of patients in each arm.

• Patient characteristics (e.g. age, gender).

• Study setting (e.g. hospital inpatients, GPs’ surgeries).

• Intervention(s) including dose(s) and route(s) of administration.

• Comparator interventions (e.g. placebo, active comparator).

• Length of follow-up.

• Outcome measure(s) and effect size(s).

• Additional comments.

The evidence table may also include some attempt to assess the quality of each study. There is no generally accepted approach to doing this but one of the more common methods is to use the Jadad score (see Table 5.1). This itemises those elements in the design and conduct of a study (i.e. randomisation and blinding) that contribute most to a study’s internal validity. A score of 5 would indicate that the particular study appeared to avoid both selection and ascertainment biases. A score of 0 would cast considerable doubt on a study’s internal validity.

Table 5.1 Jadad score calculation

Item Score
Was the study described as randomized? 0/1
Was the method of randomization described and appropriate? 0/1
Was the study described as double blind? 0/1
Was the method of double blinding described and appropriate? 0/1
Was there a description of withdrawals and dropouts? 0/1
Deduct 1 point if the method of randomization was described and was inappropriate? 0/−1
Deduct 1 point if the study was described as double blind but the method of blinding was described and inappropriate? 0/−1

Qualitative synthesis

Almost all systematic reviews include an element of narrative or ‘qualitative’ synthesis outlining, or expanding on, aspects of the included studies. Narrative syntheses become a more significant component in systematic reviews of complex interventions (such as a comparison between an antidepressant and cognitive behavioural therapy in the treatment of mild depression). The defining characteristic of a formal narrative synthesis is the use of a textual approach that provides an analysis of the relationships within and between studies, and an overall assessment of the robustness of the evidence. It is a more subjective process than meta-analysis and, when used, needs to be rigorous and transparent to reduce the potential for bias.

Quantitative synthesis (meta-analysis)

A qualitative synthesis of the results in a systematic review may itself be sufficient. It is very common, however, to attempt a quantitative synthesis – or meta-analysis – of the individual outcomes from each study so as to provide the most reliable estimate of the overall size of a product’s effects.

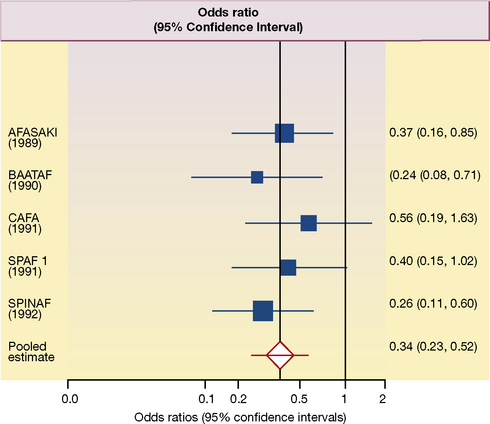
A meta-analysis (see also, Chapter 4, p. 49), at its most simple level, involves extracting the summary statistical data for each study. The relevant data are the mean differences in outcomes at the end of the study with their 95% confidence intervals. Estimates of the effect size for of the included studies, and the pooled estimate from all the studies, are often depicted as a ‘forest plot’1; an example is shown in Figure 5.1.

image

Fig. 5.1 Forest plot of five placebo-controlled trials of warfarin’s efficacy in preventing ischaemic stroke in patients with non-valvular atrial fibrillation. (Odds ratios with 95% confidence intervals.)

This forest plot summarises the results of each of five placebo-controlled trials, designed to assess the effect of anticoagulation with warfarin on the frequency of ischaemic stroke in patients with non-valvular atrial fibrillation.2 In a typical forest plot, there is an abbreviated reference to each trial on the left. The point estimate (mean) of the results of each study is represented as a square; and the horizontal line running through the square is its 95% confidence interval. The size of each square is proportional to the size of the study compared to the others. The column at the right shows the individual odds ratios (the expression of benefit used in this meta-analysis), and their 95% confidence intervals, for each study. By convention, improvement (a decrease in the frequency of ischaemic stroke) is shown to the left of the vertical ‘no effect’ line; a worsening (an increase in the frequency of ischaemic stroke) is shown to the right.

In the forest plot in Figure 5.1 the outcome is expressed as odds ratios. In each of five studies, the frequency of ischaemic stroke is reduced by treatment with warfarin and all five ‘squares’ are to the left of the ‘no effect’ (odds ratio = 1) vertical line. In three of the studies the 95% confidence interval does not cross the ‘no effect’ line and the results would be statistically significant with P values of less than 0.05. In the other two studies, the upper boundaries of the 95% confidence interval cross the ‘no effect’ line and would not reach conventional levels of statistical significance (i.e. the P value is more than 0.05). The overall pooled mean effect size, taking account of the results of all five studies, is shown as a diamond in Figure 5.1; and the horizontal line again represents its 95% confidence interval.

The value of a forest plot is that the results can be seen and interpreted almost at a glance. Although not all the studies were statistically significant the mean effects of each study showed benefit; and those that failed to meet statistical significance were the smaller studies (as evidenced by their smaller squares).

4 Drawing conclusions

The final step in a systematic review is to discuss its strengths and weaknesses, and to draw conclusions. Both strengths and weaknesses will depend in large part on the range and quality of the included studies. The veracity of any conclusions will also depend on the extent to which there might have been publication bias so that important trials with negative results were never published. There are statistical techniques that can sometimes be helpful in establishing probable publication bias.

Scrutiny of Figure 5.1 suggests that it would be reasonable, by any standards, to regard warfarin as effective in the prevention of ischaemic stroke in patients with non-valvular atrial fibrillation. Moreover, the authors were able to estimate that about 25 strokes and about 12 disabling or fatal strokes would be prevented yearly for every 1000 patients with atrial fibrillation treated with warfarin.

Cost–effectiveness

No health-care system is able to meet all the demands of its patients. The resources used to provide health care, in any individual country, are directly proportional to its wealth, so that wealthier nations with higher gross domestic products are able to devote more resources to health care than poorer ones. The manner in which health-care priorities are decided varies between countries, but rationing decisions are necessary – explicitly or implicitly – in all countries because resources are finite and demand is (almost) infinite.

A cost–effectiveness analysis attempts to provide a health-care system with a rational basis for decision-making in the face of resource constraints. In pharmacoeconomics this involves trying to estimate the extra cost to the health-care system of adopting a product in relation to the additional benefit the product might bring. If a health-care system devotes very large sums of money to a product that gives only modest benefits, other people, with other conditions, will be denied cost-effective care. The cost-effectiveness component of a health technology assessment thus attempts to provide some indication of the ‘opportunity cost’ of adopting a particular technology. In doing so, the assessment has to take account of:

• The relevant costs.

• The benefits expressed in an appropriate manner.

• The type of analysis that will be used.

1 The costs

The costs of using a particular pharmaceutical will include the acquisition costs of the product, as well as the costs associated with its use (such as any special monitoring requirements, additional visits to hospital). In using warfarin for the prevention of ischaemic stroke, the costs will therefore have to include the costs of the warfarin itself, the costs of attending a hospital anticoagulant clinic and the laboratory monitoring costs. The costs will also have to include the consequences of any adverse effects which, in the case of warfarin, would need to encompass the costs associated with warfarin-induced bleeding.

The costs will also have to take account of any savings from which a health-care system would benefit. These are often known as ‘cost offsets’ which, in the case of warfarin to prevent ischaemic stroke, would include the savings made by the reduction in strokes among treated patients.

The costs might also include the wider costs and savings to society as a whole. In this case the costs (and cost offsets) would be extended to include any reduction in time off work; or, continuing the warfarin example, the savings resulting from fewer strokes that would reduce the costs associated with unemployment or disability.

Whether the economic perspective (as economists describe it) should be based on the costs and savings to the health-care system alone, or whether it should be societal, is a complicated and controversial issue. It is a political, fiscal (relating to government revenue, especially taxes) and governmental problem rather than an economic one. For this reason there is considerable variation between countries as to the economic perspective taken. A societal perspective is adopted in Sweden, for example, but in the UK the perspective is limited to the National Health Service.

2 Benefits

For the purposes of an economic analysis, the benefits of a health technology can, broadly, be expressed either in ‘natural units’ (e.g. life years gained), or as ‘health utility’ gained.

Natural units

The number of life years saved as a result of using a product is a commonly used natural unit for products that extend life. Other natural units might include the number of additional centimetres of height gained from the use of human growth hormone in the treatment of children with congenital growth hormone deficiency; or, again using the warfarin example, the number of strokes prevented.

The use of natural units is relatively simple and they can be used effectively in comparing the costs and benefits of products that are used to treat the same condition. The disadvantage is that it is impossible to use natural units for comparing the costs and benefits of treatments for different conditions. It is for this reason that most economic analyses prefer to use health ‘utilities’ as the measure of benefit.

Health utilities

Utilities are numbers assigned to preferences according to a rule. There are a number of ways by which health utilities can be captured and all are based on an assessment, by each person, of the improvement in their quality of life. These are then aggregated across the patients using the product of interest as well as those using the comparator(s). If the study itself did not collect health-related quality of life data, there are techniques that allow it to be imputed.

The most widely used technique for capturing health-related quality-of-life data is the so-called EuroQol EQ-5D questionnaire. It is not disease-specific and captures patients’ preferences for particular health states.

The health utility measure provided by the EQ-5D ranges from 0 (dead) to 1 (perfect health). When patients benefit from a particular treatment their health state might move from (say) 0.5 to 0.8 with a corresponding utility gain of 0.3. This is multiplied by the number of years for which it is enjoyed to yield the ‘quality-adjusted life years’ (QALY). If patients could on average expect to enjoy a utility gain of 0.3 for 10 years, the quality-adjusted life years gained would be 3.0 (0.3 times 10).

3 Type of analysis

Two types of analysis are possible depending on whether the benefits are expressed in natural units or as utilities. Both require calculating an ‘incremental cost-effectiveness ratio’ (ICER) by dividing the incremental costs by the incremental benefits. Treatment pathways, however, can be extraordinarily complicated; and in arriving at an ICER health economists must of necessity construct an economic model. There is a great variety of these, and they vary in their complexity. No attempt is made to discuss them further here, and their interpretation requires considerable expertise.

Cost–effectiveness analysis

In a cost–effectiveness analysis the ICER is expressed as the incremental cost (£) per incremental gain in some natural unit. In the case of a product that, in advanced cancer, results in (say) a 6-month extension of life at a total cost of (say) £10 000, the ICER would be £20 000 per life year gained.

As already discussed, although this measure is sometimes used, it is impossible to make comparisons across conditions. How would a decision-maker make a ‘value for money’ comparison between £20 000 per life year gained for treating advanced cancer, with £20 000 per centimetre height gained from the use of growth hormone in a child with congenital growth hormone deficiency?

Cost–utility analysis

In this form of analysis the ICER is expressed as the ratio of the incremental costs to the incremental utility gain. The most common expression of this form of ICER is as cost (£) per incremental gain in the quality adjusted life years (£ per QALY). Examples of ICERs for some cancer drugs are shown in Table 5.2.

Table 5.2 Incremental cost–effectiveness ratios for some cancer drugs appraised by the National Institute for Health and Clinical Excellence (after Rawlins 2010, in Oxford Textbook of Medicine, fifth edition.)

Treatment Condition Incremental cost–effectiveness ratio (£/QALY)
Rituximab Aggressive non-Hodgkin’s lymphoma 6100
Paclitaxel Metastatic ovarian cancer 8500
Gemcitabine Metastatic pancreatic cancer 12 500
Vinorelbine Metastatic breast cancer 14 500
Trastuzumab Early breast cancer 18 000
Temozolomide Recurrent glioma 25 300
Imatinib Inoperable or metastatic gastrointestinal stromal tumour 32 000
Temozolomide Newly diagnosed glioma 35 000
Bevacizumab Metastatic colorectal cancer 62 860
Cetuximab Metastatic breast cancer 72 210

A health technology assessment may also include economic evaluations in subgroups of patients, such as those aged over 65 years, or those with other identifiable prognostic characteristics. This is usually undertaken when the overall ICER for the product is likely to represent poor value for money, but when there may be subgroups who might gain greater benefit.

In conclusion

A health technology assessment is concerned with analysing the totality of the available clinical and economic evidence. Bodies undertaking health technology assessments are not, however, decision-makers. Health technology assessments should provide decision-makers with a sophisticated analysis of the available data, together with a critical evaluation of the strengths and weaknesses of the assessment as well as the limitations in the economic analyses.

One of the most critical issues, in the assessment of the clinical data, is the extent to which the benefits in trials can be extrapolated beyond the data. In the trials depicted in Figure 5.1, the average duration of follow-up was 1.5 years. Does this mean that treatment should be stopped after this? The mean age of participants was 69 years and with very few under the age of 50 years or over the age of 80 years. Does this mean that treatment should be denied to younger people? Or to the very elderly?

These are the decisions that decision-makers themselves must make. A reasonable decision-maker could reasonably conclude that to stop warfarin treatment after 1.5 years would be wrong, and that denying the very likely benefits to those younger and older than those in the trials would be equally wrong. These decisions are ones that require judgements to be made rather than strict adherence to the tenets of health technology assessment. Health technology assessment plays a crucial role in underpinning evidence-based clinical practice but it does not supplant the place of judgement!3

Guide to further reading

Higgins J.P.T., Green S. Cochrane Handbook for Systematic Reviews of Interventions. Chichester: John Wiley; 2008.

Matthews J.N.S. An Introduction to Randomized Controlled Trials. London: Chapman and Hall; 2006.

Morris S., Devlin N., Parkin D. Economic Analysis in Health Care. Chichester: John Wiley; 2007.

Rawlins M.D., The evaluation and provision of effective medicines: Warrell. D.A., Cox T.M., Firth. J.D., Benz E.J. Oxford Textbook of Medicine, fifth ed, Oxford: Oxford University Press, 2010.

Rawlins M.D. Therapeutics, Evidence and Decision-making. London: Hodder, 2011.

1 The ‘forest plot’ is so called because (to some – though not to the author’s – eyes) the ‘plot’ resembles a forest!

2 Aguilar M I, Hart R 2005 Oral anticoagulants for preventing stroke in patients with non-valvular atrial fibrillation and no previous history of stroke or transient ischemic attacks. Cochrane Database of Systematic Reviews Issue 3, Art. No.: CD001927. DOI: 10.1002/14651858.CD001927.pub2.

3 Rawlins M D 2010 The evaluation and provision of effective medicines. In: Warrell D A, Cox T M, Firth J D, Benz E J (eds) Oxford Textbook of Medicine, 5th edn. Oxford University Press, Oxford

Related posts:

Antibacterial drugs Thyroid hormones, antithyroid drugs Neurological disorders – epilepsy, Parkinson’s disease and multiple sclerosis Neoplastic disease and immunosuppression Drugs for inflammation and joint disease Pain and analgesics