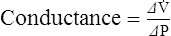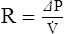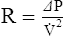General Principles of Gas Physics
I Basic Units and Relationships
A Mass: The ability of matter to occupy space, and if in motion to remain in motion, and if at rest to remain at rest.
B Weight: The quantification of the mass of an object; the effect of gravitational attraction on an object.
C Velocity: The speed that an object moves between two points; expressed in miles per hour or centimeters per second.
D Acceleration: The rate at which the velocity of an object increases. The units of acceleration are cm/sec2 or miles/hour2.
E Work: The force needed to move an object multiplied by the specific distance the object is moved.
< ?xml:namespace prefix = "mml" />
1. Force is defined as mass × acceleration. The units of force are:
2. Work is not performed unless the applied force causes movement; if no movement, no work.
F Energy is defined as the ability to do work.
1. Potential and kinetic energy are the two types of mechanical energy.
2. Potential energy (PE) is the energy of position.
where M = mass, g = gravitational attraction of the earth, and h = height.
4. Mass times gravitational attraction is frequently represented as weight (W):
5. Kinetic energy (KE) is the energy of motion.
G Pressure is the force applied per unit area. The units of pressure are:
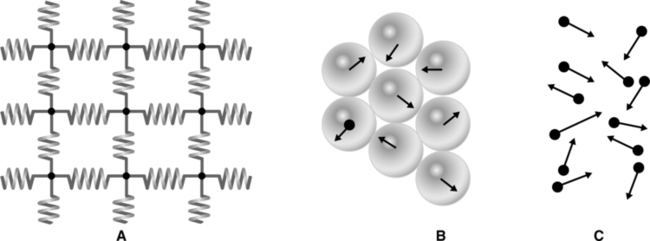
A All matter exists in one of three basic states (Figure 2-1):
1. Solid: High degree of order, little random molecular motion, and strong intermolecular attraction
2. Liquid: Limited degree of order, some freedom of movement, and moderate intermolecular attraction
3. Gas: No order, complete freedom of motion, and weak intermolecular attraction
B The state of a substance is determined by the relationship of two forces.
C The KE of a substance is directly related to temperature.
1. The greater the KE of a substance, the greater its tendency to exist as a liquid or gas.
2. Molecules of every substance are in constant motion as a result of KE.
3. At absolute zero, the KE of a substance is theoretically zero.
D Intermolecular attractive forces oppose the KE of molecules and tend to force them to exist in less free (solid or liquid) states. Basically there are three types of intermolecular attractive forces: dipole, hydrogen bonding, and dispersion.
1. Dipole forces: Forces that exist between molecules that have electrostatic polarity; the negative aspect of one molecule is lined up and attracted to the positive aspect of another molecule, as seen with NaCl. These substances frequently form crystals.
2. Hydrogen bonding: A force that exists between molecules formed by hydrogen reacting with fluorine, oxygen, or nitrogen.
a. As a result of the electronegative difference between hydrogen and fluorine, oxygen, or nitrogen, the hydrogen atom in the molecule exists essentially as a pure proton.
b. The hydrogen end of one molecule is thus attracted to the negative aspect of another molecule of the same substance.
c. Hydrogen bonding occurs only with compounds of fluorine, oxygen, and nitrogen because of these atoms’:
3. Dispersion forces (London or van der Waals forces): Forces between molecules of relatively nonpolar substances.
a. In nonpolar substances the electron cloud normally is distributed equally among all of the atoms in the molecule.
b. However, at some point in time the electron cloud may be instantaneously concentrated at one end of the molecule. When this occurs, a polarity is set up on the molecule.
c. This instantaneous polarity allows weak attraction between adjacent molecules.
d. Dispersion forces are the weakest of all intermolecular forces.
1. The first law of thermodynamics states that energy (heat) is neither created nor lost but simply transformed from one form to another.
2. That is, any energy a substance gains must be lost by its surrounding environment.
3. Heat (energy) always moves from the hotter object to the cooler object until there is thermal equilibrium between the two objects.
4. Heat transfer occurs in four ways:
a. Conduction: Transfer of heat by direct contact between objects. Thermal conductivity is a measure of a substance’s ability to absorb heat.
(1) Metals have high thermal conductivity; they tend to feel cool because they readily absorb heat from the body.
b. Convection: Heating by the mixing of two fluids (liquids or gases). Heat is allowed to freely transfer in the mixture. Fluid currents carrying heat energy are called convection currents.
c. Radiation: Heating without direct contact, heat energy in the visible and infrared light ranges transferred to the objects they encounter—heating by the sun.
d. Vaporization/condensation: Heating by the transfer of energy as water changes from one state to another.
5. Heat and moisture exchangers function by the process of vaporization and condensation. Water is condensed, and heat is transferred to the device during exhalation. During inspiration the inhaled gas picks up water vapor by vaporization, and heat as a result is transferred to the inhaled gas (see Chapter 35).
6. Calorie: Unit of heat in the metric system. Essentially it is the amount of heat necessary to cause a 1° C increase in the temperature of 1 g of water.
7. British thermal unit (BTU): Unit of heat in the British system. Essentially it is the amount of heat necessary to cause a 1° F increase in the temperature of 1 lb of water.
8. One BTU is equal to 252 calories of heat.
9. Heat capacity: Number of calories needed to raise the temperature of 1 g of a substance 1° C.
10. Specific heat: Ratio of the heat capacity of a substance compared with the heat capacity of water.
1. A specific defined amount of heat is needed to cause the molecules of a substance to change their state of matter without a change in temperature.
2. Latent heat of fusion is the amount of heat necessary to change 1 g of a substance at its melting point from a solid to a liquid without causing a change in temperature.
a. The melting point is the temperature (at 1 atm of pressure) at which a substance changes from a solid to a liquid.
b. The total volume of a substance must change from a solid to a liquid before its temperature can change.
c. Generally, a large amount of heat gain is required to change from a solid to a liquid.
d. Changing from a liquid to a solid requires the same amount of heat loss.
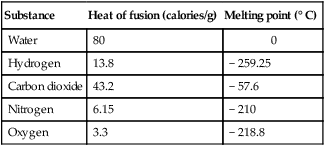
e. Latent heats of fusion and melting points for various substances:
| Substance | Heat of fusion (calories/g) | Melting point (° C) |
| Water | 80 | 0 |
| Hydrogen | 13.8 | − 259.25 |
| Carbon dioxide | 43.2 | − 57.6 |
| Nitrogen | 6.15 | − 210 |
| Oxygen | 3.3 | − 218.8 |
3. The latent heat of vaporization is the amount of heat necessary to change 1 g of a substance at its boiling point from a liquid to a gas without causing a change in temperature.
a. Boiling point is the temperature at 1 atm of pressure at which a substance changes from a liquid to a gas.
b. The total volume of a substance must change from a liquid to a gas before its temperature changes.
(1) For a substance to boil, its vapor pressure must equal the pressure of the atmosphere above it.
(2) Evaporation is a surface phenomenon whereby individual molecules of a substance gain enough heat to change their state. Boiling, on the other hand, occurs throughout the entire volume of the substance.
c. Latent heats of vaporization are generally much greater than latent heats of fusion.
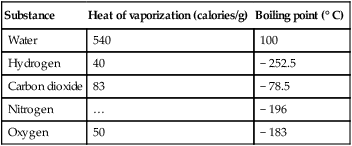
d. Latent heats of vaporization and boiling points for various substances:
| Substance | Heat of vaporization (calories/g) | Boiling point (° C) |
| Water | 540 | 100 |
| Hydrogen | 40 | − 252.5 |
| Carbon dioxide | 83 | − 78.5 |
| Nitrogen | … | − 196 |
| Oxygen | 50 | − 183 |
G Effects of pressure on melting and boiling points
1. In general, the greater the pressure over a substance, the higher the temperature necessary to cause the substance to change its state. However, pressure has a greater effect on the boiling point of a substance than on its melting point.
2. Critical temperature: The highest temperature at which a substance can exist as a liquid, regardless of the amount of pressure applied to it (O2 = −118.8° C).
3. Critical pressure: The lowest pressure necessary at the critical temperature of a substance to maintain it in its liquid state (O2 = 49.7 atm pressure).
4. Critical point: The combination of the critical temperature and the critical pressure of a substance.
H Triple point: Specific combination of temperature and pressure in which a substance can exist in all three states of matter in dynamic equilibrium.
I Sublimation: Transition of a substance from a solid directly to a gas without existence in a liquid state. The heat of sublimation equals the heat of fusion plus the heat of vaporization.
A Liquids flow and assume the shape of their containers.
B Liquids exert pressure that varies with the depth of the liquid and its density.
C According to Pascal’s principle the shape or volume of a container does not affect the pressure of a liquid; pressure is only affected by the liquid’s height and density.
D Variations in liquid pressure in a column produce an upward force referred to as buoyancy.
E As a result of buoyancy, objects in water appear to weigh less in water than in air.
F Liquids exert a buoyancy force because the pressure below a submerged object always exceeds the pressure above the object.
G According to Archimedes principle, the buoyancy force must equal the weight of the fluid displaced by the object.
H If the weight of the object exceeds the weight of the displaced water, it sinks, but if it weighs less than the displaced water, it floats.
I Archimedes principle is used to determine the specific gravity of liquids such as urine.
A The kinetic theory of gases normally is applied to relatively dilute gas volumes.
B Principles of the kinetic theory of gases are:
1. Gases are composed of molecules that are in rapid continuous random motion.
2. The molecules undergo near collisions with each other and collide with the walls of their container.
3. All molecular collisions are elastic, and as long as the container is properly insulated, the temperature of the gas remains constant.
4. The KE of molecules of a gas is directly proportional to the absolute temperature.
a. An increase in temperature causes an increase in KE of the gas.
b. The increased KE causes an increase in the velocity of the gas molecules.
c. The increased velocity causes an increase in the frequency of collisions.
d. The increased frequency of collisions causes an increase in the pressure in the system.
e. With an increase in temperature, the degree of increase in the velocity of gas molecules is indirectly related to their molecular weight (MW).
A One gram molecular weight (GMW), 1 g atomic weight, 1 g ionic weight, and so on, of a substance contains 6.02 = 1023 particles of that substance.
B The above mass of any substance is referred to as a mole.
C One mole of a gas at ° C and 760 mm Hg (standard temperature and pressure; STP) occupies a volume of approximately 22.4 L. (There is a small percent variation in this number for individual gases; e.g., CO2 = 22.3 L.)
D An equal number or fractions of moles of different gases at a specific temperature and pressure occupy the same volume and contain the same number of particles.
A Density (D) is the mass of an object per unit volume (V) and usually is expressed as g/L:
B On the surface of the earth, mass in equation 7 may be replaced by weight.
C Calculation of densities of solids and liquids is straightforward because their volumes are relatively stable at various temperatures and pressures.
D The volumes of gases, on the other hand, are severely affected by temperature and pressure.
E For this reason, the standard density of all gases is determined at STP (0° C and 760 mm Hg pressure) conditions where the volume used is 22.4 L and the weight used is the GMW of the particular gas:
F Standard densities of various substances:
G The density of a mixture of gases is determined by the following equation:
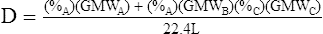 (9)
(9)Example: The density of a gas containing 40% oxygen, 55% nitrogen, and 5% carbon dioxide would be computed as follows:
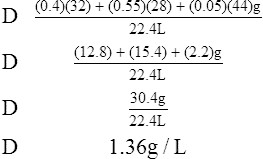
H Specific gravity: Ratio of the density of a substance to the density of a standard. The specific gravity of solids and liquids is determined using water as the (density, 1 kg/L) standard; for gases, oxygen is used as the standard. When it is stated that the specific gravity of urine is 1.10, it means the urine is 1.10 times heavier than H2O because of the dissolved substances in the urine.
A Pressure (P) in any sense is equal to force per unit area:
B The pressure of a gas is directly related to the KE of the gas (see Section II, States of Matter) and to the gravitational attraction of the earth.
C With an increase in altitude, the gravitational attraction of the earth on the molecules of gas in the atmosphere decreases.
1. This causes a decrease in density of the atmospheric gases.
2. Decreased density results in fewer molecular collisions.
3. Thus, with increasing altitude there is a nonlinear decrease in the pressure of the total atmosphere and of individual gases.
4. Even though there is a steady decrease in the pressure of the atmosphere with altitude, the concentration of gases in the atmosphere remains stable to an elevation of approximately 50 miles.
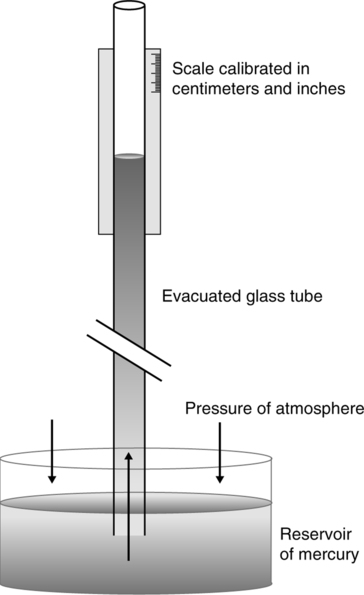
D The barometric pressure (Pb) of the atmosphere is equal to the height of a column of fluid times the fluid’s density (Figure 2-2):
If the fluid used is mercury, normal atmospheric pressure is equal to psi:
E Mercury’s density in the metric system is 13.6 g/ml; in the British system it is 0.491 lb/in.3.
F Gas pressure is frequently expressed as the height of a substance (i.e., mm Hg, cm H2O). These are not true pressure expressions, but they may be easily converted to the proper pressure notation by use of equation 11 if necessary.
G Atmospheric pressure can be determined by a number of pressure-measuring devices (Figure 2-3).
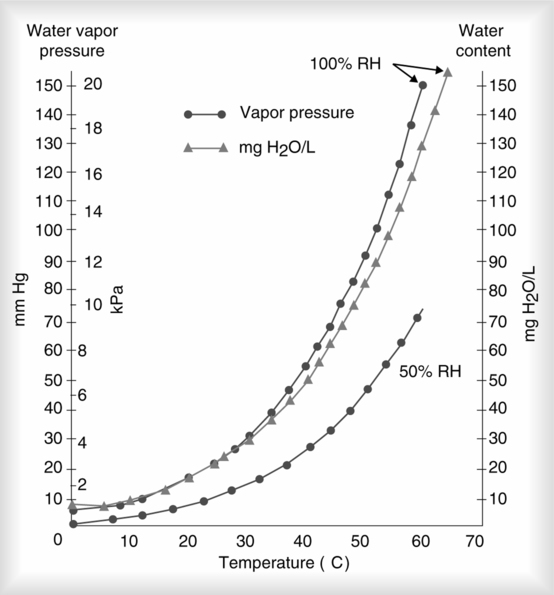
A Water vapor content of the air under atmospheric conditions is variable. Temperature is the factor that most significantly affects water vapor content in the atmosphere.
1. The process of a liquid changing into a gas at a temperature lower than its boiling point is referred to as evaporation.
2. The process of a gas changing into liquid at a temperature lower than its boiling point is called condensation.
B At a particular temperature, there is a maximum amount of water that a gas can hold, capacity for water vapor.
C Because the boiling point of water (100°C) is considerably higher than the normal temperature of the atmosphere, the maximum water vapor content of the atmosphere varies with temperature.
1. As the temperature increases, the rate of evaporation of water accelerates, and the capacity of the atmosphere to hold water increases.
2. All other standard gases in the atmosphere have boiling points much lower than atmospheric temperature. This causes stability in their concentrations.
3. Water is the only standard atmospheric gas that responds to temperature changes in this manner.
D Expressions of water vapor content
1. Absolute humidity is defined as the actual weight of water vapor contained in a given volume of gas.
a. Absolute humidity may be expressed as grams per cubic meter or milligrams per liter.
b. The maximum absolute humidity at 37° C is 43.8 g/m3, or 43.8 mg/L.
2. Partial pressure (Pp) of water vapor (PH2O), maximum PH2O at 37° C, is equal to 47 mm Hg.
3. Maximum weight of water and water vapor pressure at different temperatures:
| Temperature (° C) | Weight (mg/L) | PH2O (mm Hg) | Temperature (° C) | Weight (mg/L) | PH2O (mm Hg) |
| 20 | 17.30 | 17.5 | 29 | 28.75 | 30.0 |
| 21 | 18.35 | 18.7 | 30 | 30.35 | 31.8 |
| 22 | 19.42 | 19.8 | 31 | 32.07 | 33.7 |
| 23 | 20.58 | 21.1 | 32 | 33.76 | 35.7 |
| 24 | 21.78 | 22.4 | 33 | 35.61 | 37.7 |
| 25 | 23.04 | 23.8 | 34 | 37.57 | 39.9 |
| 26 | 24.36 | 25.2 | 35 | 39.60 | 42.2 |
| 27 | 25.75 | 26.7 | 36 | 41.70 | 44.6 |
| 28 | 27.22 | 28.3 | 37 | 43.80 | 47.0 |
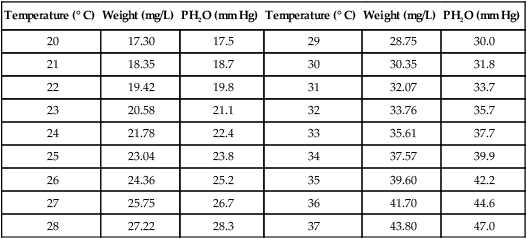
4. Relative humidity (RH) is defined as a relationship between the actual weight or pressure (content) of water in air at a specific temperature and the maximum weight or pressure (capacity) of water that air can hold at that specific temperature. RH is expressed as a percentage.
a. Expressions of actual and maximum amounts of water:
b. Formula for calculating RH:
c. If water content is kept constant and temperature is increased, RH decreases because capacity of air for water increases. As temperature decreases, the opposite effect is seen (Figure 2-4).
5. Gases in the lungs exist under body temperature and pressure saturated conditions: 37° C, RH 100%, pressure is equal to atmospheric pressure.
6. A humidity deficit exists when the actual content of water in a gas entering the lungs is less than the capacity of the gas at 37° C.
IX Dalton’s Law of Partial Pressure
A Dalton’s law states that the sum of the individual Pps of the gases in a mixture is equal to the total Pb of the system.
B The Pp of a gas is equal to the Pb times the concentration of the gas in the mixture:
Example: If the Pb is 760 mm Hg and the concentration of O2 is 21%, what is the PO2?
C The concentration of a gas is equal to the Pp of the gas divided by the Pb times 100:
Example: If the Pb is 750 mm Hg and the PO2 is 200 mm Hg, what is the concentration of O2?
X Effect of Humidity on Dalton’s Law
A Water vapor pressure does not follow Dalton’s law because under normal atmospheric conditions, the PH2O is dependent primarily on temperature and available water for evaporation.
B When the Pp of a gas is calculated and water vapor is present, the total Pb of the system must be corrected for water vapor before the Pp of any other gas can be calculated.
C The following is a modification of Dalton’s law to account for the presence of water vapor:
Example: If Pb is 770 mm Hg, PH2O is 30 mm Hg, and the concentration of O2 is 50%, what is the PO2?
D When the temperature is 37° C with Pb 760 mm Hg, the gas saturated with water vapor, and the oxygen concentration 21%, the PO2 is 149.7 mm Hg:
A The ideal gas laws apply to dilute gases at temperatures above the gases’ boiling point.
B The closer the temperature to the boiling point of a gas, the greater the error involved in using the gas laws.
C The ideal gas law demonstrates the interrelationships among volume, pressure, temperature, and amount of gas.
1. According to the ideal gas law, multiplying the pressure of the system by the volume of the system and dividing this by the product of the absolute temperature and amount of gas in any gas system yields a constant. This is referred to as Boltzmann’s constant, which can be applied to all gas systems.
D Boyle’s law states that pressure and volume of a gas system vary inversely if the temperature and amount of gas in the system are constant.
1. Boyle’s law mathematically is:
where nRT is equal to a constant, thus
2. In a system where temperature and amount of gas are constant, the original pressure and volume equal the final pressure and volume:
E Charles’ law states that the temperature and volume of a gas system vary directly if the pressure and amount of gas in the system are constant.
1. Charles’ law mathematically is:
2. In a system where the pressure and amount of gas are constant, the original temperature and volume equal the final temperature and volume:
F Gay-Lussac’s law states that the pressure and temperature of a gas system vary directly if the volume and amount of gas in the system are constant.
1. Gay-Lussac’s law mathematically is:
2. In a system where the volume and amount of gas are constant, the original pressure and temperature equal the final pressure and temperature:
G The combined gas law states that pressure, temperature, and volume of gas are specifically related if the amount of gas remains constant.
1. The combined gas law mathematically is:
2. In a system where the amount of gas in a system is constant, the original pressure, temperature, and volume are equal to the final pressure, temperature, and volume:
H All gas law calculations must use temperature on the Kelvin scale for accurate results.
I Water vapor does not react as an ideal gas; therefore, in a system where water vapor is present, water vapor pressure must be subtracted from the total system pressure before calculations are made.

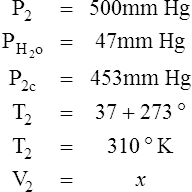
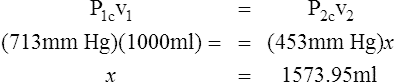
J When precision is needed, the Pb reading should be corrected for the expansion of mercury as affected by temperature.
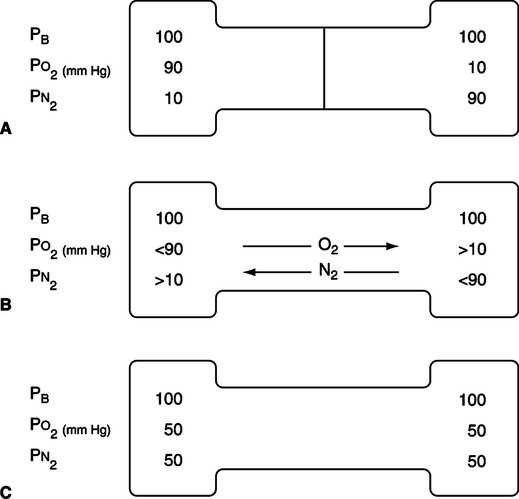
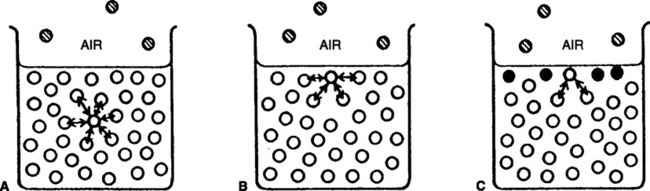
A Diffusion is movement of gas from an area of high concentration of a gas to an area of low concentration of that gas (Figure 2-5).
B As diffusion occurs, gases occupy the total container volume as if they were the only gas present; in other words, a gas in a container distributes itself with time equally throughout the whole container volume.
C The rate of diffusion of a gas through another gas is affected by the following factors:
1. The concentration gradient, which is directly related to the rate of diffusion.
2. The temperature, which is directly related to the rate of diffusion.
3. The cross-sectional area available for diffusion, which is directly related to the rate of diffusion.
4. The MW, which is indirectly related to the rate of diffusion.
5. The distance the gas has to diffuse, which is indirectly related to the rate of diffusion:
D Henry’s law states that the amount of a gas that can dissolve in a liquid is directly related to the Pp of the gas over the liquid and indirectly related to the temperature of the system.
1. Henry’s law establishes the solubility coefficients of gases in liquids.
2. Solubility coefficients of oxygen and carbon dioxide in plasma at 37° C:
E Graham’s law states that the rate of diffusion of a gas through a liquid is indirectly related to the square root of the GMW of the gas.
F If Henry’s law and Graham’s law are combined, the rates of diffusion of carbon dioxide to oxygen can be compared under conditions of equal pressure gradients, distances, cross-sectional areas, and temperatures.
1. When the aforementioned variables are equal, the only factors affecting the comparison would be the GMWs of the gases and their solubility coefficients.
2. The comparison may be mathematically represented as follows:
3. Thus, under the previously mentioned conditions, carbon dioxide would diffuse approximately 19 times faster than oxygen.
4. However, at the alveolar capillary membrane, pressure gradients for oxygen and carbon dioxide are not equal.
a. Diffusion gradient for oxygen is 60 mm Hg.
b. Diffusion gradient for carbon dioxide is 6 mm Hg.
c. As a result of these pressure gradients, oxygen equilibrates across the alveolar-capillary membrane slightly faster than carbon dioxide.
d. Oxygen equilibrates in approximately 0.23 second, whereas carbon dioxide equilibrates in approximately 0.25 second.
A Elastance (E) is the ability of a distorted object to return to its original shape.
B Compliance (C) is the ease with which an object can be distorted.
C Compliance and elastance are inversely related:
D If the compliance of a system increases, the elastance of the system decreases.
E If the compliance of a system decreases, the elastance of the system increases.
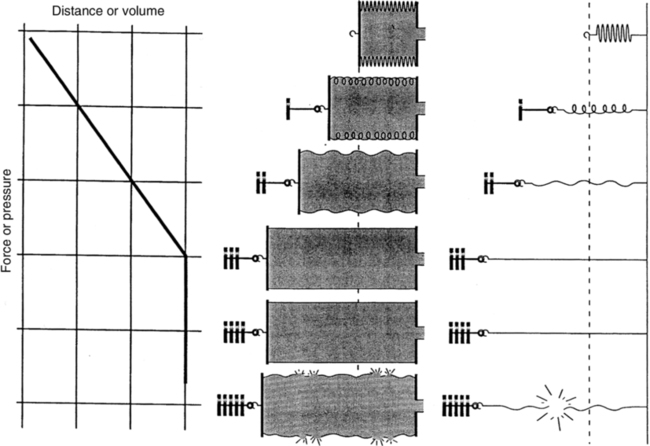
F Hook’s law defines the response of elastic bodies to distorting forces (Figure 2-6).
1. It states that an elastic body stretches equal units of length or volume for each unit of weight or force applied to it.
2. This relationship holds until the elastic limit of the system is reached.
3. Beyond the elastic limit, each unit of weight or force produces smaller and smaller changes in length or volume.
4. With a true spring, exceeding the elastic limit results in permanent distortion of the spring.
5. This principle can be applied to the lung. Overstretching with large tidal volumes results in disruption to the alveolar-capillary membrane and the development of ventilator-induced lung injury (see Chapter 23).
G Elastance can be mathematically defined as:
H Compliance can be mathematically defined as:
I See Chapter 5 for more details related to respiratory physiology.
A Surface tension (ST) is a force that exists at the interface between a liquid and a gas or between two liquids.
B The ST of a liquid is the result of like molecules being attracted to each other and thus moving away from the interface. This causes the liquid to occupy the smallest volume possible (Figure 2-7).
C As a result of ST, a force is necessary to cause a tear in the surface of the liquid.
D The ST of a liquid is expressed in dynes per linear centimeter.
E ST is indirectly related to temperature.
F LaPlace’s law is used to determine the amount of pressure generated inside a system as a result of ST.
1. The law states that the P in dynes per square centimeter as a result of ST in dynes per centimeter is equal to the ST of the liquid multiplied by 1 over the radii (r) of curvature in centimeters:
2. LaPlace’s law as applied to a drop is:
 (35)
(35)Here reference is made to a perfect sphere that has only two equal radii of curvature, one in the vertical plane and one in the horizontal plane.
3. LaPlace’s law as applied to a bubble is:
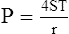 (36)
(36)There are two interfaces in a bubble, one on the inside of the bubble and one on the outside; thus, there are four radii. All radii are considered equal because the film of the bubble is only angstroms in diameter.
4. LaPlace’s law as applied to a blood vessel is:
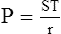 (37)
(37)When the radii of curvature of a blood vessel are considered, the only radius used in the calculation is that of the vessel’s width because the radius of length is so great. When the inverse of the radii of length is calculated, the number essentially goes to infinity and is meaningless in calculating the pressure as a result of ST.
5. It is important to remember that the pressure as a result of ST is indirectly related to the radius. The smaller the sphere, the greater the pressure as a result of ST (Figure 2-8).
6. See Chapter 5 for details on the effect of ST on lung mechanics.
G Critical volume is a volume below which the effects of ST are so great that the structure collapses. Once the critical volume is reached, collapse is always imminent.
H The force necessary to inflate a deflated object increases markedly as the critical volume is reached but rapidly decreases once the critical volume is exceeded.
I It is difficult to reinflate a collapsed lung. It requires high pressure to reopen, but once reopened the pressure needed to keep the lung open rapidly decreases.
J Chemicals referred to as surfactants reduce the ST of a fluid. Surfactants are surface-active agents that interfere with the molecules of the fluid at the surface, causing a reduction in the force (ST) that draws the fluid centrally. Soaps and detergents are common surfactants (see Figure 2-7).
1. The product of the cross-sectional area of a system and the velocity for a given flow rate is constant (Figure 2-9).
2. Thus, if the flow of gas is constant, the cross-sectional area and gas velocity are inversely related.
3. In any system with varying radii, the velocity of gas movement must change inversely as the radius changes.
1. Velocity is the speed with which movement between two points occurs (e.g., miles/hour, cm/sec).
2. Flow is the volume passing a single point per unit of time (L/min).
3. The two are related and may change directly or indirectly with each other, depending on the specific changes that occur in the structure of the system.
1. In general, resistance is defined as the force (pressure) necessary to maintain a specific flow in a particular system (Figure 2-10).
2. For gas movement to occur, there must be a pressure gradient. The overall resistance of the system determines the magnitude of the pressure gradient. Resistance to flow is defined by Ohm’s law. It states that resistance is equal to the change in pressure divided by flow:
3. Resistance is a physical property of the system.
4. The change in pressure reflects the amount of pressure necessary to maintain a specific flow in the system.
5. The resistance of a system is increased under the following situations:
6. If the resistance of a system is constant, an increase in pressure gradient results in an increase in system flow.
7. An increase in resistance with a constant pressure gradient results in a decrease in flow.
8. In general, if resistance is constant, pressure gradient and system flow are directly related.
D Series and parallel resistances (Figure 2-11)
1. Series resistances are resistance elements arranged sequentially in the direction of flow (e.g., heat and moisture exchanges attached to an endotracheal tube). The exchanger and the tube are series resistors.
(a) When resistors are placed in series their individual resistances are additive.
(b) The pressure necessary to maintain flow is equal to flow times the sum of the individual resistance.
2. Parallel resistances are resistance elements arranged next to each other where flow is divided between resistive elements. The mouth and nose are arranged in parallel.
(a) When resistors are placed in parallel the pressure gradient across them is equal, but flow through each is related to the resistance of each resistor.
(b) The pressure necessary to maintain flow across a parallel system is equal to the sum of the flow times resistance of each resistor.
 1(R1)+(
1(R1)+( 2)(R2)+(
2)(R2)+( 3)(R3) (40)
3)(R3) (40)where  1,
1,  2,
2,  3 represent the flow through each resistor, and R1, R2, and R3 represent the resistance of each resistor.
3 represent the flow through each resistor, and R1, R2, and R3 represent the resistance of each resistor.
1. Conductance is the capability of a system to maintain flow.
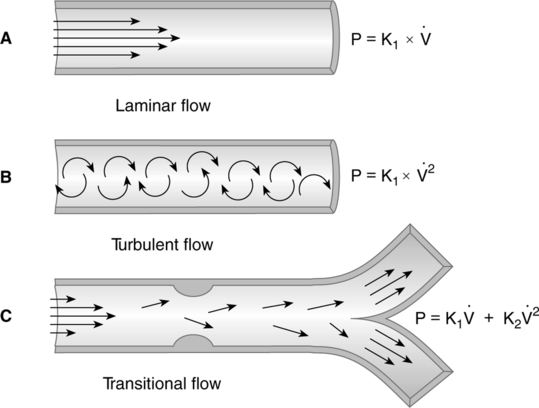
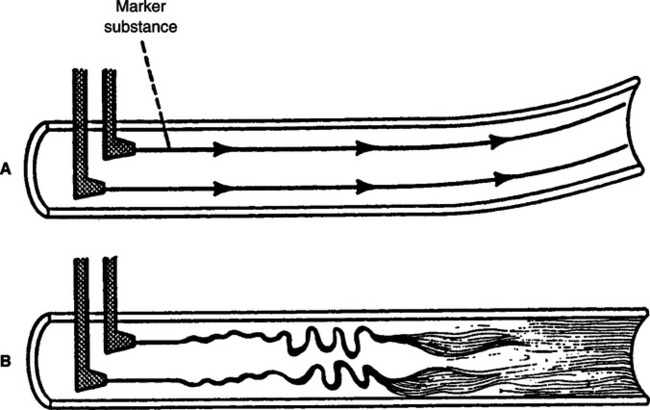
1. Laminar flow is a smooth, even, nontumbling flow.
a. Laminar flow proceeds with a cone front. The molecules of gas in the center of the system encounter the least frictional resistance and move at a greater velocity than those at the sides of the system (Figure 2-12).
b. In all laminar flow situations, the pressure necessary to overcome airway resistance is directly related to flow:
2. Turbulent flow is a rough, tumbling, uneven flow pattern.
a. Turbulent flow proceeds with a blunt front. Because of a tumbling effect, all of the molecules in the system encounter the walls of the vessel (see Figure 2-12).
b. In a turbulent flow system, the pressure necessary to overcome airway resistance is directly related to the square of the flow:
c. The pressure gradient necessary to maintain turbulent flow is much higher than that necessary to maintain laminar flow.
d. A marker substance (smoke) is rapidly mixed with the primary gas in a turbulent system but not in a laminar system (Figure 2-13).
3. Tracheobronchial flow is a combination of areas of laminar and turbulent flow. Tracheobronchial flow is believed to be the type of flow maintained throughout the respiratory system (see Figure 2-12).
1. Reynold’s number (RN) is a dimensionless number that indicates whether flow through a system is laminar or turbulent.
2. RN is calculated as follows:
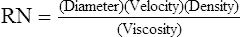 (44)
(44)where the diameter refers to the diameter of the system, and velocity, density, and viscosity refer to the gas that is flowing in the system.
3. If RN is ≥2000, the flow in the system is turbulent. If it is < 2000, the flow is laminar.
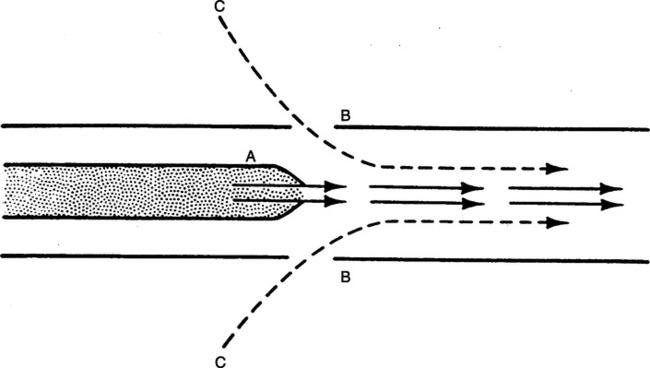
1. Poiseuille’s law was originally used to determine the viscosity of a fluid.
2. It also defines the factors that effect the pressure required to maintain laminar flow.
3. Viscosity is defined as a fluid’s resistance to deformity and for gases increases with increased temperature.
4. Poiseuille’s law states that viscosity (n) is equal to the change in pressure (ΔP) times pi (π) times the radius to the fourth power (r4) divided by eight times the length of the system (8l) times flow ( ):
):
5. Rearranging equation 45 and placing on the left side of the equation those factors that would be constant when ventilating a patient and on the right side of the equation those factors that would vary, the result is:
6. The right side of equation 46 indicates the relationship between pressure, flow, and radius of a laminar gas flow system.
7. If the radius were to decrease by one half, there would be a 16-fold change in the right side of the equation.
8. To maintain the left side of the equation constant, a 16-fold change in pressure or flow or a combination of both would be necessary to minimize the effects of the decrease in radius.
9. Thus, to minimize the effects of an airway diameter decrease, it would be necessary to increase the pressure gradient and/or decrease the flow in the system. As gas enters deeper into the respiratory tract, flow through individual segments decreases.
10. Theoretically, Poiseuille’s law can be applied only to homogeneous fluid systems that are nonpulsatile and laminar through a single cylinder.
11. Thus, Poiseuille’s law cannot be directly applied to the respiratory and cardiovascular systems, but it does provide insights into the interrelationships between pressure, flow, and system radius in physiologic systems.
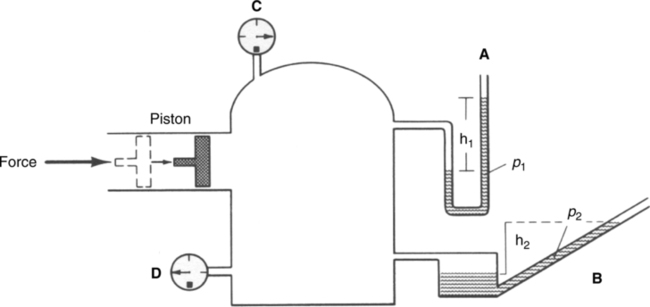
1. Bernoulli effect: As a gas moves through a free-flowing system, transmural pressure is inversely related to velocity of the gas (i.e., as the velocity of the gas increases, the transmural pressure decreases; Figure 2-14).
2. Statement 1 holds true because the total energy in a free-flowing system is equal at all points (conservation of energy).
3. In a free-flowing system of limited size functioning essentially as a non–gravity-dependent system, the total energy is equal to the sum of the KE and the transmural pressure energy.
4. Transmural pressure energy is purely a measure of the force that the gas flow exerts on the walls of the system (Figure 2-15).
5. KE in this sense is equal to 0.5 times the gas density times the gas velocity squared:
6. Thus, in a free-flowing system:
This illustrates the fact that velocity and transmural pressure are inversely related.
7. As the radius of the system decreases and velocity of the gas moving through the system increases, transmural pressure decreases, per equation 48.
8. The lower the density of a gas, the smaller the decrease in transmural pressure as the gas moves through a stenosis. This relationship demonstrates the effect of density on maintaining a more laminar flow (see Chapter 34).
a. The Venturi principle is an extension of the Bernoulli effect (see Figure 2-14).
b. It states that distal to a stenosis in a free-flowing system, prestenotic pressure can be restored if the angle of divergence of the system from the midline does not exceed 15°.
c. Also, if the stenosis in the system is small enough, subatmospheric transmural pressure can be developed and used to entrain a second gas or liquid.
d. Venturi systems can be designed to deliver specific oxygen concentrations.
e. The concentration of oxygen delivered by a Venturi system can be varied by:
f. Backpressure on a Venturi system decreases the volume of fluid or gas entrained. This causes the oxygen concentration delivered by such a system to increase.
1. The use of a constant flow of gas (jet) to entrain a second gas (Figure 2-16).
2. No pressure gradient exists between the jet flow and the ambient environment.
3. Air entrainment is a result of the viscous shearing force between a dynamic fluid and a stationary fluid resulting in a change in velocities.
4. Provided free access is allowed for the entrained gas, mixing at specific ratios can be maintained.
5. Altering the flow of the gas from the jet alters the total volume exiting the system but does not alter entrainment ratios or resulting gas concentration.
6. Changing the size of the jet orifice or the size of the entrainment port alters entrainment ratios.
7. Entrainment ratios are the same as those commonly listed for Venturi systems (see Chapter 34).
8. Backpressure on the system decreases entrainment and increases FI O2.
9. Jet mixing is responsible for the function of air entrainment masks and most other systems in respiratory care commonly attributed to the Venturi effect.
K Driving pressure as illustrated in Figure 2-15 is the pressure necessary to maintain flow between point A and B in a gas flow system.

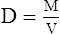
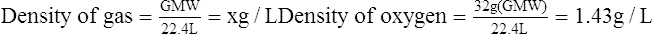
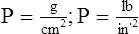


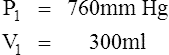
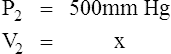
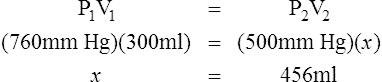
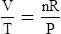
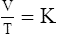
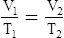
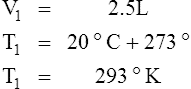
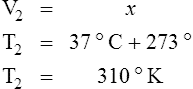
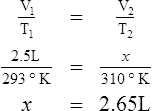
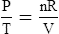
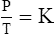

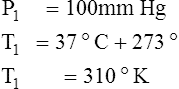
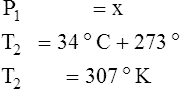
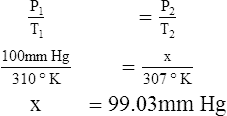
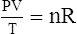
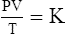
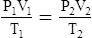

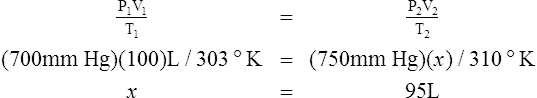
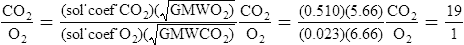
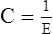
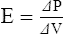
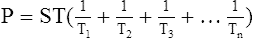



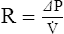
 =flow.
=flow.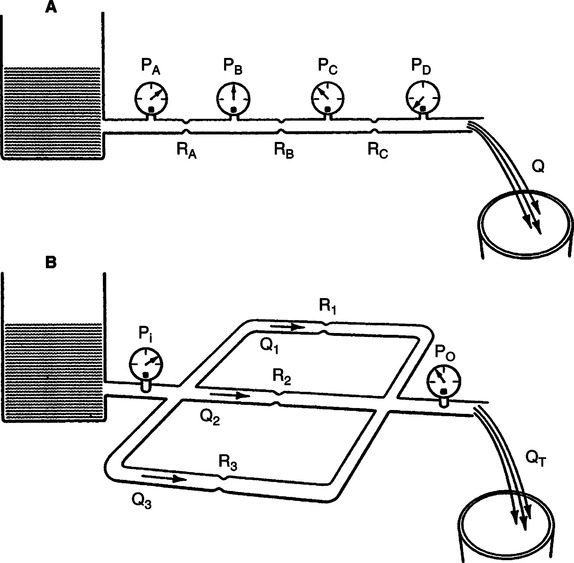
 (R1 + R2 + R3)
(R1 + R2 + R3)