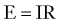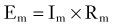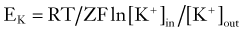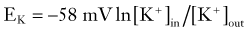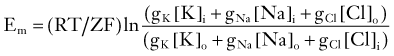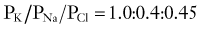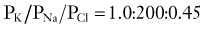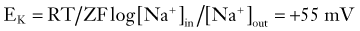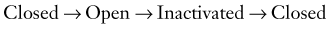CHAPTER 49 Electrophysiologic Properties of the Mammalian Central Nervous System
Electrical Properties of Mammalian Cells
The biophysical bases for maintenance of this electric potential have been extensively investigated experimentally and modeled by mathematical simulations. Under normal resting conditions, mammalian cells allow transmembrane ion currents such that the internal portion of the cell is negatively charged; the presence of nonpermeant anions such as proteins also contributes to the maintenance of transmembrane potentials. This relatively stable state results in a net transmembrane potential of several millivolts and is commonly referred to as the resting membrane potential (RMP) (Fig. 49-1).
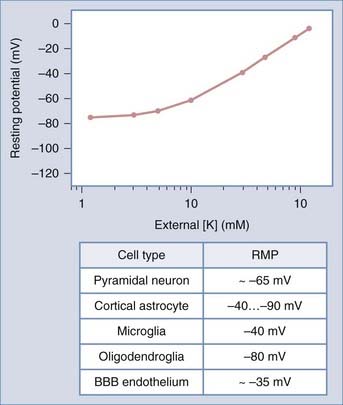
FIGURE 49-1 Relationship between resting potential and [K+]out. The line represents the “ideal” case predicted by the Nernst equation (see Equation 3). Experimental measurements show a significant departure from a linear dependency at physiologic [K+]out values. Resting potential values for excitable and nonexcitable central nervous system cells are shown. BBB, blood-brain barrier; RMP, resting membrane potential.
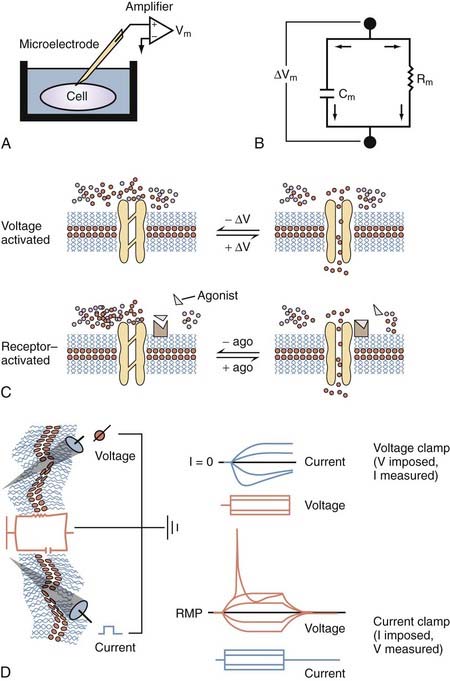
Most of what we know about the physiology of excitable cells was derived from electrical measurements (Fig. 49-2). Our knowledge of the complex properties of the CNS is based on the application to neuronal cells of simple physical rules governing the movement of charged particles. The physical principles of cell electrophysiology can be thus be compared with the biophysical rules governing flow of electric current through a so-called RC circuit (see Fig. 49-2), where electrons flow through a resistive component (in the case of living cells, represented by ion channels) set in parallel with a capacitive component (represented by the poorly conductive phospholipid bilayer). Ohm’s law describes the relationship between current flow (I) and the resulting voltage drop (E) across a resistor when no capacitive component is present. This is, of course, an abstract situation, in particular when dealing with ion fluxes across biologic membranes, but it allows one to understand the basic principles governing flow of electric current.
The following relationship constitutes Ohm’s law (or principle):
where I represents the current flowing through a resistance (R) when voltage is applied. In a hypothetical cell, this relationship can be written as follows:
where Em represents the difference in voltage (in millivolts) between the inside and the outside of the cell, Im represents the net current flowing at that particular time across the cell membrane, and Rm is the total membrane resistance. An important consequence of this relationship is that small changes in current will significantly affect cell RMP only when Rm is large. This is particularly important for inhibitory synaptic currents; for instance, in the case of γ-aminobutyric acid receptor A (GABAA) activation, inhibition is achieved not only by hyperpolarizing cell RMP further away from the firing threshold but also by greatly increasing postsynaptic conductance,* thus reducing the synaptic efficacy of concomitant excitatory signals.
A mathematical derivation of Ohm’s law useful for studies of biologic membranes was first formulated by Nernst,1 who described the relationship between intracellular and extracellular ion concentrations and changes in transmembrane potential attributable to permeation of an ion. In the case of potassium ions, the Nernst equation can be written as follows:
where R and F are constants, T is the temperature at which the observation is performed, and Z is the charge of the permeant ion. Note that if the charge (sign, or “Z” in Equation 3) of the permeant ion is changed (e.g., if we look at the Nernst equation for chloride), the direction of the gradient is changed as well. The logarithm of the ratio between intracellular and extracellular K+ dominates the right side of the equation because RT/ZF is constant under most biologic conditions when temperature can be maintained within a few degrees. This equation predicts, as expected from Ohm’s law, that net potassium flux will approach zero when intracellular and extracellular potassium levels are isosmolar, that is, when EK = 0 mV. Under physiologic conditions ([K+]out = 3.5 mM; [K+]in = 135 mM), the transmembrane potential at which potassium flux will be nil is around −90 mV.* This value constitutes the potassium equilibrium potential at these concentrations. Note that small changes in the extracellular potassium concentration will cause relatively large changes in the fraction of total membrane currents attributable to potassium ions. Because permeability to potassium is essential for maintenance of RMP, a net increase in extracellular potassium will cause a significant departure from RMP (see Fig. 49-1).
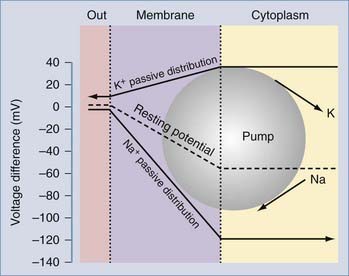
It can be seen that a 10-fold change in the concentration gradient for potassium can produce a 58-mV change in membrane potential. Because under normal conditions there is an almost 40-fold outward gradient for potassium ions and a 12-fold inward gradient for sodium ions, the resulting equilibrium potentials are −92 mV and +65 mV, respectively. Since the membrane at rest is much more permeable to potassium than to sodium (see later), RMP is closer to EK than to ENa.
Two additional considerations can help us understand the genesis of cell RMP: (1) if the membrane is exclusively permeant to K+ and no active, electrogenic transport of ions occurs, the cell potential will tend toward EK and only small movements of K+ will be sufficient to maintain RMP at −92 mV, and (2) if the membrane potential is clamped at EK, net potassium flux will be zero (as predicted by the fact that EK is the equilibrium potential for potassium). If the membrane potential is held positive with respect to EK, outward potassium currents will develop; conversely, if RMP is held at potentials negative with respect to EK, inward potassium fluxes will develop. Interestingly, the notion that cell RMP is controlled by potassium ions was first derived independently from direct observations: Julius Bernstein in 1902 correctly predicted that in most mammalian cells, potassium ions govern the transmembrane voltage difference.2 Direct experimental evidence was achieved only half a century later when a microelectrode could be placed into cells to directly measure RMP and the effects of changing [K+]out. Bernstein also proposed that selective potassium permeability was lost during the process of excitation, during which numerous “pores” opened to allow entry of other small ions (Cl− and Na+).2 This theory explained several features of the regulation of RMP and generation of action potentials, including the depolarizing effects of [K+]out.
In fact, a prediction of the formalism just presented is that RMP changes linearly with [K+]out. As shown in Figure 49-1, experimental evidence contradicts this notion, at least in the case of mammalian neurons.† Most neurons depolarize significantly after large changes in extracellular potassium, whereas changes around physiologic potassium concentrations do not significantly affect neuronal RMP. This can only be due to concomitant participation of other conductances. Although the exact nature of the ionic conductances contributing to the regulation of neuronal RMP varies between different neurons, a generic set of equations predict how these “parallel” conductances may affect Em. The most illustrious of these equations was provided by Goldman, who described the expected RMP in a cell endowed with more than one ion current mechanism as
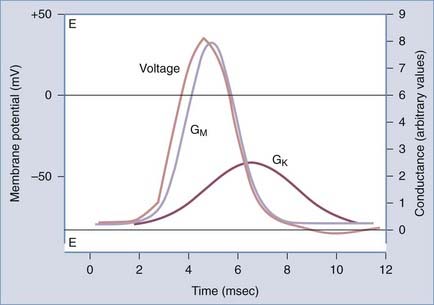
where GK, GNa, and GCl represent the conductances for potassium, sodium, and chloride.3 Note that these conductance values are multiplied by the relative chemical concentration gradient for each ion, thus combining the “passive” electro-osmotic tendency for ion permeation with the average conductance of the membrane for a particular ion. Note also that if GCl and GNa are close to zero, the transmembrane potential is governed almost exclusively by potassium ions and their conductance. This condition is common at resting potential in most neurons and glial cells, where IK (and to some extent Ipump) determines RMP (Fig. 49-3).
In 1949, Alan Hodgkin and Bernard Katz first applied the Goldman equation systematically to changes in membrane potentials evoked by altering external ion concentrations in the squid giant axon.4 They measured changes in RMP induced by changes in [K+]out, [Na+]out, and [Cl−]out. They discovered that although changes in extracellular potassium dramatically changed RMP, comparable changes in [Na+]out had little effect. Changing [Cl−]out had an intermediate effect. The following permeability ratios were obtained at rest:
whereas when PNa predominates, the following applies:
which is approximately the peak value of action potential overshoot. Direct measurement of changes in the relative permeability for Na+ and K+ contradicted one of the hypotheses formulated by Bernstein, who incorrectly predicted that neuronal excitation was due to loss of potassium permeability rather than activation of an inward sodium current (Table 49-1). Had this hypothesis been correct, the maximum depolarizing value reached during the action potential would have been around 0 mV and not at +30 mV as experimentally determined by Hodgkin and Katz.
TABLE 49-1 Glossary of Commonly Used Electrophysiologic Terms
| Inward current | Positive charges enter the cell (e.g., INa responsible for the action potential upstroke) |
| Outward current | Positive charges leave the cell (e.g., IK during action potential repolarization) |
| Depolarization | Change in RMP to less negative values (e.g., EPSP) |
| Hyperpolarization | Change in RMP to more negative values (e.g., IPSP) |
| Inward-going rectification | Tendency of some ionic currents to allow passage of inward-flowing but not outward-flowing ions (inward rectifier potassium currents) |
| Outward-going rectification | Tendency of some currents to allow passage of outward-flowing but not inward-flowing ions (most other potassium currents activated by depolarization) |
| Voltage clamp | Electrophysiologic technique allowing the study of ion currents and their modulation by voltage, or transmitters/second messengers |
| Current clamp | Technique used during intracellular recordings to determine the resting properties and excitability of cells |
| Single-channel recording | Modern variation (patch clamp) that allows study of the electrophysiologic properties of a single ion channel/protein |
| Multi–single-unit recording | Extracellular recording from a neuron or a cluster of neighboring neurons |
EPSP, excitatory postsynaptic potential; IPSP, inhibitory postsynaptic potential; RMP, resting membrane potential.
Ion Channels in Neurons and Glia
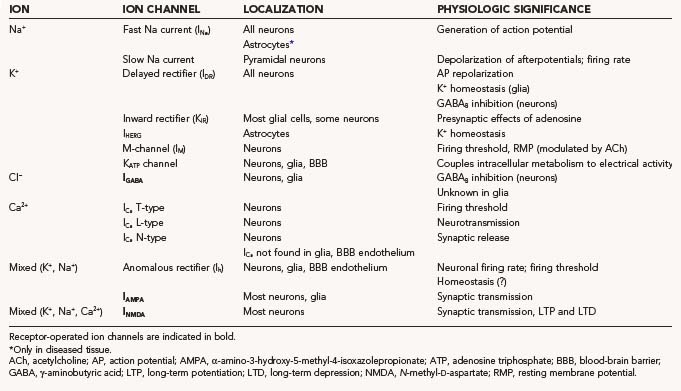
Ion channels are protein channels in cell membranes that allow ions to pass from the extracellular solution to the intracellular solution and vice versa. Similarly, transporters are specialized enzymes that carry specific ions or molecules across otherwise impermeant membranes or against electro-osmotic gradients. Not surprisingly, from a purely thermodynamic (or energetic) point of view, ion channels are less “expensive” to operate, whereas pumps or exchangers require considerable consumption of energy. Most ion channels and pumps are selective in that they allow only certain ions to pass, and an individual cell has ion channels with various ion selectivity. In the context of studies of biologic cell membranes, the term ion selectivity refers to the ability of all cell membranes to distinguish between various ions such as Na+, K+, Ca2+, and Cl−. We will focus on Na+, K+, and Ca2+ channels. All of these voltage-gated channels are made up of one or more pore-forming α subunits and variable numbers of accessory subunits, denoted β, γ, and so on. The α subunits determine ion selectivity and mediate the voltage-sensing functions of the channel. This ion selectivity involves specific pores or channels in the cell membrane, with certain channels being specific for certain ions and the opening or closing (gating) of channels depending on conditions and various interactions with ligands binding to receptors. These receptors are in some cases part of the channel itself and in other cases neighboring entities that control channel dynamics. The selectivity of an ion channel can be “gated,” with the channel effectively opened or closed, and ion channels are said to be voltage gated or ligand gated, depending on how the change in selectivity is provoked. A summary of the most studied CNS ion channels is presented in Table 49-2.
TABLE 49-2 Classification of the Most Studied Central Nervous System Ion Channels Based on the Nature of the Physiologically Permeant Ion
Genesis of Fast Sodium Action Potentials and Properties of Sodium Channels
Action potentials have a characteristic shape once a certain threshold is reached. In normal tissue, stereotyped electrical events follow the initial depolarization (Fig. 49-4). The sequence can be described as follows: (1) RMP moves from an initial negative value (−65 to −80 mV for most neurons) toward the so-called threshold for activation of sodium channels (around −40 mV). This change can be slow and may occur spontaneously as a result of fluctuations in RMP; the threshold is reached rapidly when the initial depolarization is triggered by a synaptic potential (or a summation of synaptic potentials). (2) After reaching the threshold value, an extremely rapid (1 to 2 msec) depolarization occurs because of opening of sodium channels and massive influx of sodium ions into the cell. (3) Termination of the “upstroke” phase depends on a combination of factors: voltage– and time-dependent inactivation of INa and a concomitant decrease in the driving force for sodium occurring in parallel with voltage-dependent activation of IK. (4) Further increases in the permeability to potassium ions restore the pre–action potential RMP values and force the membrane toward EK. (5) Under most circumstances, an undershoot of cell resting voltage occurs (a few millivolts from RMP) as a result of residual activation of IK and the contribution of the electrogenic sodium-potassium adenosine triphosphatase (Na+,K+-ATPase) extruding 3 Na+ ions in exchange for 2 K+. The return to pre–action potential voltage favors the so-called removal of inactivation, a necessary step that allows a subsequent cycle of depolarization-induced action potential firing. This stereotyped and relatively simple sequence of events is typically recorded in axons; other more complex interactions of various INa and IK values may lead to slightly different voltage profiles.
Early pharmacologic studies attempting to elucidate the ionic correlates of the action potential greatly benefited from the availability of naturally occurring toxins that specifically and powerfully block INa. The magic bullet for sodium channels was tetrodotoxin (TTX),5 a lethal poison produced by a selected species of puffer fish (Fugu). TTX is present in large quantities in the liver and female genital organs, but the real culinary treat is the testes of this hermaphroditic animal. Separation of the toxic portions is paramount to survival of the consumer. The sea anemone toxin (ATX) and α-scorpion toxin are also powerful blockers of INa. TTX and other natural toxins block the external portion of the ion channel. Interestingly, although most sodium channels are blocked by micromolar concentrations of TTX, genetic ablation of one amino acid (Tyr or Phe) in the sequence of the ion channel protein confers relative resistance to TTX because binding of the toxin is restricted to this region.6 The amazing specificity of TTX binding suggested that normally occurring variation in the amino acid sequence of ion channels may prove to be an extremely important determinant of not only the pharmacologic properties of the channels but also their inactivation/activation/voltage dependency. In fact, although the poisonous actions of TTX are primarily due to direct blockade of Na+ fluxes through the channel’s pore, ATX and α-scorpion toxin bind to a portion responsible for channel inactivation. Mutations in these regions cause faulty inactivation, a condition linked to neuropathogenesis.
The biophysical correlates of Na+ channel function are well understood today. The general scheme of
explains the properties of whole-cell INa recorded from neurons. The voltage dependency of each process justifies the initial depolarization required to promote the opening of channels; the consequent depolarization induced by sodium current promotes further opening of channels, the process being terminated by time- and voltage-dependent closure of the channels. The passage from closed to open (and visa versa) is referred to as activation (deactivation), whereas the passage from open to inactivated is called inactivation. Removal of inactivation occurs when the channel returns to its closed state.
From a structural point of view, Na+ channels are constituted by αβ1β2 heterotrimers, often with four repeated domains each with six-membrane–spanning subunits. The voltage sensor is located on the fourth transmembrane domain. Different subunits are represented differently in the central and peripheral nervous systems. According to the recent literature, the following tissue-specific localization and pharmacology can be derived: for α subunits, SCN1A is primarily expressed in brain tissue and is blocked by TTX and saxitoxin (SXT). The most abundant brain α subunit is encoded by SCN2A1; this subunit is also found in peripheral nerves, in the initial axonal segment, and in the nodes of Ranvier (TTX and SXT sensitive). SCN2A2 and SC2NA3 are predominantly expressed in the brain, whereas SCN4A encodes channels found in muscle. In addition to TTX, these channels are sensitive to ω-conotoxins (GIIIA, GIIIB, GIIIC). Mutations of these channels are responsible for hyperkalemic periodic paralysis, paramyotonia, and myotonia. The SCN5A subunit is expressed in the heart and in denervated skeletal muscle; in the heart, these channels are responsible for upstroke of the action potential. These subunits are resistant to blockade by TTX and SXT; mutations of these genes are involved in subtypes of long QT syndrome, a cardiac condition that is sometimes associated with epileptic seizures. SCN6A (uterus), SCN10A, SCN11A, and SCN9A (dorsal root ganglion) are all sensitive to TTX. The molecular nature of glial sodium channels and the contribution of a specific α subunit are not fully understood at present. β Subunits are bound covalently to α subunits and provide inactivation kinetics to Na+ channels. Mutations of these SCN1B and SCN1A subunits have been linked to generalized epilepsy with febrile seizures (see Catterall and colleagues7 and Gambardella and Marini8 for review of voltage-gated ion channel–related hereditary diseases).
Calcium Action Potentials and Calcium Channels
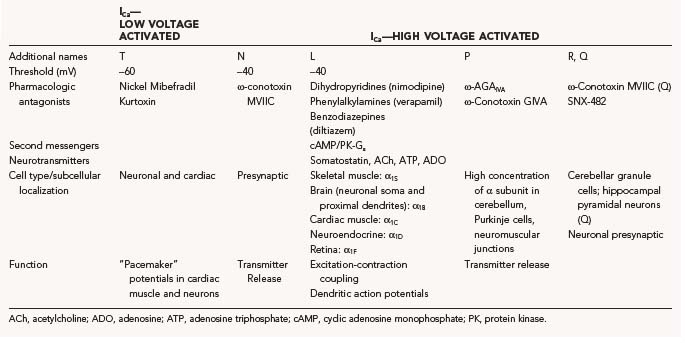
The mechanism of calcium action potentials is somewhat different, but it follows the general principles of threshold for activation and rapid gating mechanisms. As is the case with sodium channels, Ca2+ channels are distributed heterogeneously in the CNS, and even within the same cells different subspecies of Ca2+ channels may be found. This inhomogeneous expression is functionally significant in that it allows Ca2+ influx to perform several different cellular tasks, including depolarization of dendrites and propagation of signals to the cell body, synaptic release of neurotransmitter, contraction, and second messenger function. As for sodium channels, membrane depolarization is the most common trigger for opening of channels; the kinetic properties of Ca2+ channels, however, are characterized by longer time constants. This kinetic behavior underlies the different durations of neuronal/axonal action potentials (INa, 1 to 3 msec) versus cardiac action potentials (several hundreds of milliseconds; large inward currents carried by ICa).* An additional difference between Na+ and Ca2+ action potentials (or the underlying ion channel mechanisms) is the fact that the threshold for ICa activation varies greatly between different Ca2+ channel families. Low-threshold Ca2+ channels (or low voltage activated) are also characterized by relatively rapid opening and closing and are also referred to as “T-type” (transient) currents. High-threshold Ca2+ channels (or high voltage activated) can be further subdivided into neuronal (N), L, and P types. The pharmacologic properties of the calcium channel families are equally complex (Table 49-3).9,10 Although sodium action potentials are typically triggered by depolarization and terminated by depolarization (inactivation of INa and voltage-dependent activation of IK), an additional mechanism is involved in repolarization: activation by intracellular Ca2+ channels that act as powerful terminators of cell depolarization. Ca2+ channels are modulated by important intracellular signals such as cyclic adenosine monophosphate (cAMP; cAMP-dependent protein kinases) and G proteins. These modulatory signals arise from receptor stimulation, thus coupling the activity of postsynaptic (or presynaptic in the case of presynaptic receptors) Ca2+ channels to the activity of neighboring cells.
Given the large number of Ca2+ channel families and their widespread distribution in the nervous system, it is not surprising that numerous neurological disorders have been linked to mutation, autoimmune inactivation, or altered expression of ICa. Disorders affecting the presynaptic terminal of motor axons cause the aforementioned Lambert-Eaton myasthenic syndrome, and mutations of the α1A subunit are responsible for a form of episodic ataxia type 2. Lambert-Eaton myasthenic syndrome is an autoimmune disorder associated with an immunologically abnormal response to neoplasms, whereas type 2 ataxia is caused by defective production of ion channels. Familial hemiplegic migraine is associated with missense mutations in transmembrane segments, and progressive ataxia is caused by either trinucleotide repeat expansion in an intracellular region near the C-terminal or by missense mutation.11
Repolarization of Action Potentials and Maintenance of Resting Membrane Potential: Potassium Channels
Potassium channels are the major contributor to both neuronal and glial RMP. As described earlier, neuronal membranes are predominantly permeable to potassium at rest, which results in cell RMP being near the potassium reversal potential EK. Even more so than neurons, the majority of glial resting channels are K+ permeable, which results in a relatively hyperpolarized RMP. Because of their lack of electrical excitability, a hyperpolarized RMP was previously a defining criterion during physiologic recordings from glia in situ. However, it has been demonstrated over the past several years that glial cells can have a wide range of RMPs, depending on the glial cell subtype, ion channel endowment, location within the nervous system, and developmental stage.12,13
Hodgkin and Huxley initially characterized the important role of (what are now termed) delayed rectifier Kv potassium channels in action potential repolarization.14 These channels, which are blocked by tetraethylammonium (TEA), are similar to sodium channels in that the probability of channel opening is increased by membrane depolarization, with increased opening in proportion to the amount of membrane depolarization. However, delayed rectifier potassium channels differ from sodium channels in that they open more slowly and do not inactivate in the presence of persistently maintained depolarization. As discussed earlier, it is this sodium channel inactivation together with persistent activation of outward potassium channels (and inward chloride channels that produce an outward current by allowing negatively charged chloride ions to enter the cell) that results in action potential repolarization. After repolarization of the action potential, there is a refractory period during which the threshold for initiation of another action potential is elevated. The absolute refractory period, during which an action potential cannot be generated, is followed by a relative refractory period, during which an increased stimulus is necessary to generate an action potential. The refractory period results from residual sodium channel inactivation and potassium channel activation; it limits the maximum firing frequency of different classes of neurons.
The M channel has distinctly different properties from the Kv potassium channels that are responsible for repolarization of the action potential. Although activated by membrane depolarizations, these channels are inhibited by muscarinic acetylcholine receptor binding, as well as by a variety of other neurotransmitters and neuroactive compounds. Rates of channel opening and closing are approximately 100 times slower than delayed rectifier channels. Based on these different characteristics, M channels are thought to have divergent functions in the CNS. On the one hand, by means of their slow kinetics, they prevent repetitive neuronal discharges and hyperexcitability, whereas on the other hand, their inhibition by modulatory neurotransmitters results in local increases in excitation. Inhibition of these channels is thus a double-edged sword that promotes local increases in excitation important to such processes as learning and memory while also potentially rendering areas of the brain proepileptic. The M channel KCNQ1 is mutated in a subtype of long QT syndrome, whereas KCNQ2 and KCNQ3 are mutated in two different forms of benign familial neonatal convulsions.15
Several other potassium currents present in CNS neurons are beyond the scope of this chapter.16 These include (1) channels that are opened by intracellular calcium (IK(Ca)) and function in action potential repolarization and determination of the interspike interval between action potentials; (2) slowly hyperpolarizing currents (IAHP), blockade of which promotes neuronal excitation; (3) mixed cation currents (Iha) that are permeant to K+ and Na+ and are involved in rhythmic burst firing (see the later section “Expression of Ion Currents in Different Neuronal Populations”); (4) the transiently inactivating current IA, which lengthens the interspike interval between action potentials; and (5) KATP channels, an inwardly rectifying subtype that opens in response to lowered intracellular adenosine triphosphate (ATP) and has been implicated in protection from ischemia, insulin-mediated hypothalamic neuronal glucose homeostasis, and glial potassium homeostasis.
By considering the clinical manifestation of diseases caused by altered expression of INa, IK, and ICa, it is surprising that permanent changes in the normal endowment of ion channels can cause episodic diseases. This is true for a variety of inheritable cardiac conditions (arrhythmias), as well as neurological disorders such as episodic ataxia and epilepsy. How it is possible that most of the time patients affected by these disorders lack symptoms and what precipitates the clinical manifestations largely remains unknown. The modern techniques used to map and pinpoint the molecular mechanisms of diseases have thus far failed to determine the cofactors that transform a small ion channel deficit into a full-blown neurological disease. Understanding these coexisting conditions will perhaps provide information sufficient to chart an effective therapy. Channelopathies are summarized in Table 49-4.17
TABLE 49-4 Overview of Ion Channel Disorders Relevant to Neurological Surgery
| DISORDER | ION CHANNEL | MUTATION(S) |
|---|---|---|
| Generalized myotonia (Becker’s) | CLCN1 (skeletal muscle chloride channel) | Point mutations—reduced Cl− conductance; increased membrane resistance; less current required for action potential, slower repolarization; more sensitive to K+ concentration |
| Myotonia congenita (Thomsen’s) | CLCN1 (skeletal muscle chloride channel) | Missense mutations and deletions—reduced Cl− conductance; increased membrane resistance; less current required for action potential, slower repolarization; more sensitive to K+ concentration |
| Sodium channel myotonia Paramyotonia congenita Periodic paralysis, type II (hyperkalemic) |
SCN4A (skeletal muscle sodium channel) | Point mutations in regions involved in channel inactivation—impaired inactivation resulting in slowed decay of transient sodium current |
| DISORDER | ION CHANNEL | MUTATION(S) |
| Neurological | ||
| Familial hemiplegic migraine | CACNL1A (α1 voltage-sensitive calcium channel subunit) | Assorted mutations (α1 voltage-sensitive calcium channel subunit) |
| Episodic ataxia type 2 | CACNL1A | Assorted mutations (α1A calcium channel subunit) |
| Spinocerebellar ataxia | CACNL1A | Expansion of trinucleotide repeat |
| Episodic ataxia type 1/partial complex seizures | Kv1.1/KCNA1 (delayed rectifier K+ channel) | Multiple missense and stop codon mutations; rare human, severe mouse seizures |
| Benign neonatal convulsions | KCNQ2 and KCNQ3 (M-type potassium channel) | Multiple mutations, altering regulation of rapid neuronal firing |
| Generalized epilepsy with febrile seizures | SCNA1 and SCNB1 | Multiple mutations |
| DISORDER | ION CHANNEL | CAUSE |
| Acquired Channelopathies | ||
| Long QT syndrome Neurological effects prevented by BBB |
HERG K+ channel | Antiarrhythmic medications class IA or III HERG channel blockade |
| Myasthenia gravis | AChR | Autoimmune |
| Acquired myotonia | Voltage-gated K+ channel | Autoimmune |
| Eaton-Lambert syndrome | Voltage-gated Ca2+ channel | Autoimmune |
AChR, acetylcholine receptor; BBB, blood-brain barrier.
Glial Ion Channels and Glutamate Release
Glial potassium channels are the most common electrophysiologic feature of both cultured and in situ astrocytes and can be categorized as follows: channels that allow inward but not outward current flow (inward rectifiers, KIR), channels that allow outward but not inward current flow (delayed rectifier, IDR; transient outward current, IA), and channels that are opened by intracellular calcium (IK[Ca)). Glial potassium channels differ in their sensitivity to blockers: inward rectifiers are blocked by submillimolar concentrations of external cesium and barium, and outward IDR and IA are both sensitive to TEA and 4-aminopyridine (4-AP), but IA blockade by TEA requires high concentrations.18 Recently, a mixed cation channel (Iha) permeant to K+ and Na+ and ether-a-go-go currents (HERG 1)19 have been described in both cultured and in situ astrocytes and may assist in potassium homeostasis in the CNS.
Voltage-dependent, TTX-sensitive and TTX-insensitive sodium channels are also expressed in both cultured and in situ glial cells.20 Although astrocytes are incapable of producing action potential–like responses, possibly because of the relatively low Na+ current densities in these cells, a role of Na+ channels in extracellular buffering of potassium has been proposed. According to this hypothesis, Na+ influx sustains the Na+,K+-ATPase pump, which results in net uptake of K+. Finally, calcium channels are represented sparingly in glial cells and require either neuronal or otherwise differentiating factors for expression; whether ICa can be recorded from in situ hippocampal astrocytes is still unknown, but release of calcium from intracellular stores in response to neurotransmitters acting on astrocytes has clearly been demonstrated. Relevant to potassium homeostasis, micromolar [Ca+2]in can cause opening of IK(Ca) and may thus participate in the generation of outward potassium fluxes.
Astrocytes can release the excitatory transmitter glutamate, which acts on at least three families of receptors.21–25 Astrocytic release of glutamate can occur through several mechanisms, some of which are specific to glia (e.g., reversal of glutamate uptake) or occur via Ca2+-dependent exocytosis, which shares similarities to neurotransmission. In addition to glutamate, astrocytes can release a variety of neurotransmitters such as taurine and adenosine. Unlike synaptic transmission, which is specific for a postsynaptic site, release of glutamate by a single astrocyte affects several adjacent neurons, thereby simultaneously controlling the excitability of several neighboring pyramidal cells. This may constitute one of the mechanisms of neuronal synchronization in epilepsy.
If astrocytes release glutamate and have neurotransmitter receptors, what differentiates neurons from glia? Are these phenomena operating in vivo, or are these findings limited to slice preparations? For example, glial cells display intrinsic activity in the absence of neuronal stimulation, but this finding was observed only in vitro. Astrocytes greatly outnumber neurons, and the ratio of astrocytes to neurons is larger in more evolved brain. There is no question about the importance of non-neuronal cells to CNS function and human disease; however, the laboratory findings need to be confirmed in preparations in which artifacts are controlled and known. An important physiologic aspect of the astrocyte in situ is its proximity to capillaries and the perivascular space of arterioles.26 Astrocytes influence maintenance of the blood-brain barrier, which in turn regulates brain ion homeostasis.27 Whether astrocytes also release significant levels of vasodilators or constrictors remains to be proved in vivo in preparations in which the surrounding tissue is intact. However, a clear effect of astrocytes on small-diameter, capillary-like structures has been demonstrated.28 This effect may be important when capillary perfusion pressure is altered by brain edema or other disruptors of brain homeostasis.
Expression of Ion Currents in Different Neuronal Populations
This electrophysiologic heterogeneity affects the function of particular cell populations in the brain. Individual cell types possess particular combinations of the previously described Na+, K+, and Ca2+ currents that merge to result in the patterns of neuronal activity that are found in different areas of the CNS. These patterns can be investigated by in vitro isolated brain slice recordings, as well as by computer modeling simulations, to dissect the individual channel components. For example, relay neurons in the lateral geniculate nucleus that project to the visual cortex are characterized by an RMP of −70 mV during sleep versus −55 mV during the awake state, thus decreasing the transmission of information to the visual cortex during sleep. This sleep-wake variability is modulated by the low-threshold calcium current IT, which together with the hyperpolarization-activated mixed cationic current Iha generates rhythmic bursts of action potentials in thalamic relay neurons. During slow-wave sleep, thalamic relay neurons have a relatively hyperpolarized RMP that de-inactivates low-threshold calcium currents and thereby results in IT-generated slow spikes of activity. Between these spikes, a slowly depolarizing potential is generated by activation of Iha. Together, these two currents result in spontaneous synchronized bursts of low-frequency action potentials. In contrast, the transition from slow-wave sleep to either wakefulness or rapid eye movement sleep is characterized by relative depolarization of thalamic relay neurons. This depolarization inactivates IT and Iha, which results in conversion to a tonic action potential mode in which single spikes are produced one at a time in response to stimulation.16
Intercellular Communication: Electrical and Chemical Synaptic Transmission
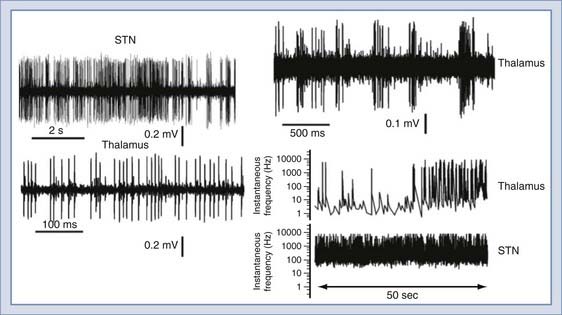
The different endowment of ion channels predictably leads to a broad variety of firing patterns (Figs. 49-5 and 49-6). Most of the traditional studies focused on cortical, cerebellar, and hippocampal neurons because of technical reasons (more densely packed neurons are easier to find) and also the popularity of brain-slicing technologies.29 More recently, with the advent of surgical procedures for deep brain stimulation, it became possible to record from other human brain regions, such as the thalamus and the subthalamic nuclei. The examples shown highlight the different firing properties derived from extracellular unit recordings. The essential feature of the action potential phenotype shown consists of frequency of discharge within a certain period. Two extremes are shown, one depicting high-frequency, non–time-dependent firing and the other showing time-dependent changes in frequency in thalamic neurons.
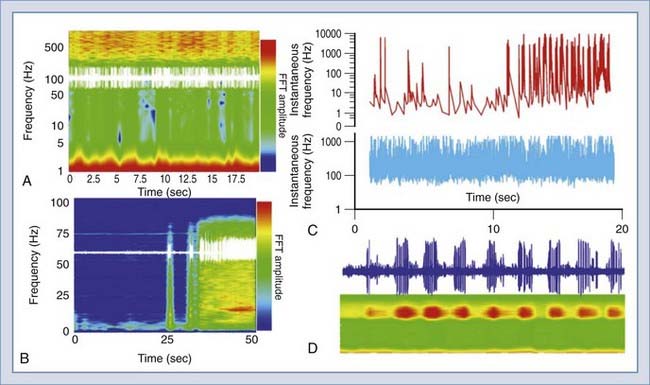
FIGURE 49-6 Examples of data analysis based on the frequency domain. The graph in A shows a trace of a unit recording (raw data, in white) superimposed on a frequency/amplitude plot. The colors depict the amplitude of the events occurring at a certain time and at a certain frequency. B shows the same protocol applied to an electroencephalographic signal recorded from a rat brain before and during a seizure. Again, the white trace refers to the raw data, whereas the color graph gives an overview of the frequency and intensity of spiking. The graph in C is the same as in Figure 49-5 but in color. D shows a ribbon trace (bottom) that has the same meaning and dimensions of the graph in A. The trace in blue is a recording from a bursting thalamic neuron. Data analysis was performed with DIADEM. FFT, fast Fourier transform.
Analysis of the data provided by these deep brain recordings has also resulted in the quest for novel quantitative approaches to describe neuronal behavior. In other words, the comparably sparse firing of hippocampal and cortical neurons can easily be described by plotting the digitized versions of the recordings themselves. Thus, if the application of stimuli is superimposed, the reader may quickly and easily derive the effect of any given manipulation by limiting the presentation to the time domain. When dealing with recordings such as those in Figure 49-5, transformation of data in the frequency domain becomes necessary. This can be achieved with a variety of software of increasing complexity (and cost!). The results in Figure 49-6 show examples of this analysis. Data can be shown as either two- or three-dimensional plots. Fast Fourier transform (FFT) analysis reveals time-dependent changes over a time interval, as well as the “FFT amplitude” of firings at a given range of frequency.
Electrical Synaptic Transmission
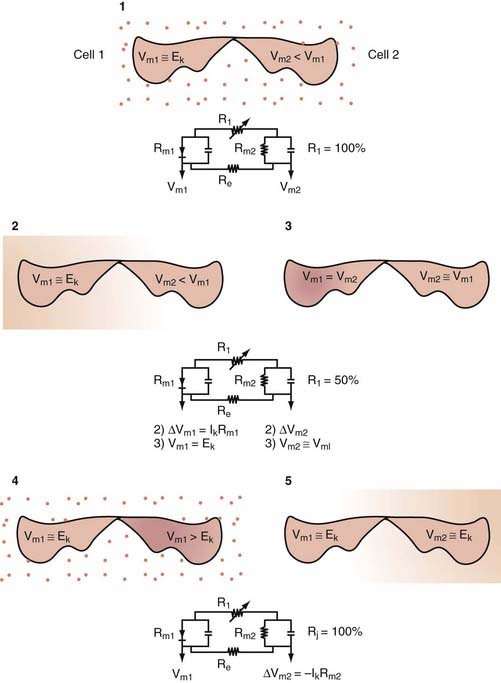
Intercellular electrical communication occurs through specialized channels called gap junctions. Each gap junction channel is made up of a pair of hemichannels contributed by the presynaptic and postsynaptic cell. The hemichannels together form an approximately 1.5-nm channel pore that directly communicates with the cytoplasm of the two cells and allows the passage of small molecules up to 1000 daltons, ions, and intercellular dyes to facilitate the study of gap junction function. Each hemichannel is composed of a connexon, which in turn consists of six identical connexin proteins. The cytoplasmic side of gap junction channels is sensitive to various modulators, including pH and intracellular calcium. Intracellular acidification and elevated intracellular calcium both result in closure of the gap junction channels by electrically uncoupling cells from one another. In contrast, alkalinization increases the degree of intercellular coupling. Electrical neurotransmission can be either bidirectional (nonrectifying) or directionally selective (rectifying), depending on whether the gap junction channels joining the two cells are voltage sensitive. The strength of electrotonic coupling between two cells can be changed by altering the shape or duration of the presynaptic impulse, the junctional conductance, or the conductance of nearby nonjunctional membrane.30,31
Electrical synaptic transmission is extremely rapid, which facilitates the synchronous firing of large groups of neurons. Although the degree of neuronal electrical synaptic activity is probably underappreciated at the present time, the functional importance of this form of intercellular communication is increasingly being recognized. For example, the normal development of neuronal columnar domains is dependent on gap junction–mediated intercellular signaling. Spontaneous excitation of one or a few trigger neurons subsequently activates other columnar cells via gap junctions. Gap junctions may also coordinate hippocampal CA1 oscillatory behavior. Parvalbumin-containing GABAergic interneurons in the rat hippocampal CA1 region, known to form a network by mutual axosomatic chemical synaptic contacts, also form another network connected by dendrodendritic gap junctions. Gap junctions linking this dendritic network may facilitate the synchronization of oscillatory activities generated in the interneuron network.32,33
Gap junction communication is found to a much larger degree between glial cells than between neurons in the adult mammalian brain. Glial cell gap junction signaling can be either homotypic (i.e., between two astrocytes) or heterotypic (between an astrocyte and an oligodendroglial cell). Astrocytes are extensively coupled by gap junctions, thus potentially forming a functional syncytium for the regulation of extracellular homeostasis of potassium ion concentration and pH. Neuronal stimulation causes an activity-dependent release of potassium, which results in a local increase in extracellular potassium ([K+]out). After a single action potential, [K+]out increases by 0.01 to 0.02 mM. Despite the firing of large populations of neurons, [K+]out is extremely tightly regulated and even during seizure activity in the hippocampus does not rise above a ceiling level of 12 mM. Additionally, [K+]out returns to normal in a relatively short period. Experiments have suggested that glial uptake and distribution via gap junctions play a pivotal role in conditions in which there is massive [K+]out accumulation, such as epilepsy. Gap junctional communication between glial cells also provides a pathway for long-range metabolite or second messenger signaling. In response to direct astrocytic or neuronal stimulation, intercellular waves of Ca2+ can be generated in astrocytes. These waves spread from cell to cell by one of two mechanisms: either directly through gap junctions or via an extracellular route whereby ATP or glutamate released from astrocytes subsequently propagates via binding to P2 purinergic or glutamatergic receptors.30,31
Chemical Synaptic Transmission
Similar to the neuromuscular junction, most CNS neurons use ionotropic receptors for rapid intercellular signaling. However, in contrast to the monosynaptic excitatory input at the neuromuscular junction, CNS neurons are usually innervated by both excitatory and inhibitory input from multiple cells using both excitatory and inhibitory neurotransmitters. Input from a single excitatory neuron generates a depolarizing excitatory postsynaptic potential (EPSP), whereas inhibitory innervation generates a hyperpolarizing inhibitory postsynaptic potential (IPSP). Excitatory and inhibitory synapses are morphologically different, as summarized in Table 49-5.
TABLE 49-5 Morphologic Differences between Central Nervous System Synapses
| GRAY TYPE I | GRAY TYPE II |
|---|---|
| Usually glutamatergic/excitatory | Usually GABAergic/inhibitory |
| Prominent round synaptic vesicles | Less prominent flattened synaptic vesicles |
| Larger synaptic cleft (30 nm) and active zone (1-2 µm) | Smaller synaptic cleft (20 nm) and active zone (<1 µm) |
GABAergic, transmitting γ-aminobutyric acid.
Maintenance of Extracellular Homeostasis
Contribution of Astrocytes to Regulation of Neuronal Excitability: Spatial Buffering
Several mechanisms have been suggested to explain the rapid clearance of K+ from the ECS: passive diffusion through the ECS, active removal by blood flow, and neuronal reuptake. However, these mechanisms alone are not fast enough to account for the rapid removal of K+ from the ECS seen under experimental conditions. Several lines of evidence suggest that brain glial cells support homeostatic regulation of the neuronal microenvironment. CNS astrocytes are strategically located in proximity to excitable neurons and are sensitive to the changes in extracellular ion composition that follow neuronal activity.34–39 Experiments have suggested that glial uptake plays a pivotal role in conditions in which there is massive Kout accumulation. In cortical regions, glial cells participate in genesis of the changes in extracellular field potential associated with neuronal depolarization and efflux of potassium in the ECS. The combination of potassium uptake into glial cells immediately followed by redistribution through electrotonically coupled glial gap junctions (“spatial buffering”) provides a valid working hypothesis to explain some of the features of K+ movement in the ECS (Fig. 49-7). Although a direct demonstration that KIR or Iha plays a role in CNS extracellular potassium homeostasis is still lacking, evidence from studies on cultured neocortical astroglia has demonstrated K+-induced inward currents sensitive to KIR blockers. In addition, recent work has demonstrated evidence of glial spatial buffering during slow sleep oscillations in spike wave seizures in rodents.40
It has long been known that in conditions involving high levels of neuronal activity (e.g., seizures), [K]out accumulation is accompanied by cell swelling. The swelling that accompanies epileptiform neuronal discharge is due to excessive activity of the ionic mechanisms normally involved in the control of ECS homeostasis. One of the several proposed mechanisms associated with cell swelling, the Na+/K+/2Cl− cotransporter, is also believed to participate in uptake of K+ into glia. This transporter is blocked by the loop diuretic furosemide. Treatment of “epileptic” hippocampal slices (treated with bicuculline, 0 Ca2+, or 4-AP) with furosemide has been shown to inhibit spontaneous burst discharge. It has been hypothesized that this mechanism is related to furosemide’s blockade of the swelling induced by the large ionic (and water) shifts that accompany Na+/K+/2Cl− cotransporter activity.41,42 More recent experimentation has suggested that furosemide-induced opening of glial inwardly rectifying potassium channels may contribute to the antiepileptic mechanism.43
Loss of Brain Homeostasis and Resultant Effects
The delicate homeostatic electrophysiologic balance of the CNS is readily perturbed in association with or as a result of various pathologic conditions such as seizures, brain edema, and brain tumors. In various forms of epilepsy, alterations in neuronal and glial ion channel expression, ECS size, and intercellular astrocytic gap junction coupling may all contribute to the development or maintenance of seizure activity. In temporal lobe epilepsy, the most common surgically treated form of epilepsy, a number of pathologic features are characteristically found, including selective neuronal loss in the CA1, CA3, and hilar regions of the hippocampus, reactive gliosis in these same subfields, and sprouting of granule cell excitatory axon collaterals (mossy fibers). Epileptic granule cells are characterized by alterations in GABA receptors that increase their zinc sensitivity at a time when “mossy fiber sprouting” of zinc-positive granule cell axonal projections has occurred.44,45 In addition, alterations in either glial or neuronal electrotonic gap junction coupling may promote seizure activity. Neuronal synchrony is enhanced in conditions of increased intercellular coupling, whereas uncoupling agents that block gap junctions may prevent neuronal synchronization.
Glial regulation of ECS size and [K+]out may similarly contribute to epileptogenesis. Astrocytes from animal model or human limbic epilepsy are characterized by decreased expression of the inwardly rectifying potassium channel KIR.46 This channel alteration would be expected to result in raised [K+]out, as well as the need to use other glial mechanisms for potassium uptake such as the Na+,K+-ATPase pump and the Na+/K+/2Cl− cotransporter. Together, these changes would be expected to increase epileptogenicity both by increasing [K+]out and by decreasing ECS size. These hypotheses have been confirmed in normal rodent tissue with pharmacologic blockade of the inwardly rectifying potassium channel KIR,12 as well as in an animal model of traumatic brain injury.47 Investigation is ongoing in human epileptic tissue.
Brain tumors are also associated with various electrophysiologic abnormalities. Gliomas are characterized both by selective expression of a chloride channel not expressed by normal astrocytes and by alterations in astrocytic mechanisms for the uptake of glutamate. The chloride currents expressed by glioma cells are volume activated and are proposed to contribute to the changes in cell shape and volume that are necessary for extracellular tumor cell migration.48 Synaptically released glutamate and GABA are both removed from the ECS through the action of electrogenic Na+-dependent transporters. In the case of glutamate, five transporter subtypes have been identified, including the astrocytic transporters GLAST and GLT-1, which are the most abundant glutamate transporters in brain. In glioma cells, there is very little expression of GLAST and mislocalization of GLT-1 to the nuclear rather than the cytoplasmic membrane. Rather than take scavenging neuronally released glutamate, glioma cells locally release internally generated glutamate, thereby resulting in increased neurotoxicity and invasiveness. Blockade of glioma glutamate release may hold promise as a novel therapy for malignant gliomas.49
Electrophysiologic Techniques in Neurosurgery
Origin of Field Potentials in the Brain and Spinal Cord
Recording Methods in Neurosurgery
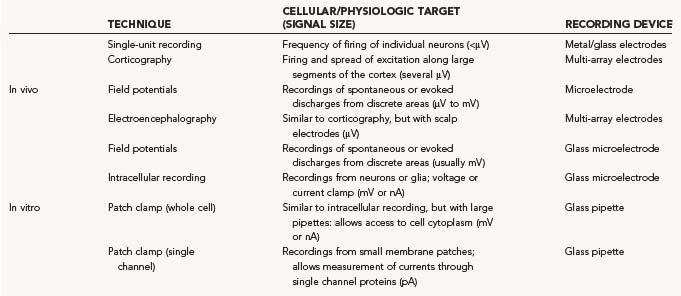
The different recording methods used in the neurosurgical treatment of epilepsy, movement disorders, and pain syndromes are summarized in Table 49-6. Although single-unit recordings carried out with microelectrodes are used for research purposes in epilepsy patients, the majority of epilepsy recordings are EEG recordings using scalp electrodes, subdural or epidural electrode arrays, or intracerebral targeted-depth electrodes. These techniques allow both the lateralization and localization that is required in medically refractory patients before focal cortical resection of their seizure focus. Intraoperative electrocorticography (ECoG) is often used in patients with lesional epilepsies, such as those caused by tumors, focal cortical dysplasia, or cavernous malformations with refractory seizures, to determine whether the epileptogenic zone extends beyond the borders of the pathologic lesion. The use of ECoG in mesial temporal lobe epilepsy to guide surgical resection is more controversial. Intraoperative hippocampal ECoG can potentially be used to determine how much hippocampus to remove to maximize seizure-free outcome. Neocortical ECoG has not been shown to be of clear benefit in the intraoperative management of mesial temporal lobe epilepsy.50
Ion Channels in Neurological Disorders
Excitotoxicity
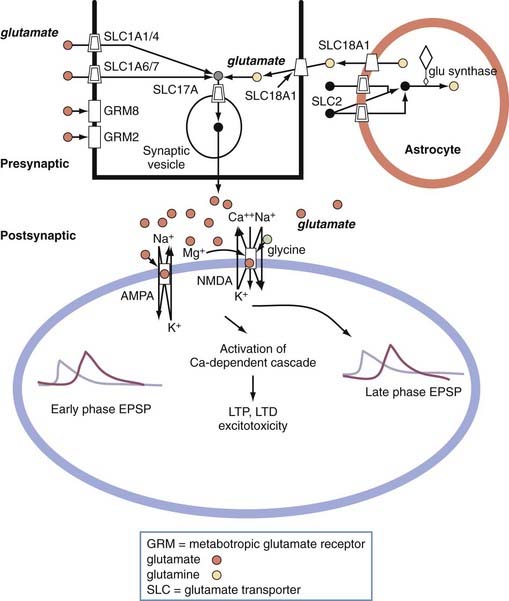
Excitotoxicity refers to the ability of glutamate or other amino acid agonists at the glutamate receptors to mediate the death of central neurons. The most common excitotoxic mechanism consists of sustained exposure to large quantities of these agonists. Excitotoxic neuronal death is almost always a pathologic feature of CNS disorders and may contribute to the pathogenesis of human brain or spinal cord disease. Excitotoxicity has substantial cellular specificity and, in most cases, is mediated by glutamate receptors. N-Methyl-D-aspartate (NMDA) receptor activation is the most common signaling event that causes excitotoxicity, and NMDA triggers injury more rapidly than do α-amino-3-hydroxy-5-methyl-4-isoxazoleproprionate (AMPA) or kainate receptors (Fig. 49-8). It is commonly accepted that this depends on NMDA’s greater ability to induce calcium influx and subsequent cellular calcium overload. A good example of excitotoxicity is hippocampal sclerosis.51,52 Hippocampal sclerosis is the most frequent pathologic finding in patients with temporal lobe epilepsy undergoing resective neurosurgery, and it is a common neuroimaging finding.53
Epilepsy and Channelopathies
Epileptic seizures are electrical events that produce a complex behavioral response ranging from absence seizures to convulsions. Several investigators have studied the link between ion channels and seizure disorders. Animal data show that several features of epilepsy can be reproduced in rodents. Electrophysiologic recordings performed both in vivo and in vitro allowed the discovery of several important features that may contribute to the development of seizures. For example, the response to GABA and NMDA varies during development, and an attempt has been made to link abnormal GABA responses to infantile seizures.54,55
In addition to developmental changes, several insults that are cofactors in human epilepsy have been shown to cause similar effects in animal models. Virtually all animal models have shown either altered excitatory or altered inhibitory loops, but more recent research has revealed a significant role for non-neuronal cells. For example, a specific deficit in potassium channels involved in glial potassium buffering has been discovered in both human tissue and animal model brain.47,56,57 More recently, involvement of other members of the neurovascular unit has expanded the electrophysiologic mechanisms to other nonexcitable cells (e.g., blood-brain barrier endothelial cells).58 Finally, it has to be emphasized that most of the work of the neurovascular unit consists of keeping the neuronal cells well nourished and living in a tightly controlled environment. As also mentioned in other sections of this chapter, altered potassium or calcium can have profound effects on neuronal firing.
A genetic contribution to the epilepsies has long been suspected, but progress in elucidating the specific genetic influences was relatively slow. A recent flurry of new experimental tools has allowed the discovery of several genetic features associated with epileptic disease. Among those that are most likely to influence neuronal discharges are “channelopathies,” or conditions involving the altered electrical property of neuronal or glial cells. Thus far, almost all of the progress in discovering “epilepsy genes” has come from analysis of rare families with mendelian modes of inheritance, and all but two of these genes encode voltage-gated or ligand-gated ion channels. Among these are KCNQ2 and KCNQ3 for potassium channels; SCN1A, SCN1B, and SCN2A for sodium channels; and GABRG2 for inhibitory chloride channels, among others. Genetic analysis of these genes is confounded by the numerous overlapping properties of ion channels. In other words, a specific mutation in a potassium channel may cause a variety of diseases in which seizures are not most prominent. On the other hand, it is possible that environmental or pharmacologic factors can mimic the genetic ablation of function even in the presence of a normal genotype. An example is the impotence drug Viagra (sildenafil), which acts on the KCNQ2 potassium channel. This compound acts as a specific phosphodiesterase type V inhibitor with a selective inhibitory effect on cyclic guanosine monophosphate (cGMP). Its enhancement of the release of nitric oxide (NO) leads to an increase in cGMP concentration, which is responsible for its main clinical effect, relaxation of smooth muscle in the corpus cavernosum. Sildenafil also affects KCNQ2 channels, which are regulated by cGMP/NO pathways. Not surprisingly, four instances of patients experiencing epileptic seizures during the clinical trials of sildenafil were reported, and anecdotal evidence supports the association between sildenafil and potassium channels expressed in the brain.59
, Bordey A, Sontheimer H. Properties of human glial cells associated with epileptic seizure foci. Epilepsy Res. 1998;32:286-303.
, Catterall WA, Dib-Hajj S, Meisler MH, et al. Inherited neuronal ion channelopathies: new windows on complex neurological diseases. J Neurosci. 2008;28:11768-11777.
, Coulter DA. Epilepsy-associated plasticity in gamma-aminobutyric acid receptor expression, function, and inhibitory synaptic properties. Int Rev Neurobiol. 2001;45:237-252.
, del Zoppo GJ. Virchow’s triad: the vascular basis of cerebral injury. Rev Neurol Dis. 2008;5(suppl 1):S12-S21.
, Goldman DE. Potential, impedance, and rectification in membranes. J Gen Physiol. 1943;27:37-60.
, Hodgkin AL, Huxley AF. A quantitative description of membrane current and its application to conduction and excitation in nerve. J Physiol (London). 1952;117:500-544.
, Hodgkin AL, Katz B. The effect of sodium ions on electrical activity of the giant axon of the squid. J Physiol. 1949;108:37-77.
, Hugenaard J, McCormick DA. Electrophysiology of the Neuron. New York: Oxford University Press; 1994.
, Oby E, Janigro D. The blood-brain barrier and epilepsy. Epilepsia. 2006;47:1761-1774.
, Ransom BR, Sontheimer H. The neurophysiology of glial cells. J Clin Neurophysiol. 1992;9:224-251.
, Rozental R, Giaume C, Spray DC. Gap junctions in the nervous system. Brain Res Brain Res Rev. 2000;32:11-15.
1 Nernst W. On the kinetics of substances in solution. Z Physik Chem. 1888;2:613-622. 634-637
2 Bernstein J. Untersuchungen zur Thermodynamic der Bioelektrische Strome. Pflugers Arch. 1902;92:521-562.
3 Goldman DE. Potential, impedance, and rectification in membranes. J Gen Physiol. 1943;27:37-60.
4 Hodgkin AL, Katz B. The effect of sodium ions on electrical activity of the giant axon of the squid. J Physiol. 1949;108:37-77.
5 Halstead BW. Poisonous and Venomous Marine Animals of the World. Princeton, NJ: Darwin Press; 1978. 233
6 Chen LQ, Chahine M, Kallen RG, et al. Chimeric study of sodium channels from rat skeletal and cardiac muscle. FEBS Lett. 1992;309:253-257.
7 Catterall WA, Dib-Hajj S, Meisler MH, et al. Inherited neuronal ion channelopathies: new windows on complex neurological diseases. J Neurosci. 2008;28:11768-11777.
8 Gambardella A, Marini C. Clinical spectrum of SCN1A mutations. Epilepsia. 2009;50(suppl 5):20-23.
9 Randall A, Benham CD. Recent advances in the molecular understanding of voltage-gated Ca2+ channels. Mol Cell Neurosci. 1999;14:255-272.
10 Stotz SC, Zamponi GW. Structural determinants of fast inactivation of high voltage-activated Ca(2+) channels. Trends Neurosci. 2001;24:176-181.
11 Pietrobon D. Calcium channels and channelopathies of the central nervous system. Mol Neurobiol. 2002;25:31-50.
12 D’Ambrosio R, Wenzel J, Schwartzkroin PA, et al. Functional specialization and topographic segregation of hippocampal astrocytes. J Neurosci. 1998;18:4425-4438.
13 McKhann GM2nd, D’Ambrosio R, Janigro D. Heterogeneity of astrocyte resting membrane potentials and intercellular coupling revealed by whole-cell and gramicidin-perforated patch recordings from cultured neocortical and hippocampal slice astrocytes. J Neurosci. 1997;17:6850-6863.
14 Hodgkin AL, Huxley AF. A quantitative description of membrane current and its application to conduction and excitation in nerve. J Physiol (London). 1952;117:500-544.
15 Cooper EC. Potassium channels: how genetic studies of epileptic syndromes open paths to new therapeutic targets and drugs. Epilepsia. 2001;42(suppl 5):49-54.
16 Hugenaard J, McCormick DA. Electrophysiology of the Neuron. New York: Oxford University Press; 1994.
17 Kullmann DM, Hanna MG. Neurological disorders caused by inherited ion-channel mutations. Lancet Neurol. 2002;1:157-166.
18 Bordey A, Sontheimer H. Ion channel expression by astrocytes in situ: comparison of different CNS regions. Glia. 2000;30:27-38.
19 Emmi A, Wenzel HJ, Schwartzkroin PA, et al. Do glia have heart? Expression and functional role for ether-a-go-go currents in hippocampal astrocytes. J Neurosci. 2000;20:3915-3925.
20 Sontheimer H, Black JA, Waxman SG. Voltage-gated Na+ channels in glia: properties and possible functions. Trends Neurosci. 1996;19:325-331.
21 Araque A, Parpura V, Sanzgiri RP, et al. Tripartite synapses: glia, the unacknowledged partner. Trends Neurosci. 1999;22:208-215.
22 Parpura V, Basarsky TA, Liu F, et al. Glutamate-mediated astrocyte-neuron signaling. Nature. 1994;369:744-747.
23 Carmignoto G, Pasti L, Pozzan T. On the role of voltage-dependent calcium channels in calcium signaling of astrocytes in situ. J Neurosci. 1998;18:4637-4645.
24 Bezzi P, Carmignoto G, Pasti L, et al. Prostaglandins stimulate calcium-dependent glutamate release in astrocytes. Nature. 1998;391:281-285.
25 Pasti L, Volterra A, Pozzan T, et al. Intracellular calcium oscillations in astrocytes: a highly plastic, bidirectional form of communication between neurons and astrocytes in situ. J Neurosci. 1997;17:7817-7830.
26 del Zoppo GJ. Virchow’s triad: the vascular basis of cerebral injury. Rev Neurol Dis. 2008;5(suppl 1):S12-S21.
27 Janigro D. Blood-brain barrier, ion homeostasis and epilepsy: possible implications towards the understanding of ketogenic diet mechanisms. Epilepsy Res. 1999;37:223-232.
28 Carmignoto G, Gomez-Gonzalo M. The contribution of astrocyte signalling to neurovascular coupling. Brain Res Rev. 2010;63:138-148.
29 Schwartzkroin PA. Hippocampal slices in experimental and human epilepsy. Adv Neurol. 1986;44:991-1010.
30 Dermietzel R, Spray DC. Gap junctions in the brain: where, what type, how many and why? Trends Neurosci. 1993;16:186-192.
31 Rozental R, Giaume C, Spray DC. Gap junctions in the nervous system. Brain Res Brain Res Rev. 2000;32:11-15.
32 Deans MR, Gibson JR, Sellitto C, et al. Synchronous activity of inhibitory networks in neocortex requires electrical synapses containing connexin 36. Neuron. 2001;31:477-485.
33 Traub RD, Bibbig R, Piechotta A, et al. Synaptic and nonsynaptic contributions to giant IPSPs and ectopic spikes induced by 4-aminopyridine in the hippocampus in vitro. J Neurophysiol. 2001;85:1246-1256.
34 Keyser DO, Pellmar TC. Synaptic transmission in the hippocampus: critical role for glial cells. Glia. 1994;10:237-243.
35 Ransom BR, Sontheimer H. The neurophysiology of glial cells. J Clin Neurophysiol. 1992;9:224-251.
36 Ransom BR, Walz W, Davis PK, et al. Anoxia-induced changes in extracellular K+ and pH in mammalian central white matter. J Cereb Blood Flow Metab. 1992;12:593-602.
37 Ransom BR, Carlini WG. Electrophysiological properties of astrocytes. In: Fedoroff S, Vernadakis A, editors. Astrocytes. Orlando, FL: Academic Press; 1986:1-49.
38 Dietzel I, Heinemann U, Lux HD. Relations between slow extracellular potential changes, glial potassium buffering, and electrolyte and cellular volume changes during neuronal hyperactivity in cat brain. Glia. 1989;2:25-44.
39 Lux HD, Heinemann U, Dietzel I. Ionic changes and alterations in the size of the extracellular space during epileptic activity. Adv Neurol. 1986;44:619-639.
40 Amzica F, Massimini M, Manfridi A. Spatial buffering during slow and paroxysmal sleep oscillations in cortical networks of glial cells in vivo. J Neurosci. 2002;22:1042-1053.
41 Hochman DW, Baraban SC, Owens JW, et al. Dissociation of synchronization and excitability in furosemide blockade of epileptiform activity. Science. 1995;270:99-102.
42 Hochman DW, D’Ambrosio R, Janigro D, et al. Extracellular chloride and the maintenance of spontaneous epileptiform activity in rat hippocampal slices. J Neurophysiol. 1999;81:49-59.
43 Barbaro NM, Takahashi BS, Baraban SC. Furosemide and blockade of seizure activity in vitro. Epilepsia. 2002;42:A.05.
44 Brooks-Kayal AR, Shumate MD, Jin H, et al. Selective changes in single cell GABA(A) receptor subunit expression and function in temporal lobe epilepsy. Nat Med. 1998;4:1166-1172.
45 Coulter DA. Epilepsy-associated plasticity in gamma-aminobutyric acid receptor expression, function, and inhibitory synaptic properties. Int Rev Neurobiol. 2001;45:237-252.
46 Hinterkeuser S, Schroder W, Hager G, et al. Astrocytes in the hippocampus of patients with temporal lobe epilepsy display changes in potassium conductances. Eur J Neurosci. 2000;12:2087-2096.
47 D’Ambrosio R, Maris DO, Grady MS, et al. Impaired K(+) homeostasis and altered electrophysiological properties of post-traumatic hippocampal glia. J Neurosci. 1999;19:8152-8162.
48 Ransom CB, O’Neal JT, Sontheimer H. Volume-activated chloride currents contribute to the resting conductance and invasive migration of human glioma cells. J Neurosci. 2001;21:7674-7683.
49 Takano T, Lin JH, Arcuino G, et al. Glutamate release promotes growth of malignant gliomas. Nat Med. 2001;7:1010-1015.
50 McKhann GM2nd, Schoenfeld-McNeill J, Born DE, et al. Intraoperative hippocampal electrocorticography to predict the extent of hippocampal resection in temporal lobe epilepsy surgery. J Neurosurg. 2000;93:44-52.
51 Mohamed A, Wyllie E, Ruggieri P, et al. Temporal lobe epilepsy due to hippocampal sclerosis in pediatric candidates for epilepsy surgery. Neurology. 2001;56:1643-1649.
52 Proper EA, Oestreicher AB, Jansen GH, et al. Immunohistochemical characterization of mossy fibre sprouting in the hippocampus of patients with pharmaco-resistant temporal lobe epilepsy. Brain. 2000;123:19-30.
53 Abbott DF, Pell GS, Pardoe H, et al. Voxel-based iterative sensitivity (VBIS) analysis: methods and a validation of intensity scaling for T2-weighted imaging of hippocampal sclerosis. Neuroimage. 2009;44:812-819.
54 Janigro D, Schwartzkroin PA. Dissociation of the IPSP and response to GABA during spreading depression-like depolarizations in hippocampal slices. Brain Res. 1987;404:189-200.
55 Janigro D, Schwartzkroin PA. Effects of GABA and baclofen on pyramidal cells in the developing rabbit hippocampus: an ‘in vitro’ study. Brain Res. 1988;469:171-184.
56 MacFarlane SN, Sontheimer H. Electrophysiological changes that accompany reactive gliosis in vitro. J Neurosci. 1997;17:7316-7329.
57 Bordey A, Sontheimer H. Properties of human glial cells associated with epileptic seizure foci. Epilepsy Res. 1998;32:286-303.
58 Oby E, Janigro D. The blood-brain barrier and epilepsy. Epilepsia. 2006;47:1761-1774.
59 Gilad R, Lampl Y, Eshel Y, et al. Tonic-clonic seizures in patients taking sildenafil. BMJ. 2002;325:869.
* Because one is most commonly interested in permeation (or flux) of charges across the membrane rather than its nonconductive properties, the term conductance (Gm, which equals 1/Rm) is used instead of Rm.
* The reader should bear in mind that ionic concentrations are not always constant. In reality, large changes occur during sustained neuronal activation or in pathologic states in which ion homeostasis is impaired (e.g., ischemia).
† A linear dependence of RMP on [K+]out is found in other CNS cells, such as glia and brain microvascular endothelium.
* The overall duration of action potentials is also determined by other factors, such as the duration of repolarizing potentials.
* These potentials are commonly called field EPSP and population spike.