Electrical signalling in neurons
The neuron at rest
There is a small difference in electrical potential across the plasma membrane of all living cells, the inside usually being slightly negative compared to the outside. This potential difference is referred to as the membrane potential of the cell. It is due to a slight excess of negative charge on the inner face of the plasma membrane and is measured in millivolts (mV). The resting membrane potential can be recorded with an intracellular microelectrode and its value is typically around –70 mV in nerve cells (Fig. 6.1).
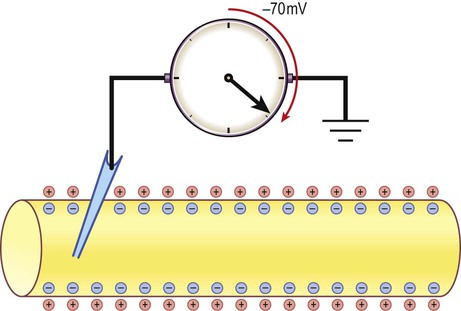
The potential difference across the cell membrane of a typical neuron is around –70 millivolts (negative on the inside).
Origin of the resting membrane potential
The sodium pump
The transmembrane gradients for sodium and potassium are maintained in the long term by the sodium-potassium exchange pump (‘sodium pump’) which works continuously in the background (Fig. 6.2). The sodium pump is a membrane-bound protein that hydrolyses adenosine triphosphate (ATP) and uses the energy released to move ions across the plasma membrane against their concentration gradients. In each cycle the sodium-potassium pump (or Na+/K+-ATPase) transfers three sodium ions out of the cell and moves two potassium ions into the cell, consuming a single molecule of ATP in the process. In this way, the intracellular potassium concentration is maintained at approximately 140 mM compared to the extracellular concentration of around 3–5.5 mM, representing a potassium gradient of around 35 : 1 (higher on the inside). In contrast, the sodium ion concentration is around 12 mM on the inside and 140 mM on the outside, which equates to a 12 : 1 gradient for sodium ions (higher on the outside).
Ionic basis of the resting membrane potential
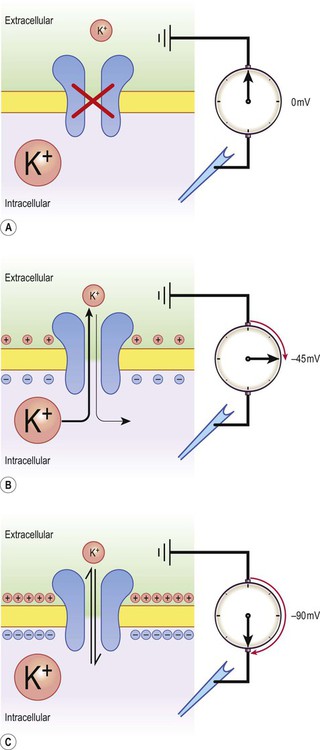
Consider the hypothetical membrane-bound cell depicted in Figure 6.3A. It contains a concentrated solution of potassium salt and is immersed in saline (a solution of sodium chloride). It is important to emphasize that although only potassium (K+) is illustrated in the figure, the intracellular and extracellular fluids contain many different positive and negative ions and are electrically neutral overall.
Now suppose that the cell membrane is exclusively permeable to potassium. Since the intracellular concentration is much higher, potassium will passively diffuse out of the cell down its steep concentration gradient (Fig. 6.3B). A slight excess of negative charge will therefore build up on the inner face of the membrane, since each potassium ion that leaves the cell carries a single positive charge. However, this generates a growing electrical field that acts in the opposite direction to the concentration gradient and tends to attract potassium back inside the cell. The net efflux of potassium ions is therefore gradually reduced as the opposing electrical field builds up.
Ultimately the rate of potassium efflux (down its concentration gradient) is exactly counterbalanced by potassium influx (down the electrical gradient) and there is no net movement of potassium ions into or out of the cell (Fig. 6.3C). At this equilibrium point the membrane potential is stable and will be slightly more negative on the inside. The potential difference across the membrane at this point is the equilibrium potential for potassium and is around –90 mV. It should be emphasized that this process is very rapid (the equilibrium point is reached almost instantaneously).
Calculating the equilibrium potential
Under normal physiological conditions, such as constant body temperature, the equilibrium potential for a particular ion is mainly determined by the concentration difference between the inside and outside of the cell. Its value is given by the Nernst equation (Fig. 6.4). This takes into account the size of the transmembrane gradient together with a number of physical and chemical factors including the absolute temperature (measured in Kelvin) and the charge carried by the ion.
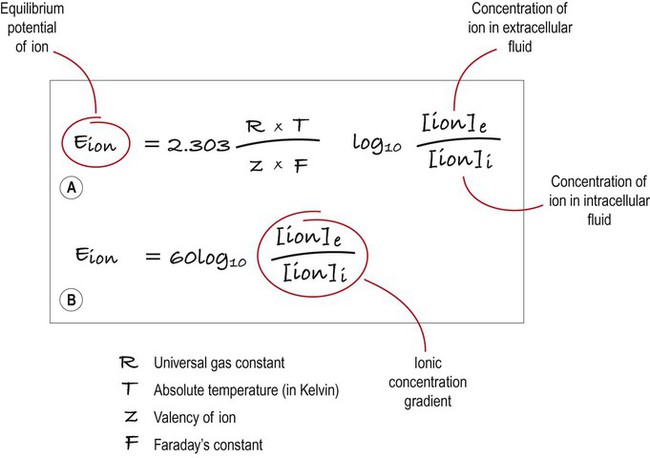
(A) This equation is used to calculate the equilibrium potential for any particular ion, taking into account variables such as temperature and ionic charge; (B) This shows exactly the same expression, but the numerical part of the equation has been simplified. Once this has been done, it is clear that the main determinant of the equilibrium potential for a particular ion is the concentration gradient (in other words: the difference in ionic concentration between the inside and outside of the cell).
Effect of membrane permeability
The resting membrane potential can be calculated by considering the equilibrium potentials for sodium, potassium and chloride ions and factoring in the membrane permeability for each. This information is combined in the Goldman equation (Fig. 6.5) which gives a predicted membrane potential that closely matches recordings from intracellular electrodes.

This equation combines the equilibrium potentials for each of the main ions (determined from the Nernst equation) in a single expression. The relative permeability of each ionic species is also factored in (e.g. if the membrane were mostly permeable to one particular ion, then the membrane potential would be closer to the equilibrium potential for that ion; if there were two main ionic species of equal permeability, the membrane potential would be halfway between the two equilibrium potentials).
The reversal potential
Increasing permeability to a particular ion causes the membrane potential to shift towards the equilibrium potential for that ion. Depending on the starting value of the membrane potential, this may therefore depolarize or hyperpolarize the cell. If the membrane potential is already the same as the equilibrium potential for that particular ion, then opening more ion channels will not alter its value. This concept is illustrated in Figure 6.6 with reference to the chloride channel, which has an equilibrium potential of –65 mV.
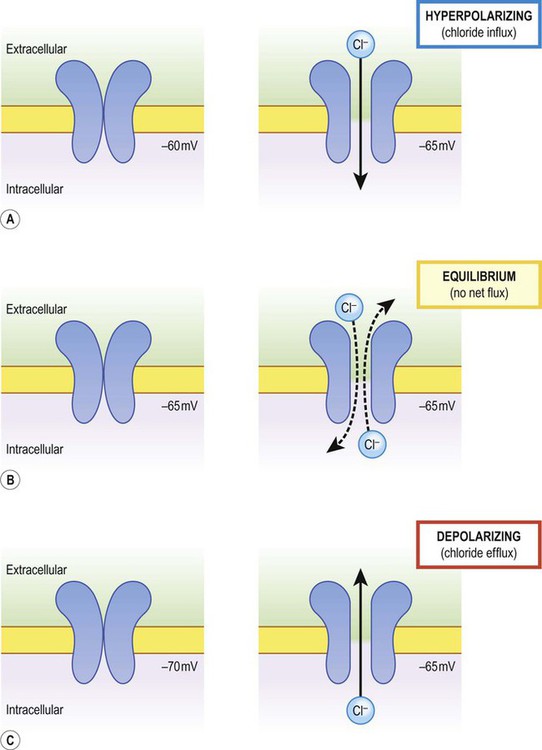
The net direction of ion flux through a membrane channel depends on the initial membrane potential of the cell and the reversal potential of the particular ion. Increasing ion conductance by opening additional channels may therefore (A) hyperpolarize the cell; (B) have no net effect on the membrane potential; or (C) depolarize the cell [see text for explanation].
Figure 6.6A shows the effect of opening additional chloride channels in a membrane that is initially polarized to a value of –60 mV. In this case the membrane is hyperpolarized (from –60 mV to –65 mV). In Figure 6.6B the cell membrane is already at the equilibrium potential for chloride (–65 mV) when the additional chloride channels are opened, so there is no change in membrane voltage (no net ion flux). In Figure 6.6C, the cell membrane starts at a value of –70 mV, which is more negative than the chloride equilibrium potential. Therefore, as the chloride conductance is increased the membrane is depolarized (from –70 mV, towards –65 mV).
Excitability
Types of ion channel
The neuronal membrane is composed of a lipid bilayer. This is a natural barrier to charged species, but water molecules are able to cross freely by passing through channels called aquaporins. The plasma membrane also contains specific ion channels. These are large, transmembrane proteins, usually made up of multiple subunits surrounding an aqueous pore (Fig. 6.7).
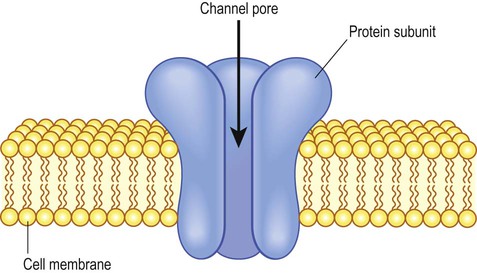
Multiple, membrane-spanning protein subunits are arranged around a central, aqueous pore. The channel may open or close in response to the binding of extracellular ligands or changes in the membrane voltage.
Gated channels
There are two types of ‘gated’ ion channel. Ligand-gated channels open in the presence of a particular signalling molecule, such as a neurotransmitter or peptide, which acts at a binding site on the extracellular aspect of the channel. This type of channel is discussed further in Chapter 7 in the context of synaptic transmission. Voltage-gated ion channels open and close in response to changes in the membrane potential and are involved in the generation and propagation of action potentials. The presence of a selectivity filter means that a channel only allows certain types of ion to pass (by exploiting the physical and chemical properties of amino acids lining the channel pore).
Voltage-gated channel structure
Voltage-gated ion channels are integral membrane proteins. They have a similar molecular structure that includes a repeating motif with six membrane-spanning alpha helices (Fig. 6.8A). There is also a pore loop that contributes to the selectivity filter and a charged domain that acts as a voltage sensor. During depolarization the inner face of the cell membrane becomes more positive and the voltage sensor (which carries a positive charge) is thrust upwards through the membrane by electrostatic repulsion. This movement induces a conformational change in the channel complex which opens the pore. Conductance changes steeply, increasing 150-fold with a 10 mV shift in membrane potential.

(A) The channel subunits are composed of six membrane-spanning alpha-helices (S1–S6) together with a pore loop that is responsible for ion selectivity. The charged domain (S4) acts as a voltage sensor; (B) The voltage-gated sodium channel consists of a single large protein with four repeating motifs (each with six membrane-spanning domains and a pore loop). The potassium channel has a similar structure (once assembled) but is composed of four separate subunits arranged as a tetramer.
Sodium and potassium channels
The voltage-gated sodium channel is composed of a single large protein with four repeating motifs labelled I, II, III and IV. Each motif contains the six membrane-spanning regions, a pore loop and a voltage sensor. In contrast, the voltage-gated potassium channel is composed of four separate subunits, each with the characteristic motif. Once assembled, the overall molecular structure of sodium and potassium channels is therefore similar (Fig. 6.8B). The sodium channel also has an inactivation gate. This closes when the neuronal membrane is fully depolarized and only opens again (‘resets’) once the cell has repolarized.
The action potential
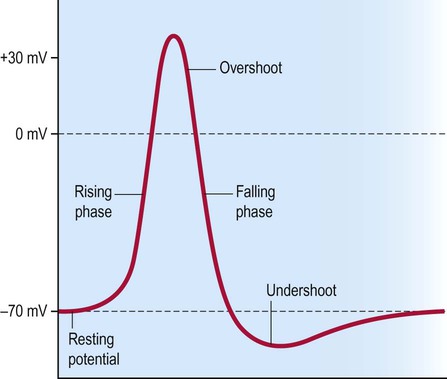
The electrical changes that occur during an action potential are illustrated in Figure 6.9. The membrane first depolarizes rapidly from its normal resting value of –70 mV with a slight overshoot to a positive value of around +30 mV. The normal membrane polarity is thus briefly reversed. The membrane very quickly repolarizes to its normal (negative) value and there is a slight undershoot, before eventually returning to baseline. The timescale is about 1–2 milliseconds.
Properties of the action potential
Nerve impulse generation
To trigger an action potential, a stimulus must be large enough to depolarize the neuronal membrane to a particular threshold value (typically –55 mV). Once this point has been reached a full action potential will occur. It is not possible for an action potential to vary in magnitude like a graded potential: a full action potential either occurs or does not occur. This is referred to as the ‘all or none’ law. Since each action potential depolarizes the adjacent membrane to threshold, the nerve impulse propagates along the full length of the axon like a row of falling dominoes (Fig. 6.10).
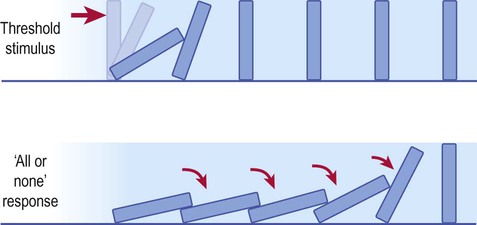
The dominoes will only fall if the minimum effective (threshold) stimulus has been applied, but once the threshold has been reached, all dominoes will fall. Application of even greater (suprathreshold) stimuli has exactly the same effect.
Refractory periods
The absolute refractory period is due to inactivation of the voltage-gated sodium channels (Fig. 6.11). Another action potential is not possible until the sodium channel inactivation gate reopens (which does not happen until the membrane has repolarized). The relative refractory period is due to the after-hyperpolarization (undershoot) that follows the action potential, when the membrane is more negative than it was at rest; a larger than usual excitatory stimulus is therefore needed to overcome this and depolarize the membrane to threshold. Most local anaesthetic agents inhibit voltage-gated sodium channels and prolong the refractory period in sensory neurons (Clinical Box 6.1).
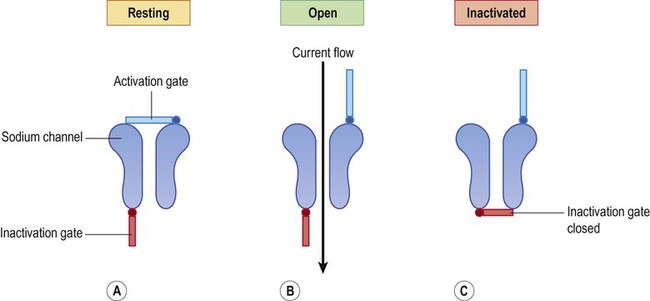
(A) At rest, the activation gate is closed and the inactivation gate is open; (B) During the depolarizing phase of the action potential both gates are open; (C) Once the inactivation gate has closed it is not possible to generate another action potential until the sodium channels have reset, corresponding to the absolute refractory period.
Ionic basis of the action potential
Depolarization (Na+ influx)
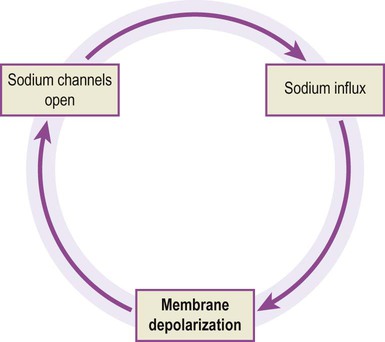
Sodium channels open rapidly and are responsible for the depolarizing phase of the action potential in which there is brisk sodium influx. A threshold stimulus is one that is just strong enough to open the minimum number of channels necessary to set up a ‘positive feedback loop’ in the neuronal membrane, referred to as the Hodgkin cycle (Fig. 6.12). Once this critical threshold is reached, the membrane depolarization caused by inflowing sodium ions triggers more voltage-gated sodium ions to open, leading to a self-reinforcing cycle. Sodium influx drives the membrane potential towards zero, before overshooting to a positive value (+30 mV) which approaches the equilibrium potential for sodium (+60 mV). At this point the sodium channels close and inactivate.
Summary of ionic events
The ionic events responsible for the different phases of the action potential can be summarized as follows (Fig. 6.13):
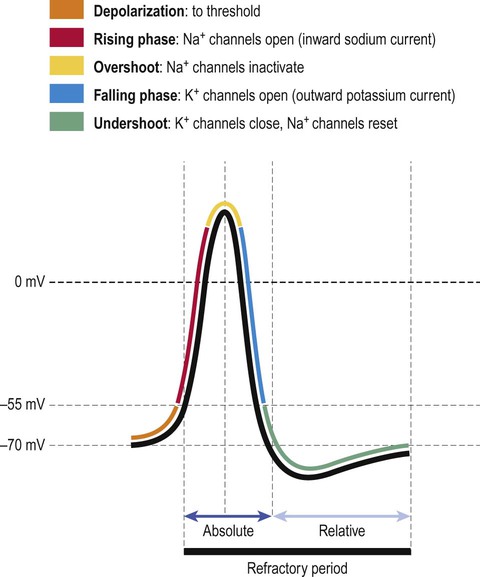
The ionic events responsible for each part of the action potential are shown. The absolute and relative refractory periods are also indicated.
 At rest: voltage-gated Na+ and K+ channels are closed but responsive.
At rest: voltage-gated Na+ and K+ channels are closed but responsive.
 Depolarization (rising) phase: Na+ channels open; K+ channels remain closed.
Depolarization (rising) phase: Na+ channels open; K+ channels remain closed.
 Maximum depolarization (overshoot): Na+ channels inactivate; K+ channels open.
Maximum depolarization (overshoot): Na+ channels inactivate; K+ channels open.
 Repolarization (falling) phase: K+ channels remain open, Na+ channels remain inactivated.
Repolarization (falling) phase: K+ channels remain open, Na+ channels remain inactivated.
 At rest: Na+ channels reset; both channels closed but responsive.
At rest: Na+ channels reset; both channels closed but responsive.
The after-hyperpolarization that follows an action potential (corresponding to the relative refractory period) occurs because some of the delayed rectifiers are still open and the membrane is therefore more permeable to potassium than it was at rest. This means that the membrane potential is closer to the equilibrium potential for potassium (closer to –90 mV). As the remainder of the voltage-gated potassium channels close the membrane returns to its resting value of –70 mV.
Axonal conduction
Passive current flow
Each action potential is associated with a brisk influx of positively charged sodium ions which enter the cell via voltage-gated channels. This creates an electrotonic wave of positive charge that enters the nerve fibre in the region of action potential generation and then spreads passively along the axon (in both directions). The electrotonic wave travels quickly, but rapidly dissipates as positive charge ‘leaks out’ across the plasma membrane, particularly in fibres that do not have a myelin sheath (Fig 6.14A).
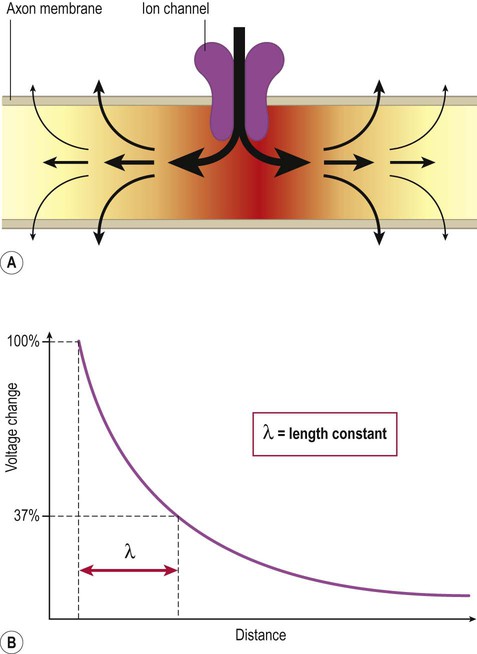
(A) At the point of action potential generation, the inflowing (depolarizing) current spreads in both directions for a variable distance along the axon but quickly dissipates by passive leakage through the axonal plasma membrane; (B) The length constant (lambda) quantifies the rate of current leakage across the membrane and reflects the distance that an electrotonic wave is able to travel along an axon before dissipating.
Depolarization is therefore maximal in the part of the membrane where the action potential was initiated, falling rapidly on either side of this point as the distance increases. This can be plotted as an exponential decay curve and expressed mathematically as the length constant (lambda) of the axon (Fig. 6.14B). The length constant is defined as the distance along the axon at which the voltage change has decayed to 37% of its maximum value.
Conduction in unmyelinated fibres
In fibres that lack a myelin sheath, the nerve impulse propagates gradually from one end of an axon to the other, like a slow-burning fuse (often travelling at speeds below 1.5 metres per second). As each action potential is generated, the electrotonic wave spreads passively along the axon for a short distance and generates a new action potential in the adjacent patch of membrane (Fig. 6.15). The impulse always continues in the forward direction since the more proximal or ‘upstream’ part of the axon (which has just generated an action potential) is refractory. By the time it has recovered, the nerve impulse has passed.
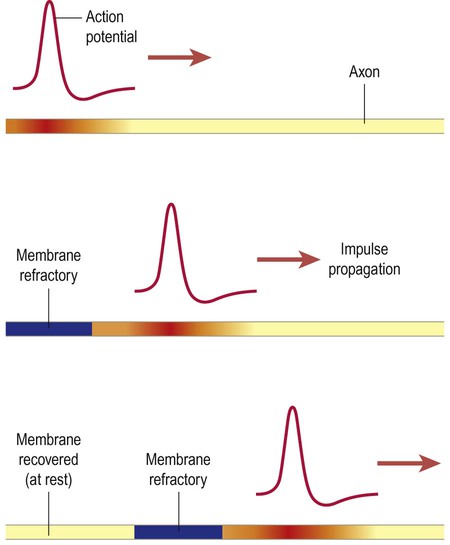
In unmyelinated fibres the nerve impulse spreads gradually and continuously along the full length of the axon, like a slow-burning fuse (travelling at 0.5–2.0 metres per second). At each point the action potential brings the adjacent membrane to threshold and triggers a new action potential.
Axonal conduction velocity
In the vertebrate (including human) nervous system, rapid axonal conduction is achieved more efficiently by investing axons with multiple layers of lipid-enriched plasma membrane, creating a fatty myelin sheath (see Ch. 5). The insulating effect of myelin (reducing current leakage across the membrane and extending the reach of the electrotonic wave) has already been discussed. Myelin also increases conduction speed by reducing membrane capacitance (discussed below).
Conduction in myelinated fibres
In myelinated fibres, each action potential arises at a node of Ranvier. This is a small gap between adjacent myelinated segments where the axon is in direct contact with the extracellular fluid. The myelinated segments are called internodes (Latin: inter-, between) and are about 1 mm long. Figure 6.16A illustrates the sodium current flowing into the axon at a node of Ranvier and the electrotonic wave spreading away from the node in both directions, reaching the two adjacent nodes (both ‘upstream’ and ‘downstream’ of the active node). Note also that local circuit currents are generated in the extracellular fluid in response to the ion flow.
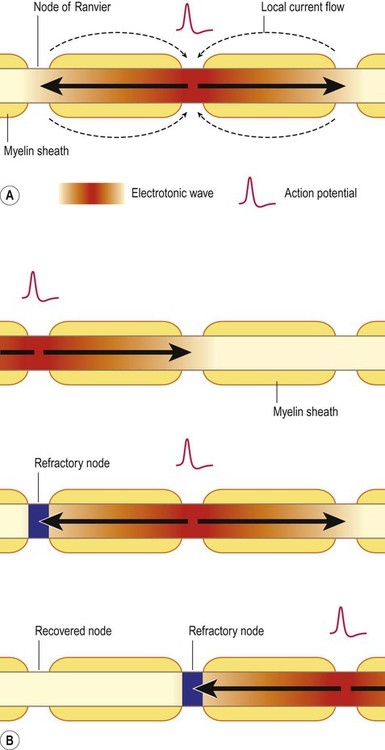
(A) When an action potential is triggered at a node of Ranvier, an inward sodium current (electrotonic wave) enters the axon and flows rapidly in both directions, triggering local current flow in the surrounding extracellular fluid; (B) Illustration of a nerve impulse moving from left to right along a single myelinated axon by causing a threshold depolarization at three successive nodes of Ranvier. Due to the presence of the myelin sheath, the electrotonic wave is able to reach the next node of Ranvier before dissipating and trigger a new action potential there. The previous node is always refractory, ensuring one-way propagation of the impulse.
Figure 6.16B illustrates the process of nerve impulse propagation along a myelinated axon. This is referred to as saltatory conduction since the action potential ‘jumps’ from node to node (Latin: saltere, to leap). As discussed above, myelination (i) lowers membrane capacitance (decreasing the time constant) and (ii) reduces current leakage (increasing the length constant). In this way the electrotonic wave depolarizes the membrane very quickly and is easily able to reach the next node of Ranvier before dissipating, triggering a new action potential there.