Conversions among Measurement Systems
• Convert among metric, household, and apothecary systems using ratio and proportion
• Convert among metric, household, and apothecary systems using dimensional analysis
Introduction
In the previous chapter you learned the basic measurements found in the household, metric, and apothecary systems of measurements. Each of these is used today in prescribing and administering medications. Another measurement system, avoirdupois, is also available, but this system is not normally found in calculations or conversions. In this system, 16 ounces = one pound (7000 grains = one pound). Two other measures are used in dosage calculations—milliequivalents and units—that will be discussed in Chapter 6.
Conversions among the systems are only necessary if the two factors needed for calculation are not found within the same measurement system. If both factors are already in the metric system, then moving within the system is all that is necessary, as seen in Chapter 4. This is likewise true for the apothecary and household measurements. However, if one factor is in one system, such as the metric system, and the other factor is in another system, such as household, proportional equations are used to find the unknown approximation.
Using Ratio and Proportion for Conversion of Units
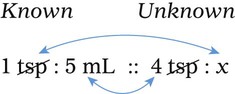
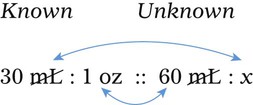
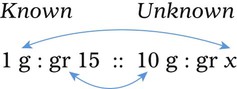
Ratio is the relationship of one quantity to another, whereas proportion is the relationship between two equal ratios. In ratio and proportion, an unknown is solved using “x” as the unknown. This provides a logical and systematic means of finding the equivalent unknown when knowns are used for calculations. Two equal ratio sets (or the relationship between two equivalents, such as a [extreme] : b [mean] :: c [mean] : d [extreme]) is indicated for calculating proportional equivalents. When one of the equivalents is unknown, an “x” is used to indicate the unknown. (See Chapter 2 if you need to review this material.)
When the ratios have been properly aligned into proportion(s), multiply the two inside numbers (means, or “insies”) and the two outside numbers (extremes, or “outsies”) and then solve for “x.” Remember that what is done to numbers on one side of the equation must be done to numbers on the other side of the equation. If you need more review for ratio and proportion, refer to Chapter 2.
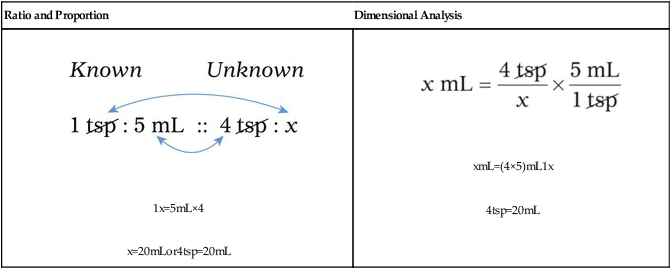
Using Dimensional Analysis for Converting Among Units
1. Find the known, or given, quantity—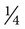 c.
c.
2. What is the desired, or wanted, amount?—x tablespoons.
3. What are the conversion factors that are needed to make the necessary calculation? In this case, we need to know that 2 tablespoons equals 1 oz and 8 oz equals 1 c.
4. Set up the problem with factors that are available for conversion factors. You want to cancel out like factors by placing them in a numerator of the first fraction followed by the denominator in the next fraction as follows:
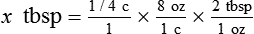
5. Cross out the unwanted units. Just as with any other mathematical equation, if units appear in both the numerator and the denominator, you may cancel them to find the unit that is desired. In this case, the remaining unit is a tablespoon, which is the unit you are seeking.
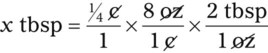
6. Multiply the numerators, multiply the denominators, and divide the product of the numerators by the product of the denominators. This will give you the desired quantity that was originally your unknown factor.
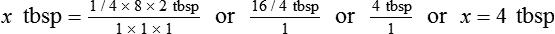
So, after completing the problem:

Now let’s look at other examples found within the same measurement systems.
Conversions Between Household and Apothecary Systems
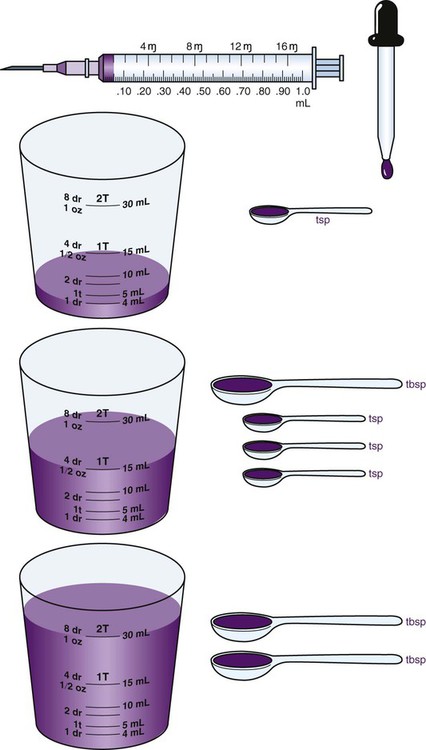
The apothecary system has only a few significant measurements that, although not commonly used, do convert into household measurements. Of importance are minims to drops, drams to teaspoons, and ounces to tablespoons (Figure 5-1). Cups, pints, quarts, and gallons are used by both systems. Length is not found in the apothecary system, so the conversions are not included in Table 5-1. As the chapter unfolds, the metric system will be added to combined tables for conversions among measurement systems.
TABLE 5.1
Conversions between Apothecary and Household Systems of Measurement
| PARAMETER | APOTHECARY UNITS | HOUSEHOLD UNITS | METRIC UNITS |
| Volume | 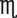 i (1 minim) i (1 minim) |
1 gtt (1 drop) | — |
 i (1 dram, i (1 dram, 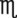 60) 60) |
1 tsp (1 teaspoon) | — | |
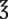 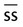 ( (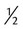 ounce) ounce) |
1 tbsp (1 tablespoon, 3 tsp) | — | |
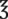 i (1 oz) i (1 oz) |
2 tbsp (2 tbsp, 6 tsp) | — | |
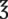 viii viii |
1 c (8 oz, 1 cup, 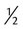 pint) pint) |
— | |
1 pt (1 pint, 2 c, 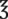 xvi) xvi) |
1 pt (1 pint, 2 c, 16 oz) | — | |
1 qt (1 quart, 2 pt, 4 c,  32) 32) |
1 qt (1 quart, 2 pt, 4 c, 32 oz) | — | |
1 gal (4 qt, 8 pt, 16 c, 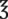 128) 128) |
1 gal (4 qt, 8 pt, 16 c, 128 oz) | — | |
| Mass/Weight | 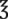 i (1 oz, 60 gr)* i (1 oz, 60 gr)* |
1 oz | — |
1# (1 lb, 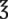 xii) xii) |
1# or 1 lb (16 oz)* | — | |
| Length | N/A | N/A | — |
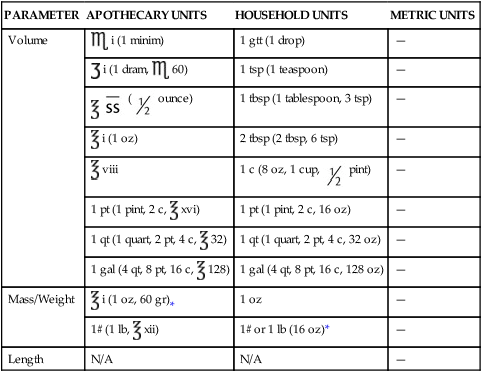
*Note that an apothecary pound contains only 12 oz, while a household pound contains 16 oz.

Conversions Between Household and Metric Units
Now that the household system has been compared with the apothecary system, it is time to compare the household system with the metric system, which is more frequently used in drug measurements (Table 5-2). Recall that the metric system is formed on the base 10 for ease of conversion. Most conversions from metric to household, such as milliliters to teaspoons, or milliliters to ounces, are volume conversions, although length from inches to centimeters is used in the medical field. Also notice that conversions between household and metric measurements are most commonly found in volume, but length and weight are found minimally when converting between these two systems for pharmaceutical purposes (Figure 5-2).
TABLE 5.2
Conversions between Household and Metric Systems of Measurement
| PARAMETER | APOTHECARY UNITS | HOUSEHOLD UNITS | METRIC UNITS |
| Volume | — | 1 gtt (1 drop) | N/A |
| — | 15 or 16 gtts* | 1 mL | |
| — | 1 tsp (1 teaspoon) | 5 mL or cc | |
| — | 1 tbsp (1 tablespoon, 3 tsp) | 15 mL | |
| — | 2 tbsp (2 tablespoons) | 30 mL | |
| — | 1 oz (2 tbsp) | 30 mL | |
| — | 1 c (8 oz, 1 cup, 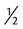 pint) pint) |
240 mL | |
| — | 1 pt (1 pint, 2 c, 16 oz) | 480 mL | |
| — | 1 qt (1 quart, 2 pt, 4 c, 32 oz) | 960 mL | |
| — | 1 gal (4 qt, 8 pt, 16 c, 128 oz) | 3840 mL | |
| Mass/Weight | — | 2.2# | 1 kg |
| Length | — | 1″ | 2.54 cm |
*Remember that the equivalents are approximate and not exact when doing conversions.

Conversions Between Metric and Apothecary Systems
Remember that the metric system uses grams, liters, and meters, whereas the apothecary system frequently uses grains, minims, drams, and ounces. Also remember that in converting between two systems of measure, the equivalents are approximate. This is important when converting between apothecary and metric systems. If the answer is a portion of a minim, you should round to the closest full amount because minims cannot be divided (e.g., if the calculation is for 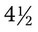 minims, the amount should be rounded to 5 minims; if the calculation is
minims, the amount should be rounded to 5 minims; if the calculation is 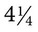 minims, the amount should be rounded to 4 minims). Portions of grains, milligrams, grams, and other measures can be expressed with fractional units. Again, with these conversions, ratio and proportion or dimensional analysis may be used, depending on the method that is most comfortable for you. Table 5-3 shows the equivalents between the apothecary system and the metric system.
minims, the amount should be rounded to 4 minims). Portions of grains, milligrams, grams, and other measures can be expressed with fractional units. Again, with these conversions, ratio and proportion or dimensional analysis may be used, depending on the method that is most comfortable for you. Table 5-3 shows the equivalents between the apothecary system and the metric system.
TABLE 5.3
Conversions between Apothecary and Metric Systems of Measurement
| PARAMETER | APOTHECARY UNITS | HOUSEHOLD UNITS | METRIC UNITS |
| Volume | 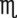 xv (15) (or xvi [16])* xv (15) (or xvi [16])* |
— | 1 mL |
 i i |
— | 4 or 5 mL * | |
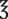 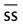 |
— | 15 mL | |
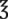 i i |
— | 30 mL | |
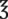 viii viii |
— | 240 mL | |
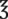 xvi or 1 pt xvi or 1 pt |
— | 480 mL | |
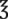 32 or 1 qt 32 or 1 qt |
— | 960 mL | |
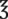 128 or 1 gal 128 or 1 gal |
— | 3840 mL | |
| Mass/Weight | gr i | — | 60 mg |
| gr xv | — | 1 g |
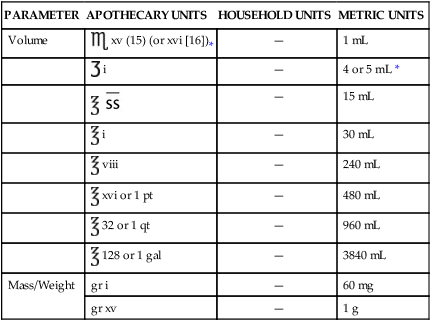
*Remember that all equivalents are approximates when converting between measurement systems.
| MASS | VOLUME |
| gr i = 60 mg (or 65 mg) | 1 mL = 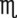 xv or xvi (use the figure that will give you as close to a whole number as possible) xv or xvi (use the figure that will give you as close to a whole number as possible) |
| 1 g = gr xv |  i = 4 or 5 mL i = 4 or 5 mL |
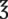 i = 30 mL i = 30 mL |

A quick way to remember conversions between grains and milligrams is to use a clock as the basis for conversions. There are 60 minutes in an hour just as there are 60 mg to a gr. Figure 5-3 shows how this can be used.
If you use the clock as a basis for conversions, gr 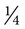 or
or 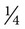 hour is 15 milligrams or minutes; gr
hour is 15 milligrams or minutes; gr 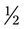 is 30 milligrams, while
is 30 milligrams, while  hour is 30 minutes; gr
hour is 30 minutes; gr 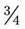 or
or 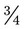 hour equals 45 milligrams or hours; and finally gr i equals 60 milligrams, while 1 hour equals 60 minutes. This same clock can be used for 1/6, 1/3, and 2/3 grains or hours just as easily. See Figure 5-3, A and B.
hour equals 45 milligrams or hours; and finally gr i equals 60 milligrams, while 1 hour equals 60 minutes. This same clock can be used for 1/6, 1/3, and 2/3 grains or hours just as easily. See Figure 5-3, A and B.
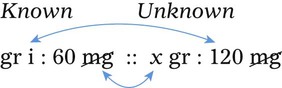
The clock can also be used to convert drams to minims as shown in Figure 5-3, C. As with the other clock examples, drams can be converted to minims by keeping the minim on the outside of the clock and the drams on the inside.

Putting It All Together—Metric, Household, and Apothecary Measurements and Their Conversions
Throughout this chapter you have converted between two measurement systems at a time. Now you need to put all of the conversions together. Table 5-4 is a combination of all tables previously shown in this chapter. Please remember that all conversions are approximations and could be changed depending on the conversion used for calculation, such as the number of mL in a dram. The conversion should always be made on the basis of a measurable dose.
TABLE 5.4
Conversions among Metric, Apothecary, and Household Systems of Measurement
| PARAMETER | APOTHECARY UNITS | HOUSEHOLD UNITS | METRIC UNITS |
| Volume | 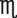 i i |
1 gtt | N/A |
 xv (or xvi)* xv (or xvi)* |
15 or 16 gtts | 1 mL | |
 i i |
1 tsp | 4 or 5 mL | |
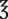 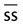 |
1 tbsp or 3 tsp | 15 mL | |
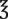 i i |
2 tbsp or 6 tsp | 30 mL | |
 viii viii |
1 c (8 oz, 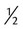 pt) pt) |
240 mL | |
 xvi or 1 pt xvi or 1 pt |
1 pt (2 c, 16 oz) | 480 mL | |
 32 or 1 qt 32 or 1 qt |
1 qt (2 pt, 4 c, 32 oz) | 960 mL | |
 128 or 1 gal 128 or 1 gal |
1 gal (4 qt, 8 pt, 16 c, 128 oz) | 3840 mL | |
| Mass/Weight | gr i | N/A | 60 mg |
| gr xv | N/A | 1 g | |
 i (60 gr) i (60 gr) |
1 oz | 4 g | |
| N/A | 2.2# | 1 kg | |
| Length | N/A | 1″ | 2.54 cm |
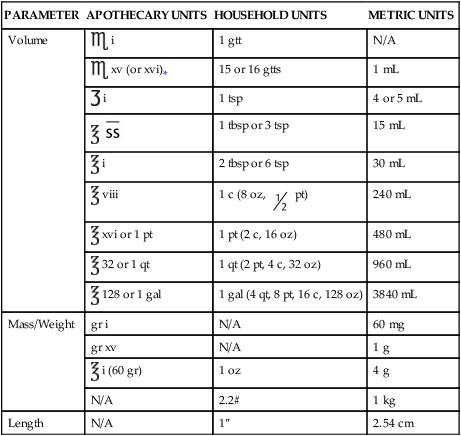
*Remember that all equivalents are approximates when converting among measurements.
Now add one last conversion to the clock (see Figure 5-3, D). Remember that you are now adding a liquid measure that should not be confused with the weight or solid measure.
Review of Rules
Rules of Conversion among Measurement Systems Using Ratio and Proportion
• Set up the conversion ratio with the known conversion units on the left of the equation.
• Set up the second ratio of the proportion with the conversion units for the unknowns.
• Label the units so that the like unit is placed in the same position within each ratio and proportion. This sets the ratios so that they are equal to each other.
Rules for Using Dimensional Analysis to Solve Conversions
• Use dimensional analysis for working with two quantities that are proportional to each other or that can be converted to find the proportional amounts.
• Use the common equivalencies or conversion factors to find the proportional amounts that are desired. Be sure the conversion factors used are in direct proportion to the previously used conversion factor.
• Always express the equation as fractional units.
• Cross out the common unwanted units before finding the products of the numerators and denominators.
• Complete the mathematical problem as you would any fractional equation.

 __________
__________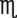 xxxii = __________ mL
xxxii = __________ mL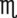 vi = __________ gtts
vi = __________ gtts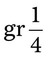 = __________ mg
= __________ mg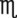 viii = __________ mL
viii = __________ mL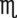 __________
__________ __________
__________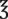 __________
__________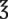 __________
__________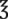 __________
__________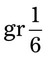 = __________ mg
= __________ mg = __________ mg
= __________ mg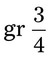 = __________ mg
= __________ mg vi = __________ tsp
vi = __________ tsp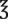 xv = __________ tbsp
xv = __________ tbsp = __________ mg
= __________ mg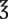 vi = __________ tbsp
vi = __________ tbsp
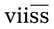 = __________ tsp
= __________ tsp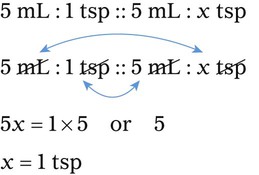
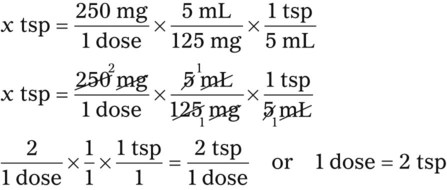


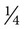 cup of an ingredient for a cake. At the time of baking, the only available measurement device is a tablespoon. How can you help the person baking the cake know the proper amount of the ingredient to be used when only a tablespoon is available? (
cup of an ingredient for a cake. At the time of baking, the only available measurement device is a tablespoon. How can you help the person baking the cake know the proper amount of the ingredient to be used when only a tablespoon is available? (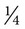 c = __________ tbsp)
c = __________ tbsp)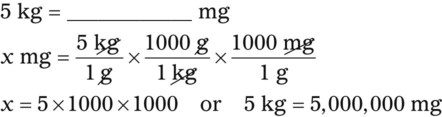
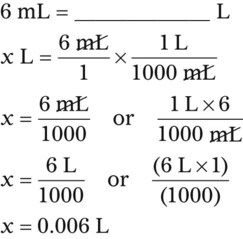
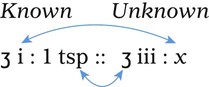
 (dram) and
(dram) and  (ounce).
(ounce).
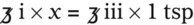
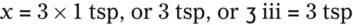
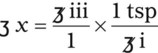
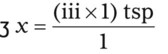
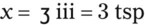



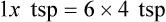
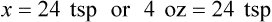
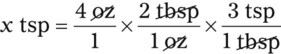
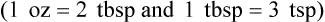

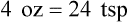
 __________
__________ __________
__________ __________
__________ __________
__________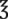
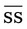 = __________ tsp
= __________ tsp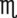 __________
__________ v = __________ tsp
v = __________ tsp __________
__________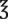 __________
__________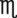 __________
__________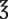 vi =
vi =  __________
__________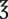 __________
__________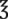 xxiv = __________ c
xxiv = __________ c __________
__________ __________
__________ __________
__________ __________
__________ xxx = __________ tbsp
xxx = __________ tbsp
 =
=  __________
__________ xxiv = __________ tsp
xxiv = __________ tsp vi =
vi =  __________
__________ __________ =
__________ =  __________
__________ ii of Robitussin cough medication q4h.
ii of Robitussin cough medication q4h.
 every 3 to 4 hours as needed for indigestion.
every 3 to 4 hours as needed for indigestion. viii daily.
viii daily. viii.
viii.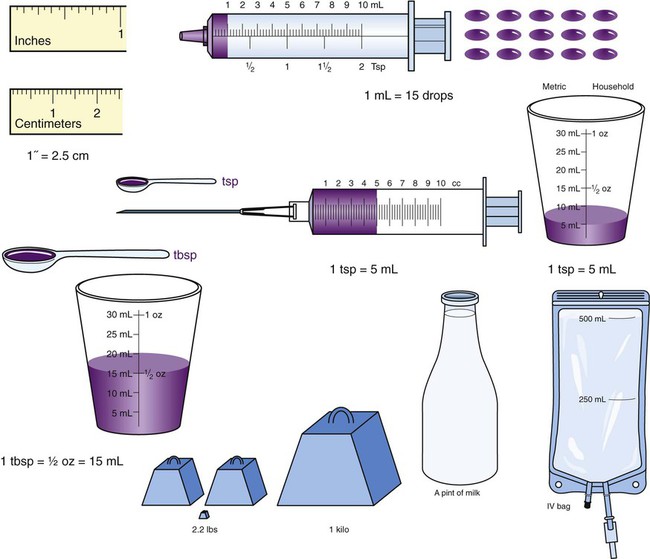

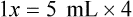
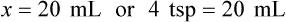
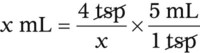
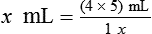
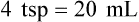

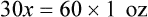
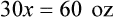
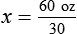
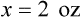
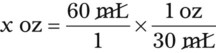
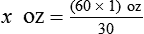
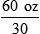

 iv = __________ tsp
iv = __________ tsp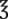 ii = __________ tbsp
ii = __________ tbsp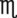 x = __________ gtts
x = __________ gtts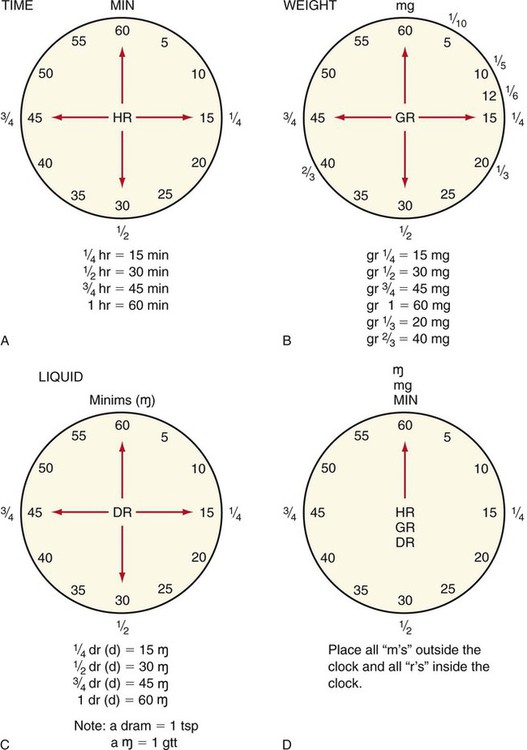
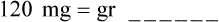
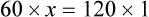
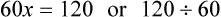

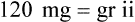
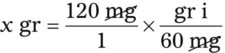
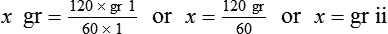

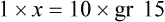
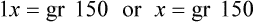
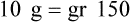
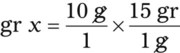
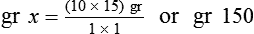
 drop would be 2 drops because a drop cannot be divided for administration. Show all of your calculations.
drop would be 2 drops because a drop cannot be divided for administration. Show all of your calculations. xvi = __________ mL
xvi = __________ mL iv = __________ mL
iv = __________ mL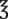 __________
__________ __________
__________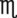 __________
__________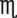 __________
__________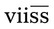 = __________ g
= __________ g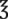 __________
__________ iv =
iv = 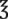 __________
__________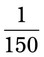 = __________ mg
= __________ mg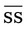 = __________ mg
= __________ mg __________
__________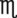 = __________ mL
= __________ mL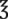 __________
__________ __________
__________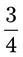 = __________ mcg
= __________ mcg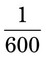 = __________ mg
= __________ mg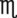 __________
__________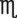 48 =
48 = 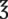 __________
__________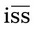 . The available medication is Seconal 100 mg/capsule.
. The available medication is Seconal 100 mg/capsule. . The medication stock bottle reads phenobarbital 30 mg per unscored tablet.
. The medication stock bottle reads phenobarbital 30 mg per unscored tablet.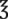 __________
__________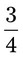 = __________ mg
= __________ mg v = __________mL __________ mL
v = __________mL __________ mL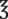 24 = __________ c
24 = __________ c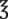 __________
__________ __________
__________ __________
__________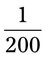 = __________ mg
= __________ mg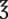 __________
__________ __________
__________ __________
__________ __________
__________ stat for pain.
stat for pain.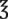 iii of water.
iii of water.


