Chapter 22 Computational Modeling of the Spine
Finite Element Models
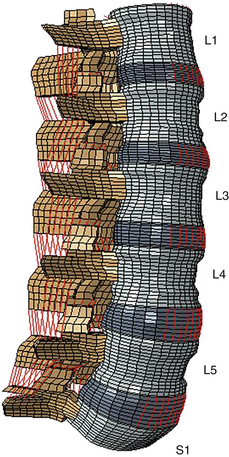
Even though the finite element method has been applied to structural engineering problems since the 1950s, it was first applied to the biomechanics of the spine in the 1970s.1,2 With improvements in numerical techniques and computer technology, its use in the field has gained momentum and it has become an integral part of spine biomechanics that is viewed as a complementary and insightful analysis (Fig. 22-1).
Modeling of Spinal Elements
Three-Dimensional Reconstruction and Structural Modeling
Several methods have been commonly used to model spinal units, including touch probe digitizer,3 laser scanner,4 CT,5 and MRI.6 Even though precise, highly accurate geometric models can be obtained using the touch probe digitizer and laser scanner methods, noninvasive techniques such as CT and MRI often are preferred because of their ability to retrieve data on internal features of the specimens—and even from live subjects—with ease. Some techniques also combine some of the methods mentioned earlier for the reconstruction of spinal units.7
In thorough finite element models, vertebral bodies usually are modeled in several sections, as cortical shell, cancellous core, dorsal bony elements, bony end plates, and cartilage layers, due to their unique material properties.5,7,8
In almost all studies, intervertebral discs are formed by three significant parts: the nucleus pulposus, the anulus fibrosus, and the cartilaginous end plates. The anulus is further divided into subcomponents such as ground substance and anulus fibers. Anulus ground substance is modeled as several layers surrounding the nucleus. The anulus fibers are angled 30 degrees and 150 degrees with respect to the transverse plane in adjacent layers.9,10 Some studies have used more realistic approaches in the design of these fibers by considering the increase in fiber angle from ventral to dorsal, and also fiber angle variation between anulus layers5,11 motivated by the histologic findings.12,13
After a solid model of the spine is built, each of its components is carefully divided into simpler substructures called “elements” for mathematical calculation purposes. Generally, hard tissues such as cortical shell, trabecular core, and dorsal elements are composed of tetrahedral (pyramid) and pentahedron (wedge) elements.14,15 With soft tissues, such as the anulus ground substance or cartilage layers, it is necessary to use hexahedral (rectangular prism) elements due to low-elasticity modulus and high Poisson ratio properties. In most studies, bilinear link or spring elements (cables), which are only capable of sustaining tension, are employed for ligaments and anulus fibers.5, 9–11
Material Definition
Vertebral Bodies, End Plates, and Facet Cartilages
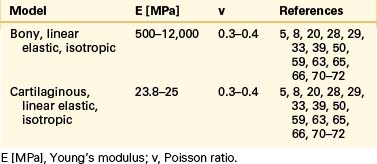
Even though bone is a poroelastic, anisotropic, and viscoelastic structure, in reality,16 vertebral cortical shell and cancellous bone usually are considered as linear elastic isotropic or transversely isotropic. Dorsal bony elements most commonly are modeled as linear elastic and isotropic (Tables 22-1 to 22-3). Researchers have either neglected the end plate due to its low elasticity module or modeled it as a composite structure (i.e., bony and cartilaginous layers). End plates most commonly were modeled as linear elastic and isotropic bone with a cartilaginous layer (Table 22-4). Cartilage layers also are added to the facets in most modeling paradigms (Table 22-5).
Intervertebral Disc: Anulus Fibrosus and Nucleus Pulposus
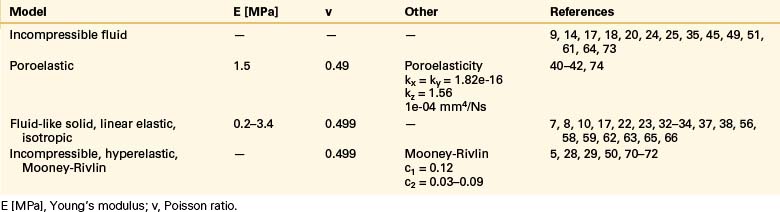
The intervertebral disc plays a crucial role in the movement and load-bearing functions of the spinal segments. It probably is the most intricate part of the functional spinal unit (i.e., vertebra-disc-vertebra complex) in finite element modeling, due to the composite structure of the anulus fibrosus and fluid-like behavior of the nucleus pulposus. The anulus fibrosus is formed by a matrix, anulus ground substance, and direction-dependent fibers. Even though there are a few homogeneous models for the anulus fibrosus, more realistic composite models that include matrix and angled fibers have been widely accepted and used (Tables 22-6 to 22-8). Anulus fibers are most commonly modeled with bilinear link, truss, or spring elements, and, in a few cases, with reinforced membrane elements. The material modeling of fibers is almost independent of the modeling technique.
Ligaments
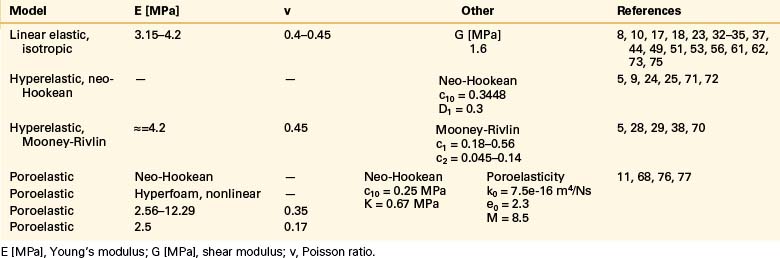
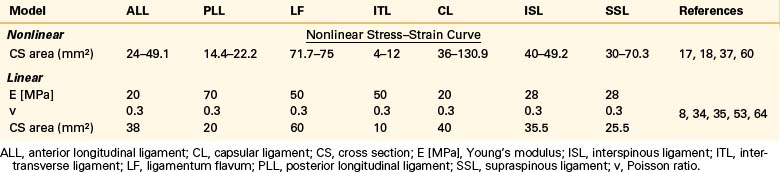
Ligaments are uniaxial structures that do not bear compressive loads. Like the anulus fibers, ligaments are modeled with link, truss, spring, or membrane elements. In general, it is assumed that linear, multilinear, or nonlinear elastic constitutive laws apply for these tissues (Table 22-9).
Articular Facet Joints
The facet joint plays an important role in load bearing and restriction of motion in segmental movements. It functions in tandem with the intervertebral disc in load transfer between adjacent vertebral bodies.17,18 The articulating structure must be modeled with realistic attributes and proper procedures in computational modeling of spinal segments because it has a significant effect on the quality and quantity of the motion. The articulation characteristics and relative motion depend on many factors, including cartilage layers, gap distance, the condition of the intervertebral disc, loading type, and geometric features of the articulating surface.
Kumaresan et al.19 compared different techniques for modeling of cervical facet joints. They reconstructed the joint capsule using four different methods: slide-line, contact plane, hyperelastic, and fluid models. The slide-line and contact plane models lacked the synovial fluid and synovial membrane. In the slide-line model, interaction was defined by using slide-line elements (gap elements), whereas in the contact plane model it was achieved by defining a contact plane between the cartilage surfaces. A friction coefficient of 0.01 was assigned for both models. The other models, hyperelastic and fluid, did not have elements for contact modeling; instead, they included synovial fluid between the cartilage layers modeled using noncompressible hyperelastic solid elements and hydrostatic noncompressible fluid elements, respectively. They concluded that fluid modeling of the facet joint matched both actual facet joint anatomy and its function better than the other three models. Similarly, Wheeldon et al.20 used full anatomic parts, such as facet joint cartilage, facet joint synovial fluid, and facet joint membrane, for modeling of the articular facet joints.
Shirazi-Adl et al.17,18 viewed the articulation process as a general moving contact problem and assigned 1 mm for the initial gap between the articulating surfaces. Guan et al.7,21 used 3D surface-to-surface contact to simulate the articulation phenomenon and assigned the initial gap between the surfaces according to CT images. Three-dimensional eight-noded compression-only gap elements were used to simulate the articulation between the facets in a study by Goel et al.22 Based on the CT images, they assigned the value of 0.45 mm for the initial gap between the surfaces.
The facet joints also are modeled with 3D gap contact elements with cartilage layers modeled using a parameter of “softened contact,” which exponentially adjusts force transfer between facet surfaces, according to the size of the gap.9,23–27 An initial gap of 0.5 mm was assigned, and at full closure, the joint was assumed to have the same stiffness as the surrounding bone material.
Schmidt et al.28,29 modeled the facet joints as nonlinear, with frictionless contact. They assigned the value of 0.6 mm for the initial gap between the cartilage layers. In other studies,30,31 the facet joints were simulated using frictionless surface-to-surface contact elements in combination with the penalty algorithm with a normal contact stiffness of 200 N/mm, and the initial gap between the cartilage layers assumed to be 0.4 mm.
Some researchers viewed the facet joints as a 3D contact problem with friction.8,32–34 To allow random motion of the surfaces, such as separation, sliding, and rotation, they defined a finite sliding interaction. For the friction characteristic, they chose a classic isotropic Coulomb friction model and assigned a relatively high friction coefficient of 0.1 as a worst-case scenario.
Lu et al.35 modeled the facet joints using sliding contact elements and assumed the contact pressure to be between 0 and 5000 megapascals (MPa), depending on the gap size. Pressure has been considered to be 0 MPa at a gap size of 0.5 mm and 5000 MPa when the gap is closed completely.
Loads and Boundary Conditions
Shirazi-adl et al.17,18 and Polikeit et al.8,34 applied a linearly varying distribution of axial loads to the top of the upper vertebra to simulate pure bending moments, with no net axial force. Kumaresan et al.36 and Wheeldon et al.20 succeeded in producing pure moments by using a force couple acting on the rigid plate attached to the superior vertebra.
Sharma et al.37 simulated pure flexion-extension moments using a pair of concentrated axial loads on top of the upper vertebra. They also studied the effect of anteroposterior shear during sagittal motion by a horizontal force applied at the center of the upper vertebral body. Two equal and opposite forces at the nodes at the edge of the sagittal or medial periphery of the upper vertebral body were applied to produce a force couple yielding a pure moment.38–42
Researchers have used the follower load technique, suggested by Patwardhan et al.,43 extensively for the last decade to simulate upper-body weight and the stabilizing effects of muscle forces seen in vivo without inducing any intervertebral rotations.9,25–28,30,44,45
Biomechanical Applications
Disc Degeneration and Vertebral Osteoporosis Simulation
In one of the earliest studies, Shirazi-Adl et al.45 modeled the degenerated disc by simply omitting a nucleus section. In another study, Shirazi-Adl et al.18 modeled the healthy disc as noncompressible fluid and suggested the loss of noncompressibility as a means to simulate the degenerated disc.
Goel et al.10 modeled the aging disc with a great deal of complexity by realistically simulating the radial and circumferential fissures in the anulus fibrosus that appear with age and discectomy. They simulated the radial crack in two ways: “out-in” injury started from the outermost layer and went through the innermost anulus layer with step-wise removal of the anulus elements, whereas “in-out” injury started from the innermost layer and went through the last layer of anulus simulated by replacing material of the anulus’s elements with nucleus material. They simulated the circumferential injury by removing the fourth anulus layer along the circumference, starting from posterior and extending through lateral.
Rohlmann et al.24 investigated the mechanical effects of three different grades of intervertebral disc degeneration—mild, moderate, and severe—compared with the healthy disc. They modeled the degeneration by reducing the disc height to 20%, 40%, and 60% of the healthy disc for mildly, moderately, and severely degenerated discs, respectively. In the finite element model, the laxity in all disc fibers and surrounding ligaments, seen on in vivo conditions after reduction of the disc height, was simulated by offsetting their nonlinear stiffness curves. They assigned the compressibility values for the nucleus pulposus of 0.0005, 0.0503, 0.0995, and 0.15, respectively, for healthy disc and mildly, moderately, and severely degenerated intervertebral discs. They assumed no effect on the material properties of the anulus fibrosus from degeneration of the disc.
Hussain et al.41,42 modeled two different degenerated discs, moderately and severely degenerated, to study the effects of disc degeneration on the facet loads. They simulated the degeneration according to the signs of Thompson disc grades 2 and 3 (moderate) and 4 and 5 (severe). They decreased the disc height, increased the disc area, and reduced the nucleus portion to simulate the degenerated disc. They also reduced the Poisson’s ratio in severely degenerated discs and increased the Young’s modulus of anulus and nucleus in both moderately and severely degenerated discs.
Galbusera et al.11 meticulously modeled the degeneration of the disc based on five different degenerative characteristics: (1) loss of water content in nucleus and anulus, (2) calcification and thickness reduction in end plates, (3) loss of disc height, (4) formation of osteophytes, and (5) diffuse sclerosis. They obtained ten different spinal segments by scaling the size of the finite element model to represent different stages of each degeneration level (mild, moderate, and severe). They changed the initial void ratio to model the degeneration in the nucleus and anulus, and they formed three different types of anular lesions: a rim lesion, a radial tear, and a circumferential tear. They modeled end plate cartilage degeneration by reducing its height and changing its material properties. Degeneration of the disc also was modeled with reduction of its height. When simulating the osteophytes, they used solid elements with the same material attributes of bone and anulus between them. They simulated sclerosis by interchanging the material properties of cancellous bone with the cortical bone in certain areas. They divided the lower half of L4 and the upper half of L5 into four regions and randomly assigned the sclerosis deficiency to these sections.
Polikeit et al.46 investigated the effects of osteoporosis and disc generation on the load transfer characteristics of an L2-3 segment. Initially, they modeled an osteoporotic vertebra by decreasing the elasticity modulus of trabecular bone by 66% and other bony parts by 33% compared with healthy model. Next, they simulated the progress of osteoporosis by modeling the cancellous bone transversely isotropic (i.e., the elastic modulus in the horizontal direction was one third of that in the vertical direction, using the same material properties as for the isotropic case) and increasing the anisotropy gradually. They postulated five steps of degeneration based on the isotropic osteoporotic vertebra model. At the first step, they changed the material definition of the nucleus pulposus from noncompressible to deformable. In the second step, the nucleus pulposus was hardened by assigning the same material properties as the ground substance of the anulus, and subsequently the Young modulus of the whole disc was doubled. In the fourth step, the innermost anulus layer was removed, other layers were thickened, and increased space between the fibers resulted. In the last step, they further reduced the elasticity modulus of the last remaining fiber layers. They also modeled a worst-case scenario by using transversely isotropic osteoporotic vertebral bodies in conjunction with the degenerated intervertebral disc.
Modeling and Analysis of the Instrumented Spine
Analysis of Fusion
Guan et al.21 studied the range of motion, disc pressure, and facet joint loading following ventral fusion at L4-5 or L5-S1 under flexion-extension loading. They simulated fusion by replacing the whole disc with either a bone graft or a porous tantalum. They assumed an elasticity modulus of 100 MPa and 3.3 gigapascals (GPa), respectively, and a Poisson’s ratio of 0.2 and 0.1, respectively, for bone graft and porous tantalum. They found that caudal fusion, compared to rostral, and tantalum, compared to bone graft, caused less range of motion, and that rostral fusion induced more facet joint loads and less adjacent disc stress than caudal fusion.
Park et al.33 investigated the biomechanical effects of the number of ventral fixation rods, with or without dorsal fixation, on the spinal stability of thoracolumbar burst fracture constructs. They prepared ten separate models, composed of combinations of the following parameters: ventral rod number (0 to 2), with or without midcolumn compression and with or without dorsal fixation. They used different corpectomy procedures for the compression. They placed a cage in the center of L1. To simulate the surgical effects of the posterior fixation, the supraspinal ligament, interspinal ligament, and ligamentum flavum were removed. Pedicle screws and a ventral screw also were placed to simulate dorsal and ventral fixation. They concluded that two-rod ventral fixation ensured enough spinal stability and one-rod ventral fixation with posterior fixation hindered excessive motion.
Kim et al.47 focused on the biomechanical alterations after removal of the dorsal stabilization device in a fused lumbar segment. They modeled the fusion mass between the transverse processes of L3 and L4 as bilateral rectangular columns. To model the decompressed condition, the supraspinous ligament, the interspinous ligament, a portion of the spinous process, the distal region of the L3 lamina, and the ligamentum flavum were removed. Fixation was achieved with posterior pedicle screws. They inserted the screws into the pedicles at an inward angle of 10 degrees with respect to the horizontal plane and used a rod 5.5 mm in diameter. After intact testing, the fusion state with or without posterior support was studied. They concluded that removal of pedicle screws could lower the stiffness value of the fused segment, which would, however, decrease the stress levels at the adjacent discs.
Polikeit et al.8 investigated the effects of intervertebral cage applications on the load transfer and stress levels of adjacent tissues. They used a box-shaped cage model with titanium and carbon fiber for the material properties. They simulated the surgical effects by removing the anterior longitudinal ligament, nucleus pulposus, and ventral portion of the anulus. The gap elements with a high friction coefficient of 0.8 were used to define contact between cage surfaces and end plates. They found that intervertebral cage application increased the stress and changed the load transfer at the adjacent segments.
In an optimization study, Zhong et al.32 sought to devise a new intervertebral cage design that would allow more bone graft volume. They used a dorsal approach to implant the titanium cages and then carried out laminectomy and partial discectomy procedures on the model. They removed the dorsal elements, supraspinous ligament, interspinous ligament, ligamentum flavum, and part of the disc to simulate the procedure. The posterior support was modeled with pedicle screws and rods. The cages were placed between the vertebral bodies within two-thirds of the area of the disc. Cages could bear only compression loads. In the optimization step, they prioritized the gain of volume for bone ingrowth without sacrificing the biomechanical characteristics. They obtained a new cage with a volume of 1603 mm3 in comparison with the initial cage model with a volume of 2058 mm3. The new design was satisfying in terms of range of motion and stress levels at the adjacent disc, but had higher stress levels than the original cages.
Analysis of Arthroplasty
Goel et al.23 used a hybrid approach, a combination of finite element method and biomechanical testing, to investigate the mechanical effects of the Charité artificial disc (DePuy Spine, Inc., Raynham, MA) on the adjacent segments. They assumed that the surfaces of the artificial disc were smooth and flat. Furthermore, they also simulated the surgical procedure by resecting the anterior longitudinal ligament and ventral anulus and excising the nucleus pulposus. They concluded that arthroplasty increases mobility in flexion and extension by 19% and 44%, respectively, with minimal adjacent disc pressure changes. They also found that shear stress levels were higher at the superior bone interface with the artificial disc than at the inferior interface.
Rohlmann et al.48 investigated the biomechanical effects of artificial disc implant position and height, as well as gradual removal of the disc and contribution of the anterior longitudinal ligament to the biomechanical behavior of the lumbar spine. They used three different disc heights—10, 12, and 14 mm—placed in various locations in the anterior-posterior plane. Removal of the disc was modeled in steps: the ventral anulus, the nucleus, and, finally, excision of the whole disc. To study the contribution of the anterior longitudinal ligament, two models were used, with and without the ligament, simulating a ligament repair after implantation. They concluded that implant position had a great effect on intersegmental rotation for standing and flexion. The increase in disc height increased intersegmental rotation, and when lateral portions of anulus were preserved, intersegmental rotations were found similar to the intact model.
Schmidt et al.30 studied two hypotheses: (1) that increasing the artificial disc implanted segment number increased the mobility of the spine and facet joint loads, and (2) that incorrect positioning of the implanted disc caused instability. They used the SB Charité 3 Disc in the finite element model. They used chrome-cobalt alloy for the metallic end plates, with an elasticity modulus of 300 GPa and a Poisson’s ratio of 0.27. They chose ultra-high-molecular-weight polyethylene for the core with a Young’s modulus of 2 GPa and a Poisson ratio of 0.3. The anterior longitudinal ligament, ventral anulus, and nucleus were removed. They obtained a perfect osteointegration between the metallic end plates and the vertebral bodies by using a perfect bond contact. Eleven cases were studied, involving combinations of two, three, or four levels of implantation. The effect of misalignment of the discs also was studied. The results showed that the increase in motion ranged from 51% for two implants up to 91% for four implants. The increase in facet joint loads was 24% for two implants and up to 38% for four implants for the centrally positioned, extension situation. They found that misalignments in the position of the artificial disc induced high facet joint loads, unfavorable kinematics, and lift-off phenomena.
Analysis of Dynamic Systems
Zander et al.49 studied a hybrid construct with a dynamic implant placed adjacent to a fused segment with a spinal fixator. A pedicle screw–based dynamic implant was placed at the L3-4 segment. An L2-3 fusion initially was modeled with a bone graft and a rigid dorsal fixator. The location of the fusion was tested by moving the fusion and fixators to the L4-5 level. They concluded that the dynamic implant decreased intersegmental rotation of the implanted level in walking, flexion, and extension, and reduced facet joint loads in axial rotation.
Rohlman et al.9 compared the mechanical performance of dorsal dynamic implants and dorsal rigid fixators. They inserted a pair of dorsal dynamic implants with fictional material attributes to the L3-4 segment. To compare the dynamic and rigid devices, the dynamic system was substituted with the rigid system. They also divided the dynamic implant investigation by studying the construct both with and without distraction to the height of a healthy disc. Furthermore, they studied the effect of implant stiffness on intersegmental rotation by changing the longitudinal rod stiffness in several steps. They found that a dynamic implant decreased the intersegmental rotation and facet joint loads at the implanted level, and that it reduced intradiscal pressure in a healthy disc in extension and standing. They also found that intradiscal pressures were reduced only for the rigid fixator after distraction.
In a recent probabilistic study, Rohlmann et al.27 investigated the effects of ten variables inherent in a pedicle screw–based motion preservation system on the intradiscal pressure, facet loads, and intervertebral rotations. They used different lengths of implants in the study with titanium screws and polycarbonate-urethane rods. The parameters that varied were elastic modulus, diameter of the rods, angular rigidity of the screw head, interval between the rod and the pedicle screw entry point, orientation of the screws, whether cranial or caudal levels were bridged, and several kinds of defects. They observed that motion preservation systems reduced levels of intersegmental rotation, intradiscal pressure, and facet joint loads in most cases. They concluded that the loading conditions, Young’s modulus and the diameter of the rod, the distraction of the segment, and the torsional stiffness of the connection between the screws and rod had a greater effect on the output parameters.
In a parametric study, Schmidt et al.29 sought the optimal axial and bending stiffness values for a dorsal dynamic implant while validating their findings with an in vitro study. They used a simplified model of the stabilization system, including rod and screws, to investigate the range of axial and bending stiffness of the rod, which represented the nonfixed and fixed situations. They found that lower stiffness values of the rod provided acceptable stiffening to the segment and higher stiffness values of the rod had negligible effects.
Analysis of Cement Augmentation
Polikeit et al.34 investigated the influence of cement augmentation on load transfer by using an L2-3 finite element model. After adapting the material properties of the osteoporotic vertebral body, they considered polymethylmethacrylate (PMMA) as the bone cement material. In the first case, they simulated the effects of cement augmentation of the whole trabecular bone by changing the cancellous bone material properties to that of PMMA in L2 and L3, subsequently. They modeled unipedicular and bipedicular cement augmentations with one or two vertically placed cement barrels filling up one sixth of the vertebral body volume according to observations on radiographs of treated patients. The results of the study showed that augmentation increased the intradiscal pressure and deflection of the end plate into the adjacent vertebra. They found that augmentation changed the stress levels and distribution in the adjacent vertebrae.
Baroud et al.50 investigated the effects of vertebroplasty on load transfer in the segment. They modeled the material properties of bone cement composition after vertebroplasty as linear isotropic elastic, 46 times stronger and 12 times stiffer than the osteoporotic bone. To simulate the cement-infiltrated vertebra, they modeled the whole volume of L5 as augmented cement. They found that augmentation reduced bulging of the end plate of the augmented vertebra, which caused stiffening of the intervertebral joint.
Rohmann et al.51 studied vertebroplasty and kyphoplasty for compression fractures and to investigate the importance of the center of gravity shift compensation of the upper torso on muscle forces and intradiscal pressure. They prepared an intact model, a vertebroplasty model, and a kyphoplasty model. They simulated the vertebroplasty model by reducing the ventral height of L3 by 35% compared with an intact disc, forming a wedge fracture. They simulated the kyphoplasty model by reducing the ventral height of L3 by 90% of the intact disc, assuming a nearly full fracture. In addition, they simulated the upper torso center of gravity shift compensation with three different scenarios. They concluded that the shift of the upper body center of gravity played a greater role in vertebral body fractures at the adjacent segments compared with kyphoplasty or vertebroplasty.
Galbusera F., Schmidt H., Neidlinger-Wilke C., et al. The mechanical response of the lumbar spine to different combinations of disc degenerative changes investigated using randomized poroelastic finite element models. Eur Spine J. 2011;20(4):563-571.
Goel V.K., Monroe B.T., Gilbertson L.G., Brinckmann P. Interlaminar shear stresses and laminae separation in a disc. Finite element analysis of the L3-L4 motion segment subjected to axial compressive loads. Spine (Phila Pa 1976). 1995;20(6):689-698.
Kumaresan S., Yoganandan N., Pintar F.A. Finite element modeling approaches of human cervical spine facet joint capsule. J Biomech. 1998;31(4):371-376.
Polikeit A., Ferguson S.J., Nolte L.P., Orr T.E. Factors influencing stresses in the lumbar spine after the insertion of intervertebral cages: finite element analysis. Eur Spine J. 2003;12(4):413-420.
Polikeit A., Nolte L.P., Ferguson S.J. Simulated influence of osteoporosis and disc degeneration on the load transfer in a lumbar functional spinal unit. J Biomech. 2004;37(7):1061-1069.
Rohlmann A., Zander T., Bergmann G. Spinal loads after osteoporotic vertebral fractures treated by vertebroplasty or kyphoplasty. Eur Spine J. 2006;15(8):1255-1264.
Schmidt H., Heuer F., Drumm J., et al. Application of a calibration method provides more realistic results for a finite element model of a lumbar spinal segment. Clin Biomech (Bristol, Avon). 2007;22(4):377-384.
1. Yoganandan N., Kumaresan S., Voo L., Pintar F.A. Finite element applications in human cervical spine modeling. Spine (Phila Pa 1976). 1996;21(15):1824-1834.
2. Moroney S.P., Schultz A.B., Miller J.A., Andersson G.B. Load-displacement properties of lower cervical spine motion segments. J Biomech. 1988;21(9):769-779.
3. Lee K.K., Teo E.C., Qiu T.X. Finite element modeling of L2-L3 using digitizer. Int J Comput Applications Technol, special issue on Biomedical Engineering and IT. 2003;20:1-9.
4. Heuer F., Schmidt H., Claes L., Wilke H.J. A new laser scanning technique for imaging intervertebral disc displacement and its application to modeling nucleotomy. Clin Biomech (Bristol, Avon). 2008;23(3):260-269.
5. Schmidt H., Heuer F., Drumm J., et al. Application of a calibration method provides more realistic results for a finite element model of a lumbar spinal segment. Clin Biomech (Bristol, Avon). 2007;22(4):377-384.
6. Pfirrmann C.W., Metzdorf A., Zanetti M., et al. Magnetic resonance classification of lumbar intervertebral disc degeneration. Spine (Phila Pa 1976). 2001;26(17):1873-1878.
7. Guan Y., Yoganandan N., Zhang J., et al. Validation of a clinical finite element model of the human lumbosacral spine. Med Biol Eng Comput. 2006;44(8):633-641.
8. Polikeit A., Ferguson S.J., Nolte L.P., Orr T.E. Factors influencing stresses in the lumbar spine after the insertion of intervertebral cages: finite element analysis. Eur Spine J. 2003;12(4):413-420.
9. Rohlmann A., Burra N.K., Zander T., Bergmann G. Comparison of the effects of bilateral posterior dynamic and rigid fixation devices on the loads in the lumbar spine: a finite element analysis. Eur Spine J. 2007;16(8):1223-1231.
10. Goel V.K., Monroe B.T., Gilbertson L.G., Brinckmann P. Interlaminar shear stresses and laminae separation in a disc. Finite element analysis of the L3-L4 motion segment subjected to axial compressive loads. Spine (Phila Pa 1976). 1995;20(6):689-698.
11. Galbusera F., Schmidt H., Neidlinger-Wilke C., et al. The mechanical response of the lumbar spine to different combinations of disc degenerative changes investigated using randomized poroelastic finite element models. Eur Spine J. 2011;20(4):563-571.
12. Eberlein R., Holzapfel G.A., Schulze-Bauer CAJ. An anisotropic constitutive model for annulus tissue and enhanced finite element analysis of intact lumbar disc bodies. Comput Methods Biomech Biomed Engin. 2001;4:209-230.
13. Cassidy J.J., Hiltner A., Baer E. Hierarchical structure of the intervertebral disc. Connect Tissue Res. 1989;23(1):75-88.
14. Rundell S.A., Guerin H.L., Auerbach J.D., Kurtz S.M. Effect of nucleus replacement device properties on lumbar spine mechanics. Spine (Phila Pa 1976). 2009;34(19):2022-2032.
15. Charriere E., Sirey F., Zysset P.K. A finite element model of the L5-S1 functional spinal unit: development and comparison with biomechanical tests in vitro. Comput Methods Biomech Biomed Engin. 2003;6(4):249-261.
16. Cowin S.C. Bone poroelasticity. J Biomech. 1999;32(3):217-238.
17. Shirazi-Adl A., Ahmed A.M., Shrivastava S.C. Mechanical response of a lumbar motion segment in axial torque alone and combined with compression. Spine (Phila Pa 1976). 1986;11(9):914-927.
18. Shirazi-Adl A., Ahmed A.M., Shrivastava S.C. A finite element study of a lumbar motion segment subjected to pure sagittal plane moments. J Biomech. 1986;19(4):331-350.
19. Kumaresan S., Yoganandan N., Pintar F.A. Finite element modeling approaches of human cervical spine facet joint capsule. J Biomech. 1998;31(4):371-376.
20. Wheeldon J.A., Stemper B.D., Yoganandan N., Pintar F.A. Validation of a finite element model of the young normal lower cervical spine. Ann Biomed Eng. 2008;36(9):1458-1469.
21. Guan Y., Yoganandan N., Maiman D.J., Pintar F.A. Internal and external responses of anterior lumbar/lumbosacral fusion: nonlinear finite element analysis. J Spinal Disord Tech. 2008;21(4):299-304.
22. Goel V.K., Kong W., Han J.S., et al. A combined finite element and optimization investigation of lumbar spine mechanics with and without muscles. Spine (Phila Pa 1976). 1993;18(11):1531-1541.
23. Goel V.K., Grauer J.N., Patel T., et al. Effects of charite artificial disc on the implanted and adjacent spinal segments mechanics using a hybrid testing protocol. Spine (Phila Pa 1976). 2005;30(24):2755-2764.
24. Rohlmann A., Zander T., Schmidt H., et al. Analysis of the influence of disc degeneration on the mechanical behaviour of a lumbar motion segment using the finite element method. J Biomech. 2006;39(13):2484-2490.
25. Dreischarf M., Rohlmann A., Bergmann G., Zander T. Optimised loads for the simulation of axial rotation in the lumbar spine. J Biomech. 2011;44(12):2323-2327.
26. Rohlmann A., Zander T., Rao M., Bergmann G. Realistic loading conditions for upper body bending. J Biomech. 2009;42(7):884-890.
27. Rohlmann A., Nabil Boustani H., Bergmann G., Zander T. Effect of a pedicle-screw-based motion preservation system on lumbar spine biomechanics: a probabilistic finite element study with subsequent sensitivity analysis. J Biomech. 2010;43(15):2963-2969.
28. Schmidt H., Heuer F., Wilke H.J. Interaction between finite helical axes and facet joint forces under combined loading. Spine (Phila Pa 1976). 2008;33(25):2741-2748.
29. Schmidt H., Heuer F., Wilke H.J. Which axial and bending stiffnesses of posterior implants are required to design a flexible lumbar stabilization system? J Biomech. 2009;42(1):48-54.
30. Schmidt H, Galbusera F, Rohlmann A, et al: Effect of multilevel lumbar disc arthroplasty on spine kinematics and facet joint loads in flexion and extension: a finite element analysis. Eur Spine J April 2, 2010 [Epub ahead of print].
31. Schmidt H., Midderhoff S., Adkins K., Wilke H.J. The effect of different design concepts in lumbar total disc arthroplasty on the range of motion, facet joint forces and instantaneous center of rotation of a L4-5 segment. Eur Spine J. 2009;18(11):1695-1705.
32. Zhong Z.C., Wei S.H., Wang J.P., et al. Finite element analysis of the lumbar spine with a new cage using a topology optimization method. Med Eng Phys. 2006;28(1):90-98.
33. Park W.M., Park Y.S., Kim K., Kim Y.H. Biomechanical comparison of instrumentation techniques in treatment of thoracolumbar burst fractures: a finite element analysis. J Orthop Sci. 2009;14(4):443-449.
34. Polikeit A., Nolte L.P., Ferguson S.J. The effect of cement augmentation on the load transfer in an osteoporotic functional spinal unit: finite-element analysis. Spine (Phila Pa 1976). 2003;28(10):991-996.
35. Lu Y.M., Hutton W.C., Gharpuray V.M. Do bending, twisting, and diurnal fluid changes in the disc affect the propensity to prolapse? A viscoelastic finite element model. Spine (Phila Pa 1976). 1996;21(22):2570-2579.
36. Kumaresan S., Yoganandan N., Pintar F.A., et al. Biomechanical study of pediatric human cervical spine: a finite element approach. J Biomech Eng. 2000;122(1):60-71.
37. Sharma M., Langrana N.A., Rodriguez J. Role of ligaments and facets in lumbar spinal stability. Spine (Phila Pa 1976). 1995;20(8):887-900.
38. Ruberte L.M., Natarajan R.N., Andersson G.B. Influence of single-level lumbar degenerative disc disease on the behavior of the adjacent segments–a finite element model study. J Biomech. 2009;42(3):341-348.
39. Hussain M., Nassr A., Natarajan R.N., et al. Biomechanical effects of anterior, posterior, and combined anterior-posterior instrumentation techniques on the stability of a multilevel cervical corpectomy construct: a finite element model analysis. Spine J. 2011;11(4):324-330.
40. Hussain M., Natarajan R.N., Chaudhary G., et al. Simulation of inhomogeneous rather than homogeneous poroelastic tissue material properties within disc annulus and nucleus better predicts cervical spine response: a C3-T1 finite element model analysis under compression and moment loadings. Spine (Phila Pa 1976). 2011;36(4):E245-E255.
41. Hussain M., Natarajan R.N., An H.S., Andersson G.B. Reduction in segmental flexibility because of disc degeneration is accompanied by higher changes in facet loads than changes in disc pressure: a poroelastic C5-C6 finite element investigation. Spine J. 2010;10(12):1069-1077.
42. Hussain M., Natarajan R.N., An H.S., Andersson G.B. Patterns of height changes in anterior and posterior cervical disc regions affects the contact loading at posterior facets during moderate and severe disc degeneration: a poroelastic C5-C6 finite element model study. Spine (Phila Pa 1976). 2010;35(18):E873-E881.
43. Patwardhan A.G., Havey R.M., Meade K.P., et al. A follower load increases the load-carrying capacity of the lumbar spine in compression. Spine (Phila Pa 1976). 1999;24(10):1003-1009.
44. Rohlmann A., Zander T., Bergmann G. Comparison of the biomechanical effects of posterior and anterior spine-stabilizing implants. Eur Spine J. 2005;14(5):445-453.
45. Shirazi-Adl S.A., Shrivastava S.C., Ahmed A.M. Stress analysis of the lumbar disc-body unit in compression. A three-dimensional nonlinear finite element study. Spine (Phila Pa 1976). 1984;9(2):120-134.
46. Polikeit A., Nolte L.P., Ferguson S.J. Simulated influence of osteoporosis and disc degeneration on the load transfer in a lumbar functional spinal unit. J Biomech. 2004;37(7):1061-1069.
47. Kim H.J., Chun H.J., Moon S.H., et al. Analysis of biomechanical changes after removal of instrumentation in lumbar arthrodesis by finite element analysis. Med Biol Eng Comput. 2010;48(7):703-709.
48. Rohlmann A., Zander T., Bergmann G. Effect of total disc replacement with ProDisc on intersegmental rotation of the lumbar spine. Spine (Phila Pa 1976). 2005;30(7):738-743.
49. Zander T., Rohlmann A., Burra N.K., Bergmann G. Effect of a posterior dynamic implant adjacent to a rigid spinal fixator. Clin Biomech (Bristol, Avon). 2006;21(8):767-774.
50. Baroud G., Nemes J., Heini P., Steffen T. Load shift of the intervertebral disc after a vertebroplasty: a finite-element study. Eur Spine J. 2003;12(4):421-426.
51. Rohlmann A., Zander T., Bergmann G. Spinal loads after osteoporotic vertebral fractures treated by vertebroplasty or kyphoplasty. Eur Spine J. 2006;15(8):1255-1264.
52. Brolin K., Halldin P. Development of a finite element model of the upper cervical spine and a parameter study of ligament characteristics. Spine (Phila Pa 1976). 2004;29(4):376-385.
53. Cheung J.T., Zhang M., Chow D.H. Biomechanical responses of the intervertebral joints to static and vibrational loading: a finite element study. Clin Biomech (Bristol, Avon). 2003;18(9):790-799.
54. Lavaste F., Skalli W., Robin, et al. Three-dimensional geometrical and mechanical modelling of the lumbar spine. J Biomech. 1992;25(10):1153-1164.
55. Wang J.L., Parnianpour M., Shirazi-Adl A., Engin A.E. Viscoelastic finite-element analysis of a lumbar motion segment in combined compression and sagittal flexion. Effect of loading rate. Spine (Phila Pa 1976). 2000;25(3):310-318.
56. Denoziere G., Ku D.N. Biomechanical comparison between fusion of two vertebrae and implantation of an artificial intervertebral disc. J Biomech. 2006;39(4):766-775.
57. Williams J.R., Natarajan R.N., Andersson G.B. Inclusion of regional poroelastic material properties better predicts biomechanical behavior of lumbar discs subjected to dynamic loading. J Biomech. 2007;40(9):1981-1987.
58. Anasetti F., Galbusera F., Aziz H.N., et al. Spine stability after implantation of an interspinous device: an in vitro and finite element biomechanical study. J Neurosurg Spine. 2010;13(5):568-575.
59. Kumaresan S., Yoganandan N., Pintar F.A. Finite element analysis of the cervical spine: a material property sensitivity study. Clin Biomech (Bristol, Avon). 1999;14(1):41-53.
60. Argoubi M., Shirazi-Adl A. Poroelastic creep response analysis of a lumbar motion segment in compression. J Biomech. 1996;29(10):1331-1339.
61. Rohlmann A., Bauer L., Zander T., et al. Determination of trunk muscle forces for flexion and extension by using a validated finite element model of the lumbar spine and measured in vivo data. J Biomech. 2006;39(6):981-989.
62. Jebaseelan D.D., Jebaraj C., Yoganandan N., Rajasekaran S. Validation efforts and flexibilities of an eight-year-old human juvenile lumbar spine using a three-dimensional finite element model. Med Biol Eng Comput. 2010;48(12):1223-1231.
63. Ng H.W., Teo E.C. Nonlinear finite-element analysis of the lower cervical spine (C4-C6) under axial loading. J Spinal Disord. 2001;14(3):201-210.
64. Little J.P., de Visser H., Pearcy M.J., Adam C.J. Are coupled rotations in the lumbar spine largely due to the osseo-ligamentous anatomy? A modeling study. Comput Methods Biomech Biomed Engin. 2008;11(1):95-103.
65. Lee S.H., Im Y.J., Kim K.T., et al. Comparison of cervical spine biomechanics after fixed- and mobile-core artificial disc replacement: a finite element analysis. Spine (Phila Pa 1976). 2011;36(9):700-708.
66. Yoganandan N., Kumaresan S.C., Voo L., et al. Finite element modeling of the C4-C6 cervical spine unit. Med Eng Phys. 1996;18(7):569-574.
67. Schmidt H., Shirazi-Adl A., Galbusera F., Wilke H.J. Response analysis of the lumbar spine during regular daily activities—a finite element analysis. J Biomech. 2010;43(10):1849-1856.
68. Galbusera F., Schmidt H., Noailly J., et al. Comparison of four methods to simulate swelling in poroelastic finite element models of intervertebral discs. J Mech Behav Biomed Mater. 2011;4(7):1234-1241.
69. Maurel N., Lavaste F., Skalli W. A three-dimensional parameterized finite element model of the lower cervical spine. Study of the influence of the posterior articular facets. J Biomech. 1997;30(9):921-931.
70. Schmidt H., Heuer F., Simon U., et al. Application of a new calibration method for a three-dimensional finite element model of a human lumbar annulus fibrosus. Clin Biomech (Bristol, Avon). 2006;21(4):337-344.
71. Noailly J., Lacroix D., Planell J.A. Finite element study of a novel intervertebral disc substitute. Spine (Phila Pa 1976). 2005;30(20):2257-2264.
72. Noailly J., Wilke H.J., Planell J.A., Lacroix D. How does the geometry affect the internal biomechanics of a lumbar spine bi-segment finite element model? Consequences on the validation process. J Biomech. 2007;40(11):2414-2425.
73. Lu Y.M., Hutton W.C., Gharpuray V.M. Can variations in intervertebral disc height affect the mechanical function of the disc? Spine (Phila Pa 1976). 1996;21(19):2208-2216. discussion 2217
74. Hussain M., Natarajan R.N., Chaudhary G., et al. Relative contributions of strain-dependent permeability and fixed charged density of proteoglycans in predicting cervical disc biomechanics: a poroelastic C5-C6 finite element model study. Med Eng Phys. 2011;33(4):438-445.
75. Goel V.K., Clausen J.D. Prediction of load sharing among spinal components of a C5-C6 motion segment using the finite element approach. Spine (Phila Pa 1976). 1998;23(6):684-691.
76. Malandrino A., Planell J.A., Lacroix D. Statistical factorial analysis on the poroelastic material properties sensitivity of the lumbar intervertebral disc under compression, flexion and axial rotation. J Biomech. 2009;42(16):2780-2788.
77. Ferguson S.J., Ito K., Nolte L.P. Fluid flow and convective transport of solutes within the intervertebral disc. J Biomech. 2004;37(2):213-221.
78. Schmidt H., Heuer F., Claes L., Wilke H.J. The relation between the instantaneous center of rotation and facet joint forces: a finite element analysis. Clin Biomech (Bristol, Avon). 2008;23(3):270-278.
79. Meijer G.J., Homminga J., Hekman E.E., et al. The effect of three-dimensional geometrical changes during adolescent growth on the biomechanics of a spinal motion segment. J Biomech. 2010;43(8):1590-1597.
80. Fagan M.J., Julian S., Siddall D.J., Mohsen A.M. Patient-specific spine models. Part 1: Finite element analysis of the lumbar intervertebral disc—a material sensitivity study. Proc Inst Mech Eng H. 2002;216(5):299-314.