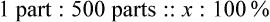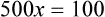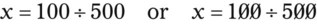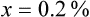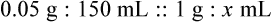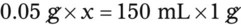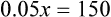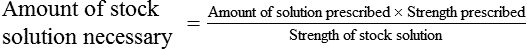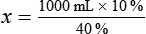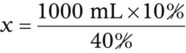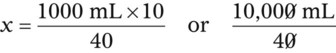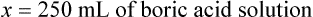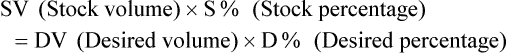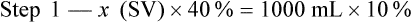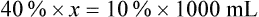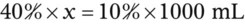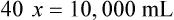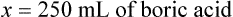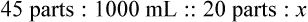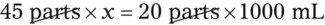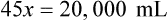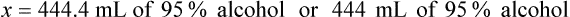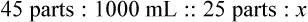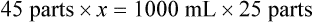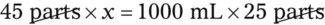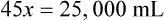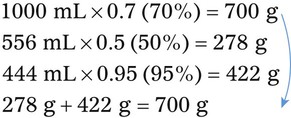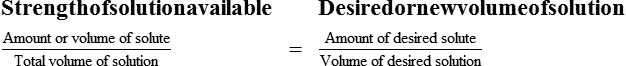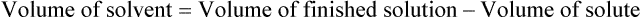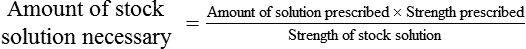Calculation of Mixtures from Stock Medications
• Interpret labels for the weight/volume of solute in solvent
• Dilute stock medications to the required strength using strengths expressed as percentages, fractions, and ratios
• Calculate the weight/volume of active ingredient in a substance
• Using alligation, calculate the weight/volume of stock medications needed to prepare a desired compound
Interpreting Solution Labels and Calculating Solutions In Percentages
With percentage preparations, the easiest method for calculation is the ratio and proportion method. If a review of the ratio and proportion method is necessary, see Chapter 2.
Reducing and Enlarging Ordered Preparations
When a volume of a known solution requires reducing or enlarging to meet a physician’s order, the original strength of the preparation may be used for the calculation of the new volume or weight of the preparation. For example, using the above calculations in Example 13-4, if the physician desires 100 mL, the answer can be figured using ratio and proportion.
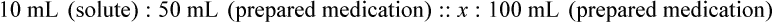
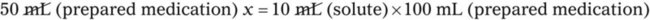
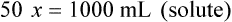
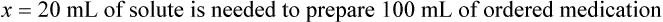
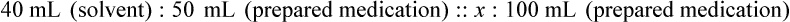
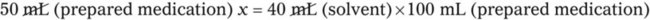
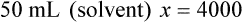
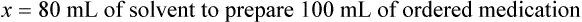
Calculating The Dilution of Stock Solutions
Two rules are important in simplifying this process:
Rule 1—When ratio strengths are given, convert these to percentage strengths using ratio and proportion. It is much easier to calculate in a percentage than in the fraction equivalent found with ratio strengths, such as 1 : 20, which would become 5%.
Rule 2—Reduce proportional parts to the lowest terms if these must be used, such as 75 parts : 50 parts becomes 3 : 2.
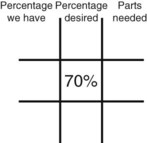
Calculating Medication Dilutions Using Alligation
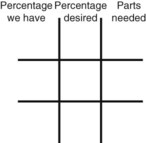
Step 2—Place the strength to be calculated in the center box.
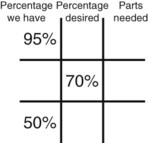
Step 3—Place the highest percentage concentration in the left upper corner.
Step 4—Place the lowest percentage concentration in the lower left corner.
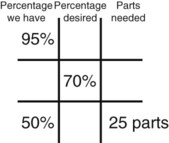
Step 5—Subtract the center square from the left upper square and place in the lower right square to reveal the parts of the lowest percentage concentration to be used in the new mixture.
Step 6—Subtract the lower left square from the center box and place in the upper right corner to reveal the parts of the highest percentage concentration to be used in the new mixture.
Step 7—Add the calculated parts together to find the total parts of the two ingredients in the compound.
Step 8—When the total quantity of the mixture is included in the prescription, then the parts of the mixture are placed into two ratio and proportion equations to calculate the exact amount of each ingredient to use. The total number of calculated parts is placed in the first ratio with the total amount of compound. The second ratio set in the proportion is the calculated number of parts of the stock ingredients to the unknown total compound amount. This step must be calculated for each part of the compound.
Review of Rules
Interpreting Solution Labels
• A solute expressed as a percentage shows the number of grams of solute in 100 mL of solvent or the parts of the solute/100 parts of solvent.
Calculating Medication Dilutions Using Alligation
Step 2—Place the strength to be calculated in the center box.
Step 3—Place the highest percentage concentration in the upper left corner.
Step 4—Place the lowest percentage concentration in the lower left corner.
• Alligation medial is another means of checking calculations for accuracy, using the following formula:
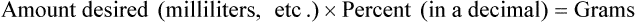
• Alligation medial may be used when two or more substances are to be mixed. The quantities to be mixed must be in a common denomination whether in weight or in volume.

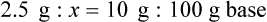
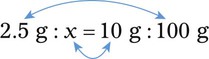
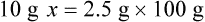
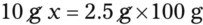
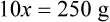
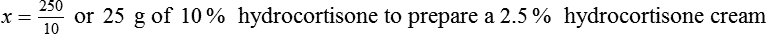
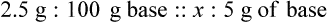
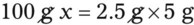


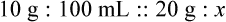
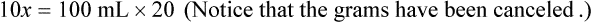
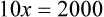
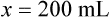
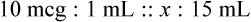
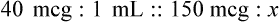
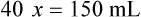
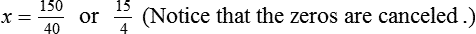
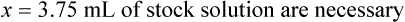
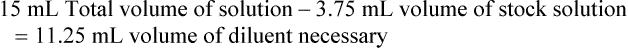
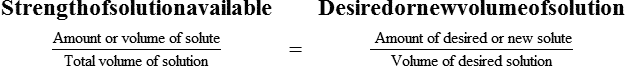
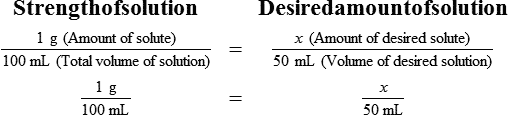
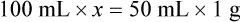
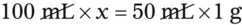
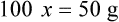
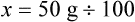
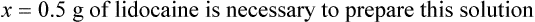
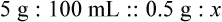
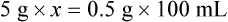
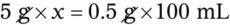
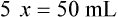
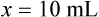
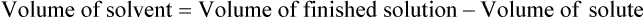
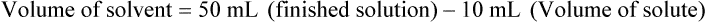
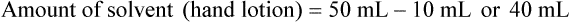
 qs 120 mL
qs 120 mL