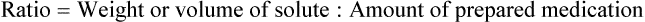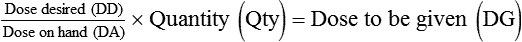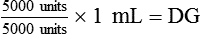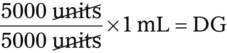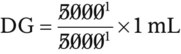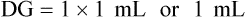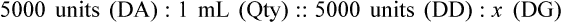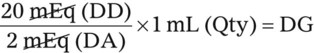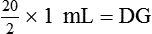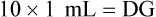Calculation of Medications Measured in Units, Milliequivalents, and Percentages of Concentration
• Calculate doses of antibiotic medications measured in units
• Calculate insulin doses measured in units
• Calculate anticoagulant doses measured in units
• Calculate medications measured in milliequivalents
• Interpret dosage when the medication is expressed as a percentage
• Interpret dosage of solutions expressed in ratio strength
• Calculate weight of active ingredients expressed in percentage or ratio and proportion
Introduction
Percentages are the concentration of weight of a substance or medication dissolved in a solute, either by volume with liquids or weight with solids. (To review how to change a percentage to whole or decimal numbers see Chapter 2.) These medications have the label showing the percentage strength such as Lidocaine 1% or epinephrine 0.1%. Solutions expressed in ratio strengths provide information concerning the ratio of medication to the amount of solute.
Calculating Dosages in Unit and Milliequivalent Measurements
Calculating Antibiotics Measured in Units
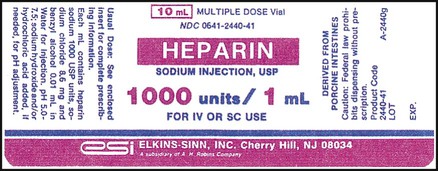
Penicillins G and V are products measured in the unit system, as are other antimicrobials such as nystatin suspension. In many cases, these medications are available in a powdered form that requires reconstitution before administration. The information on the drug label will inform you about the type and amount of needed diluent. If the label does not specify the needed diluent, in most cases the diluent will be provided with the powdered medication. In some cases the label also provides different strengths for the medication that can be prepared by the amount of diluent added (Figure 11-1). If you need to review the necessary steps for reconstitution of medications, see Chapter 9.
Calculating Insulin Doses in Units
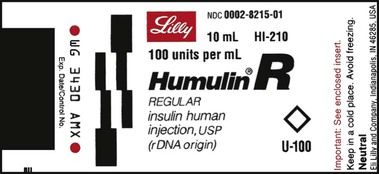
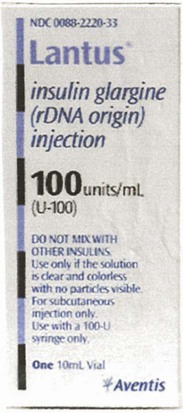
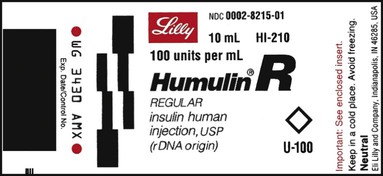
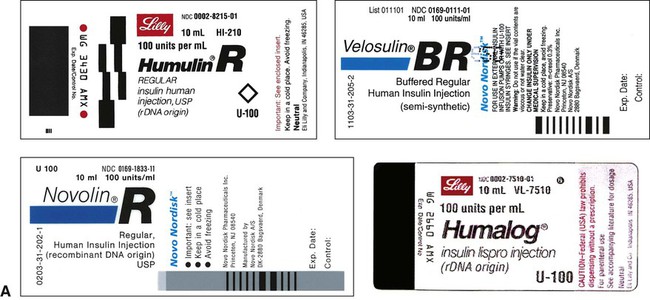
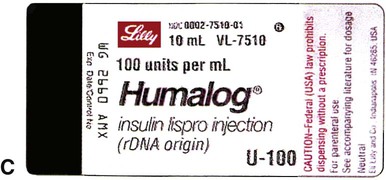
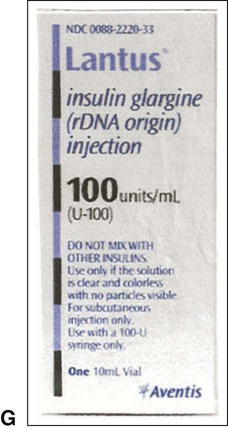
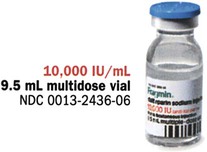
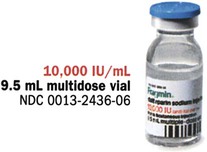
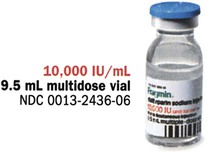
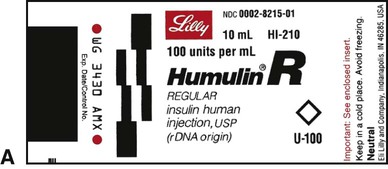
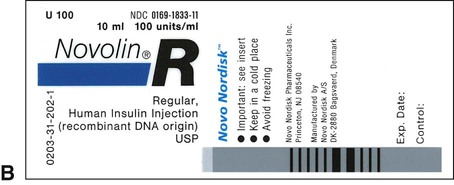
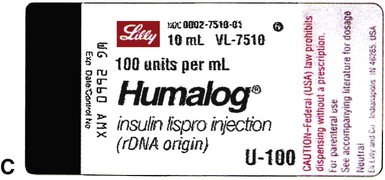
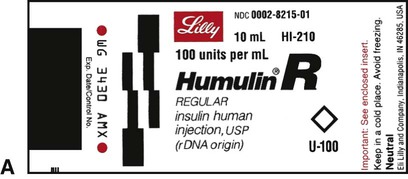
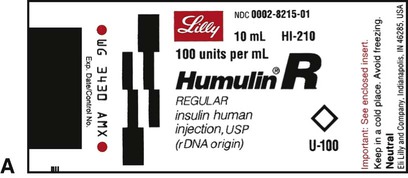
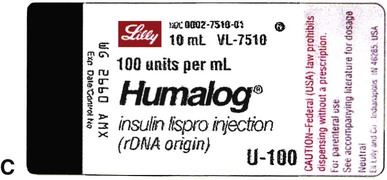
Insulin, which is used to control type 1 diabetes mellitus (T1DM) and type 2 diabetes mellitus (T2DM) in some persons whose elevated blood sugar cannot be adequately controlled with oral hypoglycemics, is prescribed and measured in units. Most insulin preparations are only available in U-100 strength, meaning that each milliliter of insulin contains 100 units of medication. Even insulin preparations that are combinations of regular insulin and intermediate-acting insulins are in U-100 specifications. See Figure 11-2 for labels for different insulin preparations.
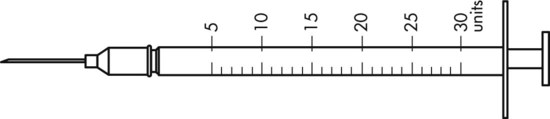
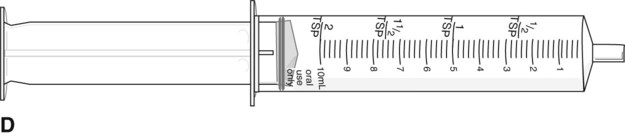
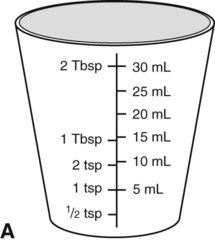
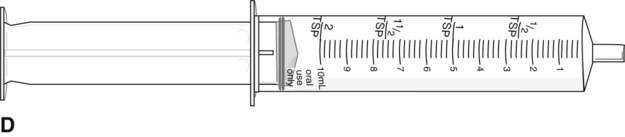
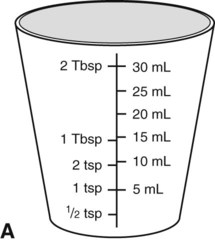
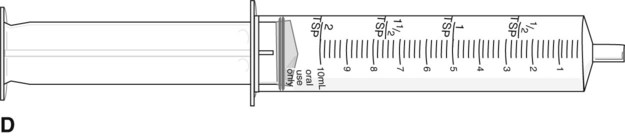
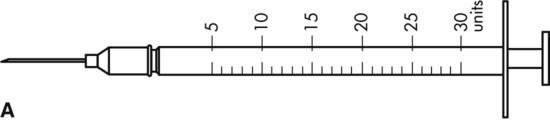
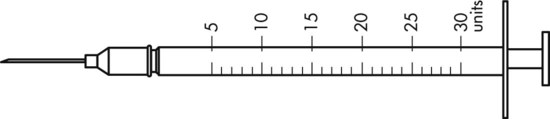
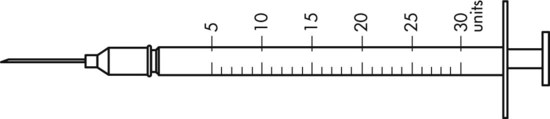
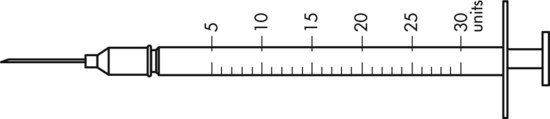
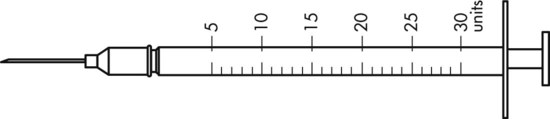
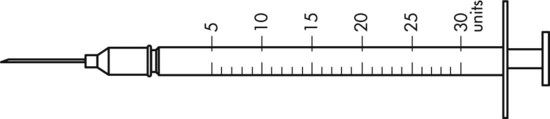
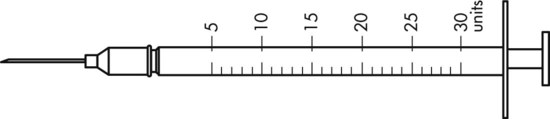
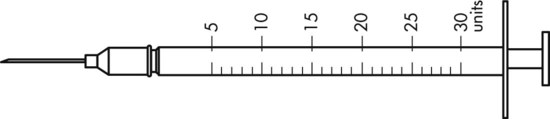
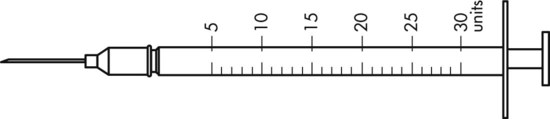
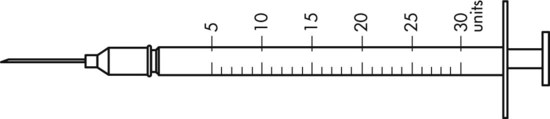
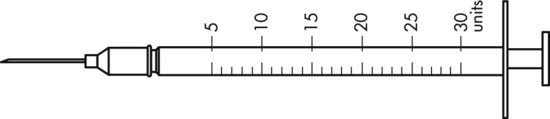
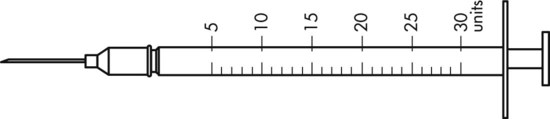
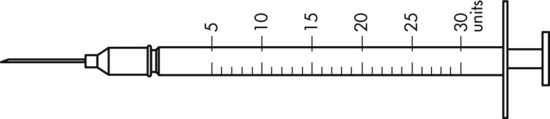
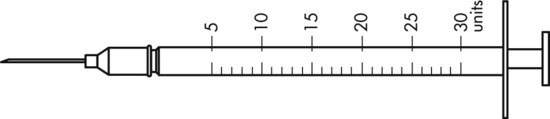
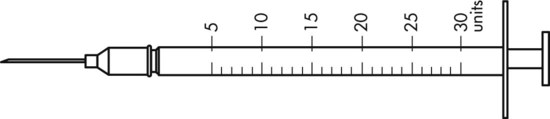
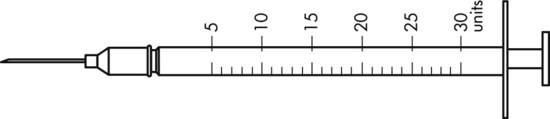
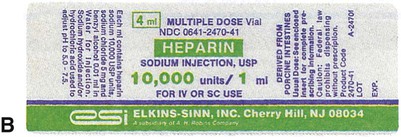
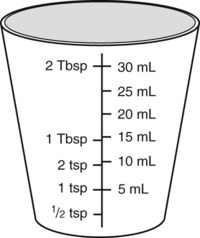
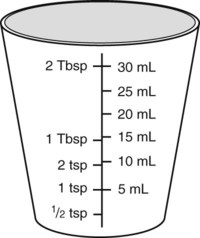
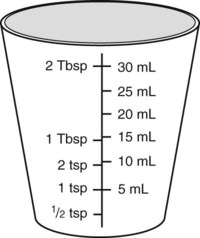
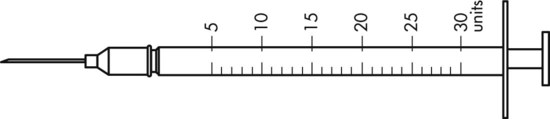
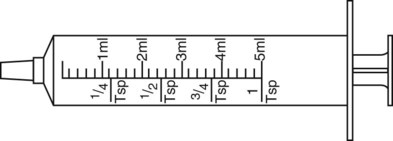
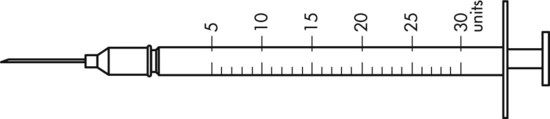
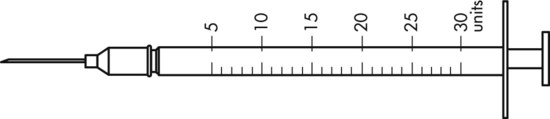
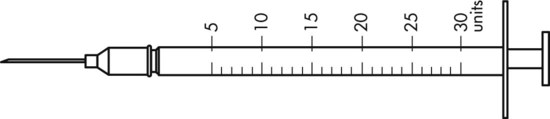
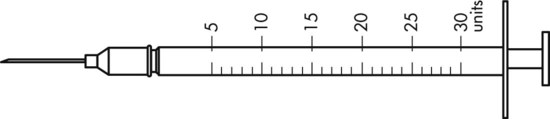
To administer insulin preparations, insulin syringes that are calibrated in 100 units/mL must be used; no other syringe is based in units for insulin (in an emergency a tuberculin syringe could be used because it is also calculated in hundredths of milliliters). The design of the syringe makes it easy to ensure that the exact dose of medication ordered is administered. Syringes come in 30-, 50, and 100-unit calibrations (Figure 11-3). Some 100-unit insulin syringes are available in two-unit increments, while others are marked in one-unit increments with two-unit increments of odd/even on each side of the syringe barrel. To further complicate matters when preparing insulin for administration, you will find some syringes are in one-unit increments with the markings on the same side of the syringe. Please note that syringes holding a smaller quantity such as 30-unit and 50-unit syringes are in one-unit increments and are easier to use by patients who have visual problems, a common complication of long-term or uncontrolled diabetes mellitus. Insulin syringes should not be used for measuring any medication other than insulin—not even for heparin or antibiotics.
Insulin preparations are also labeled by the type of insulin in the vial. An abbreviation of “R” indicates that the medication is rapid, short-acting, regular insulin. NPH insulin that is intermediate acting with a longer onset of action is marked with “N” (Table 11-1). Care must be taken to ensure that the correct insulin is chosen and delivered to the patient. For that reason, manufacturers have placed large letters on the vials showing the exact type of insulin contained.
TABLE 11.1
Action of Insulin Preparations
| INSULIN TYPE | LETTER/BOTTLE | ONSET | PEAK | DURATION |
| QUICK-ACTING | ||||
| lispro–Humalog | 15-30 min | 30 min-2.5 hr | 3-6.5 hr | |
| aspart–Novolog | — | 10-20 min | 1-3 hr | 3-5 hr |
| gluisine–Apidra | — | 10-15 min | 1-1.5hr | 3-5 hr |
| SHORT-ACTING | ||||
| Regular insulin–Humulin R or Novolin R | R | 30 min-1 hr | 1-5 hr | 6-10 hr |
| INTERMEDIATE-ACTING | ||||
| NPH insulin–Humulin N or Novolin N | N | 1-2 hr | 6-14 hr | 16-24 hr |
| LONG-ACTING | ||||
| glargine–Lantus | — | 70 min (Last for 24 hr with no evident peak and duration to last to next injection) | None, usually a once-per-day insulin preparation | 24 hr |
| detemir–Levemir | — | 6-8 hr | 12-24 hr | up to 24 hr |
| COMBINATION | ||||
| NPH/regular mixtures | 50/50 | 30 min | 7-12 hr | 16-24 hr |
| 70/30 | ||||
| insulin aspart | 70/30 | |||
| NPH/lispro | 75/25 | 30 min | 7-12 hr | 16-24 hr |
| 50/50 | ||||
Interpreting Medication Dosage in Percentage and Ratio Strength
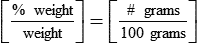
or 1 g of hydrocortisone is found in 100 g of solvent in a 1% hydrocortisone cream.
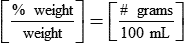
or 0.9 g of sodium chloride is found in 100 mL of solution in a 0.9% NaCl solution.
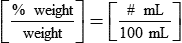
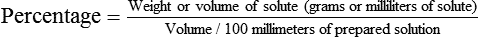
The following formula shows the mathematical calculation for medications expressed as ratios:
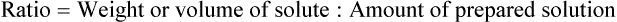
Review of Rules
Calculations of Medications Measured in Units and Milliequivalents
• Medications found in units are expressed as the number of units per liquid volume.
• Medications in milliequivalents may be shown as the number of milliequivalents per liquid or solid measure.
• Labels on medications given in units/volume must be read carefully and interpreted for the strength of the medication.
• Use either formula (Dose desired/Dose available × quantity = Dose to be given), dimensional analysis method, or ratio and proportion to calculate medications in units.
Interpreting Medications in Percentage and Ratio Concentrations
• Percentage and ratio solutions are expressed to indicate the weight of solute found in the solvent.
• The solute is an active ingredient found in either a solid or liquid solvent.
• The percentage would be amount of solute found in 100 mL or 100 g of solvent.
• The ratio would be the amount of medication found in a total prepared volume of solution, usually milliliters.
• Percentage is expressed using % as an indication of the amount of active ingredient in a medication. The ratio is divided by a colon (:) to separate the solute and solvent.
• To calculate the amount of drug in the prepared solution, write the solution strength as a ratio to show the amount of medication found in the total solution. (Refer to Chapter 2 if necessary to review percentage and ratio.)
• To calculate the ratio in a medication preparation, whether solid, semi-solid, or liquid, the total amount of prepared medication minus the amount of solute equals the amount of solvent that should be added for the total volume desired.
• The following formula expresses the actual mathematical formula that would be used to provide a percentage relationship:
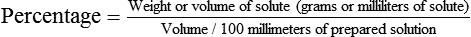
• The formula below shows the mathematical calculation for medications expressed as ratios: