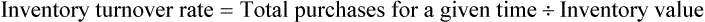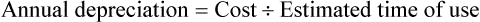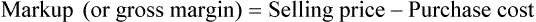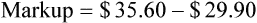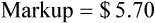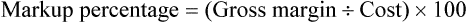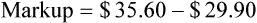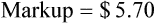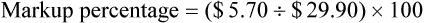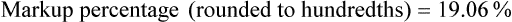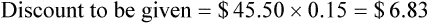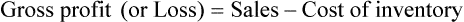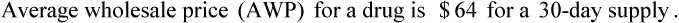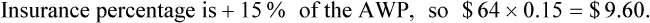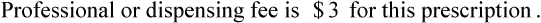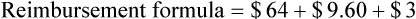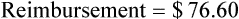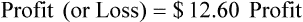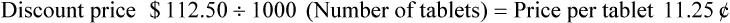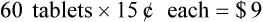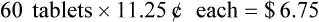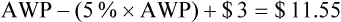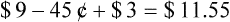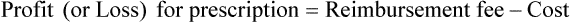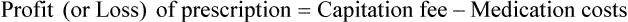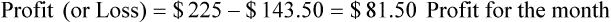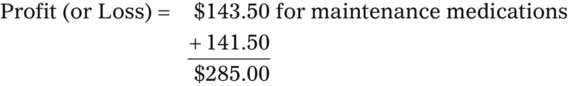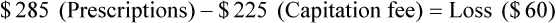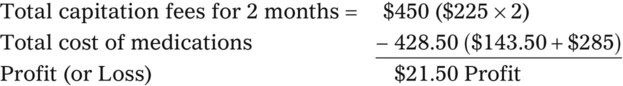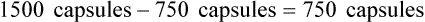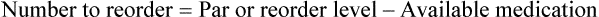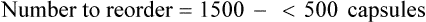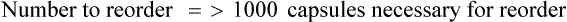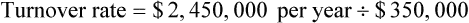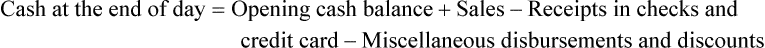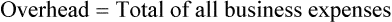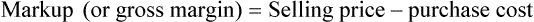Business Math for Pharmacy Technicians

Published on 02/03/2015 by admin

Filed under Basic Science

Last modified 22/04/2025

Print this page

rate 1 star rate 2 star rate 3 star rate 4 star rate 5 star
Your rating: none, Average: 0 (0 votes)

This article have been viewed 6369 times

Chapter 15

Business Math for Pharmacy Technicians

John L. Fulcher, CPA

Objectives

• Calculate overhead expenses for a specified period of time including calculating annual depreciation

• Calculate prescription markup or gross margin

• Calculate discounts on merchandise

• Calculate gross profit for a specified period of time

• Calculate net income

• Calculate insurance reimbursement using average wholesale prices and capitation fees

• Manage inventory including par levels and inventory turnover rate

• Perform a daily cash report

Key Words

Pretest

Perform the following business math calculations. Round answers to the nearest tenth or dollars and cents as appropriate.

1. A pharmacy sells a prescription for $43.50. The medication costs the pharmacy $22.65.

2. A pharmacy buys a medication at a discount rate of $555 for 1000 tablets. The selling price for the medication is $45.50 for 50 tablets.

3. A customer brings in a discount coupon for 25% off the first prescription and 10% off the second prescription. One prescription costs $15 while the other costs $24.50. The pharmacist tells you to take the 25% off the most expensive prescription.

4. A pharmacy has a monthly income of $535,356 with inventory purchases of $456,980, salaries and wages of $76,000, and maintenance costs of $1567.50.

5. What would be the percentage markup based only on cost of a prescription that has an inventory cost of $14.50 and is sold for $21? ___________________

6. A pharmacy buys a new computer program for $9500 in January. The expected time of use is 3 years and will be discarded at the end of 3 years.

7. A pharmacy has a reorder level of 2500 capsules for antibiotic during the winter influenza season. The pharmacy technician checks inventory today and finds 950 capsules are still available as inventory. The wholesaler has a deal for 5000 capsules for $1500 with a 10% discount. The average use of the capsules is 3000 capsules per week.

8. A pharmacy is contracted with an insurance company for a reimbursement of AWP plus 15% and a dispensing fee. The prescription costs the pharmacy $12.50. The dispensing fee is $7.50.

9. The pharmacy is contracted with another insurance company for reimbursement based on capitation for the medication found in question 8. The capitation fee is $45 per month for this patient. The patient has already received a prescription for $16.50.

10. A pharmacy has an opening cash drawer of $150. At the end of the day the purchases are $1895.67. The drawer contains $14.50 in coupons, discounts of $12.50, refunds of $13.50, and credit card purchases of $45.60.

Introduction

Pharmacy technicians in retail settings, as well as in hospital settings, must know how to perform some basic business calculations. For a business to remain profitable, the net income, or net profit, derived from the sales of medications must exceed the costs for doing business. The mathematical calculations may include using percentage to find discounts and markups as well as addition and subtraction to obtain the necessary par level for inventories and evaluate the financial picture for the overall business. The pharmacist(s) in charge must be sure that an adequate markup is in place so the receipts of the business are in excess of the expenses and that the supply of inventory is adequate to cover demand but not so excessive that it would tie up the cash flow of the business with stale or unwanted merchandise on the shelf. The monitoring of pricing and inventory, as well as obtaining the necessary inventory levels, may become a task of the pharmacy technician, who, therefore, has the responsibility of arriving at the actual profit of the pharmacy. The cash flow of the pharmacy is directly related to the mathematical calculations performed for inventory and profit (or loss) that are calculated on a routine basis. Therefore, costs of new inventory must be carefully checked each time the stock arrives to be sure cost of the stock has not changed since the last order. If inventory prices change and the basic costs or prices for sales are not changed simultaneously, profits will be affected. As a pharmacy technician, you have a major role in inventory control and reorders that affect turnover rates, overhead, and gross/net profits.

Overhead Expenses

In business, the receipts from sales must exceed the overhead for doing business for the retailer to be profitable. Overhead is the actual cost of doing business. It includes all costs for the pharmacy such as salaries, equipment purchases and repairs, utilities, telephone, insurance, and rent—those expenses that are required for the business to operate efficiently. The net profit for the pharmacy is based on the gross profit less the overhead. Overhead should be kept to a minimum while still providing quality services for the customers. As equipment, building, and the like age, the value is lessened by depreciation expense.

Depreciation

Depreciation represents the decrease in value of an asset (equipment, building, fixtures) based on the age related to the asset and the expected time the asset is to be used. For example, a computer is bought for $1000 to be used for 5 years. The amount to depreciate is $1000 taken over 5 years as part of the overhead. If the depreciation is taken as equal value over all years, the amount would be $200 per year.

< ?xml:namespace prefix = "mml" />Annual depreciation=Cost÷Estimated time of use

image

To calculate overhead, the total of all business expenses should be added together.

Example 15-1

A pharmacy spends $12,585 for inventory for a week; the salaries for all persons involved are $12,500. The rent is $1600 per month, and utilities cost $800 per month. In addition, the costs for insurance are $1000 per month, and depreciation on equipment is $2500 per month. Taxes are $2400 per month. What is the overhead for each week?

Inventory $12,585
Salaries 12,500
Rent 400 ($1600 ÷ 4 weeks/month)
Utilities 200 ($800 ÷ 4 weeks/month)
Insurance 250 ($1000 ÷ 4 weeks/month)
Depreciation 625 ($2500 ÷ 4 weeks/month)
Taxes 600 ($2400 ÷ 4 weeks/month)
Total overhead $27,160/week

Practice Problems A

Calculate the overhead in the following problems. Be careful to read entire problems. Show your calculations. All final answers should be shown in dollars and cents.

1. A pharmacy has a monthly cost for medication inventory of $46,725, salaries of $58,000, utilities of $2534, rent of $770, insurance of $1575, taxes of $7844, depreciation of equipment of $965, and business supplies and postage of $650.

2. A hospital pharmacy is asked to calculate the overhead necessary to maintain safety for the patients when medications are dispensed. The following amounts would be necessary per year: salaries for pharmacists—$264,000; four pharmacy technician salaries—$22,500 each; medication inventory—$56,525 each month; utilities—$750 per month; salaries for relief pharmacists—$12,500/year; computers and software updates—$56,000 yearly; yearly liability insurance for pharmacists and pharmacy technicians—$3500; and use of hospital space—$3600/year.

3. A pharmacist needs to know how much income each month is necessary to meet the overhead for the business he owns. The expenses are salaries of $72,000 per year for the pharmacist, $27,500 per year each for two pharmacy technicians, $560,430 per year for inventory costs, $5600 per year for utilities and rent, $27,500 per year for equipment replacement, and taxes and other business expenses of $1560 per month.

4. A retail pharmacy wants to ensure that sufficient income is being obtained for a new branch that has just opened. The monthly expenses are $6500 for the pharmacist’s salary, total of $1250 for two pharmacy technicians who both work part-time while in school, $25,340 for inventory, $560 for taxes, business expenses of $980, utilities and rent of $11,500, and payment for equipment of $4500 per month.

5. A pharmacy needs to compute the amount of overhead the store has in a year. The salaries are $54,000 per month, rent is $1250 per month, utilities are $22,500 per year, inventory is $86,950 per month, equipment costs $60,000 per year in replacements, supplies are $1250 per month, and miscellaneous expenses are $1550 per month. The depreciation rate is $950 per month.

Markup Of Prescriptions

The markup for a prescription is the same as the gross margin. The actual markup amount is the difference in the purchase cost of the drug and the selling price of the same drug. The formula is as follows:

Markup(or gross margin)=Selling price−Purchase cost

image

Markup rates on brand name drugs are generally lower than the markup rate on generics. For instance, if a brand name drug, such as Keflex, costs $100 and has a 6% markup, the cost to the customer is $106 ($100 × 0.06 [6%]). A generic brand for the same drug, cephalexin, may cost $40, and the pharmacy has a 25% markup on generics. The cost will be $50 ($40 × 0.25 [25%]) to the customer. As you can see, pharmacies have a higher profit margin available in generics than they do in brand name drugs. Use of generics allows pharmacies to offer “teaser” prices on these drugs as a way to gain business. This marketing ploy is often used by major chain pharmacies.

Example 15-2

A prescription sells for $35.60, and the cost is $29.90. What is the markup?

Markup=$35.60−$29.90

image

Markup=$5.70

image

Practice Problems B

Calculate the monetary markups on the following problems:

1. A medication has a selling price of $56 and a cost of $45.

2. A medication has a selling price of $34.50 and a cost of $15.60.

3. A medication has a selling price of $43.50 and a cost of $39.90.

4. A medication has a selling price of $10.20 and a cost of $9.20.

5. A medication has a selling price of $125 and a cost of $93.50.

6. A medication has a selling price of $37 and a cost of $22.25.

7. A medication has a selling price of $47.80 and a cost of $29.35.

8. A medication has a selling price of $77.43 and a cost of $46.90.

9. A medication has a selling price of $7 and a cost of $6.45.

10. A medication has a selling price of $285 and a cost of $219.25.

Percentage of Markup

Markup percentage or the gross margin percentage is calculated by dividing the gross margin by the cost and then multiplying by 100 to figure the percent. Using percentage of markup provides the calculation of which prescription medications have the greatest percentage of profit. The formula is as follows:

Markup percentage=(Gross margin÷Cost)×100

image

Example 15-3

A prescription sells for $35.60, and the cost is $29.90. What is the markup percentage?

Markup=$35.60−$29.90

image

Markup=$5.70

image

Markup percentage=($5.70÷$29.90)×100

image

Markup percentage(rounded to hundredths)=19.06%

image

Practice Problems C

Calculate the percentage of markup in the following problems. Show your calculations. Round all final answers to tenths.

1. A medication has a selling price of $56 and a cost of $45.

2. A medication has a selling price of $34.50 and a cost of $15.60.

3. A medication has a selling price of $43.50 and a cost of $39.90.

4. A medication has a selling price of $10.20 and a cost of $9.20.

5. A medication has a selling price of $125 and a cost of $93.50.

6. A medication has a selling price of $45 and a cost of $42.

7. A medication has a selling price of $27.90 and a cost of $23.60.

8. A medication has a selling price of $33.75 and a cost of $30.

9. A medication has a selling price of $12.90 and a cost of $9.20.

10. A medication has a selling price of $255 and a cost of $193.50.

Discounts

Discounts or markdowns, may be calculated on prescriptions, over-the-counter (OTC) drugs or other merchandise by subtracting a percentage of the original selling price for the item to lower the price the patient pays; this is also called the markdown price. Discounts and markdowns are used as an incentive to encourage the customer to purchase the item by realizing a savings on the previous total price. Markdowns and discounts may be in the form of manufacturers’ coupons or special discounts for reasons such as senior citizens’ initiatives. Discounts are one of the simplest business-related calculations—a concept used for sale items throughout retail businesses, such as an end-of-season 40% off sale at your local department store. The amount of the discount is always based on the selling price, not on the cost of the item. This mathematical calculation is the opposite of what was accomplished previously when the percentage of markup was accomplished. A discount decreases the sales price based on the previous sales price, while a markup is based on the wholesale price to increase the selling price to cover overhead. The formulas for discounts are as follows:

Discount amount=Selling price×Discount percentageANDDiscounted price=Selling price−Discount amount

image

When discounts are given based on manufacturers’ or other coupons, the amount of the coupon should be subtracted from the selling price and the coupon placed in the cash drawer to be used at the end of the day to balance the cash drawer. These coupons are actually a type of refund.

Example 15-4

A medication that sells for $45.50 has a manufacturer’s coupon for 15% off as an incentive to try the medication. What is the cost to the patient following the use of the discount coupon?

Hint: Change percentage to a decimal number for each calculations.

Discount to be given=$45.50×0.15=$6.83

image

Discount price=$45.50−$6.83=$38.67

image

Practice Problems D

Calculate the discount price in the following problems. Show your work. The discount should always be in the favor of the customer.

1. A patient has a manufacturer’s discount coupon in the amount of 25% for a new prescription medication item. The selling price is $42.50.

2. An ad in the local paper offers 1/3 off a medication that is taken regularly by one of your customers. The patient brings in the coupon for the medicine that costs $33.

3. A drug supplier has a deal that will provide a 25% discount for 10 tubes of a new dermatological preparation. The cost for the 10 tubes is $525.

4. An older patient on a fixed income comes to the pharmacy with a new prescription. The pharmacist knows that the patient will not be able to afford the medication at the selling price as calculated. He tells the patient that he will provide a 12% discount for the medication, which costs $65.

5. An insurance company has a contract with the pharmacy to provide a 5% discount for any prescription for its members. The prescription for John W. has a retail price of $75.50.

6. A retail pharmacy has advertised a 35% off sale on all pain relievers during the first 2 weeks of April, because of the tax-filing deadline. Tylenol’s regular price is $7.59 while at the regular price Motrin IB costs $7.79, and Aleve’s price is $8.29.

7. An ad in the local paper offers 30% off antacid liquid this week with a regular price of $4.54.

8. A manufacturer’s coupon offers a 20% discount on cough syrup. You go to the drug store and find what you need. The retail price is $5.79.

9. A manufacturer supplies a discount of 40% off on the first prescription of a hypolipidemic agent that sells for $75 retail.

10. The pharmacy has bought an over-the-counter medication at a 30% discount of the usual wholesale price. The usual wholesale price is $12.00 for the item.

Gross Profit

The gross profit is the difference in the sales price and the cost of the inventory with no other expenses of the business considered.

The formula for finding gross profit is:

Gross profit(or Loss)=Sales−Cost of inventory

image

Tech Note

On financial statements, amounts that signify losses are often placed within parentheses.

Example 15-5

If a pharmacy’s sales were $200,000 and its purchases were $175,000, its gross profit would be $25,000.

Practice Problems E

Calculate the following problems. A month should be calculated as 4 weeks with a week being six working days.

1. A pharmacy has sales of $1,253,000 with a cost of inventory of $1,125,566.

2. A pharmacy sells $25,420 a week with a monthly cost of inventory of $19,986.

3. A pharmacy has income of $31,567 for the month of June.

4. A pharmacy that is open 7 days a week has sales amounting to $6500/day with inventory costs of $5990/day.

5. John the pharmacist is asked by the bank for the gross profit of his store for a quarter. The sales are $65,432/month with inventory costs of $64,120 for the same time period.

Net Income

Net income (sometimes referred to as the bottom line or net profit) is gross profit less overhead. Using Example 15-5, if the overhead for the same store were $18,000 for the month, the net income would be $7,000.

The net income is the difference between the sales and all the costs related to the business (inventory and overhead). A positive net income is necessary for the business to remain fiscally sound.

Net income=Sales−(Inventory+Overhead)

image

If a pharmacy’s sales were $200,000 and its purchases were $175,000, its gross profit would be $25,000.

Net income(or gross profit)=$200,000−($175,000+$18,0000)

image

Net income=$200,000−$193,000

image

Net profit=$7,000

image

The profit margin, or the percentage of net profit as related to sales, is derived by applying a markup rate to the purchase price of inventory with 5% being ideal.

Example 15-6

A pharmacy has monthly sales of $425,600, inventory purchases of $310,000, salaries and wages of $60,000, utilities of $2500, insurance of $1100, and maintenance of $775.

What is the gross profit? $115,000 ($425,000 − $310,000)

What is the markup rate for this month? 37.10% ($115,000 ÷ $310,000) × 100

What is the overhead for the month? $64,375 ($60,000 + $2500 + $1100 + $775)

What is the net profit? $50,625 ($115,000 − $64,375)

Practice Problems F

Calculate the gross profit in the following problems. Round the gross markup rate of inventory to tenths and other answers to dollars and cents.

1. A retail pharmacy has monthly sales of $204,300. Inventory purchases were $177,700, salaries and wages were $21,350, utilities were $1750, rent was $1800, insurance was $750, and repairs were $900.

2. A retail chain location has monthly sales of $354,740. Inventory purchases were $317,600, salaries and wages were $27,000, utilities were $2400, rent was $3800, insurance was $1200, and repairs were $80.

3. A hospital pharmacy’s charges to patients are $454,000 for a month. Inventory purchases were $377,400, salaries and wages were $26,000, utilities allocated to the pharmacy were $850, licenses were $450, and supplies were $1900.

4. A retail pharmacy has monthly sales of $174,080. Inventory purchases were $146,220, salaries and wages were $16,200, utilities were $1950, rent was $1400, insurance was $800, and repairs were $270.

5. A retail pharmacy has monthly sales of $379,300. Inventory purchases were $317,300, salaries and wages were $31,400, utilities were $2675, rent was $3500, insurance was $1400, and supplies were $775.

Insurance Reimbursement

In today’s pharmacies, insurance or third-party reimbursements are a big factor in a pharmacy’s income. The pharmacy signs contracts with insurance carriers for predetermined reimbursement amounts that could be specific to a medication or calculated based on the average wholesale price. To get the reimbursement, a pharmacy must submit a claim electronically, using a generic form with the correct codes and the agreed-upon reimbursement fee. Upon receipt of the claim, the insurance company processes the claim according to the terms of the contract with the pharmacy and submits reimbursement appropriately. Reimbursement claims must be kept current and submitted in a timely manner. The timetable for reimbursement varies by insurance carrier and can take several weeks to process. With many computer programs used in pharmacies today, the prescription is immediately submitted to the insurance carrier electronically.

Average Wholesale Price

The price for a prescription may be computed using items such as professional fees, average wholesale price (AWP), and overhead. Because discounts are provided to pharmacies that order large quantities of drugs or for payment of orders within a specified time, the AWP is based on the national average wholesale price of the medication when medication is purchased from a wholesale market. Fast-selling medications are often ordered in large quantities to obtain these discounts, thus increasing the profit on prescriptions. In the past, patients were responsible for payment of their medications, but in today’s world of health care, most patients have third-party payers to reimburse the pharmacy on the basis of AWP. In some instances insurance contracts may provide reimbursement that is less than the AWP. In other instances, reimbursement may be greater, if rebates from manufacturers and purchasing discounts are considered. In most cases, the AWP is the basis for prescription reimbursement to ensure the necessary profit for the pharmacy is maintained. The formula is as follows:

Reimbursement of prescription=AWP±Percentage of AWP allowed+Dispensing fee(if applicable)

image

Example 15-7

Average wholesale price(AWP)for a drug is$64for a30-day supply.

image

Insurance percentage is+15%of the AWP,so$64×0.15=$9.60.

image

Professional or dispensing fee is$3for this prescription.

image

Reimbursement formula=$64+$9.60+$3

image

Reimbursement=$76.60

image

Profit(or Loss)=$12.60Profit

image

Example 15-8

A pharmacy purchases 1000 tablets of medication at the wholesale price of $125. The wholesale distributor allows a 10% discount on invoices paid in 10 days. The payment is made according to the discount. The AWP for this medication is 15¢ a tablet. Insurance reimbursement is AWP less 5% plus $3 dispensing fee. The prescription is written for 60 tablets. What is the profit (or loss) on this prescription?

Practice Problems G

Calculate the following problems indicating the formula used. For profit or loss, calculate using the AWP as the cost of the medication. If a dispensing fee is shown assume the contract allows a dispensing fee unless otherwise stated.

1. A prescription has AWP of $25.60. The insurance percentage is +18% of AWP. The professional dispensing fee is $3.50.

2. A compounded prescription has a collected AWP of $35.65. The insurance percentage is +9% of AWP. The professional dispensing fee is $7.50.

3. A 3-day prescription of a once-daily medication has an AWP of $7.90. The insurance percentage is +12% of AWP. The professional dispensing fee is $5.

4. An antibiotic prescription for 10 days has an AWP of $46.50. The insurance percentage of payment is +7.5% of AWP. The professional dispensing fee is $12.50.

5. A prescription for a month’s supply of daily medication has an AWP of $120. The insurance percentage is –2% on monthly prescriptions. Professional dispensing fees are increased to $15 for this medication.

6. A maintenance drug prescription has AWP of $15.20. The insurance percentage is +9% of AWP. The professional dispensing fee is $5.23.

7. A compound prescription has a collected AWP of $49.90. The insurance percentage is +7% of AWP. The professional dispensing fee is $13.

8. A 7-day prescription of a medication taken three times daily has an AWP of $14.45. The insurance percentage is +6.5% of AWP. The professional dispensing fee is $6.

9. A topical ointment prescription for 14 days has an AWP of $32.40. The insurance percentage of payment is +12.25% of AWP. The professional dispensing fee is $9.

10. A prescription for a 90 day supply of daily medication has an AWP of $190. The insurance percentage is +6% on these prescriptions. The professional dispensing fee is $18.

Capitation

Capitation fees, usually paid on a monthly basis, are a set amount of reimbursement to the pharmacy paid by a third party for a person whether the person receives a single prescription, multiple prescriptions, or no prescriptions. The capitation fee is a contracted amount with the third-party payer to provide medications to the insured patient. All prescriptions presented must be filled even if the cost exceeds the fee provided to the pharmacy. This type of reimbursement may provide the pharmacy with a loss during a 1-month period but may provide a profit over several months depending on the individual’s prescription costs.

Profit(or Loss)of prescription=Capitation fee−Medication costs

image

Example 15-9

The pharmacy accepts a capitation fee of $225 for a senior citizen who has multiple monthly standing prescriptions, most of which are available as generic drugs. The AWP prices for the monthly drug supplies are $9.50, $27, $65, and $42.

AWP Medication costs per month :$143.50

image

Profit(or Loss)=$225−$143.50=$81.50Profit for the month

image

However the next month, the person has a severe sinus infection requiring additional prescriptions of $45 and $55 for antibiotics, $15 for a decongestant, and $26.50 for pain medication. The patient still receives her regular medications as scheduled. What is the profit or loss for month 2?

image

$285(Prescriptions)−$225(Capitation fee)=Loss($60)

image

What is the profit or loss over the 2-month time period?

image

Practice Problems H

Calculate the profit or loss using the capitation fee supplied. Show your work.

1. A pharmacy agrees to a monthly capitation fee of $175 for a patient who has standing prescriptions of $43 and $27. This month, the person had two other prescriptions for $35 and $18.

2. The pharmacy agrees to a capitation fee of $425 for a family of four. Prescriptions for the family in 1 month are $12.50, $25, $30, and $62.50.

3. A capitation fee for a year for a patient is $1800. Prescriptions for this person for routine medications cost $25, $30, and $15 per month.

4. The capitation fee accepted by the pharmacy for a child is $125 per month. The child has a total of $1650 in prescriptions for the year.

5. A pharmacy is asked to accept a capitation fee of $350/month for an elderly patient who had six routine prescriptions of $25, $40, $35, $15, $80, and $75 monthly. Additional medications for acute conditions this month were $120, $25, and $160.

Inventory Management

An inventory is a listing of the available stock of the business on a specific date. Inventories may be done in the pharmacy and in the remainder of the store separately, by departments separately, or for the entire store. All items for sale are listed using the value based on acquisition cost of each item. Also, inventories may be done at separate times for different sections of the store or pharmacy. Controlled drugs are often inventoried more often than other medications, but this depends on the protocol of the place of business and state/federal law. Because space is allocated to the drugs most frequently ordered by physicians in the locale of practice, these medicines must be inventoried on a regular basis to ensure the medicine is available at the time needed (e.g., antibiotics and antivirals may have an increase of stock during the winter, while antihistamines may have more stock in the spring during allergy season). Often-used antihypertensives may have a consistently larger inventory than lesser-used drugs for specific conditions such as multiple sclerosis. Thus, an inventory of the available medication is an important task that ensures the pharmacy will operate smoothly during peak times.

In many cases today, perpetual inventories are automatically maintained using computer programs designed specifically for the application. Restocking occurs on a continuous basis with this type of system because the computer submits the order to the wholesaler electronically as stock is used or purchased by customers. As medication is sold it is subtracted from inventory, and when medication is received it is added to the inventory with the computer automatically ordering medication when the drug inventory level gets to a minimal or reorder level. This minimal/reorder level is predetermined by sales history or human input. This predetermined point is called the par level. To maintain the inventory flow and minimize the need for extra shelf space, replacements for medications should arrive shortly before the need for use. For seasonal medications, as mentioned earlier, the inventory or par level may increase at certain times because seasonal needs must be taken into account when inventorying stock and placing the necessary order to have the needed medications. The inventory needs may vary depending on the drug and the local ordering protocol.

Example 15-10

The par level or reorder point for amoxicillin during the winter is 1500 capsules. Prescriptions for a certain day show dispensing of 750 capsules. The bottle of 1000 capsules has been opened and appears to be less than half full. If the medication is available in 100-capsule, 500-capsule, and 1000-capsule sizes, what should the order contain?

Needed available inventory=Par or reorder level−Amount dispensedprior to inventory

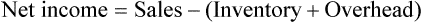
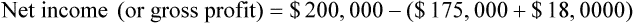
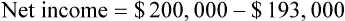
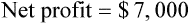
image

First determine that 750 capsules have been used in 1 day and fewer than 500 capsules are available.

1500capsules−750capsules=750capsules

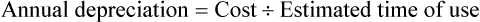
image

In this case, the bottle shows fewer than 500 capsules are available, and the medication had not been reordered on the basis of the use. To reorder to the necessary stock supply, the total number of capsules available should be more than 1500. The approximate AWP cost for 100 capsules is $25; for 500 capsules, $95; and for 1000 capsules, $156. Remember that fewer larger containers require less storage space and are usually less expensive per tablet or other unit measure.

Number to reorder=Par or reorder level−Available medication

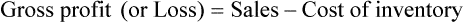
image

Number to reorder=1500−< 500capsules

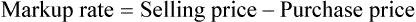
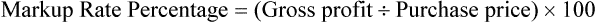
image

Number to reorder=> 1000capsules necessary for reorder

image

Number to reorder=Two bottles of1000capsules to reach the stock number(use two)bottles because this medication is being used rapidly on a dailybasis,and one bottle would not restock to the level necessary

image

The cost per capsule for the 100-capsule size is 25¢ each; 500-capsule size, 19¢ each; and 1000-capsule size, 15.6¢ each. So the extra capsules on the shelf will also save money on the AWP cost. With rapid seasonal use of the medication, the savings per capsule would be appropriate when reordering.

Practice Problems I

Calculate the amount of product to order for the medications in the following problems. The pharmacist desires the most efficient stock replacement using the lowest AWP cost of the medication if the difference in replacement need and the drug availability are within 500 tablets on the rapidly used medications shown below. Round all prices to tenths of a cent. Show your work.

1. The par (reorder) level for furosemide 20 mg is 200 tablets. The inventory available is 50 tablets. Available sizes of medications with the AWP for each size are as follows: 30 tablets for $3.50; 90 tablets for $9.50; 100 tablets for $12.50; and 500 tablets for $44.

2. The par (reorder) level for digoxin 0.25 mg is 150 tablets. The inventory available is 25 tablets. The available medications from the wholesaler are 25 tablets for $6.50; 50 tablets for $6.75; and 100 tablets for $17.25.

3. The par (reorder) level for levothyroxine 0.1 mg is 225 tablets. The inventory available is 75 tablets. Available sizes of medications with the AWP for each size are as follows: 50 tablets for $4.75; 100 tablets for $8.50; and 250 tablets for $12.50.

4. The par (reorder) level for ibuprofen 800 mg is 1500 tablets. The inventory available is 250 tablets. The available medications from the wholesaler are 100 tablets for $7.50; 200 tablets for $13.75; and 500 tablets for $27.45.

5. The par (reorder) level for Paxil 20 mg is 400 tablets. The inventory available is 180 tablets. Available sizes of medications with the AWP for each size are as follows: 40 tablets for $9.30; 90 tablets for $17; 150 tablets for $24.50; and 250 tablets for $40.

6. The par (reorder) level for tetracycline 250 mg is 420 tablets. The inventory available is 205 tablets. The available medications from the wholesaler are 100 tablets for $16.50; 300 tablets for $27.50; and 500 tablets for $40.25.

Inventory Turnover Rate

Inventory turnover rate is the frequency at which medications sell over a specified time. The turnover rate is important in setting the reorder point or par level for medications. This number helps the pharmacy determine if inventory should be increased or decreased, thus controlling the amount of cash that is tied up in inventory. The turnover rate is calculated by obtaining the total value of the pharmacy inventory that is ordered during a specified time and dividing it by the amount of the average inventory. If a pharmacy does not maintain a computerized inventory, a physical inventory must be taken periodically, and an average of the physical inventories must be calculated to figure average inventory. The formula for the turnover rate is as follows:

Inventory turnover rate=Total purchases for a given time%Inventory value

image

Example 15-11

The average inventory for the pharmacy is $350,000 at a given time. The pharmacy spends $2,450,000 per year for inventory. Using the previous formula, the equation is as follows:

Turnover rate=$2,450,000per year÷$350,000

image

Turnover rate=7times per year

image

Practice Problems J

Calculate the inventory turnover rate in the following situations. Round all answers to tenths. Show your work.

1. A pharmacy has an average inventory of $225,000. The purchases for 6 months are $1,250,000.

2. A hospital has an average inventory of $450,000. The purchases for the past 2 months are $750,000.

3. A pharmacy has an average inventory of $125,000. The purchases for 6 months are $2,250,000.

4. A hospital has an average inventory of $70,000. The purchases for the past 2 months are $270,000.

5. A pharmacy has an average inventory of $22,500. The purchases for the year are $775,200.

6. A pharmacy has an inventory of $125,275. The pharmacist is concerned that he has too much stock. He spends $870,000 per year for medications. He likes a turnover rate of 2.5 every 2 months or less.

Daily Cash Report

A daily duty in the pharmacy may be to prepare the daily cash or sales report or to check the payments received during a day to be sure that the cash shown as received balances with the amount of money in the cash drawer. This calculation is accomplished by balancing the cash drawer. To calculate this information, the opening cash balance in the register drawer is needed. Calculate total cash received as well as calculating checks and credit card receipts separately. Discounts, discount coupons, and other miscellaneous income will need to be documented and totaled. Finally calculate miscellaneous disbursements such as refunds or small payments for supplies. The total sales (checks, cash, and credit cards) and the opening balance should equal the amount of sales receipts minus disbursements from the drawer and discounts and the like in the drawer at the end of the day. When the total money entered as the payment into the cash register is incorrect, the amount in excess of the actual payment is called an overring. The erroneous amount balance would be subtracted from the cash drawer and an overring slip added to the cash drawer to indicate the error. Voids include sold items that were rung in the cash register but then the customer decided not to buy the item. This requires voiding the sale and placing a slip in the cash register receipts indicating the voiding of the sale. The formula is:

Cash at the end of day=Opening cash balance+Sales−Receipts in checks andcredit card−Miscellaneous disbursements and discounts

image

Some pharmacies require that this process be completed at the end of every shift; thus, you may have multiple cash reports in a day. The difference between the calculated amount and the actual amount is called the cash overage or shortage depending upon whether the amount is positive or negative. A positive amount would be an overage, and a negative amount would be a shortage. Any overage/shortage should be handled according to the protocol of the place of business. It is extremely important that technicians know how to count money from customers as payments and to customers as change to avoid overages/shortages.

Tech Note

When an overage/shortage occurs, the person using the cash register for the shift should attempt to find the error.

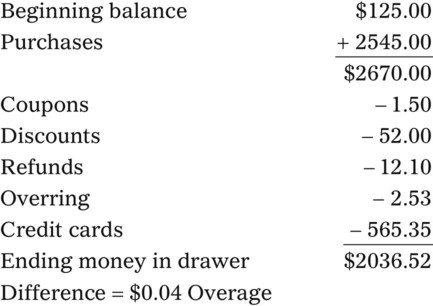
image Tech Alert

Most companies will terminate an employee for excessive shortages/overages.

The cash drawer should be balanced at the end of each shift. The formula to balance the cash drawer is:

Cash in drawer=Opening cash balance+Sales for day−Credit cardpayments−Checks−Miscellaneous disbursements

image

Example 15-12

The opening balance of the cash drawer is $125 in change. Prescriptions sales for the day are a total of $2545. Discounts total $52, coupons are $1.50, refunds are $12.10, overrings are $2.53, and credit cards are $565.35. The cash on hand at the end of the day is $2036.48. What should be the daily cash report ending balance?

image

Practice Problems K

Prepare daily cash reports for the following situations. Show your calculations.

1. A pharmacy has an extremely busy day, and the sales for the day are $3654. Coupons of $1.25 were accepted. Discounts to professionals were $25.05, voids were $15.55, refunds were $10.45, credit cards were $658.45, and overrings were 50¢. The opening balance was $100, and the closing cash is $3061.75.

2. A pharmacy has sales from one cash register of $1565.32 for a day. The opening balance in the cash register for the day was $75. Patients presented coupons in the amount of $2.50, three prescriptions totaling $45.50 were voided, a physician received a discount of $12.50 for medication to be used in his office, and credit card purchases for the day were $652.90. No refunds were made. There was one overring of $18.90. The closing cash at the end of the day is $908.08.

3. A pharmacy has a rather slow day, and the sales of prescriptions for the day are $640. Coupons of $1.25 were accepted. Discounts to professionals were $5, voids were $30.25, refunds were $1.70, and credit cards were $152. The opening balance was $150, and the closing cash is $601.54.

4. A pharmacy has sales of $2460.25 for a day. The opening balance in the cash register for the day was $140. Patients presented coupons in the amount of $7.50, a physician paid cash for medication and received a discount of $20 for medication to be used in his office, checks found were $111.21, and credit card purchases for the day were $1200.70. No refunds were made. The closing cash at the end of the day is $1260.84.

5. A pharmacy has another busy day because of the flu season, and the sales for the day are $3342. Coupons of $11.40 were accepted. Discounts to professionals were $12.50, voids were $75, refunds were $30.70, and credit cards were $1950.75. The opening balance was $100, and the closing cash is $1358.15.

6. A pharmacy has sales on Saturday of $2130.45. The opening balance in the cash register for the day was $50. Patients presented coupons in the amount of $5.50, voids were $22.75, no discounts were given, credit card purchases for the day were $485, checks totaled $300, refunds were $8.50. The closing cash at the end of the day is $1358.70.

Posttest

Before taking the Posttest, retake the Pretest to check your understanding of the materials presented in this chapter.

Calculate the following business math, rounding to dollars and cents. When calculating for a month use four weeks as the typical month and 28 days as the typical days per month.

1. The pharmacy spends $10,587.43 a week for the inventory for medications. Salaries for the two registered pharmacists total $12,360 for the 4 week period. During the month, rent is $1825 per month, utilities are $1450, telephone is $576.08, liability insurance on the building is $254, professional malpractice insurance is $243 per pharmacist, sales tax is $5615.89, other personnel taxes are $3856. Pharmacy techs are paid $2650 per week. Depreciation on equipment is $4320 per month.

2. A pharmacy buys new shelving costing $34,000 to be depreciated over 5 years. The cost for repairs of $2500 for the insertion of the shelves should be added to the cost of the new equipment.

3. A pharmacy has received an order of medication containing 1000 tablets costing $560. The markup on these tablets is to be 45%. What is the gross markup on the container of medication? ___________________

4. During the past year, the pharmacy spent $1,600,000 for inventory supplies. The average inventory value during the past year was $250,000.

5. The pharmacy has announced a 25%-off sale on all generic medications for the last Friday of the month. A customer arrives and wants to buy the following generic OTC medications with a retail cost as shown:

Acetaminophen $7.99

Multiple vitamins $10.75

Stool softener $9.99

Neomycin cream $6.50

6. A medication has an AWP of $75.60 for 50 tablets. The contract with the third-party payer is AWP + 15% + $7.85 filling fee for the prescription for 50 tablets.

7. A pharmacy has a capitation contract with an insurance company to pay the pharmacy $250 a month for an elderly patient who takes multiple medications. The patient takes prescriptions costing the pharmacy $7.68, $15.98, $46.32, and $48.21.

8. The par level for reorder of Enablex is 500 tablets. The pharmacy technician takes an inventory on Monday for reorder on Tuesday. The count on the tablets is 150. The medication is available in containers of 250 tablets.

9. Joseph is on an insurance plan that pays AWP plus 12.5% and a filling fee of $12.75. He brings prescriptions to the pharmacy for medications with an AWP of $34.50, $12.35, and $5.35.

10. A pharmacy has depreciation of $4325/month, inventory costs of $2678.36 an average week, utilities of $1025.25 per month, telephone of $568 per month, and salaries of $4500 a week for the pharmacist and $1500 a week for two pharmacy technicians. The income for the month is $65,342.

What would be the total overhead expense for the month? ___________________

What would be the net profit or loss for the month? ___________________

If the pharmacist gives a 5% discount on all merchandise for a week during the month, what would be the average total of the discount for a week based on the inventory costs? ___________________

If the pharmacy has a basic 20% markup on all inventory, what would be the discount based on average sales after markup for the week? ___________________

Using the figures given above, what would be the overhead spent in a day? ___________________

What would be the daily gross profit, using the above figures to calculate a daily profit? ___________________

What would be the net profit for the day? ___________________

What would the 5% discount cost the pharmacy per day based on a 7-day week and the price after markup? ___________________

Review of Rules

Calculation of Annual Depreciation

Insurance Reimbursements

• The third-party price for a prescription may be computed using AWP or the average wholesale price nationally.

Reimbursement of prescription=AWP±Percentage of AWP allowed+Dispensing fee(if applicable)

image

• The pharmacy needs to know if the reimbursement provides a profit or loss using the reimbursement fee less the cost of preparing the prescription.

Profit(or Loss)for prescription=Reimbursement fee−Cost

image

• Capitation fees are a set reimbursement fee usually paid to the pharmacy per month by the third-party insurance carrier.

Profit(or Loss)of prescription=Capitation fee−Medication costs

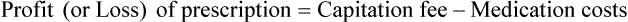
image

• A minimal/reorder level is predetermined by sales history or human input and is used to maintain the drug flow and minimize the need for extra shelf space while replacing medications as needed to maintain business efficiency. This predetermined point is called the par level.

Needed available inventory=Par or reorder level−Amount dispensed

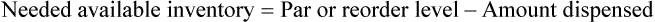
image

• Inventory turnover rate is the frequency at which medications sell over a specified time. This calculation is used to control the amount of cash that is tied up in inventory.

Inventory turnover rate=Total purchases for a given time÷Inventory value

image

Related posts:

Assessment of Mathematical Calculation Skills Needed for Pharmacy Technicians Reconstitution of Powders or Crystals into Liquid Medications Calculation of Mixtures from Stock Medications Interpretation of Medication Labels and Orders Interpreting Physicians’ Orders for Dosages Calculation of Medications for Special Populations Based on Body Weight and Patient Age