Chapter 3 Biomechanics of the Elbow
Range of motion and kinematics related to the joint geometry
Flexion–extension: range of motion
The accepted nomenclature for describing elbow flexion–extension range of motion is that of the American Academy of Orthopaedic Surgeons.1 They defined the fully extended position, with a straight arm, as 0°, and the fully flexed position to be approximately 146°. Some earlier papers had used the ‘elbow angle’, which is the angle between the limb segments, but that convention has fallen from use among orthopaedic surgeons, although it remains common among veterinary surgeons. A review of the literature shows that many papers have merely estimated the range of normal motion, but those where it has actually been measured have reported a mean range from 0° to 142° of active elbow flexion.2 The distribution of range of motion was investigated by West,3 who found that of 517 elbows that were measured 25% hyperextended by 5° or more, and more than 90% had maximum active flexion of between 140° and 150°.
There are several factors which can affect the range of elbow flexion–extension. Glanville and Kreezer4 examined the difference between active and passive elbow flexion, and found that passive movement allowed the range to increase from 141° to 146°. Active motion is limited by apposition of the soft tissues between the humerus and forearm and, as such, motion with the flexor muscles relaxed would be expected to be greater.
The final factor that affects the range of flexion–extension is the sex of the subject. Studies have shown that females have 5–8° more hyperextension than males.2
Flexion–extension and the carrying angle kinematics
Elbow motion results largely from the articular geometry, particularly the shape of the humeral trochlea and capitellum. These have been approximated as a spool and hemisphere placed coaxially across the distal humerus. In the past, some authors have produced diagrams which showed relative axial motion of the radius alongside the ulna, as the elbow flexed and extended, suggesting that this resulted from the capitellum being displaced from the trochlear axis, thus acting like a cam. However, there has been clear radiographic evidence of the coaxiality of the articular surfaces, as long as the X-ray beam is aligned accurately.5 Provided this is the case, the articular features are seen as a series of concentric circles and arcs of circles representing the waist of the trochlea, the capitellum and the medial lip of the trochlea. These structures are situated anterior to the shaft of the humerus, with the medial epicondyle hanging back posteriorly and proximal to the axis. The lateral view also shows the coronoid and olecranon fossae, which approach each other from anteriorly and posteriorly to produce a thin membrane of bone immediately proximal to the waist of the trochlea. This membrane may actually be perforated in elbows that hyperextend, and this supratrochlear foramen has an ethnic basis.6 The presence of these fossae increases the range of elbow flexion–extension before it is limited by bony impingement from the coronoid and olecranon processes. There is also a matching shallow anterior fossa that accommodates the rim of the radial head in terminal elbow flexion. However, in life elbow flexion is more likely to be limited by apposition of the bulky soft tissues between the shafts of the humerus and forearm bones. This tendency is reduced by the anterior offset of the distal humeral articulations and also the anterior position of the trochlear notch of the ulna, in relation to its shaft. These features combine to widen the gap between the bone shafts in deep elbow flexion. As much of the soft tissue is muscle, it follows that the range of passive elbow flexion is greater than that of active flexion.
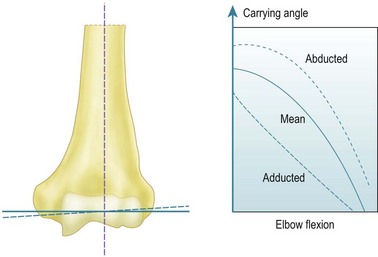
The early work that described the axes of the trochlea and capitellum as being eccentric when viewed laterally suffered from lack of appreciation of the orientation of the axis about which flexion occurs. The key to this is the carrying angle and how that angle varies with elbow flexion. The carrying angle has been defined in many specific ways, but all of these seek to describe the lateral deviation of the extended forearm from the sagittal plane, that is, aligned along the anatomical axis of the shaft of the humerus. Specific definitions have depended on how the axis of the forearm has been defined, either in terms of a line passing from the centre of the capitellum to the centre of the ulnar head distally, an axis based on bony anatomical features, or else as a line which passes along the centre of the forearm, irrespective of the structures within it.7 It is widely recognized that the carrying angle is maximal when the elbow is extended, and reduces until the forearm overlays the upper arm in maximum elbow flexion. Provided that the humero-ulnar joint acts as a uniaxial hinge this variation can be obtained by inclining the flexion axis so that it bisects the carrying angle. While the coaxial circles seen on an accurate lateral radiograph5 suggest this to be true, the literature has found it contentious until the recent advent of more modern 3-D kinematic measurement methods. In particular, it is possible to define the motion of one limb segment in relation to another in terms of the ‘instantaneous screw axis’, which allows a series of axes to be defined as the motion progresses incrementally. It has been shown8 that these instant axes are close to being parallel and intersect through a small zone at the centre of the trochlea. For this reason we can assume for all practical purposes that the elbow acts like a simple hinge under defined loads. The orientation of the hinge axis is not perpendicular to the sagittal plane of the humerus, but is abducted from that orientation by one-half of the carrying angle (Fig. 3.1).9
The literature shows that the carrying angle is larger in females than in males, typically being 14° and 11°, respectively.2,7,10 It has also been shown that the carrying angle relates to build, with carrying angle increasing with heaviness of body type.10 Although Paraskevas et al10 found that the carrying angle was larger in the dominant limb than in the non-dominant limb, that difference was small, and most authors have found that they are effectively symmetrical. That observation is useful in children, because the carrying angle develops up to puberty and so there is no standard value. Smith11 found that 9% of children aged less than 11 years had a zero carrying angle and a further 36% had less than 5°. The biomechanical and clinical importance of the carrying angle relates to both its effect on the appearance of the whole of the upper limb and its effect on the distribution of forces across the distal humerus. Inaccurate reduction of supracondylar humeral fractures will result in deformity and alteration of the carrying angle, while heavily loaded activities will result in significant force transmission across the elbow, which may affect the overall stability of the joint.
Summary Box 3.1 Elbow flexion and carrying angle kinematics
| Elbow flexion | Uniaxial hinge motion |
| Flexion axis | Abducted by a half of the carrying angle |
| Carrying angle | Maximal in extension. Approximately 14° in women and 11° in men |
| Carrying angle | Increases throughout childhood and differs between subjects. To assess accurately examine for abnormal alignment by side-to-side comparison |
Pronation–supination motion
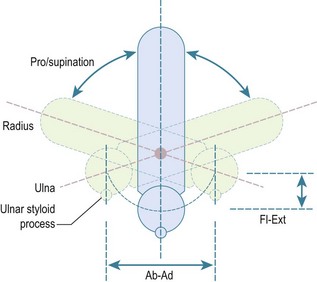
The second principal component of elbow motion is rotation of the forearm. The early literature assumed that this motion took place about a fixed axis, with the ulna not moving in relation to the humerus. This was thought to be due to the constraint of the congruent humero-ulnar joint, with the coronoid and olecranon processes gripping the waist of the trochlea. However, it has since been appreciated that the joint is not so closely constrained, with the carrying angle typically varying by ±5°, due to sloppiness of the fit of the articular surfaces and some slackness of the collateral ligaments.9 The classic paper that showed this variation was by Ray et al,12 who took double-exposure radiographs of their own elbows and forearms in pronation and supination. They immobilized the humerus using transcutaneous pins into the epicondyles, and applied traction to the fingers using a Chinese finger basket. They showed that if the forearm rotation axis was aligned through the ulna, due to traction on the little finger, it resulted in the ulna remaining stationary, with the forearm swinging around it like the handle on a bucket. However, if the axis was aligned through the centre of the wrist, with traction on the long finger, then the centreline of the forearm did not move during forearm rotation and the ulna did move in relation to the fixed humerus. Thus, pronation from neutral rotation entailed ulnar abduction, and supination entailed adduction, with the range of ulnar ab–adduction motion corresponding to the ligamentous laxity noted above. It has been suggested that the ulnar abduction during pronation is a reason for the anconeus muscle. As the forearm rotates away from neutral rotation, so the ulna also flexes a little, as it moves alongside the radius. It was shown long ago13 that this was a circumduction motion, in which the distal ulna moves in a part-circular path, yet does not itself rotate (Fig. 3.2). This has been investigated again using modern technology, with the same findings.14
At the elbow, forearm rotation is accommodated by the radial head rotating in the ulnar notch on the lateral side of the coronoid. This notch is less than 180° in extent and therefore the radial head is vulnerable to subluxation under the anterior force vector applied to the radial tuberosity by the biceps tendon. This vulnerability is controlled by the tension in the surrounding annular ligament, which envelops the radial head and attaches securely to the ridges at the anterior and posterior edges of the ulnar notch. At the wrist, the axis of rotation passes through the centre of the head of the ulna, so the axis of rotation slants across from the capitellum proximally to the ulna distally, when viewed in the coronal plane. In the sagittal plane, the axis of forearm rotation is relatively anterior proximally, again being centred in the capitellum, and is anterior to the interosseous border of the ulna. This has great significance for the function of the interosseous membrane which, when the forearm is in neutral rotation, will be tightest when the radius is furthest away from the interosseous border of the ulna,. It will then slacken when the forearm rotates away from that posture.15 In particular, the interosseous membrane is slack when the forearm is in pronation, which is the posture taken up during falls onto the outstretched hand, when load transmission along the forearm is important. This will be discussed below.
Range of forearm rotation motion
Various methods have been used to measure forearm rotation. These comprise devices held in the hand, such as a rotational pendulum or bubble goniometer, or those which seek to eliminate accessory motion at the wrist and hand (a very common way in which patients try to ‘cheat’), by using a device located around the wrist. Patrick15 found that hand grip motion was 27° greater than that measured simultaneously at the wrist, which is true forearm rotation. Also, when the radius was vertically above the ulna at the wrist, the hand grip was supinated 11°. An analysis of the then published literature2 found that the mean motion reported from hand-gripping devices was 77/106° pronation/supination, while wrist cuff devices led to means of 76/80°. A comparative study by Darcus and Salter16 found that wrist cuff goniometers resulted in much more repeatable readings for forearm rotation, and for this reason they are recommended for research studies. An updated version of this method uses an electromagnetic sensor from a motion analysis system attached to the wrist via a strap.
The literature clearly shows that forearm rotation varies between normal subjects and, therefore, when being measured after injury it should always be compared to the contralateral normal limb. This recommendation is supported by a number of studies that have found no significant difference between the dominant and non-dominant arms. Salter and Darcus17 found that females had a mean of 8° more active forearm rotation than males, while Glanville and Kreezer4 found that there was a mean of 31° more forearm rotation when the hand was held and rotated passively, presumably because that allowed muscles to relax, which might otherwise block motion between the radius and ulna.
Muscle actions causing forearm rotation
Both pronation and supination are each driven by two principal muscles,18 and in each case one is relatively long, while the other consists of a compact bulk of fibres that cross transversely from the ulna to the radius. Travill and Basmajian19,20 found that unresisted rotation was driven by the short supinator and pronator quadratus muscles, with the longer muscles becoming active as the motion was resisted.
Forceful supination is driven primarily by the biceps, the tendon of which wraps around the proximal radius inserting into the radial tuberosity. The biceps is augmented by the supinator muscle, the fibres of which are oriented anterodistally from the lateral supinator ridge to the radius. The supinator has a more extensive ulnar origin than radial attachment, with superficial fibres that spiral around the neck of the radius, attaching both proximal and distal to the biceps tuberosity. Although not usually seen during surgery, the supinator also has a deep layer of fibres which are oriented transversely to the axis of the forearm, and which wrap directly around the proximal neck of the radius from the supinator ridge. This fibre group is well oriented to resist the tendency of the biceps to cause anterior subluxation of the head of the radius when the forearm is actively flexed. Forceful supination demands coordinated action from many muscles, because of the subluxing and flexing effects of biceps contraction. Thus at least the triceps will also act to stabilize the elbow, but also probably almost all of the other forearm muscles, as they cause the hand to grasp whatever object is being rotated and also stabilize the wrist. In particular, the brachioradialis may act to return the forearm to neutral rotation from either pronation or supination.21
Clinical Pearl 3.2
The range of forearm rotation is approximately 80° of pronation and 90° of supination.
Summary Box 3.2 Forearm rotation
| Forearm rotation | Must be assessed by comparison with the contralateral limb due to variability between subjects |
| Forearm rotation – supination | Achieved by biceps and supinator |
| Forearm rotation – pronation | Achieved by pronator teres and pronator quadratus |
Passive soft tissue stabilizers of the elbow
Medial collateral ligament complex
The principal structures crossing the joint are the anterior and posterior bands of the medial collateral ligament (MCL). The humeral attachment is spread around the base of the medial epicondyle, across its distal and posterior–distal aspects, thus spanning across the site of the flexion–extension axis, which emerges from the centre of the circular medial end-face of the trochlea, at the distal edge of the epicondyle. This means that the most anterior fibres of the anterior band of the MCL are close to being isometric, and therefore tight throughout the range of elbow flexion–extension. Moving posteriorly across the width of the MCL complex, there is an increasing tendency for the ligament fibres to slacken as the elbow is extended.22 Thus the posterior band of the MCL is only tightened completely when it becomes wrapped around the distal aspect of the epicondyle beyond 90° of elbow flexion.23 Ciccotti et al22 found that the progressive tightening of the MCL fibres as the elbow flexed correlated with a reducing range of valgus laxity. Morrey and An24 found that the MCL resisted approximately one-third of the valgus moment applied to the elbow when it was extended. In addition, they noted that because the anterior joint capsule was tight in this position it also took one-third of the load, with the articular surfaces taking the remainder. As the elbow flexed, so the MCL took a larger proportion of the load, reaching 54% at 90° flexion. Thus they felt that the MCL was the primary restraint to valgus laxity. This was consistent with the findings of Sojbjerg et al,25 who reported that cutting the anterior band of the MCL led to 14° of valgus laxity at 70° of elbow flexion. At this point the posterior band became tight and if this was also cut the elbow became unstable, with up to 31° of valgus deformity.
Lateral collateral ligament complex
In general, the lateral collateral ligament structures are less important for elbow stability than the medial collateral ligament complex. Morrey and An24 found that the trochlea was more important than the lateral ligaments for resisting varus moments, contributing 75% at 90° of flexion. As the elbow reached full extension, the tightening of the anterior capsule caused the soft tissues to become more dominant, with the lateral collateral ligaments contributing 14% and the anterior capsule 32%.
The principal clinical problem associated with disruption of the lateral ligaments is posterolateral subluxation or instability. This is associated with the radial head subluxing posterior to the capitellum as a result of translation and rotation of the forearm. O’Driscoll et al26 found that it required the ulna to supinate 41° out of articulation with the trochlea, supinating the whole forearm and carrying the head of the radius posteriorly while pivoting on the intact medial collateral ligament. The proximal translation of the radial head that occurred took the forearm into 15° of valgus from its normal carrying angle. Dunning et al27 showed that all of the lateral ligamentous stabilizing structures had to be transected before they could produce posterolateral rotatory instability, reflecting the large posterior displacement of the proximal radius that must occur at the time of injury.
The strength of the elbow ligaments
The mechanical properties of the collateral ligaments were measured by Regan et al.28 They found that the anterior band of the MCL was the strongest, with a tensile strength of 261±71 N, while the posterior band had a tensile strength of 159±40 N. The lateral collateral ligament had a tensile strength of 233±116 N. By comparison, the palmaris longus tendon strength was 358±88 N and its stiffness was more than six times greater than the ligaments.
Articular contributions to elbow stability
The articular contributions to elbow stability have been reviewed by Morrey and An,29 following a series of experiments. They identified the factors that provided stability by measuring changes in the configuration of the elbow after sequential soft tissue and ligament excisions. Thus contributions to stability were inferred from changes in joint laxity or subluxation. While this approach is directly relevant to the clinical scenario, in which a radiograph may reveal joint subluxation under load, the reader should note that it does not correlate easily with the forces transmitted by the specific structures in physiological activities. This is because, unlike a ligament, a stiff bony structure will transmit a large force while deforming minimally.
The principal clinical concerns relate to instability after trauma, when elbow-stabilizing structures may be damaged either by direct trauma to the elbow or by transmission of force along the forearm. With direct trauma the olecranon may be fractured, while a fall onto the outstretched hand may cause fractures of the radial head and/or the coronoid.30 Each of these will have a specific effect on stability of the elbow; Morrey and An29 ranked their importance for axial stability, with the coronoid the most important and the olecranon the least.
The contribution of the olecranon to stability has been examined in vitro by loading the humerus axially into the trochlear notch of the flexed elbow and then imposing internal–external rotation torques.31 When this was repeated after sequential proximal to distal excision of the olecranon, elbow stability reduced in proportion to the loss of bone. From this work An et al31 suggested that after a comminuted olecranon fracture it would be acceptable to excise up to 50% of the olecranon without compromising the functional stability of the elbow.
The radial head acts as part of a strut, which transmits axial compressive loads from the wrist to the capitellum. In addition, the angulation of the carrying angle tends to bias forces onto the lateral aspect, such that a valgus moment will be resisted by a combination of compression of the radial head against the capitellum and tension in the anterior band of the medial collateral ligament. Based on clinical experience, Morrey and An suggested that an isolated comminuted radial head fracture could usually be excised without causing disabling instability. However, such an approach depends on the integrity of the MCL, and the triangular fibrocartilage of the distal radio-ulnar joint. If these are damaged by the initial injury and the interosseous membrane is torn, proximal migration of the radius under functional loads will occur:32 the so called Essex–Lopresti injury.
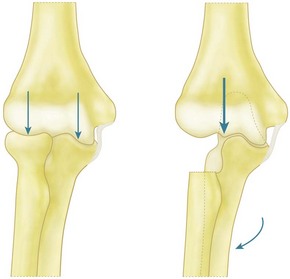
The forces carried by the radial head in relation to valgus moments imposed on the forearm have been measured, and it has been shown that the relatively rigid bony components transmitted larger forces than the relatively compliant soft tissues. This reflects the clinical observation that it is the radial head that is fractured on impact. Other studies33,34 have shown that if the radial head is excised while all other tissues remain intact then the elbow does not collapse into the valgus. The moment is resisted by tension in the medial collateral ligament and by a large compressive load on the lateral facet of the coronoid–trochlear articulation. In view of this observation, Morrey et al34 defined the radial head as a secondary restraint, taking approximately 25% of the valgus moment, and the anterior band of the MCL as the primary restraint. While these findings may accurately represent the situation for many patients, it may not always be correct since the results were obtained with very low, non-physiological, loading. The mechanism by which a valgus moment is resisted – the combination of lateral articular compression and medial soft tissue tension – is dependent on the width of the distal humerus. If that width is reduced by radial head excision, then the forces required to produce the same stabilizing moment (which is the product of force times distance) have to increase. This may lead to increased valgus angulation of the elbow as a consequence of stretching the medial collateral ligament and erosion of the lateral face of the coronoid (Fig. 3.3). This deformity occurs in the rheumatoid elbow,35 despite the reduced strength of those patients.36
Summary Box 3.3 Factors associated with osseous stability
| Osseous structure | Effect on stability |
|---|---|
| Coronoid process | Most important bony articulation resisting posterior dislocation of the elbow under axial loading |
| Olecranon process | Least important for elbow stability. 50% can be excised without causing instability |
| Radial head | Can be excised without causing functional instability but elbow will be unbalanced and stability will depend on MCL resisting large valgus moment |
Elbow strength for performing daily activities
Flexion strength
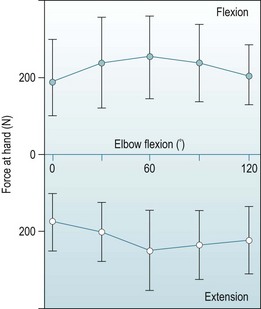
Many publications have measured elbow flexion strength because of its relevance to ergonomic design of controls and also because this action is amenable to analysis when researching muscle actions. The values reported below are for isometric strength, when the subject exerts maximum strength against a fixed handle or wrist strap. Maximum elbow flexion strength occurs at approximately 60° of flexion, declining towards both greater flexion and extension. Hunsicker,37 who produced comprehensive data, found the mean isometric elbow flexion strength was 55 N m at 0° elbow flexion, 80 N m at 60° and 65 N m at 120° flexion (80 N m flexion torque results from a force of approximately 250 N at the hand) (Fig. 3.4). There have been few studies in which male strength was compared with female, but the data available38 found that females had approximately 55% of male flexion strength.
Several studies have examined the effect of forearm rotation posture on elbow flexion strength. In general, this does not have a large effect, although Provins and Salter39 reported that strength was reduced when the hand was pulling on a handle in a direction that required dorsiflexion of the wrist, and that the handle tended to slip out of the grasp of the fingers. Thus the elbow flexion strength in mid rotation was reduced 22% when the forearm was in pronation.
The data above may be modified if the elbow flexors are not contracting isometrically: Elftman40 showed that muscles have a force–velocity relationship such that, as the speed of shortening increases (concentric muscle contraction), the tension reduces and, if the muscle is lengthening, or stretched while contracting (eccentric muscle contraction), the maximum tension increases. Following this trend, Doss and Karpovich41 reported that the mean force at the hand was reduced by 23% during concentric contraction but increased by 14% in eccentric contraction.
Elbow strength may be reduced by injury or disease. Amis et al36 measured the isometric elbow flexion strength of 102 patients with rheumatoid arthritis. A wrist strap was used in order that elbow strength was not under-assessed due to disability of the fingers. The mean force at 90° of flexion was 146 N for male outpatients, 98 N for male inpatients, and 57 N for both groups of female patients. Thus, when compared with the data for normal subjects, these rheumatoid patients had approximately 45% of normal strength. Some of this reduction in strength would have been secondary to the older age of the patients compared to the fit young adults who typically are recruited for research studies of ‘normal’ people. In addition, the rheumatoid group also included some, mostly female, subjects who had no flexion strength, due to pain.
Extension strength
There have been fewer studies leading to elbow extension strength curves, not all of which have reached the same conclusions. This disparity may reflect the study methods, particularly whether the subject was restrained in a test rig that allowed greater forces to be imposed, such as having a back rest when pushing away to extend the elbow. A study with a large number of male subjects37 found that extension strength was maximal at 60° of flexion, when a mean force of 250 N was applied to a handle, and an elbow extension torque of 75 N m. Elkins et al38 also found that the maximum extension strength was at 60°, while Currier42 found the maximum at 90° flexion. However, Hunsicker37 reported a mean strength approximately 60% higher than the other studies, and this may represent a truer attainment of maximum strength (Fig. 3.4). These papers have also included the effects of forearm rotation and shoulder position. The latter variable may have an effect because of the long head of the triceps crossing the shoulder, but the differing postures do not have significant effects on elbow extension strength.
Forearm rotation strength
Forearm rotation strength has been extensively studied by Darcus and Salter,43,44 who used hand grip dynamometers. They investigated the effects of a wide range of postures and in general found that shoulder position had very little effect on forearm rotation, despite its effect on the long head of the biceps. They also found that the greatest strength of mid-position rotation torques occurred at 90° of elbow flexion for both pronation and supination. Supination strength decreased with elbow flexion, reflecting the reduced length and hence tension of the biceps muscle. A much larger effect resulted from testing rotation strength at different positions of rotation. This related to stretching of the forearm rotation muscles. Thus pronation was strongest when the forearm had been supinated, stretching the pronator muscles, and vice versa for supination. If the hand had already been pronated 60° the pronation strength was only 2 N m, whereas if the forearm was in 60° of supination the pronation strength was 10 N m. As a reference for normal forearm rotation strength, both pronation and supination strengths were a mean of 6 N m with the forearm in neutral rotation, the elbow flexed 90° and with the humerus adducted alongside the trunk.
Summary Box 3.4 Flexion and rotation strength
| Flexion strength | Reduced in women to approximately 55% that of men |
| Flexion strength | Reduced in rheumatoid patients to approximately 45% that of normal subjects |
| Forearm rotation strength in neutral rotation | 6 N m for both pronation and supination |
| Forearm rotation strength away from neutral rotation | Increases as the rotation muscles are stretched to 10 N m for pronation from a supinated posture and supination from a pronated posture |
The forces acting on the structures of the elbow
Forces during elbow flexion
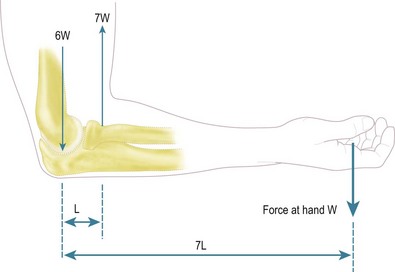
Nordin and Frankel45 have described the forces acting across the elbow during elbow flexion. The arm is illustrated with the elbow flexed 90° and with the hand supporting a weight. To maintain that position the extending moment (N m) caused by the weight is resisted by muscular activity equal to the force (N) times the distance (m) from the flexion axis of the elbow.
The muscle action is usually shown diagrammatically as only supplied by the biceps, and its tension (N) times the distance (m) of its line of action from the elbow axis gives the flexing moment (N m), which opposes the extending moment of the weight in the hand. Thus, taking typical approximate values, with the weight 350 mm from the elbow axis and a biceps tendon of 50 mm, rotational equilibrium of the moments acting about the flexion axis demands that the biceps tension must equal seven times the external load (Fig. 3.5). Further, with the load acting downwards and the biceps pulling upwards, parallel to the humerus, there is a net resultant force of six times the external load acting upwards onto the distal end of the humerus. While this is a gross simplification, it does nevertheless show how the lever arm effect causes the internal forces to be multiples of the external load.
In reality, elbow flexion actions usually entail actions by the hand, to grip the object being lifted or the handle being pulled, which means that elbow flexion inherently requires activity from the muscles which act to flex the finger and to stabilize the wrist against the combination of transverse shearing load and angulation.46 This is a difficult situation to analyse mechanically because of the large number of muscles acting simultaneously, and so a scheme for apportioning the muscle actions is needed. There are a number of well-accepted optimization criteria for predicting muscle actions when walking which are based on energy efficiency, but they are not appropriate for most upper limb actions. A starting point is electromyography, which shows which muscles are active and also indicates their relative levels of stimulation. A key paper by Dempster and Finerty47 showed how all the muscles crossing the wrist were co-contracted in order to stabilize the joint when the hand was loaded. There was a range of stimulation from most intense in the direction of the load, through to approximately 50% to stabilize the wrist in the perpendicular direction, and approximately 33% in the antagonistic direction. The net result was both a force action in the desired direction and wrist stability. Most of those muscle tensions cross the elbow, so the action of simply clenching the fist, or pulling on the handle of a suitcase, causes the elbow to be compressed along the direction of the forearm and with the load imposed on both the radial head and the coronoid process. This result is perhaps initially surprising, but a similar simple analysis to that of elbow flexion applied to the metacarpophalangeal joints shows that the finger flexor tendons are also working at multiples of the external load; thus, even if one were to hang from an overhead bar, the wrist and elbow would still be compressed.
The principal muscles acting to flex the elbow are the biceps, brachialis, brachioradialis and pronator teres. The electromyography literature shows that biceps tend to be more active when the forearm is supinated,18 but that is of little relevance when the limb is loaded heavily, when all these muscles contract maximally. It is worth noting that three of these four muscles insert distally into the radius, and a force analysis shows that the humeroradial joint is loaded heavily, as is the humero-ulnar joint, during elbow flexion.48 A further factor is the tendency for some of these muscles to cause forearm rotation, and so the supinating effect of biceps must be counterbalanced by the action of the pronator teres to ensure rotational equilibrium. The effect of flexing the elbow with the forearm in different rotational positions has not been analysed, but it can be predicted that trying to flex with the hand pronated will require the wrist extensors to work very hard, while flexing in supination will load the wrist flexors. The result of these contrasting cases is that the load on the elbow will tend to move from the radius to the ulna as the forearm is supinated.
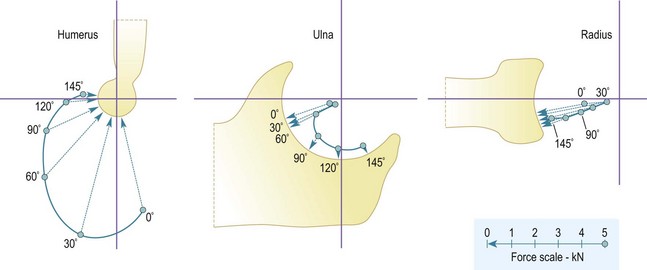
The combination of all the muscle tensions leads to a resultant force on the elbow that moves around the end of the humerus as the elbow flexes. The resultant force acts on the distal aspect of the humerus in extension, to approximately 60° from the axis of the humerus at 90° of flexion48 (Fig. 3.6). This resultant force direction follows from the combination of all the muscle actions, with the hand and wrist muscles, plus the pronator teres and brachioradialis acting along the forearm, while the biceps and brachialis act closer to the direction of the humerus. Near extension, the flexor muscles wrap closely over the anterior aspect of the elbow, and so they have a large mechanical disadvantage and flexion strength is reduced. That disadvantage reduces with flexion, as the lines of action of the muscles bridge across the decreasing gap between the humerus and forearm,49 and result in the elbow forces tending to reduce as a proportion of the external load being lifted.
Taking all the muscle actions into account, and compounding this by the large mechanical disadvantage caused by the distance from the elbow to the hand, it is not surprising to find that the elbow forces are predicted to be up to 15 times the external load held in the hand. If the maximum isometric force which can be imposed at the hand (noted above to be approximately 250 N) is multiplied by this ratio, it leads to an elbow joint load of 3 kN (four times body weight). Although this calculation relates to young adult males imposing their maximum possible strength, it indicates the size of the forces that are possible and shows that it is incorrect to assume that the elbow is not a load-bearing joint. Noting also the paths of the muscles and their attachments, particularly the distal attachments to the radius of the biceps, pronator teres and brachioradialis, it also follows that both the humero-ulnar and humeroradial joints will be loaded heavily by forceful elbow flexion activity. The joint force may be even higher than shown above, because there is also electromyographic evidence50 of antagonistic triceps activity during elbow flexion, acting to stabilize the joint. This has been estimated to raise the force on the coronoid process by up to 20% near elbow extension.
These actions on the humerus are reflected in the reaction forces acting on the radius and ulna. These are in a distal and posterior direction, which means that the joint load acts towards the base of the coronoid process and onto the posterior lip of the concave end-face of the radial head (Fig. 3.6). The head of the radius is not circular when viewed end-on. The largest dimension is oriented so that the elliptical extension beyond the circle is positioned posteriorly when the forearm is supine. This means that the posterior lip is deepest in supination, making the articulation of the radial head most stable against the anterior subluxation tendency of the biceps, which is strongest in the supinated posture. If the tendency towards anterior subluxation overcomes the stability of the articulation, then further subluxation is resisted by the annular ligament, which encircles the head of the radius attaching to the anterior and posterior edges of the articular surface of the superior radio-ulnar joint. Finally, the balance of forces across both the ulna and radius during elbow flexion is a fundamental reason for considering radial head replacement, whether as part of a total joint arthroplasty or following trauma. While load sharing clearly suggests the mechanical logic for this approach, there is no prosthesis currently available that appears to achieve reliable long-term outcomes.
Forces during elbow extension
Elbow extension is caused almost entirely by triceps tension with the humero-ulnar joint bearing most of the load. The medial head of the triceps is the principal extensor, after which the lateral and then the long heads are recruited as the load increases.51 There is also a small contribution from the anconeus. This does not mean that the radiocapitellar joint remains unloaded since the long head of triceps partly passes lateral to the olecranon with its tension dissipating into the fascia overlying the anconeus. In addition, when an object is grasped by the hand there will be contraction of the forearm muscles to stabilize the wrist. The elbow is also stabilized by antagonistic activity in the biceps, estimated to equal 7% of the triceps tension.50
The elbow forces are very large when the joint extends from a flexed posture. The triceps tendon wraps around the tip of the olecranon process and trochlea, and therefore has a small moment arm of approximately 20 mm.49 This great mechanical disadvantage means that the elbow joint force may be in excess of 20 times the external load at the hand, acting onto the distal aspect of the trochlea.48 The magnitude of the triceps tension explains the importance of obtaining secure fixation of olecranon fractures. It also means that there is a practical limit on the size of any fixation keel of the ulnar component of joint replacements, since excessive bone excavation will reduce the tensile strength of the olecranon.52
Forces during forearm rotation
There has been some work to examine the question of whether the out-of-roundness of the radial head has a significant effect on the mechanics of the elbow53 and, although statistically significant differences were noted, these were all less than 1° difference of ulnar rotation. This is therefore functionally likely to be negligible.
Forces during abduction and adduction actions
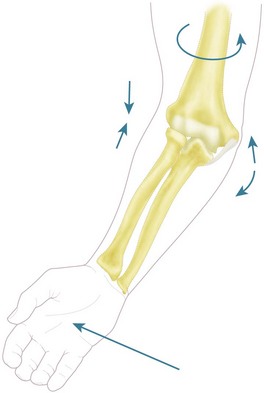
The forces that load the elbow into abduction or adduction are most easily visualized when the elbow is flexed 90° and the shoulder is rotated internally or externally. The strongest action is internal rotation, caused largely by tensions in the pectoralis muscles. This is the situation when the palms of the hands are pressed against the sides of a box, pushing towards the centreline of the body. Hunsicker37 found that inward rotation resulted in a maximum force of 218±100 N, while the external rotation force at the hand was 156±81 N.
In young adult males internal rotation of the humerus induces a torque of 65 N m in the bone. At the elbow, this torque must be countered by an equal and opposite reaction, and this arises from a coupled action between tension in the MCL and compression of the radial head onto the capitellum (Fig. 3.7). These internal forces are large multiples of the external load, because of the length of the forearm. As a result the MCL tension will be approximately six times the external force and the load on the radial head approximately eight times.
If the head of the radius is excised, it reduces the width of the base of the forearm on the distal humerus. The torque must then be resisted by the MCL tension coupled with compression onto the lateral facet of the coronoid process. The forces will be much higher than with the elbow intact because of the reduced distance between them, and can lead to increased valgus of the elbow after trauma.54
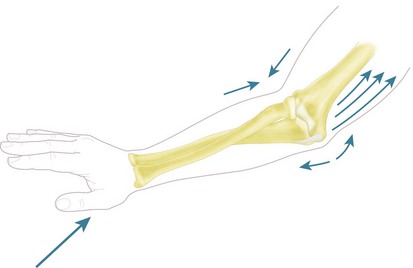
Force transmission along the forearm and during falls onto the outstretched hand
Classical studies of force transmission along the forearm found that 60% of the load applied to the hand passed to the capitellum via the radial head, with 40% passing to the trochlea from the coronoid process.55 It has more recently been shown that this load share is disrupted by the interposition of an excessively thick and stiff radial head prosthesis,56 which offloads the coronoid. These experiments applied loads axially along the forearm and although they have provided some useful data the real-life situation is more complex. Experimental work on live subjects falling forwards onto their outstretched hands57 found that they took up a characteristic posture, in which the forearm was semi-pronated, the elbow partly flexed (approximately 15°) and the shoulder flexed, abducted and partly inwardly rotated. This combination of arm posture caused the palm of the hand to be placed flat on the floor in front of the falling body (Fig. 3.8). The flexed elbow in this voluntary situation allowed energy to be dissipated by forced flexion of the elbow, stretching the triceps, plus forced retraction of the shoulder, stretching the pectoral muscles. If the subject fell onto a fully extended arm, it would act as a rigid strut, so could not then dissipate the energy of falling. It would have to be released by creating bone fractures. The characteristic falling posture means that the impact force on the palm of the hand causes a combination of axial compression and valgus moment on the forearm, which may cause a fracture of the radial head and tension in the medial collateral ligament. In that situation, the force on the head of the radius will be larger than the external load because of the MCL tension, while the load on the coronoid process may be zero.58,59
Summary Box 3.5 Elbow forces
| Elbow joint force | In extension the force acts onto the distal end of the humerus and then swings onto the anterior aspect with flexion |
| Joint force | May be 15 times the external load |
| Radio-ulnar joint forces | Low during forearm pronation–supination |
| Internal rotation of the humerus | Produces tension in the MCL and compression in the radial head typically seven times the external load |
| Fall onto the outstretched hand | Produces compression along the radius and tension in the MCL |
1 American Academy of Orthopaedic Surgeons. Joint motion: method of measuring and recording. Edinburgh: Churchill Livingstone; 1966. p. 1–97
2 Amis AA, Miller JH. The elbow. In: Measurement of joint movement. Clin Rheum Dis. 1982;8:571-593.
3 West CC. Measurement of joint motion. Arch Phys Med. 1945;26:414-425.
4 Glanville AD, Kreezer G. The maximum amplitude and velocity of joint movements in normal male human adults. Hum Biol. 1937;9:197-211.
5 London JT. Kinematics of the elbow. J Bone Joint Surg (Am). 1981;63:529-535.
6 Zimmer EA. Borderlands of the normal and early pathologic in skeletal roentgenology. New York: Grune & Stratton; 1968.
7 Van Roy P, Baeyens JP, Fauvard D, et al. Arthro-kinematics of the elbow: study of the carrying angle. Ergonomics. 2005;48:1645-1656.
8 Ericson A, Arndt A, Stark A, et al. Variation in the position and orientation of the elbow flexion axis. J Bone Joint Surg (Br). 2003;85:538-544.
9 Amis AA, Dowson D, Wright V, et al. An examination of the elbow articulation with particular reference to the variation of the carrying angle. Eng Med. 1977;6:76-80.
10 Paraskevas G, Papadopoulos A, Papaziogas B, et al. Study of the carrying angle of the human elbow joint in full extension: a morphometric analysis. Surg Radiol Anat. 2004;26:19-23.
11 Smith L. Deformity following supracondylar fractures of the humerus. J Bone Joint Surg (Am). 1960;42:235-252.
12 Ray RD, Johnson RJ, Jameson RM. Rotation of the forearm: an experimental study of pronation and supination. J Bone Joint Surg. 1951;33A:993-996.
13 Dwight T. The movements of the ulna in rotation of the forearm. J Anat (Lond). 1884;19:186-189.
14 Kasten P, Krefft M, Hesselbach J, et al. Kinematics of the ulna during pronation and supination in a cadaver study: implications for elbow arthroplasty. Clin Biomech. 2004;19:31-35.
15 Patrick J. A study of supination and pronation with especial reference to the treatment of forearm fractures. J Bone Joint Surg (Br). 1946;28:737-748.
16 Darcus HD, Salter N. The amplitude of pronation and supination with the elbow flexed to a right angle. J Anat (Lond). 1953;87:169-184.
17 Salter N, Darcus HD. The amplitude of forearm and of humeral rotation. J Anat (Lond). 1953;87:407-418.
18 Basmajian JV, DeLuca C. Muscles alive: their functions revealed by electromyography, 5th ed. Baltimore, MD: Lippincott, Williams & Wilkins; 1985.
19 Travill AA, Basmajian JV. Electromyography of the supinators of the forearm. Anat Rec. 1961;139:45-49.
20 Travill AA, Basmajian JV. Electromyography of the pronators of the forearm. Anat Rec. 1961;139:557-560.
21 Pauly JE, Rushing JL, Scheving LE. An electromyographic study of some muscles crossing the elbow. Anat Rec. 1967;159:47-54.
22 Ciccotti MG, Siegler S, Kuri JA, et al. Comparison of the biomechanical profile of the intact ulnar collateral ligament with the modified Jobe and the docking reconstructed elbow: an in vitro study. Am J Sports Med. 2009;37:974-981.
23 Safran MR, Baillargeon D. Soft-tissue stabilizers of the elbow. J shoulder Elbow Surg. 2005;14:179S-185S.
24 Morrey BF, An KN. Articular and ligamentous contributions to the stability of the elbow joint. Am J Sports Med. 1983;11:315-319.
25 Sojbjerg JO, Ovesen J, Nielsen S. Experimental elbow instability after transection of the medial collateral ligament. Clin Orthop. 1987;218:186-190.
26 O’Driscoll SW, Morrey BF, Korinek S, et al. Elbow subluxation and dislocation: a spectrum of instability. Clin Orthop. 1992;280:186-197.
27 Dunning CE, Zarzour ZD, Patterson SD, et al. Ligamentous stabilizers against posterolateral rotatory instability of the elbow. J Bone Joint Surg (Am). 2001;83:1823-1828.
28 Regan WD, Korinek SL, Morrey BF. Biomechanical study of ligaments around the elbow joint. Clin Orthop. 1991;271:170-179.
29 Morrey BF, An KN. Stability of the elbow: osseous constraints. J Shoulder Elbow Surg. 2005;14:174S-178S.
30 Amis AA, Miller JH. The mechanisms of elbow fractures: an investigation using impact tests in-vitro. Injury. 1995;26:163-168.
31 An KN, Morrey BF, Chao EY. The effect of partial removal of proximal ulna on elbow constraint. Clin Orthop. 1986;209:270-279.
32 McDougall A, White J. Subluxation of inferior radio-ulnar joint complicating fracture of radial head. J Bone Joint Surg. 1957;39B:278-287.
33 Hotchkiss RN, Weiland AJ. Valgus stability of the elbow. J Orthop Res. 1987;5:372-377.
34 Morrey BF, Tanaka S, An KN. Valgus stability of the elbow: a definition of primary and secondary constraints. Clin Orthop. 1991;265:187-195.
35 Rymaszewski L, Mackay I, Amis AA, et al. Long term effects of radial head excision in rheumatoid arthritis. J Bone Joint Surg (Br). 1984;66:109-113.
36 Amis AA, Hughes SJ, Miller JH, et al. A functional study of the rheumatoid elbow. Rheumatol Rehab. 1982;21:151-157.
37 Hunsicker P. Arm strength at selected degrees of elbow flexion. Technical Report 54-548. Wright-Patterson Air Force Base, OH: Wright Air Development Centre; 1955.
38 Elkins EC, Ledan UM, Wakim KG. Objective recording of the strength of normal muscles. Arch Phys Med. 1951;32:639-647.
39 Provins KA, Salter N. Maximum torque exerted about the elbow joint. J Appl Physiol. 1955;7:393-398.
40 Elftman H. Biomechanics of muscles. J Bone Joint Surg. 1966;48A:363-377.
41 Doss WS, Karpovich PV. A comparison of concentric, eccentric and isometric strength of elbow flexors. J Appl Physiol. 1965;20:351-353.
42 Currier DP. Maximal isometric tension of the elbow extensors at varied positions. Phys Ther. 1972;52:1043-1049.
43 Darcus HD. The maximum torques developed in pronation and supination of the right hand. J Anat (Lond). 1951;85:55-67.
44 Salter N, Darcus HD. The effect of the degree of elbow flexion on the maximum torques developed in pronation and supination of the right hand. J Anat (Lond). 1952;86:197-202.
45 Nordin M, Frankel VH. Basic biomechanics of the musculoskeletal system, 3rd ed. Philadelphia, PA: Lippincott, Williams & Wilkins; 2001.
46 Long C, Conrad PW, Hall EA, et al. Intrinsic–extrinsic muscle control of the hand in power group and precision handling: an electromyographic study. J Bone Joint Surg. 1970;53A:853-867.
47 Dempster WT, Finerty JC. Relative activity of wrist moving muscles in static support of the wrist joint: an electromyographic study. Am J Physiol. 1947;150:596-606.
48 Amis AA, Dowson D, Wright V. Elbow joint force predictions for some strenuous isometric actions. J Biomech. 1980;13:765-775.
49 Amis AA, Dowson D, Wright V. Muscle strengths and musculoskeletal geometry of the upper limb. Eng Med. 1979;8:41-48.
50 Messier RH, Duffy J, Litchman HM, et al. The electromyogram as a measure of tension in the human biceps and triceps muscles. Int J Mech Sci. 1971;13:585-598.
51 Travill AA. Electromyographic study of the extensor apparatus of the forearm. Anat Rec. 1962;144:373-376.
52 Amis AA, Miller JH, Dowson D, et al. Biomechanical aspects of the elbow: joint forces related to prosthesis design. J Med Eng Technol. 1979;3:229-234.
53 Van Riet RP, Van Glabbeek F, Baumfeld JA, et al. The effects of the orientation of the non-circular radial head on elbow kinematics. Clin Biomech. 2004;19:595-599.
54 Taylor TKF, O’Connor BT. The effect on inferior radio-ulnar joint of excision of head of radius in adults. J Bone Joint Surg (Br). 1964;46:83-88.
55 Halls AA, Travill A. Transmission of pressures across the elbow joint. Anat Rec. 1964;150:243-247.
56 Markolf KL, Tejwani SG, O’Neill G, et al. Load-sharing at the wrist following radial head replacement with a metal implant. J Bone Joint Surg (Am). 2004;86:1023-1030.
57 Carlsoo S, Johansson O. Stabilisation of, and load on, the elbow joint in some protective movements. Acta Anat. 1962;48:224-231.
58 Amis AA, Miller JH, Dowson D, et al. Axial forces in the forearm: their relationship to excision of the head of the radius. In: Stokes IAF, editor. Mechanical factors and the skeleton. London: Libbey; 1981:29-37.
59 Amis AA, Miller JH. Design, development and clinical trial of a modular elbow replacement incorporating cement-free fixation. Eng Med. 1984;13:175-179.