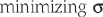CHAPTER 3 Biomechanics of the Elbow
INTRODUCTION
In our practice, a working knowledge of biomechanics has been extremely important and rewarding. Clinical relevance includes elbow joint design and technique, the rationale and execution of trauma management, and ligament reconstruction. In short, a clear understanding of biomechanics provides a scientific basis for clinical practice.5
KINEMATICS
FLEXION-EXTENSION
Because of the congruity at the ulnohumeral articulation and surrounding soft tissue constraint, elbow joint motion is considered primarily a hinge type. Yet, two separate three-dimensional studies of passive motion at the elbow revealed that the elbow does not function as a simple hinge joint.51,69 The position of the axis of elbow flexion, as measured from the intersection of the instantaneous axis with the sagittal plane, follows an irregular course. A type of helical motion of the flexion axis has been demonstrated.69 This pattern was previously suggested26,50,61 and was attributed to the obliquity of the trochlear groove along which the ulna moves.52 An electromagnetic tracking device that allows a three-dimensional measurement of simulated active elbow joint motion reveals the amount of potential varus-valgus and axial laxity that occurs during elbow flexion to average about 3 to 4 degrees. This has been confirmed with more advanced electromagnetic tracking technology.101
CENTER OF ROTATION
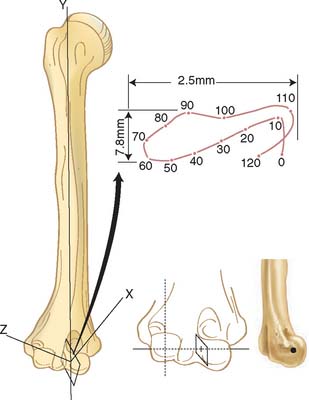
The axis of motion in flexion and extension has been the subject of many investigations.60 Fischer (1909), using Reuleaux’s technique, found the so-called locus of the instant center of rotation to be an area 2 to 3 mm in diameter at the center of the trochlea (Fig. 3-1).34 Subsequent experiments with the same technique described a much larger locus.32 In a three-dimensional study of passive motion of the elbow joint, the observations of Fischer were confirmed by using the biplanar x-ray technique.69 Based on direct experimental study as well as analytic investigation, Youm and associates109 concluded that the axis does not change during flexion-extension. In our study, however, variations of up to 8 degrees in the position of the screw axis from individual to individual have been shown. As seen from below, the axis of rotation is internally rotated 3 to 8 degrees relative to the plane of the epicondyles. In the coronal plane, a line perpendicular to the axis of rotation forms a proximally and laterally opening angle of 4 to 8 degrees with the long axis of the humerus.105 These data, coupled with the clinical information regarding implant loosening, have inspired the development of less constrained but coupled elbow joint replacement designs. It recently has been demonstrated that these designs do function as semiconstrained implants and allow for the normal out-of-plane rotations noted earlier (see Chapter 49).75
From a practical point of view, despite the different findings of various investigators, the deviation of the center of joint rotation is minimal and the reported variation is probably due to limitations in the experimental design. Thus, the ulnohumeral joint could be assumed to move as a uniaxial articulation except at the extremes of flexion and extension. The axis of rotation passes through the center of the arcs formed by the trochlear sulcus and capitellum.56
The center of rotation can be identified from external landmarks. In the sagittal plane, the axis lies anterior to the midline of the humerus92 and lies on a line that is colinear with the anterior cortex of the distal humerus.69 The coronal orientation is defined by the plane of the posterior cortex of the distal humerus.19 This axis emerges from the center of the projected center of the capitellum and from the anteroinferior aspect of the medial epicondyle (see Fig. 3-1).
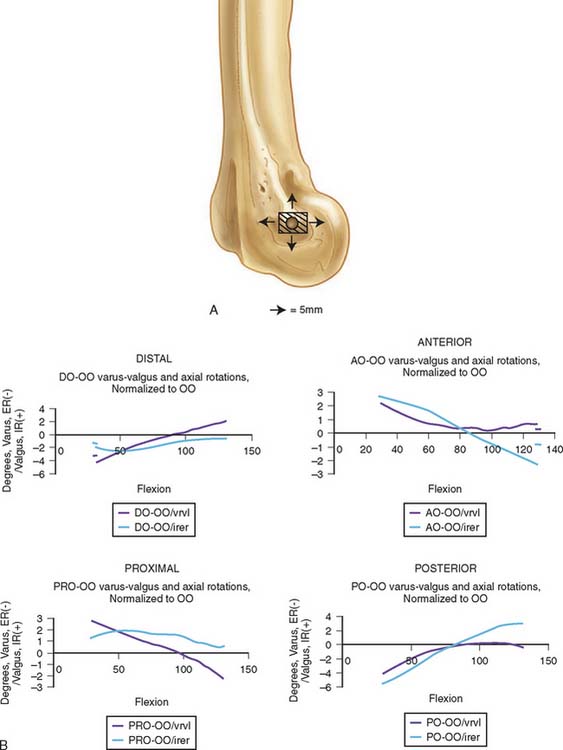
Similarly, the effect of altering the center of rotation on the kinematics of the forearm has been recently studied. Alterations of as much as 5 mm proximally, distally, anteriorly, or posteriorly have been shown to have only a slight effect on elbow kinematics (Fig. 3-2). This observation has great clinical relevance regarding the design and insertion of prosthetic replacement and articulating external fixation devices.
FOREARM ROTATION
The radiohumeral joint, which forms the lateral half of the elbow joint, has a common transverse axis with the elbow joint, which coincides with the ulnohumeral axis during flexion-extension motion. In addition, the radius rotates around the ulna, allowing for forearm rotation or supination-pronation. In general, the longitudinal axis of the forearm is considered to pass through the convex head of the radius in the proximal radioulnar joint and through the convex articular surface of the ulna at the distal radioulnar joint.34,97 The axis therefore is oblique to the longitudinal axes of both the radius and the ulna (Fig. 3-3), and rotation is independent of elbow position.45
Mori has characterized the axis of forearm rotation as passing through the attachment of the interosseous membrane at the ulna in the distal fourth of the forearm (see Fig. 3-32).62 This may have particular applications with regard to the sensitivity of forearm rotation to angular deformity in this particular portion of the bone. Clinically and experimentally, less than 10% angulation of either the radius or the ulna causes no functionally significant loss of forearm rotation.91
In the past, ulnar rotation was described as being coupled with forearm rotation.106 This observation could not be reproduced in a subsequent study by Youm and associates.108 By using a metal rod introduced transversely into the ulna, extension, lateral rotation, and then flexion of the ulna was described with rotation from pronation to supination. The axial rotational movements of the ulna were also observed by others.14,22,30,43,69,88,108
Ray and associates88 also suggested that varus-valgus movement of the ulna occurs if the forearm rotates on an axis extending from the head of the radius to the index finger. Experiments from our laboratory76 have demonstrated external axial rotation of the ulna with forearm supination. Internal rotation or closure of the lateral ulnohumeral joint occurs with pronation.
Finally, the radius has been shown to migrate 1 to 2 mm proximally with pronation.67 This observation had not been reported previously but has been confirmed by observations at the wrist.82
CARRYING ANGLE
The carrying angle is defined as that formed by the long axis of the humerus and the long axis of the ulna. It averages 10 to 15 degrees in men and is about 5 degrees greater in women.1,18,53,97
However, uncertainty has arisen over the use of the term carrying angle in the dynamic setting. Dempster27 described an oscillatory pattern during elbow flexion, whereas Morrey and Chao69 reported a linear change, with the valgus angle being the greatest at full extension and diminishing during flexion. The confusion arises because three descriptions based on different reference systems have been adopted for the measurement of carrying angle changes.
Definition 1
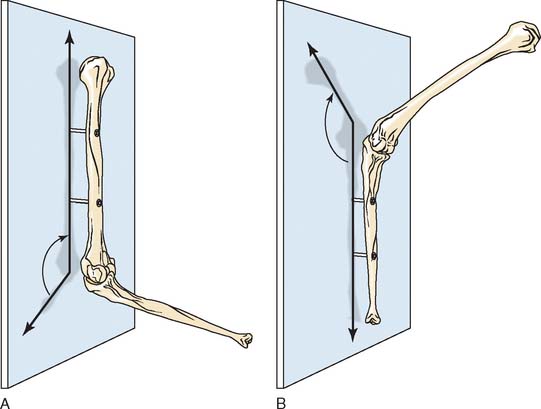
The carrying angle is the acute angle formed by the long axis of the humerus as the long axis of the ulna projects on the plane containing the humerus (Fig. 3-4A).
Definition 2
The carrying angle is described as the acute angle formed by the long axis of the ulna and the projection of the long axis of the humerus onto the plane of the ulna (see Fig. 3-4B).
Definition 3
From an anatomic point of view, it is not difficult to conclude that the existence of the carrying angle is due to the existence of obliquities, or cubital angles, between the proximal humeral shaft, the trochlea, and the distal ulnar shaft. By assuming that the ulnohumeral joint is a pure hinge joint and that the axis of rotation coincides with the axis of the trochlea, the change in the carrying angle during flexion can be defined as a function of anatomic variations of the obliquity of the articulations according to simple trigonometric calculations.8 If the first or second definition is accepted, the carrying angle changes minimally during flexion. The specific varus/valgus relationship of the forearm to the humerus during flexion therefore depends on the relative angular relationship of the humeral and ulnar articulations (Fig. 3-5).
RESTRICTION OF MOTION
In normal circumstances, elbow flexion ranges from 0 degrees or slightly hyperextended to about 150 degrees in flexion. Forearm rotation averages from about 75 degrees (pronation) to 85 degrees (supination) (see Chapter 2). The cartilage of the trochlea forms an arc of about 320 degrees, whereas the sigmoid notch creates an arc of about 180 degrees. Generally, the arc of the radial head depression is about 40 degrees,97 which articulates with the capitellum, presenting an angle of 180 degrees.
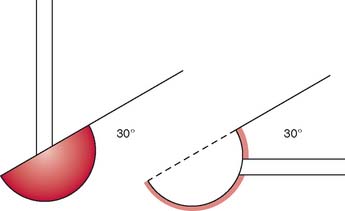
The significance of the 30-degree anterior angulation of the trochlea with the 30-degree posterior orientation of the greater sigmoid notch to flexion and extension and stability of the elbow joint is discussed in detail in Chapter 1 (Fig. 3-6). Impact of the olecranon process on the olecranon fossa and the tension of the anterior ligament and the flexor muscles as well as tautness of the anterior bundle of the medial collateral ligament have been described as serving as a check to extension.40,52 The anterior muscle bulk of the arm and forearm, along with contraction of the triceps, is also reported to prevent active flexion beyond 145 degrees.52 However, the factors limiting passive flexion include the impact of the head of the radius against the radial fossa, the impact of the coronoid process against the coronoid fossa, and tension from the capsule and triceps.
For pronation and supination, Braune and Flugel20 found that passive resistance of the stretched antagonistmuscle restricts the excursion range more than that of the ligamentous structures. Spinner and Kaplan,96 however, have shown that the quadrate ligament does provide some static constraint to forearm rotation. Impingement of tissue restrains pronation, especially by the flexor pollicis longus, which is forced against the deep finger flexors. The entire range of active excursion in an intact arm is about 150 degrees, whereas when the muscles are removed from a cadaver specimen, the range increases to 185 to 190 degrees. With cutting the ligaments, the range increased up to 205 to 210 degrees.
CAPACITY AND CONTACT AREA OF THE ELBOW JOINT
The capacity of the elbow joint recently has been shown to average about 25 mL. The maximum capacity is observed to occur with the elbow at about 80 degrees of flexion.78 This explains the clinical observation that stiff elbows tend to have fixed deformities at about 80 to 90 degrees of flexion.63
Accurate measurement of the contact points of the elbow is extremely difficult, and several techniques have been applied to this highly congruous joint.99 Silicone casting, Fuji Prescale film, and reversible cartilage staining are most commonly used. Each has advantages and disadvantages. The contact area of the articular surface during elbow joint motion has been investigated by Goodfellow and Bullough, using a staining technique.39 They found that the central depression of the radial head articulates with the dome of the capitellum and that the medial triangular facet was always in contact with the ulna. The upper rim of the radial head made no contact at all. At the humeroulnar joint, the articular surfaces were always in contact during some phases of movement. Others have verified these observations.107 The contact areas on the ulna occurred anteriorly and posteriorly and tended to move together and slightly inward from each side from 0 to 90 degrees of flexion and with increasing load.31,74 Using a wax casting technique, in full extension, the contact has been observed to be on the lower medial aspect of the ulna, whereas in other postures, the pressure areas described a strip extending from posterolateral to anteromedial.37 The radiocapitellar joint also revealed contact during flexion without externally applied load. Investigations in our laboratory show that the contact areas of the elbow occur at four facets: two at the coronoid and two at the olecranon (Fig. 3-7). Only a slight increase in total surface area occurred with elbow flexion and with a sevenfold increase in load.99 With a 10-N load, about 9% contact of the articular surfaces occurs, and with 1280 N, the area increased to about 73%.31
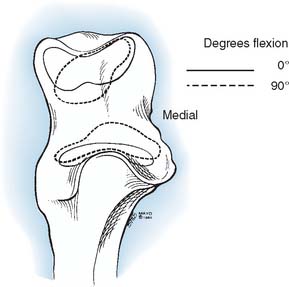
FIGURE 3-7 Contact in the sigmoid fossa moves toward the center of the fossa during elbow flexion.
(Redrawn from Walker, P. S.: Human Joints and Their Artificial Replacements. Springfield, IL, Charles C. Thomas, 1977.)
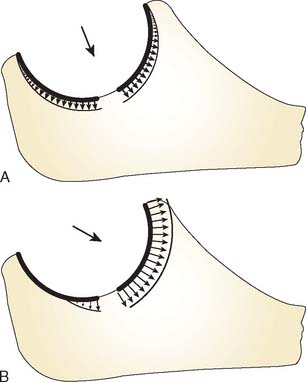
When varus and valgus loads are applied to the forearm, the contact changes medially and laterally. This implies a pivot point about which the radioulnar articulation rotates on the humerus in the anteroposterior (AP) plane in extension with varus and valgus stress. In vivo experiments have demonstrated the varus-valgus pivot point of the elbow to reside in the midpoint of the lateral face of the trochlea (Fig. 3-8).
ELBOW STABILITY
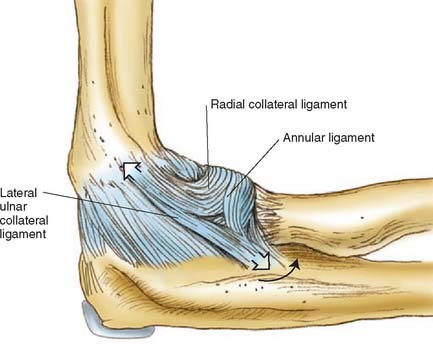
The static soft tissue stabilizers include the collateral ligament complexes and the anterior capsule. Studies from our laboratory regarding the anatomy of the lateral collateral ligament68,77 and others36,79,95 have been discussed previously (see Chapter 2). The lateral collateral ligament and the anterior bundle of the medial collateral ligament originate from points through which the axis of rotation passes. Furthermore, the medial collateral ligament has two discrete components.66,93 The anterior bundle has been shown to be taut in extension; the converse is true for the posterior fibers of the anterior bundle. Because elbow joint motion occurs about a nearly perfect hinge axis through the center of the capitellum and trochlea, the posterior bundle of the medial collateral ligament complex will be taut at different positions of elbow flexion (Fig. 3-9). The lateral collateral ligament and the anterior bundle lying on the axis of rotation will assume a rather uniform tension, regardless of elbow position. Furthermore, the lateral ulnar collateral ligament has inserts on the ulna and, as such, helps to stabilize the lateral ulnohumeral joint (Fig. 3-10).23,66,77,81 In experiments performed in our laboratory, O’Driscoll and associates have demonstrated that the lateral ulnar collateral ligament is essential to control the pivot shift maneuver (see Chapter 4). Further evidence of the contribution of the lateral ligament complex to elbow stability is offered by S∅︀jbjerg and associates.94 These investigators also attributed a major role in varus and valgus stability to the annular ligament. Although our work suggests that the major component in the varus and rotatory stability is the structure termed the lateral ulnar collateral ligament, the parallel findings of these investigators suggest that the lateral complex is, in fact, a major valgus stabilizer of the elbow joint and functions with or without the radial head.80
ARTICULAR AND LIGAMENTOUS INTERACTION
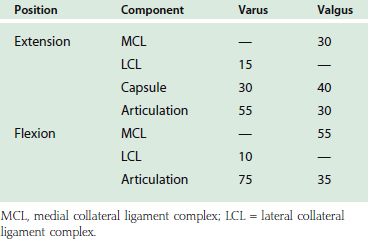
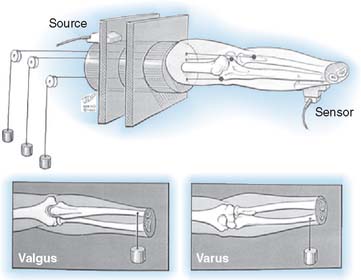
The influence of the ligamentous and articular components on joint stability are usually studied with the use of the materials testing machine by imparting a given and controlled displacement to the elbow.47,65,87 The relative contribution of each stabilizing structure can be demonstrated by sequentially eliminating each element and observing the load recorded by the load cell for the constant displacement imparted, usually 2 to 5 degrees95 (Fig. 3-11).
A simplified summary of the observations from such an experiment is shown in Table 3-1. In extension, the anterior capsule provides about 70% of the soft tissue restraint to distraction, whereas the medial collateral ligament assumes this function at 90 degrees of flexion. Varus stress is checked in extension equally by the joint articulation (55%) and the soft tissue, lateral collateral ligament, and capsule. In flexion, the articulation provides 75% of the varus stability. Valgus stress in extension is equally divided between the medial collateral ligament, the capsule, and the joint surface. With flexion, the capsular contribution is assumed by the medial collateral ligament, which is the primary stabilizer (54%) to valgus stress at this position. Furthermore, for all practical purposes, the anterior portion of the medial collateral ligament provides virtually all of the structure’s functional contribution.
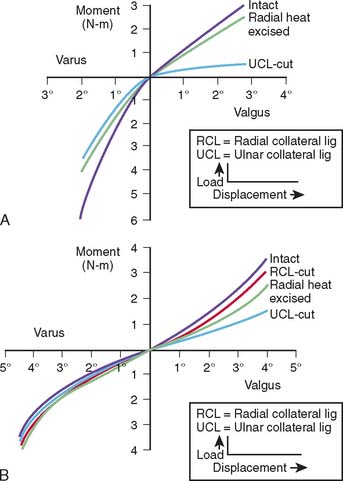
Limitations of this experimental model have resulted in an overestimation of the role of the radial head inresisting valgus load.47,65,90 This has prompted the development of an experimental technique that allows simultaneous and accurate measurement of three-dimensional angular and translational changes under given loading conditions (Fig. 3-12). Using the electromagnetic tracking device, an accurate technique for measuring the function of the articular and capsuloligamentous structures was developed.70 More accurate and relevant data were generated.70 Valgus stability is resisted primarily by the medial collateral ligament. With an intact medial collateral ligament, the radial head does not offer any significant additional valgus constraint. With a released or compromised medial collateral ligament, the radial head does resist valgus stress. This important experiment documents that the radial head is a secondary stabilizer for resisting valgus stress, whereas the medial collateral ligament is the primary stabilizer against valgus force (Fig. 3-13). In a laboratory investigation, the hyperextension trauma produces lesions of the anterior capsule, the avulsion of proximal insertions of both medial and lateral collateral ligaments.103 The degree of extension increased by 17 degrees and induced significant joint laxity in forced valgus internal-external rotation, but not varus.103
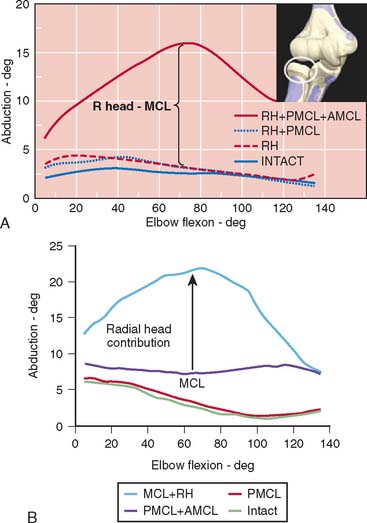
It has been recently observed that the valgus and varus laxity of the elbow is dependent on forearm rotation.86 Increased valgus/varus laxity with forearm pronation, particularly in medial collateral ligament deficient elbows, implies a possible additional factor in throwing kinematics that might put professional baseball pitchers at risk of medial collateral ligament injury due to chronic valgus overload. The forearm rotation should be considered during the clinical examination of elbow instability. The stabilizing effects of monoblock and bipolar designs of radial head replacements in cadaver elbows with a deficient medial collateral ligament were studied.85 The constraint mechanism inherent in the implant design significantly affected the mean valgus laxity. The implants all performed similarly except in neutral forearm rotation, in which the elbow laxity associated with the Judet implant was significantly greater than that associated with the other two implants.
Comminuted radial head fractures associated with an injury of the medial collateral ligament can be treated with a radial head implant. However, lengthening and shortening of the radial neck by 2.5 mm significantly alters the kinematics and contact pressure through the radiocapitellar joint in the medial collateral ligament-deficient elbow104 (Fig. 3-14). Radial neck lengthening caused a significant decrease in varus-valgus laxity and ulnar rotation, with the ulna tracking in varus and external rotation. Shortening caused a significant increase in varus-valgus laxity and ulnar rotation, with the ulna tracking in valgus and internal rotation. Therefore, a radial head replacement should be performed with the same level of concern for accuracy and reproducibility of component position and orientation as is appropriate with any other prosthesis.
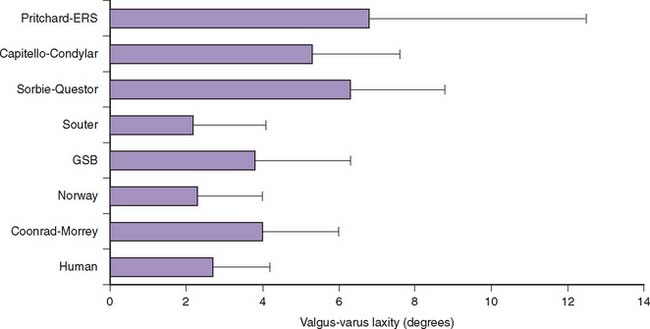
Total elbow arthroplasty has been a valuable procedure for treating patients with rheumatoid arthritis, post-traumatic arthritis, osteoarthritis, and failed reconstructive procedures of the elbow. The development of elbow prostheses diverged into two general types: linked and unlinked. The main concern with such development of unlinked elbow replacements is instability, which is attributable to numerous factors including prosthesis design, ligament integrity, and position of the prosthesis. A series of laboratory studies have been performed to examine the intrinsic constraint of various total elbow arthroplasty designs, as well as the joint laxity after implantation in cadaveric specimens6 (Fig. 3-15).
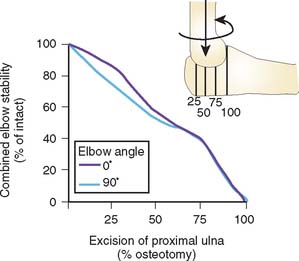
The contribution of the articular geometry to elbow stability was further evaluated by serial removal of portions of the proximal ulna, as shown in Figure 3-16.13 Valgus stress, both in extension and at 90 degrees of flexion, was primarily (75% to 85%) resisted by the proximal half of the sigmoid notch, whereas varus stress was resisted primarily by the distal half, or the coronoid portion of the articulation, both in extension (67%) and in flexion (60%).
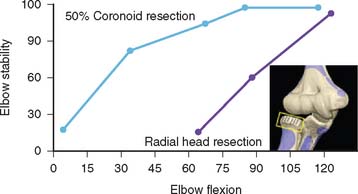
As demonstrated in subsequent chapters, the central role of the coronoid to provide elbow stability is emerging. As serial portions of the coronoid are removed, the elbow becomes progressively more unstable. If the radial head has been resected, as little as 25% resection causes elbow subluxation at about 70 degrees of flexion. Our preliminary studies indicate at least 50% of the coronoid is necessary for elbow stability if the radial head is removed (Fig. 3-17).
FORCE ACROSS ELBOW JOINT
TWO-DIMENSIONAL ELBOW FORCE ANALYSIS
In sagittal plane motion, the elbow joint is assumed to be a hinge joint. Forces and moments created at the joint, due to the loads applied at the hand, are balanced by the muscles, tendons, ligaments, and contact forces on the articular surfaces. The amount of tension in the muscles and the magnitude and direction of the joint forces are determined by the external loading conditions as well as the responses of muscles-that is, force distribution among these muscles.
in which | Fi | = magnitude of the tension in ith muscle;
fxi, fyi = components in x and y direction for the unit vector along the line of action of muscle;
Rx, Ry = x and y components of the joint contact force;
P, Px, Py = magnitude of the applied forces on the forearm and its associated components; and
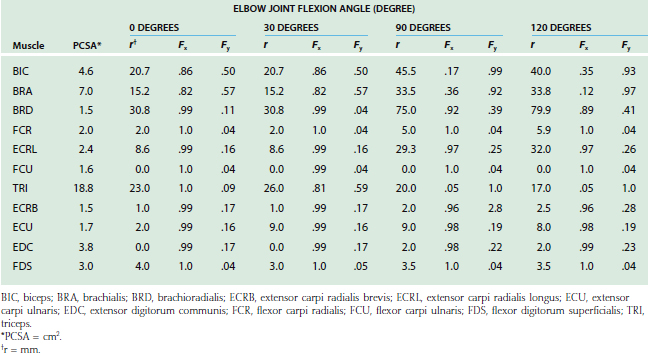
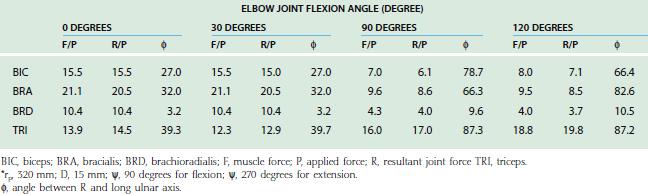
The lines of action of muscles crossing the joint have been reported.2,8,84 In the sagittal plane, based on the magnitude of moment arms, the major elbow muscles consist of biceps, brachialis, brachioradialis, extensor carpi radialis longus, triceps, and anconeus (Table 3-2). The other forearm muscles for the hand and wrist provide various but limited contributions to elbow flexion-extension. Unfortunately, the contributions of these forearm muscles are not consistently reported in the literature.
TABLE 3-2 Physiologic Cross-Sectional Area (PCSA), Unit Force Vector (Fx, Fy), and Moment Arm (r) of Elbow Muscles in Sagittal Plane
Single-Muscle Analysis
Thus, an intimate relationship between the joint force and muscle forces in balancing the externally applied force on the forearm (Table 3-3) exists. The magnitude of muscle force required for balancing the external force reflects the changes of the muscle’s moment arm, or mechanical advantage, with changes of the joint configuration.
Effect of Muscle Moment Arm
The effect of a changing muscle moment arm on the resultant joint force is demonstrated graphically in Figure 3-18. If the loading configuration does not change, both the muscle force and the joint reaction force decrease as the muscle moment arm increases. The orientation of the resultant force also changes from the middle portion of the trochlear notch toward the border of the articular cartilage.
Clinically, the concept of increasing the moment arm of the biceps muscle by moving the insertion distally has been adopted for increasing weak flexion force of the elbow in patients with brachial plexus injury.72
Effect of Orientation on Muscle Line of Action
Under the same loading condition, the effect of changing the orientation of the muscle line of action under a constant moment arm is demonstrated (Fig. 3-19). The applied force is again assumed to be perpendicular to the forearm. Both magnitudes of muscle and joint reaction forces change slightly with the change of the muscle’s line of action. However, the orientation of the resultant joint force is sensitive to changes in the muscle force line. The orientation of the resultant joint force, therefore, moves from the central portion of the trochlea toward the rim as the direction of muscle pull relative to the forearm changes from vertical to parallel. This is especially true for the resultant joint force in the trochlear notch brought about by the contraction of the upper arm muscles, whose direction relative to the forearm axis changes with the elbow joint flexion angle. On the other hand, the directions of forearm muscles with respect to the resultant joint forces are thus reasonably constant. When considering the direction of resultant joint forces applied on the trochlea, the effects of upper arm and forearm muscles are just reversed. These changes have been confirmed and directly measured with a force transducer at the proximal radius and different orientation of the line of action of the flexors and extensors.67
Effect of the Direction of the Externally Applied Force
When the force applied at the wrist changes direction from vertical to horizontal, the effective moment arm of this applied force changes. The resultant segmental moment about the elbow joint center due to this force changes as well (Fig. 3-20). Furthermore, when the resultant segmental moments change from flexion to extension, the required muscles also change from flexors to extensors.
Effect of Change in Axis of Rotation
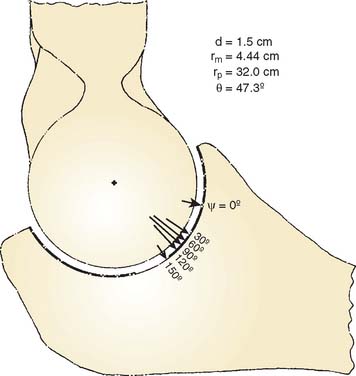
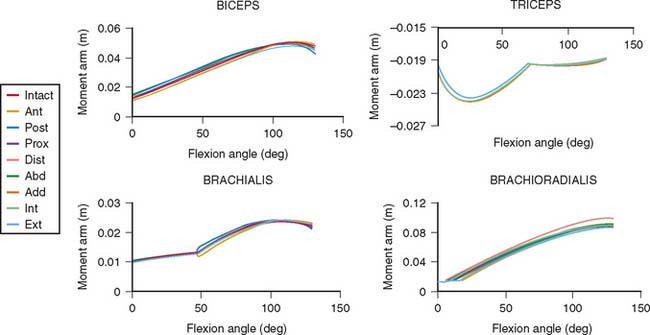
The sensitivity of the muscle moment arm to the axis of rotation is a critically important consideration in the clinical setting. Altering the axis by 1 cm anterior, posterior, proximal, and distally has a surprisingly small effect on the muscle moments at the elbow. Such axis changes result in less than 10% change in muscle moment arm values (Fig. 3-21).
In summary, the parametric analysis demonstrates that the magnitude and orientation of the resultant joint forces in the trochlear notch depend very much on whether the upper arm or forearm muscles are used, as well as the location and orientation of the external load applied on the forearm and the joint flexion angle that alters the moment arm and orientation of the muscle line of action. However, alterations of the flexion axis have little impact on muscle moment arm.
Multiple Muscle Analysis
Several methods have been employed to resolve the indeterminate problem. Electromyographic (EMG) data and the physiologic cross-sectional area may be used to provide an additional equation.35,49 The most commonly adopted techniques are analytic reduction and optimization methods.
With the use of the optimization method, a unique solution to an indeterminate problem is obtained by minimizing a preselected objective function or cost function.11 Although the solution to the problem is still nonunique, each solution generally is associated with some physiologic phenomenon or condition on which the objective function is constructed and selected. This technique has been described in more detail elsewhere.9 Recently, the results based on various object functions have been compared with EMG data regarding the muscles. The dependence of muscle coordination is related more to the degree of freedom considered, and less to the cost function selected.21
The most commonly used objective functions for resolving the indeterminate force analysis problem include linear and nonlinear weighted combinations of the unknown variables. An analytic model for the determination of muscle force across the elbow joint during isometric loading has been developed.10 In addition to the equilibrium equations obtained from free-body analysis, constraints for muscle tensions based on the physiologic considerations of muscle length-tension and velocity-tension relationships were included:
Major Elbow Muscles
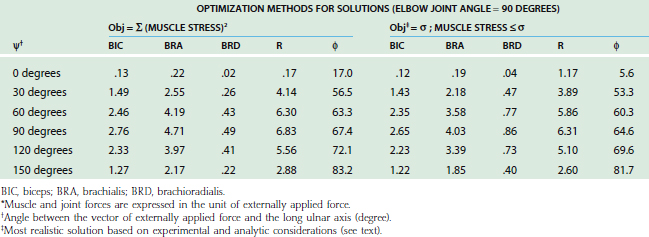
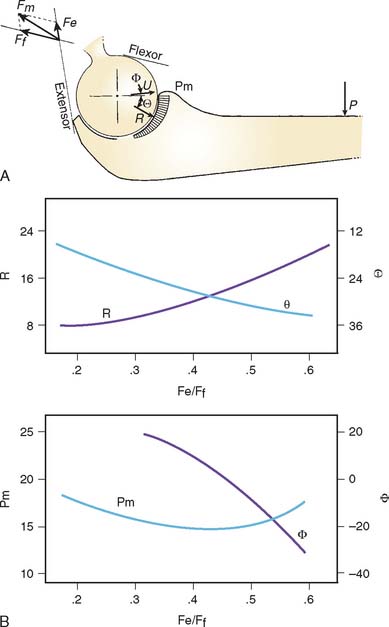
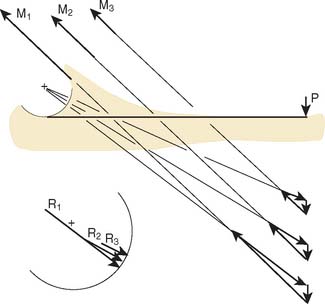
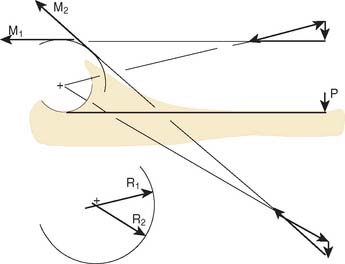
For the loading case of force applied nonperpendicularly at the wrist, the solutions of two types of optimization procedures are shown in Table 3-4. The magnitude (R) and direction (φ) of the resultant joint forces correspond to various loads. The resultant joint force shows more variation along the articular surface with changes of joint flexion (Fig. 3-22). This is because the line of action of the upper arm muscle undergoes a tremendous change in direction with respect to the ulnar axis during flexion, as discussed earlier.
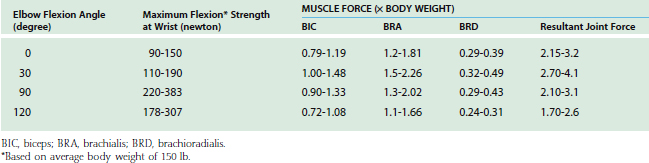
The maximum elbow flexion strength occurs at 90 degrees59,71 (see Chapter 5). From the measured lifting strength data, the maximal muscle force per unit of cross-sectional area can be calculated to be in the range of 10 to 14 kg/cm2. About one third to one half of the maximum lifting force can be generated with the elbow in the extended or 30-degree flexed position. At these positions, a force almost three times the body weight can be encountered in the elbow joint during strenuous lifting at about 30 degrees of flexion (Table 3-5).
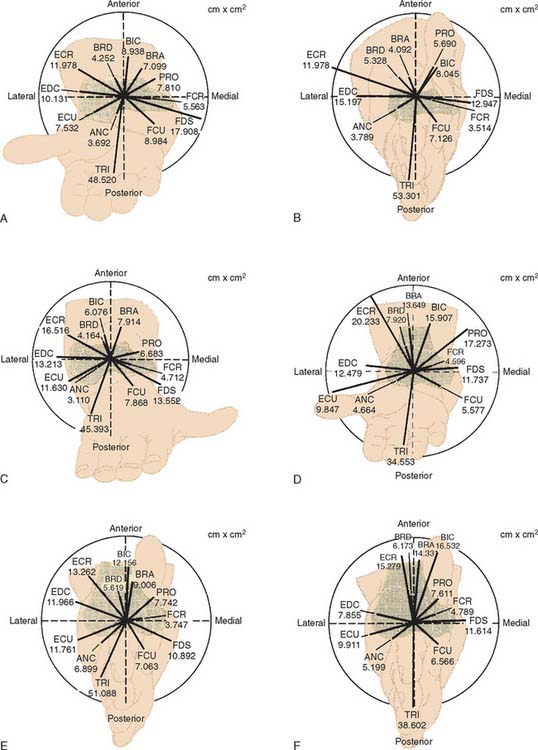
During strenuous actions, the maximum tension that could possibly be provided by each individual muscle is usually considered to be proportional to the physiologic cross-sectional area. This has been carefully measured for muscles crossing the elbow.8 The potential moment contribution of each muscle at the elbow joint can thus be estimated by multiplying its moment arm by its physiologic cross-sectional area. The moment contributions for all of the muscles crossing the elbow joint have been calculated (Fig. 3-23). Of note, the potential moment in varus appears to be balanced by the valgus moment under all of the functional configurations. When flexed, the flexion potential moment seems to be balanced by the extension moment. However, the extension moment exceeds the flexion moment when the elbow is extended.
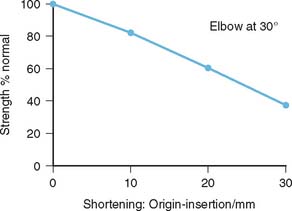
In constructing these moment potential diagrams, it is assumed that all muscles simultaneously and maximally contract to their optimal lengths. To apply these data for more general conditions, consideration should be given and adjustment made for length-tension and force-velocity relationships. In addition, when activities involve submaximal contraction, a proper scaling system based on experimental measurements, such as EMG,3,28,33,35,61 is required. In more refined models, themuscle physiology, including the length-velocity-tension relationship, should be considered.10,38 In an analytic modeling, the effect of distal humeral shortening on the triceps force production and thus the elbow extension strength has been demonstrated48 (Fig. 3-24).
Flexors
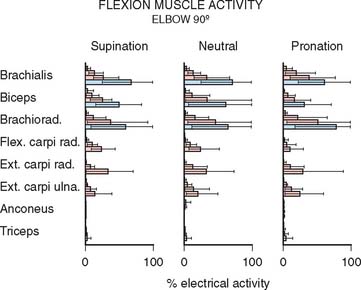
Surface electrodes along the belly of the biceps were first used100 to record electrical activity during dynamic flexion and extension, with and without load. This early study showed a decrease in biceps activity in pronation compared with supination, and that the biceps acted in extension to “brake” the forearm.
Subsequent studies have presented inconsistent data, but in almost all investigations, the biceps demonstrates no16 or decreased activity when flexion occurs in pronation.35,58,98 As expected, little influence is reflected in the brachialis muscle with forearm rotation.35,98 The brachioradialis demonstrates electrical activity with flexion, especially with the forearm rotated to the neutral position17,29 or in pronation.35,54,98
These data are summarized for the 90-degree flexion position, because this is the position of maximum strength15,54 and of greatest electrical activity of the elbow flexors35 (Fig. 3-25).
Extensors
EMG investigations of the elbow extensor muscles were first completed by Travill in 1962.102 The medial head of the triceps and anconeus muscles were found to be active during extension; the lateral and long head of the triceps acted as auxiliaries. The anconeus also was active during resisted pronation and supination. In fact, the anconeus has been demonstrated to be active during flexion and abduction-adduction resisted motions.35,83 Thus, the anconeus may be considered a stabilizer of the elbow joint, being active with almost all motions.
In 1972, Currier studied the same muscles at 60, 90, and 120 degrees of elbow flexion. The greatest electrical activity occurred at the 90-degree and 120-degree positions, consistent with the position of greatest strength.24 Others55 found there was no difference between position and muscular electrical activity.
Forearm Muscles
Some of the forearm muscles originating at the medial and lateral aspects of the distal humerus had been considered in stabilizing the elbow joint. Flexor carpi ulnaris and flexor digitorum superficialis muscles, because of their positions and proximities over the medial collateral ligaments, were potentially the muscles best suited to provide medial elbow support.25 However, in the EMG investigations, no significant activities of these muscles were noted when valgus and varus stresses were applied.35 In a recent study of baseball pitchers with medial collateral ligament insufficiency, the data did not demonstrate increased electrical activity of these muscles.42 These findings suggested that the muscles on the medial side of the elbow do not supplement the role of medial collateral ligaments.42
Distributive Forces on the Articular Surfaces
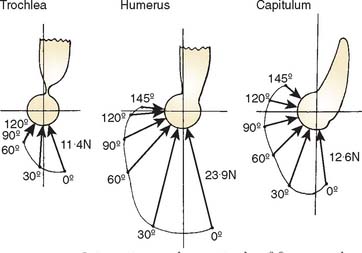
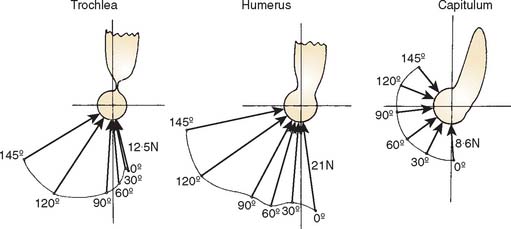
Joint compressive forces on various facets of the elbow joint have been reported in the literature.3,73 During the activities of resisting flexion and extension moments at various elbow joint positions, the components of force along the mediolateral direction, causing varus-valgus stress, are small compared with those acting in the sagittal plane directed anteriorly or posteriorly. The resultant joint forces on the trochlea and capitellum have been described in the sagittal plane for flexion (Fig. 3-26) and extension (Fig. 3-27) isometric loads. With the elbow extended and axially loaded, the distribution of stress across the joint has been calculated to be approximately 40% across the ulnohumeral joint and 60% across the radiohumeral articulation (Fig. 3-28).41,107 More recently, based on a cadaveric study,46,57 it has been noted that with the elbow in valgus realignment, only 12% of the axial load is transmitted through the proximal end of the ulna, but with the elbow in varus alignment, 93% of the axial force is transmitted to proximal ulna. Because of the poor mechanical advantage with the elbow in extension, the largest isometric flexion forces occur in this position (see Fig. 3-27).3,49 Isometric extension produces a posterosuperior compressive stress across the distal humerus. These analytic calculations have undergone experimental confirmation. Using a force transducer at the proximal radius, the greatest force was transmitted across the radiohumeral joint in full extension, a position in which the muscles have poor mechanical advantage.68
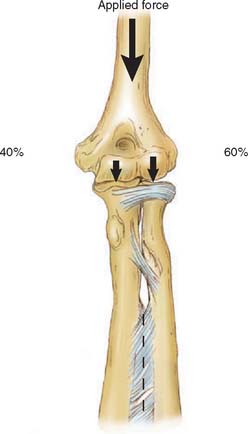
FIGURE 3-28 Static compression of the extended elbow places more force on the radiohumeral than the ulnohumeral joint.
When the elbow is flexed, inward rotation of the forearm against resistance imposes large torque to the joint. The magnitudes have been calculated as approaching twice body weight tension in the medial collateral ligament and three times body weight at the radiohumeral joint.4 Experimental data from the force transducer study suggest that the analytic estimate is probably too high. The greatest force on the radial head from the transducer data occurs with the forearm in pronation (Fig. 3-29). Even in this position, however, the maximum possible force transmission at the radiohumeral joint was measured as approximately 0.9 times the body weight.67
Considerably less knowledge is available regarding the distributed forces at the elbow during use. Nicol and associates73 have demonstrated significant forces with daily activities that not only occur at the radiohumeral and ulnohumeral joints but also are generated in the collateral ligaments. An example of such a force pattern is shown in Figure 3-30. The actual distributive forces occurring at this joint with daily activity constitute an important avenue of further investigation.
Contact Stress on the Joint Articular Surface
With the magnitude, direction, and point of application of the resultant joint force available, the stress on the articular cartilage can now be determined.84 Because the joint is not a simple geometric shape, a method based on the concept of a rigid body spring model was adopted for solution.11 In the results, it was found that if the line of action of the resultant force is at the middle of the articular surface, the stress is almost equally distributed throughout the entire articular surface (Fig. 3-31A). On the other hand, as the resultant force is directed toward the margin of the articulation anteriorly or posteriorly, the weight-bearing surface becomes smaller, the maximum compressive stress becomes elevated, and the stress distribution over the joint surface becomes more uneven (see Fig. 3-31B). It should be further noted that the position of maximum stress does not necessarily correspond with the point of intersection of the resultant joint force through the articular surface. Based on this model, the role of antagonistic muscles on the magnitudesand directions of the resultant joint forces, and thus the articulating pressure distribution and joint stability, were extensively examined (Fig. 3-32).7
Finite Element Analysis of Composite Fixation for Total Elbow Prosthesis
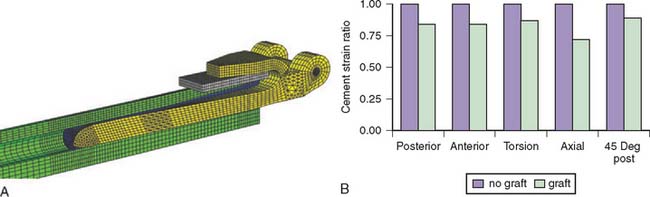
In total elbow arthroplasty implant loosening remains a challenging complication. Achieving rigid fixation using a combination of bone ingrowth and cementing should improve the implant longevity. The semiconstrained Coonrad-Morrey elbow prosthesis employs this philosophy. It has shown generally satisfactory clinical results for a variety of cases including inflammatory arthritis and distal humerus fracture.44,89 The humeral component of the implant incorporates an anterior flange that has the theoretical benefit of transferring stress from the elbow to the humeral bone and relieving stress concentrations at the vulnerable distal humerus cement interface. Finite element analysis was used to evaluate the biomechanical effects of bone graft between the anterior flange and the bone cortex.
Models were created that consisted of the humeral component of the Coonrad/Morrey elbow prosthesis, bone cement surrounding the implant stem, simulated distal humerus, and bone graft between the distal humerus and anterior flange of the prosthesis. Material properties were prescribed as linear elastic with Poisson ratio of 0.3 and elastic modulus values of implant (E = 114 GPa), humerus (E = 17 GPa), bone cement (E = 3 GPa), and bone graft (E = 0.65 GPa). Perfect bonding between the bone-cement and cement-implant interfaces was assumed.
Finite element analysis shows that stress and strain in the distal humerus and distal cement mantle can be reduced 10% to 30% when using a bone graft compared with no bone graft between the anterior flange and the bone cortex (Fig. 3-33). Furthermore, when the distal humerus had a simulated defect of 2 cm, extension of the bone graft more proximally than the anterior flange reduced the stress and strain up to 17% compared with bone graft just under the flange. Finally, when selecting the stem size, there was up to a 15% reduction in distal cement stress and strain when choosing a 6-inch stem over a 4-inch stem or when choosing an 8-inch stem over a 6-inch stem. These findings confirmed the clinical experience that rigid fixation and stress relief due to the anterior flange of the implant reduce the complication rate for primary and revision total elbow arthroplasty.
1 Amis A.A., Dowson D., Unsworth A., Miller J.H., Wright V. An examination of the elbow articulation with particular reference to variation of the carrying angle. Eng. Med. 1977;6:76.
2 Amis A.A., Dowson D., Wright V. Muscle strengths and musculoskeletal geometry of the upper limb. Eng. Med. 1979;8:41.
3 Amis A.A., Dowson D., Wright V. Elbow joint force predictions for some strenuous isometric actions. J. Biomech. 1980;13:765.
4 Amis A.A., Miller J.H., Dowson D., Wright V. Biomechanical aspects of the elbow: Joint forces related to prosthesis design. IEEE Eng. Med. Biol. Mag. 1981;10:65.
5 An K.N. Biomechanics: Basic relevant concepts. Section 1 basic science. In: Morrey B.F., editor. Joint Replacement Arthroplasty. New York: Churchill Livingstone; 1991:7.
6 An K.N. Kinematics and constraint of total elbow arthroplasty. J. Shoulder Elbow Surg. 2005;14:168S.
7 An K.N., Himeno S., Tsumura H., Kawai T., Chao E.Y. Pressure distribution on articular surfaces: Application to joint stability evaluation. J. Biomech. 1990;23:1013.
8 An K.N., Hui F.C., Morrey B.F., Linscheid R.L., Chao E.Y. Muscles across the elbow joint: A biomechanical analysis. J. Biomech. 1981;14:659.
9 An K.N., Jacobsen M.C., Berglund L.J., Chao E.Y. Application of a magnetic tracking device to kinesiologic studies. J. Biomech. 1988;21:613.
10 An K.N., Kaufman K.R., Chao E.Y. Physiological considerations of muscle force through the elbow joint. J. Biomech. 1989;22:1249.
11 An K.N., Kwak B.M., Chao E.Y., Morrey B.F. Determination of muscle and joint forces: A new technique to solve the indeterminate problem. J. Biomech. Eng. 1984;106:364.
12 An K.N., Morrey B.F., Chao E.Y. Carrying angle of the human elbow joint. J. Orthop. Res. 1984;1:369.
13 An K.N., Morrey B.F., Chao E.Y. The effect of partial removal of proximal ulna on elbow constraint. Clin. Orthop. 1986;209:270.
14 Anderson R. Rotation of the forearm. Lancet. 1901;2:1333.
15 Askew L.J., An K.N., Morrey B.F., Chao E.Y. Isometric elbow strength in normal individuals. Clin. Orthop. 1987;222:261.
16 Basmajian J.V., Latif S. Integrated actions and functions of the chief flexors of the elbow. J. Bone Joint Surg. [Am.]. 1957;39:1106.
17 Basmajian J.V., Travill A.A. Electromyography of the pronator muscles in the forearm. Anat. Rec. 1961;139:45.
18 Beals R.K. The normal carrying angle of the elbow. A radiographic study of 422 patients. Clin. Orthop. 1976;119:194.
19 Blewitt N., Pooley J. An anatomic study of the axis of elbow movement in the coronal plane: Relevance to component alignment in elbow arthroplasty. J. Shoulder Elbow Surg. 1994;3:151.
20 Braune W., Flugel A. Uber pronation and supination des menschlichen vorderarms und der hand. Arch. Anat. Physiol. 1882:169-196.
21 Buchanan T.S., Shreeve D.A. An evaluation of optimization techniques for the prediction of muscle activation patterns during isometric tasks. J. Biomech. Eng. 1996;118:565.
22 Capener N. The hand in surgery. J. Bone Joint Surg. [Br.]. 1956;38:128.
23 Cohen M.S., Hastings H.Jr. Rotatory instability of the elbow. The anatomy and role of the lateral stabilizers. J. Bone Joint Surg. [Am.]. 1997;79:225.
24 Currier D.P. Maximal isometric tension of the elbow extensors at varied positions. Part II. assessment of extensor components by quantitative electromyography. Phys. Ther. 1972;52:1265.
25 Davidson P.A., Pink M., Perry J., Jobe F.W. Functional anatomy of the flexor pronator muscle group in relation to the medial collateral ligament of the elbow. Am. J. Sports Med. 1995;23:245.
26 Deland J.T., Garg A., Walker P.S. Biomechanical basis for elbow hinge-distractor design. Clin. Orthop. 1987;215:303.
27 Dempster, W. T.: Space Requirements of the Seated Operator: Geometrical, Kinematic and Mechanical Aspects of the Body with Special Reference to the Limb. Wright Air Development Center, Project No. 7214, Wright-Patterson AFB, Ohio, 1955.
28 Dempster W.T., Finerty J.C. Relative activity of wrist-moving muscles in static support of the wrist joint: An electromyographic study. Am. J. Physiol.. 1947;150:596.
29 De Sousa O.M., De Moraes J.L., Viera F.L. Electromyographic study of the brachioradialis muscle. Anat. Rec.. 1961;139:125.
30 Dwight T. The movements of the ulna in rotation of the forearm. J. Anat. Physiol.. 1884;19:186.
31 Eckstein F., Lohe F., Muller-Gerbl M., Steinlechner M., Putz R. Stress distribution in the trochlear notch. A model of bicentric load transmission through joints. J. Bone Joint Surg. [Br.]. 1994;76:647.
32 Ewald F.C. Total elbow replacement. Orthop. Clin. North Am.. 1975;6:685.
33 Fidelus K. The significance of the stabilizing function in the process of controlling the muscle groups of upper extremities. In: Cerquiglin S., Venerando A., Wartenweiler J., editors. Medicine and Sports, Vol. 8, Biomechanics III. Basel: Karger; 1973:129.
34 Fischer G., Fick R. Handbuch der anatomie und mechanik du gelenke, unter berucksichtigung der bewegenden muskeln. Jena. 1911;2:299.
35 Funk D.A., An K.N., Morrey B.F., Daube J.R. Electromyographic analysis of muscles across the elbow joint. J. Orthop. Res. 1987;5:529.
36 Fuss F.K. The ulnar collateral ligament of the human elbow joint. Anatomy, function and biomechanics. J. Anat. 1991;175:203.
37 Goel V.K., Singh D., Bijlani V. Contact areas in human elbow joints. J. Biomech. Eng. 1982;104:169.
38 Gonzalez R.V., Hutchins E.L., Barr R.E., Abraham L.D. Development and evaluation of a musculoskeletal model of the elbow joint complex. J. Biomech. Eng. 1996;118:32.
39 Goodfellow J.W., Bullough P.G. The pattern of aging of the articular cartilage of the elbow joint. J. Bone Joint Surg. [Br.]. 1967;49:175.
40 Guttierez L.F. A contribution to the study of the limiting factors of elbow flexion. Acta Anat. 1964;56:146.
41 Halls A.A., Travill A.A. Transmission of pressures across the elbow joint. Anat. Rec. 1964;150:243.
42 Hamilton C.D., Glousman R.E., Jobe F.W., Brault J., Pink M., Perry J. Dynamic stability of the elbow: Electromyographic analyses of the flexor pronator group and the extensor group in pitchers with valgus instability. J. Shoulder Elbow Surg. 1996;5:347.
43 Heiberg J. The movement of the ulna in rotation of the forearm. J. Anat. Physiol. 1884;19:237.
44 Hildebrand K.A., Patterson S.D., Regan W.D., Mac-Dermid J.C., King G.J. Functional outcome of semiconstrained total elbow arthroplasty. J. Bone Joint Surg. [Am.]. 2000;82:1379.
45 Hollister A.M., Gellman H., Waters R.L. The relationship of the interosseous membrane to the axis of rotation of the forearm. Clin. Orthop. 1994;298:272.
46 Hotchkiss R.N., An K.N., Sowa D.T., Basta S., Weiland A.J. An anatomic and mechanical study of the interosseous membrane of the forearm: Pathomechanics of proximal migration of the radius. J. Hand Surg. [Am.]. 1989;14:256.
47 Hotchkiss R.N., Weiland A.J. Valgus stability of the elbow. J. Orthop. Res. 1987;5:372.
48 Hughes R.E., Schneeberger A.G., An K.N., Morrey B.F., O’Driscoll S.W. Reduction of triceps muscle force after shortening of the distal humerus: A computational model. J. Shoulder Elbow Surg. 1997;6:444.
49 Hui F.C., Chao E.Y., An K.N. Muscle and joint forces at the elbow during isometric lifting. Orthop. Trans. 1978;2:169. Abstract.
50 Hultkrantz J.W. Das ellbogengeleck and seine mechanik. Jena Fisher. 1897.
51 Ishizuki M. Functional anatomy of the elbow joint and three-dimensional quantitative motion analysis of the elbow joint. J. Jpn. Orthop. Assoc. 1979;53:989.
52 Kapandji I.A.. 2nd ed.. The Physiology of the Joint: The Elbow, Flexion and Extension, Vol. 1. Livingstone, London, 1970.
53 Keats T.E., Tuslink R., Diamond A.E., Williams J.H. Normal axial relationship of the major joints. Radiology. 1966;87:905.
54 Larson R.F. Forearm positioning on maximal elbow-flexor force. Phys. Ther. 1969;49:748.
55 Le Bozec S., Maton B., Cnockaert J.C. The synergy of elbow extensor muscles during dynamic work in man. Part I. Elbow extension. Eur. J. Appl. Physiol. 1980;44:255.
56 London J.T. Kinematics of the elbow. J. Bone Joint Surg. [Am.]. 1981;63:529.
57 Markolf K.L., Lamey D., Yang S., Meals R., Hotchkiss R. Radioulnar load-sharing in the forearm. A study in cadavera. J. Bone Joint Surg. [Am.]. 1998;80:879.
58 Maton B., Bouisset S. The distribution of activity among the muscles of a single group during isometric contraction. Eur. J. Appl. Physiol. 1977;37:101.
59 McGarvey S.R., Morrey B.F., Askew L.J., An K.N. Reliability of isometric strength testing. Temporal factors and strength variation. Clin. Orthop. 1984;185:301.
60 Meissner G. Lokomotion des ellbogengelenkes ber ubd. Fortschr. Anat. Physiol. 1856.
61 Messier R.H., Duffy J., Litchman H.M., et al. The electromyogram as a measure of tension in the human biceps and triceps muscles. Int. J. Mech. Sci. 1971;13:585.
62 Mori K. Experimental study on rotation of the forearm-functional anatomy of the interosseous membrane. J. Jpn. Orthop. Assoc. 1985;59:611.
63 Morrey B.F. Post-traumatic contracture of the elbow. Operative treatment, including distraction arthroplasty. J. Bone Joint Surg. [Am.]. 1990;72:601.
64 Morrey B.F. Complex instability of the elbow. J. Bone Joint Surg. [Am.]. 1997;79:460.
65 Morrey B.F., An K.N. Articular and ligamentous contributions to the stability of the elbow joint. Am. J. Sports Med. 1983;11:315.
66 Morrey B.F., An K.N. Functional anatomy of the ligaments of the elbow. Clin. Orthop. 1985;201:84.
67 Morrey B.F., An K.N., Stormont T.J. Force transmission through the radial head. J. Bone Joint Surg. [Am.]. 1988;70:250.
68 Morrey B.F., Askew L.J., An K.N. Strength function after elbow arthroplasty. Clin. Orthop. 1988;234:43.
69 Morrey B.F., Chao E.Y. Passive motion of the elbow joint. J. Bone Joint Surg. [Am.]. 1976;58:501.
70 Morrey B.F., Tanaka S., An K.N. Valgus stability of the elbow. A definition of primary and secondary constraints. Clin. Orthop. 1991;265:187.
71 Motzkin N.E., Cahalan T.D., Morrey B.F., An K.N., Chao E.Y. Isometric and isokinetic endurance testing of the forearm complex. Am. J. Sports Med. 1991;19:107.
72 Nemoto K., Itoh Y., Horiuchi Y., Sasaki T. Advancement of the insertion of the biceps brachii muscle: A technique for increasing elbow flexion force. J. Shoulder Elbow Surg. 1996;5:433.
73 Nicol A.C., Berme N., Paul J.P. A biomechanical analysis of elbow joint function. In: Joint Replacement in the Upper Limb. London: Institute of Mechanical Engineers; 1977:45.
74 Nobuta S. Pressure distribution on the elbow joint and its change according to positions. J. Jpn. Soc. Clin. Biomech. Res. 1991;13:17.
75 O’Driscoll S.W., An K.N., Korinek S., Morrey B.F. Kinematics of semi-constrained total elbow arthroplasty. J. Bone Joint Surg. [Br.]. 1992;74:297.
76 O’Driscoll S.W., Bell D.F., Morrey B.F. Posterolateral rotatory instability of the elbow. J. Bone Joint Surg. [Am.]. 1991;73:440.
77 O’Driscoll S.W., Horii E., Morrey B.F., Carmichael S. Anatomy of the ulnar part of the lateral collateral ligament of the elbow. Clin. Anat. 1992;5:296.
78 O’Driscoll S.W., Morrey B.F., An K.N. Intraarticular pressure and capacity of the elbow. Arthroscopy. 1990;6:100.
79 Olsen B.S., Henriksen M.G., Sojbjerg J.O., Helmig P., Sneppen O. Elbow joint instability: A kinematic model. J. Shoulder Elbow Surg. 1994;3:143.
80 Olsen B.S., Sojbjerg J.O., Dalstra M., Sneppen O. Kinematics of the lateral ligamentous constraints of the elbow joint. J. Shoulder Elbow Surg. 1996;5:333.
81 Olsen B.S., Vaesel M.T., Sojbjerg J.O., Helmig P., Sneppen O. Lateral collateral ligament of the elbow joint: Anatomy and kinematics. J. Shoulder Elbow Surg. 1996;5:103-112.
82 Palmer A.K., Glisson R.R., Werner F.W. Ulnar variance determination. J. Hand Surg. [Am.]. 1982;7:376.
83 Pauly J.E., Rushing J.L., Scheving L.E. An electromyographic study of some muscles crossing the elbow joint. Anat. Rec. 1967;159:47.
84 Pauwels F.. Maquet P., Furlong R., editors. Biomechanics of locomotor apparatus. Berlin: Springer-Verlag, 1980.
85 Pomianowski S., Morrey B.F., Neale P.G., Park M.J., O’Driscoll S.W., An K.N. Contribution of monoblock and bipolar radial head prostheses to valgus stability of the elbow. [see comment]. J. Bone Joint Surg. [Am.]. 2001;83:1829.
86 Pomianowski S., O’Driscoll S.W., Neale P.G., Park M.J., Morrey B.F., An K.N. The effect of forearm rotation on laxity and stability of the elbow. Clin. Biomech. 2001;16:401.
87 Pribyl C.R., Kester M.A., Cook S.D., Edmunds J.O., Brunet M.E. The effect of the radial head and prosthetic radial head replacement on resisting valgus stress at the elbow. Orthopedics. 1986;9:723.
88 Ray R.D., Johnson R.J., Jameson R.M. Rotation of the forearm: An experimental study of pronation and supination. J. Bone Joint Surg. [Am.]. 1951;33:993.
89 Ray P.S., Kakarlapudi K., Rajsekhar C., Bhamra M.S. Total elbow arthroplasty as primary treatment for distal humeral fractures in elderly patients. Injury. 2000;31:687.
90 Regan W.D., Korinek S.L., Morrey B.F., An K.N. Biomechanical study of ligaments around the elbow joint. Clin. Orthop. 1991;271:170.
91 Sarmiento A., Ebramzadeh E., Brys D., Tarr R. Angular deformities and forearm function. J. Orthop. Res. 1992;10:121.
92 Schlein A.P. Semiconstrained total elbow arthroplasty. Clin. Orthop. 1976;121:222.
93 Schwab G.H., Bennett J.B., Woods G.W., Tullos H.S. Biomechanics of elbow instability: The role of the medial collateral ligament. Clin. Orthop. 1980;146:42.
94 Sojbjerg J.O., Ovesen J., Gundorf C.E. The stability of the elbow following excision of the radial head and transection of the annular ligament. An experimental study. Arch. Orthop. Trauma Surg. 1987;106:248.
95 Sojbjerg J.O., Ovesen J., Nielsen S. Experimental elbow instability after transection of the medial collateral ligament. Clin. Orthop. 1987;218:186.
96 Spinner M., Kaplan E.B. The quadrate ligament of the elbow—its relationship to the stability of the proximal radio-ulnar joint. Acta Orthop. Scand. 1970;41:632.
97 Steindler A. Kinesiology of the Human Body Under Normal and Pathological Conditions. Springfield, IL: Charles C. Thomas, 1955;493.
98 Stevens A., Stijns H., Reybrouck T., Bonte G., Michels A., Rosselle N., Roelandts P., Krauss E., Verheyen G. A polyelectromyographical study of the arm muscles at gradual isometric loading. Electromyogr Clin Neurophysiol. 1973;13:465-476.
99 Stormont T.J., An K.N., Morrey B.F., Chao E.Y. Elbow joint contact study: Comparison of techniques. J. Biomech. 1985;18:329.
100 Sullivan W.E., Mortensen O.A., Miles M., Greene L.S. Electromyographic studies of m. biceps brachii during normal voluntary movement at the elbow. Anat. Rec. 1950;107:243.
101 Tanaka S., An K.N., Morrey B.F. Kinematics and laxity of ulnohumeral joint under valgus-varus stress. J. Musculoskel. Res. 1998;2:45.
102 Travill A.A. Electromyographic study of the extensor apparatus of the forearm. Anat. Rec. 1962;144:373.
103 Tyrdal S., Olsen B.S. Combined hyperextension and supination of the elbow joint induces lateral ligament lesions. An experimental study of the pathoanatomy and kinematics in elbow ligament injuries. Knee Surg. Sports Traumatol. Arthrosc. 1998;6:36.
104 Van Glabbeek F., Van Riet R.P., Baumfeld J.A., Neale P.G., O’Driscoll S.W., Morrey B.F., An K.N. Detrimental effects of overstuffing or understuffing with a radial head replacement in the medial collateral-ligament deficient elbow. J. Bone Joint Surg. [Am.]. 2004;86:2629.
105 Von Lanz T., Wachsmuth W. Praktische Anatomie. Berlin: Springer-Verlag, 1959.
106 Von Meyer H., Steindler A. Kinesiology of the Human Body Under Normal and Pathological Conditions. Springfield, IL: Charles C. Thomas, 1955;490.
107 Walker P.S. Human Joints and Their Artificial Replacements. Springfield, IL: Charles C. Thomas, 1977;182.
108 Youm Y., Dryer R.F., Thambyrajah K., Flatt A.E., Sprague B.L. Biomechanical analyses of forearm pronation-supination and elbow flexion-extension. J. Biomech. 1979;12:245.





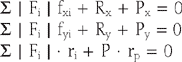
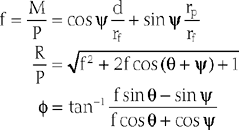

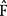 is the normalized muscle force as adjusted by the muscle length, PCSA represents the muscle physiologic cross-sectional area, and σ is the upper bound of muscle activation level. The maximum stress could be generated by the muscle. The word activation is used to describe both the number of active units (recruitment) and their degree of activity (firing frequency). The muscle force distribution was then determined by using the optimization method of
is the normalized muscle force as adjusted by the muscle length, PCSA represents the muscle physiologic cross-sectional area, and σ is the upper bound of muscle activation level. The maximum stress could be generated by the muscle. The word activation is used to describe both the number of active units (recruitment) and their degree of activity (firing frequency). The muscle force distribution was then determined by using the optimization method of