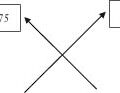
Figure 3.1 Emmetropia: light from a distant object forms an image on the retina
Refractive error (ametropia)
‘Refractive error’ (ametropia) means that an eye does not allow light from a distant source to be focused perfectly on the retina. Approximately one-third of the population has a refractive error of more than 1 dioptre, and thus may need spectacles. Myopia is just as common as hypermetropia.
The refractive power of an eye is a function of the corneal curvature (accounting for two-thirds of the power; this cannot be altered) and lens (accounting for one-third of the power; this can be altered by accommodation, provided there is no presbyopia). This is a surprise to most people, since most assume that the lens is the most powerful refractive element. The air–cornea interface is in fact the most powerful refractive element – this becomes quite obvious when you dive into water without any goggles.
Refractive error (ametropia) occurs when the refractive power of the eye does not correlate with the axial length of the eye, so an image from a distant object does not fall on the retina.
Myopia
‘Myopia’ (short-sightedness) means that the refractive power of the eye is too great relative to the axial length of the eye; as a result, the image of a distant object lies in front of the retina (see Figure 3.2). Therefore, myopia will result if the refractive power is too high or if the eye is too long. Myopia is corrected by a minus (concave) lens, which effectively weakens the refractive power to allow the image to be shifted back on to the retina (see Figure 3.3).
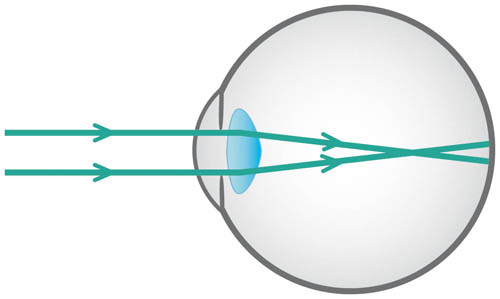
Figure 3.2 Myopia: light from a distant object forms an image in front of the retina
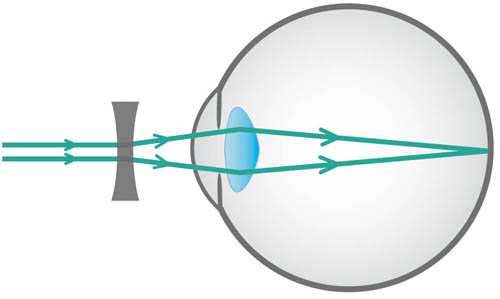
Figure 3.3 Myopia corrected by a minus (concave) lens that diverges rays
Hypermetropia
‘Hypermetropia’ (long-sightedness) means that the refractive power of the eye is too weak relative to the axial length of the eye; as a result, the image of a distant object lies behind the retina (see Figure 3.4). Therefore, hypermetropia will result if the refractive power is too low, or if the eye is too short. Hypermetropia is corrected by a plus (convex) lens, which effectively strengthens the refractive power to allow the image to be shifted forwards on to the retina (see Figure 3.5).
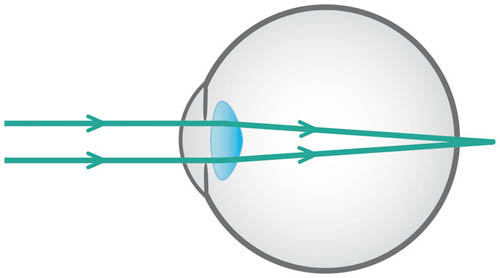
Figure 3.4 Hypermetropia – light from a distant object forms an image behind the retina
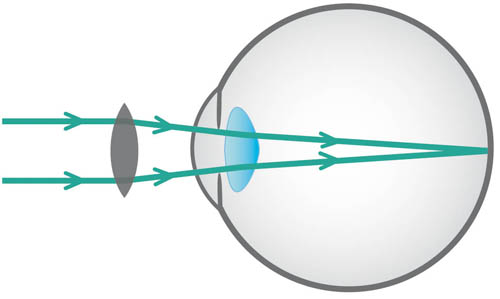
Figure 3.5 Hypermetropia corrected by a plus (convex) lens that converges rays
Astigmatism
‘Astigmatism’ refers to the refractive power of the eye being different in different meridians. Therefore, light from a point of a distant object cannot form a single point of an image (see Figure 3.6).
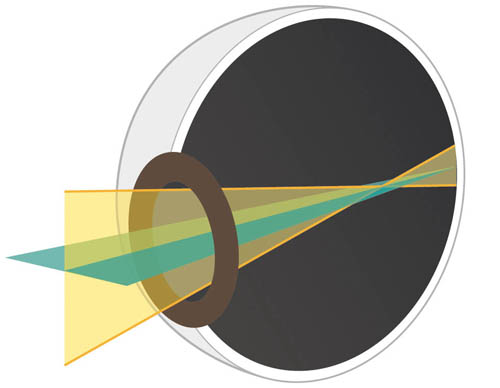
Figure 3.6 Astigmatism: light from the same distant point object does not form a single point image, as light is refracted by different amounts in different meridians
An eye with astigmatism behaves as a sphero-cylindrical (toric) lens. The principal meridians form separate line foci and between them is Sturm’s conoid. Where these lines intersect is the circle of least confusion, which is situated at the focal point for the lens spherical equivalent value (see Figure 3.7).
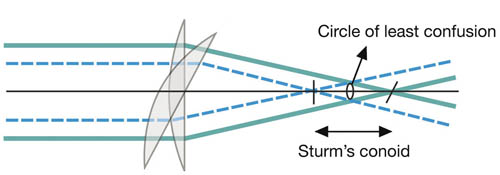
Figure 3.7 An eye with astigmatism behaves as a sphero-cylindrical lens, with the circle of least confusion of Sturm’s conoid lying at the focal point for the lens spherical equivalent value
The spherical equivalent of a sphero-cylindrical lens is equal to the sum of the sphere plus half the cylinder (cyl) and is used to establish whether an eye with astigmatism can be considered to be myopic or hypermetropic overall (for more information, see ‘Notation, transposition and spherical equivalent’, p. 17).
This may sound quite complex, but, basically, if an eye with astigmatism behaves as a sphero-cylindrical lens (i.e. a sphere lens with a cylindrical lens superimposed upon it), it follows that to correct astigmatism a sphero-cylindrical lens is required. This is different to myopia or hypermetropia, which can simply be corrected with a spherical lens alone.
The origin of astigmatism is usually corneal, where the corneal curvature and, therefore, the refractive power is different in different meridians. This is why we often explain to patients that astigmatism implies that their eye is shaped like a rugby ball rather than a football.
The degree of corneal astigmatism can be assessed by a keratometer, which gives ‘K’ values for the refractive power in different meridians. The steeper the cornea in a given meridian, the greater the numerical value of the K value for that meridian.
If cataract surgery is proposed, it is important to consider the keratometer K values, since the site of the incision will flatten the cornea in this meridian. By placing the incision on the steepest K meridian the degree of corneal astigmatism is reduced, which can be beneficial to the patient since astigmatism has no refractive advantage.
If astigmatism is present despite having a spherical cornea, it will be due to the lens (lenticular astigmatism). Lenticular astigmatism is eliminated by the placement of a spherical intra-ocular lens implant at the time of cataract surgery.
Some further terms used to describe astigmatism follow.
Regular astigmatism
This applies when the meridians of maximum and minimum refractive power are perpendicular to each other. This is further divided into:
‘with the rule’ regular astigmatism, in which:
- the cornea is steepest in the vertical meridian and flattest in the horizontal meridian
- the maximal refractive power of the cornea acts vertically (the steepest K meridian will be near 090)
- the weakest refractive power of the cornea acts horizontally (the flattest K meridian will be near 180)
- the axis of a correcting plus lens will be vertical (090), since its power needs to act horizontally to strengthen the relatively weaker horizontal meridian
- this is an example of an eye that has with the rule regular astigmatism: +1.00/+1.50 @ 090. There is a +1.50 dioptre cyl, which has its axis at 090. This cyl is super-imposed on a +1.00 dioptre sphere. In the absence of any lenticular astigmatism one would expect the K value in the vertical meridian to be greater than the horizontal meridian.
‘against the rule’ regular astigmatism, in which:
- the cornea is steepest in the horizontal meridian and flattest in the vertical meridian
- the maximal refractive power of the cornea acts horizontally (the steepest K meridian will be near 180)
- the weakest refractive power of the cornea acts vertically (the flattest K meridian will be near 090)
- the axis of a correcting plus lens will be horizontal (180), since its power needs to act vertically to strengthen the relatively weaker vertical meridian
- this is an example of an eye that has against the rule astigmatism: +2.00/+1.75 @ 180. There is a +1.75 dioptre cyl with its axis at 180. This cyl is superimposed on a +2.00 dioptre sphere. In the absence of any lenticular astigmatism one would expect the K value in the horizontal meridian to be greater than the vertical meridian.
‘oblique’ regular astigmatism, in which:
- the maximal and minimal meridians are perpendicular to each other but they are not acting in the vertical or horizontal plane; for example, a maximal meridian along 070 and a minimal meridian along 160.
Irregular astigmatism
This applies when the meridians of maximum and minimum refractive power are not perpendicular to each other. The most common cause for this is keratoconus (which gives a scissor-like retinoscope reflex that is difficult to neutralise). Retinoscopy is of limited value for irregular astigmatism and it is useful to more accurately map the corneal curvature with corneal topography. Irregular astigmatism is also common following corneal surgery such as ‘penetrating keratoplasty’ (full-thickness corneal graft).
Simple astigmatism
This is when the eye is plano (emmetropic) in one meridian (i.e. the rays in this meridian focus on the retina) and cylindrical in another (i.e. the rays in this meridian do not focus on the retina).
For example, 0.00/+1.50 @ 055 implies that no spherical correction is required, but a +1.50 cyl lens is required with an axis at 055 (power acting perpendicularly at 145) to correct the refractive error.
Compound astigmatism
This applies when both meridians are hypermetropic (i.e. the rays in all meridians come to focus behind the retina) or both are myopic (rays in all meridians come to focus in front of the retina).
For example, +1.00/+2.00 @ 090 implies that a +1.00 spherical lens with a +2.00 cyl lens with axis at 090 (power acting perpendicularly at 180) is required to correct the refractive error.
Mixed astigmatism
Applies when one meridian is myopic (rays fall in front of the retina) the other is hypermetropic (rays fall behind the retina).
For example, –1.50/+2.50 @ 040 implies that a –1.50 spherical lens with a +2.50 cyl lens with axis at 040 (power acting perpendicularly at 130) is required to correct the refractive error.
Notation, transposition and spherical equivalent
A refractive error is expressed by the spectacle (or contact lens) prescription required to correct the refractive error in the form:
Refractive error = sphere/cyl @ 000 (angle of cyl axis).
It is important to denote + or – for the sphere and the cyl value, and these values should be expressed to two decimal places (e.g. +0.75, –3.25). The angle of the cyl axis is expressed as a value from 000 to 180 (from right to left, anticlockwise, for either eye), and should always be three significant figures; the degree symbol should be omitted. For example, instead of writing ‘40°’, write ‘040’.
If you get confused or cannot remember that the angle of the cyl axis runs from 000 to 180 from right to left (anticlockwise) for either eye, simply pick up a trial frame, as the angles are clearly demarcated on this (see Figure 3.8).

Figure 3.8 The trial frame provides demarcation for the cyl axis
A spectacle prescription may be written in plus cyl notation or minus cyl notation – these are the two equivalent ways in which any single refractive error can be corrected. Both plus and minus cyl notations are acceptable, so either may be used. Always ensure that for any single patient both eyes are in the same notation (that is, both eyes in plus cyl notation or both eyes in minus cyl notation – never use plus cyl for one eye and minus cyl for the other eye). The notation that is chosen by someone usually reflects their training in retinoscopy. To obtain the equivalent notation, one form has to be transposed to the other form (transpose the plus cyl notation to the minus cyl notation, or vice versa).
Transposition involves three steps:
- add the cyl to the sphere to give the new sphere
- change the sign of the cyl to give the new cyl
- the new axis is perpendicular to the old axis.
Transposition example
Transpose –8.00/+3.00 @ 165.
New sphere = (–8.00) + (+3.00) = –5.00 (adding the cyl to the sphere to give new sphere)
New cyl = –3.00 (changing the sign of the cyl to give the new cyl)
New axis = 165 – 090 = 075 (the new axis is perpendicular to the old axis)
To give –5.00/–3.00 @ 075.
Therefore, –8.00/+3.00 @ 165 (plus cyl format) will correct the same refractive error as the transposed equivalent prescription –5.00/–3.00 @ 075 (minus cyl format).
It does not matter if you choose to record in plus or minus cyl notation, but it is crucial that you are consistent and for the eyes of any single patient always use either plus cyl notation throughout for both eyes or minus cyl format throughout for both eyes. Do not use plus cyl for one eye and minus cyl for the other eye of the same patient, since such inconsistency is confusing and unacceptable in the Refraction Certificate Examination.
Given that refractive prescriptions can be written in both plus or minus cyl format, it can be confusing at first to appreciate whether or not somebody is myopic or hypermetropic overall.
For example, consider –1.50/+4.00 @ 020, which is equivalent to +2.50/–4.00 @ 110. This person obviously has a significant amount of astigmatism, but are they myopic or hypermetropic overall? This can be simplified by the concept of the ‘spherical equivalent’, which combines the effect of the sphere and cyl to decide if the eye is myopic or hypermetropic overall.
Spherical equivalent = sphere + (cylinder/2).
The spherical equivalent can be obtained from the refractive prescription in either the plus or the minus cyl format.
So, for the above example (–1.50/+4.00 @ 020, which is equivalent to +2.50/–4.00 @ 110), the spherical equivalent would be –1.50 + (+4.00/2) = +0.50. Note that this is equal to +2.50 + (–4.00/2) = +0.50. Therefore, in this case, the eye can be considered to be mildly hypermetropic overall.
This concept of spherical equivalent is particularly important to understand when choosing the intra-ocular lens power in cataract surgery because if the incorrect target spherical equivalent is chosen anisometropia may result. ‘Anisometropia’ is when the difference in refractive errors between the two eyes is sufficiently large to result in troublesome symptoms such as aniseikonia (different image size of single object between eyes) and asthenopia (eye strain – patients are often non-specific but complain of fatigue, blurred vision and headache).
This is different for different patients but is a significant risk when the difference in spherical equivalent between the two eyes is more than 1.5 dioptres. Therefore, it is crucial to discuss with the patient undergoing cataract surgery:
- their target refraction (often the target is emmetropia, but myopes may like to be left a little myopic, whereas there is no refractive advantage of being left hypermetropic unless this is done to avoid anisometropia in hypermetropic patients keen for cataract surgery in one eye only)
- the plan for the other eye (since a patient undergoing sequential, bilateral cataract surgery will often choose to be emmetropic but should be warned of anisometropia whilst awaiting second eye surgery).