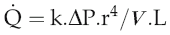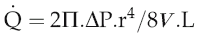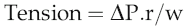Vessel length

The pressure of fluid flowing through a tube falls progressively along the tube, due to friction between the fluid and the tube wall. Thus, vessels of different lengths must contribute differently to overall peripheral resistance, with short vascular beds such as that of the stomach having less resistance (and correspondingly faster circulation times) than those of the limbs.

Even though some vessels travel in the walls of organs that change size dramatically, such as the bladder, stretching of these organs does not alter the length of the vessels. When the organs are at their minimum volume, the vessels are coiled and stretching just straightens out these coils.

Vessel radius

Since there is friction between a flowing fluid and the tube in which it is contained, the ratio between the cross-sectional area and the surface area of the tube constitutes a second determinant of resistance. This means that small tubes have higher resistance per unit length than large tubes. Because the critical factor is cross-sectional area rather than radius, resistance changes in proportion to the fourth power of the radius, with the result that only small incremental changes in vessel size confer very large changes in resistance. For example, halving the radius would increase resistance 16-fold.

The fact that resistance is greater in small vessels indicates that absolute resistance must be lower in veins than in arteries, since all segments of veins are around twice the size of the equivalent arterial vessels. The relatively low venous resistance is essential for efficient circulation, since the role of the venous system is simply to drain blood back to the heart as rapidly as possible and is reflected in the fact that the same left cardiac output requires a pressure gradient of around (100–30) or 70 mmHg to deliver it to the capillaries but only (20–0) or 20 mmHg to return it from the capillaries to the heart.

The dependence of resistance on absolute vessel size also indicates that the major component of total peripheral resistance must be localized to the smaller precapillary vessels (the microcirculation) rather than the large distributing arteries. Not only are these microcirculatory vessels smaller in radius but they also branch repeatedly every mm or so. Although total cross-sectional area increases with each branching, total surface area increases even more, so that resistance rises rapidly along quite a short distance.

While most textbooks talk about the arterioles as being the primary site of peripheral resistance, this is an oversimplification. The arterioles are the smallest of the precapillary vessels, with luminal diameters of 200 μm or less, but in fact all the small muscular arteries less than around 1 mm in diameter that give rise to these arterioles also constitute a major source of resistance.

What may appear paradoxical is that the high resistance is restricted to the precapillary vasculature, while systemic capillaries have diameters of around 7 μm and so are rather narrower than even the smallest arteriole, yet impose less resistance to flow. The lower resistance in capillaries than arterioles reflects the fact that several capillaries arise from each arteriole, so that the total capillary cross-sectional area:surface area ratio is very much greater than is associated with any generation of arterioles. In terms of functional efficiency, it is of course essential for local resistance not to limit flow through the capillary bed.

Blood viscosity

The viscosity of a moving fluid represents the amount of friction between the components of the fluid, in contrast to the friction that occurs by interaction of the fluid with the surrounding tube surface. Any friction will increase the amount of energy that is needed to move a fluid along a tube, so viscosity must constitute a further factor contributing to flow resistance.

Different fluids have very different viscosities – think of water and honey – but all fluids that consist only of molecules in solution have viscosities that remain constant regardless of the velocity of fluid movement. Such solutions are termed Newtonian fluids. By contrast, fluids that contain suspended material (non-Newtonian fluids) have viscosities that vary with flow velocity, being greater at low rates of movement. This property is termed anomalous viscosity. Because blood is a suspension of cells in plasma, it behaves in a non-Newtonian fashion and this has several implications.

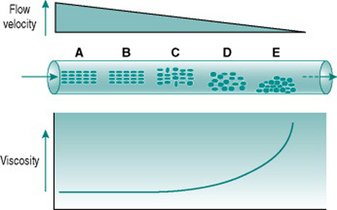
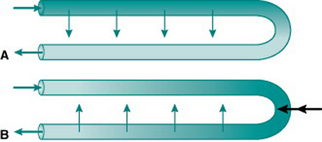
Figure 5.1 illustrates the processes that underlie anomalous viscosity in the bloodstream. When the blood is flowing relatively fast (A–B), the cellular components travel as a core in the centre of the vessel, surrounded by a cell-free layer of plasma. The cells are oriented so that they travel edge-on, producing minimal friction between the cell layers and between cells and plasma. The viscosity of the blood in this situation is around 50% greater than that of plasma alone. If the flow velocity falls sufficiently then the orientation of the suspension becomes less organized, with some cells starting to rotate and collide with adjacent cells. This process absorbs some of the energy creating the pressure gradient and so viscosity rises (C–D). If flow rate falls even further, the cellular constituents fall out of suspension and form an aggregate on the gravitationally lowest surface of the vessel. Because of the mass of the aggregate, a substantial amount of energy is required to lift the cells back into suspension again, reflected in a very high viscosity (E).

Figure 5.1 Changes in viscosity and the associated changes in red blood cell behaviour as the velocity of blood flow falls. A & B represent velocities typical of flow in the normal, intact circulation.

The dependence of blood viscosity on the cellular components has several implications. First, alteration of the haematocrit will change the size of the cell-rich core relative to surrounding plasma. Therefore, increased haematocrit will proportionately elevate viscosity. This can impose a substantial extra cardiac workload particularly during exercise. Thus, ‘blood doping’ with erythropoietin, although it is likely to improve maximal exercise performance by enhancing oxygen delivery to muscles, also carries a significant risk of damage to the heart. A second consequence of anomalous viscosity is that very low rates of blood flow can result in cells falling out of suspension. If the cell aggregates remain unsuspended for more than a few minutes, they begin to stick together and, in small vessels, may completely obstruct the lumen. This situation is most likely to occur in the postcapillary venules and will be discussed in Chapter 10 in relation to hypotensive states associated with prolonged exercise.

Blood flow through systemic capillaries is rather different to that through either precapillary or postcapillary vessels. All these other vessels have diameters greater than that of blood cells, whereas the typical capillary diameter of around 6 μm is marginally less than that of an erythrocytes (8 μm). In consequence, blood cells have to be partially folded in order to pass along the capillary. This process is important in that it ensures the closest contact possible between erythrocyte and endothelial membranes and so minimizes the distance for gas diffusion between blood and tissue. However, in theory it should also produce very high frictional forces between blood cells and the capillary wall, greatly increasing local viscosity and impeding the efficiency of capillary perfusion. To avoid such a disadvantageous situation, the endothelium of capillaries secretes a lubricant mucopolysaccharide that virtually eliminates frictional interaction with the blood cells and results in local viscosity that is almost as low as that of cell-free plasma.

Poiseuille’s law

The equation relating flow, pressure and resistance (see p. 45) can be rewritten by substitution of vessel radius (r) and length (L) and blood viscosity (V) for resistance, and adding a factor for numerical accuracy (k), thus:

This equation was derived by the scientist Poiseuille and is known as Poiseuille’s law. In its full form, with the factor k expressed numerically, it reads:

The practical importance of Poiseuille’s law is that it describes the main factors affecting the relationship between flow and pressure. It does not of course take account of homeostatic feedback so does not necessarily predict the end result of manipulating these factors in the whole body. For example, if blood pressure were elevated by a sudden increase in blood volume, there would normally be baroreflex compensation that would lower peripheral resistance and return the pressure to its initial level (see Chapter 7, p. 81). A second difference from the events in the intact circulation is that Poiseuille’s law assumes that the vasculature is a system of rigid tubes. As soon as we deal with tubes that might distend in response to internal pressure, then obviously the association between pressure and flow becomes different.

Roles of connective tissue and muscle in determining distensibility

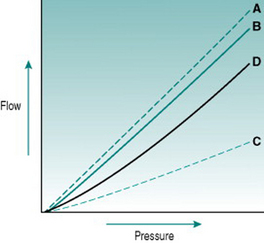
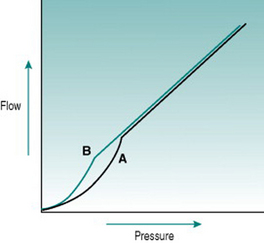
In rigid tubes, there is a linear relationship between the pressure gradient and the resulting volume flow, presuming that resistance remains constant (Fig 5.2A). In distensible tubes, by contrast, increased internal pressure will cause some increase in tube volume, so that the rate of volume flow rise with pressure will be lower. In blood vessels, distensibility is conferred by the presence of elastin in the vessel wall, while the presence of collagen confers rigidity (Fig. 5.2B–D). The property of distensibility is usually referred to as compliance.

Figure 5.2 Passive flow–pressure relationships in (A) a rigid tube, (B) an idealized artery in which the wall contains collagen but no elastin, (C) an idealized artery in which the wall contains elastin but no collagen and (D) a typical real artery containing both elastin and collagen.

For any given mix of elastin and collagen, absolute vessel compliance depends also on the amount of smooth muscle and whether the muscle cells are relaxed or contracted. Although arterioles have elastin in their walls, they behave as virtually rigid tubes because of the thickness of the muscle layer. The walls of large veins contain large amounts of elastin and relatively small amounts of muscle, so they are normally highly distensible. However, if the muscle contracts fully then this has the effect of stiffening the vein dramatically, so that even high internal pressure does not cause distension. This transition becomes practically important when one is inserting an intravenous needle for blood sampling. Unsuccessful insertion frequently causes local muscle spasm in the vein wall, with the result that the vessel shrinks so much that it is impossible to cannulate.

Measurement of arterial distensibility

The compliance of the arterial system determines the magnitude of arterial pulse pressure, the pulsatility of peripheral blood flow and the velocity of blood flow through the larger arteries. This will in turn affect shear stress on the endothelium and the release of endothelial factors that alter peripheral resistance (see Chapter 6, p. 64). The arteries become progressively stiffer with age due to loss of elastin: at any given age higher stiffness is predictive of cardiovascular morbidity, while reduction of blood pressure associated with, for example, chronic exercise programmes is linked to reduced stiffness. Measuring arterial stiffness is, therefore, potentially useful not only for evaluating the basis of circulatory parameters such as blood pressure, but also for assessing cardiovascular health and monitoring the beneficial effects of interventions like exercise.

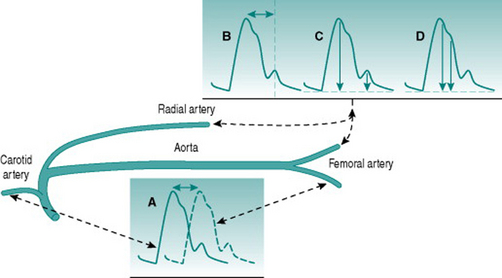
A number of techniques exist for evaluating arterial stiffness, all of which utilize non-invasive detection of the phasic blood pressure waveform and varying degrees of technology. Conceptually simplest, and the original standard, is measurement of pulse wave velocity by timing arrival of the peak pressure wave at two sites different distances away from the heart, traditionally in the carotid and the femoral arteries (Fig. 5.3A). Other methods can utilize pressure waves recorded from one peripheral arterial site (usually the femoral or radial) and involve measurement of the time interval between the systolic pressure peak and the reflected wave that follows it (Fig. 5.3B), comparison of the amplitudes of these two events (Fig. 5.3C) or assessment of the shape of the primary systolic pressure waveform (Fig. 5.3D).

Figure 5.3 Some of the approaches used for assessment of arterial stiffness from non-invasive analysis of the arterial pulse wave. (A) Pulse wave velocity. (B) Reflection time. (C) Peripheral augmentation index. (D) Central augmentation index.

All of these methods involve some assumptions about the physics of the circulation and some require significant amounts of computation. For example, the central augmentation index method (Fig. 5.3D) involves a computerized transfer function that estimates the aortic waveform from the shape of a peripheral systolic wave. Comparison of values obtained with a range of methods in healthy subjects and patient groups has indicated that there is relatively poor agreement between different techniques. This is not surprising since some methods use central and some use peripheral arteries: these two types of artery have different wall characteristics and are at very different distances from reflection sites in the peripheral microcirculation. Optimal assessment of arterial wall behaviour should, therefore, employ more than one technique, so as to involve both vessel types. However, it remains to be determined which combination of methods is most useful. For the present, the choice is based primarily on what facilities are available in particular laboratories.

Laplace’s law and large vessel function

In rigid tubes, it is clear that wall tension is independent of intravascular pressure. If the tube is distensible, by contrast, increased intravascular pressure will not only increase r, but also reduce w, so that wall tension rises rapidly. With the magnitudes of pressure and vessel size characteristic of the aorta during systolic ejection, increases in vessel radius by around 50% would be likely to cause wall rupture. The protection against this is the presence of a non-distensible layer of collagen fibres around the aorta. These are arranged so that they allow aortic radius to increase by about 20% during systolic ejection, consistent with its function in facilitating diastolic flow (see Chapter 4, p. 31), but form a rigid outer sleeve to the vessel that prevents further increases in radius (Fig 5.4). Although this protective mechanism is highly effective, it can be disrupted in people with pathologies that cause selective loss of collagen from the body. If these individuals are subject to sudden rises in blood pressure, they may, therefore, experience uncontrolled aortic distension leading to wall rupture (a dissecting aneurysm) and potentially fatal haemorrhage.

Figure 5.4 Pressure–flow relationship in the aorta. (A) The collagen elements of the wall are arranged so as to allow some distension but when this reaches its limits the collagen behaves like a rigid sheath. (B) When the aortic smooth muscle is contracted, this tightens the collagen matrix and reduces distensibility. Note that under these conditions a given value of flow is achieved at a lower pressure.

Laplace’s law is not important for venous integrity, because the relatively low intravascular pressures do not produce significant wall tension. The large veins, therefore, do not require restrictive collagen layers in their walls and are able to distend to several times their resting diameters in their role as blood storage reservoirs.

Laplace’s law and small vessel function

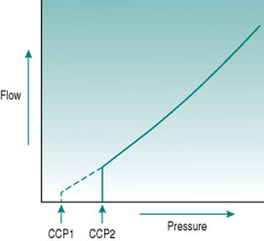
In the precapillary microcirculation, although intravascular pressure is of the same order of magnitude as in the aorta, the luminal size is too small for absolute wall tension to ever reach values that might cause wall damage. In these small arterial vessels, Laplace’s law has functional significance of another sort. The walls of small arteries and arterioles contain little connective tissue and consist primarily of smooth muscle that usually has some degree of active tone – that is, is in a state of partial contraction – due to sympathetic vasoconstrictor nerve activity and circulating vasoconstrictor hormones. Under these circumstances, the vessel luminal size must reflect a balance between the outwardly directed pressure of the blood and the inwardly directed pressure exerted by the muscle. If intravascular pressure falls suddenly, then the vessel will constrict without opposition down to a minimal luminal diameter. The absolute pressure necessary to balance muscle tone is termed the critical closing pressure, and imposes a further modification on the relationship between pressure and flow, since it means that in the microcirculation flow ceases while there is still a measurable pressure gradient (Fig. 5.5). In arterioles with high vasoconstrictor tone, the critical closing pressure may be as great as 60–70 mmHg. If the vessels are fully dilated, then flow would persist with very low pressure gradients of the order of 4–5 mmHg.

Figure 5.5 Flow–pressure relationship in an arteriole. The arteriolar wall behaves almost like a rigid tube because of its thick smooth muscle coat, but flow ceases due to vessel closure when perfusion pressure falls below a critical pressure (critical closing pressure, CCP).

The vessel segment most likely to be subject to critical closure is the region of transition between arteriole and capillary, known as the metarteriole, because within the muscular arteriolar tree this last region is the smallest in diameter and has least supporting tissue. The relationship between contractile state and metarteriolar closure is an important determinant of blood flow distribution in tissues, such as skeletal muscle, and will be discussed further in the next chapter (pp. 69–73).

Temperature

Skin temperature reflects a balance between the rate at which heat arrives from the body core in the cutaneous blood supply and the rate at which this heat is lost into the environment. Provided that the local environmental conditions can be controlled, therefore, skin temperature is often used as a semi-quantitative index of skin blood flow. The main advantage of this technique is that it can provide moment-to-moment indicators of skin perfusion over a wide area of the body surface, making it useful, for example, for evaluating cutaneous vasomotor responses to thermoregulatory stimuli. Aside from the obvious fact that no calibration of flow is possible, other limitations of this technique include the need to prevent interference from sweat-induced evaporative heat loss and the fact that high metabolic rates of underlying tissues, such as muscle, may distort the temperature recorded at the skin surface.

Pulse transduction

The haemoglobin content of red blood cells means that they differentially reflect electromagnetic radiation frequencies that pass through the other tissue constituents. Since the absolute volume of red blood cells within a tissue varies proportionately with blood flow, this provides a method by which pulsatile blood flow can be visualized and, to some extent, the level of flow assessed. In human experimentation, the application of these pulse transduction techniques is for monitoring of skin blood flow. In relatively thin tissues, such as fingers and ear lobe, red light can be shone through the tissue and detected using a photoelectric cell on the opposite side. Measurement of superficial blood flow in other areas can be achieved by detection of reflected light with photoelectric elements adjacent to the light emitter or by measuring the Doppler shift in frequency of the reflected beam.

With all these devices, pulsatile signal amplitude rises with cutaneous arteriolar dilation and so is roughly proportional to blood flow. The devices that rely on photoelectric detection, however, have the limitation that no calibration of flow is possible. By contrast, the more sophisticated devices that utilize Doppler shift detection and which involve laser light sources, have inbuilt algorithms that allow estimation of zero flow and so can be calibrated. Pulse transduction cannot be used for measurement of muscle blood flow because the path length of the practicable light sources is insufficient to penetrate that far below the skin.

Venous occlusion plethysmography

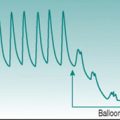
If venous outflow from a tissue is obstructed, the continued arterial inflow will initially produce an equivalent increase in tissue volume. At the same time, intravascular pressure in the tissue capillaries and veins rises progressively towards arterial pressure. When venous pressure reaches the occluding pressure then venous outflow is re-established and no further increase in tissue volume occurs. Provided that the tissue involved is able to swell in response to arterial inflow for at least a few heart beats, which is the case for most tissues, then the volume change gives an accurate measurement of regional blood flow.

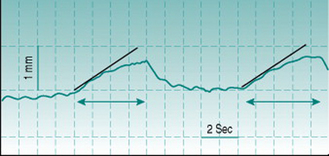
In practice, this technique of measuring volume change (plethysmography) in response to venous occlusion is usually applied to measurement of limb blood flow, and then most commonly to that in forearm. The subject is seated with the forearm in a horizontal position and at or slightly above the level of the heart. An occlusive cuff is applied to the upper arm and inflated repetitively for periods of several seconds to a pressure above that in the arm veins but below diastolic arterial pressure – this pressure is typically set at 40 mmHg and the inflation–deflation cycle is typically of the order of 4 s–6 s. Tissue volume is quantified from arm circumference, measured by a stretchable strain gauge wrapped around the midpoint of the forearm. Without cuff inflation, it is usually possible to observe small pulsatile changes in arm circumference with every pulse wave (Fig. 5.6). Cuff inflation causes a progressive rise in circumference that becomes less pronounced after the first few heart beats as venous pressure rises and will plateau after some seconds when venous pressure exceeds the cuff pressure. Flow is calculated by measuring the gradient of the early, steepest part of the curve and converting this to the rate of volume change of the tissue slice beneath the strain gauge (Fig. 5.6).

Figure 5.6 Venous occlusion plethysmography of the forearm. Periods of cuff inflation are denoted by the horizontal arrows. During the periods between inflation, pulsatile changes in arm circumference are associated with each cardiac cycle. Note that during inflation the first few cardiac cycles are associated with a rapid rise in circumference but that this plateaus as venous pressure in the arm rises. Blood flow is measured from the rate of rise in circumference during the first two cardiac cycles of the inflation period, as indicated by the red lines. Initial forearm circumference was 200 mm, so its radius was 32 mm, and the strain gauge covered a 1 mm length of arm. The initial tissue volume at the measurement site was therefore Π. 32² or 3215 mm³, approximating to 3.2 g tissue. Venous occlusion caused swelling by 1 mm circumference (0.16 mm radius)/4 s, equating to a volume change of 33 mm³/4 s or 495 mm³/min per 3.3 g tissue, which corresponds to 0.495 mL/min/3.3 g or 15 mL/min/100 g.

Because the distensible tissues of the forearm consist of both muscle and skin, venous occlusion plethysmography measures blood flow through both and interpretation of the vascular bed responsible for experimentally induced flow changes is based largely on the situation. For example, skin perfusion can be held at a low and stable level by maintaining a cool environment and hyperaemia following brief isometric forearm exercise must by definition be primarily localized to muscle. By contrast, increases in flow associated specifically with body warming can be assumed to occur primarily in skin. For accurate assessment of skin blood-flow responses to thermal stimuli it is preferable to measure not only forearm, but also finger blood flow, because the fingers are devoid of muscle. As well, since the finger circulation contains arteriovenous shunts (see Chapter 5, p. 60), simultaneous monitoring of arm and finger flows sometimes provides differential information on the responses of shunt and arteriolar vessels to thermal stimuli.

Finger volume is measured in an identical way to that used for forearm. Some investigators favour placement of the occlusive cuff at the wrist on the basis that leaving the whole forearm venous supply intact damps the rate of finger swelling: on the other hand, the initial inflation artefact is much larger when using a wrist cuff and this can lead to inaccuracy of flow measurement. On balance, this author recommends retaining the cuff on the upper arm.

Similar principles are used for measurement of leg blood flow, but in a standing posture the gravitational forces result in venous distension and high intra-tissue pressure that may interfere with volume changes during venous occlusion. Greater accuracy is, therefore, assured if the subject is sitting or lying.

Doppler imaging

Positioning a pulsed Doppler transducer over a relatively superficial artery allows the velocity of blood flow at that site to be quantified. An adjacent Doppler head can provide an image of the arterial diameter, so together these pieces of information can be transcribed into absolute volume flow. This technique can be used on the brachial artery to measure blood flow to the forearm or on the femoral artery to measure blood flow to the leg. However, the need to have extremely accurate placement of the Doppler heads makes it possible to measure flow during exercise only if the limb segment involved is immobilized. Thus, for leg exercise, only movements of the lower leg are possible.

Thermal dilution

If a known amount of an indicator (in this case, cold) is introduced into the arterial blood supply, then it will appear at a more distal part of the vascular bed at a rate that reflects the volume flow. This technique is used routinely in some exercise laboratories that are skilled in invasive procedures, for measurement of leg blood flow. The radial artery is cannulated in the groin and a bolus of cold saline is injected. The rate at which this cold fluid travels through the leg circulation is determined by a thermistor placed in the femoral vein and an algorithm allows calculation of volume flow. Since no movement artefacts occur, this technique is compatible with even high intensity whole-body exercise and the accuracy is high. However, the invasive nature of the procedure obviously restricts its application.

Countercurrent exchangers

When the arterial and venous limbs of a circulatory bed are closely apposed to each other, two streams of blood travel parallel to each other but in opposite directions. Under these circumstances, any substance that is in a higher concentration in one limb tends to diffuse down its concentration gradient into the other limb. If the higher concentration is in the arterial blood then some substance is returned into the venous bloodstream rather than reaching the capillaries: if the higher concentration is in the venous blood then some will be recycled into the arterial stream rather than travelling on into the central veins.

Different types of substance can be exchanged in these counter-current loops dependent on whether the loop involves large or microcirculatory vessels. Thermal energy diffuses rapidly over quite long distances through body tissues, so heat can easily be transferred between large arteries and veins. By contrast, solute exchange can occur only in the microcirculation because molecular diffusion is efficient only over distances of a few microns.

Countercurrent heat exchange

Countercurrent exchange of heat in large vessels is an essential part of thermoregulation since it is used to vary the amount of core body heat that is lost into the environment. A large fraction of total heat exchange takes place in the hands and feet and especially in the digits. These are sites of very large surface area:volume ratio and afford a large area for exchange and a relatively efficient pathway for diffusion of heat from bloodstream to skin surface. This can be used to optimize heat loss under conditions of heat stress or exercise by removal of sympathetic vasoconstrictor tone to the limb vessels, which both increases extremity blood flow and ensures that the venous drainage from these areas travels in veins close to the skin surface.

When the body is exposed to a cold environment, by contrast, then even the relatively small volume of blood reaching the extremities under vasoconstricted conditions loses a lot of its internal heat and places an additional metabolic load on the body if core body temperature is to remain stable. For metabolic economy it is, therefore, sensible to minimize heat loss in the extremities. This is achieved by sympathetic changes in venous tone that divert drainage in the limbs to deep veins lying adjacent to the main arteries. In this situation, heat is transferred from arterial to venous blood as it travels down the limbs, and recycled back into the central circulation (Fig. 5.7A).

Figure 5.7 Countercurrent exchange between an arterial and a venous vessel in parallel. In (A), material entering in the arterial bloodstream (dark shading) is partially lost into the venous return before it reaches the most distal portion of the vascular bed. In (B), material diffusing into the capillaries forming the end of the loop (dark shading) is partially recycled through the loop, slowing the rate of venous clearance.

Arteriovenous shunts

In the previous section we saw that the digits are a major site of heat loss from the body because of their large surface area:volume ratios. A similar thermoregulatory function is served by other small superficial tissues with large surface areas, the ears and the nose. In all these tissues, heat exchange is optimized further by the presence of short, large diameter vessels that connect large arterioles directly to large venules, bypassing the resistance of the smaller arterioles. These so-called arteriovenous anastomoses or shunts have thick walls containing circular bands of smooth muscle, which can shut off the lumen of the vessel entirely when contracted. Under those conditions, all flow takes place through capillaries. If the shunt muscle is relaxed, the low resistance of the shunt vessels means that total blood flow to these areas of the skin rises dramatically. Like other vascular smooth muscles, the shunt muscle receives a sympathetic innervation and, therefore, the withdrawal of sympathetic tone to the skin circulation that occurs during during body heating not only increases skin blood flow generally but in addition opens up the shunts.

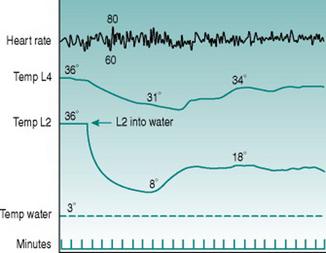
The shunt vessels subserve a second thermoregulatory function in that they open not only during heat stress but also when local skin temperature reaches a value just above freezing point. At these local temperatures, therefore, blood flow through the fingers, toes, ears and nose suddenly rises dramatically from the low values that are characteristic of skin perfusion during sympathetic vasoconstriction (Fig. 5.8). This response, termed cold vasodilatation, is potentially important for preventing freezing of peripheral tissues that cool down particularly rapidly. While this role imposes a significant extra thermal load on the body because it involves loss of additional body heat into the environment, this is minimized for the limbs, where total flow and, therefore, potential heat loss is highest, by the countercurrent recycling of arterial heat into the deep veins (see Countercurrent heat exchange, above).

Figure 5.8 Skin temperatures recorded from the plantar surfaces of second and fourth fingers of the left hand (L2, L4) during immersion of L2 in water at 3° C for 20 min. Note that the immersed finger begins to rewarm once skin temperature falls below 8° C and that the temperature is subsequently maintained at 16–18°C. Note also that the temperature oscillation is not restricted to the immersed finger.

From Bell & Robbins (1997), reproduced with permission of the publishers.

The mechanism of cold vasodilatation is not well understood. Smooth muscle cells lose their contractile ability when they are cooled below about 10° C, so shunt opening could be due to this cold-induced paralysis overriding the constrictor effect of sympathetic nerve activity. Some data, however, suggest that this is too simplistic an explanation. For one thing, the increased local blood flow that accompanies shunt opening can rewarm the skin to values considerably above those that cause muscle paralysis, but this is not always followed by another bout of shunt closure and recooling. As well, when cooling is restricted to one digit, less exaggerated increases in blood flow occur synchronously in adjacent fingers (Fig. 5.8). Finally, some studies have reported deficits in cold vasodilatation in limbs with damaged innervation and noted that the response normalized as nerve regeneration took place. Together, these findings suggest that the cold vasodilator response may involve activation of dilator nerves rather than being a purely local phenomenon.