Chapter 3
The Electrochemical Basis of Nerve Function
T.M. Dwyer
Combined Forces of Chemical Gradients and Electrical Potentials
Forces Due to Concentration Gradients
Ohm’s Law and the Equivalent Electrical Circuit of the Neuron
Pain and a Syndrome of Periodic Paralysis
Attack by the Immune System: Membrane Attack Complexes and Porins
Microbial Attacks: Antibiotics
Synaptic Structure and Function: The Neuromuscular Junction
Receptor Binding and Channel Gating
Specific Responses via Increases in Ionic Permeability
Muscle Weakness: Failure of Transmission at the Neuromuscular Junction
Action Potentials in the Nerve and in the Neuron
Cable Properties of Nerve Processes
Regenerative Potentials Using a Single Active Current
Sodium Channel Activated by Depolarization
Gating, Selectivity, and the Structure of the Sodium Channel
Use-Dependent Block and the Treatment of Epilepsy
Genetic Defects, Toxins, and Venoms
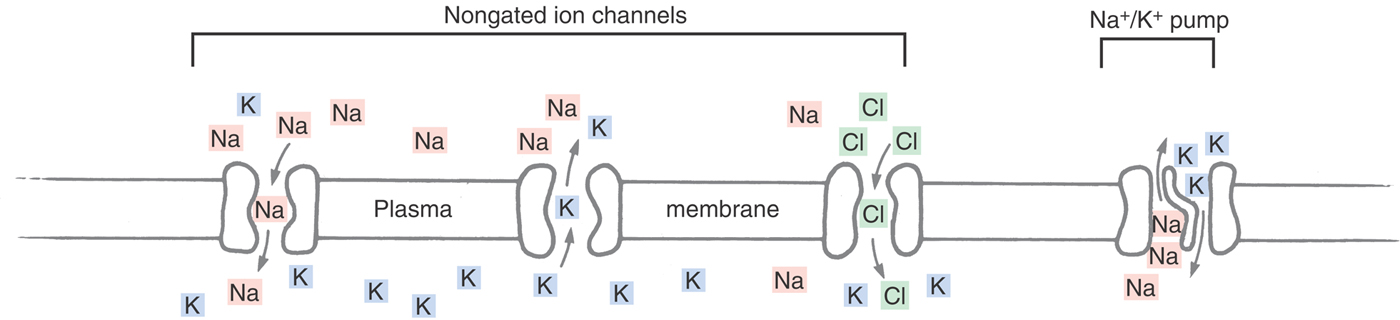
Membranes composed of a lipid bilayer enclose all cells in the body as well as all the organelles within those cells. Being lipid, these membranes are impermeant to small ions and macromolecules alike. A variety of transport proteins, selected from among hundreds available in the genome (Table 3-1), are inserted into the lipid bilayer to bring specific functions to one cell type or another. Together, these cell types in the nervous system function to harness electrical and chemical forces in their efforts to gather information, to analyze data, and to encode meaning as a string of action potentials (APs). This chapter begins with a discussion of the fundamental electrical and chemical properties of the solutions of small ions and large proteins that comprise the interior of the cell and its environs and shows how a neuron uses those forces to ensure its own integrity—and how bacteria and our own immune system broach these defenses to destroy neurons. Next are the electrical properties of the nerve that allow us to sense our environment and to integrate neural data. This chapter then concludes with the active changes in the nerve cell membrane that generate APs to encode data and to bring about distant activity.
Table 3-1 Families of Ion Channels*
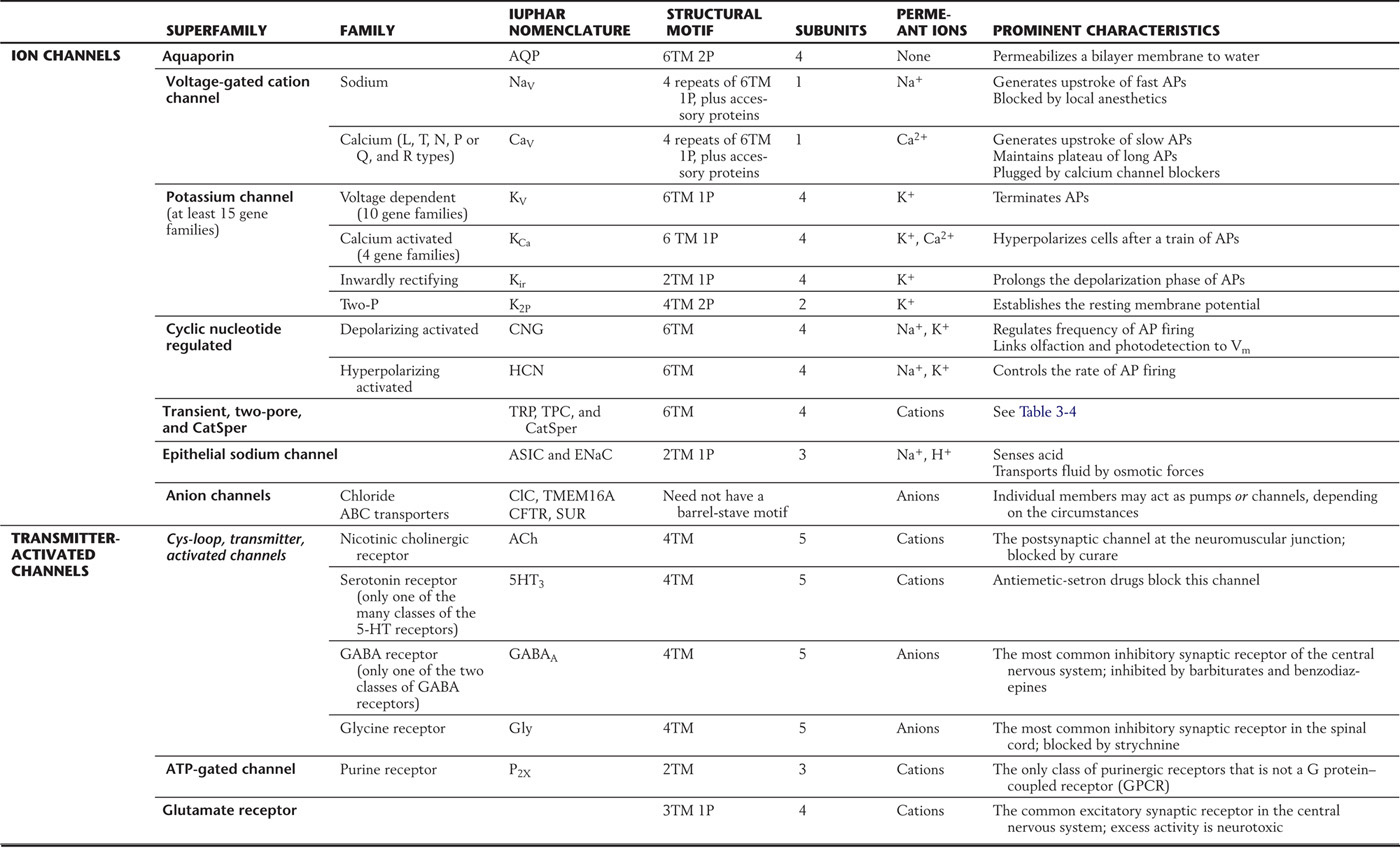
*Presented here is a sample of the important channels found in nerve membranes. Individual channels are grouped into families and then into superfamilies on the basis of structural homologies. Most channels have a barrel-stave structural motif, with characteristic numbers of transmembrane segments (TM) and pore domains (P). These channels may be open constitutively; be regulated by membrane voltage, by cell calcium, or by second messengers; or be signaled to open by synaptic transmitters. Abbreviations have been assigned by IUPHAR, the International Union of Basic and Clinical Pharmacology.
AP, action potential.
COMBINED FORCES OF CHEMICAL GRADIENTS AND ELECTRICAL POTENTIALS
Because cell membranes are composed of a lipid bilayer, large molecules such as proteins can neither enter nor leave the cell by simple diffusion, whereas small molecules like water can diffuse with relative ease. These impermeant molecules exert an osmotic force that draws water into the cell, causing it to swell and ultimately to burst unless an opposing force intervenes first. As a result, the very first task of the cell is to ensure its own physical integrity, both by minimizing osmotic flow of water and by removing that excess water that does enter the cell. The mechanisms that perform this feat have been further adapted by the nervous system both to generate specialized fluids necessary for its proper function (such as the cerebrospinal fluid and the perilymph and endolymph of the ear) and to detect stimuli, to transport signals, and to integrate information.
Forces Due to Concentration Gradients
Pure water is 55.5 M (mol/kg) in concentration. The logic behind this startling notion is that the molecular weight of water is 18 and the weight of a liter of water is a kilogram: 1000 ÷ 18 = 55.5. Any solute added to water takes up space, displacing water molecules and so reducing their concentration. Table 3-2 provides one example of how common ions might be found in a peripheral nerve cell and its surrounding fluid. Also shown are the protein concentrations, with the cell protein content being 10-fold greater than the protein in the body’s interstitium and 100-fold greater than that in the cerebrospinal fluid, which is the brain’s interstitial fluid. Because of this higher concentration inside the cell, the cell protein displaces, and thus dilutes, the neuron’s water. Since all substances spontaneously tend to move from regions of a higher concentration to regions of a lower concentration, water will tend to move into the cell from the interstitium, causing the cell to swell.
Table 3-2 Distribution of Osmotically Active Particles
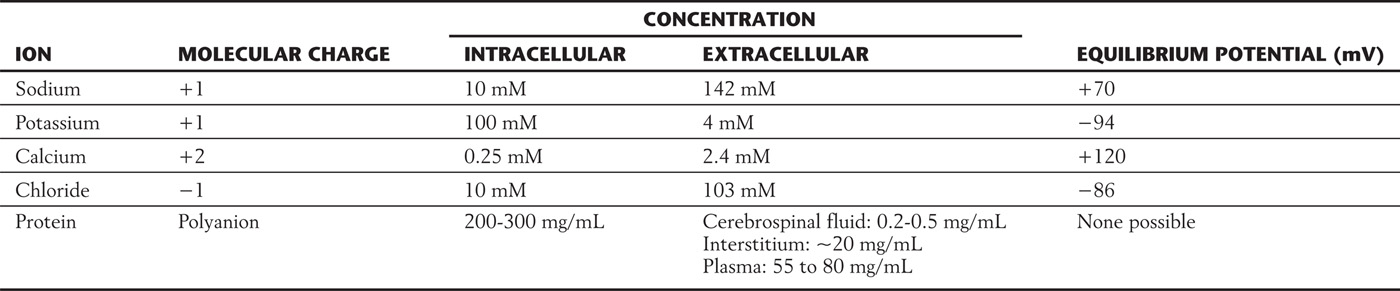
Maintenance of proper cell volume is so important that a variety of systems have evolved to counter the presence of cell proteins and to adjust to changing interstitial conditions. Indeed, pathologists generally see abnormal swelling in metabolically compromised cells, when the processes that counter this tendency are no longer adequately functioning. The following sections explain the physical principles used by these systems.
Osmotic forces measure the tendency of water to move down its concentration gradient; but our analytic instruments measure the solutes (sodium, potassium, chloride, sucrose—the dissolved substance), not the water. Hence it is the solute that gets all the attention and not the water. As a result, we dissemble when we say that osmotic forces tend to move water from a more dilute solution (of solute, that is) to a more concentrated one. In truth, the higher concentration of water is in the solution that has the lower concentration of solute, and water does in fact move as required by the laws of entropy, namely, from the solution of higher (water) concentration to the solution of lower (water) concentration.
Aquaporins (AQPs, Fig. 3-1) are the proteins in cell membranes that allow cells to reach osmotic equilibrium rapidly. AQPs contain transmembrane pores so specialized for the transport of water that they allow it to move almost as fast as in bulk solution—3 × 109 molecules per second for each pore—while excluding all other molecules. (Such a membrane is termed semipermeable.) At least 10 distinct aquaporins are present in various cells in the human body, distributed in a tissue-specific manner. Congenital abnormalities result from the absence of specific AQPs: lack of AQP0 leads to cataracts; lack of AQP4 leads to deafness because it is needed for proper cochlear function; and AQP1 is required for adequate intraocular pressure.
Cells counter the osmotic force exerted by the high intracellular concentrations of protein by making a predominantly extracellular particle (sodium) impermeant as well. Consequently, sodium is generally more concentrated outside the cell (extracellular) than inside the cell (intracellular) (Table 3-2). The osmotic force (Π for pressure) exerted by this one ionic gradient is huge, being proportional to the difference between the two concentrations (Table 3-3, the van’t Hoff equation):
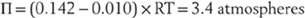
Table 3-3 Equations Governing Electrical and Chemical Forces at Equilibrium
Thus it is supremely important for the integrity of the cell that the contributions of all osmotically active particles sum to as close to zero as possible. The adjustments available to the cell that correct for small imbalances are the topic of the next section.
Electrical Forces
Cell proteins generally carry negative charges, and this large quantity of impermeant charge has important electrical consequences. In any solution, the number of positive and negative charges must be equal—the principle of microscopic electroneutrality. Because many of the cell’s negative charges are on proteins, the remaining intracellular anions (like chloride) must be reduced relative to their extracellular concentration. In osmotic terms, this concentration gradient acts together with sodium to minimize water flux across the cell membrane. In addition, chloride is also charged, and so electrical forces (measured as voltages) must also come into play as can best be understood by examining the numerical consequences of these interactions.
The best way to visualize the electrical forces involved in this chloride gradient is an approach that is analogous to the van’t Hoff equation (Table 3-3), namely, to calculate the force (in this case a voltage) that is generated by the ionic gradient by use of the Nernst equation (also in Table 3-3). For instance,
This mental image of chemical forces giving rise to electrical forces can be expressed in three equivalent ways: first, this voltage (VCl) is the potential at which Clo (chloride outside) is in equilibrium with Cli (chloride inside); second, the concentration gradient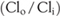 
is just offset by electrical forces at VCl; and third, at VCl, chloride movements into the cell are just equal to chloride movements out of the cell. Hence, this Nernst potential is also called the equilibrium potential for chloride, or simply the chloride potential.
Cations have the opposite valence of anions (the z term in the Nernst equation), and so (by the properties of the logarithm) the concentration gradient is inverted. Thus, for potassium, whose equilibrium potential is similar to that of chloride, the intracellular concentration exceeds the extracellular concentration (Table 3-2).
Returning to the case of sodium, its equilibrium potential is very different from that of potassium or chloride:
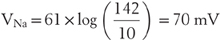
This difference is easily tolerated because sodium is the effectively impermeant ion in most cells. Indeed, the steep sodium concentration gradient is used to great advantage in the effective transport of fluid and generation of APs, as we shall soon see.
Membrane Potential
In the long run, individual neurons exist at a steady state, with osmotic forces across the cell membrane balanced and with the concentration gradients of the permeant ions offset by a characteristic voltage (Fig. 3-2). The relationship among these electrochemical parameters was first visualized by Goldman and further developed by Hodgkin and Katz as being governed by the permeabilities of ions across the cell membrane (Table 3-3). This relation is derived from the Nernst-Planck equation, with the algebraic contributions of individual ions being in proportion to PS, their steady-state membrane permeability. Although the PS is itself difficult to measure and awkward to express, relative permeabilities are more straightforward concepts. For instance, it is easily demonstrated experimentally that the potassium permeability of a nonmyelinated nerve axon is 100 times that of sodium (and then easy to say that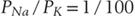 
). By use of these relative permeabilities, and postponing consideration of chloride until later, a more tractable form of the Goldman-Hodgkin-Katz voltage equation would be
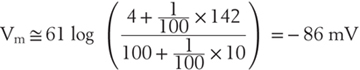
Potassium is now obviously the dominant ion in this calculation, with only a modest contribution from extracellular sodium.
This calculation is exactly the reason that we have introduced the concepts of electrical and concentration forces, namely, to demonstrate that the membrane potential is primarily due to the diffusion of potassium from the cell, withdrawing positive charges until the electrical potential across the membrane becomes approximately equal—but opposite—to the force generated by the potassium concentration gradient.
Cell chloride differs from the cations we have discussed not only because it is negatively charged but also because it is often in electrochemical equilibrium with its surroundings, which is to say that VCl = Vm. This is true in some nerve and muscle cells in which chloride serves to stabilize the membrane potential. In these cases in which the chloride equilibrium potential equals the membrane potential, VCl contributes nothing to the Goldman-Hodgkin-Katz calculation and can be safely omitted, as shown in the previous example. In other cells, chloride ions are pumped out, making VCl more negative than Vm. This is true in some postsynaptic nerve terminals, and when inhibitory neurotransmitters open chloride permeant channels, chloride ions diffuse passively into the neuron, transiently making the membrane potential more negative and thus more difficult to trigger an AP. Finally, chloride is actively accumulated in epithelial cells that secrete fluid, which is the subject of the next section.
Fluid Transport by Epithelia
The nervous system requires highly specialized fluids in the extracellular spaces of the brain, cochlea, and eye for the proper function of these organs. The brain is bathed in cerebrospinal fluid (CSF), a solution low in protein that is generated by the choroid plexus and removed through the arachnoid villi. The cochlear endolymph is high in potassium, and the ciliary body of the eye is continuously producing a nutrient solution that flows past the lens and is taken up by specialized veins along the margin of the iris.
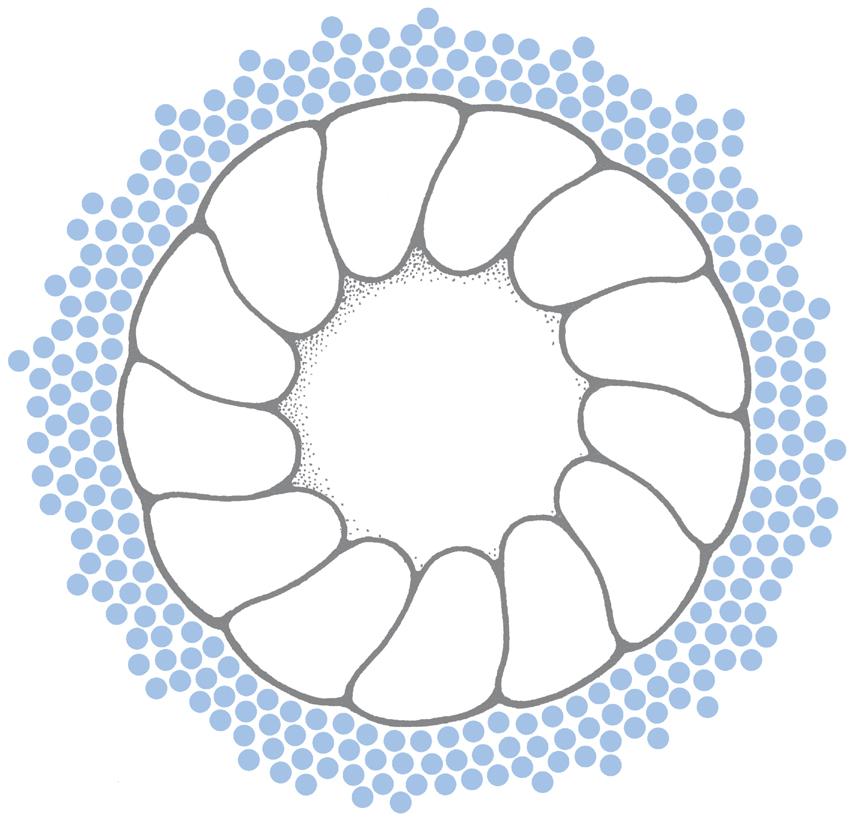
In each case, the specialized fluid is generated across an epithelial layer by the judicious placement of membrane pumps and channels (Fig. 3-2). Epithelial cells have two functionally distinct surfaces: the base and the sides (or basolateral surface), which are in contact with the interstitial fluid of the body; and the apical surface, which faces the lumen. Almost all epithelia restrict the sodium pump to the basolateral surface; the two exceptions are the choroid plexus and the retinal pigmented epithelium, in which the sodium pump is exclusively in the apical membrane. Individual epithelia then distinguish themselves by distributing characteristic channels and transporters on their apical and basolateral surfaces.
The sodium pump (a sodium-potassium adenosine triphosphatase, or ATPase) is a molecule present in all cells that moves sodium out of the cell and potassium into the cell (Fig. 3-2). This exchange generates a steep concentration gradient for the two ions, fueled by the chemical energy stored in molecules of ATP (hence, primary active transport). We have already seen that the potassium gradient determines the steady-state membrane potential. The sodium gradient is not only the basis of the AP, but it can also be harnessed to move large quantities of fluid. For instance, Na/2Cl/K cotransport pumps are present on the apical (ventricular) surface of the cells in the choroid plexus. The sodium electrochemical gradient provides the energy for this secondary active transport mechanism to drive potassium and chloride into the cell; specialized chloride channels on the apical surface then allow those ions to diffuse out of the cell. In addition, large quantities of carbonic anhydrase are present in the cells lining the choroid plexus, generating HCO–3 ions that accompany chloride into the CSF. These chloride and bicarbonate ions are accompanied by passive movements of sodium and water molecules as dictated by electrical and osmotic forces. (Potassium channels on the basolateral surface recycle that ion back into the interstitium.) Other cotransport mechanisms move nutrients, antibiotics, and a wide variety of other organic molecules into the CSF, generating liters of CSF a week, all the time keeping an effective barrier against erythrocytes, leukocytes, and plasma proteins.
Modifying the placement and nature of the cell’s pumps and channels alters the composition of the secreted fluid. For instance, cochlear endolymph is high in potassium because its epithelial cells have their potassium channels on the apical side, causing the potassium and chloride pumped into the cell by the basolateral Na/2Cl/K cotransporter to exit the cell together into the scala media. Thus it can be seen that the large and effective concentration gradients and the osmotic and electrical forces present in neurons require energy input by the sodium-potassium pump. However, the body has adapted these forces, each required for the physical integrity of the cell, to a wide variety of other purposes.
Ohm’s Law and the Equivalent Electrical Circuit of the Neuron
The resting membrane potential refers to the neuron at a steady state and is largely the result of the potassium, chloride, and sodium diffusion potentials; in addition, membrane currents—electrical charges carried by ions crossing the cell membrane—modify this voltage as described by Ohm’s law:
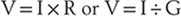
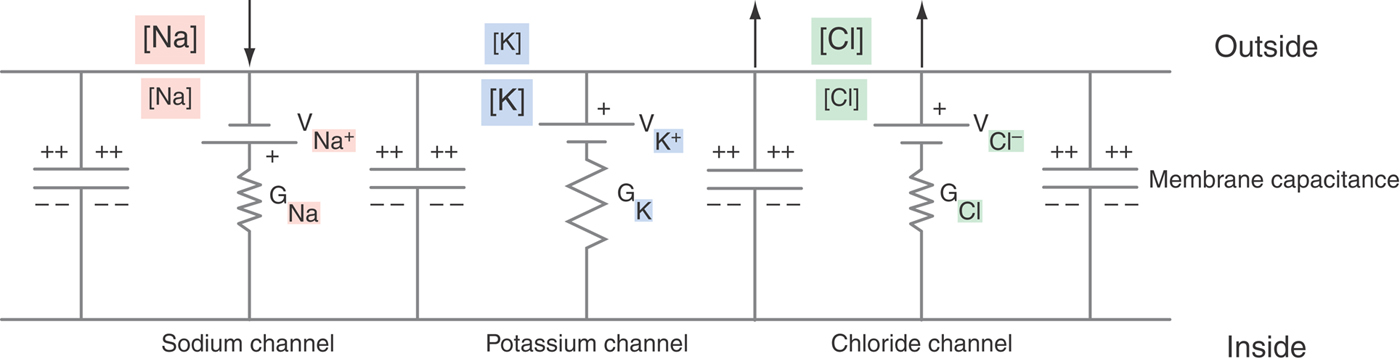
Thus current (I, in amperes) flowing through a conductance (G, in siemens) or across a resistance (R, in ohms) will generate a voltage drop (Fig. 3-3). By a convention established by Benjamin Franklin, electrical current is the flow of positive charges: positive charges leaving the cell are defined as a positive current. Equivalently, negative charges entering the cell are also a positive current. Conversely, positive charges entering the cell are a negative current, as is the exit of negative charges. A familiar example is the sodium pump, which is electrogenic because it cycles three sodium ions out of the cell for every two potassium ions in; this net positive current removes positive charges from the cell interior, causing the membrane potential to be more negative than predicted by the Goldman-Hodgkin-Katz voltage equation. In a cell as large as a skeletal muscle fiber, this amounts to ~2 to 5 mV. In small nerve terminals, where the input resistance is much greater, this current can hyperpolarize the membrane by 15 mV or more.
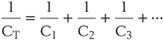
Of even more interest is the flow of current through open membrane channels because the number of open channels varies when the nerve is stimulated in any of a wide variety of ways. From Ohm’s law, the magnitude and direction of the flow of an individual ion S through the cell membrane equals the driving force on that ion times its conductance:
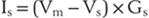
The electrical driving force on S is the difference between the voltage across the membrane (Vm) and that voltage where the ion is at electrochemical equilibrium (VS, the Nernst potential for substance S). These relationships are summarized diagrammatically, for those familiar with electrical circuits, in Figure 3-4. Thus the magnitude of the ionic flow will increase as the driving force—or the conductance—of the ion increases and decrease as it decreases. In the face of an increasing conductance and a decreasing driving force, a situation that is described in the section on the AP, specific calculations are required to determine the final outcome.
We can use the circuit theory in Figure 3-3 to calculate the number of charges (Q) on a cell membrane that has a given voltage (V) because Q = V × Cm, and the capacitance of a cell membrane (Cm) has been measured to be 0.9 µF/cm2. If a hypothetical neuron were spherical (for simplicity) and 20 µm in diameter, it would have a surface area of almost 1300 µm2, a capacitance of 11 pF per cell, and thus a charge of 1 pC (picocoulomb) when the membrane voltage is 90 mV. The 1 pC of charge on the membrane represents 6 million ions. Although this may seem to be a lot, the cell volume of this neuron would be 4 pL (picoliters) and contain ~250 billion potassium ions and ~25 billion chloride ions. Together, these two ions alone are ~40,000 times the number required to charge the membrane.
Pain and a Syndrome of Periodic Paralysis
Pathologic conditions may alter the concentration of ions ordinarily seen in nerve cells (Table 3-2). For instance, tissue injury causes a local increase in the potassium concentration as these cells release their contents. This increased extracellular potassium moves the steady-state membrane potential toward 0 mV, which generates APs when it is done quickly enough. Thus one source of pain is simply the direct stimulation of nerve endings by elevated potassium concentration in the tissue interstitium.
In rare individuals who have certain genetic abnormalities, extracellular concentration of potassium can fall dramatically when epinephrine or insulin stimulates its uptake by muscle cells, leading to muscle weakness and even paralysis. This condition is called hypokalemic periodic paralysis. Surprisingly, the muscle membrane potentials are less negative than normal, just the opposite of what the Nernst equation predicts. For reasons not yet fully understood, the cell membrane loses its ability to select potassium over sodium, which is to say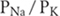 
declines markedly. The effect is so great that the cell is depolarized because the membrane potential moves away from VK toward VNa, as the Goldman-Hodgkin-Katz voltage equation predicts. This membrane potential change is slow, allowing the muscle fiber to undergo accommodation and so become inexcitable. (Accommodation is explained more fully in the section on APs.)
Attack by the Immune System: Membrane Attack Complexes and Porins
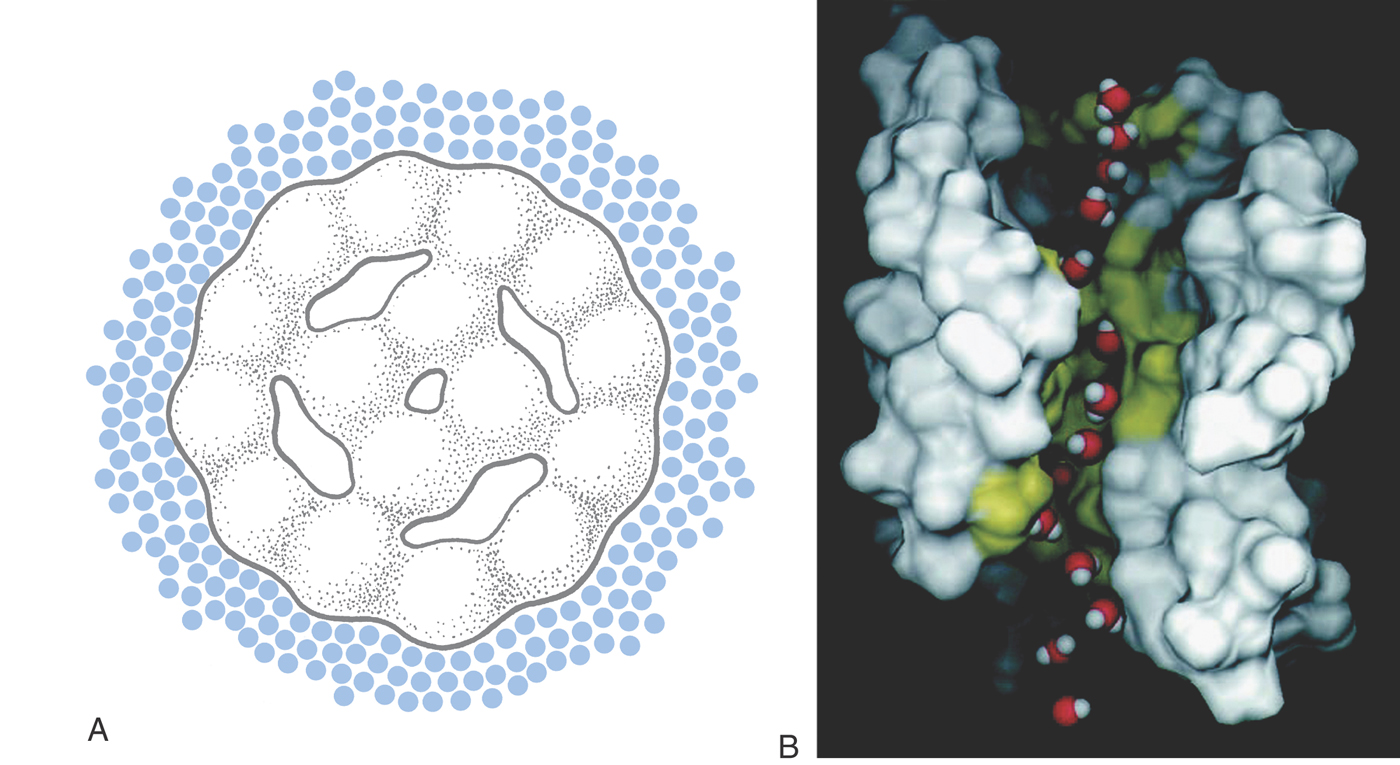
The nervous system can be attacked by bacteria and even the body’s own immune system in ways that short-circuit membrane potentials and destroy the cell’s integrity. Attack by the immune system depolarizes the cell membrane by insertion of nonselective channels into cell membranes. This mechanism is one weapon of self-defense used by the human body’s own cellular and humoral immune systems. The pore-forming elements of the body’s immune system are the porins, from killer T lymphocytes; defensins, produced by phagocytes and epithelial cells; and two elements of the complement cascade, C8 and C9. C8 forms individual, <3-nm pores; C9 aggregates to form >10-nm pores, termed membrane attack complexes (MACs, Fig. 3-5). (MACs attack myelin sheaths of motor neurons, causing a paralysis discussed later in this chapter.) At 16 nm, porins are even larger.
The channels through MACs and porins are wide enough to easily pass sodium, potassium, chloride, and sucrose, discriminating little among them. The channels’ conductances are correspondingly large: 2 nS (nanosiemens) for the MAC and 6 nS for porin. As a consequence, the formation of just a single C9 aggregate or insertion of a single porin molecule results in a large flow of ions. As in all nonselective channels, the currents flowing through MAC and porin channels are carried primarily by sodium ions because the magnitude of the driving force for sodium is the greatest: |Vm − VNa| >> |Vm − VCl| > |Vm − VK|. If Vm = −90 mV (to take a simple example), the driving force on the sodium will be
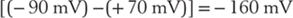
and the current flowing through the MAC is easy to calculate:
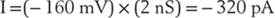
Because one ampere is the flow of 6.3 × 1018 charges per second, the number of sodium ions flowing through a single MAC is 2 × 109 per second, a rate so fast that the membrane potential of our previous example (the 20-µm neuron) would be neutralized in [(6 × 106) ÷ (2 × 109)] = 3 × 10−3 seconds.
By following the movements of the various ions due to the electrical forces on them, it is possible to see that the cell gains osmotic particles and so swells. For instance, because the net driving force on sodium is negative, it will enter the cell, with its positive charge tending to cancel the negativity of the membrane potential. In fact, the cell membrane potential will rapidly go to zero and remain there as long as the MACs are in the membrane. As a consequence, the driving force on chloride will increase; (Vm − VCl) being positive, the current will be positive, meaning that chloride is entering the cell along with the sodium. Thus, when sodium and chloride enter the cell, water follows, and the cell swells. Even more important, the MAC complexes are so large that molecules the size of ATP can diffuse from the cell. Thus attack by complement or killer T lymphocytes leads inexorably to cell swelling and lysis both because important metabolic contents are lost and because the osmotic pressures exerted by the remaining cell proteins cause cell swelling and death.
Microbial Attacks: Antibiotics
Insertion of ion channels into cell membranes is also a weapon deployed by many microorganisms. Antibiotics such as amphotericin and gramicidin, and α-staphylotoxins from Staphylococcus aureus, lyse cells by broaching their membranes with large pores. When it is used clinically, amphotericin preferentially attacks fungal cells in fungal meningitis, but there is a narrow therapeutic range because amphotericin also attacks cell membranes in the nervous system. In overwhelming sepsis, α-staphylotoxins attack all cells of the body, leading to multiple organ failure and cardiovascular collapse, primarily due to the loss of the integrity of cell membranes.
GRADED POTENTIALS
Electrical events underlie much of the nerve activity in our body. Indeed, many of our ordinary feelings and sensations begin with graded potentials that are due to continuous changes in the ionic conductance of the sensory receptor’s cell membrane and, consequently, the cell membrane potential itself. Similarly, nervous input is electrically integrated by the combined actions of excitatory and inhibitory synapses on nerve cell bodies. Finally, APs are regenerative electrical signals that transmit the information to distant cells. The remainder of this chapter explains how the principles governing chemical and electrical forces contribute to the function of the nervous system.
Generator Potentials
All body sensations are graded, with transduction mechanisms generating bigger electrical signals—and consequently more APs—for bigger stimuli. These graded responses are generator potentials that can be the direct result of the stimulus opening membrane channels or increasing the current through existing membrane channels. More often, intermediary chemical signals connect the initial sensation to the opening of membrane channels, the identity of which is just now being elucidated in experimental settings (Table 3-4).
Table 3-4 The Graded Potentials of Sensation Are Mediated by a Variety of Gene Families*
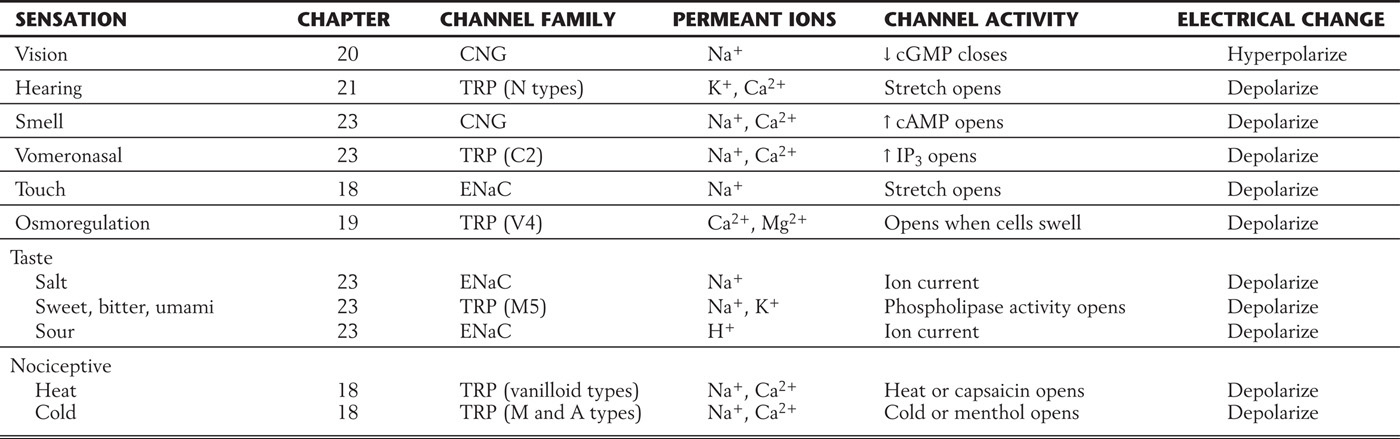
*Members of several large gene families are used for sensing stimuli, including CNG, the cyclic nucleotide–gated family of potassium channels; TRP, the transient receptor protein family; and ENaC, the epithelial sodium channel family.
Many sensations are transduced by more than one mechanism, depending on the importance of the sensation or the strength of the signal—for instance, the sensing of changes in osmotic pressure by both visceral and hypothalamic receptors. Indeed, this ability is widespread throughout the body, in which many cells respond autonomously to the shrinking or swelling of their volume. Considering the fundamental importance of the maintenance of intracellular proteins, it is not surprising that osmosensors are present in lower animals as well. The best understood of these stretch-activated channels (MscL, the mechanosensitive channel of large conductance, Fig. 3-6) is tethered to the cytoskeleton and cell membrane and is closed off at its inner edge by loose coils of its C-terminal sequence. With stretch, the whole MscL molecule dilates as the cytoskeleton tugs on it, initially uncoiling the redundant structure at the channel’s inner mouth and finally opening a 4-nm-wide channel that spans the full width of the membrane. The action of the MscL gives an example of a transient, graded sensory system with negative feedback: if the extracellular osmotic pressure falls, the cell swells, opening MscL channels, resulting in the loss of osmotically active particles and thus water. As a consequence, the cell shrinks and the channels again close.
Synaptic Potentials
Vertebrate nervous systems use chemicals to communicate between cells, as already introduced in Chapter 1 and Chapter 2, and these signals alter the target nerve or effector cell by a combination of electrical and metabolic mechanisms, as is more fully described in Chapter 4. The most specialized structure supporting this chemical signaling is the synapse, and the best understood synapse is the neuromuscular junction (NMJ), in large part because it is readily accessible for experimental investigation (see Chapter 2, Chapter 4 and Chapter 24). For this reason, the NMJ will be used extensively to illustrate the nature of the synaptic potential.
Like generator potentials, neurotransmitters may act to open membrane channels either directly or via intermediary signals. For instance, acetylcholine (ACh) opens the nicotinic receptor at the NMJ directly. In contrast, the cholinergic muscarinic receptor is a G protein, in which case ACh acts indirectly by two mechanisms. The first is to release the Gβγ subunit, which opens certain potassium channels. The second is to stimulate or to inhibit adenylate cyclase and various lipases, altering the concentrations of cyclic adenosine monophosphate (cAMP), the inositol phosphates, diacylglycerol, and calcium. Closely related structurally to the nicotinic ACh receptor are the ligand-gated channels for GABA (the GABAA receptors), serotonin, and glycine, and the behavior and pharmacology of those channels are similar in many ways to those of the ACh receptor. The glutamate and the purinergic receptors are evolutionarily and functionally distinct from this family and from each other.
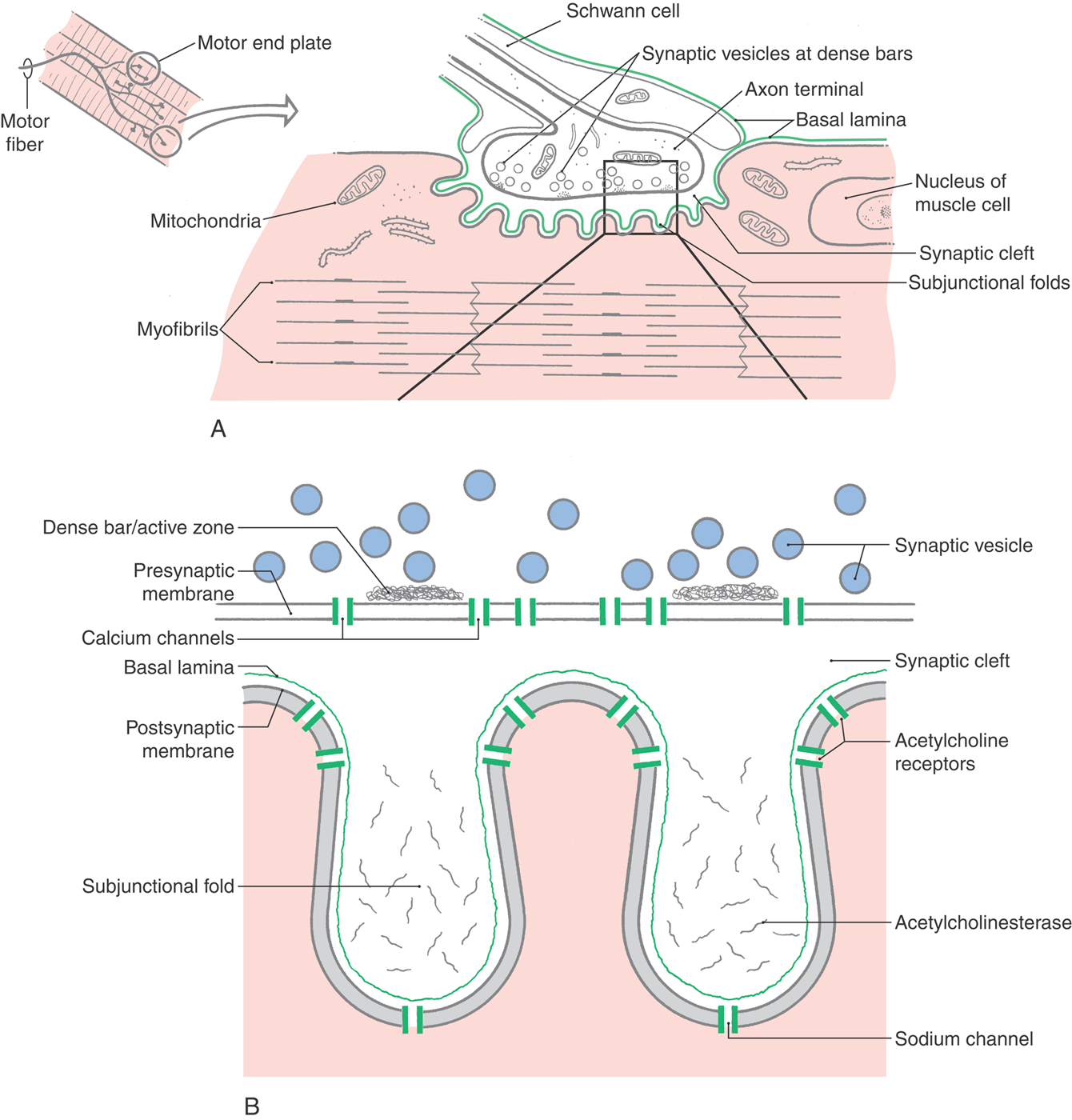
Synaptic Structure and Function: The Neuromuscular Junction
Motor nerve axons branch at their termini to innervate many muscle fibers, all of which contract together as a motor unit. The myelin sheath stops at each nerve terminal, exposing the naked axon to the muscle membrane at a specialized disk-shaped region called the motor end plate (Fig. 3-7). In this region, numerous transmitter-filled vesicles are gathered about release points, the active zones, which are stripes of docking proteins close to voltage-sensitive calcium channels. In electron microscopy, these aggregations of proteins are called dense bars. Such an arrangement allows an efficient coupling of the motor nerve’s AP, the resulting voltage-dependent calcium influx, and finally the calcium-dependent release of the transmitter vesicles’ contents.
The membrane of the skeletal muscle fiber is thrown up into numerous subjunctional folds in the end plate region, with the tops of the folds situated immediately opposite the active zones of the nerve terminal. Clustered on the top of the folds are nicotinic acetylcholine receptors (AChRs), which respond to released neurotransmitter (acetylcholine) by increasing the conductance of the muscle membrane to sodium and potassium. The released transmitter reaches the AChRs within tens of microseconds after release, ensuring a speedy transmission. Equally important, the transmitter will not have time to disperse, guaranteeing that the dense cluster of AChRs will be exposed to a high concentration of transmitter; consequently, almost all the released transmitter will be bound to and act on the receptors. Clustered at the base of the folds are large numbers of voltage-dependent sodium channels, guaranteeing that one muscle AP will fire for each AP in the motor nerve.
Between the nerve and the muscle lies a narrow but very deep synaptic cleft. The cleft matrix contains a basal lamina with collagen and laminin that combine to keep the nerve and muscle in close approximation and precise register during the active muscle activity. The depths of the synaptic cleft contain a high concentration of acetylcholinesterase (AChE) molecules that are held in place by their long collagen-like tail. Thus one purpose of the synaptic cleft is to trap ACh and to rapidly hydrolyze the transmitter into choline and acetate. This positioning ensures that little ACh diffuses out from under the nerve terminal and that the transmitter is present for only a brief (~1 ms) time.
Receptor Binding and Channel Gating
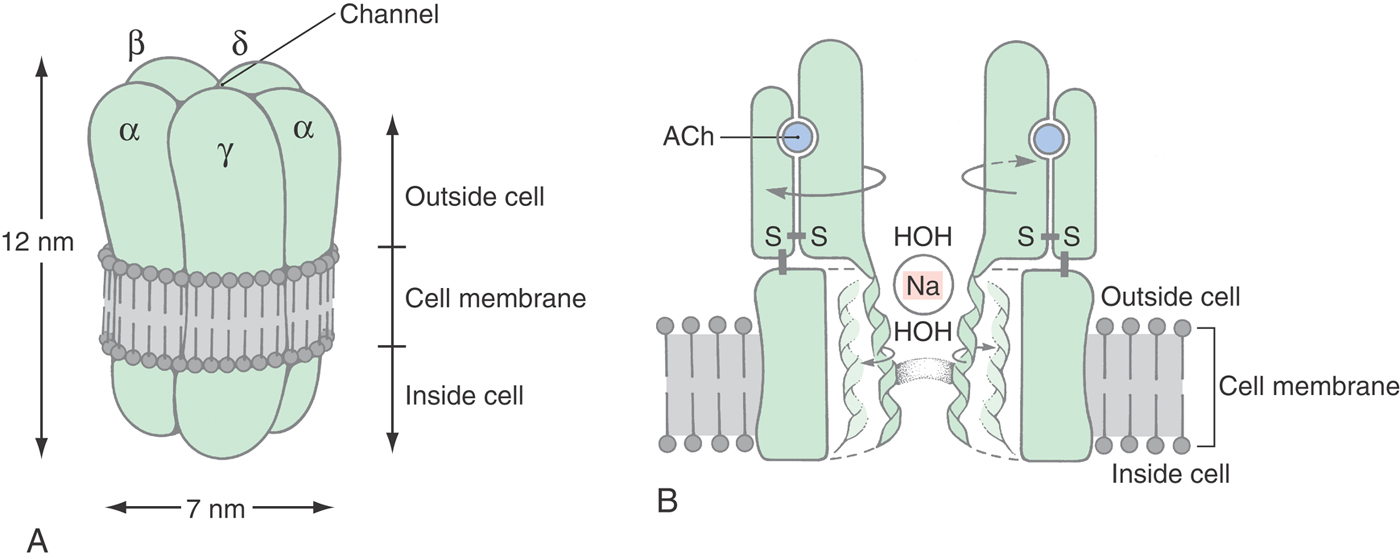
All synaptic receptor molecules have a distinct region that specifically binds the transmitter. In the case of the NMJ, one or two ACh molecules bind in a highly specific manner to the large extracellular portion of the AChR molecule (Fig. 3-8). The binding sites each span two subunits: the αε (or γ) and the αδ interfaces. In the presence of the transmitter, three loops of the α subunit come together with a loop of the ε or δ subunit to form a box of nonpolar and aromatic amino acids, primarily tryptophans and tyrosines. The open, conducting conformation is stabilized when ACh is in this box. Because there are two α subunits in the receptor complex, two ACh molecules must be bound before ion flow can begin. Once the first ACh leaves, its α subunit is free to close, at which time ion flow ceases.
The specificity of the AChR binding site has been used by pharmacologists to design molecules that specifically relax skeletal muscle fibers (for instance, during surgery) but have no unwanted side effects on heart or vascular smooth muscle contractility. Curare, a plant product, was the first of these muscle relaxants; succinylcholine and many more have been designed for particular purposes. The duration of action and potency of effect are largely due to the affinity of the drug to the binding site, which in turn reflects how well the drug fits into the box-like geometry of the amino acids that comprise the αε and the αδ interfaces.
Just as specific muscle relaxants bind to the AChR, other receptors also have characteristic activators and inhibitors. Strychnine binds to the glycine receptor, blocking its inhibitory activity and leading to a hyperexcitable state, a tool used long ago by medical students to remain alert for exams; this was effective but only within a very narrow range of dosing because slightly higher doses cause convulsions. Benzodiazepines bind to GABAA receptors, increasing the effectiveness of the endogenous GABA; barbiturates bind to GABAA receptors, inhibiting their activity. Thus specificity of action within the nervous system reflects in part the different structures of receptor molecules in their transmitter-recognition region.
Specific Responses via Increases in Ionic Permeability
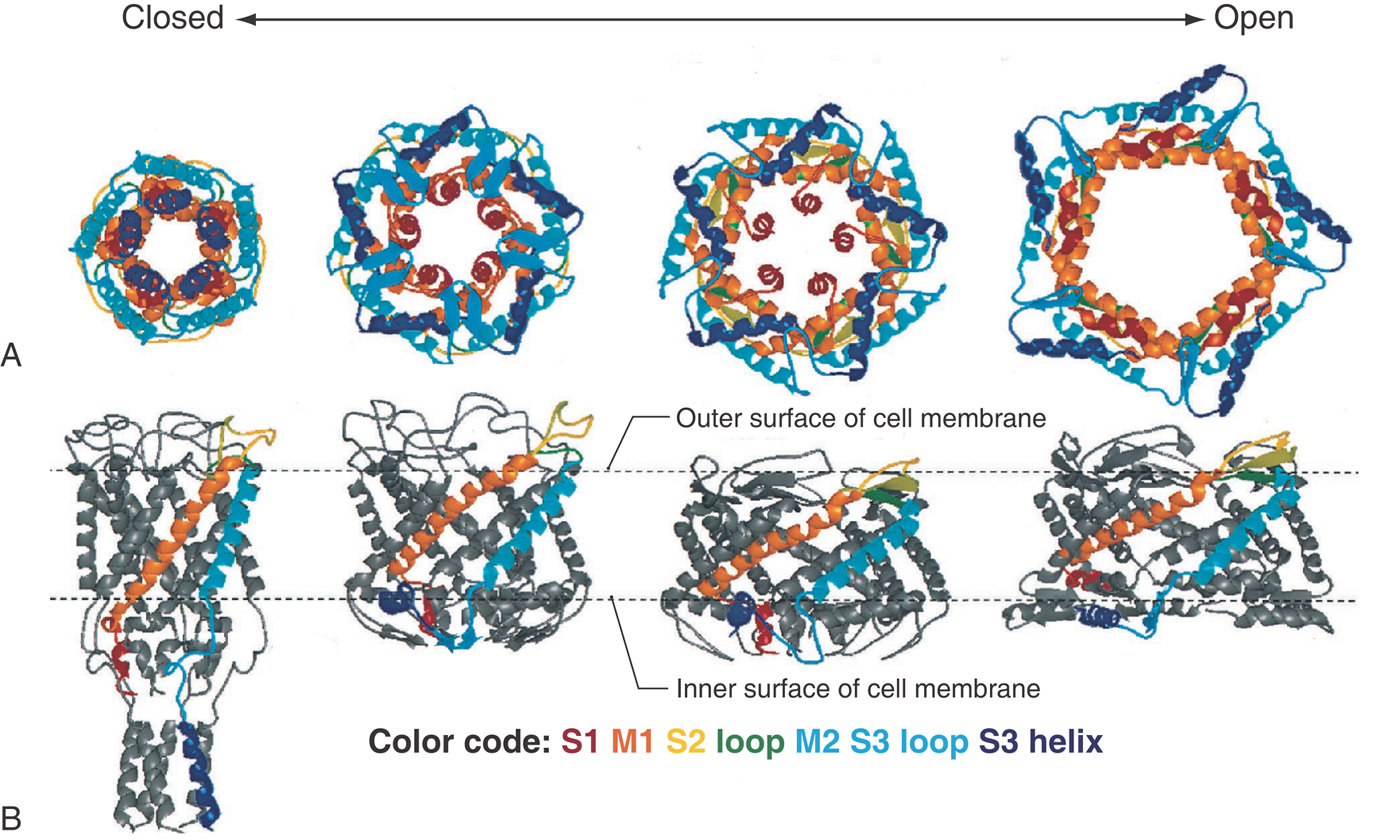
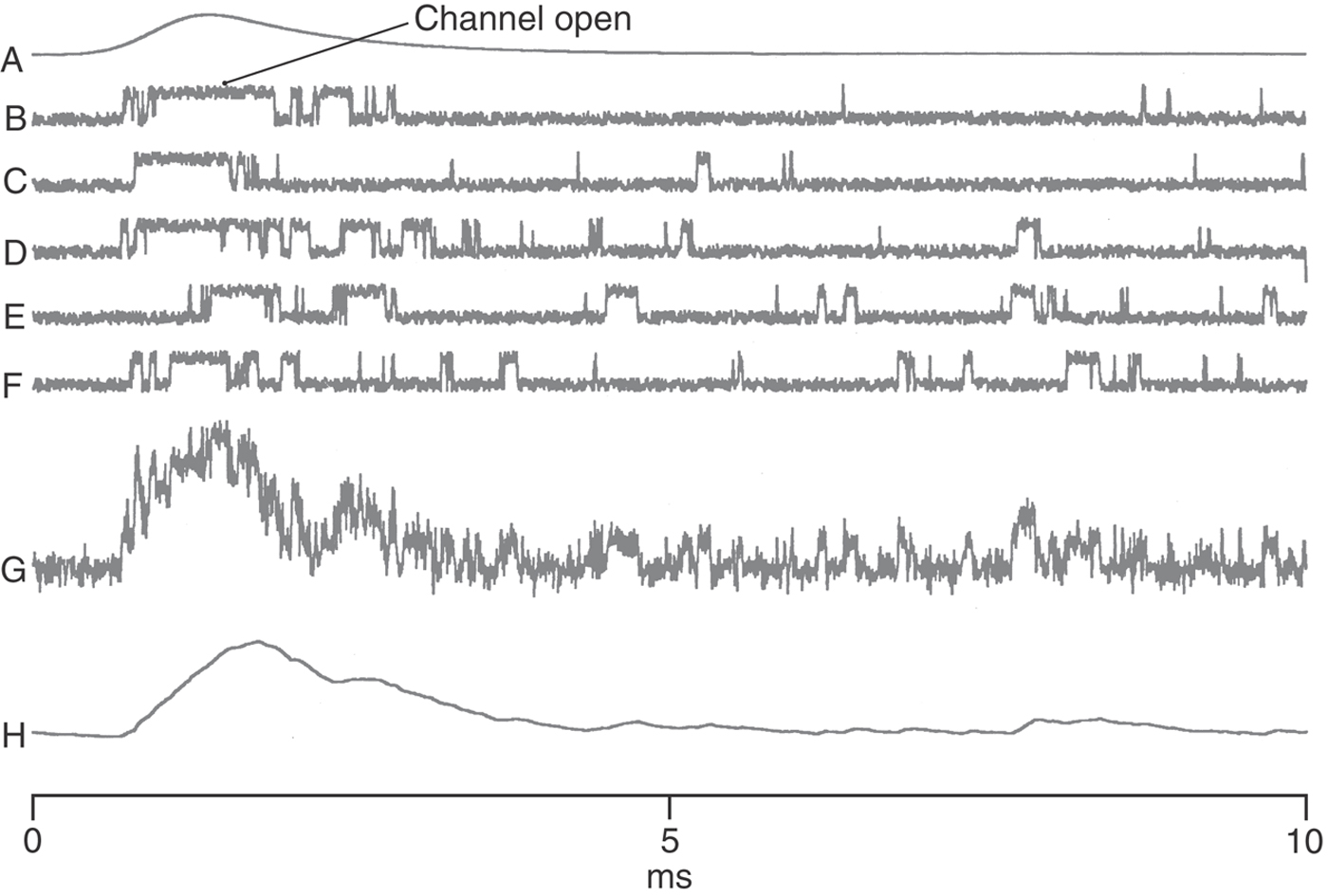
The specific recognition of a transmitter molecule is only one of the two necessary functions of a receptor molecule; the second is to effect a change in the target cell. The nicotinic AChR is an example of those receptors that open to expose a water-filled channel that spans the membrane and that selectively allows ionic currents to flow down their electrochemical gradients. The narrowest region of the AChR channel is girdled by the hydrophobic amino acids leucine and valine and forms a gated barrier to the movement of charged atoms (Fig. 3-8). When this gate is open, uncharged and positively charged molecules smaller than 0.65 nm × 0.65 nm can pass through; negative ions are excluded by multiple rings of negatively charged amino acids. Individual channel activity can be demonstrated electrically by the patch clamp technique (Fig. 3-9).
Because ACh activates cation-permeable receptors at the NMJ, this transmitter generates an end plate potential (EPP), which is one specific type of excitatory postsynaptic potential (EPSP), and which is explained in the following way. The conductance of the postsynaptic membrane (ΔG) increases in proportion to the number of channels opened (n) and the conductance of an individual AChR (γ):
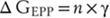
In the case of this AChR, the channel is permeable to both sodium and potassium, so the reversal potential (VACH) is approximately 0 mV. Consequently, the current flowing through this new conductance will be negative—or inward—and so will depolarize the muscle fiber (again assuming a resting membrane potential of −90 mV):
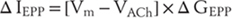
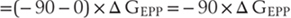
Other synapses in the nervous system act to inhibit neuron activity. These include synapses activated by glycine and GABA, both of which open anion-selective chloride channels because chloride carries most of the synaptic current. Since the chloride equilibrium potential is slightly more negative than the steady-state membrane potential of most neurons, the current of the inhibitory postsynaptic potential (IPSP) will be positive and will tend to hyperpolarize the cell:
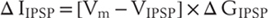
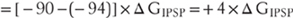
Muscle Weakness: Failure of Transmission at the Neuromuscular Junction
Under normal circumstances, the EPSP at the NMJ is always large enough to provide an adequate stimulus for an AP to fire, and so there is a one-to-one correspondence between the firing of the motor nerve and the muscle’s AP. Alcohols and local anesthetics interfere with NMJ transmission by preventing ion permeation; the vestibule of the AChR is large enough to admit local anesthetic molecules, which bind tightly and prevent ions from passing. The region behind the gating α helix is also water filled and contains a specific site for alcohol and the binding of local anesthetics such as lidocaine (arrow in Fig. 3-8).
Toxins also specifically interfere with synaptic transmission at the NMJ. The three botulinum toxins are metalloproteinases that specifically attack the docking proteins syntaxin, synaptobrevin, and SNAP-25 on the presynaptic side of the NMJ. This effectively interrupts exocytosis and causes a paralysis that lasts until new docking proteins are synthesized. α-Latrotoxin, the toxin of the black widow spider, specifically binds to neurexin, another docking protein, causing first a massive emptying of the nerve terminal of neurotransmitter vesicles and then a complete loss of that end plate’s function.
Acquired myasthenias—those diseases characterized by muscle weakness—can be due to the activity of the immune system. Myasthenia gravis is the most common syndrome, characterized by the fluctuating severity of the weakness, by the early involvement of ocular muscles, and by its response to cholinergic drugs. In myasthenia gravis, a small area of the extracellular region of the AChR—nanometers away from the transmitter binding site—is vulnerable to autoimmune attack. These amino acids form an epitope that is shared by peptides expressed during certain viral illnesses and by cells in the thymus that can activate antigen-specific T lymphocytes. Antibodies generated as a consequence of this activity may cross-link AChRs, increasing their rate of endocytosis and consequent lysosomal destruction, and reducing their normal lifetime from a week to half that value. When the increased rate of loss becomes sufficient, the current generated during the end plate potential will be insufficient to trigger the nerve AP, and muscle weakness will ensue. In other individuals, the antibodies bind complement, leading to the formation of MACs and lysis of the muscle cell. In still other individuals, the antibodies are of no pathologic consequence whatsoever, so a simple determination of antibody titer is not absolutely predictive of the severity of the disease. In the longer term, the severity of the immune response is reduced by the use of corticosteroids or more powerful immunosuppressive agents, or the thymus may be removed. The most direct treatment is the use of drugs that inhibit cholinesterase activity, such as the anticholinesterase pyridostigmine.
Anticholinesterase therapy is designed to increase and to prolong the synaptic concentrations of ACh. An untoward consequence of intensive anticholinesterase therapy is the desensitization of AChRs by the prolonged exposure to ACh. When the desensitization progresses too far, the loss of functional AChRs overtakes the benefit of the prolonged exposure to transmitter, and the patient becomes weaker. This condition, termed a cholinergic crisis, is a therapeutic dilemma; any individual patient might become weaker because the immune disease worsens or because the number of AChRs is being reduced through desensitization. The test to distinguish between the two possibilities is the double-blind use of a short-acting cholinesterase inhibitor (with a ventilator nearby in case the patient becomes too weak to breathe): if the patient’s strength is improved, then the immune disease is becoming worse and the anticholinesterase therapy must be increased; if the patient weakens, then he or she is in a cholinergic crisis, and the anticholinesterase therapy must be reduced.
Muscle weakness may also accompany small cell carcinoma of the lung owing to the production of antibodies to calcium channels in the presynaptic nerve terminal. In this situation, the weakness is a paraneoplastic process—a syndrome that is associated with a primary neoplasm elsewhere in the body. Such a condition is variously called the myasthenic syndrome or the Lambert-Eaton syndrome. Characteristically, these patients gain strength with repeated muscle activity, unlike those with myasthenia gravis, who fatigue more rapidly than normal. This improvement is due to repeated firing of the nerve AP that causes potentiation or facilitation of transmitter release as more calcium enters the nerve terminal with each succeeding AP. With sufficient activity, many of the affected nerve terminals will again have adequate calcium to release transmitter to generate a muscle AP.
ACTION POTENTIALS IN THE NERVE AND IN THE NEURON
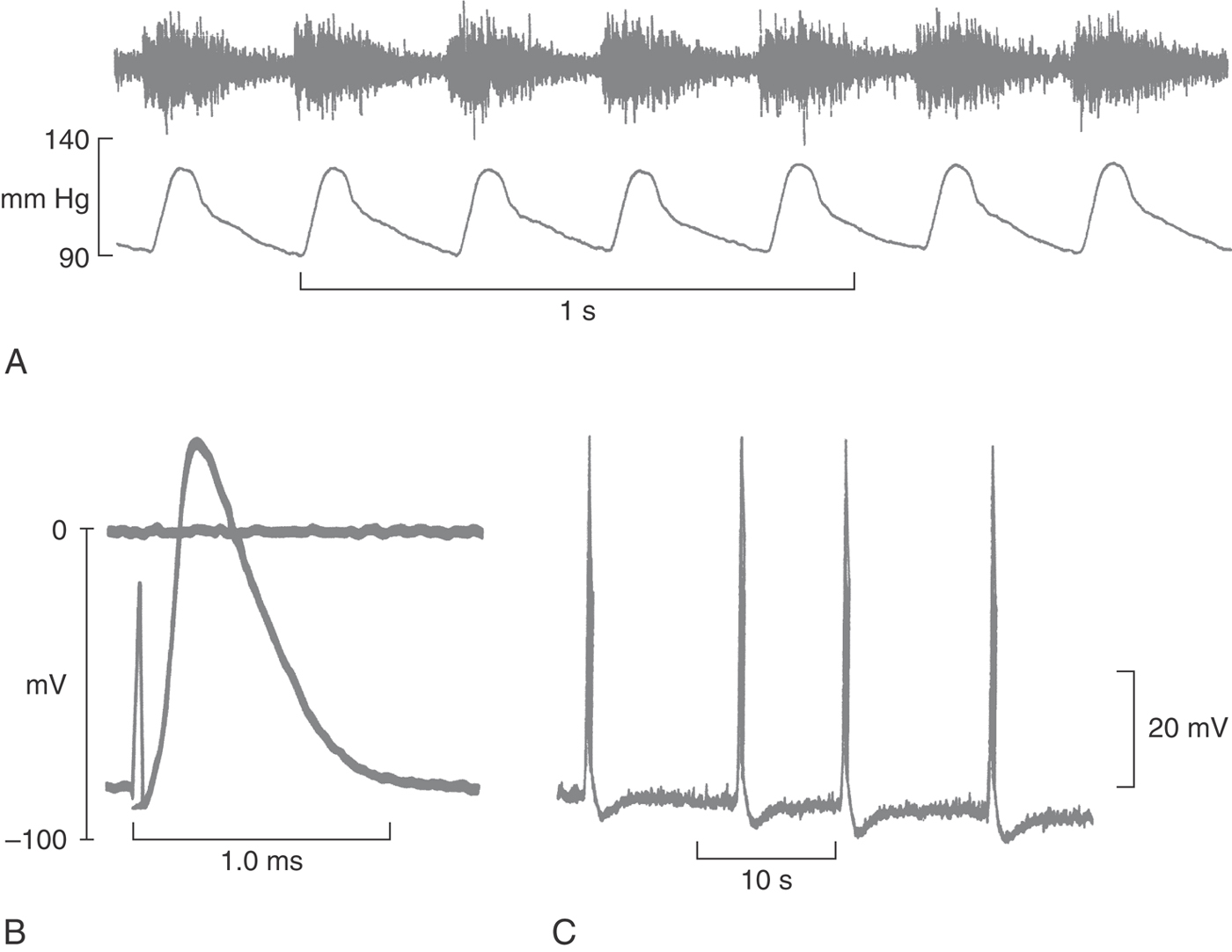
APs are brief electrical transients, visible when recorded as intracellular voltages or extracellular currents (Fig. 3-10). APs occur throughout the body’s tissues, regulating secretion of insulin from the islets of Langerhans and secretion of aldosterone from the zona glomerulosa and even signaling fertilization of the egg by the sperm. In the nervous system, APs serve to integrate the generator potentials from sense organs and the synaptic input to cell bodies, with the magnitude of the result being sent down the neuron’s axon encoded as a frequency. Axonal APs can travel for a meter or more without decrement and without distortion, at speeds that can be maximized by increasing the axon diameter or by adding insulating layers of myelin. Such fidelity is possible because the AP is a self-regenerating electrical signal that is automatically produced by the inherent properties of specific membrane proteins.
Extracellular recordings of nerve activity monitor APs in many nerve fibers at once (Fig. 3-10A). In this case, afferent nerve fibers from the carotid body baroreceptors are seen to fire rhythmically in response to the increase in arterial blood pressure during systole. These fibers have a low degree of tonic activity plus a superimposed phasic discharge proportional to the rate of change in blood pressure.
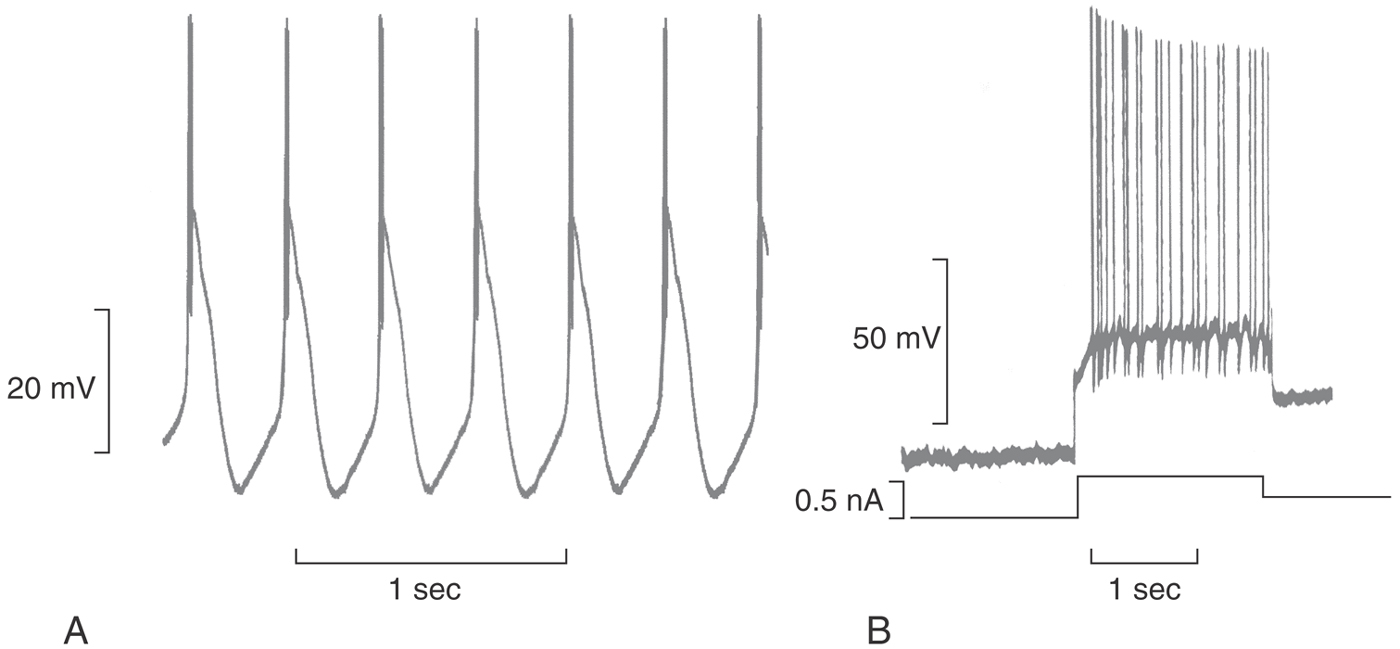
An understanding of the many varieties of APs in individual nerve cells is made possible by intracellular recordings. At one extreme is the axon of a myelinated nerve (Fig. 3-10B), which is electrically silent except when an AP is triggered at the axon hillock of the cell body. The AP is complete within a millisecond and reflects the activity of a single active current. More complex APs are seen in pyramidal cells of the hippocampus (Fig. 3-10C), which are entrained to the firing of other pyramidal cells. These APs contain three or four spikes and end with a hyperpolarizing afterpotential. The remainder of this chapter characterizes these APs more fully and describes the mechanisms that generate their complex waveforms.
Compound Action Potentials
Much of the nerve activity described in this book was demonstrated in experiments that used extracellular electrodes to record the combined firings of many individual nerve fibers (such as electroencephalograms, which are recordings from regions of the brain, and electromyograms, which are recordings from peripheral nerves, such as Figs. 3-10A and 3-11). The electrical basis for these recordings lies in the membrane currents that flow during the APs. As the sodium ions first enter the nerve cell and then potassium ions leave, electrical charges are removed and then added to the extracellular fluid. Because the extracellular fluid is a solution of various salts, it has electrical resistance, and so the flow of these ions is an electrical current that generates a voltage (Ohm’s law).
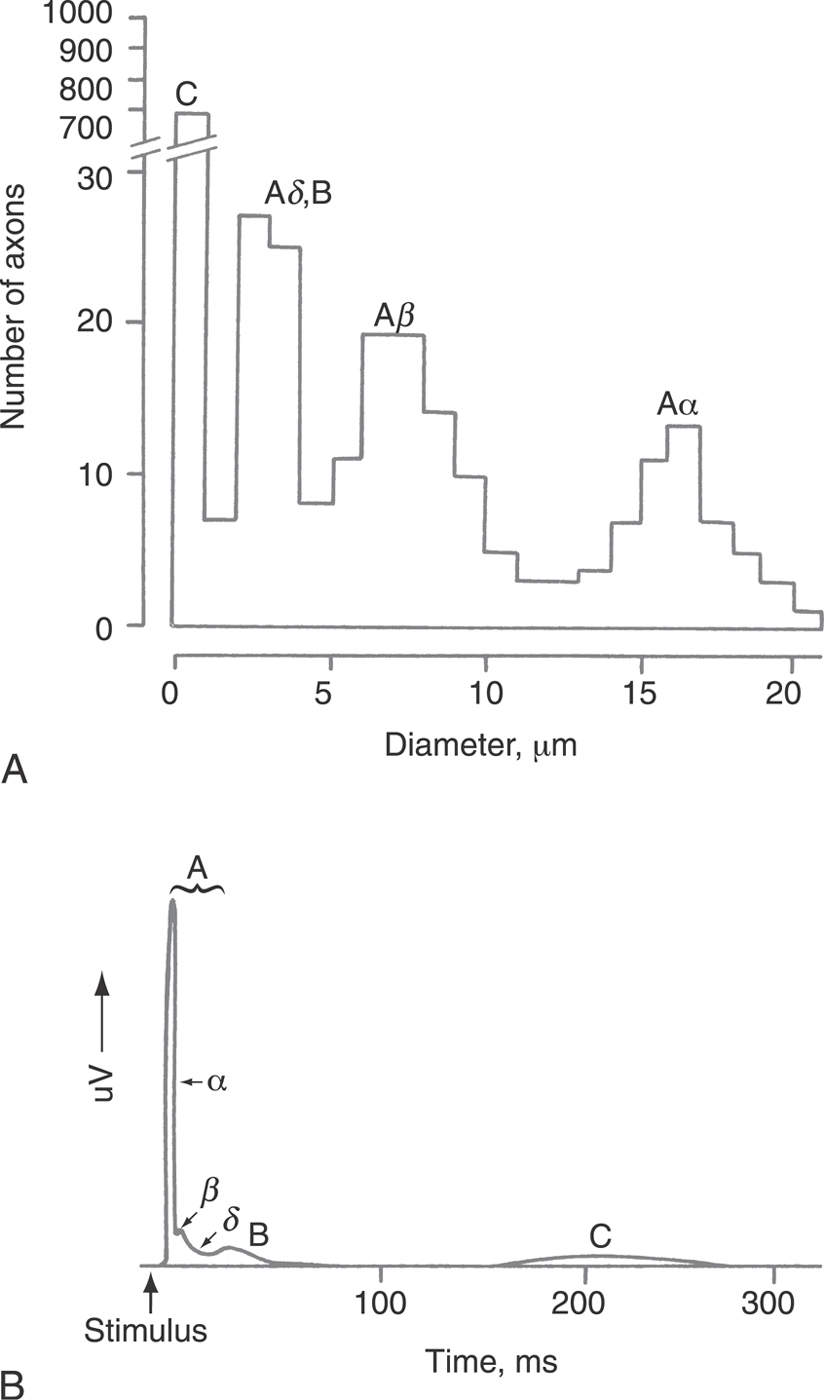
Whereas nerve axons vary in size from less than 1 µm to more than 20 µm, their sizes generally cluster into four groups (Fig. 3-11). The smaller axons conduct APs more slowly than do the larger axons, so it is reasonable that any given nerve bundle or tract of nerves contains fibers that can be grouped by their conduction velocities. The four different groups each have a characteristic set of functions, which is more fully described in Chapter 17.
In clinical practice, nerve conduction velocity measurements are often performed to determine if nerve transmission is slower than normal by stimulating a peripheral nerve with a pair of electrodes and recording the resulting compound AP at a distance (Fig. 3-11B). For instance, an electrophysiologist might stimulate the median nerve at the elbow and record the compound AP in the volar aspect of the hand to test if there is a compression neuropathy in the carpal tunnel. At a low stimulus strength, only the Aα peak appears, as the largest fibers have the lowest thresholds. For a 30-cm separation between the stimulating and the recording electrodes, the delay should be 4 ms because the expected conduction velocity is expected to be 80 m/s or more. In a diabetic or a compression neuropathy, the speed would decline or conduction would fail altogether. With increasing stimulus intensity, smaller and smaller fibers are recruited, and additional peaks appear at longer latencies; they are later because they are slower. Significantly, the magnitude of the signal is not a good indicator of the number of fibers of a given group; the larger diameter nerves have proportionately greater amounts of membrane and so will contribute much larger signals than will small nerves. In fact, Figure 3-11A shows that there are many more C fibers than A or B fibers, yet the C fiber electrical signature is much smaller than the A fiber peak (Fig. 3-11B).
Cable Properties of Nerve Processes
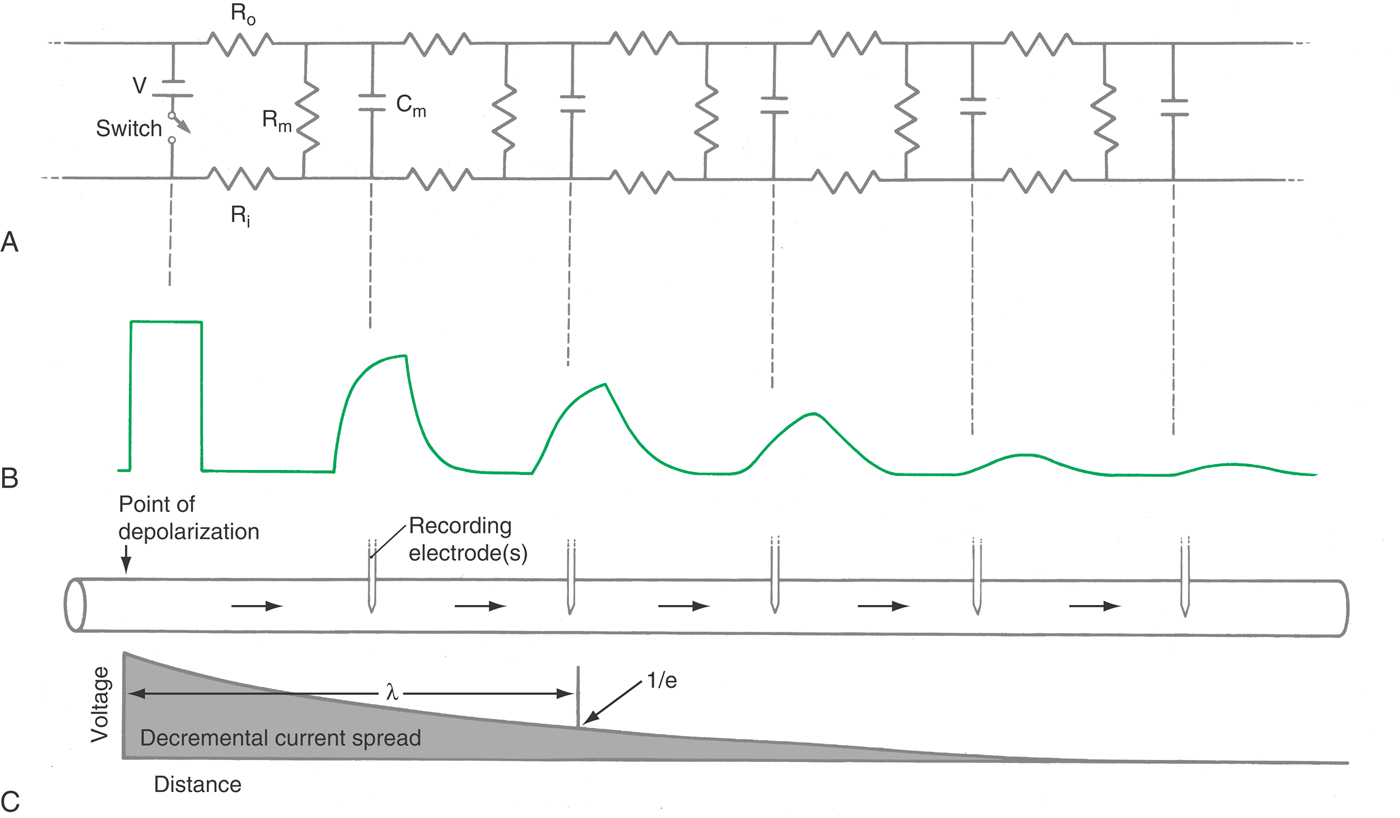
Electrical events in real neurons are complicated by the fact that neuronal activity exists in time and over distance. Those familiar with electrical circuitry will recognize similarities between nerve cells and telephone or network cables laid in the ground: an electrical signal is transmitted down the length of a core conductor but tends to leak through an imperfect insulating sheath. Furthermore, there is often a shield around the cable that protects it electrically but that also degrades the signal as a result of the capacitative coupling between the two.
Because the lipid bilayer effectively separates charge, the cell membrane has a large capacitance, on the order of 0.9 µF/cm2 (microfarads per square centimeter). Consequently, time is required for the currents to change the membrane capacitance (Fig. 3-12). As shown in Figure 3-9, synaptic currents charge the postsynaptic membrane, generating the postsynaptic potentials. The speed with which a current charges a membrane is characterized by τ (tau), its time constant, defined as the time required for a signal to decay to 1/e or 37% of its initial value (e being 2.71828…, the base of the natural logarithm). With a resistor (R) and a capacitor (C) in series, τ = RC, and so increasing the access resistance or the membrane capacitance will slow the time constant.
The spatial properties of the neuron are characterized by its length constant, which is the distance required for a signal to decay to 1/e (37%) of its initial value and which varies according to the neuron’s structure and activity. For instance, the length constant is dramatically increased by myelin, resulting in much faster nerve conduction because of the increased linear reach of any given node’s depolarization. In contrast, the length constant of a nerve dendrite is reduced by inhibitory activity that increases the chloride conductance; in so doing, the resistance of the dendrite membrane declines, and its length constant is shortened. As a consequence, any nearby excitatory input will decay rapidly and so have diminished influence over whether an AP is triggered at the initial segment of the cell’s axon (Fig. 3-13).
Nerve Conduction Velocity
The speed of nerve conduction is very important for somatomotor activity, but less so for visceromotor (autonomic) control of the body. Consequently, the nervous system has optimized some fibers for high velocity of nerve conduction and relaxed that requirement for other fibers. One way to speed conduction is to reduce the electrical resistance of the cytoplasm of the nerve. This is accomplished with an increase of the cross-sectional surface area, which is proportional to the nerve diameter squared, in order to get more highly conductive ionic media per unit length. This comes at a cost, as more membrane is included in the larger diameter, whose capacitance slows the AP in proportion to the diameter; hence the speed of the AP increases simply as the diameter, averaging 1.7 m/s per micron of axon diameter for unmyelinated nerve fibers of the size found in humans. Invertebrates take this modification to extremes, with the giant motor axon of the squid reaching 100 to 500 µm in diameter to obtain the speeds necessary for rapid motor activity.
The alternative approach, which is more practical for the size limitations of the vertebral bony canal, is to insulate the axon with a myelin sheath. The insulation provided by the myelin greatly augments the resistance already provided by the nerve membrane as well as decreases its effective capacitance. Both changes work together to increase the length constant of the fiber, which reduces how quickly the electrical signal generated at the node decays away passively. Consequently, distant nodes reach threshold more rapidly, and conduction velocity is boosted. For example, a 10-µm myelinated fiber (axon plus its myelin sheath) has the same speed as a 500-µm unmyelinated axon (20 m/s at 20° C, comparing a frog motor nerve with a squid giant axon) but occupies only [10/500]2 or 1/2500 of the space. Thus vertebrates always use myelinated nerves to achieve the fastest conduction times, averaging 6 m/s per micron diameter (see Chapter 17).
REGENERATIVE POTENTIALS USING A SINGLE ACTIVE CURRENT
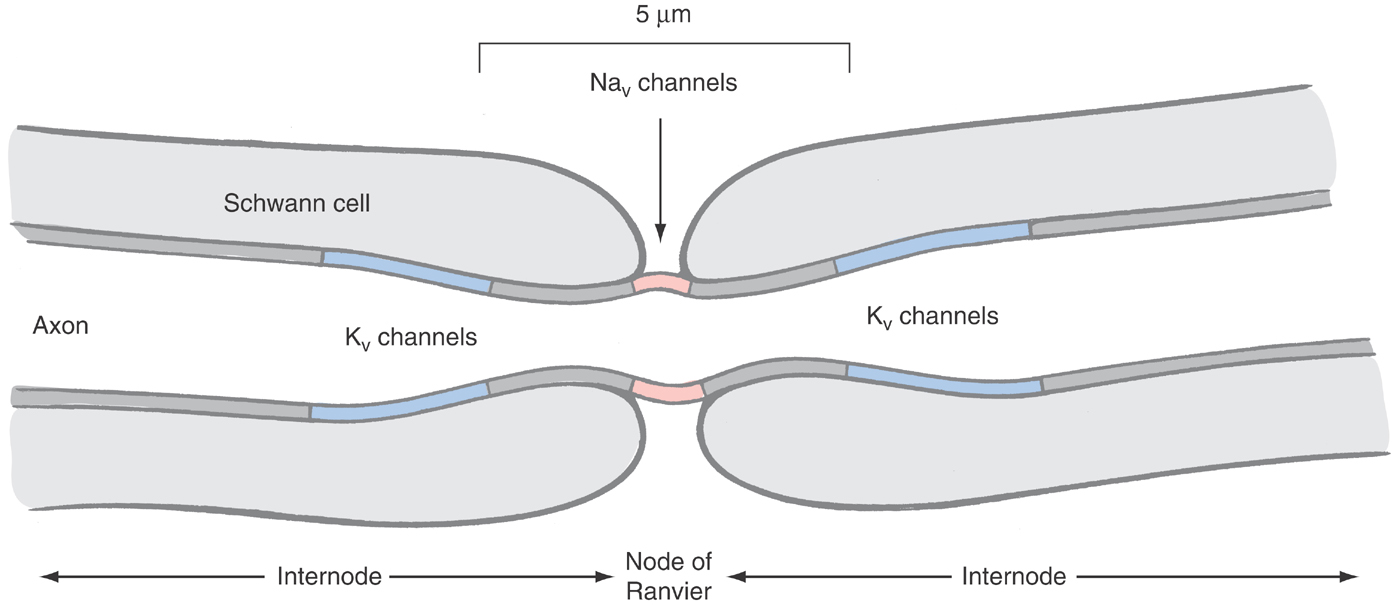
The simplest example of the AP mechanism occurs in the myelinated nerve. Much of this neuron’s axon is well insulated by multiple lipid bilayers applied by oligodendrocytes in the central nervous system and Schwann cells in the periphery (see Chapter 2). Active currents are generated only in short intervals of naked axonal membrane—the nodes of Ranvier. Because the exposed axonal membranes at the nodes comprise no more than 0.05% of the total axon, it is economically possible to pack in 100-fold more voltage-activated sodium and always-open potassium channels than would be found in nonmyelinated axons (Fig. 3-14).
Sodium Channel Activated by Depolarization
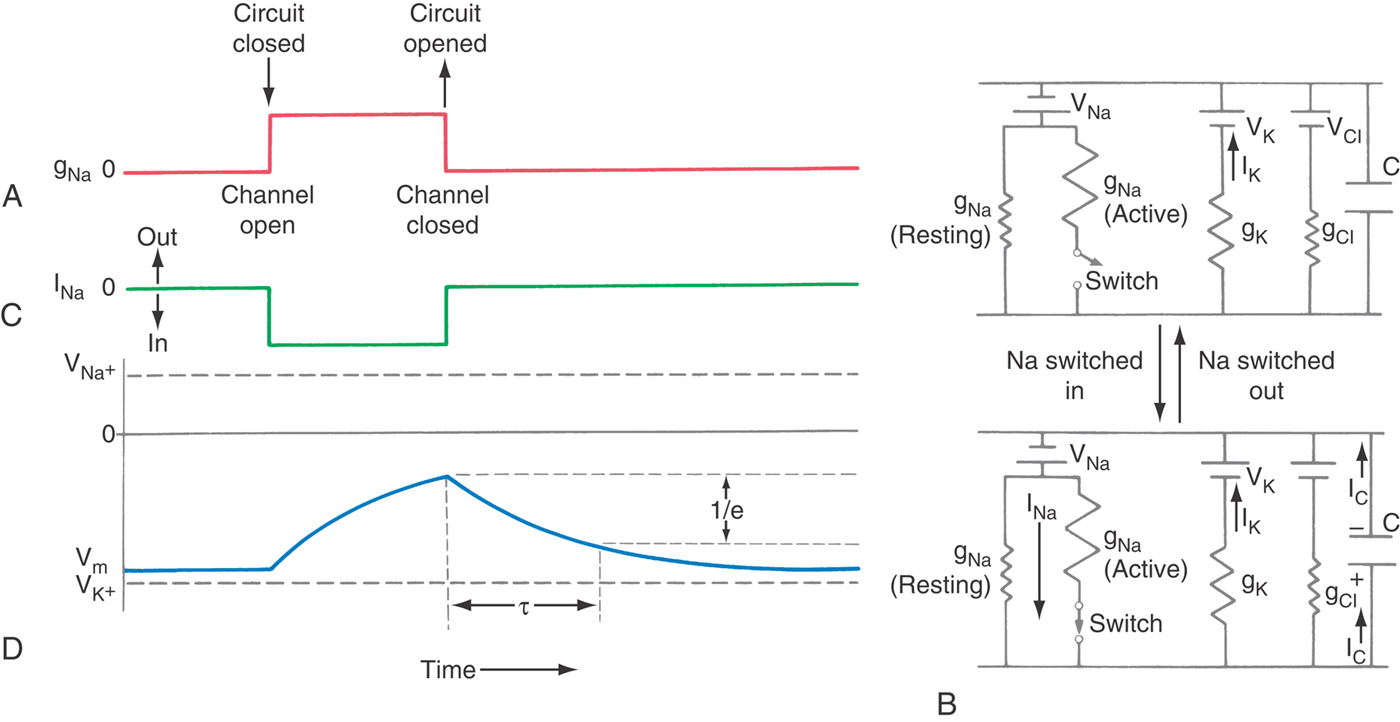
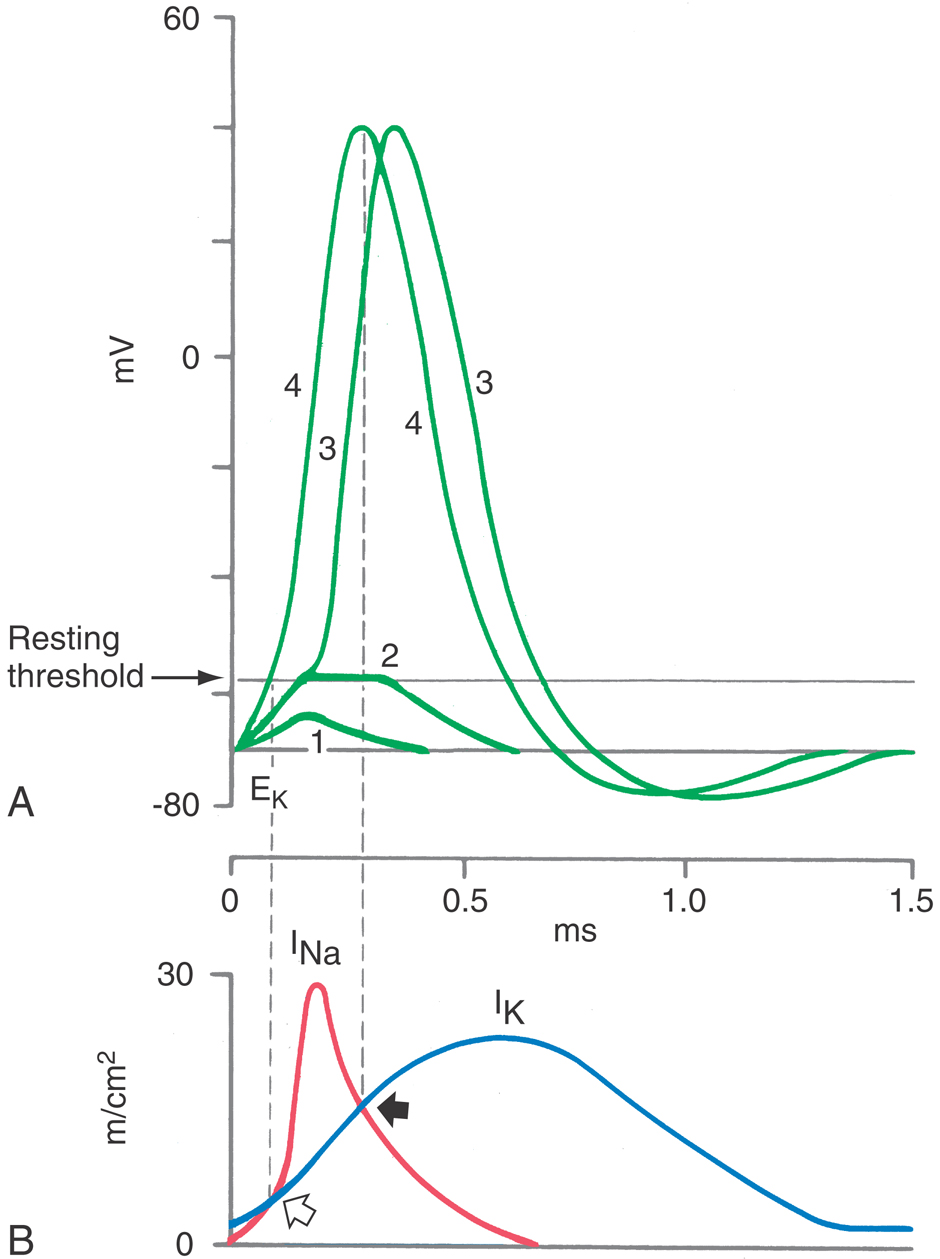
The key to the self-regenerative nature of the AP was fully characterized by Hodgkin, Huxley, and Katz during the summer of 1951, after a dozen years of reflection during World War II and its aftermath. They simplified the complex nature of an AP—which involves the flow of various ions down their electrochemical gradient through conductances that change continuously—by studying the open and shut behavior of the sodium or potassium conductance at defined voltages by the method of the voltage clamp. In so doing, they could separate out the contribution of a single ion (sodium or potassium) and focus on its conductance as the membrane potential was varied in a controlled manner.
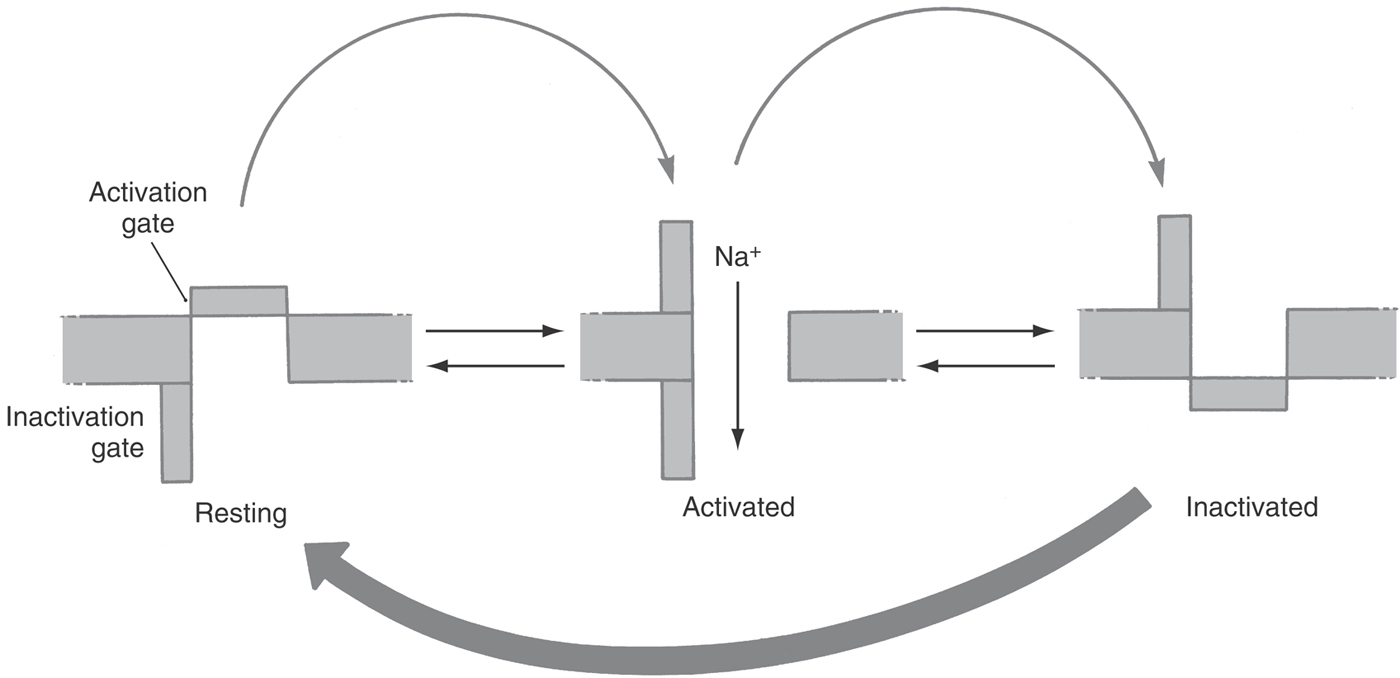
Two general principles emerged from these experiments that have been shown to be true for virtually all APs. First is the notion of separate currents flowing through different and highly characteristic channels: the depolarization being due to the influx of sodium or calcium ions and the repolarization being due to the efflux of potassium or influx of chloride ions. Second is the notion of multiple conformations, or states, for a channel. For instance, a closed sodium channel is stimulated to open when the cell membrane potential becomes more positive, that is, when it is depolarized. The open state does not last forever but changes to a nonconducting inactive state during a period measured in milliseconds (Fig. 3-15) and can return to the closed state only when the membrane potential is returned to a more negative value. The three states of the sodium channel—closed, open, and inactive—are the key to our understanding of almost all the known characteristics of the AP.
Regeneration
Opening of sodium channels causes sodium current to flow, with the sodium ions moving down both an electrical gradient and a concentration gradient. The entrance of these positive ions causes the membrane potential to become less negative. This voltage change is exactly the stimulus for opening of more sodium channels, resulting in more inward current, resulting in more depolarization, and resulting in an even stronger stimulus for the remaining closed sodium channels to open. Such a process is a feed-forward system, which repeatedly generates a full-blown electrical signal that spreads down the entire length of an axon, using only the native characteristics of a node’s sodium channel.
Repolarization
The lifetime of the open sodium channel is limited to a few milliseconds. After this brief period, the sodium channel passes into the inactive state, a nonconducting state in which it cannot return to the open state, regardless of the membrane potential. Without the voltage-dependent inward sodium current, and in the presence of a large resting potassium conductance, the membrane potential rapidly returns to the resting level, hence repolarization. Thus not only is the regenerative upstroke of the AP an automatic feature of the nodal sodium channel, but so is its conclusion.
Threshold Voltage
APs are initiated when generator potentials cross a narrowly defined range—the threshold voltage. A millivolt less and no AP will be triggered; a millivolt more and the AP abruptly takes off, all because three events are competing among themselves. The closed sodium channels are opening at a rate that becomes faster and faster as the membrane is depolarized; however, at the same time, the newly opened sodium channels do not last forever, as they undergo inactivation. Finally, the membrane conductances to potassium and chloride will tend to damp out the signal. These dynamic changes also mean that the rate of depolarization is also important, as will be described more completely in the section on accommodation. The outcome of these competing events is the basis of the Hodgkin-Huxley formulation of the mechanism of the AP.
Refractory Period
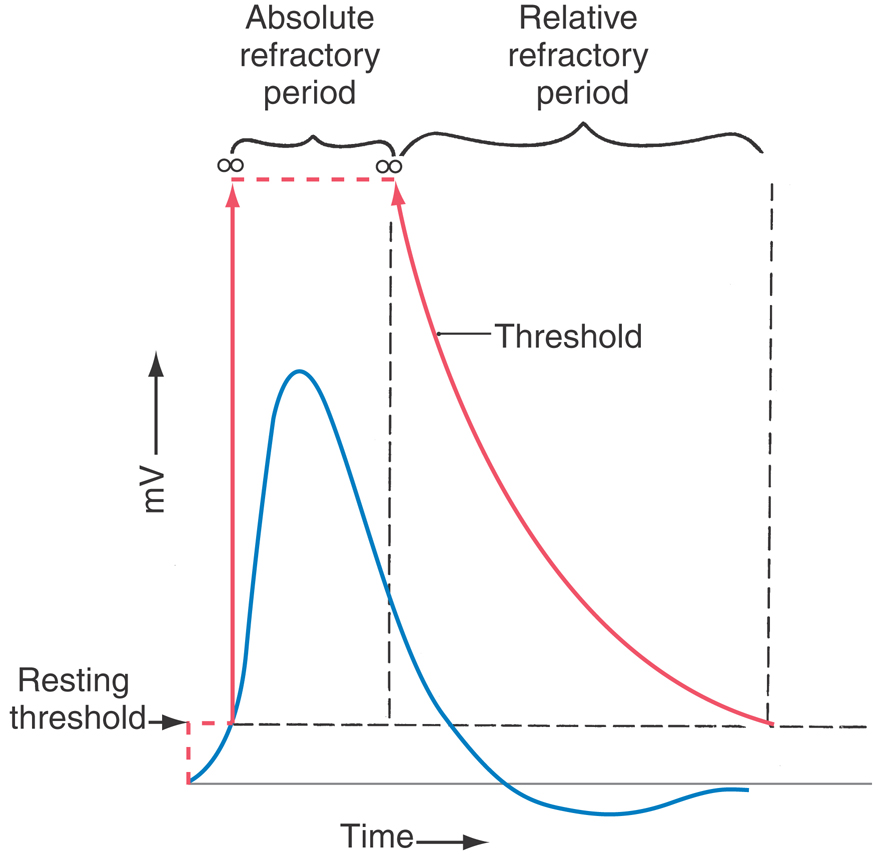
It is not possible to elicit a second AP for a brief time after any given AP, and this is the absolute refractory period when most of the neuron’s sodium channels are inactivated and cannot be opened (Fig. 3-16). With time, the inactivated channels do return to the closed state, but the entire process takes many milliseconds. During this time, it is relatively more difficult than normal to elicit a second AP—the relative refractory period.
Unidirectional Propagation
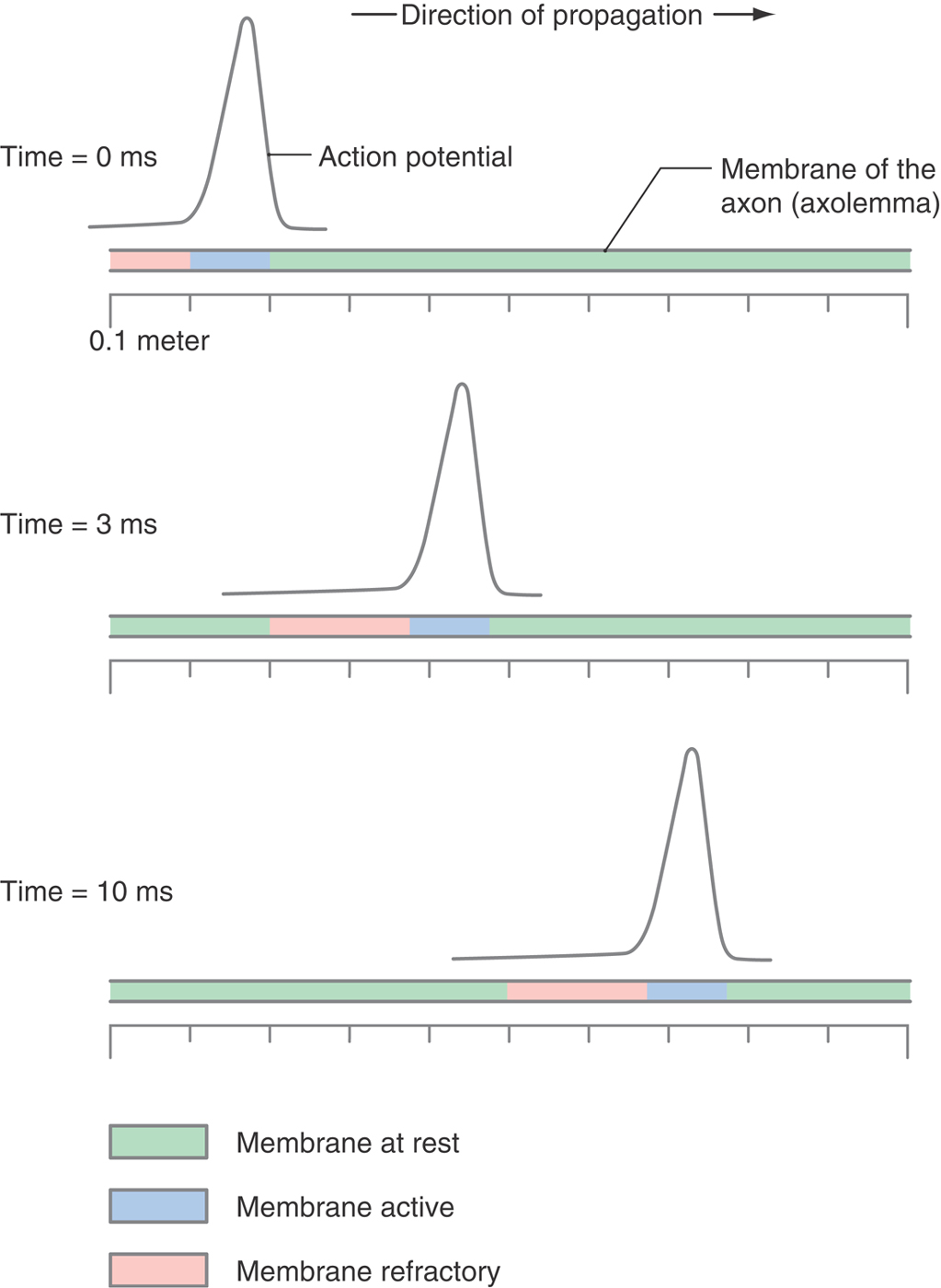
There are no echoes in the nervous system: once an AP is sent down a motor nerve, the job is done and the AP does not bounce back and forth across the length of the axon (Fig. 3-17). Propagation is unidirectional. Again, it is the inactive state of the sodium channel that prevents the AP from changing its direction of propagation; once the AP passes, the sodium channels left behind are in the inactivated state and are refractory to any further stimulation. The AP stops at the end of the axon because there are no more closed sodium channels to activate, neither ahead, because there is no more nerve, nor behind, because they are inactivated.
Saltatory Conduction
The AP of the myelinated nerve moves by saltatory conduction, which is to say that the AP jumps (from Latin, saltus) from node to node because active currents are possible only in the 1-µm node of the myelinated nerve; the adjacent ~2 mm of internode is well insulated by up to 300 layers of membrane laid down by the oligodendrocytes or Schwann cells (Fig. 3-14). This insulation is both resistive and capacitative. With each additional layer of membrane, the passive conductance to potassium and chloride is reduced by a factor of 2, 3, 4…. Equally important, the capacitance is reduced by an equal factor. Thus, as the electrical signal generated at the nodes travels down the internal conductor of the axon—down the cytoplasm—little can leak through the internodal membrane by ionic flow and little is needed to charge the membrane capacitance, as it is so small. Quantitatively, whereas the internode is ~2000 times the length of the node, the conductance and capacitance are each 600-fold less than at the node. Consequently, the whole of the internode requires approximately half the charge to depolarize it as would a single node [2000 ÷ (600 × 600)]. In effect, the myelinated AP dances from node to node, being largely unencumbered by the intervening internodal membrane (the saltator and saltatorix being dancers of sometimes ill repute in ancient Rome).
A brief snapshot in time would show that the AP extends over many inches of axon. The speed at which the AP travels is great: 60 m/s for a 10-µm axon at body temperature. Because the duration of the AP is ~1.2 ms, the linear extent of the AP is ~72 mm, or 36 nodes, at 2 mm per internode.
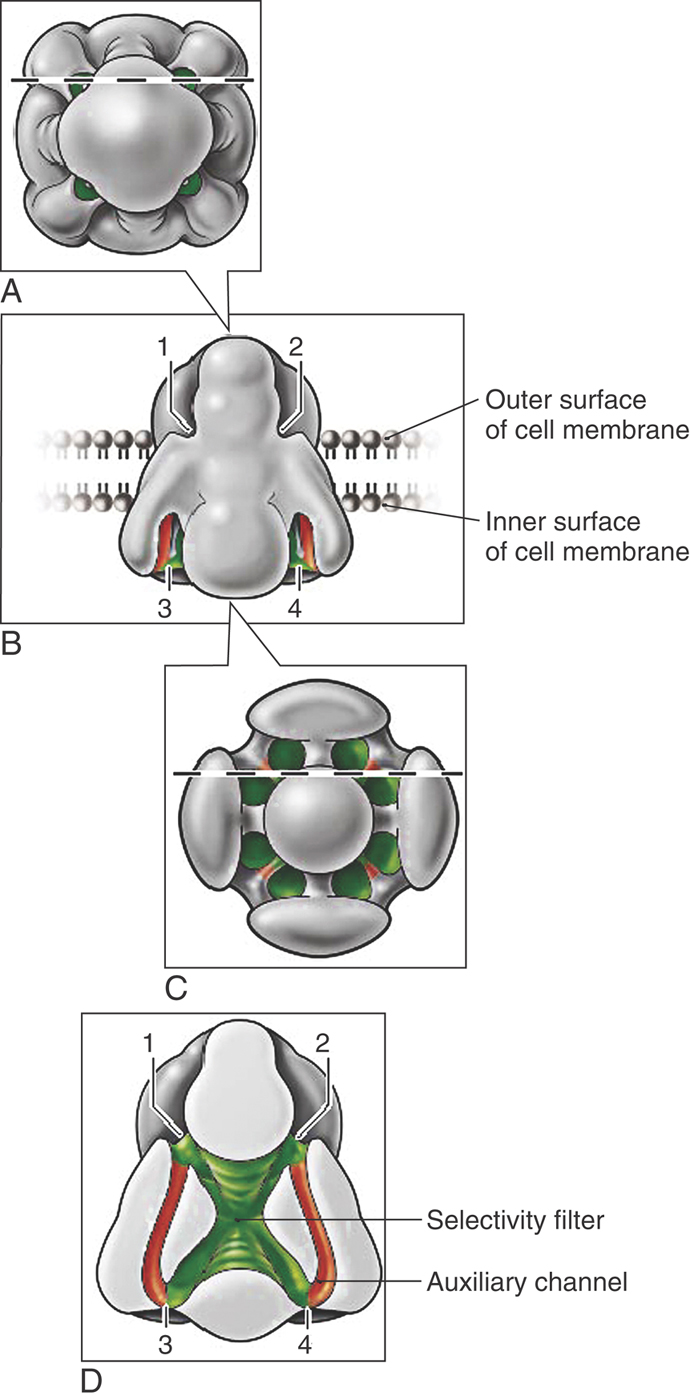
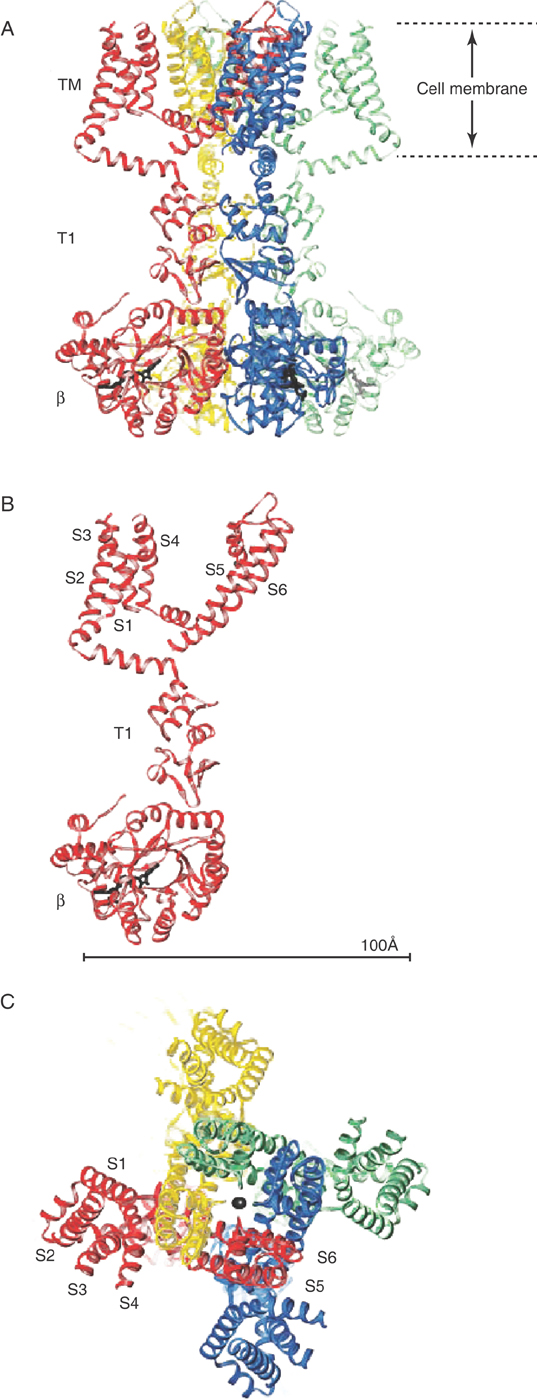
Gating, Selectivity, and the Structure of the Sodium Channel
A score of voltage-dependent sodium and calcium channels (NaV and CaV) are known to exist in humans. These homologues appear globose and contain a surprisingly complex array of water-filled passages (Fig. 3-18). Sodium ions enter NaV only to find the interior lined with aspartate-glutamate-lysine-alanine sequences. These negatively charged amino acids create a high field strength site within the channel pore that closely mimics what had been the sodium ion’s immediate surroundings in bulk water. Because the channel’s interior is similar to the external solution, sodium enters the pore, sheds some of its surrounding water as it in turn displaces resident water molecules in the high field strength region, and then reenters bulk water on the far side with relative ease. Exclusion of large ions such as potassium is due to their weaker field strength, which cannot effectively dislodge water molecules from the high field strength sites within the pore.
A highly mobile sequence of amino acids with a positive charge acts as the voltage sensor, not only for NaV and CaV but also for voltage-dependent potassium channels. Negative membrane potentials move these gating charges toward the inside of the cell; depolarizations cause these amino acids to move outward and to open the pores to ion flow.
MODIFIERS OF EXCITABILITY
Clinicians have long known that magnesium sulfate stabilizes nerve membranes, as do local and general anesthetics. Conversely, low levels of calcium increase membrane excitability, producing unwanted spontaneous activity in nerves that are ordinarily quiescent. With the knowledge that regenerative currents derive from specific voltage-dependent sodium channels, it is now possible to understand the molecular mechanisms by which clinical interventions easily modify excitability and how demyelinating diseases lead to loss of nerve function.
Accommodation
A slow but prolonged application of a subthreshold stimulus will cause a nerve to lose the ability to generate an AP; the nerve is said to accommodate to the stimulus. Again, knowing that the sodium channel can exist in one of three conformations—closed, open, and inactive—means that a subthreshold stimulus will stimulate channels to open, but at a rate that is too slow for there to be a sufficient number of open channels at any one time to fire an AP. Instead, the channels will inactivate. If the subthreshold stimulus lasts long enough, all sodium channels will be inactivated and no AP will be possible. This process causes nerves to “go to sleep” when pressure is applied for a long time.
Two distinct types of inactivation exist in all sodium channels: fast and slow. Fast inactivation was introduced earlier and is the process that terminates the AP within milliseconds and controls features such as the refractory period and unidirectional AP transmission. Slow inactivation requires depolarizations that last tens or hundreds of milliseconds, such as illustrated in Figure 3-10C, where the excitability of the hippocampal pyramidal cell declines during a 40-ms period as fewer and fewer sodium channels are in the closed state and so available to generate a new AP. Slow inactivation also contributes to adaptation in the neocortex, in motor neurons, in neurons of the subthalamic nucleus, and in nociceptor cell bodies in the posterior (dorsal) root ganglion.
Anode Break
APs can be triggered at the end of a hyperpolarizing pulse of current, as would have been delivered from the anode of an old-fashioned vacuum tube stimulator of the early twentieth century (the anode break). This is the opposite of the usual stimulus, a depolarizing pulse of current that sends the membrane potential positive to the threshold voltage. However, this observation led to understanding of the behavior of nerves that fire spontaneously at a fixed rate (Fig. 3-10C). In these pacing neurons, each AP is followed by a deep hyperpolarization. As this hyperpolarization relaxes back to a more positive voltage, it triggers another AP when the threshold voltage is again crossed. Whereas details vary from cell to cell, the basic mechanism relates to the three states of the sodium channel: during the hyperpolarizing pulse, more and more sodium channels switch over from the inactive to the closed state. The greater the fraction of closed channels, the lower the threshold and the easier it is to trigger an AP. Hence, it is actually possible that the passive return to the normal resting potential is fast enough to be a sufficient stimulus to fire an AP while most of the sodium channels are still closed.
Tetany
Abnormal levels of calcium, magnesium, and hydrogen ions alter nerve activity. Increased concentrations stabilize nerve membranes, leading to fatigue, depression, anorexia, and constipation. Indeed, large infusions of magnesium sulfate have long been the accepted safe treatment for the life-threatening hypertension and seizures accompanying the eclampsia of pregnancy. Reduced levels of these ions increase excitability, causing tetany (a combination of tingling sensations and muscle spasms), mental irritability, and ultimately seizures. Metabolic or respiratory alkalosis exacerbates symptoms of low calcium or magnesium and can trigger overt symptoms in borderline or latent tetany, as will tapping of the facial nerve in front of the ear (Chvostek sign) or causing a brief period of ischemia by inflation of a blood pressure cuff (Trousseau sign).
The mechanism by which divalent cations like calcium modify the excitability of nerves is subtle and is closely associated with the detailed structure of the membrane lipid bilayer. The explanation begins with the fact that the phospholipids and the oligosaccharide groups decorating membrane proteins have negative surface charges at the surface of the bilayer. These negative surface charges are present in large numbers and create a voltage drop of ~30 mV across the last few nanometers immediately above the cell surface. Having this negative surface potential means that the cell’s membrane potential is divided into two parts, one portion occurring across the surface charges on the membrane exterior and the remaining drop falling across the 3-nm lipid portion of the membrane bilayer. Being doubly charged, divalent cations bind tightly to the negative surface charges, so high concentrations of divalent cations neutralize the anionic surface charges, abolish the negative surface potential, and shift the entire membrane potential onto the lipid interior of the bilayer. A transmembrane protein such as the voltage-dependent sodium channel would then experience a more negative voltage and have a reduced tendency to open: the neuron becomes stabilized. Conversely, when the concentrations of calcium or magnesium fall, divalents leave the membrane surface and more anionic charges are exposed. The surface potential becomes more negative and assumes a greater fraction of the membrane potential. Transmembrane proteins then experience a less negative voltage, the sodium channels become more likely to open, and an AP can be triggered by a much smaller stimulus: the neuron becomes hyperexcitable. When this condition is severe, the axons of sensory and motor nerves spontaneously fire volleys of APs, thus generating the signs and symptoms known as tetany.
Use-Dependent Block and the Treatment of Epilepsy
Seizures are excessive and paroxysmal neuronal activity, either locally in a small region of the brain or spreading across the entire cortex. Optimal drug treatment of epilepsy targets the high-frequency APs of the seizure while preserving normal function as much as possible. Fortunately, sodium channels (like ACh receptors) have a binding site for local anesthetics like lidocaine and phenytoin. The site is inside the pore and is accessible only when the channel is open. As a consequence, local anesthetic block of sodium channels is use dependent—the more the channel is used, the more channels are plugged, and the more complete the block is. No more entry is possible once the channel is closed, but the local anesthetics can exit, releasing the block during periods of inactivity. Thus use-dependent block can augment the endogenous mechanisms that ordinarily bring a burst of nerve activity to an end (see Fig. 3-10C).
Genetic Defects, Toxins, and Venoms
The exact balance among the three states of the sodium channel is critical for proper function of the AP. This is readily apparent in a rare inherited cause of epilepsy (generalized epilepsy with febrile seizures), two motor diseases (hyperkalemic periodic paralysis and paramyotonia congenita), and a cardiac arrhythmia (long QT syndrome, type 3). Slowed inactivation leads to repeated AP firing in each case and to a refractory state and paralysis in some cases. Toxins also interfere with sodium channel function, most famously tetrodotoxin (from the puffer fish and a North American salamander) and saxitoxin (from diatoms that cause the red tide). These all bind to the closed sodium channel, preventing it from opening. Scorpion stings cause pain, spasms, and ultimately paralysis because their venom slows NaV inactivation and causes activation to occur at more negative voltages.
Demyelinating Disease
The loss of the myelin sheath, as in multiple sclerosis, interrupts myelinated AP transmission for three reasons. First, the internodal membrane contains no sodium channels, so it cannot contribute to the regenerative currents needed for an AP. Second, the loss of the electrical insulation of the myelin means that the capacitance of the internode increases and the resistance of the internode decreases. Third, voltage-activated potassium channels are clustered in the internodal regions immediately adjacent to—but normally electrically insulated from—the nodes; once the myelin is lost, these potassium channels oppose the nodal sodium currents. All three factors act together to reduce the length constant of the nerve, causing the currents at the active nodes of Ranvier to have less of an effect at the distant resting nodes. With sufficient destruction, the length constant becomes less than the internodal distance. Transmission then ceases when it becomes impossible to reach threshold.
POTASSIUM AND THE VARIETY OF NEURONAL ACTIVITY
Diverse patterns of activity are required of neurons, which in turn differ greatly in their geometries. Individual cells adapt to their particular functions by expressing sodium, calcium, potassium, and chloride channels drawn from scores of families and a multitude of transcripts. Three of these functions require particular potassium channels (Fig. 3-19) and are discussed next: terminating the AP, controlling excitability, and pacing a rhythmic pattern.
Repolarizing the Neuron
Neurons use a variety of strategies to terminate their APs. The nodes of Ranvier simply have a high resting potassium conductance. Unmyelinated axons are more ambitious in that they terminate their APs promptly by opening potassium channels: the depolarization of the AP activates a potassium current through one or more KV channels (Fig. 3-20). KV channels are normally gated shut, saving the neuron energy that would otherwise be spent to pump potassium out of a leaky cell, but open in response to the upstroke of an AP. The resulting pore sieves ions by size, allowing only the smallest hydrated monovalent cations to pass. Potassium is a large ion, so its charge density is not strong enough to attract as many water molecules as sodium; consequently its hydrated radius will be smaller, and its passage will be easier. KV remains open as long as the membrane is depolarized; closing is guaranteed because the KV current will return the membrane potential toward VK, the potassium equilibrium potential, repolarizing the membrane and allowing KV to close. The AP is thus brought to a conclusion, and the membrane returns to its high resistance state as well.
Controlling Excitability
Whereas the brief, definitive AP of the myelinated axon is well suited for a motor nerve, other nerve axons and cell bodies require signals that are more prolonged, by either extending the duration of a single AP or repeating the AP in bursts of 2, 6, 12, or more. Some of these needs are met by INaV, which can be carried by any one of the nine NaV channels. More often the task is performed by one or more of the 10 voltage-dependent calcium channels (CaV), which are abundant throughout the nervous system and varied in their nature. The ability of CaV channels to extend the duration of the AP is most dramatically seen in heart muscle but also apparent in Figure 3-10. CaV channels are also well adapted for firing bursts of APs.
Neurons that fire calcium-dependent APs (for instance, the hippocampal pyramidal neuron in Fig. 3-10C) often have an additional current that repolarizes and stabilizes the cell membrane, which is due to the opening of the calcium-dependent potassium channel KCa. Both CaV and NaV contribute to each of the APs in the burst that is characteristic of isolated pyramidal cells. Whereas the little bit of calcium that enters during a single AP is readily buffered by the cell, a train of APs will effectively raise internal calcium, open KCa channels, drive the membrane potential to hyperpolarized potentials, and thence break off the train of APs. In the intact hippocampus, networks of pyramidal cells fire single APs rhythmically, entrained by the response of NaV, CaV, and KCa to the cell’s synaptic inputs. In this way, the hippocampus can respond by altering the AP frequency while automatically limiting the number of APs in a sequence, avoiding the excessive and uncontrolled activity characteristic of a seizure.
Simply changing the membrane potential by the action of one or more of the membrane channels may have highly complex consequences. Whereas hyperpolarization of a membrane would seem to move the neuron away from its threshold, the opposite may actually be the case. APs are more easily triggered at the more negative membrane potentials because more NaV channels are closed (versus inactivated). Other voltage-dependent channels are modified as well. Figure 3-21B illustrates the actions of the transient A-current due to KA channels, which open at negative potentials. The experiment in this figure is one in which the neuron is first conditioned with a short hyperpolarization and then tested with a depolarizing stimulus. As illustrated, there is a delay before the stimulus is adequate to trigger a train of APs. This delay is the time required for the KA channels to close, and with longer or weaker hyperpolarizing conditioning, the delay is less. So a rhythmic pacing like Figure 3-21A is very complex and can be predicted in detail only by thorough computer simulations.
Pacing APs
Individual nerve, muscle, and endocrine cell types differ widely in their need for rhythmic firing of APs modulated by Vm, synaptic inputs, and metabolic conditions. Thalamocortical relay neurons fire APs in two distinct patterns: a train of single APs much like that shown in Figure 3-21B and a rhythmic pattern as in Figure 3-21A. A dozen channel types are involved in the specifics, with four NaV and CaV channels contributing to the spike activity. As with the solitary nucleus, currents through KA and KCa channels terminate the burst of APs. However, it is the current through the hyperpolarization-activated cyclic nucleotide–binding (HCN) channels that is the pacing current that determines the rhythmicity of this neuron (and the sinoatrial node of the heart as well). Like cyclic nucleotide–gated (CNG) channels (see Table 3-1), HCN channels are permeable to both sodium and potassium ions and are activated by cyclic nucleotides. Most important, HCN channels are activated at hyperpolarizing membrane potentials but inactivate with time. Thus HCN channels are open at the end of the AP burst, joining with the currents through KA and KCa to repolarize the neuron. HCN channels then slowly inactivate, allowing the membrane potential to drift toward 0 mV, away from VK, and toward the AP threshold and a new burst of APs.
Modifying a pacing neuron’s frequency is key to controlling its signal. HCN channels, for instance, can bind cAMP, increasing the AP frequency. KATP is a current that increases when cell ATP levels fall, reducing the AP frequency. Finally, synaptic input can change the background sodium, potassium, or chloride currents, modifying the effectiveness of the HCN channels and increasing or decreasing AP frequency.
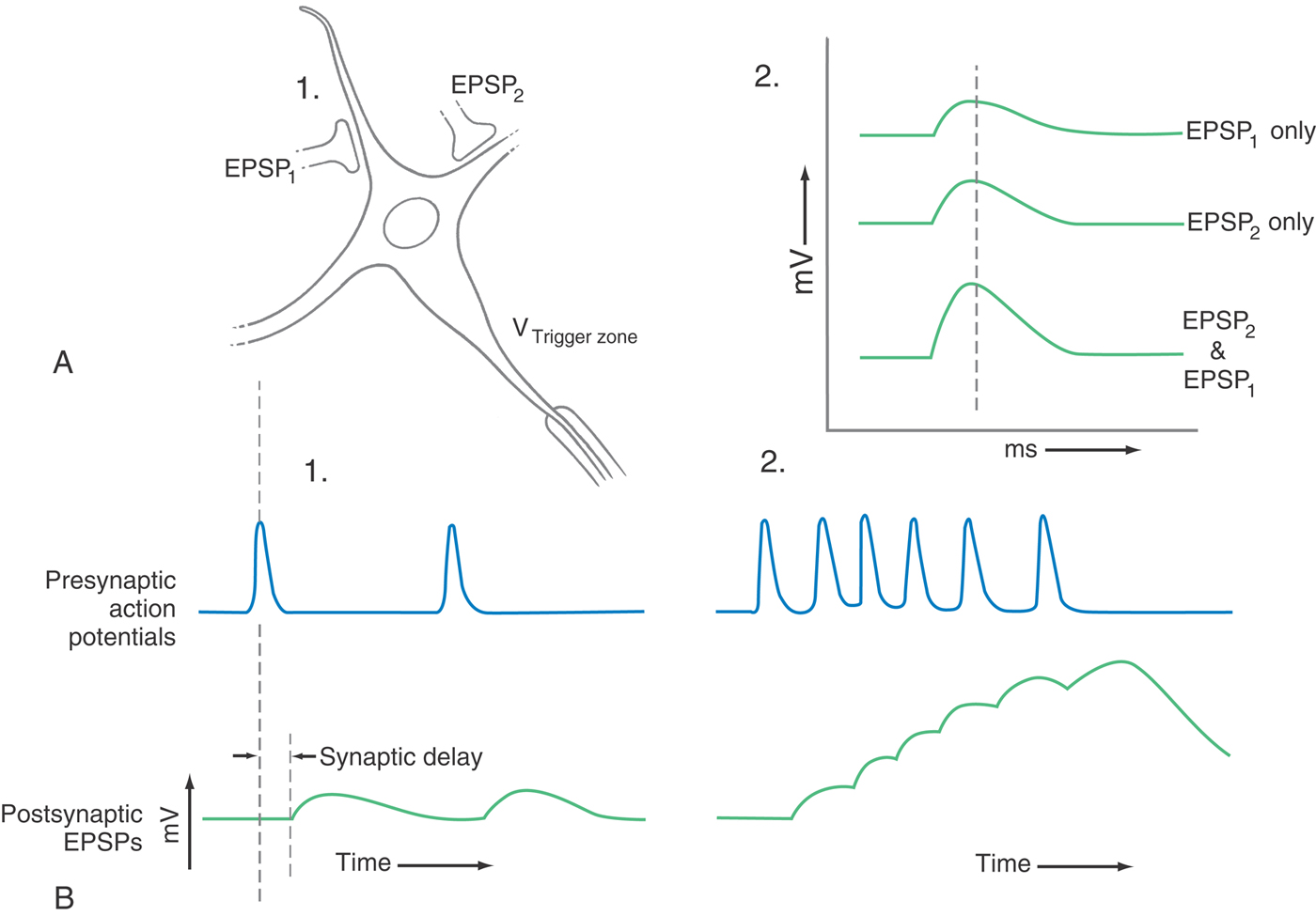
NEURONAL ACTIVITY AS INFORMATION
The neurons that were introduced in the preceding chapter and that will be discussed throughout the remainder of the book can be highly complex in structure, having a vast number of inhibitory and excitatory synaptic inputs on the dendrites and on the cell body (Fig. 3-22). Their information is encoded as APs, and whether the neuron fires an axonal AP is determined by how synaptic activity modulates the cell’s intrinsic electrical activity. Recall that synaptic potentials are graded in nature, spreading passively along the cell’s membrane, decreasing in size with distance and time. Consequently, the geometry and timing of synaptic activity are crucial. For instance, as synaptic input increases in frequency, the resulting changes in membrane potential begin to add together and thus become more effective than any one single postsynaptic potential; this is called temporal summation. Similarly, as more and more excitatory synaptic inputs become active, the cell body is depolarized to a greater and greater extent; this is called spatial summation. Inhibitory synaptic inputs do the converse. It is the combined effects of all these factors that modulate the intrinsic electrical activity of the neuron cell body to determine whether the axon fires an AP—whether a bit of information is sent down the axon.
Sources and Additional Reading
Ashcroft FM. Ion Channels and Disease. San Diego: Academic Press; 2000.
Clapham DE. TRP channels as cellular sensors. Nature. 2003;426:517–524.
Hille B. Ion Channels of Excitable Membranes. ed 3 Sunderland, Mass: Sinauer Associates; 2001.
Kaupp UB, Siefert R. Cyclic nucleotide–gated ion channels. Physiol Rev. 2002;82:769–824.
