Adult: Author	Year	Journal
Crapo	1982	Bull Eur Physiopathol Respir 1982; 18:419-427
Goldman	1969	Am Rev Respir Dis 1969; 79:457-467
Quanjer	1993	Eur Respir J 1993; 6(Suppl 16):5–40
Stocks	1995	Eur Respir J 1995; 8:492–506
Pediatric:
Quanjer	1989	Eur Respir J 1989; 1(Suppl 4): 184 S–261 S
Hsu	1979	J Pediatr 1979; 95:14-23

Diffusing Capacity

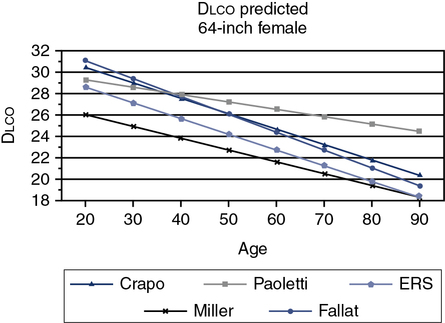
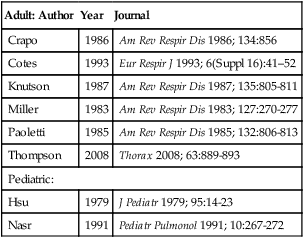
The ATS-ERS did not recommend a specific set of reference equations for diffusing capacity, citing inter-laboratory variability as their reason. Published data have shown even in a well controlled clinical trial that intersession variability can range from 10%-25%. The ATS-ERS statement did recommend that predicted values for alveolar volume (V_A), inspired volume (V_I), and Dlco should come from the same source. Figure 13-1 demonstrates the difference in a subject between various Dlco predicted equations. A 60-year-old female of average height can have a predicted value ranging from approximately 21-27 mL/min/mm Hg, depending on the reference set selected. Thompson and others published a reference set in middle aged to older subjects (ages 45-71), which complied entirely with the 2005 ATS-ERS recommendations for testing technique and quality assurance. Their equations compared favorably with those previously published by Miller. Several common reference authors are listed in Table 13-2.

Table 13-2

Common Reference Authors for Diffusing Capacity

Adult: Author	Year	Journal
Crapo	1986	Am Rev Respir Dis 1986; 134:856
Cotes	1993	Eur Respir J 1993; 6(Suppl 16):41–52
Knutson	1987	Am Rev Respir Dis 1987; 135:805-811
Miller	1983	Am Rev Respir Dis 1983; 127:270-277
Paoletti	1985	Am Rev Respir Dis 1985; 132:806-813
Thompson	2008	Thorax 2008; 63:889-893
Pediatric:
Hsu	1979	J Pediatr 1979; 95:14-23
Nasr	1991	Pediatr Pulmonol 1991; 10:267-272

Figure 13-1 A comparison of five diffusing capacity reference sets for a 64 inch female. Depending on the author selected the predicted value for a 20 y.o. would range from a low of 26 to 31 units or for a 70 y.o. 20 to 26 units.

Several methods for applying reference values are used:

• Tables of reference values

• Nomograms

• Graphs

• Regression equations used in calculators or software

Tables, nomograms, and graphs are rarely used because of the widespread availability of computerized systems. Peak flowmeters and other simple devices designed for use outside of the clinic or laboratory sometimes use a nomogram or printed graph to allow the user to look up a predicted value. The use of computers (or calculators) allows regression equations to be available in software. In most automated systems, the user selects sets of prediction equations best suited to the population being tested. Some software allows users to enter their own equations or modify published equations. This provides a means of adding new reference equations as they become available.

Establishing what is abnormal

Determining the lower limit of normal (LLN) should be done by analyzing some measure (e.g., FVC, FEV₁) in healthy subjects and then determining the variability of that measurement. In clinical medicine, the 5th percentile is often defined as the LLN because it represents the segment of healthy subjects farthest below the average. Even though subjects in the 5th percentile are healthy, they are arbitrarily defined as “abnormal” for clinical purposes. Figure 13-2 depicts the predicted and the LLN for white females from ages 8–80 years (NHANES III). It is noteworthy that the statistical LLN is approximately the same across the adult age range.

Figure 13-2 Predicted and lower limit of normal.
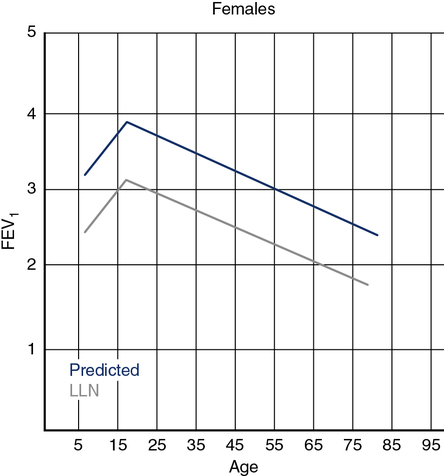
The predicted FEV₁ for females ages 8 to 80 years is shown by the upper line (blue) based on the third National Health and Nutrition Evaluation Survey (NHANES III) regression equations for white adults. The lower line (gray) represents the statistical lower limit of normal (LLN) for the same group. FEV₁ increases from ages 8 to 18 years, with the LLN showing a similar pattern. The LLN line represents the 95th percentile.

Some clinicians use a fixed percentage (measured value divided by the reference value × 100) of the reference value to determine the degree of abnormality. Eighty percent (80%) is often used as the limit of normal. Unfortunately, this method leads to errors because the variability around the predicted value is relatively constant in adults. In other words, the scatter of normal values does not vary with the size of the predicted value. Figure 13-3 illustrates why using fixed percentages, such as 80% of the predicted, can lead to misclassification. In tall, young subjects 80% of the predicted is often less than the 5th percentile; using 80% as the limit can allow a patient who really does have decreased lung function (in the 5th percentile or lower) to be misclassified as normal. This situation is a false-negative result; the patient has disease but the test does not indicate abnormality. Similarly, an elderly patient who is short may have a lung function parameter that is less than 80% of predicted but well within the statistically normal range (above the 5th percentile). This short elderly subject would be misclassified as having lung disease when in fact she is within the “normal” range (i.e., a false-positive result). Using percents of predicted introduces both age and height biases. The situation is slightly different in children because the variability of lung function measures tends to change proportionately with the size of the predicted value. For this reason, percents of predicted values may be appropriate for classifying lung function in children.

Figure 13-3 Bias introduced by using percents of predicted.
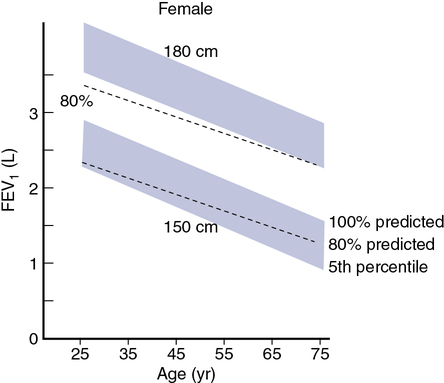
The graph illustrates the fall in predicted FEV₁ for tall (180 cm) and short (150 cm) females with age. The shaded areas represent the “normal” range from 100% of the predicted value down to the 5th percentile. The *dashed line* shows a fixed percentage of the predicted—in this case, 80%, as is sometimes used to represent the lower limit of normal. For a young tall female, 80% is less than the statistical lower limit. A subject with a low FEV₁ (below the 5th percentile) might still be above 80% of predicted; this would result in a false-negative finding on spirometry. Similarly, a short, older female might have an FEV₁ below 80% of predicted and be considered to have disease when her FEV₁ is actually above the 5th percentile. In this instance, the result is false-positive. Similar bias occurs when percents of predicted are used from adult males because the variability of FEV₁ (and other pulmonary function parameters) does not tend to vary with the size of the predicted value. Clinical decisions should be based on well-defined lower limits of normal rather than fixed percents of predicted (in adults).

A more statistically sound approach for classifying abnormality is to compute the z score or standard deviation score (SDS). If lung function varies in a normal fashion (a Gaussian or bell-shaped distribution curve; Figure 13-4), the mean ± 1.96 standard deviation (SD) defines the 95% confidence interval. Statistically, 95% of the healthy population falls within approximately 2 SD of the mean. The remaining subjects fall into either the highest or lowest 2.5% of the distribution. The z score or SDS can be calculated easily if the variability (residual standard deviation (RSD)) of the reference population is known:

Figure 13-4 Gaussian distribution curve with z scores and percentile ranks.
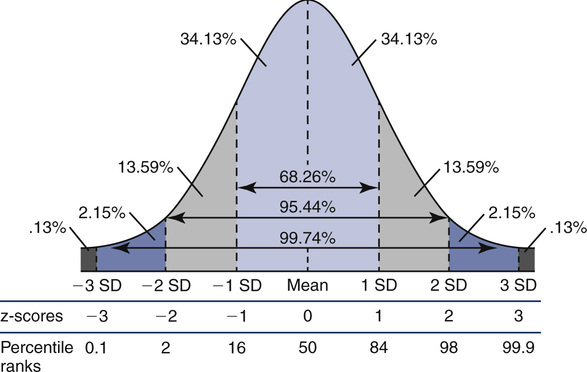
Lowest 5% of the reference population is defined as “abnormal.”

< ?xml:namespace prefix = "mml" />zscore=(measured−predicted)RSD

where:

RSD = residual standard deviation

The RSD is the normal variability that remains when all other sources of variability have been accounted for in the regression. If an individual’s z score is less than −1.65, there is only a 5% chance that the test result is normal. If the z score is less than −1.96, the measured value is found in only 2.5% of healthy subjects.

For example, consider a male subject who is 70 years old and 69 inches (175 cm) tall. His FEV₁ is measured as 2.40 L; his predicted FEV₁ is 3.12 L. His FEV₁ is 77% of predicted; is this abnormal? Using 80% as the cutoff suggests that this patient has mild lung disease. However, if the patient’s z score is calculated as:

zscore=(2.40−3.12)0.468 =−0.720.468 =−1.53

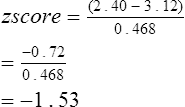
where 0.468 is the residual standard deviation from the reference population, the z score of −1.53 suggests that this subject is above the 5th percentile and likely has normal lung function. The advantage of z scores is that they can be used for any index that is normally distributed. Because the z score accounts for the variability occurring in healthy subjects, it tells how common, or uncommon, the finding may be in the patient being studied.

For many pulmonary function variables, only the LLN (i.e., below the mean) is significant. For example, it is not usually clinically significant if FVC is greater than predicted, only if it is lower. For normally distributed variables, 1.645 × RSD can be considered the LLN. Variables that can be abnormally high or low (e.g., RV, TLC, Paco₂) must consider the upper limit of normal (ULN) in a similar manner.

The LLN can be easily calculated when the variable of interest (e.g., FEV₁, FVC) is normally distributed in the population. Using the 5th percentile to define the LLN, however, does not require the pulmonary function variable to be normally distributed in the population. Simple counts can determine the level for a specific variable that separates the lowest 5% of the subjects from the remainder. Lower limits of normal using the 5th percentile are sometimes defined for specific groupings of age or gender.

There are several areas in which the definition of lung function abnormality may have important clinical consequences. One such area is the use of a fixed ratio to define airway obstruction, as is frequently done with the FEV₁/FVC (FEV₁/VC). The World Health Organization’s Global Initiative for Obstructive Lung Disease (GOLD) recommends the use of 70% as a cutoff, with ratios less than this value defining the presence of airway obstruction. However, because the FEV₁/FVC ratio falls with age (sex, height, and ethnicity also may play a role), using a fixed ratio may misclassify younger subjects as normal (false negative) and older subjects as obstructed (false positive) (Figure 13-5). Similarly, using fixed percentages of predicted (e.g., 80%, 50%) to categorize the severity of obstruction may misclassify subjects who are young and tall or old and short (as discussed in a preceding paragraph). These misapplications of fixed ratios and fixed percents of predicted can have serious consequences for individual patients and for large groups of subjects when research is involved. Misclassifying an elderly subject as having COPD may mean the inappropriate prescription of drugs that can have serious side effects. Using an inappropriate classification, such as an FEV₁/FVC ratio of 70%, to exclude subjects from a clinical trial (because they are incorrectly classified as “obstructed”) means that otherwise healthy subjects are not exposed to the treatment or drug being evaluated.

Figure 13-5 Theoretical sample population of females for the NHANES III data set.
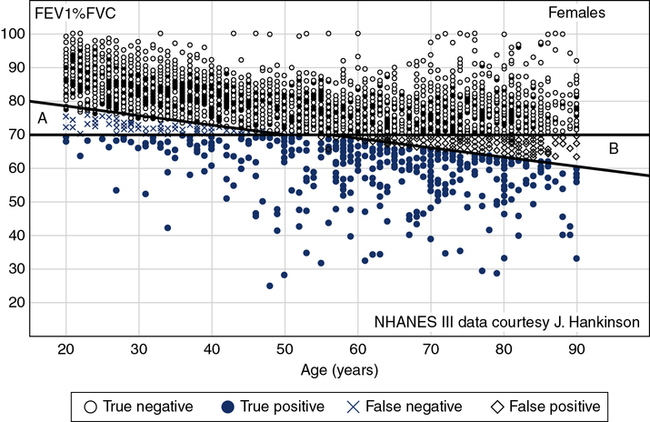
The Figure shows a theoretical sample population of females whose data fit the NHANES III equation for FEV₁/FVC ratio. All subjects plotted as black dots are truly within the normal range. Those plotted in light grey are below the LLN and represent true positives. The subjects less than 40 years of age and plotted in blue “x”s are false negatives (GOLD recommendations falsely state they are normal [>70%] but are in fact below the LLN) and the black “◇”s in the older population group are those where GOLD recommendations state they are abnormal when in fact they are above the LLN (false positives).

Pulmonary function laboratories should try to choose reference studies from a population similar to the patients they test. The following factors may be considerations in selecting reference values:

1. Type of equipment used for the reference study: Does equipment comply with the most recent recommendations of the ATS-ERS (See Chapter 11.)

2. Methodology: Were standardized procedures used in the reference study similar to those to be used, particularly for spirometry, lung volumes, and Dlco?

3. Reference population: What were the ranges of ages of the individuals in the reference population? Were both males and females tested? Did the study generate different regressions for different ethnic origins? Did the study include smokers or other “at-risk” individuals as healthy individuals? If a specific group of subjects was studied, are the results applicable to the population in general?

4. Statistical analysis: Are lower limits of normal specifically defined (e.g., 5th percentile, 1.645 × RSD)? Are adequate measures of variability available (RSD, SEE) so that upper or lower limits of normal can be calculated along with the predicted values?

5. Conditions of the study: Was the study performed at a different altitude or under significantly different environmental conditions?

6. Published reference equations: Do reference values generated using the study’s regressions differ markedly from other published references?

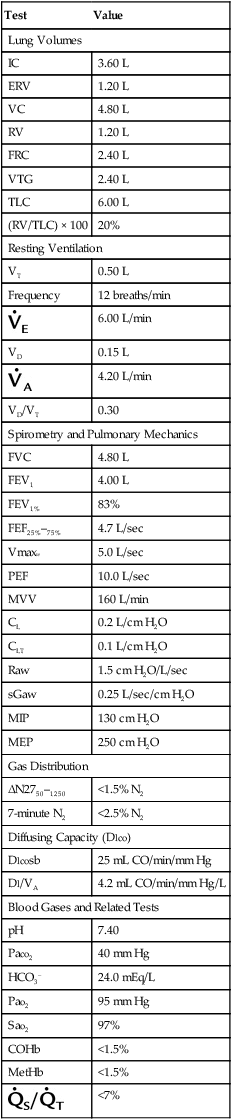
Individual laboratories may wish to perform measurements on subjects who represent a healthy cross-section of the population that the laboratory usually tests. Doing this in a statistically meaningful way may require testing a large number of subjects. However, measured values from these individuals can then be compared with expected values using various reference equations. Equations that produce the smallest average differences (measured – predicted) may be preferable. Evaluation of a small number of individuals may not show much difference between equations for FVC and FEV₁. However, there may be noticeable discrepancies for Dlco or maximal flows. Equations for spirometry, lung volumes, and Dlco should be taken from a single reference, if possible. If healthy individuals fall outside of the limits of normal, the laboratory should examine its test methods, how the individuals were selected, and the prediction equations being used. Table 13-3 lists “typical” normal values for pulmonary function and blood gas parameters.

Table 13-3

Typical Values for Pulmonary Function Tests
Values are for a healthy young male, 1.7 m² body surface area.

Test	Value
Lung Volumes
IC	3.60 L
ERV	1.20 L
VC	4.80 L
RV	1.20 L
FRC	2.40 L
VTG	2.40 L
TLC	6.00 L
(RV/TLC) × 100	20%
Resting Ventilation
V_T	0.50 L
Frequency	12 breaths/min
	6.00 L/min
V_D	0.15 L
	4.20 L/min
V_D/V_T	0.30
Spirometry and Pulmonary Mechanics
FVC	4.80 L
FEV₁	4.00 L
FEV_1%	83%
FEF_25%–_75%	4.7 L/sec
Vmax_⁵⁰	5.0 L/sec
PEF	10.0 L/sec
MVV	160 L/min
C_L	0.2 L/cm H₂O
C_LT	0.1 L/cm H₂O
Raw	1.5 cm H₂O/L/sec
sGaw	0.25 L/sec/cm H₂O
MIP	130 cm H₂O
MEP	250 cm H₂O
Gas Distribution
ΔN27₅₀–₁₂₅₀	<1.5% N₂
7-minute N₂	<2.5% N₂
Diffusing Capacity (Dlco)
Dlcosb	25 mL CO/min/mm Hg
Dl/V_A	4.2 mL CO/min/mm Hg/L
Blood Gases and Related Tests
pH	7.40
Paco₂	40 mm Hg
HCO₃^–	24.0 mEq/L
Pao₂	95 mm Hg
Sao₂	97%
COHb	<1.5%
MetHb	<1.5%
	<7%

Pulmonary function testing interpretation, “bringing it all together”

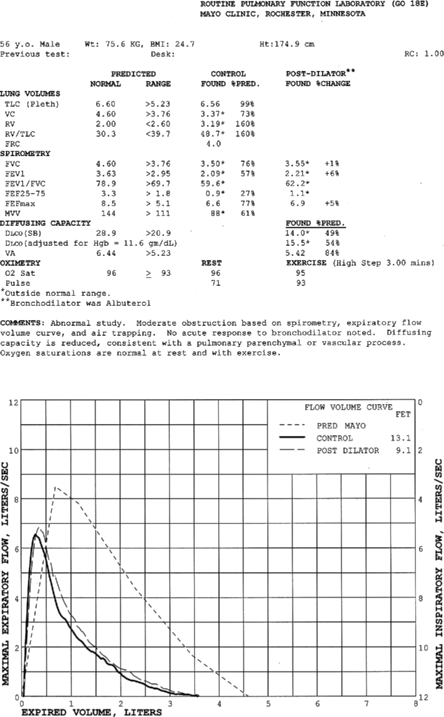
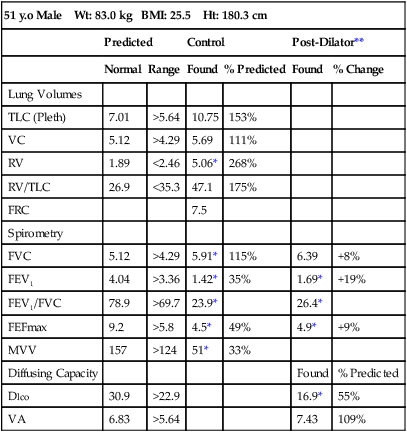
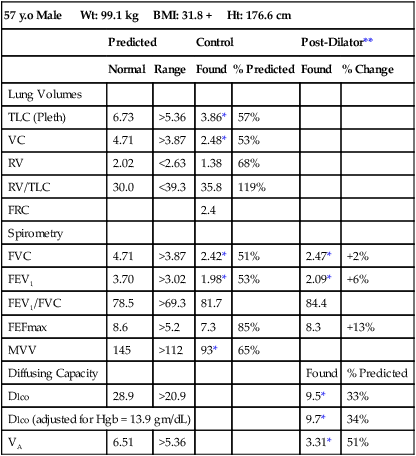
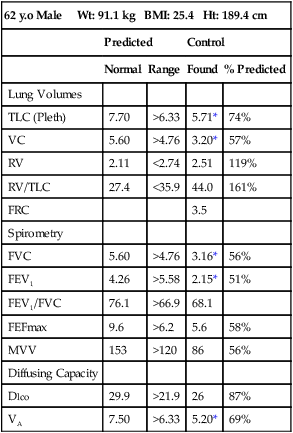
Pulmonary function test interpretation should be structured to facilitate an understanding of the test results by the attending clinician and not to further confuse them. Simply reiterating numbers will not accomplish this goal. Clear, succinct terminology, such as “normal study” or “abnormal study” followed by a brief organized review of the data will be more useful to the ordering physician in caring for their patient (Box 13-1). The reported data should be structured in an organized manner to facilitate the interpretation and understanding of the clinician. Spirometers can calculate a virtual sea of parameters, and, even though they may have benefit in specific circumstances, they serve only to confuse the novice user. Figure 13-6 is an example of a PFT report with groupings of data under major section headers that assist in presenting the data in an organized fashion. Values that fall outside of the LLN (or ULN) can be highlighted (colored) or accompany an asterisk to visually bring them to the attention of the viewer.

Box 13-1 Example PFT Interpretation

Abnormal study. Severe airway obstruction with hyperinflation and air trapping. A significant response to bronchodilator. Diffusing capacity is reduced, which is consistent with a pulmonary parenchymal or vascular process. Oxygen saturation at rest is normal.

Signature, MD

Figure 13-6 **Example of PFT report** with major and minor headings and only clinically significant parameters displayed.

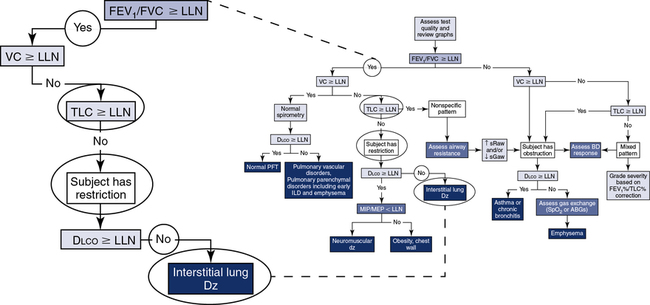
Interpretation algorithm

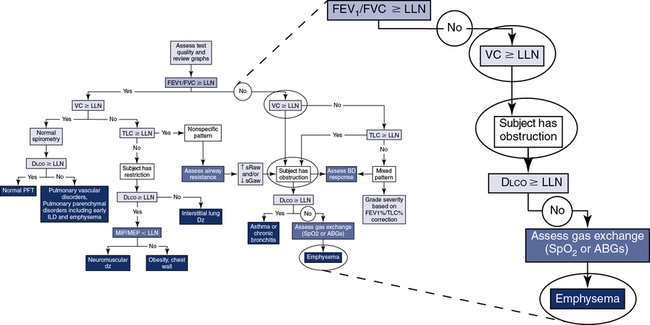
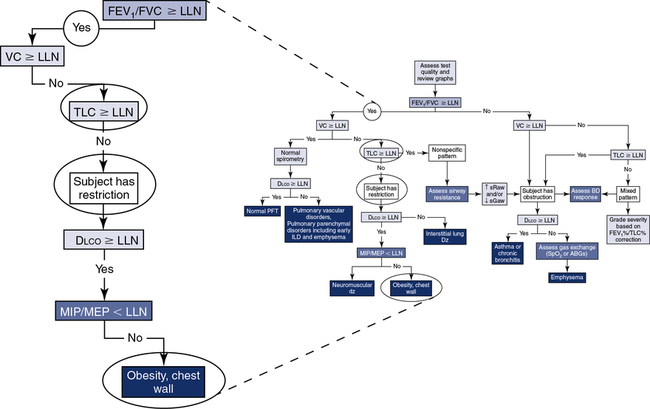
The application of a simple algorithm to define the major characteristics of lung function allows for a systematic approach to interpretation (Figure 13-7), although it does not fully describe all of the clinical nuances an interpreter may encounter.

Quality Review and “the Graph”

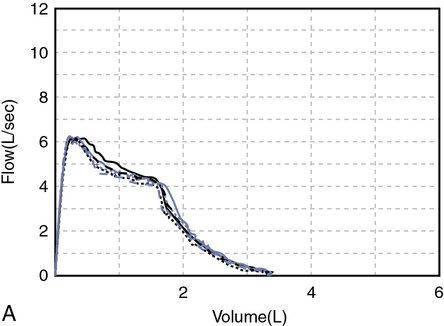
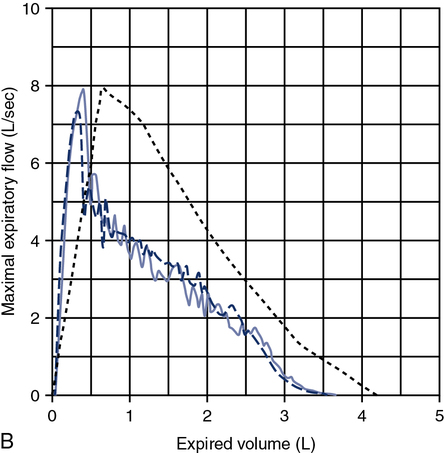
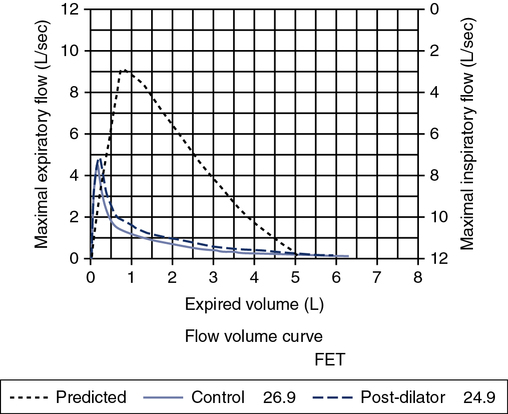
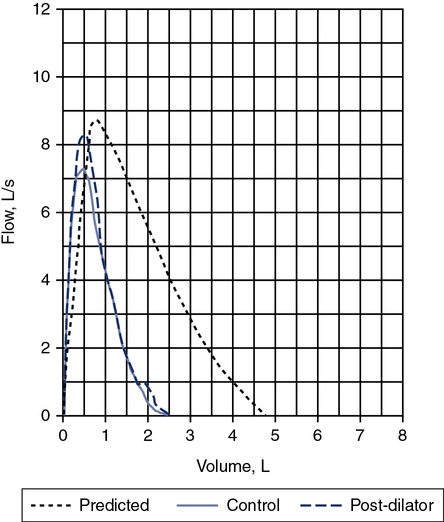
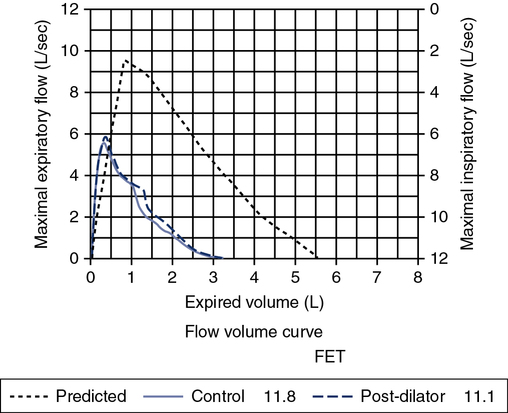
A review of the quality of each testing module data (see Chapter 12) and any comments documented by the testing staff are quintessential in the interpretation process. The interpretation of data that do not meet the ATS-ERS recommendations for acceptability and repeatability or include technologist’s comments related to poor effort should be conducted with caution. Data that are not repeatable but still “usable” should be noted by the interpreter in their comments (e.g., subject could not perform repeatable FVCs). Reviewing the flow volume and volume time curves can also help the interpreter in assessing quality. A slow start (e.g., back extrapolation error), cough in the first second, sharp peak flow (e.g., effort), and end-of-test criteria can all be evaluated visually from the graphical data. The FV curve can help define obstructive and restrictive patterns, aid in the assessment of upper airway obstruction (see Chapter 2), and possibly identify normal variants or other abnormalities that may not affect the numbers but be relevant to the patient’s condition (Figure 13-8, A and B). Any spirometry data without the presence of the flow volume curve graph, in particular, are just numbers and subject to question.

Figure 13-8 Variants of the flow-volume curve.
A, Normal variant termed a “knee.” B, Airway noise (not coughing) secondary to “floppy airways” or “redundant tissue” of the upper airway, which is neither specific nor sensitive for but often seen in patients with obstructive sleep apnea.

“The Ratio”

After reviewing the test quality, the first step of the interpretation process is to assess the FEV₁/FVC (FEV₁/VC) ratio. If the ratio is less than the LLN, the subject has obstruction. Other parameters such as FEF_75% or FEF_25%-75% and/or the shape of the flow volume curve (concave) may be affected earlier in the obstructive disease process and lead the interpreter to make a statement such as “borderline” obstruction. Next is the assessment of the vital capacity. If the ratio and the vital capacity are reduced, the measurement of lung volumes (e.g., TLC) is required to further define the abnormality. If the TLC is reduced, the subject has a mixed pattern. If the TLC is normal or elevated, this pattern is consistent with air trapping or hyperinflation along with their obstructive disease. If the vital capacity is greater than the LLN, the subject has obstruction. TLC can still be of benefit in defining hyperinflation and air trapping, in particular, with values >125% of predicted (RV greater than ULN). Assessment of the subject’s bronchodilator response may be useful in determining hyperreactive airways disease.

The subject has normal spirometry if the ratio is greater than or equal to the LLN and the VC is also greater than or equal to LLN. However, if the VC is less than LLN, TLC is required to further evaluate the abnormality. If the TLC is greater than or equal to the LLN, it is defined as the nonspecific pattern. In a study published by Hyatt and others, approximately 70% of their subjects with this pattern had obstruction and/or developed obstruction on follow-up, and the other 30% were morbidly obese. The term parallel shift is also used to describe the pattern when both FVC and FEV₁ are reduced with a normal TLC. Airways resistance and bronchodilator response can be used to further assess the nonspecific pattern.

If the ratio is greater than or equal to LLN and the vital capacity is reduced, spirometry suggests restriction; however, restriction needs to be defined by some measurement of TLC (lung volumes, CXR, or CT). If the measured TLC is less than LLN, the subject has restriction.

Gas Exchange

Gas exchange can be evaluated by several parameters. Diffusing capacity is used to evaluate the integrity of the alveolar-capillary membrane interface (transfer factor; see Chapter 3), and arterial blood gases or pulse oximetry is used to assess the physiologic impact of a gas exchange abnormality (see Chapter 6). In our simple algorithmic scheme, we will use the former to determine the impact of the disease process on gas exchange.

If the patient has obstruction, mixed pattern, and nonspecific pattern included (see Figure 13-7, B), and the Dlco is greater than or equal to LLN, the data would be consistent with asthma or chronic bronchitis. Whereas if the Dlco is less than LLN, the data would be consistent with emphysema. According to Hadeli and others, when the Dlco is <60%, there is a high probability of exercise desaturation, and further assessment (i.e., ABGs or pulse oximetry) may be warranted.

If the patient has normal spirometry (see Figure 13-7, A) and the Dlco is greater than or equal to LLN, the subject has a normal PFT. Whereas if the Dlco is less than LLN, the data would be consistent with a pulmonary vascular disorder (e.g., pulmonary emboli, A-V malformation) and/or early pulmonary parenchymal disorders (e.g., interstitial lung disease, emphysema).

If the patient has restriction (see Figure 13-7) and the Dlco is greater than or equal to LLN, consider neuromuscular disease, obesity, and/or chest wall deformities. Further evaluation with respiratory muscular strength measurements (see Chapter 10) may be helpful in differentiating the abnormality. Whereas if the Dlco is less than LLN, the data would be consistent with interstitial lung disease (e.g., pulmonary fibrosis).

Bronchodilator Response

Assessing bronchodilator response may be indicated in patients complaining of chest tightness, wheeze, and/or shortness of breath. Furthermore, patients who fall into the categories of obstruction, mixed pattern, and/or nonspecific pattern may specifically warrant bronchodilator testing to further differentiate their underlying abnormality. A complete description of the test methodology and assessment of the response is described in Chapter 2. However, as a review, a significant response (positive response) is an increase in the FEV₁ greater than 12% and 200 mL or if airways resistance is assessed, a 30% to 40% change occurs (↓ sRaw or ↑ sGaw).

Grading Severity and Assessing Change in Lung Function

Table 13-4 summarizes grading of the severity of pulmonary function test parameters. The 2005 ATS-ERS recommendations do not address grading of lung volumes (also known as restriction) separate from grading the severity of the FEV₁ from spirometry, noting that the overall impact of the ventilatory dysfunction can be described with this single variable. However, practically all clinicians are still requesting grading of the lung volume measurements and may make clinical/treatment decisions based on that grade. The 1991 ATS interpretation recommendations have a scheme for the grading of lung volumes, which are included in Table 13-4. Zechariah and others recently published recommendations for grading the severity of obstruction in a patient with mixed obstruction-restriction. In their paper, they applied an adjustment by dividing the FEV_1% predicted by the TLC% predicted.

Table 13-4

Grading Severity of PFT Parameters

*Spirometry FEV₁/FVC < LLN	FEV₁ % Pred
Mild obstruction	>70%
Moderate obstruction	60%-69%
Moderately severe obstruction	50%-59%
Severe obstruction	35%-49%
Very severe obstruction	<35%
**Lung Volumes FEV₁/FVC ≥ LLN	TLC % Pred
Mild restriction	<LLN but >70%
Moderate restriction	<70 and >60%
Moderately severe restriction	<60%

*DLCO	DLCO % Pred
Mild	>60% and <LLN
Moderate	40%-60%
Severe	<40%

^*Adapted from the ATS-ERS Interpretation guideline. Eur Respir J. 2005; 26:948–968.

^**Adapted from the ATS Selection of reference values and interpretive strategies. Am Rev Respir Dis. 1991; 144:1202.

Example:

TLC	2.82 L	61% pred
FVC	1.11 L	44% pred
FEV₁	0.68 L	34% pred = Very severe obstruction
FEV₁/FVC		61.6%

FEV_1% pred

TLC% predicted = 34/61 = 56% = Moderately severe obstruction

In evaluating a patient’s change in lung function over time, you need to take into account the test-to-test variability. The normal rate of decline in FEV₁ is approximately 30 mL per year in subjects greater than 30 years of age. However, when you factor in the test variability, the ATS-ERS recommends a change of 15% before you interpret any change as clinically significant. A laboratory can also establish its own variability by analyzing their BioQC (see Chapter 12) data. The Mayo Clinic Pulmonary Laboratory variability is as follows:

FVC 250 mL FEV₁ 220 mL, TLC 320 mL, Dlco 3.2 units

Table 13-5 summarizes the ATS-ERS recommendations for a clinically significant change over time.

Table 13-5

Significant Change Over Time

	FVC	FEV₁	Dlco
Week to Week
Normal subjects	≥11%	≥12%	>6 units
COPD	≥20%	≥20%	>4 units
Year to Year	≥15%	≥15%	10%

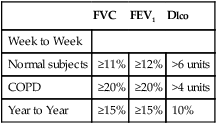
Adapted from the ATS-ERS Interpretation guideline. Eur Respir J. 2005; 26:948–968.

Summary

• The chapter describes the selection of reference values for spirometry, lung volumes, and diffusing capacity.

• It’s important to identify the lower limit of normal and list some of the more commonly used reference sets, such as for spirometry, lung volumes, and diffusing capacity.

• A simple algorithm for the interpretation of pulmonary function test can be used and will help establish the cut-points used to grade severity.

• More detailed information related to test interpretation is found in specifically labeled chapters.

Case Studies

Case 13-1

51 y.o Male Wt: 83.0 kg BMI: 25.5 Ht: 180.3 cm
	Predicted		Control		Post-Dilator**
	Normal	Range	Found	% Predicted	Found	% Change
Lung Volumes
TLC (Pleth)	7.01	>5.64	10.75	153%
VC	5.12	>4.29	5.69	111%
RV	1.89	<2.46	5.06*	268%
RV/TLC	26.9	<35.3	47.1	175%
FRC			7.5
Spirometry
FVC	5.12	>4.29	5.91*	115%	6.39	+8%
FEV₁	4.04	>3.36	1.42*	35%	1.69*	+19%
FEV₁/FVC	78.9	>69.7	23.9*		26.4*
FEFmax	9.2	>5.8	4.5*	49%	4.9*	+9%
MVV	157	>124	51*	33%
Diffusing Capacity					Found	% Predicted
Dlco	30.9	>22.9			16.9*	55%
VA	6.83	>5.64			7.43	109%

^*Outside normal range.

^**Bronchodilator was Albuterol.

Step 1: Assess quality and review graphs.

• Good quality—no hesitation, good peak, no cough, expiratory time 26 seconds

• Concave curve would suggest obstruction.

Step 2: Evaluate “the ratio.”

• Less than LLN = obstruction

Step 3: Assess the vital capacity.

• Normal

Step 4: Assess TLC.

• Elevated TLC (>125%) and RV (greater than ULN) suggest hyperinflation and air trapping.

Step 5: Assess Dlco.

• Less than LLN

Step 6: Consider the addition of airway resistance, bronchodilator response, respiratory muscle strength, and ABGs/pulse oximetry.

• >12% and 200 mL; significant BD response

Interpretation

Abnormal study. Very severe obstruction with hyperinflation and air trapping. There is a significant response to bronchodilator. Diffusing capacity is moderately reduced, which is consistent with a pulmonary parenchymal or vascular abnormality.

The subject had Alpha-1 antitrypsin deficiency.

^*For these case studies use the simple interpretation flow chart to characterize the abnormality.

Case 13-2

57 y.o Male Wt: 99.1 kg BMI: 31.8 + Ht: 176.6 cm
	Predicted		Control		Post-Dilator**
	Normal	Range	Found	% Predicted	Found	% Change
Lung Volumes
TLC (Pleth)	6.73	>5.36	3.86*	57%
VC	4.71	>3.87	2.48*	53%
RV	2.02	<2.63	1.38	68%
RV/TLC	30.0	<39.3	35.8	119%
FRC			2.4
Spirometry
FVC	4.71	>3.87	2.42*	51%	2.47*	+2%
FEV₁	3.70	>3.02	1.98*	53%	2.09*	+6%
FEV₁/FVC	78.5	>69.3	81.7		84.4
FEFmax	8.6	>5.2	7.3	85%	8.3	+13%
MVV	145	>112	93*	65%
Diffusing Capacity					Found	% Predicted
Dlco	28.9	>20.9			9.5*	33%
Dlco (adjusted for Hgb = 13.9 gm/dL)					9.7*	34%
V_A	6.51	>5.36			3.31*	51%

^*Outside normal range. +weight exceeds 95th percentile.

^**Bronchodilator was Albuterol.

Step 1: Assess quality and review graphs.

• Good quality—no hesitation, good peak, no cough, expiratory time 7 seconds

• Peaked “witch’s hat” curve would suggest restriction.

Step 2: Evaluate “the ratio.”

• Greater than LLN = normal or restriction

Step 3: Assess the vital capacity.

• Reduced vital capacity suggests restriction by spirometry.

Step 4: Assess TLC.

• Reduced TLC is consistent with restriction.

Step 5: Assess Dlco.

• Less than LLN

Step 6: Consider the addition of airway resistance, bronchodilator response, respiratory muscle strength, and ABGs/pulse oximetry.

• No BD response

• High probability of exercise-induced desaturation

Interpretation

Abnormal study. Moderately severe restriction with no response to bronchodilator. Diffusing capacity is moderately reduced, which is consistent with a pulmonary parenchymal or vascular abnormality.

Subject has pulmonary fibrosis.

^*For these case studies use the simple interpretation flow chart to characterize the abnormality.

Case 13-3

62 y.o Male Wt: 91.1 kg BMI: 25.4 Ht: 189.4 cm
	Predicted		Control
	Normal	Range	Found	% Predicted
Lung Volumes
TLC (Pleth)	7.70	>6.33	5.71*	74%
VC	5.60	>4.76	3.20*	57%
RV	2.11	<2.74	2.51	119%
RV/TLC	27.4	<35.9	44.0	161%
FRC			3.5
Spirometry
FVC	5.60	>4.76	3.16*	56%
FEV₁	4.26	>5.58	2.15*	51%
FEV₁/FVC	76.1	>66.9	68.1
FEFmax	9.6	>6.2	5.6	58%
MVV	153	>120	86	56%
Diffusing Capacity
Dlco	29.9	>21.9	26	87%
V_A	7.50	>6.33	5.20*	69%