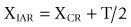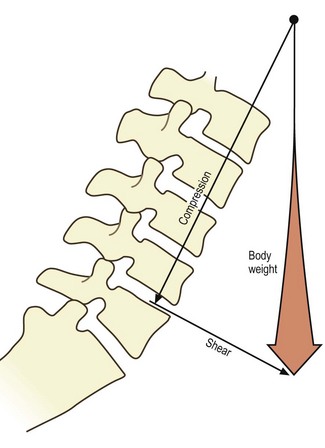
Axial compression

Axial compression is the movement that occurs during weight-bearing in the upright posture, or as a result of contraction of the longitudinal back muscles (see Ch. 9). With respect to the interbody joints, the weight-bearing mechanisms of the intervertebral discs have already been described in Chapter 2, where it was explained how the nucleus pulposus and anulus fibrosus cooperate to transmit weight from one vertebra to the next. It is now appropriate to add further details.

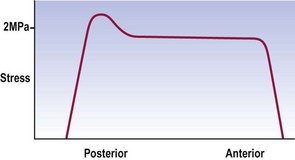
During axial compression, both the anulus fibrosus and nucleus pulposus bear the load and transmit it to the vertebral endplates (see Ch. 2). In a normal disc, the outermost fibres of the anulus do not participate in bearing the load. Otherwise, the compression load is borne uniformly across the inner, anterior anulus and nucleus, but with a peak stress over the inner, posterior anulus (Fig. 8.1).^2–4 In older discs this posterior peak is larger.^3,4

Figure 8.1 The stress profile of an intervertebral disc from the posterior to the anterior anulus during axial compression.

(Based on Adams et al. 1993.¹)

Compression squeezes water out of the disc.^5–7 Under a 100 kPa load, the nucleus loses some 8% of its water and the anulus loses 11%.^8–10 The loss of water results in a relative increase in the concentration of electrolytes remaining in the disc, and this increased concentration serves to re-imbibe water into the disc once compression is released.⁹

Under compression, the vertebral bodies around a disc approximate and the disc bulges radially.^6,8,11 The vertebral bodies approximate because the vertebral endplates bow away from the disc.^11–13 Indeed, the deflection of each endplate is almost equal to half the displacement of the vertebrae.¹² This amounts to a strain of approximately 3% in the endplate.¹² The disc bulges because, as the anulus loses height peripherally, the redundant length must somehow be accommodated, i.e. the lamellae of the anulus must buckle. Nuclear pressure normally prevents buckling inwards, leaving outward radial bulging as the only means of accommodating loss of disc height. The bulging is greater anteriorly than at the posterolateral corner of the disc, and induces a strain in the anulus fibrosus of about 2% per mm loss of disc height.¹⁴ Removing part of the nucleus (as occurs in discectomy) increases both the loss of disc height and the radial bulge.¹⁵

The load on the endplate during compression is evenly distributed over its surface, there being no greater load over the nucleus pulposus than over the anulus fibrosus.¹⁶ The endplate bows, however, because its periphery its strongly supported by the underlying cortical bone of the vertebra, whereas its central portion is supported by the slightly weaker trabecular bone of the vertebral body. This trabecular support is critical to the integrity of the endplate.

When excessive loads are applied to normal intervertebral discs, the trabeculae under the endplates fracture and the endplates themselves fracture, typically in their central region, i.e. over the nucleus pulposus, rather than over the anulus.^5,17–20 With the application of very great loads the entire endplate may fracture.^19–21

In this context, it is noteworthy that the endplates are the weakest components of the intervertebral disc in the face of axial compression. Provided the anulus is healthy and intact, increasing the load causes one or other of the endplates to fail, by fracturing, sooner than the anulus fibrosus fails, by rupturing.^5,19,20 This phenomenon has particular ramifications in the pathology of compression injuries of the lumbar spine and disc degradation (see Ch. 15), and has its basis in the relative strengths of the anulus fibrosus and the bone of the vertebral body. Calculations have shown that the anulus fibrosus can withstand a pressure of 3.2 × 10⁷ Nm⁻² but cancellous bone yields at 3.4 × 10⁶ Nm⁻².⁸ Consequently, endplates would be expected to fail sooner than the anulus fibrosus when the disc is subjected to axial compression.

With respect to the vertebral bodies, in adults under the age of 40, between 25% and 55% of the weight applied to a vertebral body is borne by the trabecular bone;^11,22,23 the rest is borne by the cortical shell. In older individuals this proportion changes, for reasons explained in Chapter 13. Overall, the strength of a vertebral body is quite great but varies considerably between individuals. The ultimate compressive strength of a vertebral body ranges between 3 and 12 kN.^24,25 This strength is directly related to bone density^24,26,27 and can be predicted to within 1 kN on the basis of bone density and endplate area determined by CT scanning.²⁸ It also seems to be inversely related to physical activity, in that active individuals have stronger vertebrae.²⁹

Another factor that increases the load-bearing capacity of the vertebral body is the blood within its marrow spaces and intra-osseous veins (see Ch. 11). Compression of the vertebral body and bulging of the endplates causes blood to be extruded from the vertebra.⁶ Because this process requires energy, it buffers the vertebral body, to some extent, from the compressive loads applied to it.²⁰

During compression, intervertebral discs undergo an initial period of rapid creep, deforming about 1.5 mm in the first 2–10 min depending on the size of the applied load.^30–32 Subsequently, a much slower but definite creep continues at about 1 mm per hour.³² Depending on age, a plateau is attained by about 90 min, beyond which no further creep occurs.³¹

Creep underlies the variation in height changes undergone by individuals during activities of daily living. Over a 16-hour day, the pressure sustained by intervertebral discs during walking and sitting causes loss of fluid from the discs, which results in a 10% loss in disc height¹⁰ and a 16% loss of disc volume.³³ Given that intervertebral discs account for just under a quarter of the height of the vertebral column, the 10% fluid loss results in individuals being 1–2% shorter at the end of a day.^34–36 This height is restored during sleep or reclined rest, when the vertebral column is not axially compressed and the discs are rehydrated by the osmotic pressure of the disc proteoglycans.¹⁰ Moreover, it has been demonstrated that rest in the supine position with the lower limbs flexed and raised brings about a more rapid return to full disc height than does rest in the extended supine position.³⁶

The pressure within intervertebral discs can be measured using special needles,^37–39 and disc pressure measurement, or discometry, provides an index of the stresses applied to a disc in various postures and movements. Several studies have addressed this issue although for technical reasons virtually all have studied only the L3–4 disc.

In the upright standing posture, the load on the disc is about 70 kPa.³⁸ Holding a weight of 5 kg in this posture raises the disc pressure to about 700 kPa.^38,40 The changes in disc pressure during other movements and manoeuvres are described in Chapter 9.

Although the interbody joints are designed as the principal weight-bearing components of the lumbar spine (see Ch. 2), there has been much interest in the role that the zygapophysial joints play in weight-bearing. The earliest studies in this regard provided indirect estimates of the load borne by the zygapophysial joints based on measurements of intradiscal pressure, and it was reported that the zygapophysial joints carried approximately 20% of the vertical load applied to an intervertebral joint.³⁷ This conclusion, however, was later retracted.⁴¹

Subsequent studies have variously reported that the zygapophysial joints can bear 28%⁴² or 40%⁴³ of a vertically applied load. To the contrary, others have reported that ‘compression did not load the facet joints … very much’,⁴⁴ and that ‘provided the lumbar spine is slightly flattened … all the intervertebral compressive force is resisted by the disc’.⁴⁵

Reasons for these differences in the conclusions relate to the experimental techniques used and to the differing appreciation of the anatomy of the zygapophysial joints and their behaviour in axial compression.

Although the articular surfaces of the lumbar zygapophysial joints are curved in the transverse plane (see Ch. 3), in the sagittal and coronal planes they run straight up and down (although see Ch. 11). Thus, zygapophysial joints, in a neutral position, cannot sustain vertically applied loads. Their articular surfaces run parallel to one another and parallel to the direction of the applied load. If an intervertebral joint is axially compressed, the articular surfaces of the zygapophysial joints will simply slide past one another. For the zygapophysial joints to participate in weight-bearing in erect standing, some aberration in their orientation must occur, and either of two mechanisms may operate singly or in combination to recruit the zygapophysial joints into weight-bearing.

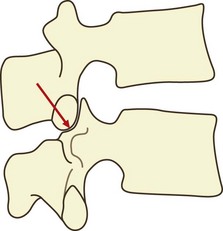
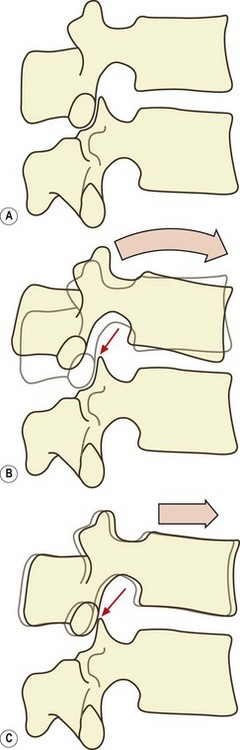
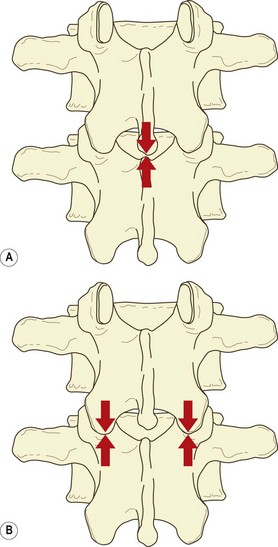
If a vertebra is caused to rock backwards on its intervertebral disc without also being allowed to slide backwards, the tips of its inferior articular processes will be driven into the superior articular facets of the vertebra below (Fig. 8.2). Axial compression of the intervertebral joint will then result in some of the load being transmitted through the region of impaction of the zygapophysial joints. By rocking a pair of lumbar vertebrae, one can readily determine by inspection that the site of impaction in the zygapophysial joints falls on the inferior medial portion of the facets. Formal experiments have shown this to be the site where maximal pressure is detected in the zygapophysial joints of vertebrae loaded in extension.⁴⁶

Figure 8.2 When a vertebra rocks backwards, its inferior articular processes impact the lower face of the superior articular processes of the vertebra below.

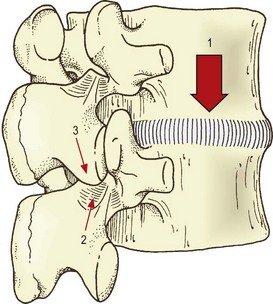
Another mechanism does not involve the zygapophysial joint surfaces but rather the tips of the inferior articular processes. With severe or sustained axial compression, intervertebral discs may be narrowed to the extent that the inferior articular processes of the upper vertebra are lowered until their tips impact the laminae of the vertebra below (Fig. 8.3).⁴⁷ Alternatively, this same impact may occur if an intervertebral joint is axially compressed while also tilted backwards, as is the case in a lordotic lumbar spine bearing weight.^46–49 Axial loads can then be transmitted through the inferior articular processes to the laminae.

Figure 8.3 If an intervertebral joint is compressed (1), the inferior articular processes of the upper vertebra impact the laminae below (2), allowing weight to be transmitted through the inferior articular processes (3).

It has been shown that under the conditions of erect sitting, the zygapophysial joints are not impacted and bear none of the vertical load on the intervertebral joint. However, in prolonged standing with a lordotic spine, the impacted joints at each segmental level bear an average of some 16% of the axial load.^45,48 In this regard, the lower joints (L3–4, L4–5, L5–S1) bear a relatively greater proportion (19%), while the upper joints (L1–2, L2–3) bear less (11%).⁴⁸ Other studies have shown that the actual load borne by impaction of inferior articular processes varies from 3–18% of the applied load, and critically depends on the tilt of the intervertebral joint.⁴⁹ It has also been estimated that pathological disc space narrowing can result in some 70% of the axial load being borne by the inferior articular processes and laminae.⁴⁵

It is thus evident that weight-bearing occurs through the zygapophysial joints only if the inferior articular processes impact either the superior articular facets or the laminae of the vertebra below. Variations in the degree of such impactions account for the variations in the estimates of the axial load carried by the zygapophysial joints,⁴⁹ and explain why the highest estimates of the load borne are reported in studies in which the intervertebral joints have been loaded in the extended position.^{42,43,50–52}

Although the preceding account of axial compression emphasises the role of the discs and zygapophysial joints in weight-bearing, other components of the lumbar spine also participate. The shape of the lordotic lumbar spine allows the anterior longitudinal ligament and the anterior portions of the anuli fibrosi to be involved in weight-bearing. Because of the curvature of the lordosis, the posterior parts of the intervertebral discs and the zygapophysial joints are compressed, but the anterior ligaments are stretched. Axial loading of a lordotic spine tends to accentuate the lordosis and, therefore, to increase the strain in the anterior ligaments. By increasing their tension, the anterior ligaments can resist this accentuation and share in the load-bearing.

In this way, the lordosis of the lumbar spine provides an axial load-bearing mechanism additional to those available in the intervertebral discs and the zygapophysial joints. Moreover, as described in Chapter 5, the tensile mechanism of the anterior ligaments imparts a resilience to the lumbar spine. The energy delivered to the ligaments is stored in them as tension and can be used to restore the curvature of the lumbar spine to its original form, once the axial load is removed.

Axial distraction

Compared to axial compression and other movements of the lumbar spine, axial distraction has been studied far less. One study provided data on the stress–strain and stiffness characteristics of lumbar intervertebral discs as a whole, and revealed that the discs are not as stiff in distraction as in compression.⁵¹ This is understandable, for the discs are designed principally for weight-bearing and would be expected to resist compression more than tension. In a biological sense, this correlates with the fact that humans spend far more time bearing compressive loads – in walking, standing and sitting – than sustaining tensile loads, as might occur in brachiating (tree-climbing) animals.

Other studies have focused on individual elements of the intervertebral joints to determine their tensile properties. When stretched along their length, isolated fibres of the anulus fibrosus exhibit a typical ‘toe’ region between 0% and 3% strain, a failure stress between 4 and 10 MPa, and a strain at failure between 9% and 15%; their stiffness against stretch ranges from 59 to 140 MPa.⁵⁴ If the anulus is tested while still attached to bone and distracted along the longitudinal axis of the vertebral column, as opposed to along the length of the fibres, the failure stress remains between 4 and 10 MPa but the stiffness drops to between 10 and 80 MPa.⁵⁵ These tensile properties seem to vary with location but the results between studies are conflicting. Isolated fibres seem to be stiffer and stronger in the anterior region than in the posterolateral region of the disc, and stiffer in the outer regions of the anulus than in the inner regions.¹ On the other hand, in intact specimens, the outer anterior anulus is weaker and less stiff than the outer posterior anulus.⁵⁵

The capsules of the zygapophysial joints are remarkably strong when subjected to longitudinal tension. A single capsule can sustain 600 N before failing.⁵⁶ Figuratively, this means that a pair of capsules at a single level can bear twice the body weight if subjected to axial distraction.

However, the significance of these results lies not so much in the ability of elements of the lumbar spine to resist axial distraction but in their capacity to resist other movements that strain them. The anulus fibrosus will be strained by anterior sagittal rotation and axial rotation, and the zygapophysial joint capsules by anterior sagittal rotation. Those movements are considered below.

There has been one study⁵⁷ that has described the behaviour of the whole (cadaveric) lumbar spine during sustained axial distraction, to mimic the clinical procedure of traction. Application of a 9 kg weight to stretch the lumbar spine results in an initial mean lengthening of 7.5 mm. Lengthening is greater (9 mm) in lumbar spines of young subjects, and less in the middle-aged (5.5 mm) and the elderly (7.5 mm). Sustained traction over 30 min results in a creep of a further 1.5 mm. Removal of the load reveals an immediate ‘set’ of about 2.5 mm, which reduces to only 0.5 mm by 30 min after removal of the load. Younger spines demonstrate a more rapid creep and do not show a residual ‘set’. The amount of distraction is greater in spines with healthy discs (11–12 mm) and substantially less (3–5 mm) in spines with degenerated discs.

Some 40% of the lengthening of the lumbar spine during traction occurs as a result of flattening of the lumbar lordosis, with 60% due to actual separation of the vertebral bodies. The major implication of this observation is that the extent of distraction achieved by traction (using a 9 kg load) is not great. It amounts to 60% of 7.5 mm of actual vertebral separation, which is equivalent to about 0.9 mm per intervertebral joint. This revelation seriously compromises those theories that maintain that lumbar traction exerts a beneficial effect by ‘sucking back’ disc herniations, and it is suggested that other mechanisms of the putative therapeutic effect of traction be considered.⁵⁷

The other implication of this study relates to the fact that the residual ‘set’ after sustained traction is quite small (0.5 mm), amounting to about 0.1 mm per intervertebral joint. Moreover, this is the residual set in spines not subsequently reloaded by body weight. One would expect that, in living patients, a 0.1 mm set would naturally be obliterated the moment the patient rose and started to bear axial compression. Thus, any effect achieved by therapeutic traction must be phasic, i.e. occurring during the application of traction, and not due to some maintained lengthening of the lumbar spine.

Flexion

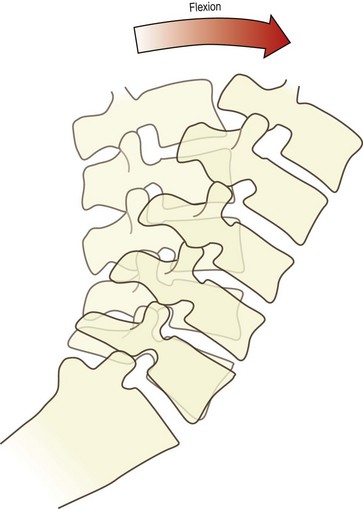
During flexion, the entire lumbar spine leans forwards (Fig. 8.4). This is achieved basically by the ‘unfolding’ or straightening of the lumbar lordosis. At the full range of forward flexion, the lumbar spine assumes a straight alignment or is curved slightly forwards, tending to reverse the curvature of the original lordosis (see Fig. 8.3). The reversal occurs principally at upper lumbar levels. Reversal may occur at the L4–5 level but does not occur at the L5–S1 level.^58,59 Forward flexion is therefore achieved for the most part by each of the lumbar vertebrae rotating from their backward tilted position in the upright lordosis to a neutral position, in which the upper and lower surfaces of adjacent vertebral bodies are parallel to one another. This relieves the posterior compression of the intervertebral discs and zygapophysial joints, present in the upright lordotic lumbar spine. Some additional range of movement is achieved by the upper lumbar vertebrae rotating further forwards and compressing their intervertebral discs anteriorly.

Figure 8.4 During flexion, the lumbar lordosis unfolds, and the lumbar spine straightens and leans forwards on the sacrum. The curvature of the lordosis may be reversed at upper lumbar levels but not at L5–S1.

It may appear that during flexion of the lumbar spine, the movement undergone by each vertebral body is simply anterior sagittal rotation. However, there is a concomitant component of forward translation as well.^59,60 If a vertebra rocks forwards over its intervertebral disc, its inferior articular processes are raised upwards and slightly backwards (Fig. 8.5A). This opens a small gap between each inferior articular facet and the superior articular facet in the zygapophysial joint. As the lumbar spine leans forwards, gravity or muscular action causes the vertebrae to slide forwards, and this motion closes the gap between the facets in the zygapophysial joints (Fig. 8.5B). Further forward translation will be arrested once impaction of the zygapophysial joints is re-established, but nonetheless a small forward translation will have occurred. At each intervertebral joint, therefore, flexion involves a combination of anterior sagittal rotation and a small amplitude anterior translation.

Figure 8.5 The components of flexion of a lumbar intervertebral joint. (A) The lateral parts of the right superior articular process have been cut away to reveal the contact between the inferior and superior articular facets in the neutral position. (B) Sagittal rotation causes the inferior articular processes to lift upwards, leaving a gap between them and the superior articular facets. This gap allows for anterior sagittal translation. (C) Upon translation, the inferior articular facets once again impact the superior articular facets.

The zygapophysial joints play a major role in maintaining the stability of the spine in flexion, and much attention has been directed in recent years to the mechanisms involved. To appreciate these mechanisms, it is important to recognise that flexion involves both anterior sagittal rotation and anterior sagittal translation, for these two components are resisted and stabilised in different ways by the zygapophysial joints.

Anterior sagittal translation is resisted by the direct impaction of the inferior articular facets of a vertebra against the superior articular facets of the vertebra below, and this process has been fully described in Chapter 3. This mechanism becomes increasingly important the further the lumbar spine leans forward, for with a greater forward inclination of the lumbar spine, the upper surfaces of the lumbar vertebral bodies are inclined downwards (Fig. 8.6), and there will be a tendency for the vertebrae above to slide down this slope.

Figure 8.6 When the lumbar spine is flexed, the weight of the trunk exerts compressive and shearing forces on the intervertebral joints. The forces are proportional to the angle of inclination of the interbody joint.

The cardinal ramification of the anatomy of the zygapophysial joints with respect to forward shear is that in joints with flat articular surfaces, the load will be borne evenly across the entire articular surface (see Ch. 3), but in joints with curved articular surfaces the load is concentrated on the anteromedial portions of the superior and inferior articular facets (see Ch. 3). Formal experiments have shown that during flexion, the highest pressures are recorded at the medial end of the lumbar zygapophysial joints,⁴⁶ and this has further bearing on the age changes seen in these joints (see Ch. 13).

The anterior sagittal rotation component of flexion is resisted by the zygapophysial joints in a different way. The mechanism involves tension in the joint capsule. Flexion involves an upward sliding movement of each inferior articular process, in relation to the superior articular process in each zygapophysial joint, and the amplitude of this movement is about 5–7 mm.⁶¹ This movement will tense the joint capsule, and it is in this regard that the tensile strength of the capsule is recruited. Acting as a ligament, each capsule can resist as much as 600 N.^14,56 Indeed, the tension developed in the capsules during flexion is enough to bend the inferior articular processes downwards and forwards by some 5°.⁶²

The other elements that resist the anterior sagittal rotation of flexion are the ligaments of the intervertebral joints. Anterior sagittal rotation results in the separation of the spinous processes and laminae. Consequently, the supraspinous and interspinous ligaments and the ligamenta flava will be tensed, and various types of experiments have been performed to determine the relative contributions of these structures to the resistance of flexion. The experiments have involved either studying the range of motion in cadavers in which various ligaments have been sequentially severed,⁶⁰ or determining mathematically the stresses applied to different ligaments on the basis of the separation of their attachments during different phases of flexion.³

In young adult specimens, sectioning the supraspinous and interspinous ligaments and ligamenta flava results in an increase of about 5° in the range of flexion.⁶⁰ (Lesser increases occur in older specimens but this difference is discussed in Ch. 13.) Sectioning the zygapophysial joint capsules results in a further 4° of flexion. Transecting the pedicles, to remove the bony locking mechanism of the zygapophysial joints, results in a further 15° increase in range.

In a sense, these observations suggest the relative contributions of various structures to the resistance of flexion. The similar increases in range following the transection of ligaments and capsules suggest that the posterior ligaments and the zygapophysial joint capsules contribute about equally, but their contribution is overshadowed by that of the bony locking mechanism, whose elimination results in a major increase in range of movement. However, such conclusions should be made with caution, for the experiments on which they are based involved sequential sectioning of structures. They do not reveal the simultaneous contributions of various structures, nor possible variations in the contribution by different structures at different phases of movement. Nevertheless, the role of the bony locking mechanism in the stability of the flexed lumbar spine is strikingly demonstrated.

To determine the simultaneous contribution by various structures to the resistance of flexion, mathematical analyses have been performed.³ The results indicate that in a typical lumbar intervertebral joint, the intervertebral disc contributes about 29% of the resistance, the supraspinous and interspinous ligaments about 19%, the ligamentum flavum about 13%, and the capsules of the zygapophysial joints about 39%. It is emphasised that these figures relate only to the resistance of anterior sagittal rotation, which is the movement that tenses these ligaments. They do not relate to the role played by the bony locking mechanism in preventing anterior translation during flexion.

Within the disc, the posterior anulus is tensed during flexion and the anterior anulus is relaxed. The posterior anulus exhibits a strain of 0.6% per degree of rotation, and the anterior anulus exhibits a reciprocal strain of –0.6% per degree.¹⁴ With respect to anterior translation, the anulus exhibits a strain of about 1% per mm of horizontal displacement.¹⁴ An isolated disc can withstand a flexion moment of about 33 Nm, and can sustain flexion angles of about 18°,⁶³ but in an intact specimen it is protected by the posterior ligaments. In an intact intervertebral joint, the posterior ligaments protect the disc and resist 80% of the flexion moment and restrict the segment to 80% of the range of flexion that will damage the disc.⁶³

Extension

In principle, extension movements of the lumbar intervertebral joints are the converse of those that occur in flexion. Basically, the vertebral bodies undergo posterior sagittal rotation and a small posterior translation. However, certain differences are involved because of the structure of the lumbar vertebrae. During flexion, the inferior articular processes are free to move upwards until their movement is resisted by ligamentous and capsular tension. Extension, on the other hand, involves downward movement of the inferior articular processes and the spinous process, and this movement is limited not by ligamentous tension but by bony impaction.

Bony impaction usually occurs between the spinous processes.⁶⁹ As a vertebra extends, its spinous process approaches the next lower spinous process. The first limit to extension occurs as the interspinous ligament buckles and becomes trapped between the spinous processes. Further extension is met with further compression of this ligament until the spinous processes virtually come into contact (Fig. 8.7A).⁶⁹

Figure 8.7 Factors limiting extension. Posterior sagittal rotation is usually limited by impaction of the spinous processes (A) but may be limited by impaction of the inferior articular processes of the laminae (B).

In individuals with wide interspinous spaces, extension may be limited before spinous processes come into contact.⁶⁹ Impaction occurs between the tip of one or other of the inferior articular processes of the moving vertebra and the subjacent lamina (Fig. 8.7B). This type of impaction is accentuated when the joint is subjected to the action of the back muscles,⁴⁷ for in addition to extending the lumbar spine, the back muscles also exert a substantial compression load on it (see Ch. 9). Consequently, during active extension, the inferior articular processes are drawn not only into posterior sagittal rotation but also downwards as the entire intervertebral joint is compressed. Under these circumstances, the zygapophysial joints become weight-bearing, as explained above (see ‘Axial compression’).

The posterior elements, however, are not critical for limiting extension. Resection of the zygapophysial joints has little impact on the capacity of a lumbar segment to bear an extension load.⁷⁰ The extension load, under these conditions, is adequately borne by the anterior anulus.⁷⁰

Axial rotation

Axial rotation of the lumbar spine involves twisting, or torsion, of the intervertebral discs and impaction of zygapophysial joints.

During axial rotation of an intervertebral joint, all the fibres of the anulus fibrosus that are inclined toward the direction of rotation will be strained. The other half will be relaxed (see Ch. 2). Based on the observation that elongation of collagen beyond about 4% of resting length leads to injury of the fibre (see Ch. 7), it can be calculated that the maximum range of rotation of an intervertebral disc without injury is about 3°.⁸ Beyond this range the collagen fibres will begin to undergo micro-injury. Moreover, observational studies have determined that the anulus fibrosus exhibits a strain of 1% per degree of axial rotation,¹⁴ which also sets a limit of 3° before excessive strain is incurred.

Experiments on lumbar intervertebral discs have shown that they resist torsion more strongly than bending movements, and the stress–strain curves for torsion rise very steeply in the range 0–3° of rotation.⁵¹ Very large forces have to be applied to strain the disc beyond 3°, and isolated discs (the posterior elements having being removed) fail macroscopically at about 12° of rotation.⁷¹ This suggests that 12° is the ultimate range for rotation before disc failure occurs but this relates to total macroscopic failure. Analysis of the stress–strain curves for intervertebral discs under torsion (Fig. 8.8) reveals an inflection point just before 3° of rotation, which indicates the onset of microscopic failure in the anulus fibrosus.⁷¹ The range between 3° and 12° represents continued microfailure until overt failure occurs.

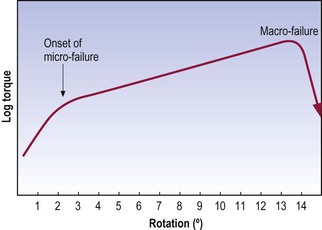
Figure 8.8 Stress–strain curve for torsion of the intervertebral disc.

(Based on Farfan et al. 1970.⁷¹)

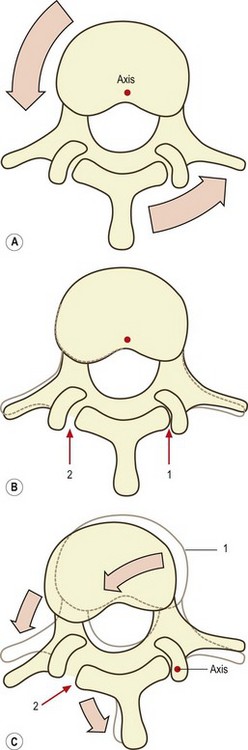
In an intact intervertebral joint, the zygapophysial joints, and to a certain extent the posterior ligaments, protect the intervertebral disc from excessive torsion. Because the axis of rotation of a lumbar vertebra passes through the posterior part of the vertebral body,⁷² all the posterior elements of the moving vertebra will swing around this axis during axial rotation. As the spinous process moves, the attachments of the supraspinous and interspinous ligaments will be separated, and these ligaments will be placed under slight tension. Furthermore, one of the inferior articular facets of the upper vertebra will be impacted against its apposing superior articular facet (Fig. 8.9). In the case of left axial rotation, it will be the right inferior articular facet that impacts (and vice versa). Once this impaction occurs, normal axial rotation is arrested.

Figure 8.9 The mechanism of left axial rotation of a lumbar intervertebral joint. Two consecutive vertebrae, superimposed on one another, are viewed from above. The lower vertebra is depicted by a dotted line. (A) Initially, rotation occurs about an axis in the vertebral body. (B) As the posterior elements swing around, the right inferior articular process of the upper vertebra impacts the superior articular process of the lower vertebra (1). The opposite zygapophysial joint is gapped (2). (C) Rotation beyond 3° occurs about an axis located in the impacted zygapophysial joint. The intervertebral disc must undergo lateral shear (1), and the opposite zygapophysial joint is gapped and distracted posteriorly (2).

Because the joint space of the zygapophysial joint is quite narrow, the range of movement before impaction occurs is quite small. Such movement as does occur is accommodated by compression of the articular cartilages, which are able to sustain compression because their principal constituents are proteoglycans and water. Water is simply squeezed out of the cartilages, and is gradually reabsorbed when the compression is released.

Given that the distance between a zygapophysial joint and the axis of rotation is about 30 mm, it can be calculated that about 0.5 mm of compression must occur for every 1° of axial rotation. Furthermore, given that the articular cartilages of a lumbar zygapophysial joint are about 2 mm thick (see Ch. 3), and that articular cartilage is about 75% water,⁷³ it can be calculated that to accommodate 3° of rotation, the cartilages must be compressed to about 62% of their resting thickness and must lose more than half of their water. The zygapophysial joints therefore provide a substantial buffer during the first 3° of rotation, and the zygapophysial joint must be severely compressed before rotation exceeds the critical range of 3°, beyond which the anulus fibrosus risks torsional injury. Nevertheless, if sufficiently strong forces are applied, rotation can proceed beyond 3°, but then an ‘impure’ form of rotation occurs as the result of distortion of other elements in the intervertebral joint.

To rotate beyond 3°, the upper vertebra must pivot on the impacted joint, and this joint becomes the site of a new axis of rotation. Both the vertebral body and the opposite inferior articular process will then swing around this new axis. The vertebral body swings laterally and backwards, and the opposite inferior articular process swings backwards and medially (see Fig. 8.9C). The sideways movement of the vertebral body will exert a lateral shear on the underlying disc^71,72 which will be additional to any torsional stress already applied to the disc by the earlier rotation. The backward movement of the opposite inferior articular process will strain the capsule of its zygapophysial joint.

During this complex combination of forces and movements, the impacted zygapophysial joint is being strained by compression, the intervertebral disc is strained by torsion and lateral shear, and the capsule of the opposite zygapophysial joint is being stretched. Failure of any one of these elements can occur if the rotatory force is sufficiently strong, and this underlies the mechanism of torsional injury to the lumbar spine (see Ch. 15).

The relative contributions of various structures to the resistance of axial rotation have been determined experimentally, and it is evident that the roles played by the supraspinous and interspinous ligaments, and by the capsule of the tensed (the opposite) zygapophysial joint are not great.⁷⁴ The load is borne principally by the impacted zygapophysial joint and the intervertebral disc. Quantitative analysis⁷¹ reveals that the disc contributes 35% of the resistance to torsion, the remaining 65% being exerted by the posterior elements: the tensed zygapophysial joint; the supraspinous and interspinous ligaments; and principally the impacted zygapophysial joint. Experimental studies, however, have established that the zygapophysial joints contribute only between 42% and 54% of the torsional stiffness of a segment, the rest stemming from the disc.⁷⁵

Lateral flexion

Lateral flexion of the lumbar spine does not involve simple movements of the lumbar intervertebral joints. It involves a complex and variable combination of lateral bending and rotatory movements of the interbody joints and diverse movements of the zygapophysial joints. Conspicuously, lateral flexion of the lumbar spine has not been subjected to detailed biomechanical analysis, probably because of its complexity and the greater clinical relevance of sagittal plane movements and axial rotation. However, some aspects of the mechanics of lateral flexion are evident when the range of this movement is considered below.

Rotation in flexion

There has been considerable interest in the movement of rotation in the flexed posture because this is a common movement associated with the onset of back pain. However, the studies offer conflicting results and opinions that stem from the complexities and subtleties of this movement, and differences in methods of study.

Using an external measuring device, Hindle and Pearcy⁷⁷ observed in 12 subjects that the range of axial rotation of the lumbar spine increased when these subjects sat in a flexed position. This, they argued, occurred because, upon flexion, the inferior articular facets are lifted out of the sockets formed by the apposed superior articular facets, and if the inferior facets are tapered towards one another, they gain an extra range of motion in the transverse direction. Subsequently, they demonstrated this phenomenon in cadavers.⁷⁸

Gunzburg et al. (1991)⁷⁹ reported contrary data. They could not find increased rotation upon flexion either in cadavers or in living subjects in the standing position.

It has been argued that these differences can be explained by differences in compression loads.⁸⁰ If a cadaveric specimen is compressed when flexed, the zygapophysial joints will remain deeper in their sockets than when allowed simply to flex. In living subjects, stooping while standing imposes large external loads that must be resisted by the back muscles, whose contraction will compress the moving segments (see Ch. 9). Consequently, increased axial rotation may be prevented by axial compression. However, this compression is not as great during flexion in the sitting position, under which conditions the increased axial rotation becomes apparent.

The argument concludes that increased axial rotation during flexion will not be apparent if the back muscles are strongly contracted although it may be apparent during sitting or if sudden external loads are applied which exceed the force of the back muscles. Under these circumstances, the increased axial rotation renders the disc liable to injury. As long as the zygapophysial joints limit rotation to less than 3°, the anulus is protected from injury. However, if axial rotation is greater than this, the anulus must undergo a greater strain and, moreover, one that is superimposed on the strain already induced by flexion.⁸⁰

Range of movement

The range of movement of the lumbar spine has been studied in a variety of ways. It has been measured in cadavers and in living subjects using either clinical measurements or measurements taken from radiographs. Studies of cadavers have the disadvantage that because of post-mortem changes and because cadavers are usually studied with the back musculature removed, the measurements obtained may not accurately reflect the mobility possible in living subjects. However, cadaveric studies have the advantage that motion can be directly and precisely measured and correlated with pathological changes determined by subsequent dissection or histological studies. Clinical studies have the advantage that they examine living subjects although they are limited by the accuracy of the instruments used and the reliability of identifying bony landmarks by palpation.

The availability and reliability of modern spondylo-meters, and the techniques for measuring the range of lumbar spinal motion are conveniently summarised in the AMA’s Guides to the Evaluation of Permanent Impairment, which also provides modern normative data.⁸¹ These, however, pertain to clinical measurements of spinal motion. They do not indicate exactly what happens in the lumbar spine and at each segment. That can be determined only by radiography.

Radiographic studies provide the most accurate measurements of living subjects but, although there have been many radiographic studies of segmental ranges of motion, these have now been superseded by the more accurate technique of biplanar radiography. Conventional radiography has the disadvantage that it cannot quantify movements that are not in the plane being studied. Thus, while lateral radiographs can be used to detect movement in the sagittal plane, they do not demonstrate the extent of any simultaneous movements in the horizontal and coronal planes. Such simultaneous movements can affect the radiographic image in the sagittal plane and lead to errors in the measurement of sagittal plane movements.^58,59,82

The technique of biplanar radiography overcomes this problem by taking radiographs simultaneously through two X-ray tubes arranged at right angles to one another. Analysis of the two simultaneous radiographs allows movements in all three planes to be detected and quantified, allowing a more accurate appraisal of the movements that occur in any one plane.^58,59,82

There have been two principal results stemming from the use of biplanar radiography. These are the accurate quantification of segmental motion in living subjects, and the demonstration and quantification of coupled movements.^58,59,83,84 The segmental ranges of motion in the sagittal plane (flexion and extension), horizontal plane (axial rotation) and coronal plane (lateral bending) are shown in Table 8.1. It is notable that, for the same age group and sex (25- to 36-year-old males), all lumbar joints have the same total range of motion in the sagittal plane, although the middle intervertebral joints have a relatively greater range of flexion, while the highest and lowest joints have a relatively greater range of extension.

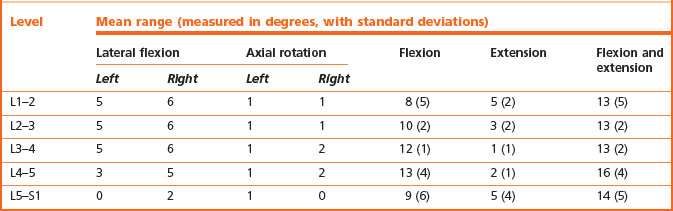
As determined by biplanar radiography, the mean values of axial rotation are approximately equal at all levels (see Table 8.1), and even the greatest values fall within the limit of 3°, which, from biomechanical evidence, is the range at which microtrauma to the intervertebral disc would occur. Conspicuously, the values obtained radiographically are noticeably smaller than those obtained both in cadavers and in living subjects using a spondylometer. The reasons for this discrepancy have not been investigated but may be due to the inability of clinical measurements to discriminate primary and coupled movements.

Coupled movements are movements that occur in an unintended or unexpected direction during the execution of a desired motion, and biplanar radiography reveals the patterns of such movements in the lumbar spine. Table 8.2 shows the ranges of movements coupled with flexion and extension of the lumbar spine and Table 8.3 shows the movements coupled with axial rotation and lateral flexion.

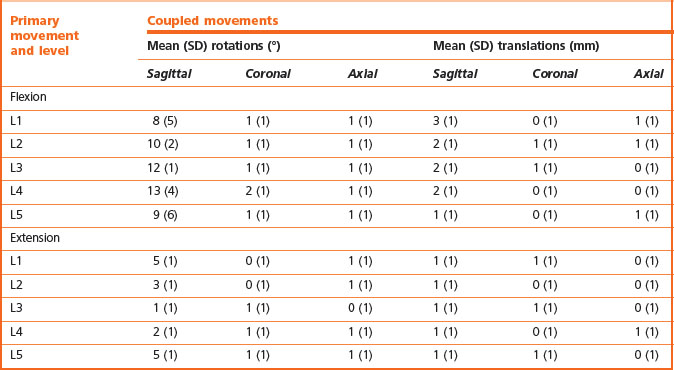
Flexion of lumbar intervertebral joints consistently involves a combination of 8–13° of anterior sagittal rotation and 1–3 mm of forward translation, and these movements are consistently accompanied by axial and coronal rotations of about 1° (see Table 8.2). Some vertical and lateral translations also occur but are of small amplitude. Conversely, extension involves posterior sagittal rotation and posterior translation, with some axial and coronal rotation, but little vertical or lateral translation (see Table 8.2).

Axial rotation and lateral flexion are coupled with one another and with sagittal rotation (see Table 8.3). Axial rotation is variably coupled with flexion and extension. Either flexion or extension may occur during left or right rotation but neither occurs consistently. Consequently, the mean amount of flexion and extension coupled with axial rotation is zero (see Table 8.3). Similarly, lateral flexion may be accompanied by either flexion or extension of the same joint, but extension occurs more frequently and to a greater degree (see Table 8.3). Therefore, it might be concluded that lateral flexion is most usually accompanied by a small degree of extension.

The coupling between axial rotation and lateral flexion is somewhat more consistent and describes an average pattern. Axial rotation of the upper three lumbar joints is usually accompanied by lateral flexion to the other side, and lateral flexion is accompanied by contralateral axial rotation (see Table 8.3). In contrast, axial rotation of the L5–S1 joint is accompanied by lateral flexion to the same side, and lateral flexion of this joint is accompanied by ipsilateral axial rotation (see Table 8.2). The L4–5 joint exhibits no particular bias; in some subjects the coupling is ipsilateral while in others it is contralateral.⁸⁴

While recognising these patterns, it is important to note that they represent average patterns. Not all individuals exhibit the same degree of coupling at any segment or necessarily in the same direction as the average; nor do all normal individuals necessarily exhibit the average direction of coupling at every segment. While exhibiting the average pattern of coupling at one level, a normal individual can exhibit contrary coupling at any or all other levels.⁵⁸ Consequently, no reliable rules can be formulated to determine whether an individual exhibits abnormal ranges or directions of coupling in the lumbar spine. All that might be construed is that an individual differs from the average pattern but this may not be abnormal.

The presence of coupling indicates that certain processes must operate during axial rotation to produce inadvertent lateral flexion, and vice versa. However, the details of these processes have not been determined. From first principles, they probably involve a combination of the way zygapophysial joints move and are impacted during axial rotation or lateral flexion, the way in which discs are subjected to torsional strain and lateral shear, the action of gravity, the line of action of the muscles that produce either axial rotation or lateral flexion, the shape of the lumbar lordosis and the location of the moving segment within the lordotic curve.

Axes of sagittal rotation

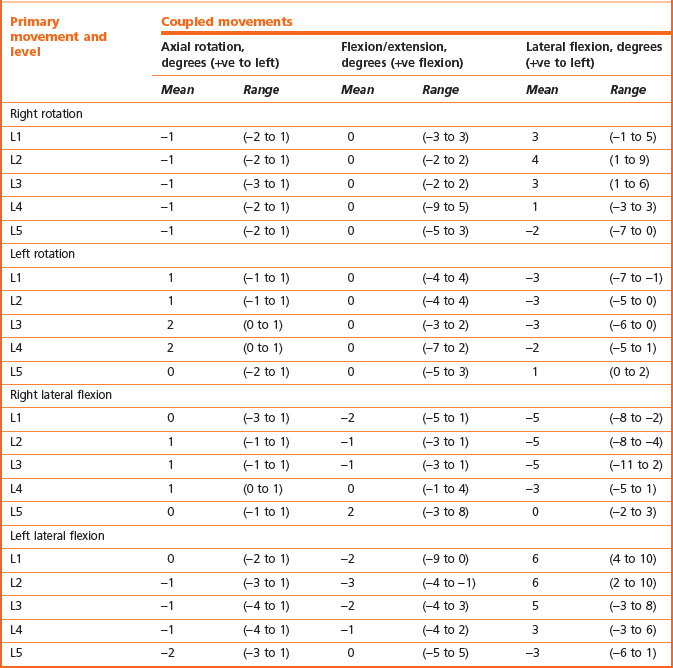
The combination of sagittal rotation and sagittal translation of each lumbar vertebra which occurs during flexion and extension of the lumbar spine results in each vertebra exhibiting an arcuate motion in relation to the next lower vertebra (Fig. 8.10). This arcuate motion occurs about a centre that lies somewhere below the moving vertebra and can be located by applying elementary geometric techniques to flexion–extension radiographs of the moving vertebrae.⁸⁸

Figure 8.10 During flexion–extension, each lumbar vertebra exhibits an arcuate motion in relation to the vertebra below. The centre of this arc lies below the moving vertebra and is known as the instantaneous axis of rotation (IAR).

For any arc of movement defined by a given starting position and a given end position of the moving vertebra, the centre of movement is known as the instantaneous axis of rotation or IAR. The exact location of the IAR is a function of the amount of sagittal rotation and the amount of simultaneous sagittal translation that occurs during the phase of motion defined by the starting and end positions selected. However, as a vertebra moves from full extension to full flexion, the amount of sagittal rotation versus sagittal translation is not regular. For different phases of motion the vertebra may exhibit relatively more rotation for the same change in translation, or vice versa. Consequently, the precise location of the IAR for each phase of motion differs slightly. In essence, the axis of movement of the joint is not constant but varies in location depending on the position of the joint.

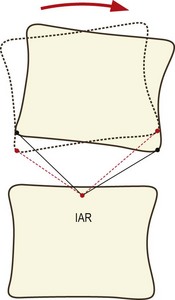
The behaviour of the axis and the path it takes when it moves can be determined by studying the movement of the joint in small increments. If IARs are determined for each phase of motion and then plotted in sequence, they depict a locus known as the centrode of motion (Fig. 8.11). The centrode is, in effect, a map of the path taken by the moving axis during the full range of motion of the joint.

Figure 8.11 As a vertebra moves from extension to flexion, its motion can be reduced to small sequential increments. Five such phases are illustrated. Each phase of motion has a unique instantaneous axis of rotation (IAR). In moving from position 0 to position 1, the vertebra moved about IAR number 1. In moving from position 1 to position 2, it moved about IAR number 2, and so on. The dotted lines connect the vertebra in each of its five positions to the location of the IAR about which it moved. When the IARs are connected in sequence they describe a locus or a path known as the centrode.

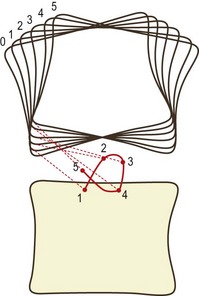
In normal cadaveric specimens the centrode is short and is located in a restricted area in the vicinity of the upper endplate of the next lower vertebra (Fig. 8.12A).^89,90 In specimens with injured or so-called degenerative intervertebral discs, the centrode differs from the norm in length, shape and average location (Fig. 8.12B).^89,90 These differences reflect the pathological changes in the stiffness properties of those elements of the intervertebral joint that govern sagittal rotation and translation. Changes in the resistance to movement cause differences in the IARs at different phases of motion and therefore in the size and shape of the centrode.

Figure 8.12 (A) The centrodes of normal cadaveric intervertebral joints are short and tightly clustered. (B) Degenerative specimens exhibit longer, displaced and seemingly erratic centrodes.

(Based on Gertzbein et al. 1985, 1986).^89,90

Increased stiffness or relative laxity in different structures such as the anulus fibrosus, the zygapophysial joints or the interspinous ligaments will affect sagittal rotation and translation to different extents. Therefore, different types of injury or disease should result in differences, if not characteristic aberrations, in the centrode pattern. Thus it could be possible to deduce the location and nature of a disease process or injury by examining the centrode pattern it produces. However, the techniques used to determine centrodes are subject to technical errors whenever small amplitudes of motion are studied.⁸⁸ Consequently, centrodes can be determined accurately only if metal markers can be implanted to allow exact registration of consecutive radiographic images. Without such markers, amplitudes of motion of less than 5° cannot be studied accurately in living subjects. Reliable observations in living subjects can only be made of the IAR for the movement of full flexion from full extension.⁸⁸ Such an IAR provides a convenient summary of the behaviour of the joint and constitutes what can be taken as a reduction of the centrode of motion to a single point.

In normal volunteers, the IARs for each of the lumbar vertebrae fall in tightly clustered zones, centred in similar locations for each segment near the superior endplate of the next lower vertebra (Fig. 8.13).⁸⁸ Each segment operates around a very similar point, with little normal variation about the mean location. This indicates that the lumbar spine moves in a remarkably similar way in normal individuals: the forces governing flexion–extension must be similar from segment to segment, and are similar from individual to individual.

Figure 8.13 The mean location and distribution of instantaneous axes of rotation of the lumbar vertebrae. The central dot depicts the mean location, while the outer ellipse depicts the two SD range exhibited by 10 normal volunteers.

(Based on Pearcy and Bogduk 1988.⁸⁸)

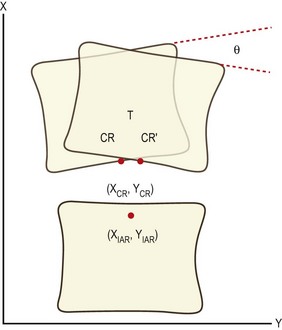
It has been shown⁹¹ that the location of an IAR can be expressed mathematically as:

where (X_IAR, Y_IAR) are the coordinates of the IAR, (X_CR, Y_CR) are the coordinates of the centre of reaction, T is the translation exhibited by the moving vertebra and θ is the angular displacement of the vertebra (Fig. 8.14). These equations relate the location of the IAR to fundamental anatomical properties of the motion segment.

Figure 8.14 The location of an instantaneous axis of rotation (IAR) in relation to a coordinate system registered on the lower vertebral body, the location of the centre of reaction (CR) of the moving vertebra and the rotation and translation (T) which that vertebra exhibits.

The centre of reaction is that point on the inferior endplate of the moving vertebra through which the compression forces are transmitted to the underlying intervertebral disc; as a point it is the mathematical average of all the forces distributed across the endplate. A feature of the centre of reaction is that it is a point that undergoes no rotation: it exhibits only translation. Its motion therefore reflects the true translation of the moving vertebra. Other points that appear to exhibit translation exhibit a combination of true translation and a horizontal displacement due to sagittal rotation.

If the compression profile of the disc is altered, the centre of reaction will move. Consequently, the IAR will move. Similarly, if the amplitude of translation or rotation is altered, the IAR will move according to the equations.

These relationships allow the displacement of an IAR from normal to be interpreted in terms of those factors that can affect the centre of reaction, translation and angular rotation. For example, posterior muscle spasm will increase posterior compression loading and will reduce angular rotation. This will displace the IAR backwards and downwards.⁹² Conversely, a joint whose IAR is located behind and below the normal location can be interpreted to be subject to excessive posterior muscle spasm.

In so far as IARs reflect the quality of movement of a segment, as opposed to its range of movement, determining the IARs in patients with spinal disorders could possibly provide a more sensitive way of detecting diagnostic movement abnormalities than simply measuring absolute ranges of movement. What remains to be seen is whether IARs in living subjects exhibit detectable aberrations analogous to the changes in centrode patterns seen in cadavers.