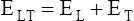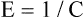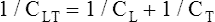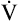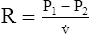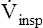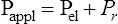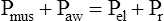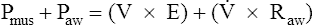Mechanics of Ventilation
After reading this chapter, you will be able to:
• Explain how elastic recoil forces of the lungs and chest wall interact to establish the resting lung volume
• Describe how static lung volumes and capacities are influenced by changes in the elastic recoil forces of the lungs and chest wall
• Explain which pressure gradients maintain alveolar volume and create airflow into and out of the lung
• Describe how spontaneous breathing and positive pressure mechanical ventilation are different and similar in the way they create pressure gradients throughout the respiratory cycle
• Describe how the rib cage, diaphragm, and abdomen components of the thorax move and interact differently in normal and abnormal conditions
• Interpret static and dynamic pressure-volume curves of the lungs, thorax, and lung-thorax system
• Determine whether high inflation pressure during mechanical ventilation is caused by a change in lung compliance or in airway resistance
• List factors that cause lung compliance and airway resistance to change
• Describe how surface tension and pulmonary surfactant influence lung compliance, inflation pressure, alveolar stability, and work of breathing
• Explain what causes the lung’s pressure-volume curve to exhibit hysteresis
• Explain how to use pressure-volume and time-pressure curves to distinguish between elastic and frictional forces that oppose lung inflation
• Describe why greater muscular effort fails to increase expiratory flow rates under certain physical conditions
• Explain how compliance and resistance are related to the emptying and filling rates of the lung during breathing
• Describe what factors predispose to incomplete exhalation and trapping of positive pressure in the alveoli at the end of expiration
• Explain the way in which work of breathing, respiratory muscular strength, and respiratory muscular fatigue are assessed
dipalmitoyl phosphatidylcholine (DPPC)
expiratory reserve volume (ERV)
frequency dependence of compliance
functional residual capacity (FRC)
maximum expiratory pressure (MEP)
maximum inspiratory pressure (MIP)
positive end-expiratory pressure (PEEP)
respiratory distress syndrome (RDS)
single breath nitrogen elimination test
tension-time index of the diaphragm (TTdi)
tension-time index of the inspiratory muscles (TTmus)
transdiaphragmatic pressure (Pdi)
Static Lung and Chest Wall Mechanics
Elastic Recoil of the Lungs and Thorax
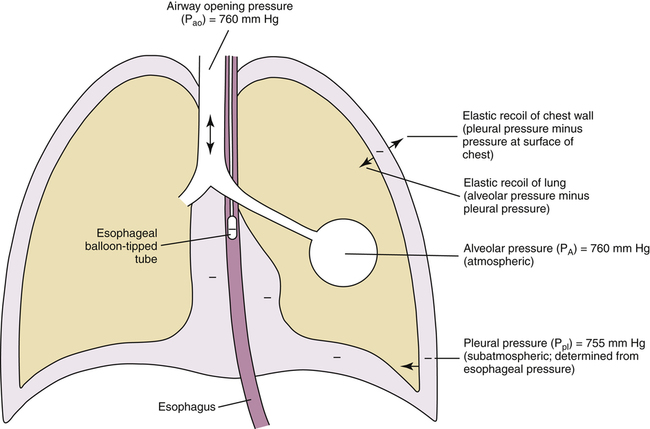
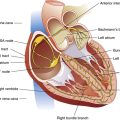
As the lung and chest wall recoil in opposite directions, the pressure between the pleural membranes decreases (Boyle’s law). No true space exists between the visceral and parietal pleurae. However, if a small tube were placed through the chest wall between these membranes, a space would be created, and the pressure measured through the tube would be subatmospheric. This method of obtaining intrapleural pressure (Ppl) would be too invasive and hazardous for clinical purposes; changes in Ppl can be measured more safely through a balloon-tipped catheter placed in the esophagus with the tip of the catheter well inside the thoracic cavity (Figure 3-1). The thin-walled esophagus has little muscle tone and easily transmits Ppl changes to the balloon on the end of the catheter. Changes in intraesophageal balloon pressure reflect changes in Ppl. Figure 3-1 shows lung and thorax recoil forces and the resulting pressures.
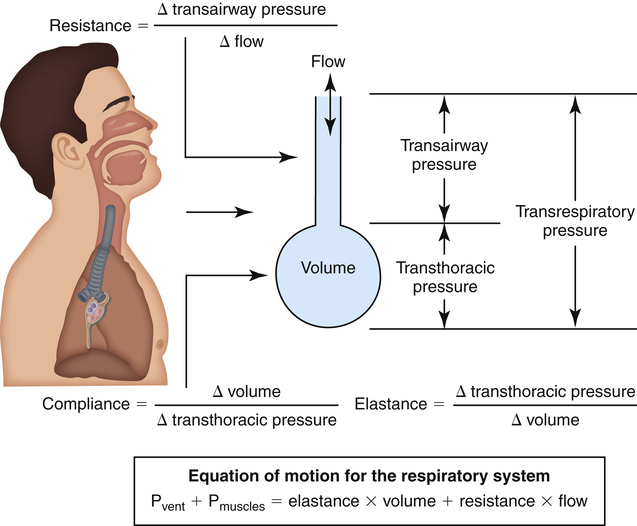
Pressure Gradients during Ventilation
Figure 3-2 illustrates various pressure differences or gradients involved in ventilation. Airway pressures are usually expressed using atmospheric pressure as the zero reference value. A pressure of 0 mm Hg does not refer to an absolute lack of pressure but to atmospheric pressure (760 mm Hg at sea level). In this sense, a subatmospheric pressure of 755 mm Hg is below 0 mm Hg, or “negative.” Likewise, a pressure of 765 mm Hg is above 0 mm Hg, or “positive.” (All pressures are positive and cannot be truly negative. However, in this book, the terms negative and positive with regard to pressure refer to subatmospheric and above atmospheric pressures.)
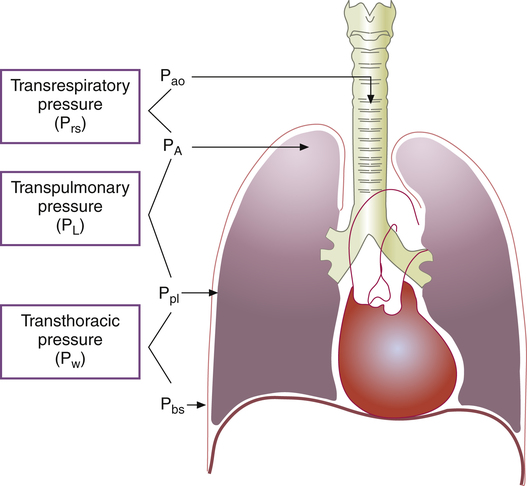
Pressure gradients are simply pressure differences between two points that cause air to move in or out of the lungs and are responsible for keeping the lungs in an inflated state. Air always flows from a point of high pressure to a point of low pressure; a pressure gradient of 0 mm Hg means there is no pressure difference between the two points and thus no airflow. Important pressure gradients in ventilation are the transpulmonary pressure (PL), transthoracic pressure (Pw), and transrespiratory pressure (Prs) (see Figure 3-2). (See Appendix I for a summary of pressure symbols in ventilatory mechanics.)
Prs is the difference between alveolar and body-surface pressures (Prs = PA − Pbs) or the pressure gradient across the entire respiratory system (lungs plus chest wall). Because both Pbs and Pao are atmospheric during normal breathing, Pao can be substituted for Pbs in the previous equation (Prs = PA − Pao, as shown in Figure 3-2). This equation shows that Prs is also equal to the pressure gradient across the airways, between the mouth and alveoli; thus, this pressure gradient is sometimes called the transairway pressure (PTA). PTA is responsible for airflow in and out of the lung. No airflow exists at the end of inspiration or at the end of expiration because PA is equal to Pao under both of these conditions; Prs or PTA is 0 mm Hg at these two points in the breathing cycle. In normal spontaneous breathing, Prs changes only when the PA changes because Pao is atmospheric and remains constant at 0 mm Hg. The magnitude of Prs (i.e., the difference between mouth and alveolar pressures) reflects the airways’ frictional resistance to airflow: the greater the pressure gradient needed to drive gas through the airways, the greater the airway resistance.
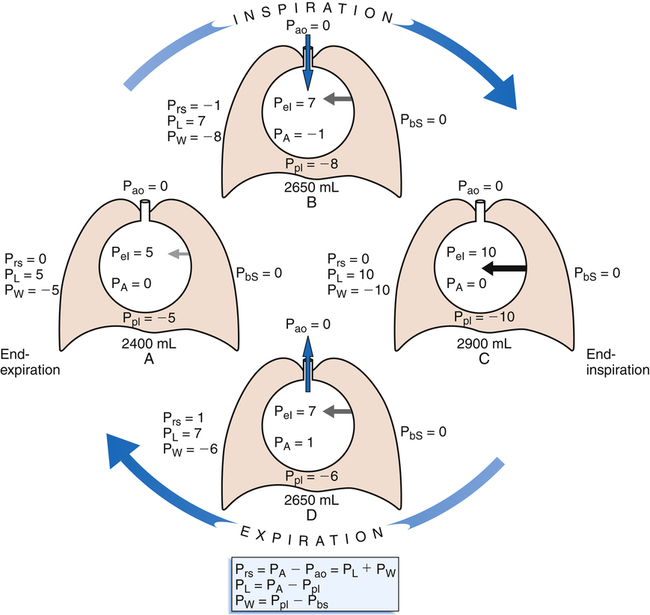
Figure 3-3 illustrates changes in pressures during the respiratory cycle (inspiration and expiration). At the end of a resting expiration when all airflow has ceased, PA = 0 cm H2O, and the elastic recoil force of the lungs (Pel) is equal to a pressure of about 5 cm H2O (Figure 3-3, A). This means Ppl must be −5 cm H2O (PA is the sum of alveolar recoil pressure plus Ppl). Therefore, transpulmonary pressure (PL) at this point is about 5 cm H2O. The PL is calculated as follows:
< ?xml:namespace prefix = "mml" />
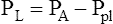
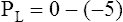
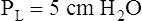
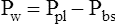

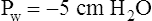
When all muscles are relaxed and no air is flowing, the inward and outward recoil forces of the lungs and thorax are in equilibrium with each another (see Figure 3-3, A). The Prs (pressure difference between the alveoli and the body surface) is the sum of PL plus Pw and is 0 mm Hg under the resting conditions just described. This is illustrated as follows:
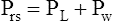
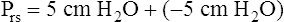
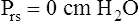
The act of inspiration (see Figure 3-3, moving from A to B to C) disrupts the equilibrium between lung and thoracic recoil forces. The ventilatory muscles contract and increase the thoracic dimensions as explained in Chapter 2. Consequently, Ppl decreases (Boyle’s law), which increases the PL gradient (PA − Ppl), “pulling” the alveoli to larger volumes. This causes PA to fall below Pao, establishing a pressure gradient for airflow into the lungs (see Figure 3-3, B). Air stops flowing into the lungs when PA equalizes with Pao (see Figure 3-3, C). At this point, PL is at its maximum value in the respiratory cycle (i.e., the difference between PA and Ppl is greatest), corresponding with an inhaled volume of 500 mL in this example.
Expiration begins when ventilatory muscles relax, allowing lung recoil forces to shrink the thoracic cavity passively (see Figure 3-3, moving from C to D). As the thoracic volume decreases, Ppl increases (becomes less negative), narrowing the gap between Ppl and PA. This decreases PL, reducing the lung’s dimensions, which compresses the lung’s air, increasing PA above Pao. Gas flows out of the lungs, reestablishing the initial preinspiratory conditions (see Figure 3-3, from D to A).
Rib Cage and Diaphragm-Abdomen Components of the Thorax
To this point, the thorax has been considered as if it were a single unit. It is more accurate to think of the thorax as having two components: the rib cage and the diaphragm-abdomen complex.1 The rib cage and diaphragm are coupled but can act independently during ventilation. Rib cage movements change the anterior-posterior and lateral dimensions of the thorax, and diaphragm movements displace the abdominal organs and change vertical thoracic dimensions. Normally, abdominal displacement predominates during quiet breathing, whereas rib cage displacement predominates when one breathes large volumes near maximum lung capacity.1 If abdominal displacement by the diaphragm is hampered by obesity, pregnancy, or an otherwise distended abdomen, breathing becomes more dependent on rib cage displacement. The work of breathing increases because it is more difficult to inflate the lung when the diaphragm resists movement.
Static Lung Volumes and Capacities
Measurement of Lung Volumes—Spirometry
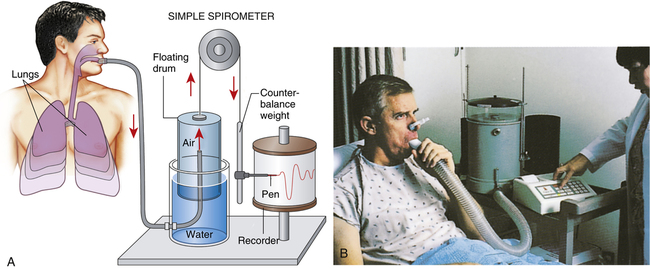
Spirometry is the process of measuring volumes of air moving in and out of the lungs. A spirometer is the device used to measure these volumes. The spirogram is a graphical volume versus time representation of the lung volumes made by the spirometer. A classic water-seal spirometer is shown in Figure 3-5. Knowledge of the function of the water-seal spirometer helps a
person understand the interrelationships between volumes and capacities. (Modern spirometers are electronic, microprocessor-controlled devices.)
While wearing nose clips to occlude the nostrils, the patient inhales and exhales through a large tube inserted snugly into the mouth (see Figure 3-5). Exhaled air enters the inverted cylinder (bell) suspended by a chain and pulley. This bell fits loosely over a smaller cylinder and floats in a water-filled sleeve. The other end of the chain is attached to a recording pen and counterweight, which exactly balance the weight of the floating bell. The water provides a seal from atmospheric air and allows nearly frictionless movement of the bell. Bell movements cause the pen to move up and down, inscribing reciprocal tracings on recording paper wrapped around a drum rotating at a constant speed, creating a graphic representation of volume (vertical axis) versus time (horizontal axis) (Figure 3-6).
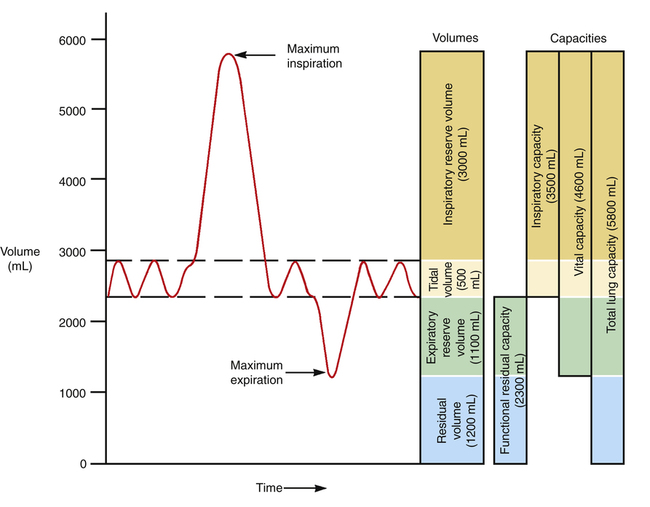
Figure 3-6 reveals that not all of the TLC is accessible to the spirometer. The residual volume (RV) cannot be exhaled, even with the greatest expiratory effort, because the rigid rib cage prevents total lung deflation. RV must be measured indirectly through other techniques (see Chapter 5).
Figure 3-6 illustrates the four lung volumes and four lung capacities. The measurements for each are approximate and vary according to an individual’s height, gender, and age. The descriptions and symbols for the static lung volumes and capacities are shown in Table 3-1. (See also Appendix I.)
TABLE 3-1
Static Lung Volumes and Capacities
| Volume and Capacity | Symbol | Definition |
| Residual volume | RV | Volume of air remaining in the lung after a maximal-effort expiration |
| Expiratory reserve volume | ERV | Volume of air that can be exhaled with maximal effort from a resting (tidal) end-expiratory level |
| Tidal volume | TV or VT | Volume of air normally inhaled or exhaled with each breath during resting, quiet breathing |
| Inspiratory reserve volume | IRV | Volume of air that can be inhaled with maximal effort from the tidal end-inspiratory level |
| Total lung capacity | TLC | Volume of air in the lung after a maximal-effort inspiration; the sum of all volumes |
| Inspiratory capacity | IC | Volume of air that can be inhaled with maximal effort from a resting (tidal) end-expiratory level; sum of TV and IRV |
| Vital capacity | VC | Maximum volume of air that can be exhaled after a maximal-effort inspiration; sum of IRV, TV, and ERV |
| Functional residual capacity | FRC | Volume of gas remaining in the lung at the end of a normal tidal exhalation (relaxed ventilatory muscles); sum of ERV and RV |
The tidal volume (VT) is the volume of air inhaled or exhaled with each breath. The vital capacity (VC) defines the maximum limits of a single breath—that is, from a maximum-effort inspiration to a maximum-effort expiration. Theoretically, the VT can increase until it equals the VC, but this never occurs, even with the most strenuous exercise. The functional residual capacity (FRC) is the amount of air in the lungs at the point of ventilatory muscle relaxation, also known as the resting level, or end-tidal exhalation level. Normally, about 40% of the TLC is contained in the lung at this resting FRC level. Expiratory (abdominal) muscle contraction is required to exhale any portion of the FRC, which involves the exhalation of expiratory reserve volume (ERV). The balance point between inward lung recoil and outward chest wall recoil determines the FRC level. Any factor that decreases lung recoil force increases the FRC and decreases the inspiratory capacity (IC). Any factor that increases lung recoil force decreases the FRC and decreases the TLC and VC. (Chapter 5 reviews these interrelationships in more detail.)
Maximum Static Inspiratory and Expiratory Pressures
Average MEP and MIP results for adults are shown in Table 3-2.2 These pressures represent high reserve muscle strength, which may become involved during a cough or the birth process. Measurements of MIP and MEP are often used clinically to assess the ability of a patient to maintain spontaneous, unassisted ventilation; MIP is more often used in this regard. Severe compromise of ventilatory muscle strength is evident when no more than −20 cm H2O MIP can be generated.3
TABLE 3-2
Maximum Inspiratory and Expiratory Pressures
| Gender | MIP—Measured at RV | MEP—Measured at TLC |
| Males | −126 cm H2O | 229 cm H2O |
| Females | −92 cm H2O | 151 cm H2O |
Static Pressure-Volume Relationships
Static Pressure-Volume Curve
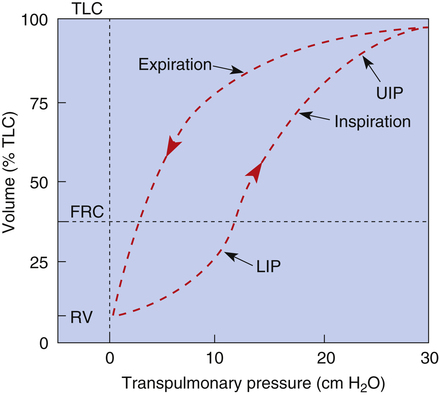
An inspiratory P-V curve can be constructed (Figure 3-7) by applying pressure to the trachea, inflating the lung in volume increments in a stepwise fashion from RV to TLC. Each volume increment is held in the lung until all airflow ceases and PL is recorded. If the lung is deflated in an identical stepwise fashion back to RV, an expiratory P-V curve is constructed. The inflation-deflation curves are traced in a counterclockwise fashion when the lung is inflated by positive pressure applied to the trachea. The curves are nonlinear, partly because the collagen and elastic fibers composing the lung parenchyma are not uniform springs. Elastic fibers are easily stretched, whereas collagen fibers are more resistant to deformation. As the lung volume approaches TLC during inspiration, collagen fibers resist stretching more, causing the slope of the P-V curve to flatten at its upper end, creating an upper inflection point (see Figure 3-7).
Hysteresis and Mechanism of Lung Volume Change
The inflation and deflation limbs of the P-V curve in Figure 3-7 trace different paths, showing that for the same distending pressure, lung volume is greater during deflation than inflation. This phenomenon is called hysteresis, which occurs because the lungs dissipate energy during inflation.4 In other words, part of the energy used to inflate the lungs is not recovered during deflation; this means it takes less force to keep the lungs inflated during deflation than it does during inflation. This phenomenon has been experimentally shown: at the same pressure, the lung volume fixed in inflation is lower than the volume fixed in deflation.4
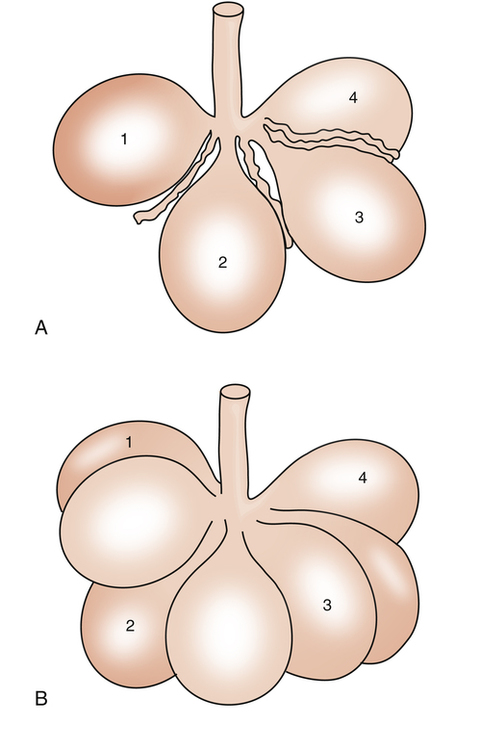
The phenomenon of hysteresis is related to the mechanism whereby lung volume changes. The idea that lung inflation and deflation are the result of collective balloon-like changes in 300 million alveolar diameters is overly simplistic. It is now widely understood that the major mechanism of lung expansion and retraction involves the sequential opening and closing (recruitment and derecruitment) of peripheral alveoli.4,5 At the end of a maximally forceful expiration (at RV), numerous alveoli are closed; lung volume increases during the subsequent inspiration mainly because an increasingly greater number of alveoli open up, not because individual alveolar diameters increase. The lungs dissipate energy in the alveolar recruitment process, mostly in overcoming the molecular adhesive forces of surface tension—forces not present during expiration when alveoli are already open.4
The lung’s recruitment expansion mechanism has been confirmed by in vivo microscopy of subpleural alveoli in animal models; inflation of the lung from 20% to 80% of TLC increased the number of recruited alveoli but did not increase individual alveolar diameters.5 A different investigation yielded similar results; when lung inflation pressure was increased from 10 cm H2O to 20 cm H2O and then again from 20 cm H2O to 30 cm H2O, alveolar size did not change, but the number of recruited alveoli changed in direct proportion to applied pressure.4
The alveolar recruitment-derecruitment mechanism is illustrated in Figure 3-8. At the beginning of inspiration (Figure 3-8, A), numerous alveoli are closed, their walls stuck together. As inspiration continues, these alveoli are forced open and recruited by the increasing PL (Figure 3-8, B). Recruitment occurs in two phases: in the first phase, from deflation to about 50% of the TLC, lung volume increases secondary to a linear increase in the number of alveoli recruited (i.e., the number recruited is directly proportional to PL). From 50% to 100% of TLC, the rate of recruitment accelerates, and the number of recruited alveoli increases exponentially. This accelerated recruitment rate is reflected by a steeper slope on the P-V curve, marked by a lower inflection point (LIP) on the inspiratory limb (see Figure 3-7).4
It was previously thought that the LIP marked the point at which alveolar recruitment was complete and that if expiratory pressure were not allowed to fall below this point in mechanically ventilated critically ill patients, alveolar closure on expiration would be prevented. It is now known that alveolar recruitment continues beyond the LIP to TLC; the entire P-V curve can be thought of as a recruitment curve.4,6 (See Clinical Focus 3-3 for a discussion of the clinically obtained P-V curve and significance of LIP.)
Lung Distensibility: Static Compliance
Compliance is a measure of the lung’s opposition to inflation. The P-V curve (see Figure 3-7) is a compliance curve. Lung compliance (CL) is defined as the change in lung volume produced by a unit of pressure change and is measured in liters per centimeter of water pressure (L/cm H2O), shown as follows:
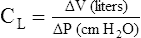
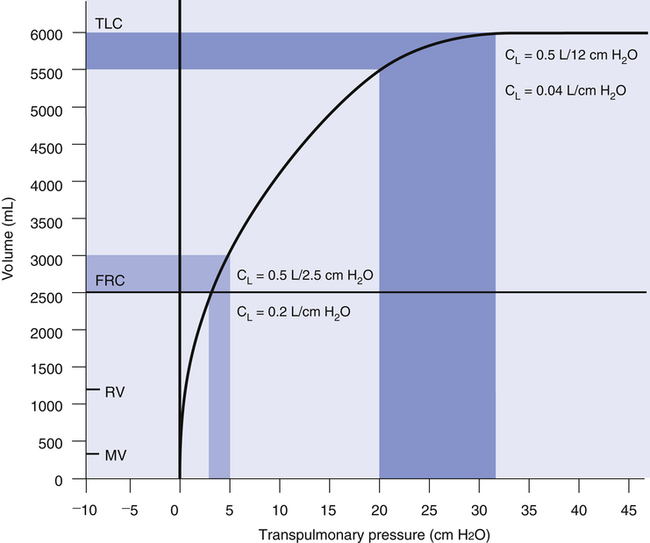
Compliance can be conceptualized as distensibility; if the lung is easily distended, it has high compliance. A lung with low compliance is stiff and difficult to inflate. Static CL can be obtained from the P-V curve in Figure 3-9 by measuring the volume change (vertical axis) produced by a pressure change (horizontal axis). Normal compliance of the lung alone (CL) is 0.2 L/cm H2O or 200 mL/cm H2O.
Compliance and Lung Volume
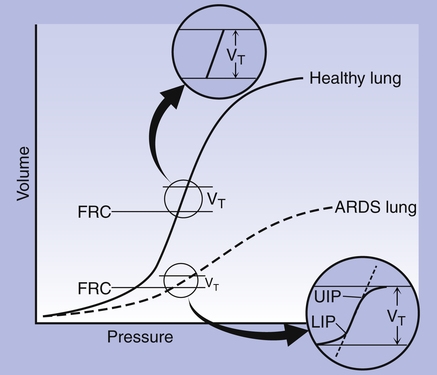
The value of CL depends on the volume at which it is measured. The compliance curve is not linear, as shown in Figure 3-9. Near TLC, lung fibers are stretched and close to their elastic limits; a 500-mL inspiration taken at a point near TLC requires more muscular effort than a 500-mL inspiration beginning at FRC. The slope of the compliance curve is steepest and CL is greatest at FRC; this is beneficial because an individual normally inhales the VT from the FRC level where volume changes require little effort. Even during strenuous exercise, people breathe over the lower 70% of the P-V curve, keeping the elastic WOB relatively low. The larger inspired volumes during exercise produce higher lung recoil, which helps provide the force needed to produce high expiratory flow rates during rapid breathing rates.
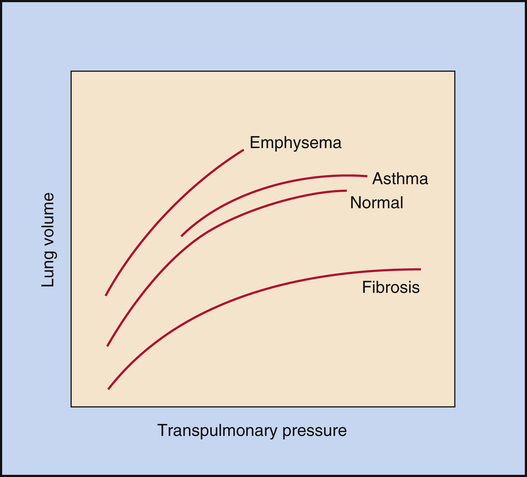
Figure 3-10 illustrates the effects of different disease types on CL. Emphysema is characterized by a loss of elastic lung tissue, which means the lungs can be easily distended and have an abnormally low recoil force. Small pressure changes produce large volume changes. Weakened elastic lung recoil changes
the equilibrium point between lung and thoracic recoil forces, which increases the FRC. Pulmonary fibrosis is characterized by high lung recoil forces. The FRC equilibrium point is displaced, this time to a lower point in the TLC than normal.
Surface Tension and Pulmonary Surfactant
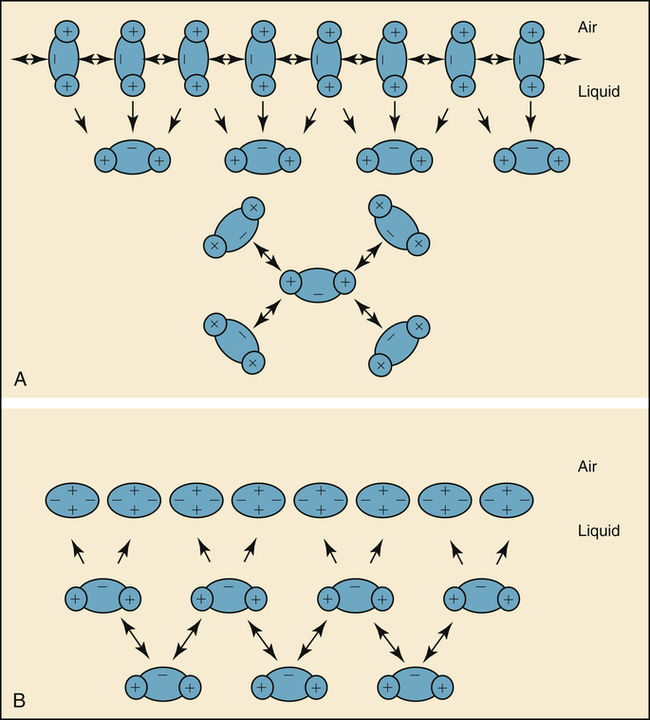
The molecules of a water surface are attracted by other water molecules below and adjacent to them. As a result, the water surface has a tendency to contract, creating a force known as surface tension (Figure 3-11, A). Surface tension causes a water droplet to take on the shape of a rounded bead because of the tight intermolecular attraction forces surrounding the droplet.
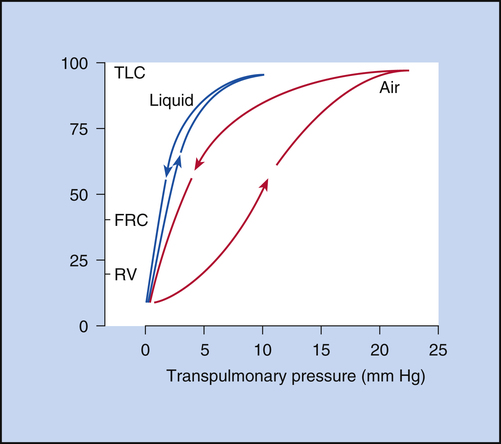
In 1929, von Neergaard conducted the now classic experiment in which he demonstrated the presence of surface tension in the alveoli. He inflated the lungs of anesthetized cats, first with air and then with a liquid saline solution. He constructed P-V curves for both air and saline inflations. Figure 3-12 illustrates that saline inflation requires much less pressure than air inflation to achieve a given volume. von Neergaard correctly concluded that alveolar air-liquid surfaces produced forces that opposed lung inflation. Saline inflations abolished the air-liquid surfaces and eliminated their opposition to lung inflation. The recoil pressure of the saline-filled lungs reflected only elastic tissue retractile forces, whereas the recoil pressure of the air-filled lung reflected retractile forces of the elastic tissues plus surface tension. von Neergaard found that surface-tension forces are responsible for more than half of the lung’s elastic recoil force.7
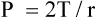
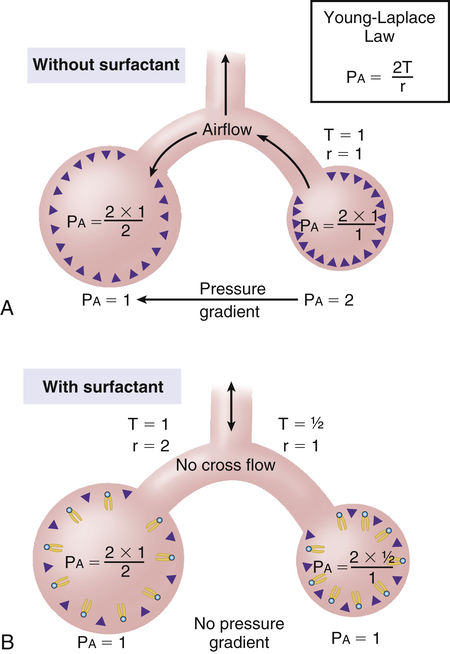
In this equation, P represents distending pressure (in dynes/cm2), T represents surface tension (in dynes/cm2), and r represents the alveolar radius (in cm). The equation shows that if surface tension remains constant, small alveoli require higher distending pressure than large alveoli (Figure 3-13, A); the equation would predict that the smaller alveoli should empty into larger alveoli—assuming that all alveoli have the same surface tension. If the surface tension were the same for all alveoli, Laplace’s law would predict serious alveolar instability; small alveoli would collapse into larger ones, producing coexisting areas of overdistention and complete collapse (Figure 3-13, B). Alveolar pressures throughout the lungs are the same, however, because they all are connected to a common airway—the trachea. How then is alveolar stability maintained, and how can the lung inflate evenly?
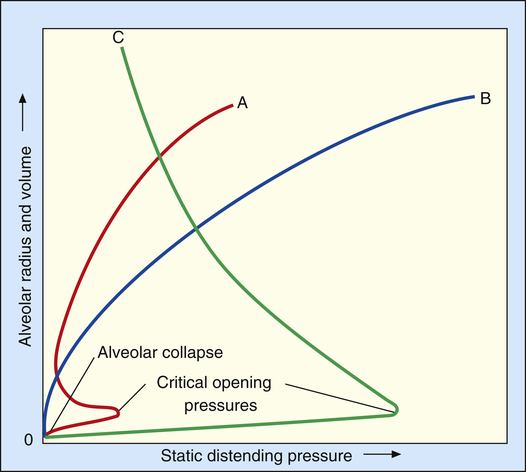
Figure 3-14 illustrates critical opening pressure and critical closing pressure. A relatively high pressure is required to expand a collapsed alveolus. When enough pressure is applied to produce an alveolar radius equal to that of the alveolar duct supplying it, the critical opening pressure has been reached. When the critical opening pressure is exceeded, the alveolus abruptly opens and expands easily. This phenomenon is similar to the inflation of a toy balloon. High pressure is required initially until the balloon abruptly expands; thereafter, the balloon inflates easily. The critical opening pressure is identical to the critical closing pressure; pressures below this measurement result in the abrupt collapse of the alveolus. The radius of the alveolar duct and the surface-tension force determine the critical opening pressure.
Adhesive molecular surface-tension forces are the major opposition to alveolar inflation when the alveolus is collapsed and below its critical opening pressure. Above the critical opening pressure, elastic tissue recoil becomes a progressively greater opposition to inflation (see Figure 3-14).
Nature and Composition of Pulmonary Surfactant
Surfactant molecules in a water medium have extremely weak attractive forces for each other and for the surrounding water molecules. Strong intermolecular attractive forces between water molecules push the neutral surfactant molecules up to the surface, forming a thin molecular film. This surfactant film floats on the surface and shields the water molecules below from contact with air (see Figure 3-11, B). The weak intermolecular attractive forces of the floating surfactant film impart a low surface tension to the solution.
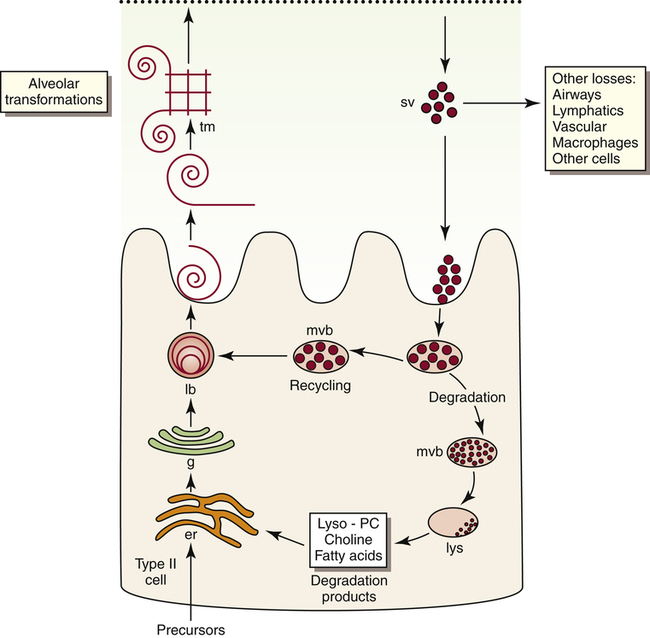
Pulmonary surfactant is a complex substance composed of 90% phospholipid and 10% protein. Dipalmitoyl phosphatidylcholine (DPPC) constitutes about 50% of surfactant’s phospholipid content and is primarily responsible for the surface-tension–lowering properties of surfactant.8 DPPC forms a tight monolayer (a single-molecule-thick film) at the air-liquid interface of the alveolus. The more this surface monolayer is compressed (as occurs in smaller alveoli), the more it concentrates the DPPC molecules and lowers the surface tension. Type II cells secrete surfactant phospholipids by discharging lamellar bodies into the liquid film that lines the inner alveolar surface; this process is known as exocytosis. Once secreted, lamellar bodies unravel and transform into a lattice-like structure called tubular myelin (Figure 3-15). Tubular myelin is the immediate precursor of the DPPC surface monolayer; when facilitated by a specialized surfactant protein (described in the following paragraphs), it quickly spreads to form a film one molecule thick on the alveolar air-liquid surface through a process called adsorption.
Normal surfactant contains four specialized proteins that can be divided into two groups: hydrophilic, or water-attracting proteins SP-A and SP-D and hydrophobic, or water-repelling proteins SP-B and SP-C. The two hydrophilic proteins SP-A and SP-D are not as critical for surfactant function as the two extremely hydrophobic surfactant proteins SP-B and SP-C; the presence of SP-B in particular is essential for the formation of tubular myelin and its adsorption on the monolayer film surface.8
Adequate functional surfactant must be present in the fetal lung at birth to allow a successful transition to air breathing; otherwise, high surface tension causes widespread alveolar collapse and severe respiratory distress. DPPC is first present in lamellar bodies of the human fetal lung at 24 weeks of gestation.8 Avery and Mead9 were the first investigators to describe low surfactant levels in premature newborns with respiratory distress syndrome (RDS). It was later confirmed that deficient synthesis and secretion of pulmonary surfactant causes RDS to occur in a premature infant. Specifically, the absence of SP-B is responsible for respiratory distress and gas exchange abnormalities in a premature newborn.8
The concentration of DPPC, also known as lecithin, increases during the last 20% of gestation in the full-term fetus. At the same time, the concentration of another phospholipid, sphingomyelin, remains relatively constant.10 The ratio of lecithin to sphingomyelin (L/S ratio) in amniotic fluid is predictive of fetal lung maturation. An L/S ratio greater than 2:1 indicates fetal lung maturity in nondiabetic pregnancies; the L/S ratio is falsely high in mothers with diabetes.10 The L/S ratio is generally 1:1 at 31 to 32 weeks of gestation and 2:1 at 35 weeks of gestation.10 Phosphatidylglycerol (PG) is another phospholipid component of surfactant that is produced quite late in gestation. Its presence in amniotic fluid almost guarantees lung maturity; the risk of RDS is low if PG is present.10 The L/S ratio and the presence of PG in amniotic fluid continue to be the “gold standard” for determining fetal lung maturity.10 More recently, the lamellar body count in amniotic fluid has been shown to correlate significantly with the L/S ratio and PG levels. The advantage of the lamellar body count is that it can be performed more quickly and easily and is less costly than phospholipid analysis; in addition, it is less subject to false elevations in diabetes.10 Maternal administration of steroids may accelerate the production of fetal DPPC.8
Physiological Significance of Pulmonary Surfactant
In Figure 3-16, curve C shows that when the alveolar diameter is small in the surfactant-deficient lung, extremely high PL is required to offset surface-tension forces and prevent alveolar collapse. Therefore, alveoli are quite prone to collapse at low lung volumes, as Laplace’s law predicts. In the presence of pulmonary surfactant, surface tension decreases dramatically as the alveolar volume decreases (curve A); this allows small alveoli to remain inflated at an extremely low PL.
Pulmonary surfactant is physiologically important because (1) it reduces WOB; (2) it reduces the distending pressure required to keep small alveoli open; and (3) it provides a stabilizing influence, allowing alveoli of different sizes to coexist at the same distending pressure. Pulmonary surfactant also helps reduce the tendency for fluid to leave pulmonary capillaries and enter the interstitial space. In the absence of pulmonary surfactant, high surface-tension–retracting forces create too much negative intrapleural and interstitial pressure, which pulls fluid out of the capillaries. By decreasing alveolar surface tension, pulmonary surfactant helps prevent the development of undue negative interstitial pressure.8
Lung and Chest Wall Interactions
Lung, Thorax, and Total Compliance
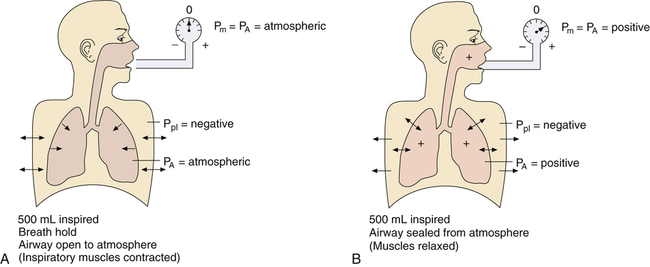
CL and CLT can be obtained simultaneously by measuring esophageal balloon pressure and mouth pressure under static conditions, which is equivalent to measuring intrapleural and alveolar pressures (mouth pressure equals alveolar pressure under static, no-flow conditions). The subject inspires a known volume of gas and holds the breath, keeping the glottis open (Figure 3-17, A). In this state, the esophageal (pleural) pressure reflects only lung recoil pressure changes (i.e., the thorax cannot contribute to recoil pressure because the ventilatory muscles hold it in a fixed position). PA is equal to atmospheric pressure because the glottis is open and air is not moving. While maintaining this lung volume, the subject pinches the nostrils shut, tightly seals the lips around the mouthpiece of the pressure gauge, and completely relaxes all muscles of ventilation (see Figure 3-17, B). Mouth pressure under these no-flow relaxed conditions equals the combined recoil pressures of the lungs and thorax. Mouth pressure also equals the PA. The negative intrapleural pressure in this situation equals the recoil pressure of only the thoracic cage; the occluded mouth and nose trap air in the lungs, creating a positive pressure splint that prevents the lungs from recoiling inward. Only outward recoil of the thoracic cage can generate negative Ppl
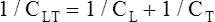
Another way to state this is as follows:
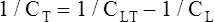
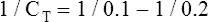
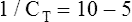
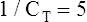
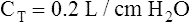
Relaxation Pressure-Volume Curves
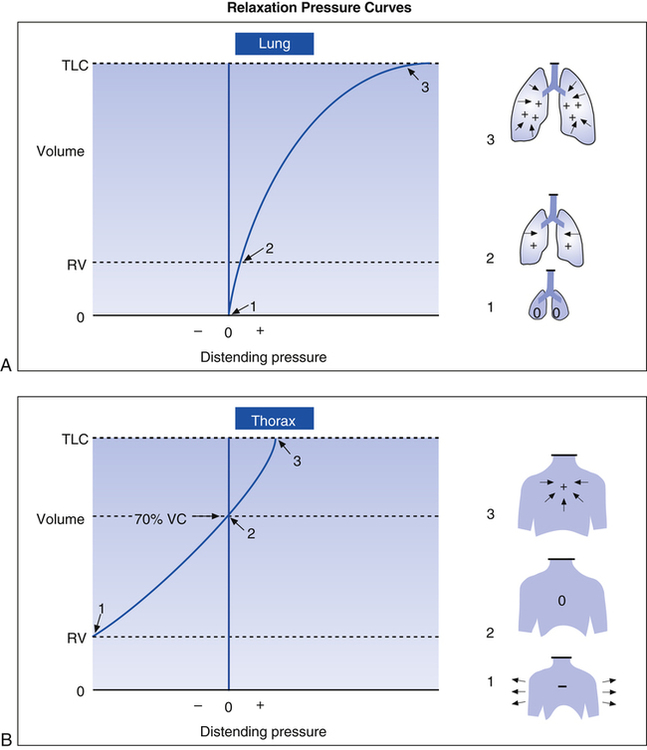
Passive relaxation P-V curves can be constructed separately for the lungs and thoracic cage. Figure 3-18, A, shows the relaxation pressures for the lung alone (as if it were outside of the thorax) plotted against TLC. Pressure in the lung is 0 at collapsed resting state (see Figure 3-18, A, 1) and increases to its maximum level as the lung is inflated to TLC, where elastic tissues are stretched maximally (see Figure 3-18, A, 3). At each lung-inflation point in the figure, the airway is sealed, airflow stops, and the positive pressure is the result of passive lung recoil. Figure 3-18, B, shows that if the empty thoracic cage is compressed to the RV level, it generates a strong outward recoil force. This force generates a negative intrathoracic pressure if the thoracic opening is sealed and the compression force is removed, allowing the thorax to recoil freely (see Figure 3-18, B, 1). When the thorax is allowed to recoil outward to the volume it would contain at 70% of the VC, the thorax is at rest, generating neither inward nor outward recoil force (see Figure 3-18, B, 2). Inflation beyond this point expands the thoracic cage above its resting level and generates an inward recoil force. In other words, from 70% of the VC to TLC, the thorax recoils in the same direction as the lungs (see Figure 3-18, B, 3).
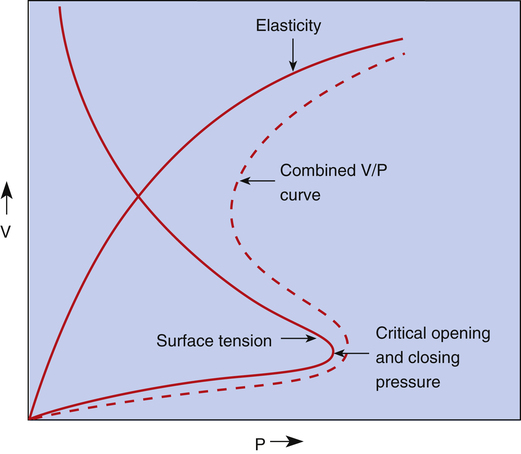
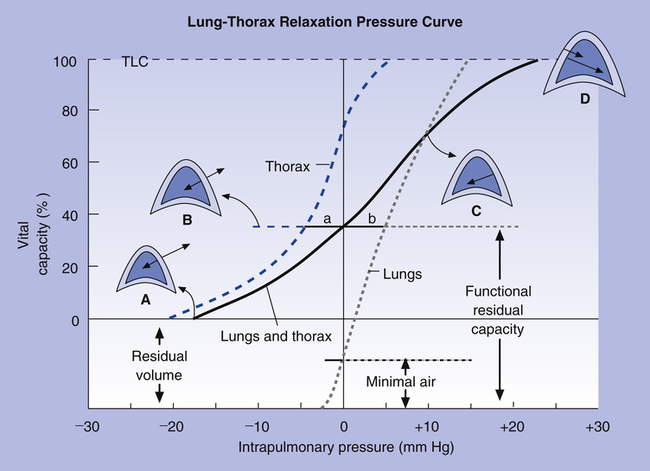
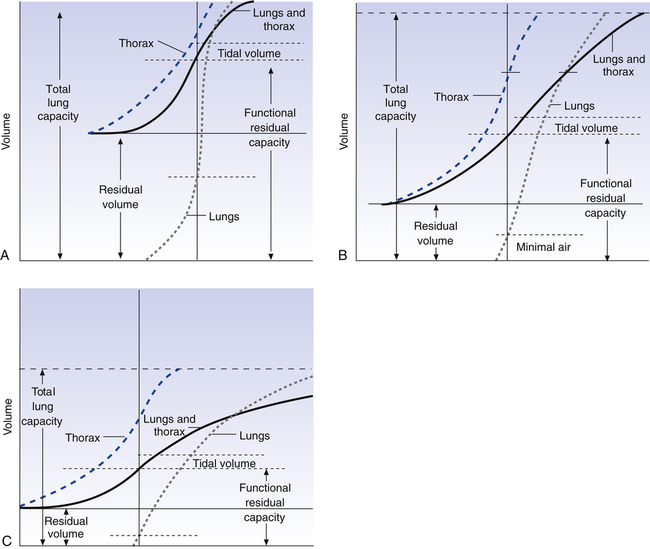
Figure 3-19 shows relaxation P-V curves for the lungs and thorax plotted on the same graph along with the coupled lung-thorax system curve. The resting equilibrium point between inward lung recoil force and outward thoracic recoil force defines FRC and normally occurs between 40% and 50% of TLC. This FRC balance point between the two opposing recoil forces is shown in Figure 3-19 as the point where the horizontal distances between 0 pressure and the two recoil curves are identical (distance a is equal to distance b in the figure).
The lung-thorax compliance curve (see solid line in Figure 3-19) is the algebraic sum of the lung (dotted line) and thorax (dashed line) compliance curves. At all points along the lung-thorax curve, its slope is less than the slope of either the lung curve or the thoracic curve, which means that the combined lung-thorax system is less compliant than either of its components alone (i.e., CLT is less than either CL or CT). Put in terms of elastance, combined lung-thorax elastance (the reciprocal of compliance) is greater than either lung or thorax elastance; this helps explain why reciprocals of CL and CT must be added to obtain the compliance of the total system. Compliance is a measure of the lung’s distensibility, whereas elastance is a measure of the lung’s resistance to inflation. The thorax and lungs actually represent elastances, not compliances, arranged in series with one another. As with an electrical circuit, total resistance is equal to the sum of the resistances in the series (RT = R1 + R2 + R3 + …). In this equation, RT represents total resistance, and R1 through R3 represent the individual resistances.
Relaxation Pressure-Volume Curves and Disease
If the lung at FRC in Figure 3-19 develops decreased elasticity, the equilibrium between lung recoil and thoracic recoil is disrupted; outward, thoracic recoil predominates, pulling the lungs outward to a larger volume. The thorax stops expanding, and the lung stops enlarging when the stretching lung generates enough recoil force to again balance the oppositely directed thoracic recoil force. This establishes a new equilibrium point at a larger volume than before (i.e., FRC is increased, and VT is breathed at a higher level in TLC). The lung curve and lung-thorax curve would shift leftward, showing that smaller pressures are required to inflate the lung to a given volume. Pulmonary emphysema, characterized by the destruction of elastic lung tissue, produces the changes just
described. Diseases that increase lung recoil force, such as pulmonary fibrosis, shift lung and lung-thorax curves to the right and reduce FRC because increased lung recoil pulls the thorax down to lower volumes.
Figure 3-20 shows P-V relaxation curves for the lungs and thorax under normal conditions (see Figure 3-20, B) compared with pulmonary emphysema (see Figure 3-20, A) and pulmonary fibrosis (see Figure 3-20, C). The lungs of the patient with emphysema in A have extremely low recoil force; they must be stretched to near TLC before they generate enough recoil to counterbalance the thoracic recoil force and establish FRC. FRC is quite large, mainly because the RV is so large. Even minimal air is increased as a result of the low lung recoil; if these lungs are removed from the chest, their recoil is so weak that they are unable to expel much of their air, and they remain hyperinflated even at rest.
The fibrotic lungs in Figure 3-20, C, recoil quite strongly, even at low lung volumes. Not much inflation is required before their recoil is equal to chest wall recoil. The FRC equilibrium point is established at an abnormally low volume. TLC is reduced because the ventilatory muscles are not strong enough to stretch the strongly recoiling fibrotic lung to greater volumes.
Dynamic Lung and Chest Wall Mechanics
Frictional (Nonelastic) Resistance
Airway Resistance
Neurogenic factors also affect Raw at different lung volumes. Stretch receptors in the lung (see Chapter 1) are stimulated at high volumes, causing a reflex decrease in parasympathetic bronchomotor tone, which dilates the bronchi. Conversely, at low volumes, parasympathetic tone is unchecked, and the airways narrow.
Flow Regimens in the Airways
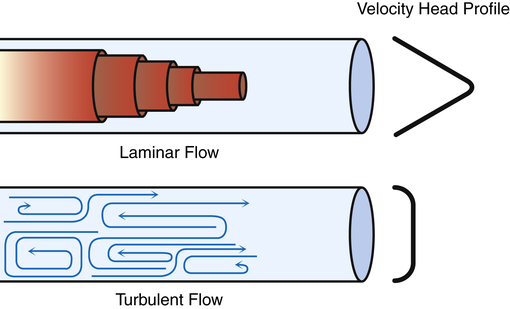
Laminar Flow
Flow is laminar when it is organized in discrete streamlines, similar to overlapping cylindrical layers moving at different speeds. The gas flowing in the central layer of the stream moves at the highest velocity, whereas the outside layer contacting the airway wall is stationary; this produces a conical stream front (Figure 3-21) or a parabolic velocity profile. The concentric cylindrical layers of gas slide over one another, creating friction between them as they travel at different velocities. This friction is determined by molecular cohesive forces (unique for each gas type) and is the source of gas viscosity. When flow is laminar, the pressure required to produce a given flow rate through the airways is influenced by gas viscosity but not by the molecular weight or density of the gas.2
Poiseuille’s Law and Airway Resistance
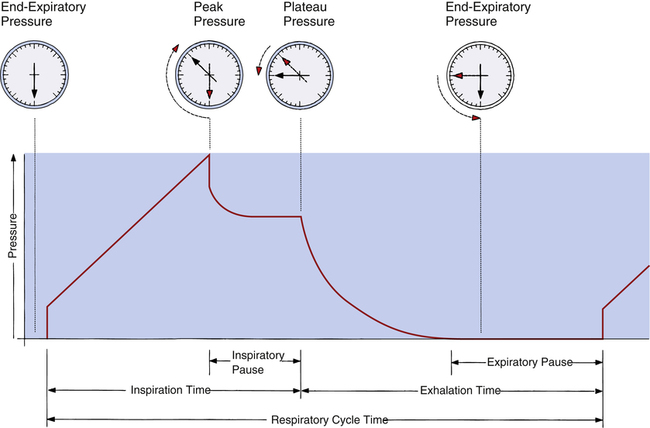
Under laminar flow conditions, the pressure required to produce a given flow rate through a tube is defined by Poiseuille’s law (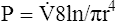 ). In this equation, P represents the pressure gradient across the tube,
). In this equation, P represents the pressure gradient across the tube, 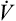 represents the gas flow rate, l represents the tube length, n represents gas viscosity, r represents the tube radius, and 8 and π represent constants. This equation states that under laminar flow conditions, the pressure required to drive a given flow through a tube increases if the tube length or gas viscosity increase. More striking is the increased pressure needed to maintain a given flow rate when tube radius decreases. The equation shows that if an airway’s radius decreases to one half of its original size (e.g., by bronchospasm or mucosal edema), 16 times more pressure is required to maintain the original flow through the airway. For practical purposes, the constants in Poiseuille’s law can be lumped together to form one constant (K), simplifying Poiseuille’s law to
represents the gas flow rate, l represents the tube length, n represents gas viscosity, r represents the tube radius, and 8 and π represent constants. This equation states that under laminar flow conditions, the pressure required to drive a given flow through a tube increases if the tube length or gas viscosity increase. More striking is the increased pressure needed to maintain a given flow rate when tube radius decreases. The equation shows that if an airway’s radius decreases to one half of its original size (e.g., by bronchospasm or mucosal edema), 16 times more pressure is required to maintain the original flow through the airway. For practical purposes, the constants in Poiseuille’s law can be lumped together to form one constant (K), simplifying Poiseuille’s law to 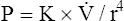 . Pressure varies with the fourth power of the tube radius. This means the denominator (r4) becomes 16 times smaller if the tube radius is cut in half, which means pressure required to keep flow constant becomes 16 times greater. Of all the factors affecting Raw, the most profound is the airway radius. In practical terms, a person must exert 16 times more effort (work) to maintain the same flow through airways that constrict to half of their original diameters. Put another way, if muscular weakness or fatigue prevents such increased effort, flow decreases to one sixteenth of its original value, drastically reducing ventilation.
. Pressure varies with the fourth power of the tube radius. This means the denominator (r4) becomes 16 times smaller if the tube radius is cut in half, which means pressure required to keep flow constant becomes 16 times greater. Of all the factors affecting Raw, the most profound is the airway radius. In practical terms, a person must exert 16 times more effort (work) to maintain the same flow through airways that constrict to half of their original diameters. Put another way, if muscular weakness or fatigue prevents such increased effort, flow decreases to one sixteenth of its original value, drastically reducing ventilation.
Turbulent Flow
In contrast to laminar flow, turbulent flow is chaotic, with many churning eddy currents (see Figure 3-21). Gas molecules swirl in lateral and forward directions. The entire gas stream moves forward with no velocity difference between its center and outside portions; this lack of difference in flow rates across the tube’s diameter gives turbulent flow a blunt rather than conical velocity profile. Turbulent flow in the lung is much noisier than laminar flow because high-velocity gas molecules strike the airway walls much more frequently. Much energy is required to generate the chaotic, swirling eddy currents of turbulent flow; turbulent flow requires a higher driving pressure than laminar flow to produce a given flow rate. In laminar flow, the pressure gradient is directly proportional to the flow rate; if pressure doubles, the flow rate also doubles. In turbulent flow, the pressure gradient is proportional to the square of the flow rate. Doubling the flow rate requires a fourfold increase in driving pressure. Poiseuille’s law does not apply to turbulent flow.
Turbulent flow is more likely to occur when the flow rate is high and when flow abruptly changes direction, for example, through narrow and sharply branching airways. Reynolds’ number (Re) predicts when the flow regimen will change from laminar to turbulent. Re, a dimensionless number, is derived from values for gas density, viscosity, velocity, and airway diameter. Generally, if Re is greater than 2000, flow is turbulent. In contrast to laminar flow, the pressure required to produce a given flow rate in turbulent flow is influenced by the molecular weight of the gas or its density (greater density requires greater pressure) but not by its viscosity. For this reason, helium, a gas with very low density, is sometimes used to reduce WOB in patients with abnormally turbulent airflow, as occurs in severe airway obstruction (see Clinical Focus 3-8).
Types of Flow in the Lung and Distribution of Airway Resistance
Flow patterns in the lung are highly turbulent in the upper airways, trachea, and major bronchi but never turbulent in smaller bronchioles and distal airspaces. Normal quiet breathing commonly produces instantaneous peak flow rates of 1 L per second, or 60 L per minute, at the mouth. Even during quiet breathing, flow is highly turbulent in the pharynx, larynx, and trachea. As the airways branch, airflow is progressively redirected into more channels until finally, at the terminal bronchiole level, flow is distributed across hundreds of millions of airways; this greatly reduces flow velocity, and flow is laminar. Even during maximal ventilation, flow in the peripheral airways remains laminar. For similar reasons, Raw is normally much lower in small airways than in large airways (see Chapter 1). The increase in the number of small airways and the increase in their collective cross-sectional area far outweigh the decrease in their individual diameters.
The upper airways, including the larynx, mouth, and nose, normally account for about 50% of total Raw at FRC; airways less than 3 mm in diameter account for less than 10% of the total Raw.12 However, in people who have severe emphysema, chronic bronchitis, or asthma, resistance to flow in the lower airways may exceed upper Raw
Dynamic Compliance
Dynamic Pressure-Volume Curves
Figure 3-22 is a plot of superimposed static and dynamic CL curves obtained during mechanical positive pressure lung
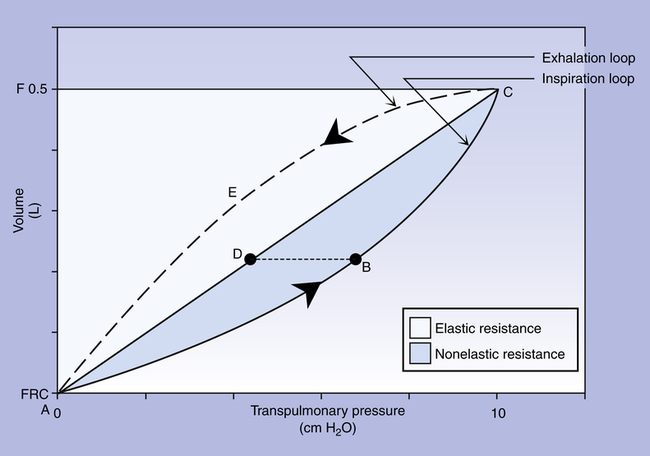
inflation with the respiratory muscles completely at rest. Lung inflation begins at FRC (point A). The straight, solid line (A-C) is the Cst curve, which is constructed by momentarily interrupting air flow at progressively greater volumes and holding the breath (ventilatory muscles relaxed) until all airflow ceases.
The curved solid line (ABC) plots pressures dynamically in real time as lung volume increases during a single uninterrupted lung inflation, defining the Cdyn curve. The Cdyn curve bows away from the straight Cst line, reflecting the “drag” that frictional airway resistance adds to elastic resistance. If lung inflation is abruptly halted and the breath is held at point B on the dynamic curve, airflow stops, and its frictional resistance ceases to exist; the pressure generated by it disappears. Airway pressure falls to point D on the static pressure curve. Pressure at point D reflects only the elastic recoil forces present at that volume, whereas pressure at point B reflects elastic recoil forces plus flow-resistive forces. Thus, pressure B minus pressure D represents the pressure required to overcome Raw. The white area in Figure 3-22 reflects static elastic resistance, and the shaded area (inspiratory portion of the loop) represents flow-dependent airway resistance. The area enclosed by the curved dashed line (CEA on the expiratory loop) and the straight static curve (ADC) reflects expiratory airway resistance. Modern positive pressure mechanical lung ventilators can graphically display breath-by-breath P-V loops (compliance curves), allowing respiratory therapists to identify and differentiate elastic and frictional resistances to ventilation.
Peak and Plateau Airway Pressure
The same positive pressure breath illustrated in Figure 3-22 can be graphically represented on a pressure versus time curve (Figure 3-23). As the ventilator inflates the lung, pressure increases to a maximum peak value (see Figure 3-23, point B). This peak pressure (Ppeak) corresponds with the pressure represented by point B on the Cdyn curve in Figure 3-22 and reflects the sum of elastic recoil force and frictional airway resistance. If the breath is held momentarily (an inspiratory pause), gas flow stops, and Raw dissipates, as does the pressure that was required to overcome it; airway pressure falls to a lower level and stays there until the person is allowed to exhale. This plateau pressure (Pplat) (see Figure 3-23, point D) reflects only the elastic recoil force of the lung-thorax system, which corresponds to point D on the static curve in Figure 3-22. The Ppeak − Pplat difference reflects only frictional Raw
Computing Lung-Thorax Compliance and Airway Resistance in Mechanical Ventilation
Respiratory system compliance (lung-thorax compliance [CLT]) and Raw can be easily computed on a mechanically ventilated patient. CLT and Raw are measures of elastic and flow-resistive opposition to ventilation. By programming the ventilator to create an inspiratory pause, as just described, the respiratory therapist can directly measure Ppeak and Pplat (see Figure 3-23). The delivered VT and the inspiratory flow rate are known values programmed into the ventilator. The CLT is calculated as follows:
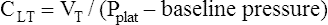
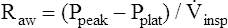
Lung Inflation Pressure and Equation of Motion
We know from the previous section that the pressure required to drive gas into the airways and inflate the lungs is caused by the elastic and resistive elements that oppose ventilation. This is illustrated in Figure 3-24. Lung inflation pressure can be expressed in terms of these two resistive elements as follows:13
In this equation, Pappl is the airway pressure applied at the mouth, Pel is the elastic recoil pressure (a function of lung volume), and Pr is the airway resistive pressure (a function of flow rate). The Pappl may be supplied totally by the respiratory muscles (Pmus), by a mechanical ventilator (Paw), or by both (Pmus + Paw). Substituting the term Pmus + Paw for Pappl, equation 1 can be written as follows:14
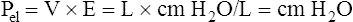
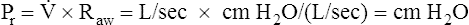
Equations 1 to 3 are consistent with Newton’s third law of motion: “For every action there is an equal and opposite reaction.” Each equation or a variation of each has been referred to as the respiratory system equation of motion (see Figure 3-24). In equation 3, if the patient breathes spontaneously, the airway pressure (Pmus) is negative during lung inflation. If the patient is attached to a mechanical ventilator and it supplies more flow than the patient demands, airway pressure becomes positive, and inspiration is assisted. If the ventilator supplies just enough flow to match the patient’s inspiratory flow demand exactly, airway pressure remains at zero throughout inspiration. The respiratory system equation of motion is the theoretical basis for this kind of mechanical ventilation, known as proportional assist ventilation (PAV).13 In PAV, the ventilator monitors volumes, pressures, and flows instantaneously as the patient breathes and uses this information to compute breath-to-breath inspiratory pressures (Pel + Pr) proportional to the patient’s inspiratory demands.
Exhalation Mechanics and Cephalad Flow Bias
During expiration, PL decreases, causing the airway diameter to decrease. The airway diameter is determined by PL and anatomical structural support. The cartilaginous airways are better able than small, noncartilaginous airways to resist pressure-induced diameter changes. Small airways depend on elastic retractile forces of surrounding lung parenchyma for their patency (see Chapter 1). Natural airway narrowing during normal tidal exhalation causes linear flow velocity to be greater than it is during inhalation, especially in small, peripheral airways—that is, for a given flow rate, gas molecules pick up speed as they move through narrowed airways. This expiratory cephalad (toward the head) flow bias enhances the normal process of mucociliary clearance because mucus tends to move in the direction of the highest flow velocity.16 This effect is exaggerated during a cough when small airways are narrowed further by bursts of high intrapleural pressures; extremely high linear flow velocities provide the shearing forces necessary to propel mucus up toward the trachea and pharynx. (One must distinguish between bulk flow rate and linear flow velocity; although airway compression can reduce bulk flow rate [liters per second], it increases linear velocity [meters per second].)
Expiratory Flow Limitation
At the start of a forced exhalation from the TLC level, the thorax contracts, causing the normally subatmospheric Ppl to become positive. As a result, PA also increases. PA is the sum of static elastic recoil pressure (Pel) and surrounding Ppl (PA = Pel + Ppl) as shown in Figure 3-25, A. Frictional resistance to airflow causes the pressure along the airway to decrease steadily from the alveolus to the mouth, where Pao is 0.
narrows the airways. Normally, this dynamic airway compression occurs only as the lung nears RV, where low elastic recoil force limits the maximum driving pressure that can be generated. In patients with emphysema, airway compression and collapse occur well above the RV level because the elastic recoil force of the lung is abnormally low in the first place.
Effort-Dependent and Effort-Independent Expiratory Flow Rate
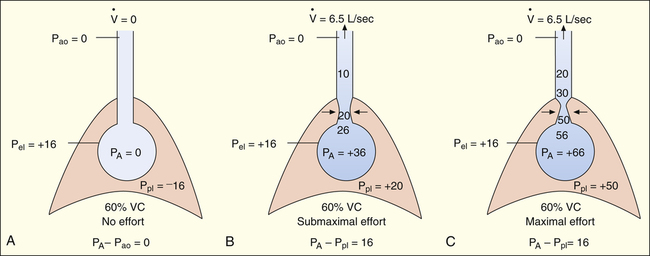
If forced exhalation starts from the TLC level, the initial flow rate is effort-dependent—that is, greater efforts produce greater initial flows as shown in Figure 3-25. In Figure 3-25, A, the subject was instructed to inhale to TLC and hold the breath, keeping the glottis open. In Figure 3-25, B, still at TLC, the subject was instructed to exhale with a submaximal effort. In Figure 3-25, C, the subject was instructed to inhale to TLC again and this time to exhale with maximal effort. The high lung volume at the beginning of these exhalations produced a high elastic recoil pressure, which made a high PA possible. Because PA is the sum of intrapleural and elastic recoil pressures, the higher the elastic recoil pressure, the greater the difference between PA and the surrounding Ppl. Therefore, in a forced exhalation beginning from TLC, the PA pressure head is high enough that pressures down the airway (toward the mouth) never fall below Ppl before gas leaves the thoracic airways. EPP and dynamic airway compression described earlier never occur at high lung volumes near TLC. In Figure 3-25, B and C, greater muscular effort produced greater PA − Pao differences and greater flow rates.
In Figure 3-26, the subject was instructed exactly as in Figure 3-25 except that the exhalation maneuvers began at 60% of VC instead of from TLC. At this smaller lung volume, the beginning lung recoil is lower, and the difference between maximum achievable PA and Ppl is relatively small. During even a submaximal exhalation effort (see Figure 3-26, B), the pressure inside the airway soon falls below Ppl, and EPP is reached well inside the thoracic cavity. A maximal expiratory effort (see Figure 3-26, C) fails to produce a greater flow rate because EPP represents a choke point between the alveolus and the mouth. In this situation, the driving pressure that produces the expiratory flow rate is not PA − Pao, as it is in Figure 3-25, B and C, but is instead PA minus EPP choke point pressure, which is identical for submaximal and maximal efforts in Figure 3-26, B and C. One can think of the airway compression at EPP as a valve that controls the flow rate, similar to the way pinching the middle of a garden hose would control the outflow of water at the hose’s end. Greater muscular effort in Figure 3-26, C, simply produced an increase in Ppl that exactly matched the increase in PA. Therefore, the flow rate remained constant and was effort-independent.
Isovolume Pressure-Flow Curve
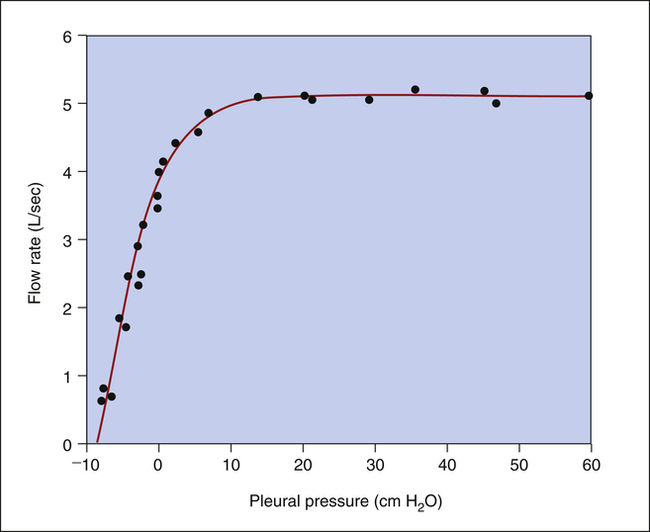
The isovolume pressure-flow curve (Figure 3-27) can be constructed after a person repeatedly inhales as deeply as possible to TLC, each time exhaling the VC with different efforts. Each time the person exhales the VC, greater effort is used, until the last VC is exhaled with maximal effort. The flow rate, volume, and Ppl (using an esophageal balloon) can be measured simultaneously during each VC maneuver. For all VC efforts performed, from weak to maximal efforts, the flow rates and the corresponding Ppl values that occurred exactly at 60% of VC are identified. Each flow rate is plotted against each corresponding Ppl value obtained at 60% of each VC effort (see Figure 3-27). This curve is called an isovolume pressure-flow curve because all flows and pressures are measured at the same volume (60% of VC).
The points on the curve represent the flow rates and pressures produced by the different efforts, all of which are measured precisely at the moment the lung deflates through 60% of the VC. The striking feature of this curve is that flow no longer increases when expiratory efforts cause pleural pressures to increase to greater than 10 cm H2O. Even maximal effort (60 cm H2O pleural pressure in Figure 3-27) fails to increase the flow rate. After the flow rate plateau is reached, the flow rate becomes effort-independent. This flow limitation is explained by the EPP phenomenon described in the previous section.
If several other pressure-flow curves are plotted at different lung volumes in exactly the same manner just described, a family of isovolume pressure-flow curves is produced, each at a different lung volume (Figure 3-28, A). At 90% of VC, increasing effort always produces increasing flows (i.e., a flow rate at 90% of the VC is effort-dependent). At lower lung volumes (60%, 30%, and 10% of VC), expiratory flows initially increase with greater efforts, but after a certain point, further effort fails to increase flow. Each lung volume has its own maximum achievable flow rate (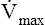 ). If each
). If each 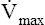 is plotted against its corresponding lung volume (instead of its corresponding pleural pressure), a flow-volume curve is produced that is identical in shape to the flow-volume curve recorded instantaneously from a single exhaled, forced VC maneuver (see Figure 3-28, B). The FVC flow-volume curve is actually a continuous plot of all the maximum flows achievable at lung volumes ranging from TLC to RV. (The use of flow-volume curves in assessing pulmonary function is discussed in Chapter 5.)
is plotted against its corresponding lung volume (instead of its corresponding pleural pressure), a flow-volume curve is produced that is identical in shape to the flow-volume curve recorded instantaneously from a single exhaled, forced VC maneuver (see Figure 3-28, B). The FVC flow-volume curve is actually a continuous plot of all the maximum flows achievable at lung volumes ranging from TLC to RV. (The use of flow-volume curves in assessing pulmonary function is discussed in Chapter 5.)
Time Constants in Ventilation
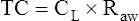
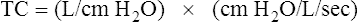

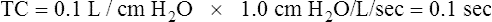
Effect of Compliance
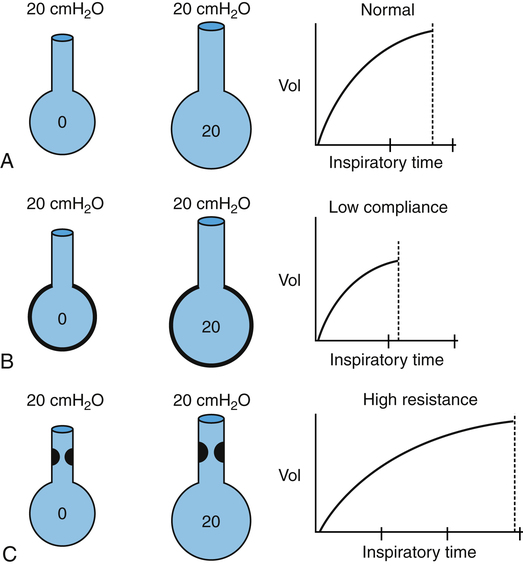
Stiff lungs with low compliance achieve equilibrium with the inflation pressure quickly but at a low volume (Figure 3-29, B). Likewise, stiff lungs empty quickly because of their high elastic recoil. Lungs with low compliance and normal Raw have short time constants. Four to five time constants are still required for complete inflation or deflation, but the absolute time required is less than for a normally compliant lung.
Effect of Airway Resistance
Figure 3-29, C, illustrates that high frictional resistance leads to long inflation and deflation times. If the same instantaneous inflation pressure is applied to normal lungs and lungs with high Raw, more time is required for pressures to equalize across the high-resistance airways. Four or five time constants are needed for pressure equalization, but each time constant is relatively long. Given adequate time, the lung with increased Raw eventually achieves the same volume as the normal lung, if inflation pressures are identical (see Figure 3-29, C). Equally important, lungs with high Raw require long expiratory (deflation) times. Inadequate expiratory time leads to incomplete lung emptying, air trapping, and hyperinflation of the lungs.
Frequency Dependence of Compliance
Because they account for less than 10% of the total Raw, small airways (<2 mm in diameter) constitute a “silent zone” in which considerable disease may go undetected by conventional pulmonary function tests. One marker of increased small airway resistance is the frequency dependence of compliance.15 Raw is so low in people without disease that Cdyn and Cst are essentially equal at normal breathing rates. Even at 60 breaths per minute (high flow rates), Cdyn and Cst are equal in normal people. Therefore, Cdyn is not normally frequency-dependent, which implies that all ventilating lung units have normal and uniformly distributed resistances and time constants.
Effects of Lung Compliance and Airway Resistance on Ventilation
Distribution of Inspired Air
Regional Pleural Pressure Gradients and Gas Distribution
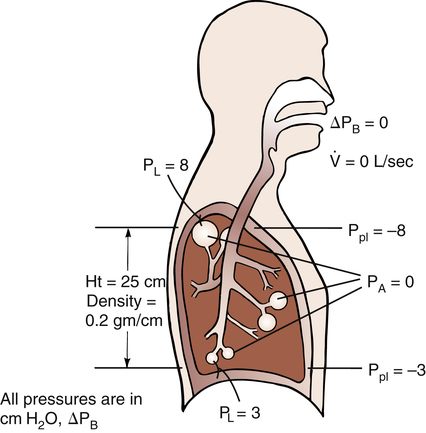
Ppl does not have the same value throughout the pleural space from lung base to apex (Figure 3-30). In the upright position, the downward pull of lung tissue and blood creates a greater negative Ppl at the apex (−8 cm H2O) than at the base (−3 cm H2O). PL is greater in the apex (PL = 8 cm H2O) than the base (PL = 3 cm H2O). As a result, apical alveoli are more distended and have higher recoil forces (are less compliant) than basal alveoli at the FRC level. Consequently, inspired tidal air preferentially flows to the more compliant basal lung units, ventilating them more than the apices. Although apical alveoli contain the greater volume, their decreased compliance allows less volume change per breath and less ventilation per minute.
During a VC inspiration from RV to TLC, the basal alveoli undergo a greater volume change than apical alveoli. If a person exhales forcefully to RV, pleural pressure at the base becomes positive and small airways collapse. However, pleural pressure at the apex is still negative, and apical airways remain patent (Figure 3-31, RV). If the person slowly inhales to TLC, air first flows into the patent airways of apical alveoli; basal alveoli cannot receive volume until the Ppl is reduced below atmospheric levels and they begin to expand.
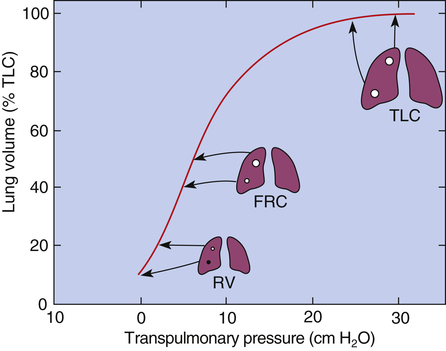
Apical alveoli at RV are small and on the steep part of the P-V curve (i.e., they are compliant and easily inflated because they are close to their resting volumes). However, at FRC (see Figure 3-31), apical alveoli are more distended and less compliant than basal alveoli. At TLC, apical and basal alveoli are nearly the same size. Although the PL values are different, they are both on the flat part of the P-V curve, and their volumes differ only slightly. The greater portion of the inspired VC enters basal alveoli because they undergo a greater size change.
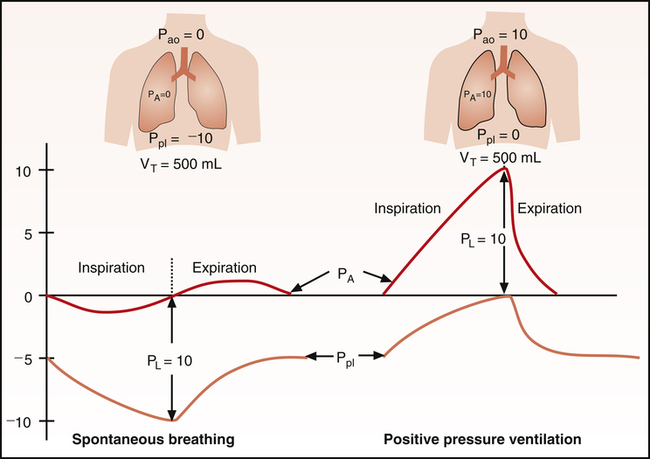
Effect of Compliance and Resistance on Pressure Gradients in Positive Pressure Ventilation
During positive pressure ventilation (PPV), compliant lungs transmit more of the alveolar pressure into the pleural space than noncompliant lungs. Under normal conditions, when CLT is about 0.1 L/cm H2O, approximately half of the applied positive pressure in the alveoli is transmitted into the pleural space.17 Diseased lungs with low compliance (high recoil force) may transmit only one third or one fourth of their pressures. High intrapleural pressures induced by PPV in critical care settings may compress the great veins in the mediastinum and impede the return of venous blood to the heart. This effect is more pronounced when CL is normal but is less evident in stiff, noncompliant lungs.
pressures, unless an inspiratory pause occurs at the end of inspiration. In high Raw, peak inspiratory mouth pressure does not reflect PA because much of the peak pressure is dissipated by the high resistance of the airways. For this reason, individuals with high Raw, such as patients with severe asthma, can be ventilated with relatively high peak upper airway pressure without subjecting the alveoli to high pressure. The best indicator of true PA is the pressure obtained during an inspiratory pause (Pplat).
Effect of Compliance and Resistance on Work of Breathing and Ventilatory Pattern
Work of Breathing
Work is performed when a force moves an object over a certain distance (work = force × distance). This equation shows that no matter how great the force, if the object does not move, no work is performed. Thus, WOB is a poor indicator of patient effort, which is one reason why it is not commonly calculated in the clinical setting. Work is measured in units of kilograms multiplied by meters (kg • m). The work equation can be modified to calculate WOB by substituting pressure for force (force equals pressure per unit of area) and lung volume for distance—WOB = P × V, which yields work units expressed in cm H2O • L. Generally, however, mechanical work is expressed in terms of either kg • m or joules (J). (To convert cm H2O • L to kg • m, divide cm H2O • L by 100; to convert to J, divide cm H2O • L by 10.)17 WOB is sometimes expressed in terms of work per unit of volume or kg • m/L. Normal WOB is about 0.05 kg • m/L or 0.5 J/L.17
The respiratory muscles affect the mechanical WOB during spontaneous ventilation because they tense and add resistance to chest wall expansion. Therefore, the work of lung inflation is best measured on a sedated patient during mechanical ventilation, when respiratory muscles are completely relaxed. The P-V curve in Figure 3-22 illustrates the elastic and resistive WOB performed on the lung-thorax system by a positive pressure ventilator. Elastic opposition to inflation is proportional to the white triangle ADCFA. The shaded area, ABCDA, represents the work required to overcome frictional resistance. The total work is represented by the sum of both areas (ABCFA). About 65% of the total work during quiet breathing is elastic work; the remaining 35% is frictional work. Of the frictional work, 80% is used to overcome Raw, and 20% is used to overcome viscous resistance, or the friction between tissues as they slide over each other.
Expiratory frictional resistance, represented by the area ADCEA in Figure 3-22, is normally overcome by stored elastic energy of the lung. The lung deflates along the line CEA and inflates along the line ABC.
Muscular Weakness and Fatigue
If the respiratory muscles are already weak, increased WOB may lead to muscle fatigue. Weakness refers to the decreased force-generating capacity of the rested muscle; fatigue refers to the decreased force-generating capacity of actively working muscles, reversible by rest.18 Respiratory muscle weakness is common in critically ill patients and predisposes them to ventilatory failure. Clinical assessment of respiratory muscle fatigue is important in determining a patient’s need for mechanical ventilation.
Overt diaphragmatic fatigue may result from excessive WOB with or without muscle weakness. Overt fatigue is defined as the inability of the diaphragm to sustain a given force of contraction throughout inspiration.21 A measure of the diaphragm’s force of contraction is the transdiaphragmatic pressure (Pdi). Pdi (pressure across the diaphragm) is measured after the subject swallows a tube with both esophageal (above the diaphragm) and gastric (below the diaphragm) balloons attached. Pdi is the difference between esophageal and gastric balloon pressures. Any force that resists lung inflation causes the diaphragm to contract more forcefully, which increases Pdi.
A key indicator of diaphragmatic fatigue is the ratio between quiet-breathing Pdi and the maximal Pdi (Pdimax) a person can generate.21 This ratio tells the clinician what percentage of the maximal force-generating capacity the patient uses for each breath. The Pdi/Pdimax ratio increases when (1) lung recoil or Raw increase or (2) muscular weakness (i.e., low Pdimax) is present. The Pdi/Pdimax ratio in normal persons breathing quietly is about 0.05. Patients with a Pdi/Pdimax ratio of 0.4 or more eventually experience diaphragmatic fatigue.18,19
The “gold standard” index of diaphragmatic fatigue is the tension-time index of the diaphragm (TTdi), which relates the Pdi/Pdimax ratio to the time spent in inspiration (Ti).20 Ti is expressed as a fraction of the total breath cycle time, Ti/Ttot,
or the so-called duty cycle. The product of these two ratios produces the TTdi, shown as follows:
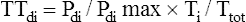
The greater the diaphragmatic fatigue, the greater the TTdi. TTdi takes into account (1) the percentage of maximum achievable inspiratory force the patient uses for each breath and (2) the length of time the force is applied. Clinical studies reveal that a TTdi of 0.15 is the fatigue threshold or critical TTdi above which healthy subjects cannot persistently maintain their breathing patterns.20 It is widely accepted that TTdi greater than 0.15 is highly predictive of diaphragmatic fatigue.21
The disadvantage of TTdi is that it is an invasive procedure involving the swallowing of esophageal and gastric balloons, which makes it impractical for routine clinical assessment. In addition, TTdi focuses on diaphragmatic function alone, and does not take into account the contribution that the rib cage and accessory muscles make to vigorous inspiratory efforts. The diaphragm and rib cage muscles are uncoupled, each able to function independently. In quiet, nonstressful inspiration, only the diaphragm is active, but as inspiratory load increases (e.g., breathing through an endotracheal tube), the rib cage muscles take on an increasingly greater share of the inspiratory work.21
An alternative noninvasive estimate of TTdi is the tension-time index of the inspiratory muscles (TTmus), which reflects the performance of all inspiratory muscles involved in respiratory effort. TTmus uses easily measured mouth occlusion pressures instead of esophageal and gastric pressures. The noninvasive TTmus has been validated and shown to correlate highly with the traditional invasive TTdi.21,22 (TTmus has also been called the pressure-time index [PTI].) TTmus is calculated as follows:
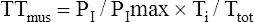
The negative inspiratory pressures, PI and PImax, are measured at the mouth while the subject breathes through a tube that the clinician can abruptly occlude to make pressure measurements. PI is the mean occlusion pressure measured during normal breathing, and PImax is the maximal occlusion pressure the patient can generate. Ti/Ttot is the fraction of the total respiratory cycle spent in inspiration. PI is estimated from the negative airway pressure generated during normal breathing 0.1 second after the airway is abruptly occluded (P0.1). (The greater the value of P0.1, the greater the TTmus. The reason P0.1 increases as muscle strength decreases is that when fatiguing respiratory muscles fail to generate adequate tension, the muscle spindles become excited and stimulate the central nervous system, which increases the nervous drive to breathe.21) The equation for estimating PI (the mean inspiratory occlusion pressure) is as follows:22
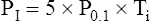
This method assumes that P0.1 is the rate at which pressure increases over the inspiratory time (cm H2O/sec). Because the pressure generated by the inspiratory muscles does not always increase linearly, this method may overestimate PI.21 However, a given individual’s inspiratory time-pressure waveform is quite stable and repeatable; thus repeated measurements of PI, P0.1, and TTmus for any one individual should be reliable.23
TTmus is easily measured at the bedside or in the emergency department with the appropriate technology and correlates extremely well with TTdi in normal subjects, patients with COPD, and patients with restrictive lung diseases.21–23 The fatigue threshold of the respiratory muscles above which patients fail to sustain adequate ventilation lies in a critical TTmus range of 0.27 to 0.43.24 (A normal TTmus in healthy control subjects was found in one study to be about 0.05.21) Because TTmus reflects the performance of all inspiratory muscles, it has an advantage over TTdi in assessing patients with high inspiratory loads, relevant especially in patients with COPD and restrictive lung disease. These patients inhale using predominantly rib cage muscles rather than the diaphragm, a pattern exaggerated by high inspiratory workloads.21,23
An increased use of accessory ventilatory muscles, coupled with rapid, shallow breathing, also signals impending diaphragmatic fatigue.25 Accessory muscle use can be detected by palpating the neck and abdomen for muscle tensing. Fatiguing breathing patterns are characterized by the loss of synchronized outward inspiratory movements of the rib cage and abdomen. Asynchrony occurs when the outward movement of the abdomen lags behind the movement of the rib cage during inspiration. Critically ill patients exhibiting asynchrony have an increased risk of ventilatory failure. A visual sign of overt diaphragmatic fatigue is abdominal paradox, in which the abdomen is sucked inward during inspiration as the rib cage expands outward; this is evidence that the rib cage muscles are predominately being used.25
Because rapid, shallow breathing invariably accompanies respiratory muscle fatigue, the frequency-to-VT (f/VT) ratio (sometimes called the rapid, shallow breathing index) is widely used in the clinical setting to assess an individual’s ability to sustain adequate spontaneous ventilation. In a landmark study of patients being weaned from mechanical ventilation, patients with f/VT ratios greater than 100 (VT is expressed in liters and f in breaths per minute) had a 95% likelihood of developing ventilatory failure, whereas patients with f/VT ratios less than 100 had an 80% probability of successfully sustaining spontaneous ventilation.26 The f/VT ratio is an attractive clinical tool for assessing WOB because it is highly predictive of ventilatory failure, is easily measured, and does not require patient effort or cooperation.
Energy Costs of Breathing
Oxygen consumed by the respiratory muscles reflects the energy costs of breathing. Oxygen consumed by the respiratory muscles alone can be assessed through a comparison of total oxygen consumption at rest with oxygen consumed at increased levels of ventilation. The oxygen cost of breathing in normal people is about 1.0 mL of oxygen consumed per liter of total ventilation; this is less than 5% of normal total body oxygen consumption. Patients with advanced COPD may have an oxygen cost of breathing as high as 10 mL of oxygen consumed per liter of ventilation.19 The efficiency of breathing is decreased in patients with COPD because respiratory muscles consume large amounts of oxygen for each liter of ventilation they produce.
The oxygen cost of ventilation is difficult to measure directly but may be indirectly estimated from WOB measures. However, WOB obtained from a P-V curve correlates poorly with oxygen consumed by ventilatory muscles because it does not take into account a patient effort that produces no volume change (no volume change means no work is performed, regardless of patient effort). A much more accurate indicator of oxygen consumption is TTdi, which takes into account the force of muscle contraction and the time over which it is applied.27 The energy cost, and thus oxygen consumption of skeletal muscle contraction, depends on the force developed, the duration of muscular contraction, and the velocity of muscle shortening. The P-V curve reflects the mechanical work performed but does not account for the intensity of muscle contraction.