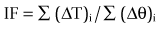Instability has been defined as a condition of a system in which the application of a small load causes an inordinately large, perhaps catastrophic, displacement.⁶ This definition conveys the more colloquial sense of something that is about to fall apart or could easily fall apart. Bioengineers have insisted that instability is a mechanical entity and should be treated as such,⁷ but how biomechanists have portrayed the definition graphically in mathematical terms has evolved over recent years, as more and more embellishments and alternatives have been added.

Stiffness

An early definition simply maintained that instability was loss of stiffness.⁷ A later elaboration introduced a clinical dimension, to the effect that instability is a

loss of spinal motion segment stiffness such that force application to the structure produces a greater displacement(s) than would be seen in a normal structure, resulting in a painful condition, the potential for progressive deformity, and that places neurologic structures at risk.⁸

Other engineers have disagreed, insisting that any definition of instability should include the sense of sudden, unpredictable behaviour; that a small load causes a large, perhaps catastrophic, displacement.⁶ They argue that loss of stiffness may simply describe loose or hypermobile segments that are not at risk of catastrophic collapse.

Indeed, any definition expressed simply in terms of stiffness is inadequate and inappropriate. It is inadequate because it raises the question ‘How much less stiff should a segment become before it is considered unstable?’. It is inappropriate because it does not convey the sense of impending failure. In that regard the definition that includes the terms ‘catastrophic displacement’ is more appropriate but there is still the question ‘What constitutes a “catastrophic displacement”?’.

There may well be conditions of the lumbar spine that involve loss of stiffness and the production of symptoms, but these do not necessarily constitute instability in the full sense of the word, and perhaps an alternative term should be applied, such as ‘segmental looseness’ or simply ‘hypermobility’.

Neutral zone

A refreshing new definition that has emerged is one that essentially defines instability as an increased neutral zone. Explicitly, the definition is

a significant decrease in the capacity of the stabilising system of the spine to maintain the intervertebral neutral zones within the physiological limits so that there is no neurological dysfunction, no major deformity, and no incapacitating pain.⁹

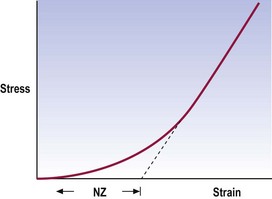
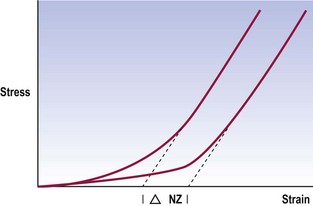
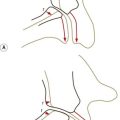
The neutral zone is that part of the range of physiological intervertebral motion, measured from the neutral position, within which the spinal motion is produced with a minimal internal resistance.⁹ In essence, although not exactly the same mathematically, it is similar to the length of the toe phase of the stress–strain curve that describes the behaviour of the segment (Fig. 16.1).

Figure 16.1 An archetypical stress–strain curve showing the location of the neutral zone (NZ).

This definition describes joints that are loose but early in range. Their ultimate strength may be normal but early in range they exhibit excessive displacement (Fig. 16.2). This definition captures the sense of excessive displacement; it captures the sense of excessive displacement under minor load but it defies the engineering sense of impending catastrophic failure. However, it does so deliberately and not totally without regard to catastrophe.

Figure 16.2 The stress–strain curve of a lumbar segment that exhibits instability in terms of an increased neutral zone (ΔNZ) compared to a normal curve.

The neutral zone concept directs attention away from the terminal behaviour of a joint to its earlier behaviour. This allows the definition to be applied to circumstances more common than those associated with impending failure of the spine; it is applicable to the conditions otherwise described as ‘looseness’. The sense of catastrophe, and hence instability, is nonetheless retained in a modified form.

As a joint moves through an extended neutral zone it is undergoing an inordinate displacement. If extrapolated, this behaviour predicts that the joint will eventually fall apart. Hence the sense of impending catastrophe applies. It transpires, however, that eventually the inordinate motion of the joint is arrested and catastrophe does not ensue. Nevertheless, during the neutral zone, the movement looks and feels inordinate and threatening.

Instability factor

The engineering definitions of instability describe what might be called terminal instability: the behaviour of a system at its endpoint. It is there that the sense of impending failure arises. Another interpretation addresses instability during movement rather than at its endpoint. It focuses on the quality of movement during range, not on terminal behaviour.

Flexion–extension of the lumbar spine is not a singular movement; it involves a combination of rotation and translation (see Ch. 8). Notwithstanding the range of motion, the quality of motion may be defined in terms of the ratio between the amplitude of translation and the amplitude of rotation. For each phase of movement there should be a certain amount of translation accompanied by an appropriate degree of rotation. If this ratio is disturbed, the motion becomes abnormal and the sense of instability may arise. In this regard, the instability would be defined as an inordinate amount of translation for the degree of rotation undergone, or vice versa.

Normal lumbar segments exhibit an essentially uniform ratio of translation to rotation during flexion–extension.¹⁰ The overall pattern of movement looks smooth; translation progresses regularly, as does rotation (Fig. 16.3). The ratio between translation and rotation at any phase of movement is the same as the ratio between total translation and total rotation.

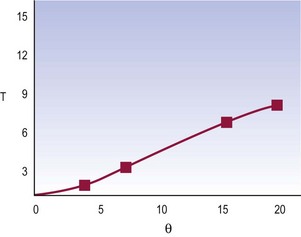
Figure 16.3 A normal movement pattern of a lumbar segment in terms of the ratio between translation and rotation.

(Based on Weiler et al. 1990.¹⁰)

It may be defined that instability occurs when, at any time in the movement, there is an aberration to this ratio. The segment suddenly exhibits an inordinate translation for the degree of rotation undergone, or may translate without any rotation (Fig. 16.4).

Figure 16.4 A movement pattern of a lumbar segment showing an aberrant ratio between translation and rotation, and an abnormally high instability factor.

(Based on Weiler et al. 1990.¹⁰)

This definition conveys the sense of inordinate displacement but places it during the normal range of motion instead of at its endpoint. The segment may be terminally stable but expresses instability during range. The sense of catastrophe does not obtain in the conventional sense, in that the segment will not fall apart, but it is present qualitatively. For that brief moment when the unexpected inordinate movement suddenly occurs, the sensation will be the same as that of impending failure. The fact that the joint is ultimately stable is not sufficiently reassuring, for during the unstable phase the movement is alarming and qualitatively the same as if the spine were about to fall apart.

Special techniques are required to detect this form of instability. They involve taking serial radiographs of the motion, at least five exposures for the entire range of motion, and determining the ratios of translation to rotation for each phase. From these ratios, an instability factor (IF) can be computed, namely.

where (ΔT)_i is the range of translation for each phase of motion (i) and (Δθ)_i is the range of rotation for each phase.¹⁰ In normal spines, the instability factor has a mean value of 25 (mm radian⁻¹) and a standard deviation of 8.7. Values beyond the upper two SD range nominally qualify for instability.

Anatomy

Although biomechanical definitions for instability are available, for them to be meaningful clinically they require translation into anatomy. For treatment to be rational and targeted, the structure must be specified which is responsible for the decreased stiffness, the increased neutral zone or the excessive translation versus rotation.

In principle, a spectrum of possibilities arises (Fig. 16.5). Instability may be related to the extent of injury to a segment and the factors that remain trying to stabilise it. At one extreme lies complete dislocation, where no factors maintain the integrity of the segment. At the opposite extreme lies an intact segment that is absolutely stable. Between lies a hierarchy of possibilities.

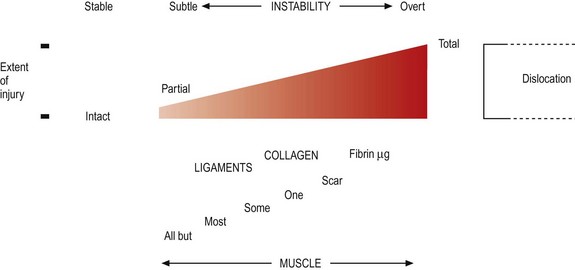
Figure 16.5 The relationship between instability, extent of injury and the factors maintaining stability.

In a totally disrupted segment, instability will be overt. Gravity may be the only factor keeping it together. As long as the patient remains upright, the compressive loads between vertebrae keep them in place. However, if the patient leans forwards, the affected segment can simply slip forwards under gravity. Friction, fibrin deposits or scar tissue may offer token resistance to displacement but are insufficient practically to stabilise the segment.

For any degree of stability, the segment requires its stabilising elements: its facets and ligaments (see Chs 3 and 4). The fewer of these that are intact, the more liable the segment is to catastrophic failure; the more that are intact, the more stable the segment becomes.

Numerous studies have been conducted that demonstrate how progressively removing each of the restraining elements progressively disables a lumbar motion segment. Transecting the posterior longitudinal ligament and posterior anulus fibrosus produces hypermobility, even when other elements remain intact.¹¹ Progressively transecting the supraspinous and interspinous ligaments, ligamentum flavum, joint capsules, facets, the posterior longitudinal ligament and the posterior anulus fibrosus leads to progressively greater displacements when a segment is loaded in flexion, with the greatest increase in displacement occurring after transection of the posterior disc.¹² Short of transecting the disc, the zygapophysial joints appear to be the major stabilising elements in flexion.^13,¹⁴

Superimposed on the facets and ligaments are muscles. These contribute to stability in two ways. The lesser mechanism is to pull directly against threatened displacements. In this regard, however, the back muscles are not well oriented to resist anterior or posterior shear or torsion; they run longitudinally and can only resist sagittal rotation (see Ch. 9). However, whenever the muscles act they exert compressive loads on the lumbar spine. This achieves a stabilising effect. By compressing joints, the muscles make it harder for the joints to move, and a variety of studies have now documented the stabilising effect of muscles on the lumbar spine.^15,¹⁶ Specifically, muscle contraction decreases the range of motion and decreases the neutral zone of lumbar spinal segments, with the multifidus contributing the strongest influence.¹⁶

Notwithstanding the range of possible explanations for instability, across the spectrum of possibilities a transition occurs from concerns about terminal failure to interest in looseness, or instability within range. Overall, a segment may have most of its restraining elements intact and not be at risk of terminal failure, but the absence of a single restraining element may allow the segment to exhibit a partial inordinate movement within range. For clinical practice, two challenges obtain:

• Overt failure or impending failure is readily recognised radiographically in conditions such as fracture-dislocation when a vertebra exhibits malposition or an excessive motion apparent to the unaided eye. In such circumstances, instability is beyond doubt because the evident motion could not possibly have occurred unless the restraining elements were totally disrupted. However, the challenge obtains to determine the threshold for instability when the abnormal motion is not readily apparent.

• For instability within range, the challenge is to demonstrate its presence and to be certain that the abnormal motion is responsible for the patient’s symptoms.

Hypothetical models

The concepts offered by biomechanists can be collated and summarised graphically using a unifying device: a force and displacement graph (Fig. 16.6). For any lumbar movement there will be a force that induces displacement. Acting against this force will be restraining forces that stem from the facets, ligaments and muscles of the segment. These restraining forces act to prevent uncontrolled acceleration of the segment, under gravity for example. Given an appropriate combination of displacing forces and restraining forces, motion occurs; displacement progresses with time, and a velocity of motion emerges. The graph (see Fig. 16.6) shows the two opposing sets of forces and the change of displacement. The slope of this latter curve will be the velocity of movement. Under normal conditions, as displacing forces build up, the segment accelerates. As long as displacing forces exceed the restraining forces, movement continues. Towards the end of range, restraining forces exceed the displacing forces and movement decelerates, eventually stopping at end of range.

Figure 16.6 A force and displacement diagram. The difference between displacing forces (DF) and restraining forces (RF) results in displacement of a motion segment. The slope of the displacement curve is the velocity of movement. In a normal coordinated movement, the velocity curve is smooth and regular. Towards the end of range, the velocity slows to zero as movement is arrested.

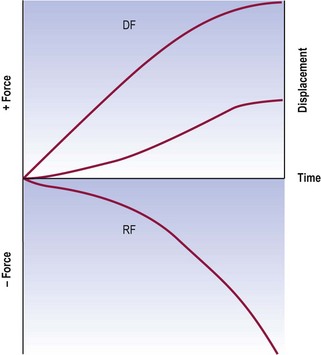
If a segment suffers a loss of stiffness, the restraining forces that resist forward flexion are reduced, but the gravitational forces that produce forward bending are unaltered and displacing forces remain the same (Fig. 16.7). As a result, the acceleration and eventual velocity of the resultant movement must, prima facie, be greater. Instability ensues if the balance between the displacing and restraining forces is insufficient to prevent inordinate displacement or the threat of failure of the segment. Such instability obtains both throughout range and at terminal range.

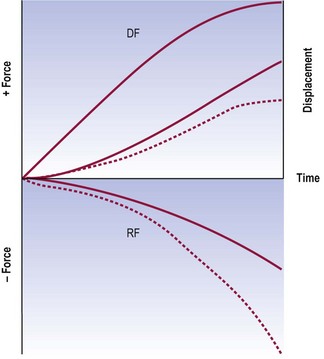
Figure 16.7 A force and displacement diagram of a motion segment with decreased stiffness. Throughout the range, the restraining forces (RF) are considerably less than the displacing forces (DF) and the segment develops a higher than normal velocity towards end of range. For comparison, the normal curves for restraining forces and displacement (see Fig. 16.6) are shown as dotted lines.

If a segment suffers a loss of restraints that operate early in range but no loss of terminal restraints, the restraining forces will exhibit an increased neutral zone, but the displacing forces are unchanged (Fig. 16.8). As a result, the motion segment exhibits an essentially normal early velocity but as the difference between displacing and restraining forces increases, it accelerates and eventually exhibits a higher than normal velocity. The sense of instability arises because the terminal velocity is excessive and unexpected. Instead of the accustomed pattern of motion, there is an unfamiliar acceleration, which is alarming because it predicts (albeit inappropriately) that, at this rate of displacement, the segment threatens to fall apart.

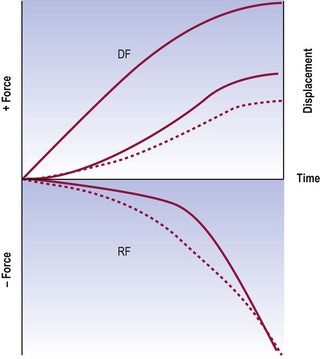
Figure 16.8 A force and displacement diagram of a motion segment with an increased neutral zone. The displacing forces (DF) and restraining forces (RF) are imbalanced early in range, and the segment accelerates towards end of range and develops a higher than normal terminal velocity. For comparison, the normal curves for restraining forces and displacement (see Fig. 16.6) are shown as dotted lines.

If a segment suffers a loss of restraints that operate in mid-range or late in range, initial movements may be normal but the loss of restraints results in an acceleration late in range (Fig. 16.9). This acceleration is alarming because it feels as if the segment is about to shoot out of control.

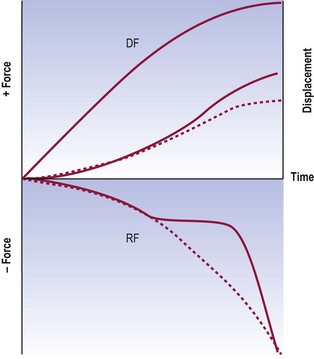
Figure 16.9 A force and displacement diagram of a motion segment exhibiting instability in mid-range. Early in range the balance between displacing forces (DF) and restraining forces (RF) is normal, and a normal velocity of movement occurs. When suddenly a restraining component fails to engage, the movement accelerates, reaching a higher than normal terminal velocity. For comparison, the normal curves for restraining forces and displacement (see Fig. 16.6) are shown as dotted lines.

These models convert the concept from one of abnormal range or abnormal displacement to one of excessive acceleration. It is the degree of acceleration that corresponds to the degree of instability. The models also implicitly invoke a neurophysiological dimension. Instability arises when there is a mismatch between the expected and actual velocity of motion.

In neurophysiological terms, the mismatch is between the proprioceptive feedback and the motor programme for the movement. For a given movement, the individual will be accustomed to a particular pattern of motion, and therefore to a particular pattern of proprioceptive feedback. Habitually, they will have used a correspondingly appropriate pattern of activity of their back muscles. When, however, the pattern of motion changes, the proprioceptive feedback will be different, but if the individual uses their habitual motor pattern it will be inappropriate for the velocity of movement occurring. In essence, at a time when the individual is accustomed to expecting ‘n’ units of velocity and ‘m’ units of motor control, they actually suffer ‘n + x’ units of velocity, for which ‘m’ units of motor control are insufficient. As a result, the segment will feel as if it is ‘getting away’ or ‘falling apart’. Hence the sensation of instability.

There is no guarantee that the nervous system can adapt to changes in the behaviour of mechanical constraints, other than in a crude way. The changes in motion occur too quickly for the proprioceptive feedback to correct the motor activity by reflex. Instead, warned of the unaccustomed acceleration, the nervous system recruits a sudden muscle contraction, as if to deal with an ‘emergency’. Clinically, this would manifest as a jerk or a ‘catch’. Otherwise, in a very unstable segment, muscles may be persistently active to guard the affected segment against any movement that risks accelerating the segment.

In terms of these models, how instability relates to pain is a vexatious issue. Notionally, a hypermobile segment, or one with loss of stiffness, should not be painful. Pain might occur only at end of range when restraints were being excessively strained. If the loss of stiffness is due to injury, pain may arise from the injured structures, but in this regard the pain is independent of the instability; the pain may be aggravated by the movement, not because of instability but simply because the injured part is being irritated.

Segments with an increased neutral zone or with mid-range loss of restraints exhibit a marked terminal acceleration. A model that might explain pain under these circumstances invokes what might be referred to as abnormal ‘attack’. Normally, terminal restraints in a segment would be engaged at a normal, accustomed velocity. However, in an unstable segment, these restraints will be engaged, or ‘attacked’, at a greater than normal velocity. Perhaps the more forceful attack on these restraints stimulates nociceptors in them.

However, notwithstanding these speculations, it may well be that there is no need to explain the pain of instability because there is no direct relationship. Pain may arise from a segment simply because it is injured. Instability may be present but in parallel. Movement is painful as in any painful segment. But if the movement is suddenly jerked or arrested, the sudden compression load exerted by the back muscles might be the aggravating factor for the pain, rather than a painful engagement of restraints.

Clinical instability

Almost antithetical to the biomechanists’ notion of instability is the concept of ‘clinical instability’. Two uses of this latter term obtain.

One use is explicitly clinical and temporal; it bears no relationship to biomechanics. It maintains that clinical instability is a condition in which the clinical status of a patient with back problems steps, with the least provocation, from the mildly symptomatic to the severe episode.¹⁷ Philosophically and semantically this does amount to instability in the sense that a trivial force causes a major displacement, but the displacement is not of a mechanical entity; it is a displacement of the patient’s symptoms or of their clinical course. This use of the term is akin to speaking of an individual’s mood or emotions being ‘unstable’. This use of the term should not be confused or equated with the biomechanical use. More seriously, because it lacks any relationship to biomechanics, a diagnosis of clinical instability does not suggest, let alone indicate, mechanical therapy. There is a risk that, because ‘clinical instability’ and ‘biomechanical instability’ sound alike, they are equivalent. They are not.

A second definition of clinical instability has a more evident and legitimate relationship to biomechanics. It refers to biomechanical instability that reaches clinical significance, in that it produces symptoms. In this regard, the clinical features are immaterial to the basic definition; the definition rests on biomechanical abnormalities. The addition of the adjective ‘clinical’ simply promotes the biomechanical instability to one of ostensible clinical relevance. However, and most particularly, it does not imply that the instability is clinical evident; it implies only that the instability is clinically relevant.

The diagnosis of instability still hinges on biomechanical tests.

Diagnosis

Instability is readily abused as a diagnostic rubric. It is easy to say a patient has instability; it is much harder to satisfy any criteria that justify the use of this term.

Most irresponsible in this regard is the fashion to label as instability any spinal pain that is aggravated by movement. This is patently flawed. Conditions can occur which are painful and which are aggravated by movement but which involve no instability of the spine. The movements of the affected segment are normal in quality and in range; they are not excessive. Indeed, the range of movement may be restricted rather than excessive. For example, a septic arthritis is very painful, and any movement may aggravate the pain, but the joint and its segment are essentially intact and there is no risk of them falling apart. Osteoarthritis may be painful and aggravated by movements, and if anything, the joint is stiffer and more stable than normal.

If an anatomic or pathological diagnosis is available, it should be used, but ‘instability’ is not an arbitrary alternative that can be applied when no other diagnosis is apparent. Instability is clearly a biomechanical term and if it is to be applied, a biomechanical criterion must be satisfied. Pain on movement is not that criterion.

Criteria

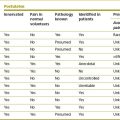
Various authorities have issued guidelines for the legitimate use of the term instability.^8,¹⁸ The major categories are shown in Table 16.1. Categories I, II and III are beyond controversy. Each involves a condition that threatens the integrity of the spine and which can be objectively diagnosed by medical imaging, perhaps supplemented by biopsy.

Table 16.1 Lumbar segmental instabilities

Category	Causes
I	Fractures and fracture-dislocations
II	Infections of the anterior elements
III	Neoplasms
IV	Spondylolisthesis
V	Degenerative

Spondylolisthesis is a controversial category. Traditionally, the appearance of this condition has been interpreted as threatening. Even under normal circumstances, the L5 vertebra appears to be precariously perched on the sloping upper surface of the sacrum. Defects in the posterior elements, notably pars interarticularis fractures, threaten to allow the L5 vertebra to slip progressively across the sacrum. However, the available data mitigate against this fear.

Spondylolisthesis rarely progresses in adults ¹⁹ or teenagers,²⁰ and therefore it appears inherently stable, despite its threatening appearance. Indeed, biplanar radiography studies of moving patients have shown that, if anything, grade 1 and grade 2 spondylolisthesis are associated with reduced range of motion rather than instability.²¹ However, some patients with spondylolisthesis may exhibit forward slipping upon standing from a lying position,²² but it is not clear whether the extent of slip in such cases is abnormal. Studies, using implanted tantalum balls in order to establish landmarks accurately, have found no evidence of instability.²³ In some patients, movement abnormalities may be revealed using special radiographic techniques, which include having the patient stand loaded with a 20 kg pack and hanging by their hands from an overhead bar.^24,²⁵ These extreme measures, however, have been criticised as unrealistic and cumbersome.⁶

It is with respect to degenerative instability that the greatest difficulties arise. A classification system of this category of lumbar instability has been proposed (Box 16.1).^8,¹⁸ The secondary instabilities are easy to accept and understand. They involve surgical destruction of one or more of the restraining elements of the spine, and are thereby readily diagnosed on the basis of prior surgery and subsequent excessive or abnormal motion. It is the primary instabilities that pose the greatest difficulties.

Rotational instability has been described as a hypothetical entity.²⁶ Based on clinical intuition, certain qualitative radiographic signs have been described¹⁷ but their normal limits have not been defined, nor has their reliability or validity been determined. Consequently, rotational instability remains only a hypothetical entity.

Translational instability is perhaps the most classic of all putative instabilities. It is characterised by excessive anterior translation of a vertebra during flexion of the lumbar spine. However, anterior translation is a normal component of flexion (see Ch. 8). The difficulty that arises is setting an upper limit of normal translation. Posner et al.¹² prescribed a limit of 2.3 mm or 8% of the length of the vertebral endplate for the L1–L4 vertebrae, and 1.6 mm or 6% for the L5 vertebra. Boden and Wiesel²⁷ however, demonstrated that many asymptomatic individuals exhibited static slips of such magnitude, and emphasised that, in the first instance, any slip should be dynamic before instability could be considered. A dynamic slip is one that is evident in full flexion but not in extension, or vice versa. Furthermore, even dynamic slips of up to 3 mm can occur in asymptomatic individuals; only 5% of an asymptomatic population exhibited slips greater than 3 mm. Accordingly, Boden and Wiesel²⁷ have advocated that 3 mm should be the threshold limit for diagnosing anterior translational instability. Hayes et al.,²⁸ however, found that 4 mm of translation occurred in 20% of their asymptomatic patients. Accordingly, 4 mm might be a better threshold limit.

Belief in retrolisthetic instability dates to the work of Knutsson.²⁹ He maintained that degenerative discs exhibited instability in the form of abnormal motions, notably retrolisthesis upon extension of the lumbar spine. This contention, however, was subsequently disproved when it was shown that similar appearances occurred in asymptomatic individuals.^28,³⁰ As a result, there are no operational criteria for instability due to retrolisthesis, other than the guidelines of Boden and Wiesel²⁷ or Hayes et al.,²⁸ which state that up to 3 mm or 4 mm of translation can be normal.

Scoliotic instability amounts to no more than rotational instability or translational instability, alone or in combination, in a patient who happens to have scoliosis. Adding the adjective ‘scoliotic’ in no way changes the difficulties in defining and satisfying the diagnostic criteria for these putative instabilities.

There is no evidence, to date, that internal disc disruption is associated with instability. Radiographic biomechanical studies simply have not been conducted on patients with proven internal disc disruption.

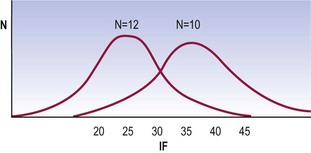
Although positive correlations are lacking between disc degeneration and retrolisthetic rotational and translational instability, there are associations between disc degeneration and a raised instability factor.¹⁰ Patients with disc degeneration exhibit a greater mean value of instability factor that is statistically significant (Fig. 16.10). However, because the technique for determining the instability factor is very demanding and time consuming, this method of studying instability has not been pursued further, to date.

Figure 16.10 The distribution of values of instability factor (IF) in a normal population (left curve) and a population of patients with degenerative disc disease (right curve).

(Based on Weiler et al. 1990.¹⁰)

Clinical diagnosis

Various clinical criteria have been proclaimed as indicative or diagnostic of lumbar instability.^17,^31,³² At best, these constitute fancy. To be valid, clinical signs have to be validated against a criterion standard. The only available criterion standard for instability is offered by radiographic signs, but the radiographic signs of instability are themselves beset with difficulties. Consequently, no studies have yet validated any of the proclaimed clinical signs of instability.