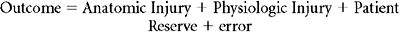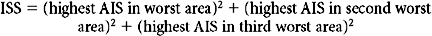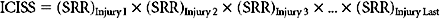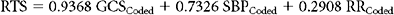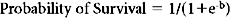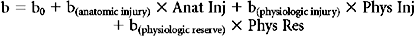INJURY DESCRIPTION AND SCORING: CONCEPTUAL BACKGROUND

Injury scoring is a process that reduces the myriad complexities of a clinical situation to a single number. In this process information is necessarily lost. What is gained is a simplification that facilitates data manipulation and makes objective prediction possible. The expectation that prediction will be improved by scoring systems is unfounded, however, since when ICU scoring systems have been compared to clinical acumen, the clinicians usually perform better.^4,5

Clinical trauma research is made difficult by the seemingly infinite number of possible anatomic injures, and this is the first problem we must confront. Injury description can be thought of as the process of subdividing the continuous landscape of human injury into individual, well-defined injuries. Fortunately for this process, the human body tends to fail structurally in consistent ways. Le Fort⁶ discovered that the human face usually fractures in only three patterns despite a wide variety of traumas, and this phenomenon is true for many other parts of the body. The common use of eponyms to describe apparently complex orthopedic injuries underscores the frequency with which bones fracture in predictable ways. Nevertheless, the total number of possible injuries is large. The Abbreviated Injury Scale is now in its fifth edition (AIS 2005) and includes descriptions of more than 2000 injuries (increased from 1395 in AIS 1998). The International Classification of Diseases, Ninth Revision (ICD-9) also devotes almost 2000 codes to traumatic injuries. Moreover, most specialists could expand by several-fold the number of possible injuries. However, a scoring system detailed enough to satisfy all specialists would be so demanding in practice that it would be impractical for nonspecialists. Injury dictionaries thus represent an unavoidable compromise between clinical detail and pragmatic application.

Although an “injury” is usually thought of in anatomic terms, physiologic injuries at the cellular level, such as hypoxia or hemorrhagic shock, are also important. Not only does physiologic impairment figure prominently in the injury description process used by emergency paramedical personnel for triage, but such descriptive categories are crucial if injury description is to be used for accurate prediction of outcome. Thus, the outcome after splenic laceration hinges more on the degree and duration of hypotension than on degree of structural damage to the spleen itself. Because physiologic injuries are by nature evanescent, changing with time and therapy, reliable capture of this type of data is problematic.

The ability to describe injuries consistently on the basis of a single descriptive dictionary guarantees that similar injuries will be classified as such. However, in order to compare different injuries, a scale of severity is required. Severity is usually interpreted as the likelihood of a fatal outcome; however, length of stay in an intensive care unit, length of hospital stay, extent of disability, or total expense that is likely to be incurred could each be considered measures of severity as well.

In the past, severity measures for individual injuries have generally been assigned by experts. Ideally, however, these values should be objectively derived from injury-specific data that is now available in large data bases. Importantly, the severity of an injury may vary with the outcome that is being contemplated. Thus, a gunshot wound to the aorta may have a high severity when mortality is the outcome measure, but a low severity when disability is the outcome measure. (That is, if the patient survives he or she is likely to recover quickly.) A gunshot wound to the femur might be just the reverse in that it infrequently results in death but often causes prolonged disability.

Although it is a necessary first step to rate the severity of individual injuries, comparisons between patients or groups of patients is of greater interest. Because patients typically have more than a single injury, the severity of several individual injuries must be combined in some way to produce a single overall measure of injury severity. Although several mathematical approaches of combining separate injuries into a single score have been proposed, it is uncertain which of these formulas is most correct. The severity of the single worst injury, the product of the severities of all the injuries a patient has sustained, the sum of the squared values of severities of a few of the injuries a patient has sustained, have all been proposed, and other schemes are likely to emerge. The problem is made still more complex by the possibility of interactions between injuries. We will return to this fundamental but unresolved issue later.

As noted, anatomic injury is not the sole determinant of survival. Physiologic derangement and patient reserve also play crucial roles. A conceptual expression to describe the role of anatomic injury, physiologic injury, and physiologic reserve in determining outcome might be stated as follows:

Our task is thus twofold: First, we must define summary measures of anatomic injury, physiologic injury, and patient reserve. Second, we must devise a mathematical expression combining these predictors into a single prediction of outcome, which for consistency will always be an estimated probability of survival. We will consider both of these tasks in turn. However, before we can consider various approaches to outcome prediction, we must briefly discuss the statistical tools that are used to measure how well predictive models succeed in the tasks of measuring injury severity and in separating survivors from nonsurvivors.

TESTING A TEST: STATISTICAL MEASURES OF PREDICTIVE ACCURACY AND POWER

Most clinicians are comfortable with the concepts of sensitivity and specificity when considering how well a laboratory test predicts the presence or absence of a disease. Sensitivity and specificity are inadequate for the thorough evaluation of tests, however, because they depend on an arbitrary cut-point to define “positive” and “negative” results. A better overall measure of the discriminatory power of a test is the area under the receiver operation characteristic (ROC) curve. Formally defined as the area beneath a graph of sensitivity (true positive proportion) graphed against 1 – specificity (false positive proportion), the ROC statistic can more easily be understood as the proportion of correct discriminations a test makes when confronted with all possible comparisons between diseased and nondiseased individuals in the data set. In other words, imagine that a survivor and a nonsurvivor are randomly selected by a blindfolded researcher, and the scoring system of interest is used to try to pick the survivor. If we repeat this trial many times (e.g., 10,000 or 100,000 times), the area under the ROC curve will be the proportion of correct predictions. Thus, a test that always distinguishes a survivor from a nonsurvivor correctly has an ROC of 1, whereas a test that picks the survivor no more often than would be done by chance has an ROC of 0.5.

A second salutary property of a predictive model is that it has clarity of classification. That is, if a rule classifies a patient with an estimated chance of survival of 0.5 or greater to be a survivor, then ideally the model should assign survival probabilities near 0.5 to as few patients as possible and values close to 1 (death) or 0 (survival) to as many patients as possible. A rule with good discriminatory power will typically have clarity of classification for a range of cut-off values.

A final property of a good scoring system is that it is well calibrated, that is, reliable. In other words, a predictive scoring system that is well calibrated should perform consistently throughout its entire range, with 50% of patients with a 0.5 predicted mortality actually dying, and 10% or patients with a 0.1 predicted mortality actually dying. Although this is a convenient property for a scoring system to have, it is not a measure of the actual predictive power of the underlying model and predictor variables. In particular, a well-calibrated model does not have to produce more accurate predictions of outcome than a poorly calibrated model. Calibration is best thought of as a measure of how well a model fits the data, rather than how well a model actually predicts outcome. As an example of the malleability of calibration, Figure 2A and B displays the calibration of a single ICD-9 Injury Severity Score (ICISS) (discussed later), first as the raw score and then as a simple mathematical transformation of the raw score. Although the addition of a constant and a fraction of the score squared add no information and does not change the discriminatory power based on ROC, the transformed score presented in Figure 2B is dramatically better calibrated. Calibration is commonly evaluated using the Hosmer Lemeshow (HL) statistic. This statistic is calculated by first dividing the data set into 10 equal deciles (by count or value) and then comparing the predicted number of survivors in each decile to the actual number of survivors. The result is evaluated as a chi-square test. A high (p>0.05) value implies that the model is well calibrated, that is, it is accurate. Unfortunately, the HL statistic is sensitive to the size of the data set, with very large data sets uniformly being declared “poorly calibrated.” Additionally, the creators of the HL statistic have noted that its actual value may depend on the arbitrary groupings used in its calculation,⁷ and this further diminishes the HL statistic’s appeal as a general measure of reliability.

Figure 2 (A) Survival as a function of Injury Severity Scores (ISS). One-half of valid ISS score values are below 25 due to the sum of squares definition of ISS. Because the data set is spread over 44 ISS scores, and higher scores occur less often, error bars for higher ISS scores are wider than for lower ISS values (691,973 patients from the NTDB). (B) ISS presented as paired histograms of survivors (above) and nonsurvivors (below). Note that only the 44 possible ISS scores are represented. In general, survivors tend to have lower ISS scores. Some ISS scores are dramatically more common, in part because these scores result from two or more combinations of AIS severity scores (691,973 patients from the NTDB).

In sum, the ROC curve area is a measure of how well a model distinguishes survivors from nonsurvivors, whereas the HL statistic is a measure of how carefully a model has been mathematically fitted to the data. In the past, the importance of the HL statistic has been overstated and even used to commend one scoring system (A Severity Characterization of Trauma [ASCOT]) over another of equal discriminatory power (TRISS). This represents a fundamental misapplication of the HL statistic. Overall, we believe much less emphasis should be placed on the HL statistic.

The success of a model in predicting mortality is thus measured in terms of its ability to discriminate survivors from nonsurvivors (ROC statistic) and its calibration (HL statistic). In practice, however, we often wish to compare two or more models rather than simply examine the performance of a single model. The procedure for model selection is a sophisticated statistical enterprise that has not yet been widely applied to trauma outcome models. One promising avenue is an information theoretic approach in which competing models are evaluated based on their estimated distance from the true (but unknown) model in terms of information loss. While it might seem impossible to compare distances to an unknown correct model, such comparisons can be accomplished by using the Akaike information criterion (AIC)⁸ and related refinements.

Two practical aspects of outcome model building and testing are particularly important. First, a model based on a data set usually performs better when it is used to predict outcomes for that data set than other data sets. This is not surprising, because any unusual features of that data set will have been incorporated, at least partially, into the model under consideration. The second, more subtle, point is that the performance of any model depends on the data evaluated. A data set consisting entirely of straightforward cases (i.e., all patients are either trivially injured and certain to survive or overwhelmingly injured and certain to die) will make any scoring system seem accurate. But a data set in which every patient is gravely but not necessarily fatally injured is likely to cause the scoring system to perform no better than chance. Thus, when scoring systems are being tested, it is important first that they be developed in unrelated data sets and second that they be tested against data sets typical of those expected when the scoring system is actually used. This latter requirement makes it extremely unlikely that a universal equation can be developed, because factors not controlled for by the prediction model are likely to vary among trauma centers.

MEASURING ANATOMIC INJURY

Measurement of anatomic injury requires first a dictionary of injuries, second a severity for each injury, and finally a rule for combining multiple injuries into a single severity score. The first two requirements were addressed in 1971 with the publication of the first AIS manual. Although this initial effort included only 73 general injuries and did not address penetrating trauma, it did assign a severity to each injury varying from 1 (minor) to 6 (fatal). No attempt was made to create a comprehensive list of injuries, and no mechanism to summarize multiple injuries into a single score was proposed.

This inability to summarize multiple injuries occurring in a single patient soon proved problematic and was addressed by Baker and colleagues in 1974 when they proposed the ISS. This score was defined as the sum of the squares of the highest AIS grade in each of the three (of six) most severely injured body areas:

Because each injury was assigned an AIS severity from 1 to 6, the ISS could assume values from 0 (uninjured) to 75 (severest possible injury). A single AIS severity of 6 (fatal injury) resulted in an automatic ISS of 75. This scoring system was tested in a group of 2128 automobile accident victims. Baker concluded that 49% of the variability in mortality was explained by this new score, a substantial improvement over the 25% explained by the previous approach of using the single worst-injury severity.

Both the AIS dictionary and the ISS score have enjoyed considerable popularity over the past 30 years. The fifth revision of the AIS⁹ has recently been published, and now includes over 2000 individual injury descriptors. Each injury in this dictionary is assigned a severity from 1 (slight) to 6 (unsurvivable), as well as a mapping to the Functional Capacity Index (a quality-of-life measure).¹⁰ The ISS has enjoyed even greater success—it is virtually the only summary measure of trauma in clinical or research use, and has not been modified in the 30 years since its invention.

Despite their past success, both the AIS dictionary and the ISS score have substantial shortcomings. The problems with AIS are twofold. First, the severities for each of the 2000 injuries are consensus derived from committees of experts and not simple measurements. Although this approach was necessary before large databases of injuries and outcomes were available, it is now possible to accurately measure the severity of injuries on the basis of actual outcomes. Such calculations are not trivial, however, because patients typically have more than a single injury, and untangling the effects of individual injuries is a difficult mathematical exercise. Using measured severities for injuries would correct the inconsistent perceptions of severity of injury in various body regions first observed by Beverland and Rutherford¹¹ and later confirmed by Copes et al.¹² A second difficulty is that AIS scoring is expensive, and therefore is done only in hospitals with a zealous commitment to trauma. As a result, the experiences of most non-trauma center hospitals are excluded from academic discourse, thus making accurate demographic trauma data difficult to obtain.

The ISS has several undesirable features that result from its weak conceptual underpinnings. First, because it depends on the AIS dictionary and severity scores, the ISS is heir to all the difficulties outlined previously. But the ISS is also intrinsically flawed in several ways. By design, the ISS allows a maximum of three injuries to contribute to the final score, but the actual number is often fewer. Moreover, because the ISS allows only one injury per body region to be scored, the scored injuries are often not even the three most severe injuries. By considering less severe injuries, ignoring more severe injuries, and ignoring many injuries altogether, the ISS loses considerable information. Baker herself proposed a modification of the ISS, the new ISS (NISS¹³), which was computed from the three worst injuries, regardless of the body region in which they occurred. Unfortunately, the NISS did not improve substantially upon the discrimination of ISS.

The ISS is also flawed in a mathematical sense. Although it is usually handled statistically as a continuous variable, the ISS can assume only integer values. Further, although its definition implies that the ISS can at least assume all integer values throughout its range of 0 to 75, because of its curious sum-of-one (or two or three) square construction, many integer values can never occur. For example, 7 is not the sum of any three squares, and therefore can never be an ISS score. In fact, only 44 of the values in the range of ISS can be valid ISS scores, and half of these are concentrated between 0 and 26. As a final curiosity, some ISS values are the result of one, two, or as many as 28 different AIS combinations. Overall, the ISS is perhaps better thought of as a procedure that maps the 84 possible combinations of three or fewer AIS injuries into 44 possible scores that are distributed between 0 and 75 in a nonuniform way.

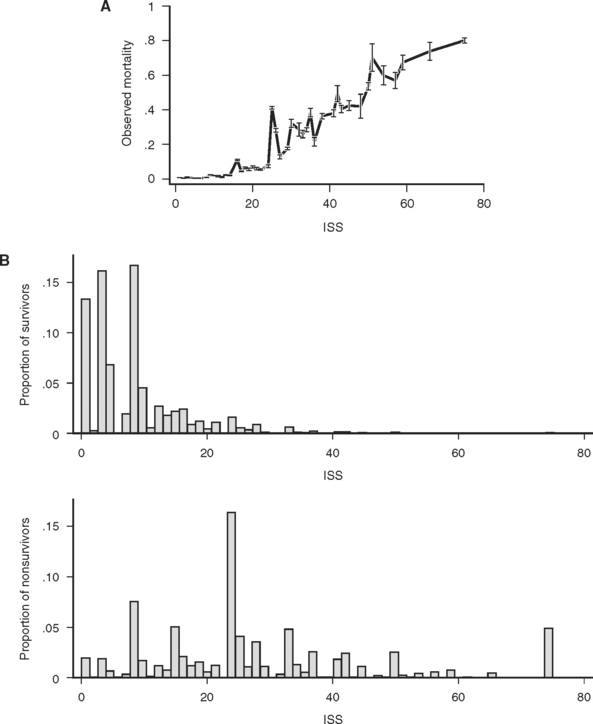
The consequences of these idiosyncrasies for the ISS are severe, as an examination of the actual mortality for each of 44 ISS scores in a large data set (691,973 trauma patients contributed to the National Trauma Data Bank [NTDB]¹⁴) demonstrates. Mortality does not increase smoothly with increasing ISS, and, more troublingly, for many pairs of ISS scores, the higher score is actually associated with a lower mortality (Figure 1A). Some of these disparities are striking: patients with ISS scores of 27 are four times less likely to die than patients with ISS scores of 25. This anomaly occurs because the injury subscore combinations that result in an ISS of 25 (5,0,0 and 4,3,0) are, on average, more likely to be fatal than the injury subscore combinations that result in and ISS of 27 (5,1,1 and 3,3,3). (Kilogo et al.¹⁵ note that 25% of ISS scores can actually be the result of two different subscore combinations, and that these subscore combinations usually have mortalities that differ by over 20%.)

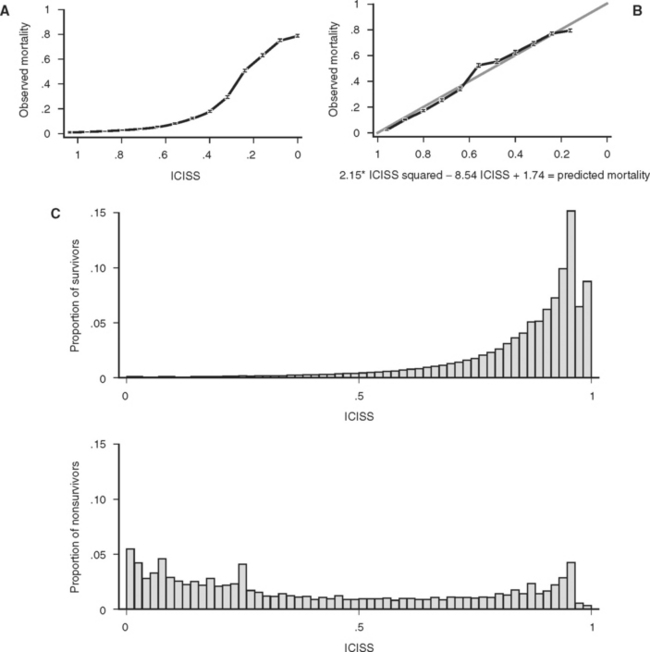
Figure 1 (A) Survival as a function of ICD-9 Injury Scoring System (ICISS) score (691,973 patients from the National Trauma Data Bank [NTDB]). (B) Survival as a function of ICISS score mathematically transformed by the addition of an ICISS² term (a “calibration curve”). Note that although this transformation does not add information (or change the discrimination [receiver operation characteristic value]) of the model, it does substantially improve the calibration of the model (691,973 patients from the NTDB). (C) ICISS scores presented as paired histograms of survivors (above) and nonsurvivors (691,973 patients from the NTDB).

Despite these dramatic problems, the ISS has remained the preeminent scoring system for trauma. In part this is because it is widely recognized, easily calculated, and provides a rough ordering of severity that has proven useful to researchers. Moreover, the ISS does powerfully separate survivors from nonsurvivors, as matched histograms of ISS for survivors and fatalities in the NTDB demonstrate (Figure 1B), with an ROC of 0.86.

The idiosyncrasies of ISS have prompted investigators to seek better and more convenient summary measures of injury. Champion and coworkers¹⁶ attempted to address some of the shortcomings of ISS in 1990 with the AP, later modified to become the modified AP (mAP).¹⁷ The AP used the AIS dictionary of injuries, and assigned all AIS values greater than 2 to one of three newly defined body regions (head/brain/spinal, thorax/neck, other). Injuries were combined within body region using a Pythagorean distance model, and these values were then combined as a weighted sum. Although the discrimination of the AP and mAP improved upon the ISS, this success was purchased at the cost of substantially more complicated calculations, and the AP and mAP have not seen wide use.

Osler and coworkers in 1996 developed an injury score based upon the ICD-9 lexicon of possible injuries. Dubbed ICISS (ICD-9 Injury Severity Score), the score was defined as the product of the individual probabilities of survival for each injury a patient sustained.

These empiric “survival risk ratios” were in turn calculated from a large trauma database. ICISS was thus by definition a continuous predictor bounded between 0 and 1. ICISS provided better discrimination between survivors and nonsurvivors than did ISS, and also proved better behaved mathematically: The probability of death uniformly decreases as ICISS increases (Figure 1A), and ICISS powerfully separates survivors from nonsurvivors (Figure 1C). A further advantage of the ICISS score is that it can be calculated from hospital discharge data, and thus the time and expense of AIS coding are avoided. This coding convenience has the salutary effect of allowing the calculation of ICISS from administrative data sets, and thus allows injury severity scoring for all hospitals. A score similar to ICISS but based on the AIS lexicon, Trauma Registry Abbreviated Injury Scale (TRAIS),¹⁸ has been described and has performance similar to that of ICISS. Because ICISS and TRAIS share a common structure, it is likely that they will allow comparisons to be made between data sets described in the two available injury lexicons, AIS and ICD-9.

Other ICD-9-based scoring schemes have been developed which first map ICD-9 descriptors into the AIS lexicon,¹⁹ and then calculate AIS-based scores (such as ISS or AP). In general, power is lost with such mappings because they are necessarily imprecise, and thus this approach is only warranted when AIS-based scores are needed but only ICD-9 descriptors are available.

Many other scores have been created. Perhaps the simplest was suggested by Kilgo and coworkers,¹⁸ who noted that the survival risk ratio for the single worst injury was a better predictor of mortality than several other models they considered that used all the available injuries. This is a very interesting observation, because it seems unlikely that ignoring injuries should improve a model’s performance. Rather, Kilgo’s observation seems to imply that most trauma scores are miss-specified, that is, they use the information present in the data suboptimally. Much more complex models, some based on exotic mathematical approaches such as neural networks²⁰ and classification and regression trees have also been advocated, but have failed to improve the accuracy of predictions.

To evaluate the performance of various anatomic injury models, their discrimination and calibration must be compared using a common data set. The largest such study was performed by Meredith et al.,²¹ who evaluated nine scoring algorithms using the 76,871 patients then available in the NTDB. Performance of the ICISS and AP were found to be similar, although ICISS better discriminated survivors from nonsurvivors while the AP was better calibrated. Both of these more modern scores dominated the older ISS, however. Meredith and colleagues²¹ concluded that “ICISS and APS provide improvement in discrimination relative to … ISS. Trauma registries should move to include ICISS and the APS. The ISS … performed moderately well and (has) bedside benefits.”

MEASURING PHYSIOLOGIC INJURY

Accurate outcome prediction depends on more than simply reliable anatomic injury severity scoring. If we imagine two patients with identical injuries (e.g., four contiguous comminuted rib fractures and underlying pulmonary contusion), we would predict an equal probability of survival until we are informed that one patient is breathing room air comfortably while the other is dyspneic on a 100% O₂ rebreathing mask and has a respiratory rate of 55. Although the latter patient is not certain to die, his chances of survival are certainly lower than those of the patient with a normal respiratory rate. Although obvious in clinical practice, quantification of physiologic derangement has been challenging.

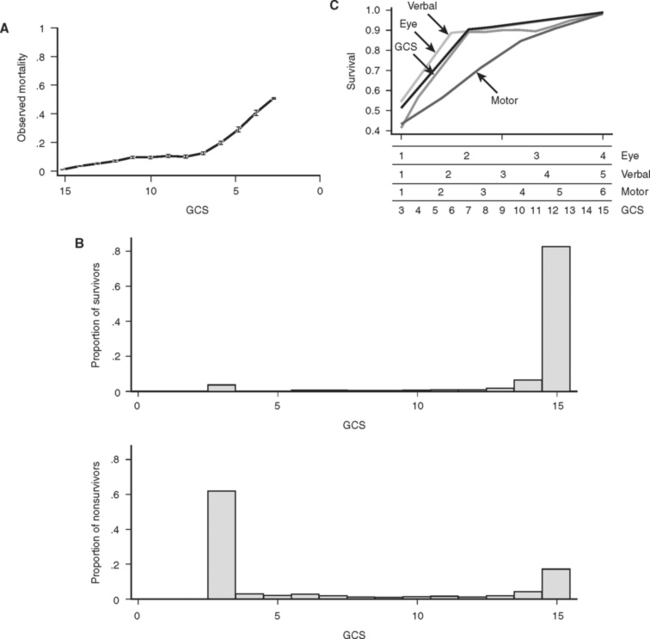
Basic physiologic measures such as blood pressure and pulse have long been important in the evaluation of trauma victims. More recently, the Glasgow Coma Score (GCS) has been added to the routine trauma physical exam. Originally conceived over 30 years ago as measure of the “depth and duration of impaired consciousness and coma,”²² the GCS is defined as the sum of coded values that describe a patient’s motor (1–6), verbal (1–5), and eye (1–4) levels of response to speech or pain. As defined, the GCS can take on values from 3 (unresponsive) to 15 (unimpaired). Unfortunately, simply summing these components obscures the fact that the GCS is actually the result of mapping the 120 different possible combinations of motor, eye, and verbal responses into 12 different scores. The result is a curious tri-phasic score in which scores of 7, 8, 9, 10, and 11 have identical mortalities. Fortunately, almost all of the predictive power of the GCS is present in its motor component, which has a very nearly linear relationship to survival^23,24 (Figure 3C). It is likely that the motor component alone could replace the GCS with little or no loss of performance, and it has the clear advantage that such a score could be calculated for intubated patients, something not possible with the three-component GCS because of its reliance on verbal response. Despite these imperfections, the GCS remains part of the trauma physical exam, perhaps because as a measure of brain function, the GCS assesses much more than simply the anatomic integrity of the brain. Figure 3B shows that GCS powerfully separates survivors from nonsurvivors.

Figure 3 (A) Survival as a function of Glasgow Coma Score (GCS) (691,973 patients from the NTDB). (B) GCS scores presented as paired histograms of survivors (above) and nonsurvivors (below) (691,973 patients from the NTDB). (C) GCS scores (691,973 patients from the NTDB). Note that the eye and verbal subscores are not linear, and as a result the summed score GCS is also nonlinear. The motor score, by contrast, is quite linear.

Currently the most popular measure of overall physiologic derangement is the Revised Trauma Score. It has evolved over the past 30 years from the Trauma Index, through the Trauma Score to the RTS in common use today. The RTS is defined as a weighted sum of coded values for each of three physiologic measures: Glasgow Coma Scale (GCS), systolic blood pressure (SBP), and respiratory rate (RR). Coding categories for the raw values were selected on the basis of clinical convention and intuition (Table 1). Weights for the coded values were calculated using a logistic regression model and the Multiple Trauma Outcome Study (MTOS) data set. The RTS can take on 125 possible values between 0 and 7.84:

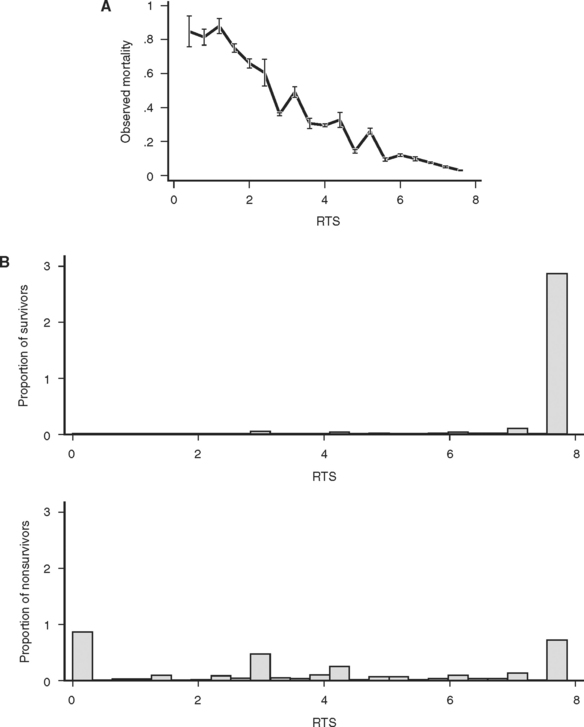
While the RTS is in common use, it has many shortcomings. As a triage tool, the RTS adds nothing to the vital signs and brief neurological examination because most clinicians can evaluate vital signs without mathematical “preprocessing.” As a statistical tool, the RTS is problematic because its additive structure simply maps the 125 possible combinations of subscores into a curious, nonmonotonic survival function (Figure 4A). Finally, the reliance of RTS on the GCS makes its calculation for intubated patients problematic. Despite these difficulties, the RTS discriminates survivors from nonsurvivors surprisingly well (Figure 4B). Nevertheless, it is likely that a more rigorous mathematical approach to an overall measure of physiologic derangement would lead to a better score.

Figure 4 (A) Survival as a function of Revised Trauma Score (RTS) (691,973 patients from the NTDB). (B) RTS presented as paired histograms of survivors (above) and nonsurvivors (below) (691,973 patients from the NTDB).

MEASURING PHYSIOLOGIC RESERVE AND COMORBIDITY RISK

Physiologic reserve is an intuitively simple concept that, in practice, has proved elusive. In the past, age has been used as a surrogate for physiologic reserve, and although this expedient has improved prediction slightly, age alone is a poor predictor of outcome. Using the example of two patients with four contiguous comminuted rib fractures and underlying pulmonary contusion, we would predict equal likelihood of survival until we are told that one patient is a 56-year-old triathlete, and the other is a 54-year-old with liver cirrhosis who is awaiting liver transplant and is taking steroids for chronic obstructive pulmonary disease (COPD). Although the latter patient is not certain to die, his situation is certainly more precarious than that of the triathlete. Remarkably, the TRISS method of overall survival prediction (see later) would predict that the triathlete is more likely to die. Although this scenario is contrived, it underscores the failure of age as a global measure of patient reserve. Not only does age fail to discriminate between “successful” and “unsuccessful” aging, it ignores comorbid conditions. Moreover, the actual effect of age is not a binary function as it is modeled in TRISS and is probably not linear either.

Although physiologic reserve depends on more than age, it is difficult to define, measure, and model the other factors that might be pertinent. Certainly compromised organ function may contribute to death following injury. Morris et al.²⁵ determined that liver cirrhosis, COPD, diabetes, congenital coagulopathy, and congenital heart disease were particularly detrimental following injury. Although many other such conditions are likely to contribute to outcome, the exact contribution of each condition will likely depend on the severity of the particular comorbidity in question. Because many of these illnesses will not be common in trauma populations, constructing the needed models may be difficult. Although the Deyo-Charlson scale²⁶ has been used in other contexts, it is at best an interim solution, with some researchers reporting no advantage to including it in trauma survival models.²⁷ As yet no general model for physiologic reserve following trauma is available.

MORE POWERFUL PREDICTIONS: COMBINING SEVERAL TYPES OF INFORMATION

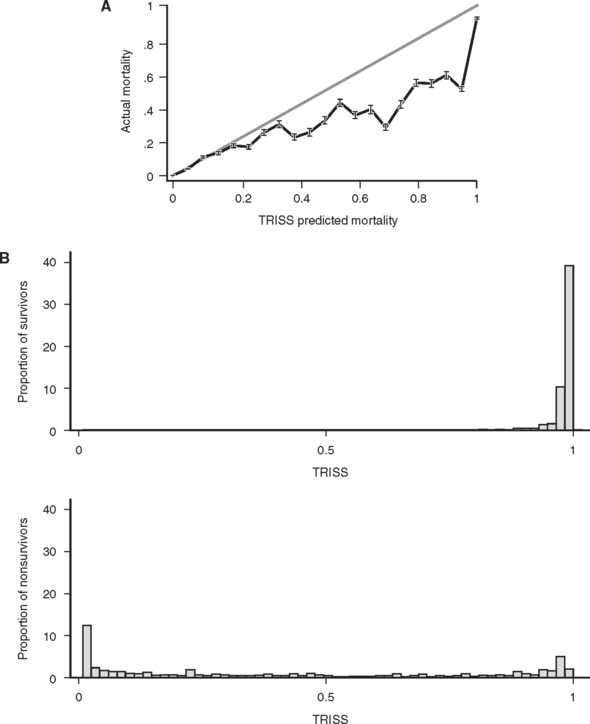
The predictive power of models is usually improved by adding more relevant information and more relevant types of information into the model. This was recognized by Champion et al.²⁸ in 1981, as they combined the available measures of injury (ISS), physiologic derangement (RTS), patient reserve (age as a binary variable: age >55 or ≤55), and injury mechanism (blunt/penetrating) into a single logistic regression model. Coefficients for this model were derived from the MTOS data set.²⁹ Called TRISS (TRauma score, Injury Severity Score age comorbidity index), this score was rapidly adopted and became the de facto standard for outcome prediction. Unfortunately, as was subsequently pointed out by its developers and others,³⁰ TRISS had only mediocre predictive power and was poorly calibrated. This is not surprising, because TRISS is simply the logit transformation of the weighted sum of three subscores (ISS, RTS, GCS), which are themselves poorly calibrated and in fact not even monotonically related to survival. Because of this “sum of subscores” construction, TRISS is heir to the mathematically troubled behavior of its constituent subscores, and as a result TRISS is itself not monotonically related to survival (Figure 5A). Although TRISS was conceived in hopes of comparing the performance of different trauma centers, the performance of TRISS has varied greatly when it was used to evaluate trauma care in other centers and other countries,^31,32 suggesting that either the standard of trauma care varied greatly, or, more likely, that the predictive power of TRISS was greatly affected by variation in patient characteristics (“patient mix”). Still another shortcoming is that because TRISS is based on a single data set (MTOS), its coefficients were “frozen in time” (in the context of the likelihood that success of trauma care improves over time). When new coefficients are calculated for the TRISS model, predictions improve, but it is unclear how often such coefficients should be recalculated, or what data set they should be based on. Thus, as a tool for comparing trauma care at different centers, TRISS seems fatally deficient.

Figure 5 (A) Survival as a function of TRISS score. Note that survival is a nonmonotonic function of the Trauma and Injury Severity Score (TRISS), and further, that for TRISS scores greater than 0.2, TRISS uniformly greatly overpredicts mortality, an anomaly that results in most trauma centers evaluated using TRISS appearing to be “above average,” a statistical impossibility (513,413 patients from the NTDB). (B) TRISS scores presented as paired histograms of survivors (above) and nonsurvivors (below) (513,413 patients from the NTDB).

In an attempt to address the shortcomings of TRISS, Champion et al. proposed a new score, ASCOT.¹⁶ ASCOT introduced a new measure of anatomic injury, the AP (see previous discussion), which was based on AIS severities of individual injuries, but summarized as the square root of the sum of squared injuries within three body regions, which were then weighed and summed. ASCOT also unbundled the RTS and included its newly coded components (GCS, RR, and SBP) as independent predictors in the model. Finally, age was modeled by decile over the age of 55. Despite these extensive and logical alterations, the discrimination of ASCOT only marginally improved over TRISS, and calibration was only slightly improved. Because ASCOT mixed anatomical and physiological measures of injury, the authors were unsure of the source of ASCOT’s modest improvement. The substantial increase in computational complexity further discouraged general adoption of ASCOT.³³ While some have advocated abandoning TRISS in favor of ASCOT, the data on which this view is based show no statistical difference in the discrimination of the two scores.³⁴ A difference in calibration was detected, but as we have argued, this is of less importance than discrimination.

STATISTICAL CONSIDERATIONS

Many statistical techniques are available to combine several predictor variables into a single outcome variable. Probably the best known is linear regression, which allows several linear predictor variables to be combined into a single continuous outcome measure. This technique might be appropriate for the prediction of such continuous outcome variables as hospital length of stay or total cost.

The outcome of overriding interest in injury severity scoring is the binary outcome survival/nonsurvival, however, and here logistic regression is the most commonly employed (although not necessarily optimal [Pepe et al.³⁵]) approach. Logistic regression provides a formula that predicts the likelihood of survival for any patient given the values for his or her predictor variables, typically summary measures of anatomic injury, physiologic derangement, and physiologic reserve. This formula is of the form:

Here,

and Anat_Inj, Phys_Inj, and Phys_Res are summary measures of anatomic injury, physiologic injury, and physiologic reserve, respectively.

The values of the coefficients b₀, b_{(anatomic injury)}, b_{(physiologic injury)}, and b_{(physiologic reserve)} are derived using a technique called maximum likelihood estimation. The details need not concern us, except to say that these coefficients are computed from a reference data set using an iterative procedure that requires a computer. The four coefficients thus capture much of the information present in the reference data set, including both the explicit information in the predictor variables and outcome, as well as implicit information included in other unmeasured variables of the data set. Logistic regression is extremely versatile, and can use both categorical and continuous variables as predictors. It does require that predictors be individually mathematically transformed to ensure that they are linear in the log odds of the outcome, however, and thus some statistical expertise is required to create and evaluate logistic models.

Despite the popularity and advantages of logistic regression, it is by no means the only approach to making a binary prediction from several predictor variables. Techniques such as neural networks and classification and regression trees have also been applied to medical prediction,^35,36 but in general prediction of mortality using these approaches is no better than standard logistic regression models.^37,38 These newer computer-intensive techniques have the further disadvantage that they are in general more difficult to implement and to explain. Occasional claims of remarkable success for such techniques²⁰ seem to be due to overfitting of the model under consideration rather than dramatically improved predictions. (Overfitting can be thought of as a technique’s “cheating” by memorizing the peculiarities of a data set rather than generalizing the relationship present between predictors and the outcome of interest. An overfit model may perform extremely well with the reference data set, but perform poorly when confronted with new data.)

IMPROVED PREDICTION IN TRAUMA SCORING

As argued previously, it is unlikely that a different statistical modeling technique will substantially improve outcome prediction. Thus, improvement must come from better measures of anatomic injury, physiologic injury, and physiologic reserve. In effect, because the “recipe” for trauma scoring is unlikely to get better, we must concentrate upon improving the “ingredients,” that is, the predictors used in our models. Fortunately, such improved measures are likely to be forthcoming, made possible by the advent of larger data sets and improved statistical methodology.

CONCLUSIONS

Injury severity scoring is still in a prolonged infancy. Although over 30 years old, the first-generation summary predictors (ISS, GCS, RTS, and TRISS) are still the standard scores in general use. The development of large trauma databases (e.g., NTDB) and better statistical software have now allowed us to see clearly the shortcomings of these early scoring techniques. In particular, the “summed subscores” approach to summary measures used in ISS, RTS, and GCS, as well as the overall survival predictor TRISS, uniformly results in probability of survival functions that are nonlinear, and, more problematically, often not monotonically related to mortality. Newer scoring systems that both better discriminate survivors from nonsurvivors and have better statistical properties have been developed (e.g., ICISS), but have failed to replace the first-generation scores. In part this is because the second generation of scores has not performed dramatically better than the older scores, and in part this is because the older scores are so firmly entrenched. Perhaps the most important reason for this inertia is that scores have as yet found no real use except in the arena of trauma research where scores that provide a rough ordering of injury severity have been adequate. However, if provider report cards, patient referrals, center certification, and revenue distribution come to depend on objective measures of the success of trauma care, it is likely that trauma scoring will elicit much greater interest. Even if reliable trauma scores are developed and adopted, the statistical challenge of comparing providers must not be underestimated.

We should continue to pursue improved trauma scores because we will learn much in the process, and substantially improved scoring systems may emerge. However, we must acknowledge that scoring systems cannot be perfect, and may never be powerful enough to be clinically useful or meet the perceived needs of monitoring organizations. We must have the courage to resist demands that injury severity scoring systems be extended into areas where they would detract from intelligent discourse or damage clinical practice until they are robust enough to perform reliably.