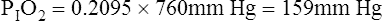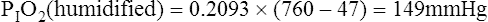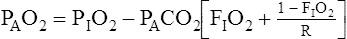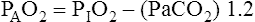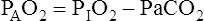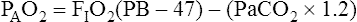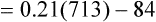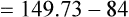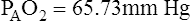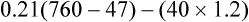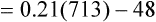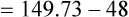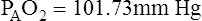Gas Diffusion
After reading this chapter, you will be able to:
• Differentiate between diffusion and bulk gas flow
• Use the alveolar gas equation
• Explain why the respiratory exchange ratio affects the calculation of alveolar oxygen pressure (PAO2)
• Identify the factors that affect diffusion, as illustrated by Fick’s law
• Use Graham’s law and Henry’s law to explain the differences in oxygen (O2) and carbon dioxide (CO2) diffusion rates in the lung
• Explain why O2 transfer from lung to blood is perfusion limited, whereas carbon monoxide (CO) transfer is diffusion limited
• Explain why CO and not O2 is the test gas normally used for measuring the diffusion capacity of the lung
• Explain how diffusion capacity is measured in a pulmonary function laboratory
• Correlate disease entities with the abnormal processes that decrease diffusion rate
• Explain why the diffusion capacity of the lung for carbon monoxide (DLCO) test detects oxygenation problems in the natural progression of disease before abnormalities in arterial blood oxygen pressure (PaO2) are evident
What is Diffusion?
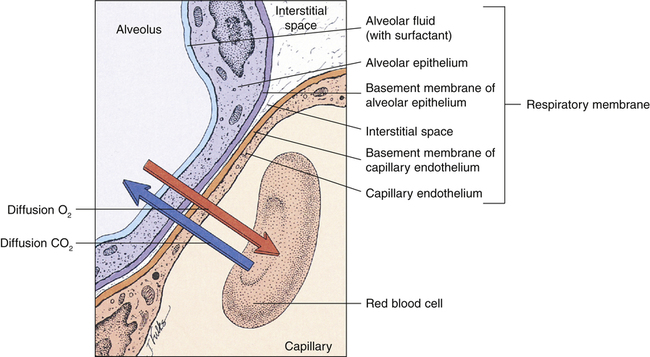
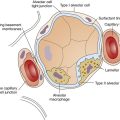
The high-speed random impacts of atmospheric air molecules on solid surfaces create the atmosphere’s pressure. Air is a gas mixture; the contribution that each gas makes to the atmospheric pressure is proportional to the number of its molecules present (i.e., each gas exerts its own partial pressure, as explained in Chapter 4). A gas diffuses from one point to another when there are differences in its partial pressures within the mixture; the direction of diffusion is always from high to low partial pressure. When no partial pressure difference exists for any gas throughout the mixture, equilibrium is present. Individual gas partial pressure differences are called diffusion gradients. During diffusion, each gas in a mixture moves according to its own diffusion gradient. That is, two different gases may simultaneously diffuse in opposite directions because of oppositely oriented partial pressure gradients. This occurs for oxygen (O2) and carbon dioxide (CO2) across the alveolar capillary membrane (Figure 7-1).
Diffusion Gradients of Respiratory Gases
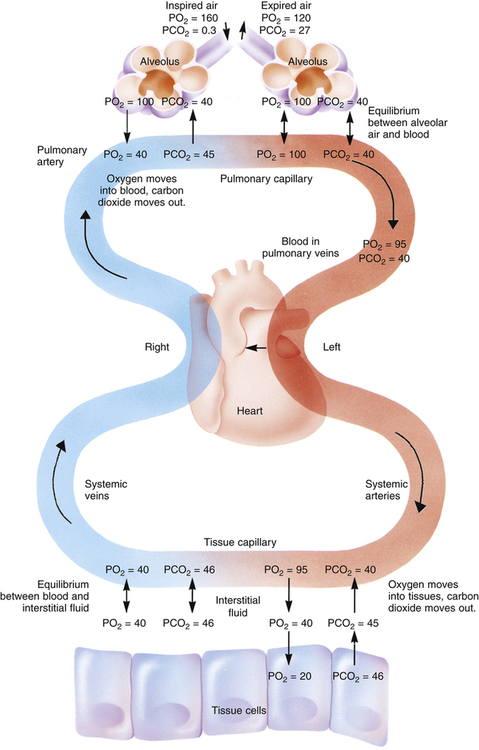
Figure 7-2 illustrates diffusion gradients between alveolar gas and blood and between blood and body tissues. Inspired air contains about 21% O2 and essentially no CO2. Inspired oxygen partial pressure (PIO2) is about 160 mm Hg, as the following calculation shows:
The diffusion gradient between alveolar gas and mixed venous blood is much larger for O2 than it is for CO2 (60 mm Hg vs. 6 mm Hg), as shown in Figure 7-2. At rest, these diffusion gradients transfer about 250 mL of O2 into the blood and 200 mL of CO2 into the alveoli each minute. By the time blood leaves the alveolar capillary, the PO2 and PCO2 of the blood have reached equilibrium with alveolar gases, even during exercise when blood flows very rapidly through the capillary. PO2 of blood entering the left atrium is never as high as PO2 of blood leaving the pulmonary capillaries (see Figure 7-2) because a small amount of deoxygenated bronchial venous blood mixes with capillary blood; this constitutes a normal anatomical shunt. Anatomical shunt is mostly responsible for the normal P(A-a)O2 (alveolar-to-arterial oxygen pressure difference). Left atrial blood normally flows unaltered into the systemic arteries.
Alveolar Air Equation
from the blood into alveoli each minute, PAO2 would be calculated by simply subtracting alveolar PCO2 (normally 40 mm Hg) from the result of equation 2. However, O2 diffuses out of the alveolus at a greater rate than CO2 diffuses into the alveolus. At rest, pulmonary capillary blood removes about 250 mL per minute of O2 from the alveoli, replacing it with only 200 mL per minute of CO2. The ratio of alveolar CO2 excretion (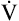 CO2) to blood oxygen uptake (
CO2) to blood oxygen uptake (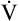 O2) is called the respiratory exchange ratio (R), and its value is normally about 0.8 (
O2) is called the respiratory exchange ratio (R), and its value is normally about 0.8 (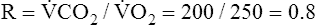 ).
).
Examination of equation 3 shows that higher FIO2 values require progressively smaller correction factors; at 100% inspired oxygen (FIO2 = 1.0), no correction is needed. A sufficiently accurate equation for clinical use is a simplified form of equation 3 for patients breathing an FIO2 of 0.60 or less. This is shown as follows:1
For FIO2 values greater than 0.60, a sufficiently accurate clinical equation is as follows:1
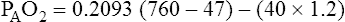

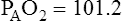
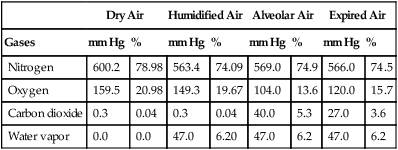
Table 7-1 summarizes respiratory gas partial pressures at sea level in dry inspired air, humidified (tracheal) air, alveolar air, and mixed expired air. Expired gas PO2, PCO2, and PN2 differ from alveolar values because expired air contains dead space gas mixed with alveolar gas.
TABLE 7-1
Partial Pressures of Gases at Sea Level
| Dry Air | Humidified Air | Alveolar Air | Expired Air | |||||
| Gases | mm Hg | % | mm Hg | % | mm Hg | % | mm Hg | % |
| Nitrogen | 600.2 | 78.98 | 563.4 | 74.09 | 569.0 | 74.9 | 566.0 | 74.5 |
| Oxygen | 159.5 | 20.98 | 149.3 | 19.67 | 104.0 | 13.6 | 120.0 | 15.7 |
| Carbon dioxide | 0.3 | 0.04 | 0.3 | 0.04 | 40.0 | 5.3 | 27.0 | 3.6 |
| Water vapor | 0.0 | 0.0 | 47.0 | 6.20 | 47.0 | 6.2 | 47.0 | 6.2 |
Modified from Seeley RR, Stephens TD, Tate P: Anatomy & physiology, ed 3, New York, 1995, McGraw-Hill.
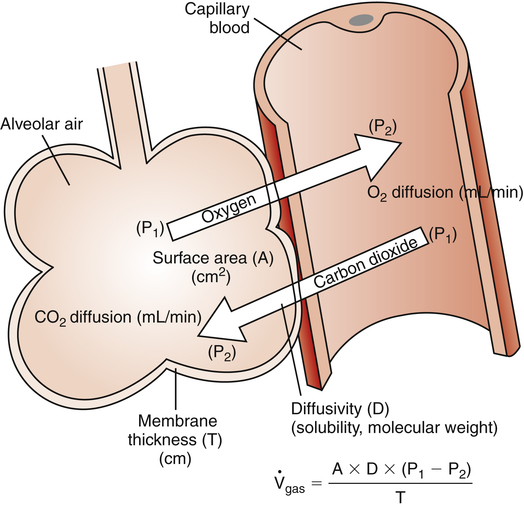
Laws Governing Diffusion
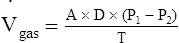
In this equation the following are represented:
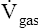 represents the volume of gas diffusing through the membrane per minute (mL per minute).
represents the volume of gas diffusing through the membrane per minute (mL per minute).
A represents the surface area of the membrane available for diffusion (cm2).
D represents the diffusion coefficient (D), or diffusivity, of a particular gas. It is directly proportional to the gas solubility (sol) but inversely proportional to the square root of the gas molecular weight (mw):
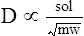
P1 − P2 represents the partial pressure difference across the membrane (i.e., diffusion pressure gradient [mm Hg]).
T represents the membrane thickness, or diffusion path distance (cm).
This equation states that 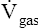 increases if there are increases in the membrane surface area, gas diffusivity, or diffusion pressure gradient. The diffusion rate decreases if membrane thickness increases. Doubling the membrane surface area or diffusion pressure gradient doubles the overall diffusion rate; doubling the membrane thickness reduces the diffusion rate by half. Figure 7-3 illustrates the factors involved in Fick’s law.
increases if there are increases in the membrane surface area, gas diffusivity, or diffusion pressure gradient. The diffusion rate decreases if membrane thickness increases. Doubling the membrane surface area or diffusion pressure gradient doubles the overall diffusion rate; doubling the membrane thickness reduces the diffusion rate by half. Figure 7-3 illustrates the factors involved in Fick’s law.
Physical Gas Characteristics and Diffusion
O2 and CO2 diffuse through gaseous and liquid phases in the lung; the alveolar capillary membrane (see Figure 7-1) is a liquid barrier. Light gases diffuse more rapidly than heavier gases, and highly soluble gases diffuse through liquids more rapidly than less soluble gases. The rate of gas diffusion in the lung is inversely proportional to its molecular weight and directly proportional to its solubility; the diffusion coefficient in Fick’s law is derived from these two factors. Specifically, the gas diffusion rate is inversely proportional to the square root of its gram molecular weight (gmw) (Graham’s law). Relative rates of diffusion for O2 (molecular weight = 32) and CO2 (molecular weight = 44) in a gaseous medium are as follows:
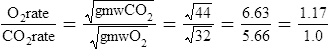
Because O2 is a lighter molecule, it diffuses through a gas medium 1.17 times faster than CO2.
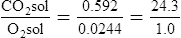
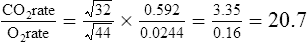
Limitations of Oxygen Diffusion
Effects of the Partial Pressure Gradient and Capillary Blood Transit Time on Gas Equilibrium
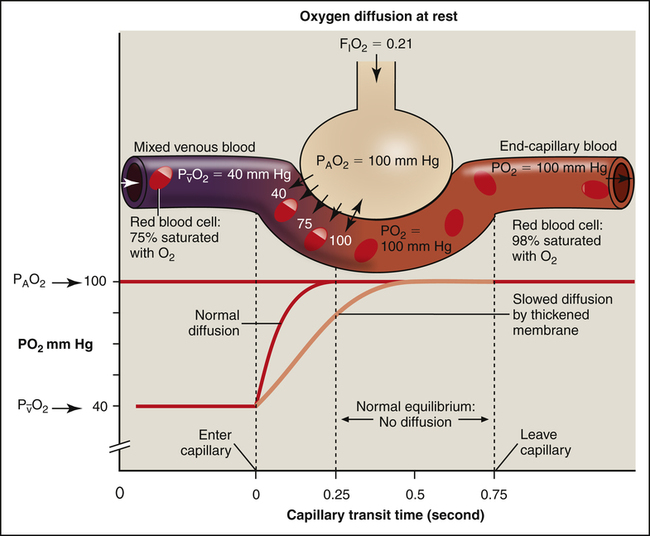
At a resting cardiac output, a red blood cell spends about 0.75 second traveling through the pulmonary capillary. Normally, the equilibrium between alveolar gas and capillary blood PO2 occurs within 0.25 second, or about one third of the distance through the capillary (Figure 7-4, dark curved line). The time to reach equilibrium may be prolonged if alveolar capillary membranes are thickened (light curved line in Figure 7-4). Even so, equilibrium is virtually always achieved at rest. The rate of diffusion is rapid at first when the partial pressure gradient across the alveolar capillary membrane is greatest. The diffusion rate continuously slows as the partial pressure gradient diminishes (notice the shape of the PO2 curve [dark line] in Figure 7-4) until diffusion completely ceases at equilibrium. Thus, during the last two thirds of travel through the pulmonary capillary, no diffusion normally occurs.
If a healthy person exercises vigorously at a high altitude, where atmospheric PO2 is very low, the O2 diffusion gradient may be so low that O2 cannot diffuse across the alveolar capillary membrane fast enough to establish equilibrium during the shortened capillary transit time. Alternatively, if disease thickens the alveolar capillary membrane, the diffusion rate across the membrane may be slowed enough to prevent complete O2 equilibrium by the time blood leaves the capillary. In the clinical setting, this situation rarely occurs at rest, even in severe lung disease.2 However, exercise immediately exposes the diffusion abnormality problem because it shortens the blood’s transit time through the capillary, making it likely that alveolar and capillary O2 equilibrium never occurs (Figure 7-5). Patients with thickened alveolar capillary membranes are most likely to show evidence of O2 diffusion impairment during exercise.3
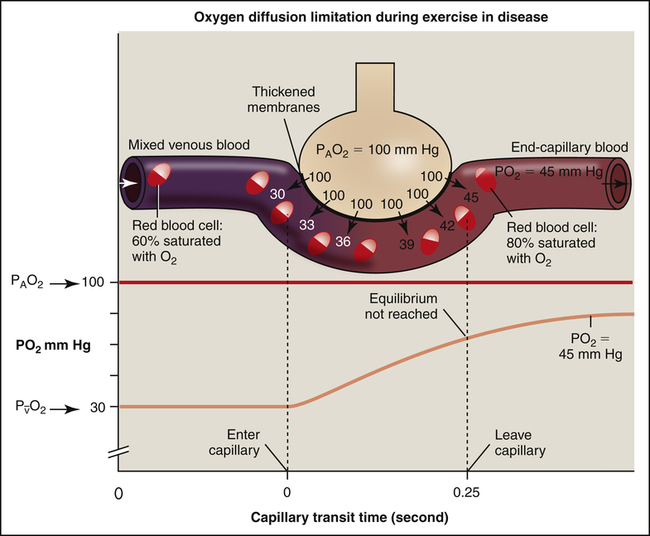
Perfusion and Diffusion Limitations to Oxygen Transfer
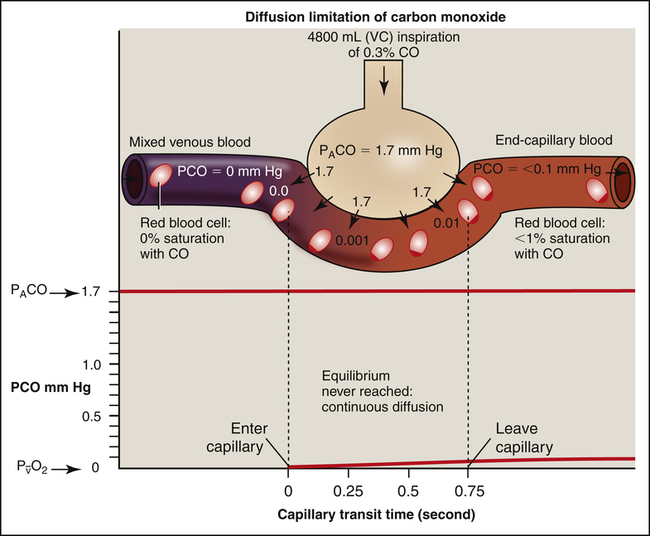
Figure 7-4 shows that diffusion normally stops when O2 equilibrium is reached between the alveolus and capillary, which occurs long before the blood travels the length of the capillary. If blood flow (perfusion) increases, more O2 leaves the lung each minute because the O2-saturated blood moves out of the capillary more quickly, which means deoxygenated blood enters more quickly to take up more O2. Therefore the O2 diffusion rate through the alveolar-capillary membrane is normally perfusion limited (see Figure 7-4); that is, a change in blood flow rate alters the number of O2 molecules that cross the alveolar-capillary membrane each minute. If O2 equilibrium between the alveolus and capillary never occurs because of thickened membranes, O2 transfer is truly diffusion limited. In such an instance, it is the alveolar capillary membrane, not blood flow rate, that influences the O2 transfer rate (see Figure 7-5).
If one wishes to evaluate the extent to which the alveolar capillary membrane itself impedes the diffusion rate (milliliters per minute of O2 transfer per millimeters of mercury pressure gradient), one should not measure the O2 diffusion rate because it is affected by blood flow rate. Instead, one should measure the diffusion rate of a gas that never reaches equilibrium between alveolar gas and capillary blood, even in resting conditions. In other words, the blood’s capacity for this gas should be so great that the gas cannot diffuse across the membrane fast enough to saturate the blood to capacity before it leaves the capillary. For such a gas, the only factor that limits diffusion is the resistance of the alveolar capillary membrane itself. Carbon monoxide (CO) is the ideal gas for this kind of measurement because blood can absorb it at a greater rate than CO can diffuse across the alveolar capillary membrane, even under resting conditions. For this reason, CO is always diffusion limited. Figure 7-6 illustrates the diffusion-limited characteristics of CO. All events that are illustrated in Figure 7-6 occur at rest; increased blood flow cannot result in greater CO uptake because CO is already diffusing through the alveolar-capillary membrane at its maximum rate. For this reason, CO is commonly used in pulmonary function laboratories to evaluate the lung’s true diffusion capacity.
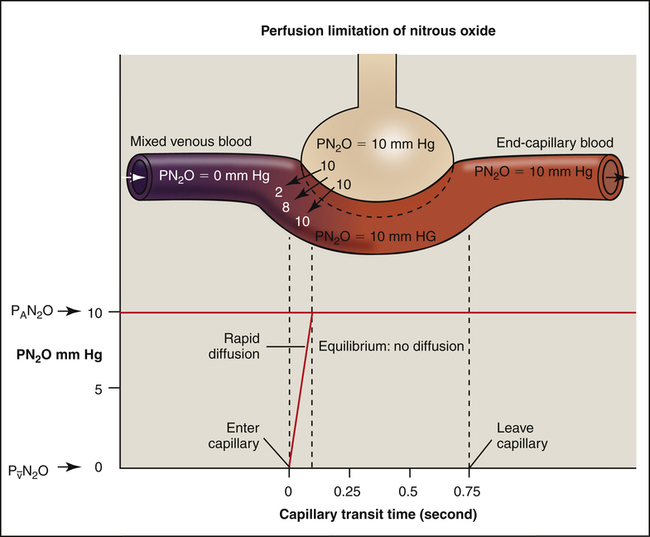
Hemoglobin in the blood makes O2 and CO much more soluble in whole blood than they are in the alveolar-capillary membrane fluid or the blood plasma. In contrast, a gas such as nitrous oxide (N2O), highly soluble in the alveolar-capillary membrane and plasma, does not chemically bind with hemoglobin; its solubility in whole blood is much less than that of CO or O2. If N2O is inhaled, the pulmonary capillary blood reaches its maximum capacity for N2O almost instantly (Figure 7-7). N2O partial pressures across the alveolar capillary membrane reach equilibrium in the first one twentieth of the distance along the capillary.
Diffusion Path Length
The distance for diffusion includes the entire path length from alveolar gas to the hemoglobin in the red blood cell. It was originally thought that the alveolar capillary membrane was the only important rate-limiting barrier to diffusion; it is now known that the red blood cell membrane and rate of O2 combined with hemoglobin limit the lung’s O2 uptake to the same extent as the alveolar-capillary membrane.4 The total diffusion path distance is normally less than 0.1 µ and includes the following (see Figure 7-1): (1) surfactant layer that is lining the alveolar surface, (2) alveolar epithelium, (3) basement membrane of the alveolar epithelium, (4) extremely thin interstitial space, (5) basement membrane of the capillary endothelium, (6) capillary endothelium, (7) plasma, (8) red blood cell membrane, and (9) intracellular fluid bathing the hemoglobin molecule.
Various abnormal conditions can increase the diffusion path length, including the following: (1) fibrotic thickening of alveolar and capillary walls; (2) interstitial edema fluid, separating alveolar and capillary membranes; (3) fluid in the alveoli; (4) interstitial fibrotic processes that thicken the interstitial space; and (5) dilated, engorged capillaries, which allow red blood cells to flow side by side. Abnormalities that increase the distance for diffusion are rarely the cause of decreased end-capillary or arterial PO2 at rest. The major cause of resting hypoxemia in these patients is a mismatch between ventilation and blood flow.2 That is, the processes that increase diffusion distance generally decrease lung compliance, which decreases ventilation in these areas. Blood perfusing these underventilated areas tends to be inadequately oxygenated.
Measuring Diffusion Capacity
General Principles

Normal Values
Normal DLCO values in healthy individuals vary considerably depending on age, body size, and body position as explained in subsequent sections. A large cross-sectional study of healthy, never-smoking adult men and women in the United States yielded a mean DLCO of 26.4 mL/min/mm Hg (single breath testing method).5 The mean DLCO was about 33 mL/min/mm Hg in men and about 24 mL/min/mm Hg in women. The diffusion capacity of the lung for oxygen (DLO2) is obtained by multiplying DLCO by 1.23. A mean DLCO of 26 mL/min/mm Hg yields a normal DLO2 of about 32 mL/min/mm Hg. It may seem odd that DLO2 is greater than DLCO, considering the much greater affinity of hemoglobin for CO than O2. This peculiarity is explained by the fact that O2 is more soluble than CO in the alveolar capillary membrane and the plasma and diffuses more rapidly. The fact that hemoglobin has 210 times greater affinity for CO than O2 simply means that at a given partial pressure (PCO or PO2), the hemoglobin carries more CO than O2. This fact is unrelated to O2 and CO diffusion rate across the alveolar capillary membrane, which is determined by molecular weight and solubility coefficients.
Factors Affecting Measured Carbon Monoxide Diffusion in the Lung
Body Size
Alveolar Partial Pressure of Oxygen and Partial Pressure of Carbon Dioxide
Increased PAO2 is associated with decreased DLCO because in the blood O2 competes with CO for binding sites on the hemoglobin molecule. In other words, the rate of CO uptake by hemoglobin is hindered by increased arterial PO2 values but is enhanced by decreased arterial PO2 values. People with severe hypoxia have higher DLCO values because of this phenomenon and because hypoxia increases cardiac output, pulmonary blood flow, and capillary recruitment and distention.4 This phenomenon also explains why elevated PACO2 increases DLCO; an elevated PACO2 means hypoventilation is present, which means PAO2 is of necessity also low.
Pulmonary Diseases
Box 7-1 lists conditions that decrease diffusion capacity. DLCO is useful in differentiating emphysema from other obstructive diseases not associated with destroyed alveolar architecture, such as chronic bronchitis and asthma. Asthma is often associated with an increased DLCO. An explanation may be that high inspiratory resistance created by narrowed airways increases negative intrathoracic pressure during maximal inspiration of the test gas, which increases the gas diffusion pressure gradient and the blood flow in lung apices.6
Clinical Use of Carbon Monoxide Diffusion in the Lung
pulmonary capillary distance, a 50% reduction in DLCO can exist without affecting end-capillary and arterial PO2. In this sense, the DLCO test is more sensitive than the PaO2 to potential O2 transfer problems (i.e., as disease progresses, DLCO becomes abnormal before PaO2). Impairment of diffusion across the alveolar capillary membrane is only one mechanism that can cause arterial hypoxemia. Many factors decrease PaO2 without affecting the diffusion path length or membrane surface area, such as ventilation–blood flow mismatches. The DLCO test can help clarify the mechanism of arterial hypoxemia; if DLCO is normal, diffusion impairment cannot be a contributing factor.