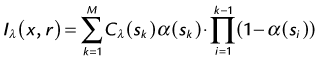CHAPTER 83 Basic Three-Dimensional Postprocessing in Computed Tomographic and Magnetic Resonance Angiography
The three-dimensional data acquired by computed tomography angiography (CTA) or magnetic resonance angiography (MRA) can be processed off-line using a variety of commercially available techniques that enable isolation and improved viewing of specific vascular segments and their anatomic relationships. The most popular and widely available postprocessing tools for CTA and MRA data are multiplanar reformation (MPR), maximum intensity projection (MIP), and volume rendering (VR).1–5 This chapter reviews these basic methods for postprocessing of CTA and MRA data, highlighting their strengths and pitfalls. For different clinical applications, the specific methods of highest value will vary. Individual techniques for various anatomic regions are covered elsewhere in this text.
MULTIPLANAR REFORMATION
MPR refers to the reconstruction of three-dimensional data into a new orientation. For example, a volumetric CTA data set acquired in the axial plane can be reconstructed for viewing in a coronal plane or a plane of any obliquity using MPR. MPR images can be reconstructed into linear (e.g., coronal, sagittal, axial, oblique; Figs. 83-1 and 83-2) or curved plane images (Fig. 83-3). The process does not change the original data or voxels. In the MPR process, interpolation is needed to rearrange data into a different coordinate system. Curved reformatting is useful for viewing tortuous vessels such as the coronary arteries on CTA because it unravels the tortuous segments for linear viewing of the vessel (i.e., straightens out the vessel in length). It is particularly useful for showing vascular detail in cross-sectional profile along the vessel length, facilitating characterization of stenoses or other intraluminal abnormalities. The pitfall is that manual definition of curved planes may not be accurate for actual measurements and is potentially a time-consuming process because operator interaction is often required. Automated curve detection methods can expedite processing but fail if there are image artifacts within the data (e.g., motion blurring or high-value nonvascular structures such as calcium on CTA). These may be erroneously labeled as vessel lumen, thereby introducing inaccurate curved vascular lumen reformation.
Nearest Neighbor Interpolation
Interpolation is an important concept in the context of image reconstruction. As demonstrated in Figure 83-4, a slice of an original acquired image is composed of known data points. In this example, the circles are known data grids. Triangles are points that need to be interpolated because of MPR needs. The left known data signal intensity (SI) value is SIa = 100, and right known signal intensity value is SIb = 100. The simplest interpolation is the nearest neighbor. In nearest neighbor interpolation, the new interpolated data point (i.e., triangle) is closer to the right data point, where SIb is, so the unknown interpolated signal intensity (SIi) is set to be the same as SIb, that is, SIi.
Linear Interpolation
Another simple method is linear interpolation. Using the same example as in Figure 83-4, the distance for the points are xa = 1, xi = 3, and xb = 4. The signal intensities for known points are SIa = 10 and SIb = 100. The interpolated value SIi for the triangle is linear interpolation as given by equation (1):
MAXIMUM INTENSITY PROJECTION
MIP is another common method for two-dimensional projectional viewing CTA and MRA three-dimensional data. In MIP, the highest signal intensity values are projected from the data encountered by a ray cast through an object to the viewer’s eye (Fig. 83-5). MIP is not averaging the average signal intensities from slice to slice along the projected axis (mean value); instead, it finds the highest value along a projection line and assigns that value to the pixel represented on the two-dimensional projected image. For CTA, the pixel values are in density or Hounsfield units; for MRA, the pixel values are in signal intensity. In this way, three-dimensional data can be collapsed into a two-dimensional projection image (see Fig. 83-2). MIP can be generated using the whole three-dimensional volume or a smaller subvolume (slab, or subvolume MIP; Figs. 83-6 and 83-7).
MIP is useful for projected viewing of CTA and MRA in views similar to conventional x-ray angiograms. MIP images provide the big picture but are often suboptimal for viewing specific segments that are tortuous, such as near vessel origins or bifurcations, where subvolume MIP may be more helpful, especially if there are overlapping vessels such as the celiac artery (Fig. 83-8). Furthermore, because it projects simply brightest value, full-volume or thick MIP processing does not provide depth perception because the three-dimensional data are collapsed for viewing of only the brightest values. Subvolume MIP provides planar viewing of thinner volumes versus single-voxel viewing using MPR but may also mask luminal abnormalities. With MIP, the pitfall is that of a loss in depth information. Therefore, MIP misrepresents anatomic spatial relationships in depth directions. Moreover, MIP shows only the highest intensity along the projected ray. A high-intensity mass such as calcification will obscure information from intravascular contrast material. Vessels with low signal intensity values may be partially or completely imperceptible on MIP images. Alternatively, the bright signal of the lumen may mask subtle detail such as an intimal tear in an arterial dissection.
VOLUME RENDERING
Volume rendering (VR) is a visualization technique that represents a three-dimensional CTA or MRA data set (see Figs. 83-2, 83-7, and 83-8) as an opaque or translucent fashion but preserves the depth information of the data set, which is not afforded by MIP reconstruction (Fig. 83-9). It has replaced most imaging applications such as surface rendering, with the notable exception of interior vessel analysis. VR assigns opacity values based on a percentage classification from 0% to 100% using a variety of computational techniques. It uses all acquired data, so it needs greater processing power than the other applications discussed. Once the data have been assigned percentages, each tissue is assigned a color and degree of transparency. Then, by casting simulated rays of light through the volume, VR generates a three-dimensional image. The color used in volume rendering is a pseudocolor, which does not represent the true optical color of the tissues. However, color enhances the human eyes’ ability to perceive depth relationships (see Fig. 83-3). On VR reconstruction, the three-dimensional data can be visualized using various degrees of opacity and transparency, which afford different viewing perspectives of the image data (Fig. 83-10).
The basic idea of volume rendering is to find the best approximation of the low-albedo volume rendering optical model that represents the relation between the volume intensity and opacity function and the intensity in the image plane. A common theoretical model on which VR algorithms are based is described in equation (2)6:
where α is the opacity samples along the ray and C is the local color values derived from the illumination model. All algorithms obtain colors and opacities in discrete intervals along a linear path and composite them in front to back order. The raw volume densities are used to index the transfer functions for color and opacity; thus, the fine details of the volume data can be expressed in the final image using different transfer functions.
KEY POINTS
 Three-dimensional data sets from CTA and MRA can be viewed using a variety of postprocessing tools, most commonly, multiplanar reformation, maximum intensity projection, and volume rendering.
Three-dimensional data sets from CTA and MRA can be viewed using a variety of postprocessing tools, most commonly, multiplanar reformation, maximum intensity projection, and volume rendering. MPR provides reconstructed viewing of three-dimensional data in an arbitrary plane that can be linear (e.g., axial, coronal, sagittal, oblique) or curved.
MPR provides reconstructed viewing of three-dimensional data in an arbitrary plane that can be linear (e.g., axial, coronal, sagittal, oblique) or curved.Cody DD. AAPM/RSNA physics tutorial for residents: topics in CT. Image processing in CT. Radiographics. 2002;22:1255-1268.
Fishman EK, Ney DR, Heath DG, et al. Volume rendering versus maximum intensity projection in CT angiography: what works best, when and why. Radiographics. 2006;26:905-922.
Calhoun PS, Kuszyk BS, Heath DG, et al. Three-dimensional volume rendering of spiral CT data: theory and method. Radiographics. 1999;19:745-764.
1 Lell MM, Anders K, Uder M, et al. New techniques in CT angriography. Radiographics. 2006;26:S45-S62.
2 Dalrymple NC, Prasad SR, Freckleton MW, Chintapalli KN. Informatics in radiology (infoRAD): introduction to the language of three-dimensional imaging with multidetector CT. Radiographics. 2005;25:1409-1428.
3 Cody DD. AAPM/RSNA physics tutorial for residents: topics in CT. Image processing in CT. Radiographics. 2002;22:1255-1268.
4 Fishman EK, Ney DR, Heath DG, et al. Volume rendering versus maximum intensity projection in CT angiography: what works best, when and why. Radiographics. 2006;26:905-922.
5 Calhoun PS, Kuszyk BS, Heath DG, et al. Three-dimensional volume rendering of spiral CT data: theory and method. Radiographics. 1999;19:745-764.
6 Levoy M. Efficient ray tracing of volume data. ACM Trans Graphics. 1990;9:245-261.

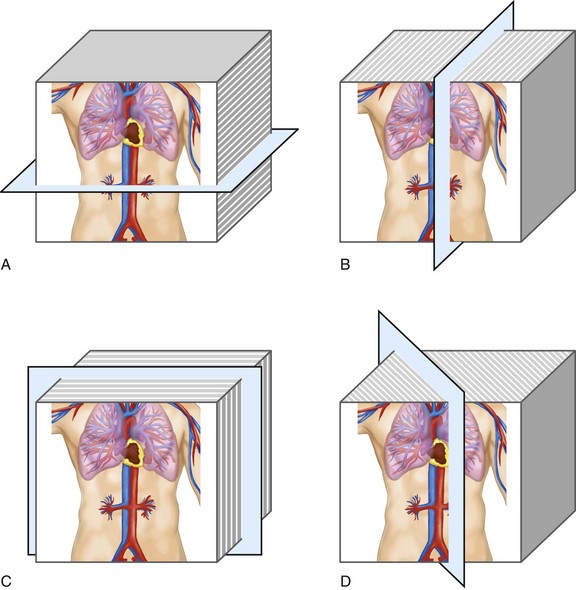
 FIGURE 83-1
FIGURE 83-1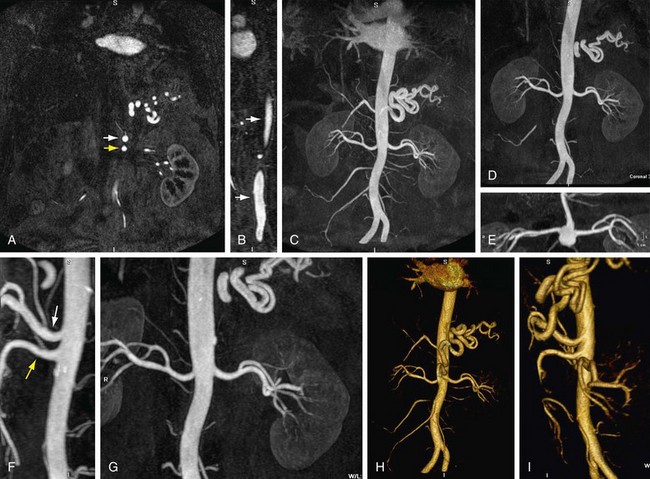
 FIGURE 83-2
FIGURE 83-2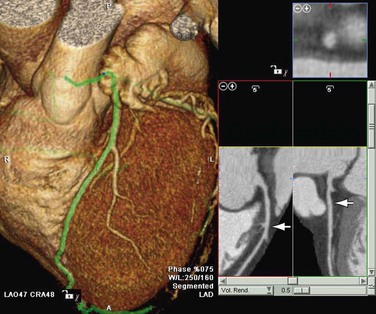
 FIGURE 83-3
FIGURE 83-3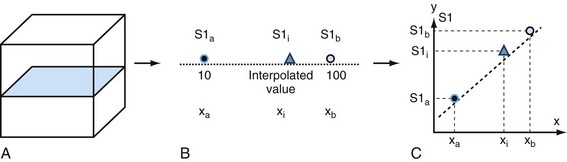
 FIGURE 83-4
FIGURE 83-4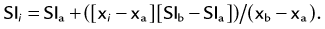
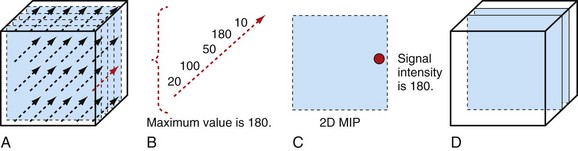
 FIGURE 83-5
FIGURE 83-5
 FIGURE 83-6
FIGURE 83-6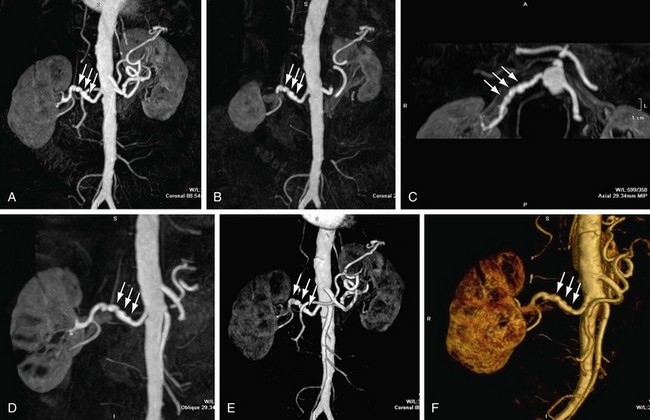
 FIGURE 83-7
FIGURE 83-7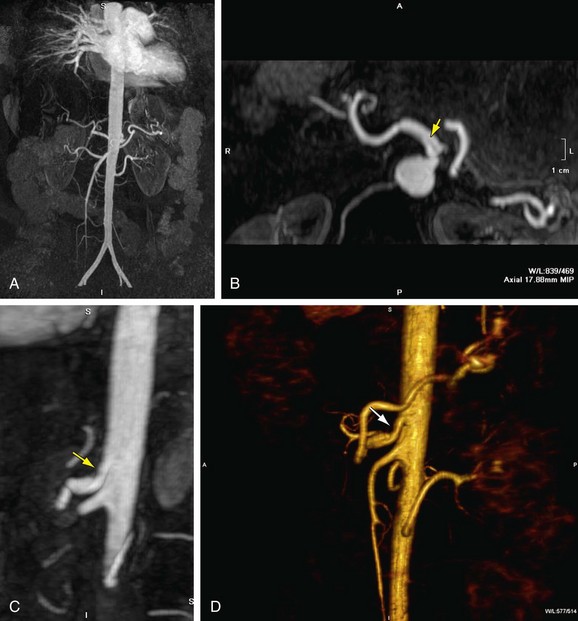
 FIGURE 83-8
FIGURE 83-8
 FIGURE 83-9
FIGURE 83-9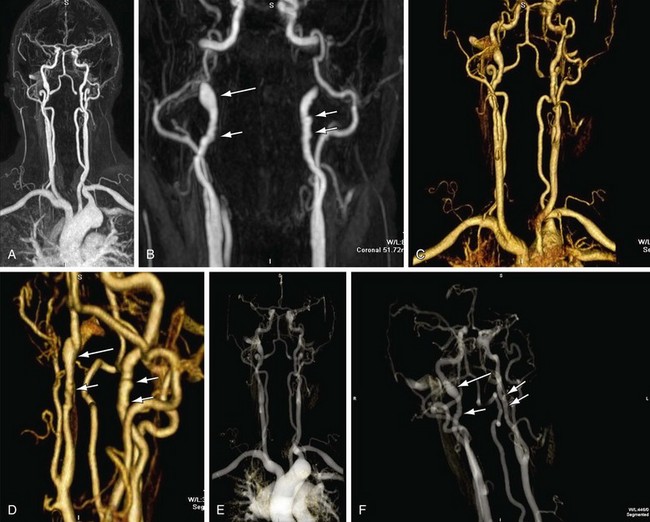
 FIGURE 83-10
FIGURE 83-10