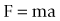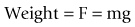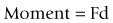Movements

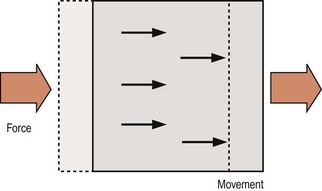
There are two types of motion that a bone may undergo: translation and rotation. The essence of translation is that every point on the bone moves in the same direction and to the same extent (Fig. 7.1). Translation occurs whenever a single force or a net single force acts on a bone, and any force that tends to cause translation is called a shear force.

Figure 7.1 Translation. A single net force causes all points in a body to move in parallel, in the same direction and to the same extent.

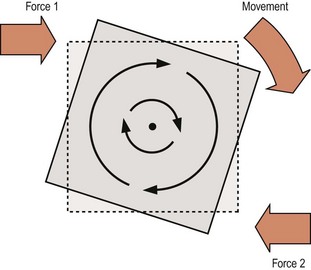
Rotation is characterised by all the points on a bone moving in parallel around a curved path centred on some fixed point. The points move in a similar direction but to different extents depending on their radial distance from the fixed point which is known as the centre of rotation (Fig. 7.2). Rotation occurs when two unaligned forces act in opposing directions on different parts of the bone, forming what is known as a force couple (see Fig. 7.2), and the net force tending to cause rotation is referred to as the torque. Depending on circumstances, torque may be the result of two opposed forces which may both be muscular actions, or they may be a muscular action and a ligamentous resistance, or they may be gravity opposed by either muscular action or ligamentous resistance.

Figure 7.2 Rotation. Two unaligned, opposite forces (a force couple) cause the points in a body to move around a stationary centre.

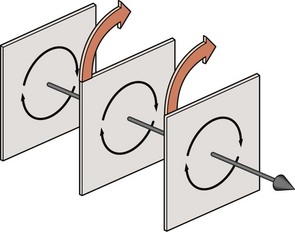
When a rotating bone is considered in three dimensions it can be seen that all the points throughout the bone can be grouped into individual planes that lie parallel to the direction of motion (Fig. 7.3). In each plane, the points move about a centre located in that plane, and when all the centres of all the planes are lined up they depict a straight line that forms what is known as the axis of rotation of the bone.

Figure 7.3 During rotation, the points in any plane of a body move around a centre located in that plane. A line formed by these centres is the axis of rotation of the body.

There is nothing special about an axis of rotation in a biological sense. The points along an axis of rotation do not have any unique biological properties. An axis of rotation is only a mathematical phenomenon created by the net effect of forces acting on a bone. For any rotation, it can be shown that there is a region where all opposing forces cancel out and no net force acts, and this will be the axis of rotation. The axis remains stationary because no net force acts on it. Meanwhile, all the points surrounding the axis are subjected to a net force, and motion will occur around the stationary axis. Thus, a formal definition of an axis of rotation can be ‘that region that does not move when two or more opposing, unaligned forces act on a bone’.

The location of any axis of rotation is not an intrinsic property of the bone that moves around it. It is a property of the forces that may happen to act on the bone, and different forces will create a different axis of rotation. So-called ‘normal’ axes of rotation occur only when, during repetitions of a movement, the same forces are consistently applied. With each repetition, the axis of rotation occurs consistently in the same place. However, if at any time one of the applied forces is altered, a new axis will occur.

Planes of movement

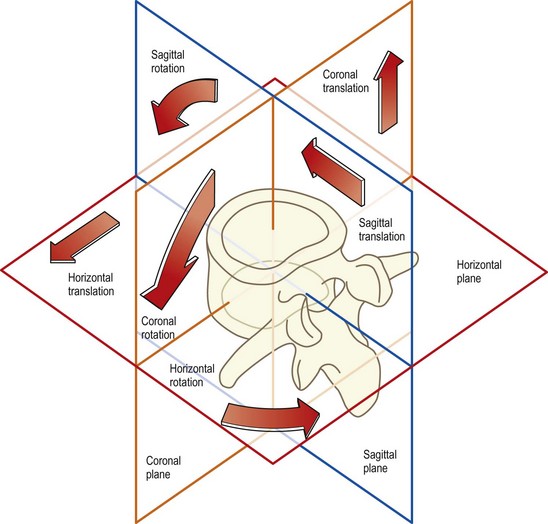
Both translation and rotation can occur in either of two opposite senses which can be variously defined according to circumstances or convention. For example, the motion can be upwards or downwards, forwards or backwards, clockwise or anticlockwise, and in some conventions positive (+) or negative (−). Furthermore, in three-dimensional space, translation or rotation can occur in any of three fundamental planes. In anatomical terms, these planes are the sagittal, coronal and horizontal planes (Fig. 7.4). Backward or forward rotations are movements in the sagittal plane, as are translations in the backward or forward direction. Side-bending is rotation in the coronal plane, and twisting is rotation in the horizontal plane. A sideways gliding movement across the horizontal plane would be horizontal translation, while movements up or down are described as coronal translations.

Figure 7.4 Planes and directions of motion: anatomical system.

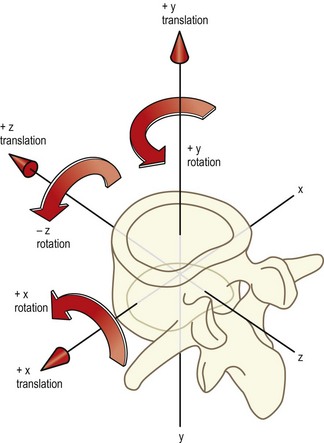
Biomechanists prefer to define movements in relation to three imaginary axes drawn through the body, which are labelled X, Y and Z.^1,2 The X axis passes sideways through the body; the Y axis passes through it vertically; and the Z axis passes through it from back to front (Fig. 7.5). Movements can then be described as along or around any particular axis. Thus, sagittal translation is translation along the Z axis; sideways gliding movements are translations along the X axis; and up and down movements are along the Y axis. Forward bending is rotation around the X axis; side-bending is rotation about the Z axis; and twisting movements are rotations around the Y axis. The key to this nomenclature lies in the prepositions used. Translations are movements along one of the axes while rotations are movements around one of the axes.

Figure 7.5 Axes and directions of motion: biomechanical system.

The advantage of the biomechanists’ convention is that the dimensions of movements are accurately and unambiguously defined. However, the terms ‘X’, ‘Y’ and ‘Z’ are unfamiliar and anonymous to all except to those who use them regularly. The terms ‘sagittal’, ‘coronal’ and ‘horizontal’ are somewhat more meaningful because of their use in other areas of anatomy, and these are the terms used in this text. In the anatomical system the movements are perceived to occur in or along the plane in question, irrespective of whether the movement is a translation or a rotation. For reference, the equivalence of various terms derived from the anatomical system, the biomechanists’ convention and colloquial vocabulary is shown in Table 7.1.

Table 7.1 Descriptive terms of motion. By convention, the direction of any rotation is defined according to the direction of movement of the most anterior point on the bone

Because of difficulties in appreciating the distinctions between translations and rotations in the horizontal and coronal planes, the term ‘axial’ has been introduced in Table 7.1. Thus, the term ‘axial rotation’ replaces ‘horizontal rotation’ to refer to rotation in the horizontal plane, i.e. around the long axis of the body. The term ‘axial translation’ replaces ‘coronal translation’ to refer to movement up or down, or along the long axis of the body, and to distinguish this movement from sideways translations in the horizontal plane, which are described as horizontal or lateral translations.

To specify the direction of axial translations, the terms ‘cephalad’, meaning towards the head, and ‘caudad’, meaning towards the tail, are used in Table 7.1. Although perhaps cumbersome and unfamiliar, these terms are accurate and applicable in all situations. The more familiar terms ‘upward’ and ‘downward’ are applicable for axial translations in the upright position but they are not strictly applicable in describing motions of vertebrae in patients who might be lying down. To overcome this difficulty, the more colloquial terms of ‘distraction’ and ‘compression’ are more usually used instead of ‘cephalad’ and ‘caudad axial translation’. Similarly, the term ‘lateral bending’ is more convenient and is preferred to ‘coronal rotation’.

In this text, the term ‘sagittal’ rotation is strictly used to refer to forward and backward rotatory movements. Although the terms ‘flexion’ and ‘extension’ are commonly used to describe this motion, these terms are insufficiently accurate when applied to movements of individual lumbar vertebrae. Flexion and extension are not pure movements of the lumbar vertebrae because, as will be shown in Chapter 8, these movements involve a combination of both sagittal translation and sagittal rotation. The terms ‘flexion’ and ‘extension’ may be used to describe forward bending and backward bending of the lumbar spine in a general sense, but in relation to movements of individual vertebrae it should be understood that the terms refer to a combination of both sagittal rotation and sagittal translation.

The relevance of these explicit definitions of motion is extensive. In the first instance, the motion of individual vertebrae is often complex, and no single term can describe the motion. Nevertheless, it can always be described as some combination of the fundamental movements listed in Table 7.1. Furthermore, each component of motion of the lumbar spine is exerted and resisted by different mechanisms, and to appreciate how these mechanisms act, each needs to be analysed in relation to the particular component of motion that it controls. This type of analysis is undertaken in Chapter 8.

Stress–strain

To stretch a collagen fibre, a force must be applied to it. Once it starts to stretch, the fibre resists elongation by generating a resisting force due to the chemical bonds between collagen fibrils, between tropocollagen molecules, between collagen fibres, and between collagen fibres and proteoglycans (see Ch. 2). By convention, the applied or elongating force is known as the applied stress and the extent to which a fibre is elongated is known as the strain. Stress is measured in units of force (newtons) and strain is measured as the fractional or percentage increase in length relative to initial length. Thus a fibre of length L₀ when stretched to a new length L₁ undergoes a strain of L₁/L₀ or L₁/L₀ × 100%.

Particular terms are used to specify different types of stress and strain according to the direction in which a structure is deformed. When a structure is stretched longitudinally, the deforming force is known as tension and the structure undergoes tension strain. If a structure is squashed, the deforming stress is compression and it undergoes compression strain. The latter is measured as the fractional or percentage decrease in height of the structure. Forces that cause two vertebrae to slide with respect to one another are referred to as shear forces and the strain that occurs in the intervening intervertebral disc is referred to as shear strain. The distinction between shear and tension is that tension conventionally applies to forces exerted along the long axis of a structure, whereas shear forces are applied across this axis. When an object twists, it is said to undergo torsion. A force that causes torsion is a torque and the resultant strain is referred to as torsion strain.

At rest, single collagen fibres are usually buckled, and the wavy shape they assume is referred to as crimp.^3–6 When stress is applied to a collagen fibre, the first effect is to straighten this crimp. Little energy is required to do this as there are no major chemical bonds that maintain it. Thus, a crimped collagen fibre will elongate in response to little applied force. However, once crimp has been removed, the collagen fibre starts to resist strongly any further elongation. The stress attempts to break the bonds between the collagen fibrils and tropocollagen molecules. Energy is required to oppose strain and perhaps eventually to break these bonds. Consequently, more force is required to produce further elongation of the collagen fibre. If sufficient force is applied, the bonds may break, and when this occurs in a substantial number of bonds, the collagen fibre ceases to resist elongation and is said to ‘fail’. Once the collagen fibre has failed, only small forces are required to tear apart its now unbonded component fibrils and molecules.

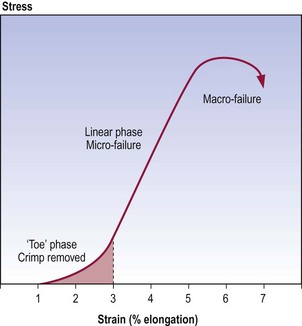
The mechanical behaviour of collagen fibres subject to stress can be depicted graphically,⁷ as in Figure 7.6; such graphs are known as stress–strain curves. The curve exhibits three main regions. The first region, known as the ‘toe’ phase, reflects the phase when crimp is being removed from the collagen fibre. The second, or linear, region is the steep slope along the middle of the curve. Mathematical calculations reveal that the junction of the toe phase and the linear region represents the point where crimp has been maximally removed from the fibre and the stress starts to stretch the collagen fibre longitudinally.^6,7 The linear region represents the phase when bonds within and between collagen fibrils are being strained and some are being broken. The peak of the curve represents the phase of failure of the collagen fibre, when substantial numbers of bonds are irreversibly broken. As depicted by the last part of the curve, once failure has occurred, elongation can continue with ever decreasing amounts of stress being required.

Figure 7.6 Stress–strain curve of collagen.

(Based on Abrahams 1967⁷ and Shah et al.1977.⁶)

A key feature of the mechanical properties of collagen is that bonds within and between collagen fibrils start to be strained and broken somewhere after 3% and 4% elongation of the fibre has occurred. Consequently, about 4% elongation is the maximum a fibre can sustain without risking microscopic damage.

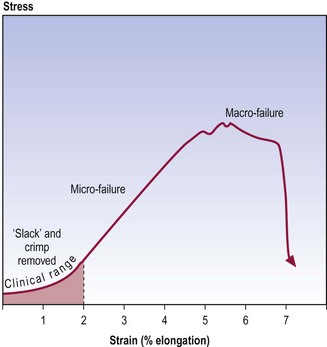
Collagenous tissues, like ligaments and joint capsules, behave in a similar manner to isolated collagen fibres, and exhibit similar stress–strain curves^5,6,8,9 but certain additional mechanical events are involved (Fig. 7.7). In addition to the removal of crimp, the toe phase may represent the removal of any macroscopic slack in the ligament. During the second phase, collagen fibres are being rearranged in the stressed structure. Fibres that, at rest, are curved or run obliquely in the three-dimensional lattice of the ligament or capsule are straightened to line up with the applied force. Thus, when the three-dimensional lattice is stressed, any bonds between separate collagen fibres and between collagen fibres and their surrounding proteoglycan matrix are strained. Furthermore, to make way for the rearrangement of collagen fibres, water and proteoglycans may need to be displaced from between the collagen fibres.

Figure 7.7 Stress–strain curve for a ligament.

(Based on Nordin and Frankel 1980⁸ and Noyes 1977.⁹)

All of these processes require energy: to strain the bonds to move the collagen fibres and proteoglycans; and to squeeze out water. Thus, to achieve continued elongation, more force must be applied and this creates the steep slope of the second phase (see Fig. 7.7). Eventually, after the collagen fibres, proteoglycans and water have been rearranged, the bonds within individual collagen fibres are strained. In the face of increasing stress, these bonds and those between collagen fibres will fail and the entire structure fails.

The proportion of collagen fibres that needs to fail before macroscopic failure of a ligament or capsule occurs is not known, and it is not possible to predict the stress–strain curves for different structures on the basis of the number or nature of their constituent collagen fibres. Therefore the mechanical behaviour of different structures has to be derived empirically by subjecting several samples of the same structure to known stresses and obtaining average stress–strain curves representative of the particular structure.

The value of stress–strain curves is that they graphically depict the mechanical properties of collagenous (and other) structures, notably their strength and the way in which they resist elongation. In turn, the mechanical behaviour reflects the biochemical properties of the structure, for alterations in the proteoglycan content and the bonding within and between collagen fibres will affect the way a ligament or a capsule can resist applied forces.

To a certain extent, physical examination involves obtaining a stress–strain curve for a joint and its capsule or ligaments. When passive movement is induced, a stress is applied, and strain is reflected in terms of both the range of movement observed and the form of the palpated resistance to movement. It is important to realise, however, that clinical examination only studies the early part of the stress–strain curve, no further than just beyond the toe phase.⁸ The limit is well within the 4% elongation at which microscopic injury occurs. Physical examination rarely (and should not) enter into the second phase, for then it is actually inducing microfailure of the structure, and risks macrofailure. Physical examination therefore gains access to only a part of the total stress–strain curve possible. Nevertheless, it does detect some of the physical properties of the structure examined, which can be interpreted in the light of knowledge of the microstructure and biochemistry of the structure examined, and knowledge of its total mechanical behaviour as determined in cadaveric and post-mortem material.

Stiffness

The stiffness of a given structure is its resistance to deformation and can be measured by the force required to produce a unit elongation or deformation.¹⁰ In mathematical terms, it is the slope of the stress–strain curve of a structure. Stiffer structures resist deformation and the slope of their stress–strain curves will be steeper. In biochemical terms, stiffness implies a greater degree of bonding between collagen fibres, or between collagen fibres and their surrounding matrix.

Initial range of movement

If a joint is moved passively or actively by a constant force, a point is reached where no further movement appears possible. The resistance in the capsule and ligaments of the joint balances exactly the force attempting to move the joint. The distance moved by the joint up to this point is known as the initial range of movement. If a stress–strain curve were constructed for the joint, the initial range of movement would be found to occur somewhere early in the second phase of the curve, just after the toe phase when collagen bonding is starting to resist the movement.

Application of a greater force would strain the resisting structures further and a new, greater initial range of movement would be perceived. The amount of increased range would be dependent both on the increase in force and on the stiffness of the joint and its ligaments. However, to obtain a substantially greater initial range of movement, considerably larger forces would need to be applied to most joints and ligaments. Such larger forces are not usually possible during normal clinical examination.

With the forces used in clinical examination, the initial range of movement remains early in the second phase of the stress–strain curve, and even if the applied force varies somewhat with the strength of the examiner, the resistance of the joint is such that the differences in perceived range of movement are not great. Consequently, the initial range of movement as perceived from clinical examination falls in a narrow range and can be called the normal range of movement.

Creep

Initial ranges of movement are usually measured on the basis of a brief application of force. The force is applied until the range of movement is maximal, and once the range is measured, the force is released. However, if a constant force is left applied to a collagenous structure for a more prolonged period, further movement is detectable. This movement is small in amplitude, occurs slowly, almost imperceptibly, and is consequently known as creep.

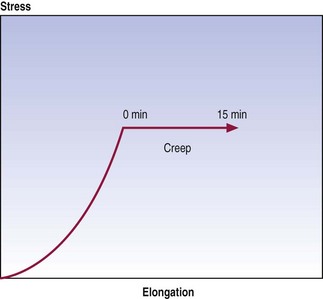
Graphically, creep is seen as continued displacement when a constant force is maintained at some point on a stress–strain curve (Fig. 7.8). The time over which creep can be measured is optional, and various studies have employed times varying from minutes to hours.^10–14

Figure 7.8 Stress–strain curve illustrating creep. Despite maintenance of a constant load, elongation occurs with the passage of time.

The biochemical and structural basis of creep is not known for certain but it appears to be due to the gradual rearrangement of collagen fibres, proteoglycans and water in the ligament or capsule being stressed. Forces of short duration may not act long enough to squeeze water out of a ligament or to allow the rearrangement of collagen that could possibly occur. The force is removed before maximal displacement has had a chance to occur. In contrast, sustained forces allow for these displacements to occur, whereupon the ligament or capsule can elongate slightly as a result of the internal readjustment of its constituents.

The academic relevance of creep is that it provides an indirect though readily obtainable measure of the interactions of collagen, proteoglycans and water in a ligament or capsule. By studying the creep of structures, one can determine how these interactions vary with age or in the face of disease processes or injury. However, creep is not just a laboratory phenomenon as it occurs regularly in activities of daily living.

Many occupational groups (e.g. stonemasons, bricklayers, roofing carpenters), regularly submit their lumbar spines to prolonged load-bearing in flexion. Once they achieve such a posture there is often little movement away from it, and their lumbar joints will creep. The possible significance of this phenomenon is discussed below.

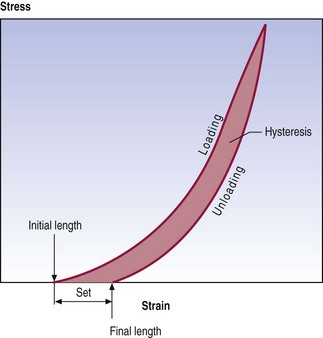
Hysteresis

Most structures, and certainly all biological tissues, exhibit differences in mechanical behaviour during loading versus unloading. Loading produces a characteristic stress–strain curve but gradual release of the load produces a different stress–strain curve. Restoration of the initial length of a ligament occurs at a lesser rate and to a lesser extent than did the deformation (Fig. 7.9). This difference in behaviour is referred to as hysteresis and reflects the amount of energy lost when the structure was initially stressed.

Figure 7.9 Stress–strain curve illustrating hysteresis. When unloaded, a structure regains shape at a rate different to that at which it deformed. Any difference between the initial and final shape is the ‘set’.

When a structure is deformed, the energy applied to it goes into deforming the structure and into straining the bonds within it. For collagenous tissues, some of the energy goes into displacing proteoglycans and water, rearranging the collagen fibres, and perhaps even into breaking some of the bonds between collagen fibres. Once used in this way, this energy is not immediately available to restore the structure to its original shape. Displaced water, for example, does not remain in the structure exerting some sort of back-pressure attempting to restore its original form. It is squeezed out of the structure, and the energy used to displace the water is no longer available to the system. If chemical bonds are broken they cannot act to restore the form of the structure.

Thus, with less energy available to restore the structure, the rate and extent of its restoration are reduced. When all applied forces are completely removed, the final length of the ligament or capsule may remain greater than its original length (or less in the case of compressed structures). This difference between initial and final length is referred to as a ‘set’.

In general, hysteresis and a residual set do not occur if a structure is stressed only in the toe phase of its stress–strain curve, as bonds within and between the collagen fibres are not broken. However, the further a structure is stressed beyond its toe phase, the more bonds are broken and the greater the hysteresis and set.⁷

In time, collagen fibres and proteoglycans in a structure may be rearranged into their usual configuration, and any displaced water is eventually reabsorbed, restoring the structure to its original form. Under these circumstances any set disappears, and the structure regains its original size.

A set often occurs after creep. When the applied force is released, the structure does not immediately spring back to its original shape, although it may do so in time. However, if bonds between or within collagen fibres have been broken, the set may not disappear until and unless the bonds are exactly reconstituted. If the original bonds are not reformed, or if new bonds are formed in the set position, the set may persist indefinitely.

This phenomenon has implications in the interpretation of trauma to ligaments or capsules. The energy lost in breaking the tissue may not be recoverable, and the original structure is not fully reformed. Healing may occur in a set position, and this may compromise the mechanical function of the structure. Healing in a set position effectively lengthens the ligament and it will therefore accommodate greater than normal initial ranges of movement, which may not be desirable.

The phenomena of creep and hysteresis are also of particular relevance to the interpretation of sustained insults to ligaments and capsules. A ligament may be subjected to forces well within its load-bearing capacity but if these forces are sustained for prolonged periods, the ligament will creep, and because of hysteresis, eventual release of the load does not result in the immediate restoration of the form and microstructure of the ligament. The ligament requires time to reform fully. In the meantime, the mechanical properties of the ligament have been altered. Its stress–strain capacity is different from normal, and until the structure is fully reformed it cannot be expected to sustain reapplied loads in the normal, or accustomed, way. Therefore, the structure may be liable to injury during this vulnerable period of restoration.

Fatigue failure

When forces are repeatedly applied to a material, it does not behave the same way each time. Each application produces a certain amount of hysteresis, and the structure of the material is altered slightly, albeit perhaps temporarily. However, if the repetitions are frequent enough, the material may not have an opportunity to recover fully. Each application, therefore, effectively weakens the material slightly. With one or two applications this weakness may not be apparent. However, following many repetitions, the small weaknesses accumulate, and weakness in the material becomes apparent. Indeed, after several frequent repetitions of a stress, the material may fail at a stress that is substantially less than that required to damage the material following a single application of a force.

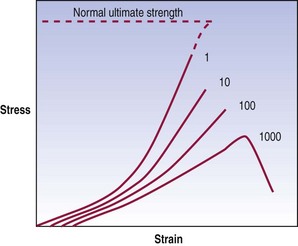
This phenomenon is referred to as fatigue failure; its behaviour is illustrated graphically in Figure 7.10. An initial loading reveals the mechanical properties of the material. Its stiffness is evident, and the ultimate tensile stress is the force that would be required to disrupt the material completely upon one application of a force. However, if the material is repeatedly stressed, it exhibits an evolution of mechanical properties. Its stiffness decreases and, in particular, the stress at failure drops. As a result, by repeatedly stressing a material at forces less than those required to break it after one loading, the material can eventually be disrupted. A common analogy is the ability to break a wire or paper clip, not by pulling or bending it once but by repeatedly bending it.

Figure 7.10 Fatigue failure. After a single application of an increasing force, a structure exhibits a typical stress–strain curve (1). However, after 10, 100 and 1000 repeated applications of a stress less than the initial ultimate tensile stress, the structure becomes less stiff and may fail at substantially less stress than its original ultimate tensile strain.

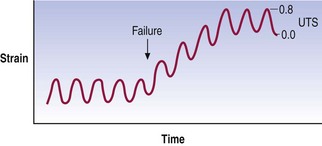
Another way of plotting fatigue failure is to display the evolution of strain over time as a force of constant peak magnitude is applied (Fig. 7.11). The graph shows the repeated cycles of force being applied. Initially, the force applied results in a relatively constant strain but at some point the strain suddenly increases and the specimen operates at a new strain even though the stress has not changed. This behaviour indicates that something in the material has failed, allowing it to exhibit greater deformation for the same stress.

Figure 7.11 Fatigue failure. When a force of constant peak magnitude is applied cyclically, the material initially deforms repeatedly to the same extent, but at some point the strain increases even though the load has not changed. This point indicates the onset of fatigue failure. UTS, ultimate tensile stress.

How rapidly a material undergoes fatigue failure is governed by the nature of the material itself and by the magnitude of the offending stress and its periodicity. Larger stresses are more likely to achieve failure sooner; smaller stresses will require more repetitions. Infrequent repetitions may allow biological materials to recover; frequent repetitions deny this recovery and may achieve failure sooner.

The clinical importance of fatigue failure is that damage to tissues may occur without a history of major or obvious trauma. Indeed, studies of human spinal tissues have shown that an anulus fibrosus typically fails after 3000 repetitions but can fail after as few as 20 repetitions of a force equal to 60% of the ultimate tensile stress.¹⁵ Fractures of the vertebral endplate occur within 1000 repetitions but in some cases they occur after as few as 30–80 applications of a stress equal to 50–80% of ultimate compressive strength.¹⁶ The forces involved are within the range of those encountered in activities of daily living, and these experimental studies warn that in the face of repetitive loading, elements of the lumbar spine can be injured by forces considerably less than those expected for an acute injury.

Forces and moments

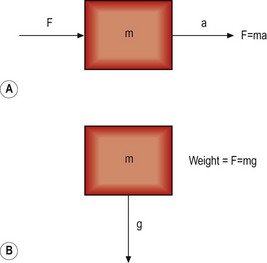
When an object is free to move and is acted upon by a force, it will accelerate in the same direction as the applied force (Fig. 7.12). The force (F) is related to the acceleration (a) by the equation

Figure 7.12 The nature of forces. (A) A force (F) acting on a mass (m) imparts an acceleration (a) on the mass in the same direction as the force. (B) When gravity acts downwards on an object, the force it exerts is the weight of the object, which is proportional to its mass (m) and the gravitational acceleration of the Earth (g).

where ‘m’ is the mass of the object in kilograms. In the MKS system, the unit of force is a newton (N) and has the dimensions of kilogram metres per second squared (kg m s⁻²).

For an object in the Earth’s field of gravity, its weight is produced by the force of gravity trying to accelerate it towards the centre of the Earth (see Fig. 7.12). The mass of the object (m) is related to its weight by the acceleration produced by the Earth’s gravitational field, i.e.

where ‘g’ = 9.8 m s⁻². An object in the Earth’s gravitational field therefore exerts a downward force whose magnitude in newtons is about 10 times its mass measured in kilograms.

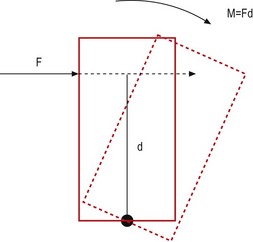
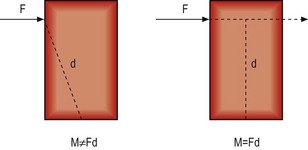
If an object is acted upon by a force but is fixed at some point, the object is not free to move in the direction of the applied force. Instead, it will tend to bend or rotate about the fixed point (Fig. 7.13). A force that causes bending is known as a moment, and its magnitude is proportional to both the magnitude of the force applied and the perpendicular distance between the line of force and the fixed point, i.e.

Figure 7.13 The nature of moments. When a force acts eccentrically on an object that is fixed at some point, the force tends to bend or rotate the object. This bending effect is a moment (M) whose magnitude is proportional to the magnitude of the force (F) and the perpendicular distance (d) between the fixed point and the direction of the force.

The unit of measure of a moment is newton-metres, the dimensions of which are kg m² s⁻².

Intuitively, it should be obvious that the bending capacity of a moment will be greater either if the force applied is greater or if the distance from the fixed point is greater. (Compare the effort required to bend a short object versus a longer object of the same material.)

It is critical to appreciate that a moment is not calculated according to the distance between the fixed point and the point on the object at which the force is applied. It is calculated according to the perpendicular distance between the fixed point and the direction of the force (Fig. 7.14). This distance is referred to as the moment arm.

Figure 7.14 Moments (M) are calculated using not the distance (d) between the fixed point and the site of application of the force (F), but the perpendicular distance (d) between the fixed point and the direction of the force (F).

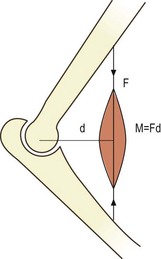
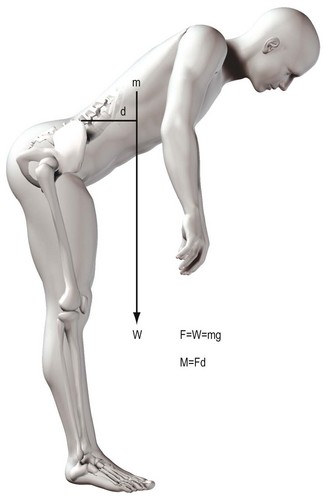
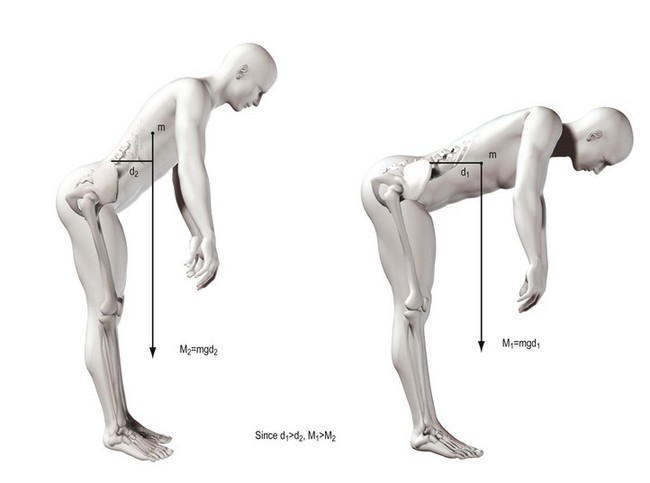
The concept of moments applies to all situations where joints bend, whether they are acted upon by muscles or gravity. The moment generated by a muscle is the product of the force exerted by the muscle and the perpendicular distance between the axis of rotation of the joint and the line of action of the muscle (Fig. 7.15). In the case of the vertebral column, movements such as flexion are frequently exerted by gravity. The force involved is the weight of the trunk leaning forwards of the lumbar spine and it is exerted vertically downwards on the centre of mass of the trunk (Fig. 7.16). The magnitude of the force acting on a given joint in the lumbar spine is calculated as the mass of the trunk above that joint multiplied by g. The moment arm is the perpendicular distance from the joint in question to the line of action of the force (see Fig. 7.16). Clearly, the further a subject leans forward, the longer this moment arm and the greater the resultant moment. Conversely, the more upright a subject stands, the shorter the moment arm and the smaller the flexion moment (Fig. 7.17).

Figure 7.15 Muscles exert moments on joints that they move. The magnitude of the moment (M) is proportional to the force (F) exerted by the muscle and the perpendicular distance (d) between the line of action of the muscle and the axis of rotation of the joint.

Figure 7.16 Flexion moments are exerted on the lumbar spine when the trunk leans forwards. The force (F) exerted is the weight (W) of the trunk above the lumbar spine. This force acts downwards from the centre of mass of the upper trunk (m). The moment arm (d) is the distance from the lumbar spine to the line of gravity (g) acting on the upper trunk. The magnitude of the flexion moment (M) is the product of the force and the moment arm.

Figure 7.17 Different angles of flexion of the trunk result in moments (M) of different magnitude being applied to the lumbar spine. Even though the mass of the trunk (m) and the gravitational acceleration of the Earth (g) remains the same, different moments result from differences in the moment arms (d) that occur.