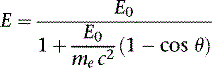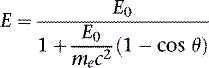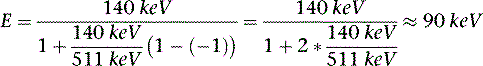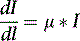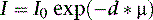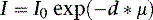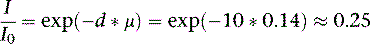INTRODUCTION

Myocardial perfusion single-photon emission computed tomography (SPECT) has in large part been successful despite significant imaging limitations. Soft-tissue attenuation, photon scatter, distance-dependent collimator blur, and partial volume artifacts are present in every single SPECT procedure performed in the world today. It is a testament to the robustness, utility, and clinical needs that SPECT continues to be such a dominant procedure for the management of patients with coronary artery disease, even with these limitations.

The field of medicine is changing dramatically, and the demands that will be placed on nuclear cardiology practitioners are increasing. Society is demanding greater accuracy, improved outcomes, and increased cost-effectiveness of procedures. To achieve these goals, attenuation correction will be a critical bridge that must be crossed if we are to achieve the gains society desires.

HISTORICAL PERSPECTIVE

The field of SPECT imaging was born out of pioneering work done at Duke University in the late 1970s under Ronald Jaszczak¹ and John Keyes.² It was demonstrated that three-dimensional radionuclide imaging could be obtained using an Anger camera rotating around a patient. As early as 1977, it was recognized that attenuation would be one of the major limitations of the new imaging modality.

The effort to solve the problem of attenuation artifacts in nuclear cardiology was carried forward by several groups around the world. Moore et al. demonstrated the feasibility of performing attenuation correction using x-ray computed tomography (CT),³ and Greer KL et al.⁴ demonstrated the feasibility of acquiring transmission data with a gamma camera system. A complete history of the development of attenuation correction can be found in King et al., 1995.⁵

The impact of attenuation was first quantitated in the work of Eisner et al. in 1988.⁶ In this work, differences between males and females were correctly identified as arising from differences in anatomy. This led to significant differences in the mean normal distribution patterns in the left anterior descending (10% to 15% higher in males than females) and right coronary artery (8% to 10% higher in females than males). Later work by Galt et al. demonstrated that with the application of attenuation correction methods, these normal distributions were similar.⁷ Depuey et al. developed techniques for identifying attenuation and presented algorithms for improving interpretive accuracy using deductive techniques.⁸

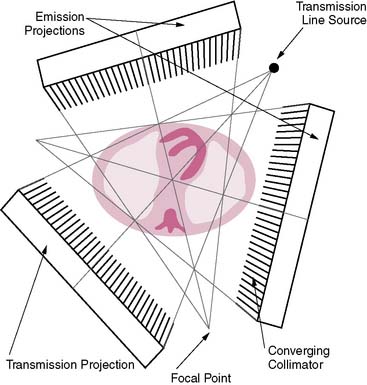
The first attempts at commercialization of attenuation correction were introduced by Picker with its STEP system (Fig. 7-1). This technique was based on the geometry proposed by Tung⁹ and Jaszczak.¹⁰ The system employed a fanning collimator design to collect photons from a fixed line source opposite the detector head on a triple-headed detector system. Early work using this system demonstrated that significant improvements in uniformity could be obtained using the fanbeam collimation system with attenuation correction.^11,12 This system failed to received widespread acceptance, because it employed a triple-detector SPECT system and fanbeam collimation. The use of fanbeam collimation led to very extreme truncation artifacts, owing to the small field of view of the fanbeam geometry (~30 cm). Furthermore, the added cost of a third detector system and loss of clinical efficiency from the 120-degree angles of the triple-head systems made this system cost prohibitive.

Figure 7-1 The Picker PRISM 3000 STEP system was the first commercially available attenuation correction system. It used a system of three fanbeam collimators and a stationary line source.

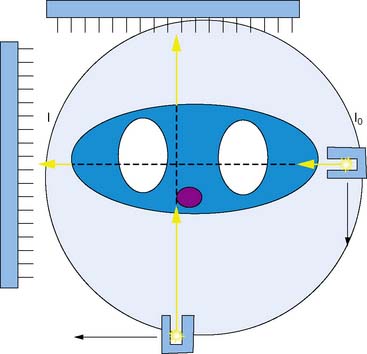
Other vendors introduced parallel-geometry scanning line source systems. The Vantage/ExSPECT system, introduced by ADAC laboratories, used a 90-degree parallel-hole geometry system for simultaneously acquiring emission and transmission data (Fig. 7-2).¹³ Using this approach, one of the few multicenter trials of attenuation correction was conducted, demonstrating significant improvement in specificity and normalcy. These results were also duplicated in several single and multicenter imaging trials using various vendor approaches.^14–21

Figure 7-2 The scanning line source geometry employs a system of two radioactive sources, typically positioned opposite the detector face. A system of gears moves the arms across the field of view of the detector.

One of the major limitations of the first-generation systems was that though they work reasonably well in clinical trials, they did not always perform well in the clinical setting.²² Quality control (QC) of the attenuations correction systems was not well understood, and systematic QC procedures were not in place in most nuclear laboratories attempting to use attenuation correction. The result of this was a very uneven application of QC standards in the field and an eventual low rate of adoption by practitioners.

To address these limitations, ADAC laboratories introduced a second-generation processing suite for its Vantage scanning line source systems, the VantagePRO (Philips Medical, Milpitas, CA). This package used a combination of pre- and post-acquisition QC tools combined with a Bayesian iterative reconstruction algorithm to improve the consistency of the resulting images.²³ Clinical trials using this approach demonstrated significant improvement in normalcy and specificity; however, because of the retrospective nature of the study, sensitivity did not show improvement over conventional non-attenuation-corrected imaging.

Another approach that was investigated was the use of x-ray computed tomography to derive the patient-specific attenuation map. Because of the high count flux, very high-quality transmission maps can be obtained. Clinical results from these systems have been reported, and they have been shown to produce significant improvement in interpreter accuracy over non-attenuation-corrected image approaches.^24,25

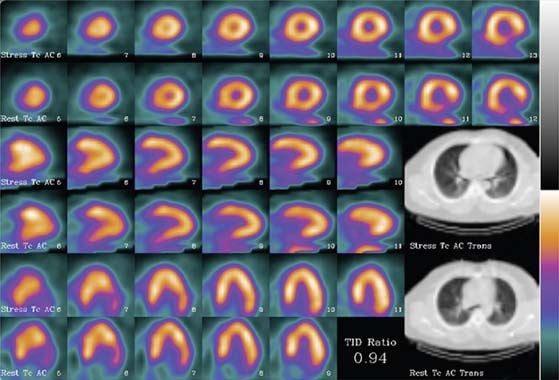
The limitation of x-ray-based approaches is that they are inherently sequential acquisition protocols. Transmission/emission image registration issues, as well as clinical efficiency concerns, have limited the acceptance of these systems. The Hawkeye System, introduced by General Electric, was a departure from the conventional line source attenuation correction, insofar as it employed a low-dose x-ray tube (140 kVp, 2.5 mAs) to generate a patient-specific x-ray-based CT attenuation map referred to as hybrid imaging SPECT/CT. This technique was capable of producing transmission maps and attenuation-corrected images of higher quality (Fig. 7-3). As the need for diagnostic-quality transmission maps has arisen, vendors have introduced SPECT/CT hybrid systems capable of detecting and measuring coronary calcium and performing vascular and coronary CT angiography (Siemens [Symbia], Philips [Precedence]).

Figure 7-3 The Hawkeye SPECT/CT system employs a low-dosage CT system to produce x-rays for measuring the patient’s anatomy. Though the CT images are not of diagnostic quality, they are of very high quality for the purpose of attenuation correction.

Pressure for SPECT to evolve is mounting as payer and patient expectations rise. Positron emission tomography (PET) and CT are setting new standards for early detection of disease and in the management of complex patients. The expectations of a perfusion test are changing, and SPECT must improve the information content of its product or face obsolescence. Attenuation and scatter correction are likely to play a critical role in allowing SPECT to survive in this increasingly competitive medical environment.

SCIENTIFIC FOUNDATION OF ATTENUATION: COMPTON SCATTERING AND THE PHOTOELECTRIC EFFECT (See Chapter 6)

Photon attenuation is a natural process of electromagnetic radiation with matter. For optical light, this process is easily recognized as the natural opacity of solid objects. Some materials—colored glass, polarizing sunglasses, and so forth—are translucent, allowing some of the photon beam to pass through the object. Logically, the thicker the translucent object, the fewer photons can survive the trip through the material.

This process is played out in a similar way in the high-energy regimen, albeit with different physical processes in play. Nuclear cardiology (and x-ray imaging as well) exists because of a very peculiar fact of nature: At these energies, the seemingly solid object of the human body is not nearly as solid as it appears. To understand this, we have to introduce an interesting concept, the wave-particle duality of photons.¹ At higher and higher energies, photons act as if they have smaller and smaller sizes. In the gamma ray and x-ray ranges, photons could pass through a solid object with little effort. To a high-energy gamma ray, the body looks less like a solid object and more like a cloud of electrons.¹

To be precise, attenuation is a misnomer. Most of what is referred to as “attenuation” in nuclear cardiology is in reality photon scatter. The dominant process for “attenuating” photon signal in the energy range used in nuclear cardiology is known as Compton scattering. This process, discovered by Arthur H. Compton in 1923 (resulting in Compton and his graduate student being awarded the Nobel Prize in physics²⁶), is the quantum scatter of light off of matter and the transfer of significant amounts of energy from the photon to the electron.

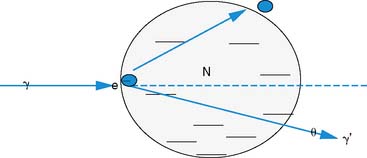
The photon in a Compton scattering event can be thought of as a billiard ball striking the electron. The electron then absorbs some of the energy from the photon, lowering the energy of the photon (Fig. 7-4). The key parameters of a Compton scattering event are the incident energy of the photon (E₀) and the scattering angle of the photon relative to its incident and (θ). The higher the incident energy, the more relative energy can be delivered to the electron. (Imagine a compact car–against-truck head-on collision versus a truck-against-truck collision: The second truck will fare worse in the latter scenario.) Furthermore, the larger the scattering angle, the more energy that can be delivered to the electron. Compton demonstrated that the exact energy of the scattered photon can be calculated from the following formula:

Figure 7-4 Compton scatter occurs when a high-energy photon collides with an electron in the media. The photon energy is changed by delivering energy to the electron, which is then ejected into the medium.

This is very important: Compton scattering does not destroy the incident photon. Each “attenuation” event is truly a scattering event. In other words, as we remove “good photons” from our signal, we add “bad photons” to the signal.

In the energy regimen of ^99mTc (140 keV), Compton scattering dominates all scattering processes in human tissue. For lower-energy photons (²⁰¹Tl, ~72 keV), the photoelectric effect also plays a role. In photoelectric-effect absorption, the photon interacts with the atomic structure of the material. In these interactions, a significant fraction of the energy of the incident photons is used in ionizing the atom. For atoms such as oxygen and hydrogen, the k-shell binding energies are very low relative to the energies of the photons used in nuclear cardiology. Because of the energy difference between the binding energy and the incident photon, the likelihood of photoelectric effect ionization is low.

Example problem 1:

A 140-keV photon is completely backscattered by an electron. What is the resulting energy of the scattered photon?

Answer:

Using the Compton formula:

where E₀ is the energy of the incident photon, m_ec² is the resting energy of an electron (511 keV), and θ is the angle of the scattered photon relative to the incident photon. For a backscattered photon: θ = 180 degrees. Solving the Compton equation:

PHYSICS OF ATTENUATION AND SCATTER COMPENSATION

Attenuation and scatter of photons in nuclear cardiology can be compensated during the reconstruction process by knowing how the medium absorbs photons. This is typically accomplished by using a patient-specific map of the soft tissue to calculate the degree to which the photon signal has been reduced as a result of attenuation.

The degree to which photons are attenuated by the medium is calculated from this simple differential equation:

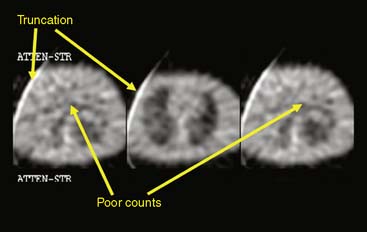
where I is the flux, μ is the linear attenuation coefficient, and is the change in I over a small distance. In other words, the change in the number of photons over a small distance of material is proportional to the single physical parameter, μ. Solving this equation yields:

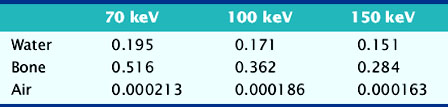
The value of μ is dependent on the characteristics of the material in question and the energy of the incident photons. Examples of linear attenuation coefficients are given in Table 7-1.

To compensate for the impact of attenuation on the photo peak images, a model for the patient-specific attenuation is applied during the reconstruction. Conventional filtered backprojection reconstruction is not well suited for attenuation compensation; the attenuation profile cannot be easily expressed as a Fourier filter that can be applied to the projection data. To incorporate the attenuation profile data into the reconstruction, an iterative algorithm must be applied.

Iterative reconstruction algorithms can be broken down into three key components: the data, the estimate (or reconstruction), and the projection matrix (the model for how photons are moved out of the patient and into the camera). Ideally, a perfect model and perfect data will result in a perfect reconstruction. However, the reality is that perfect data and perfect models do not exist.

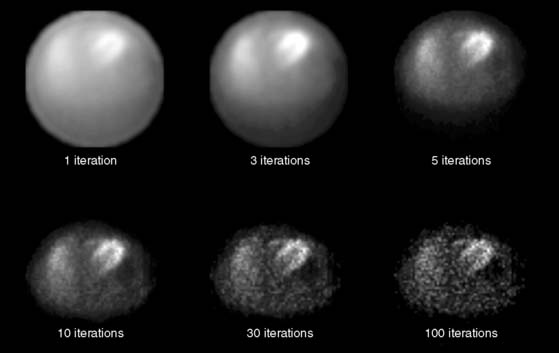
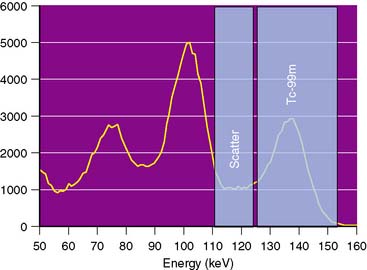
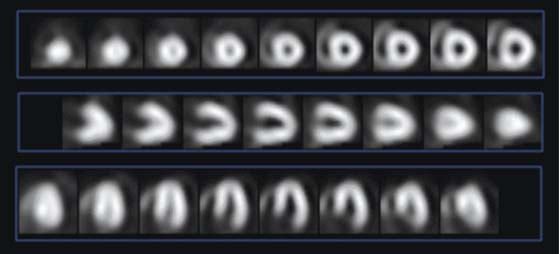
The most common iterative reconstruction algorithm is the maximum-likelihood expectation maximization (MLEM) algorithm.^27,28 This model employs an iterative approach for searching for the most likely source of the projection data, based on a physical model of how photons get from the patient to the camera. As one might expect, if the data are bad and the model is wrong, MLEM will not converge to the correct solution. The main strength of MLEM is the ease of which physics of attenuation can be modeled into the reconstruction. An example of the convergence of MLEM is given in Figure 7-5.

Figure 7-5 Iterative reconstruction successively improves the image fidelity by updating the image in small amounts at each iteration. Because the input data are not perfect, these algorithms can overfit the noise and produce a noisy reconstruction at high iteration numbers.

There are other iterative algorithms in addition to MLEM. Ordered subset expectation maximization (OSEM) is also commonly used. While its origins are similar to those of MLEM, OSEM has much more rapid convergence properties. OSEM uses pieces of the data to create each update of the data (subset). Each iteration of OSEM can result in several updates of the reconstruction map. This has the effect of greatly increasing the convergence time of the algorithm.²⁹

Example problem 2:

A beam of 140-keV photons penetrate a 10-cm slab of water. The attenuation coefficient for 140-keV photons is μ = 0.15/cm.

Answer:

where d is the thickness of the slab, I₀ is the flux of the incident beam, and I is the resulting flux.

Similar to attenuation correction, scatter correction relies on acquiring a patient-specific estimate of photon scatter. The most common technique for scatter estimation is the acquisition of adjacent energy windows to subtract the scatter component from the photo peak component (Fig. 7-6). These techniques typically use a secondary energy window placed at a lower energy from the primary photo peak to measure the distribution of Compton scatter photons.³⁰ These techniques can be effective in removing the scatter from ^99mTc, but they have been less successful in correcting Tl-201 images. Furthermore, these techniques have been unable to demonstrate measurable improvements in sensitivity.

Figure 7-6 The most simple scatter correction technique uses a neighboring energy window to acquire a measurement of the down-scatter. This measurement is then subtracted from the primary peak data to produce a scatter-corrected projection data set.

One possibility for the failure to observe improvement in sensitivity is that scatter window subtraction techniques do not model the smaller-angle scatter events responsible for defect fill-in (Fig. 7-7).³¹ Several techniques have been described for more accurately modeling photon scatter. These techniques rely upon acquiring several energy windows and using multispectral techniques for modeling the large- and small-angle scattering events.³²

Figure 7-7 More sophisticated techniques use a model of the energy response of the detector system to “reconstruct” the energy spectrum at each pixel to achieve better energy discimination.

TECHNIQUES OF ACQUIRING THE PATIENT-SPECIFIC ATTENUATION MAP

To perform attenuation correction, an estimate of the anatomy is required. This estimate of anatomy is typically obtained through the direct measurement of the patient using an external radiation source.

Quality-Control Issues

Regardless of the techniques used for acquiring the transmission map, all attenuation correction systems require a high-quality transmission map to perform attenuation correction. A high-quality transmission map is defined as:

1. Near-uniform attenuation coefficients across the mediastinal area

2. Free of truncation artifacts

3. Well-defined lung boundaries

4. Registered with the emission data

5. Breathing cycle equivalent to a free breathing state averaged over several respiratory cycles

Examples of attenuation maps that do not meet these criteria are displayed in Figure 7-8.

Figure 7-8 Low-quality transmission scans often have low counts, truncation, or both.

Prior to interpretation, all transmission data sets should be routinely inspected for image quality. Data that do not meet these criteria should be suspect.

APPLICATIONS FOR ATTENUATION CORRECTION

The American Society of Nuclear Cardiology and the Society of Nuclear Medicine recommend the routine use of attenuation correction as an important adjunct to traditional filtered backprojection images.³³ These recommendations are based on the preponderance of evidence that demonstrates that superior specificity can be achieved using attenuation correction. Though anecdotal evidence exists for the improvement of sensitivity, study selection bias and suboptimal scatter correction techniques have been unable to demonstrate improvements in sensitivity.

Applications for attenuation correction fall into two broad categories: techniques that improve conventional perfusion imaging and techniques for which routine rest/stress perfusion imaging is not possible.

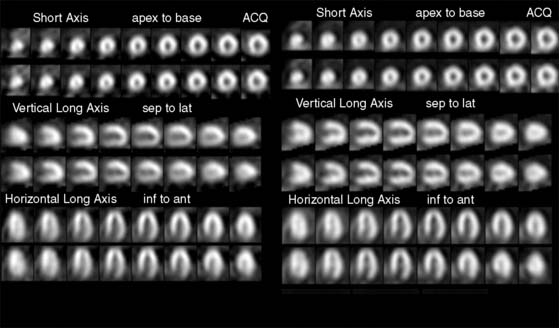
The most common application of attenuation correction is as supplementary data for rest/stress ^99mTc- imaging. In these studies, a transmission data set is acquired in conjunction with the emission data set. The data are then reconstructed using a filtered backprojection algorithm for the non-attenuation-corrected data set and an iterative reconstruction for the attenuation-corrected data set. The filtered backprojection images can then be compared to the attenuation-corrected data sets to assess the significance of attenuation on the filtered backprojection images (Fig. 7-9).

Figure 7-9 On the left is a filtered backprojection recontruction of a low-likelihood male patient. On the right is a reconstruction of the same patient, using attenuation correction. Note the change in the perfusion distribution after attenuation correction.

Stress Only

Another application that has been promoted is the use of attenuation correction for assessing myocardial perfusion images in the absence of a resting study. In this application, patients presenting with a relatively low pretest likelihood for disease are tested with a stress-first myocardial perfusion test. The physician then will make a determination of the normalcy of the study based on the stress perfusion. If the stress images are normal, the patient is not brought back for rest testing (Fig. 7-10).³⁴

Figure 7-10 Example of a patient image acquired using a 30-mCi Tc-99m-sestamibi stress-only protocol. Note: Because of the uniformity of this image, the patient would not be required to return for rest imaging.

One of the most significant challenges of stress-only imaging is the necessity of triaging patients to a stress-first protocol, which could require the patient to return for further testing on the second day.

Heller et al.^35,36 demonstrated that reader confidence was greatly improved when attenuation correction was applied. Other studies have demonstrated comparable accuracy in the normalcy rate when compared to full-rest stress studies.

Quantitative Single-Photon Emission Computed Tomography

As pressure builds for more and more accurate tests for myocardial perfusion imaging, the assessment of large epicardial disease may no longer be sufficient. Myocardial perfusion PET has already seen widespread interest in assessing true myocardial blood flow in terms of mL/g/min. These measurements, in principle, would be independent of the resting perfusion pattern, more sensitive to triple-vessel disease, and capable of measuring serial changes in perfusion.³⁸

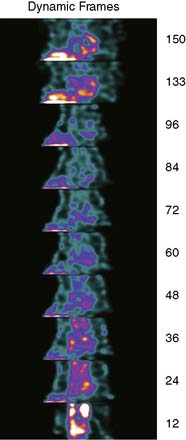
To obtain a quantitative measurement of myocardial perfusion, it is necessary to obtain a measurement in mCi/cc, the dynamic arterial tracer concentration, and the dynamic uptake of the tracer within the myocardium. To achieve this, it is necessary to acquire serial images of the input bolus in SPECT mode with attenuation. These rapid tomographic images must be acquired at such speed as to allow quantification of the input bolus to time less than 6 seconds (Fig. 7-11).

Figure 7-11 Example of an attenuation-corrected “stress input function” sequence acquired using a Siemens (Symbia) system. Despite the high noise and low image fidelity in this image, counts are sufficient for measuring the integrated blood-pool concentration of tracer.

CHALLENGES FOR ATTENUATION CORRECTION

The story of attenuation correction in SPECT is best looked at as both a glass half empty and a glass half full. Most treatments of attenuation and scatter correction focus on either one or the other of these paradigms, best illustrated by the publications of dueling opinions in the Journal of Nuclear Cardiology, 2005.^22,39 Though there is little argument that specificity is improved with attenuation correction as is, there is also little argument that attenuation correction has not seen widespread adoption. A more appropriate question is “Why isn’t the glass completely full?”—that is, what is missing to make attenuation correction an unquestionable necessity for SPECT? In fact, the “recommendation” for attenuation correction presented by the American Society of Nuclear Cardiology and the Society of Nuclear Medicine is qualified so as to relegate the attenuation-corrected images to adjunctive information to the patently incorrect noncorrected images.³³ This is hardly a ringing endorsement.

In cardiac PET imaging, attenuation correction is always applied; in fact, non-attenuation-corrected images are never produced. Because of the unique geometry of PET (two photons produced simultaneously, traveling in opposite directions), attenuation and scatter correction are robust and very accurate. There is no added reimbursement for attenuation correction for PET; it is simply recognized as the correct way to process these images. For attenuation and scatter correction for SPECT to achieve a similar level of acceptance, it must produce a substantially better image than non-attenuation-corrected SPECT.

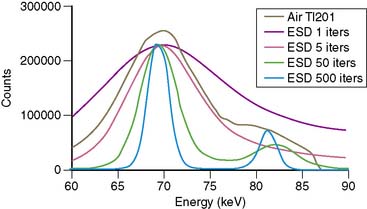
The most commonly cited limitation of attenuation-corrected SPECT is the lack of uniformity in some studies. This lack of uniformity is often referred to as overcorrection or undercorrection of the emission data.²² The mathematics of attenuation correction is straightforward,^27–29 and its implementation within computer programs is straightforward. Attenuation correction is “working” when a high-quality transmission map is available. However, this may not be all that is going on. Poor scatter correction, partial volume effects, and distance-dependent blur all produce artifacts that are patient and protocol specific.

In a sense, the world without attenuation and scatter correction is a simpler world. Attenuation artifact plays such a dominant role that other effects pale in comparison. When attenuation correction is applied, the myriad of other confounding artifacts become visible and can make the images more challenging to interpret, despite the fact they are more accurate.

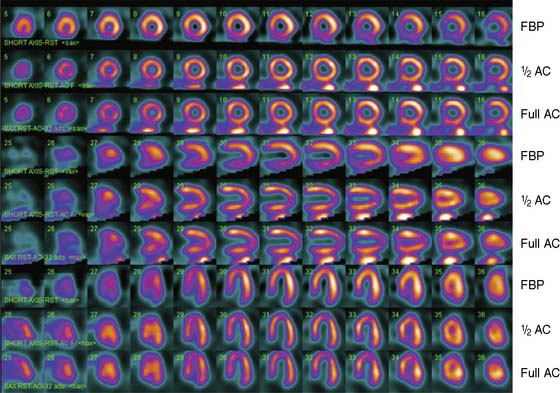
Significant advances have been made in the implementation of resolution recovery and advanced scatter correction. Flash3D (Siemens, Hoffman Estates, IL), Astonish (Philips, Milpitas, CA) and Wide Beam Reconstruction (UltraSPECT, Haifa, Israel) all use a model for the blurring of the collimator. The results are higher-resolution images with fewer partial-volume artifacts (Fig. 7-12). Improvements in scatter correction will also be necessary for improving the sensitivity of myocardial perfusion SPECT images to smaller defects.³¹

Figure 7-12 Example of attenuation correction combined with Astonish resolution recovery and scatter correction (Philips Medical Systems, Milipitas, CA). This study was performed using both full time (25/sec/stop) and half time (12.5 sec/stop). Note the clearly delineated papillary muscles in the Astonish images using both full- and half-time imaging.

CONCLUSION

It would be easy to recommend that attenuation and scatter correction should be applied in all cases; however, things are not that simple. Attenuation correction has been very well established as a technique that can yield significant and impressive improvements in specificity, and it can be useful in situations where two-stage rest/stress imaging is impossible. QC must be maintained, and protocols must be implemented to ensure accurate acquisition and reconstruction of the attenuation map, as well as the reconstruction of the emission data.

The future of attenuation correction mirrors the future of myocardial perfusion SPECT: Without a demonstrable change in the information that can be extracted from the data, SPECT will continue to lose out to other more sophisticated techniques such as CT, magnetic resonance imaging, and PET.

The next stage in the development of attenuation correction for SPECT is to create obsolescence for non-attenuation-corrected studies. This can be achieved through the further penetration of robust scatter correction and resolution recovery methodology. Many of these techniques are being brought to the commercial realm, and it is likely that attenuation, scatter, and resolution recovery methods will eclipse the techniques of today.