Calculating Drug Dosages
Objectives
1. Use formulas to determine the dosages of tablets, capsules, or liquids.
3. Use information about the metric measurement system to accurately calculate drug dosages.
5. Calculate flow rates for infusions.
6. List the rule used to calculate medication dosages for children.
Key Terms
body surface area (BSA) (p. 90)
Clark’s rule (p. 89)
drop factor (DRŎP FĂC-těr, p. 88)
flow rate (FLŌ RĀT, p. 88)
nomogram (NŌM-Ō-grăm, p. 90)
![]() http://evolve.elsevier.com/Edmunds/LPN/
http://evolve.elsevier.com/Edmunds/LPN/
Overview
How medications are ordered differs among physicians, drugs, and health care agencies. Some agencies require physicians to order generic products or only those drugs stocked by the pharmacy. Most drugs are ordered using the metric system, but occasionally another measurement system will be used; for example, heparin, a powerful blood thinner, is available in units. There are many reasons why medication orders appear in a variety of forms, and the nurse must be prepared to understand them all.
Calculation Methods
Calculating dosages involves the following three steps:
2. Simplify by reducing to the lowest terms whenever possible.
Fraction Method
When using fractions to compute drug dosages, write an equation consisting of two fractions. First, set up a fraction showing the number of units to be given over x, the unknown number of tablets or milliliters. For example, if the physician’s order states, “ibuprofen 600 mg,” you would write  . On the other side of the equation, write a fraction showing the drug dosage as listed on the medication bottle over the number of tablets or milliliters. The ibuprofen bottle label states, “200 mg per tablet,” so the second fractionis
. On the other side of the equation, write a fraction showing the drug dosage as listed on the medication bottle over the number of tablets or milliliters. The ibuprofen bottle label states, “200 mg per tablet,” so the second fractionis  . The equation then reads:
. The equation then reads:
< ?xml:namespace prefix = "mml" />
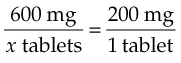
Note that the same units of measure are in both numerators and the same units of measure are in both denominators. Now solve for x:
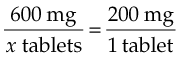
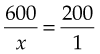
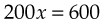
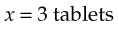
Ratio Or Proportion Method
In using the ratio method, first write the amount of the drug to be given and the quantity of the dosage (x) as a ratio. Using the previous example, this is 600 mg:x tablets. Next, complete the equation by forming a second ratio consisting of the number of units of the drug in the dosage form and the quantity of that dosage form as taken from the bottle. Again, using the previous example, the second ratio is 200 mg:1 tablet. Expressed as a proportion, this is:
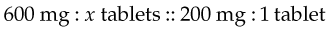
Solving for x determines the dosage:
Can errors be drawn from the previous formula to show where they are in the following problem?
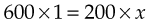


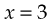
This method, again, gives a dosage of 3 tablets.
“Desired Over Available” Method
A third method for drug dosage calculation combines the conversion of ordered units into available units and the computation of drug dosage into one step. The general equation for doing this is:

If a physician orders 10 gr of a drug and the drug is available only in 300-mg tablets, the dose may be easily calculated with this formula. Substitute 10 gr (Desired) for the first element of the equation. Then use a conversion factor (60 mg/1 gr) so the desired amount can be expressed in the same units as the dose available in the second portion of the formula. The second element of the equation shows the quantity of drug form (capsule or tablet) for the dose Available (1 tablet contains 300 mg). The completed equation then is:
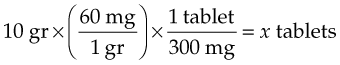
Once the conversion factor has been used, you can see the underlying relationship between dose Desired and dose Available:
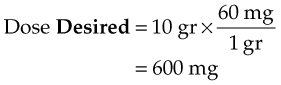
Thus the previous equation can be reduced to:
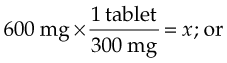
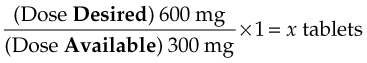
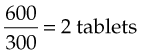
By solving for x, you will find that the patient should receive two 300-mg tablets.
As you can see, all three methods of drug calculation (fraction, proportion, and desired over available methods) use the same information and much of the same format in solving the problems. With minor variations, they do the same thing. One or another of these methods will seem to make more sense to you or be easier to follow. Throughout the calculation sections, use the method for drug calculation that makes the most sense. Return here for review if you are having difficulty.
As a final check to yourself, ask if the answer you calculated makes sense. You will learn about the usual doses for different drugs. However, you may want to develop a plan to always recalculate the problem if your answer suggests you should give more than two tablets, ounces, and so on. Give it the “Does It Make Sense?” (DIMS) test. Always imagine looking at your answer and imagining what the dose would look like if you were to bring the dose into a patient’s room. Would you bring in 45 tablespoons of a cough syrup? There is always pressure to quickly give medications. But if you always use the DIMS test, you will reduce the chance that errors will occur.
Calculating Dosages
Oral Medications
Although there are many forms of oral products, oral medications usually come in capsules, tablets, or liquids. Medications dispensed through the unit-dose system are packaged by the pharmacist, according to the dosage ordered. You usually do not have to calculate the medication dosage, but check the accuracy of the preparation.
When medication is ordered individually or through an open-stock system, you usually will calculate the proper drug dosage. Drug calculations are required when any of the following conditions are true:
• The drug available is in a smaller dose than that ordered.
• The drug available is in a larger dose than that ordered.
• The drug available is in a different unit of measure than that ordered.
Capsules and Tablets
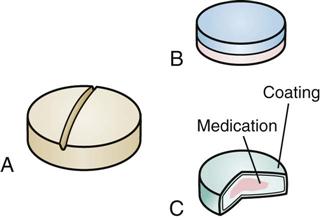
Capsules cannot be broken or divided. This makes calculating the drug dosage more difficult. Additional capsules may be given to provide an accurate dosage, but a part of a capsule cannot. Manufacturers of drugs provide capsules in different dosages to help you arrive at the proper dosage. If the calculations specify that a fraction of a capsule should be given, then it is necessary to notify the prescriber for change in order for the dose. Some tablets may be easily divided if they are “scored” (Figure 9-1, A). Examples of unscored tablets are layered tablets (see Figure 9-1, B) and coated tablets (see Figure 9-1, C). As a general rule, if a tablet is not scored, it should not be broken or cut apart. Sometimes tablets may be cut to fill a smaller drug dosage order, or they may be combined to fill a larger drug dosage order.
To illustrate, here are a few examples:
The order reads, “ASA gr x stat and prn for temperature elevation.” Acetylsalicylic acid (ASA) is labeled as 0.3 g/tablet:
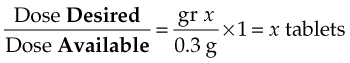
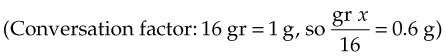
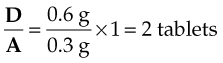
The order reads: “methocarbamol 1.5 g daily.” The medication comes in 750-mg tablets.

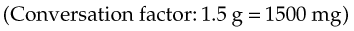
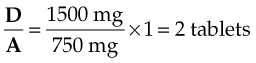
Liquids
The process and formulas used to calculate dosages of liquids are the same as those used to compute dosages of capsules or tablets. Only the unit of measure is different. To review:
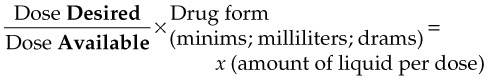
For example, the order reads: “phenobarbital elixir 0.2 g at bedtime.” The drug is available in 20 mg/5 mL. Again, the formula is a basic proportion problem:
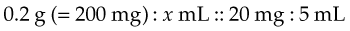
Written as an equation, this is:
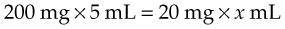
Thus:

Parenteral Medications
When medication is to be injected, it usually comes in one of three different forms:
Again, proportion is the standard method for calculating this dosage:
Please change word dilution below to solution:
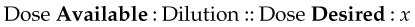
Written as an equation, this becomes:
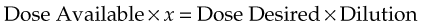
or
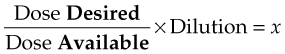
To illustrate, here are a few examples:
The order reads: “digoxin 0.2 mg IM.” The drug is available as 0.5 mg/mL.
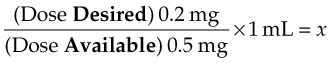
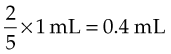
The order reads: “quinidine gluconate 200 mg IM (intramuscular) q6h.” The medication comes in a multiple-dose vial with 80 mg/mL.
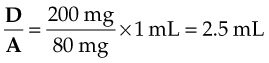
The order reads: “Demerol 35 mg IM daily.” The drug is available in 50-mg/mL ampules.
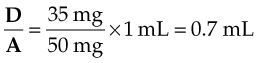
Many chemicals are very fragile. Heat, light, and time cause the medication to change or deteriorate. To avoid these problems, some medications are manufactured as powders or crystals, making them more stable. When the medication is ordered, liquid must be added to the drug to dissolve the medication and form a solution (reconstitute the drug). The medication must then be given within a few hours or it will decay. This is often true for products that will be added to IV fluids.
Some chemicals come in a single-dose vial. When the medication is ordered, usually 1 to 2 mL of liquid is added, the solution is gently shaken to dissolve it, and the whole amount is drawn into a syringe and injected. This is very common for some antibiotics.
At other times, a vial will contain several doses of the powdered medication. The instructions for adding the liquid (diluent) must be followed carefully. Some multiple-dose vials for steroids contain the diluent in the top part of the bottle, separated from the powder in the bottom part of the container. Pushing on the top part forces the liquid down into the bottom part, dissolving the medication. The instructions are usually found on the package, on the vial label, or on the package insert in the box, and they must be followed exactly. Once powders have been dissolved in liquid or reconstituted, the bottle must be carefully labeled so that further doses may be accurately given from it. It is especially important to note the date and time the powder was dissolved, as well as the concentration of the reconstituted medication. There should be information with each vial that indicates how long the medicine can be used once it has been mixed.
To illustrate, here are a few examples:
The doctor orders an antibiotic to be given 500 mg q6h IM. The drug comes in a multiple-dose vial containing 3 g of powder. Prepare it so that 500 mg equals 1 mL. First, convert 3 g to 3000 mg. Then apply the proportion formula:
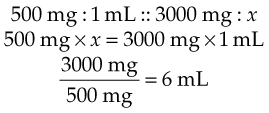
Therefore 6 mL of diluent must be added to obtain a concentration of 1 mL = 500 mg/mL. Expressed more simply:
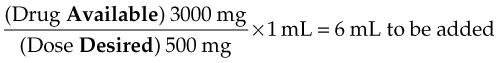
Thus you would add 6 mL to create the solution and then determine how much medicine to give.
The order reads: “Give 500,000 units penicillin IM.” Dilute 1,000,000 units of penicillin so that 500,000 units equals 1 mL. Thus:
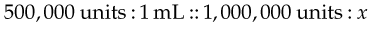
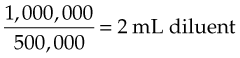
or
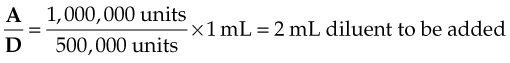
The order reads: “Give cephalosporin 200 mg in 1 mL IM.” The drug is manufactured in 1-g units of powder. What is the amount of diluent to add?

Insulin
Insulin is a parenteral medication that replaces insulin not being made by the patient’s own body. Great accuracy is important in preparing and administering insulin because the quantity given is very small, and even minor variations in dosage may produce adverse symptoms in the patient.
Calculating and preparing insulin dosages is unique in the following three ways:
1. There are many kinds of insulin, but they all come in a standardized measure called a unit. Insulin is available in 10-mL vials and in two strengths (concentrations): U-100 (100 units per 1 mL of solution) (Figure 9-2) and U-500 (500 units per 1 mL of solution). U-500 is five times stronger (more concentrated) than U-100. This preparation is rarely used except in patients with very large insulin needs.
2. Insulin should be drawn up in a special insulin syringe that is marked or calibrated in units (Figure 9-3).
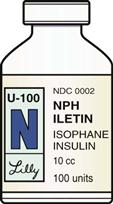

When the insulin order and the syringe are both U-100, all you have to do is draw up the number of units ordered. For example, the order reads: “48 units NPH insulin] U-100 1 hour before breakfast.” Using a U-100 syringe, you would draw up 48 units of NPH insulin.
When the order calls for two different types of insulin, both may be given at the same time in the same syringe. One will be short-acting (regular) insulin, and the other will be an intermediate or longer-acting type (neutral protamine Hagedorn [NPH]). Draw up the regular insulin first, then the longer-acting type. Give both in the same syringe. For example, the order reads: “20 units regular insulin U-100 and 30 units NPH U-100 before breakfast.” Using a U-100 syringe, draw up 20 units of regular insulin; then draw up 30 units of NPH insulin to equal 50 units in the syringe. Be certain that you are using the correct type of insulin. The newer long-acting insulins (Lantus and Detemir) cannot be mixed with regular or rapid-acting insulins.
Intravenous Infusions
Flow Rates.
Regulating the IV infusion rate is a common nursing task. Some institutions have automatic infusion pumps that make flow-rate calculations easy. Each nurse will learn to use the equipment available. However, all nurses must learn to calculate infusion rates without relying on equipment, in case of power or equipment failures or when working in agencies where no automatic pumps are available. The completeness of physicians’ orders for IV infusions varies widely. Some physicians are more specific in their instructions than others. A complete order specifies not only the type of solution and the volume to be infused (usually 500 or 1000 mL) but also the length of time the medication should be given. More commonly, the nurse is left to calculate the flow rate, or how fast the medication will be infused.
There are three mathematical procedures the nurse must be familiar with regarding IV infusions:
1. Calculating the flow rates for IV fluid administration
To calculate the flow rate for IV fluid administration, two concepts must be understood: the flow rate and the drop factor. The rate at which IV fluids are given is the flow rate, and this is measured in drops per minute. The drop factor is the number of drops per milliliter of liquid and is determined by the size of the drops. The drop factor is different for different manufacturers of IV infusion equipment, and it must be checked by reading it on the infusion set itself. Regular infusion sets generally range between 10 and 15 drops/mL. Infusion sets have different drop factors for use with blood infusion sets (usually 10 to 12 drops/mL) because the drops are larger, whereas pediatric setups use very small drops called microdrops (often with 50 or 60 microdrops/mL).
Once the nurse has learned the drop factor for the equipment being used, the flow rate may be calculated by using the following formula:
Drop factor × Milliliters/minute = Flow rate (drop/minute)
To illustrate, here are a few examples:
The order reads: “IV infusion to run at a slow rate to keep vein open.” The rate to keep a vein open is 2 mL/min. The IV infusion set delivers 10 drops/mL. The goal is to determine the flow rate in drops/minute:
10 drops/mL (drop factor) × 2 mL/min = 20 drops/min
The order reads: “1000 mL NS to be administered in 5 hours.” The drop factor is 15. To calculate the flow rate, use:

Flow Rates for Infants and Children.
Infants and small children are very sensitive to extra amounts, or volumes, of fluids. Smaller total amounts of IV fluids are often ordered, and the infusions are given in very small drops to avoid quickly overloading the infant’s circulation. This is a built-in safety mechanism to try to prevent fluid overloading as a result of accidental delivery of too much fluid.
The drop factor must be determined from the infusion setup. Usually 60 microdrops/mL is the drop factor for infants. For calculating the flow rates in infants, the same formula is used, but the microdrop drop factor must be substituted into the formula for the adult drop factor:

For example, the order reads: “Give 50 mL D5W [5% dextrose in water] IV in 4 hours.” The drop factor is 60 microdrops/mL. Thus:
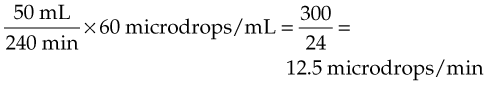
Total Infusion Time.
Sometimes physicians’ orders tell how fast they want infusions to run. To plan nursing care of the patient and to anticipate when new IV bottles may be needed, you need to calculate the total time the infusion will run.
Calculating the total administration time for IV fluid depends on calculating the total number of drops to be infused. Using this information, plus the drop factor, the total infusion time can be easily determined by using the following formula:
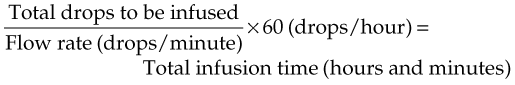
To calculate the total infusion time:
For example, the order reads: “1000 mL D5W to be given at 50 drops/min with a drop factor of 10 drops/mL.” Thus:
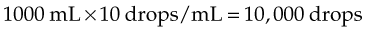
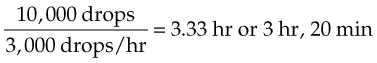
Other Factors Influencing Flow Rates.
There are many other factors that influence the flow rate of an infusion. The nurse has no control over many of them, such as the age, size, and condition of the patient; the size of the vein; the type of fluid; and the need for the fluid. Other factors may be changed or altered to assist in infusion of IV fluids: the size of the needle, the needle’s position in the vein, the height of the IV pole, the condition of the filter, the air in the air vent, and movement of the patient. If the fluid does not infuse at the calculated rate, the IV setup should be carefully checked from the IV bottle to the site of the needle’s insertion.
Calculating Dosages For Infants And Children
Drug dosages are calculated to give the highest possible blood and tissue concentration of a medication without causing overdosage or adverse effects. Because infants are very sensitive to medications, and because infants and children are so much smaller than adults, almost all dosages given to infants and children are smaller than those given to adults. Most pharmaceutical companies list the recommended dosages of their drugs for a child or infant. If this information is not listed in the instructional material provided with the medication, the nurse should question whether the medication may safely be given to a child.
Although children’s dosages were once frequently calculated, there remain only a few medications that require the nurse to determine how much to give a child. In past years, there were several general rules developed to calculate these special reduced dosages for infants and children. Some were based on age, and these have fallen out of usage because children of different ages vary so much in size.
With the growing attention on having better information available for giving medications to children, there has been greater focus on accurate drug calculation for them. The Joint Commission on Accreditation of Healthcare Organizations now asks that all dosages for children be weight based, preferably in kilograms.
One of the most widely accepted methods for determining children’s dosages based on body weight is known as Clark’s rule. Again, ratios and proportions may be used to calculate the pediatric value. If we assume that an average adult weighs 150 lb and we know the adult dosage, it follows that if we know the child’s weight, we can calculate the child’s dosage:
Adult weight : Adult dosage :: Child’s weight : x (Child’s dosage)
For example, if the 150-lb adult dose of meperidine is 100 mg, what is the dose for a 50-lb child?
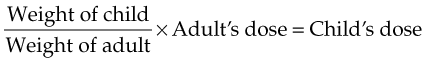
so
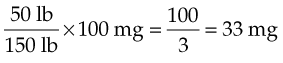
Other formulas substitute kilograms for pounds in calculating the correct dose. The formula remains the same. Using the problem information in the preceding column, the nurse simply divides the weight of the adult and the weight of the child by 2.2 to obtain the weights in kilograms. Clark’s rule is by far the most popular method of assessing children’s dosages and should be the formula used.
Medications that require very careful dosage use the body surface area (BSA), or total tissue area, of the child. This is the most accurate method for determining pediatric dosages. The reason for using the BSA is that children have a greater surface area than adults in relation to their weight. For drugs that require careful dosage, charts known as nomograms are used to calculate the BSA in square meters. A nomogram is a chart that displays the relationships between two different types of data so that complex calculations are not necessary. BSA charts are constructed from height and weight data. The ratio of BSA to weight varies inversely (opposite) to length. Thus infants would have proportionally more surface area, because they weigh less and are shorter than children. These charts may be used only if the child has normal height for weight. Even with the use of standardized charts, the calculated dosages are more accurate for children than for very young infants.
An example of a nomogram used to calculate BSA is shown in Figure 9-4. A straight edge is placed from the patient’s height in the left column to his weight in the right column, and the intersection on the BSA column indicates the patient’s BSA. The total BSA value is determined and is put into the following formula:
Surface area of the child (m2) × Usual adult dose ÷ Surface area of an adult (1.73 m2) = Child dose
Use the nomogram to solve these two sample problems, using the BSA to calculate pediatric dosages (use 1.73 m2 as the accepted adult BSA):
Dimensional analysis is a technique used in a select few LPN/LVN programs. If your program uses dimensional analysis for drug calculations, see the Evolve website (http://evolve.elsevier.com/Edmunds/LPN/) for information on using this calculation procedure and sample problems.