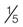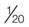Review of Mathematical Principles
Objectives
Key Terms
common denominator (dē-NŎM-ĭ-nā-tŏr, p. 73)
complex fraction (FRĂK-shŭn, p. 72)
denominator (dē-NŎM-ĭ-nā-tŏr, p. 71)
fraction (FRĂK-shŭn, p. 71)
improper fraction (ĭm-PRŎP-ěr FRĂK-shŭn, p. 72)
mixed number (p. 72)
numerator (NŪ-měr-ā-tŏr, p. 71)
percent (pěr-CĚNT, p. 76)
proper fraction (PRŎP-ěr FRĂK-shŭn, p. 72)
proportion (prŏp-ŎR-shun, p. 75)
ratio (RĀ-shē-ō, p. 75)
Roman numeral system (RŌM- ăn NŪ-měr-al SĬS-tĕm, p. 71)
![]() http://evolve.elsevier.com/Edmunds/LPN/
http://evolve.elsevier.com/Edmunds/LPN/
Overview
It is very important to give the correct dose of a medicine. This may mean that you will need to accurately calculate the dosage using basic math formulas or a calculator. Even a small error in dosage may produce a big error. (Many of you may remember that the twin babies of Actor Dennis Quaid were accidentally given a huge overdose of heparin in the neonatal intensive care unit, which made the babies’ blood fail to clot.) Accuracy with dosage ensures safety.
Although most nurses feel comfortable with addition and subtraction, many can profit from a review of basic concepts in multiplication and division, as well as fractions, percentages, and proportions, to increase their speed. These number relationships form important building blocks for tasks the nurse must master. By memorizing and drilling on these basic facts, you will have confidence and speed in calculating dosages and converting from one system of measures for drugs to another. Even if one uses a calculator, it is important to know how to manually do the math problem so you can recheck calculations at the bedside when necessary to make sure you aren’t making a mistake.
Multiplication and Division
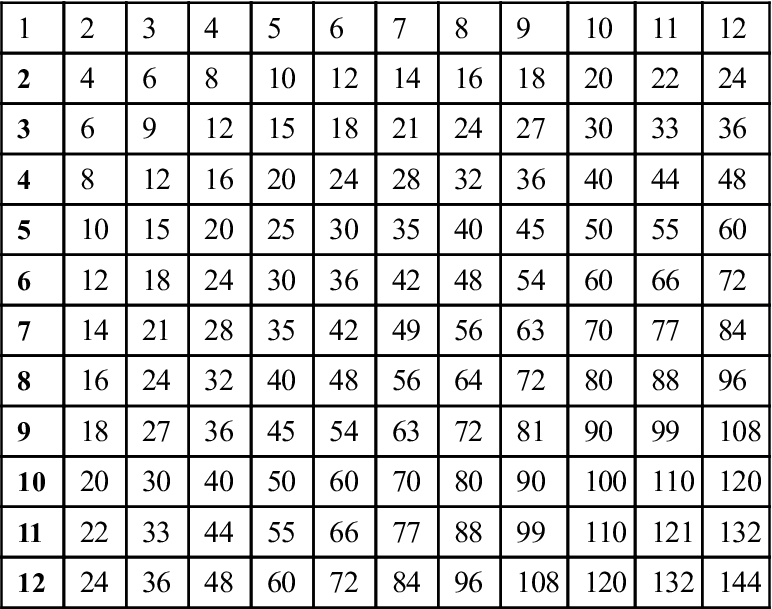
Box 7-1 presents a basic grid for multiplication and division. To multiply two numbers, find one number in the top row and the other number in the left-hand column, and follow the row leading across and the column leading down from each number to where the row and the column intersect (cross each other) within the grid.
For example: What is 7 × 8? Find the number 7 on the left and follow across to the right; find the number 8 on the top and follow down from it. The two lines intersect at 56. Therefore 7 × 8 = 56. Another way to indicate that two numbers are to be multiplied is to place them in parentheses next to each other. Therefore (30)(3) means 30 × 3.
To use this grid for division, find the number on the left-hand side of the chart that is the same as the divisor (the number you are dividing by). Follow the row to the right until you come to the exact number you are dividing or the number closest to it. Follow the column up to the top to learn the number of times that larger number may be divided by the number on the left.
For example: How many times will 9 go into 81? Find 9 in the column on the left. Follow the row across until you come to 81. Follow the column up from 81 to the top, which is 9. Therefore 81 ÷ 9 = 9. If you wanted to know how many times the whole number 9 would go into 84, you would still use the column containing the number 81, because it is the closest number in that row of the grid to 84. The answer would still be 9, but there would be a remainder of 3.
Roman Numerals
The numbers commonly used today in expressing quantity and value are called Arabic numerals. Examples of Arabic numerals are 1, 2, and 3. Another number system in common use is the Roman numeral system. Roman numerals from the values of 1 to 100 are commonly used as units of the apothecaries’ system of weights and measures in writing prescriptions. They may also be used to express dates in copyrights and in formal manuscripts. Seven numerals make up the basic building blocks of the Roman numeral system (Box 7-2).
After memorizing the seven Roman numerals and their values, it is important to learn the four rules in using Roman numerals. These rules and some examples are presented in Box 7-3.
Fractions
A good understanding of fractions is important to the nurse because all units of the apothecaries’ system are written as common fractions for all amounts less than 1. Fractions also form the foundation in dosage calculations when medication is only available in a different dose form than the form that was ordered.
Basic Principles
A fraction is one or more equal parts of a unit. It is written as two numbers separated by a line, such as 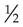 or
or 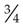 . The parts of the fraction are called the terms. The two terms of a fraction are the numerator and the denominator. The numerator is the top number (the number above the line). The denominator is the bottom number (the number below the line). In
. The parts of the fraction are called the terms. The two terms of a fraction are the numerator and the denominator. The numerator is the top number (the number above the line). The denominator is the bottom number (the number below the line). In 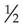 , 1 is the numerator, and 2 is the denominator.
, 1 is the numerator, and 2 is the denominator.
The denominator tells how many equal parts the whole has been divided into. The numerator tells how many of the parts are being used.
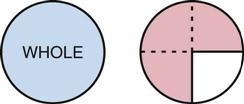
It is important not to confuse these two parts of the fraction. One way to remember which part belongs where is to think of the word NUDE. The N is on top; the D is on the bottom, like this:

To use fractions in calculations, the numerator and the denominator must be of the same unit of measure. For example, if the numerator is in milligrams, the denominator must be in milligrams.
Fractions may be raised to higher terms by multiplying both terms of the fraction by the same number. For example, to raise 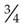 to a higher term, multiply both the numerator and the denominator by 2, converting it to
to a higher term, multiply both the numerator and the denominator by 2, converting it to 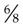 . Thus
. Thus 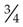 and
and 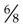 have the same value:
have the same value:
< ?xml:namespace prefix = "mml" />
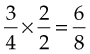
Fractions are reduced to lower terms by dividing both the numerator and denominator by the same number. For example, to lower 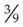 to a lower term, divide both the numerator and the denominator by 3, converting it to
to a lower term, divide both the numerator and the denominator by 3, converting it to 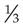 . Thus
. Thus 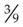 and
and 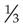 have the same value:
have the same value:
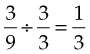
A proper fraction has a numerator smaller than the denominator. The number 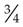 is a proper fraction because it is less than 1; its numerator is less than its denominator.
is a proper fraction because it is less than 1; its numerator is less than its denominator.
An improper fraction has a numerator the same as or larger than the denominator. The number 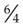 is an improper fraction because the numerator (6) is larger than the denominator (4).
is an improper fraction because the numerator (6) is larger than the denominator (4).
A mixed number is a whole number and a proper fraction. Examples of mixed numbers are 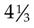 ,
, 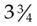 , and
, and  .
.
It is often necessary to change an improper fraction to a mixed number or to change a mixed number to an improper fraction when doing certain calculations. To change an improper fraction to a mixed number, divide the denominator into the numerator. The result is the whole number (quotient) and the remainder, which is placed over the denominator of the improper fraction. For example, 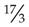 is an improper fraction. To convert it to a mixed number:
is an improper fraction. To convert it to a mixed number:
1. Divide the denominator (3) into the numerator (17):

2. Move the remainder (2) over the denominator (3).
3. Put the quotient (5) in front of the fraction:
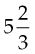
To change the mixed number 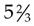 to an improper fraction, multiply the denominator of the fraction (3) by the whole number (5), add the numerator (2), and place the sum over the denominator. For example:
to an improper fraction, multiply the denominator of the fraction (3) by the whole number (5), add the numerator (2), and place the sum over the denominator. For example:

The sum (17) goes over the denominator of the fraction: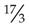 is the improper fraction.
is the improper fraction.
A complex fraction has a fraction in either its numerator, its denominator, or both. The following are examples of complex fractions:
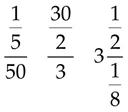
Complex fractions may be changed to whole numbers or to proper or improper fractions by dividing the number or fraction above the line by the number or fraction below the line. For example, to change the following complex number to a proper fraction, divide the fraction above the line by the number below the line:
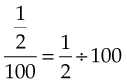
To divide by 100, or 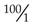 , simply invert or reverse the numerator (100) and the denominator (1) and multiply by the result, or by
, simply invert or reverse the numerator (100) and the denominator (1) and multiply by the result, or by 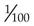 . For example:
. For example:

Adding Fractions
If fractions have the same denominator, simply add the numerators and put the sum above the common denominator. For example:
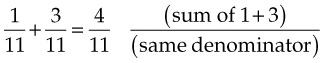
Also:
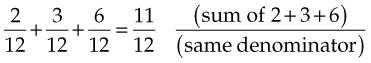
If the fractions have different denominators, they must be converted to a number that each denominator has in common, or a common denominator. One can always find a common denominator by multiplying the two denominators by one another. Sometimes, however, both numbers will go into a smaller number. For example, in the equation 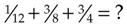 , what is the smallest common denominator?
, what is the smallest common denominator?
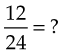
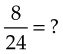
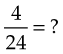
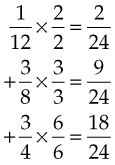
4. Then add the numerators and bring down the denominator:
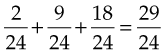
5. Change the improper fraction to a mixed number:
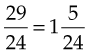
When adding mixed numbers, first change them to improper fractions and proceed as indicated previously.
Subtracting Fractions
If fractions have the same denominator, subtract the smaller numerator from the larger numerator. Leave the denominator the same, and then reduce to the lowest terms, if necessary. For example:
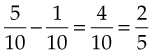
If fractions do not have the same denominator, change the fractions so they have the smallest common denominator, subtract the numerators, and leave the denominator the same. For example:
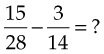
Because 28 is a multiple of 14 (14 × 2 = 28), 28 is a common denominator of 28 and 14. Divide the lowest common denominator by the denominator of each fraction to determine the quotient, and multiply the numerator and denominator of the fraction by the quotient:
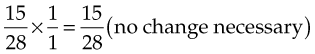
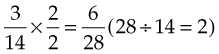
Subtract the numerators and leave the denominators the same:

When subtracting mixed numbers, first change them to improper fractions and proceed as shown in the previous examples.
Multiplying Fractions
When multiplying fractions, reduce all terms to their smallest form to simplify the calculation. For example,  is the same as
is the same as 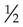 , but
, but 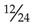 is more difficult to work with. To reduce to the lowest terms, divide the same number into both the numerator and the denominator. For example, in the fraction
is more difficult to work with. To reduce to the lowest terms, divide the same number into both the numerator and the denominator. For example, in the fraction 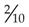 both 2 and 10 can be divided by 2; therefore,
both 2 and 10 can be divided by 2; therefore, 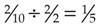 . Similarly, in the fraction
. Similarly, in the fraction 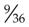 both the numerator and the denominator can be divided by 9; therefore,
both the numerator and the denominator can be divided by 9; therefore, 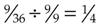 .
.
When the fractions are in their simplest form, multiply the numerators together, and then multiply the denominators together. For example:
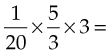

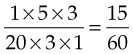
This can be simplified as follows:
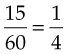
If the number is a mixed number (a whole number and a fraction), change it to an improper fraction before solving. For example:
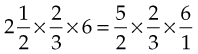
Simplify:
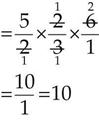
Dividing Fractions
To divide a fraction by a fraction, invert (or turn upside down) the fraction that is the divisor and then multiply. For example:
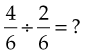
Invert the divisor:
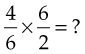
Simplify, then multiply the numerators and then the denominators:
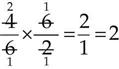
If the number is a mixed number, change it to an improper fraction before solving. For example:
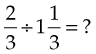
Change the mixed number to an improper fraction:

Invert the divisor:
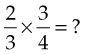
Simplify:
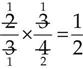
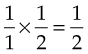
Decimal Fractions
A decimal fraction has a denominator of 10 or a multiple of 10. Instead of writing the denominator, a decimal point is added to the numerator. For example:
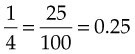
All numbers to the left of the decimal point represent whole numbers. Numbers to the right represent fractions. Zeros may be placed to the right of the decimal without changing the value of the whole number (for example, 45 is the same as 45.0 or 45.00).
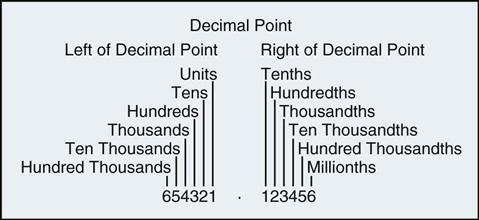
Decimals increase in value from right to left; they decrease in value from left to right. Decimals increase in value in multiples of 10. Each column in a decimal has its own value, according to where it lies in relation to the decimal point (Figure 7-1).
Adding and Subtracting Decimal Fractions
Place the numbers so that the decimal points are stacked in a straight line. Keep the columns straight. Add zeros to the right of the decimal points if necessary so that each number has an equal number of digits to the right of the decimal point. Then add or subtract as for whole numbers. The decimal point goes in the answer just below the decimal points in the problem.
For example, to add 0.0678 and 1.082:

Note that the decimal point in the answer is in line with the other decimal points.
To subtract 3.053 from 6.046:
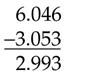
Multiplying and Dividing Decimal Fractions
To multiply decimal fractions, multiply the two numbers as for whole numbers. Then count the number of decimal places in the multiplicand (the number that is multiplied) and the number in the multiplier (the number you multiply by). Beginning at the right side of the product (answer), count off that total number of decimal places from right to left and insert a decimal point. For example:

To divide by a decimal fraction, first move the decimal point in the divisor (the number you are dividing with) enough places right to make it a whole number. Then move the decimal point in the dividend (the number you are dividing) as many places as it was moved in the divisor. Place the decimal point in the quotient (answer) directly above that in the dividend. For example, to divide 32.80 by 8.2:
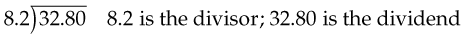
Move the decimal point in the divisor to the right to make it a whole number, then move it the same number of places in the dividend:
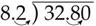
Solve the problem:

A shortcut may be taken when multiplying or dividing by 10, 100, or 1000. To multiply a decimal fraction by 10, 100, or 1000, move the decimal point as many places to the right as there are zeros in the multiplier. For example:
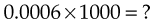
In 1000 there are three zeros, so:
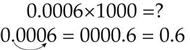
To divide a decimal fraction by 10, 100, or 1000, move the decimal place as many places to the left as there are zeros in the divisor. For example:
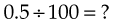
The number 100 has two zeros, so:
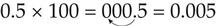
Ratios
A ratio is a way of expressing the relationship of one number to another number, or of expressing a part of a whole number. The relationship is expressed by separating the numbers with a colon (:). The colon means division. The expression 1 : 2 means there is a ratio of one part to two parts. Ratios are commonly used to express concentrations of a drug in a solution.
For example, a ratio written as 1 : 20 means 1 part to 20 parts. The relationship may also be expressed as a fraction (e.g., 1 : 10 is the same as 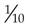 ).
).
Proportions
A proportion is a way of expressing a relationship of equality between two ratios. In other words, the first ratio listed is equal to the second ratio listed. The two ratios are separated by a double colon (::), which means “as.” The numbers at each end of the relationship are the extremes, and the two numbers in the middle are the means. In any proportion, the product of the extremes equals the product of the means. This means that if one of the terms is not known, it may be calculated. The unknown term is defined by an x. For example:
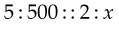
(where x is the unknown) can be read as “5 is to 500 as 2 is to x” or “The relationship of 5 to 500 is the same as the relationship of 2 to x.” Then:
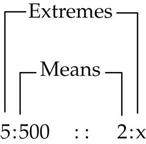
In this proportion, 5 and x are the extremes, and 500 and 2 are the means. Therefore:
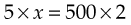
To find x, express the proportion as a relationship of two fractions, cross multiply, and solve:
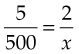
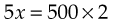
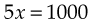
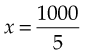
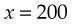
Because a proportion is a relationship of equality, both ratios in the proportion must also be written in the same system (e.g., minims are to grains as minims are to grains; milliliters are to grams as milliliters are to grams). For example:
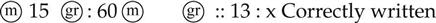
The calculation of ratios and proportions provides one of the major foundations in drug dosage calculations. Often you know the desired concentration of drug and need to calculate how much to give of a medication on hand. You will be able to figure how much medication to give by using the principles of proportion.
Percents
The term percent, or the symbol %, means parts per hundred. Thus a percentage may also be expressed as a fraction or as a decimal fraction. For example:
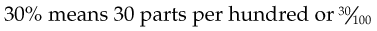

Percentages should also be reduced to their lowest common denominator, when appropriate. For example:
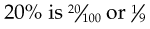
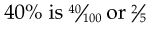
To change a fraction to a percentage, divide the numerator by the denominator, multiply the quotient (results) by 100, and add a percent sign (%). For example, to change 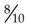 to a percentage:
to a percentage:
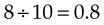
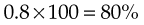
To change 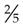 to a percentage:
to a percentage:
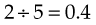
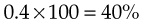
To change a mixed number to a percentage, first change it to an improper fraction, then proceed as noted previously. For example, to change 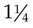 to a percentage:
to a percentage:
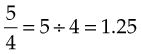
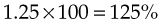
To change a ratio to a percentage, the ratio is first expressed as a fraction. The first number or term of the ratio becomes the numerator, and the second number or term becomes the denominator (e.g., 1 : 200 becomes 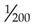 ). The fraction is then changed to a percentage:
). The fraction is then changed to a percentage:
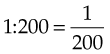
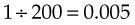
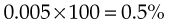
To change a percentage to a ratio, the percentage becomes the numerator and is placed over the denominator of 100. For example, to change 20% and 50% to ratios:
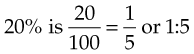
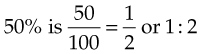
A percentage may easily be expressed as a decimal, a fraction, or a ratio. For example:
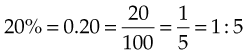
It is very easy to change between fractions, percentages, decimals, and ratios. The rules that summarize these changes are presented in Box 7-4.

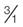 ; the 1 can be added as a denominator if it makes calculations easier to understand.
; the 1 can be added as a denominator if it makes calculations easier to understand.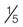 = 1 : 5
= 1 : 5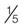 = 0.20
= 0.20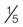 = 0.20 = 20%
= 0.20 = 20%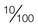 =
= 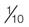
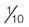 = 1 : 10
= 1 : 10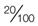 =
=